Образовательные задачи урока.
- повторить необходимые и достаточные условия
существования точек экстремума, понятия:
стационарные и критические точки; - ввести алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке - сформировать умение решать задачи на
нахождение наибольшего и наименьшего значения
степенной функции на отрезке с помощью
производной. - разобрать прототипы задач № 1 В14
экзаменационной работы в формате ЕГЭ. - Продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения писать
необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - cодействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм; - cодействовать профилактике утомляемости
школьников, используя разнообразные виды работы
на уроке.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых
уроков: точки экстремума, каково достаточное
условие точек экстремума, стационарные точки и
критические точки (учащихся отвечают с места)
Повторить таблицу производных основных
функций и основные правила нахождения
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция непрерывна и дифференцируема на
отрезке , то
для нахождения наибольшего и наименьшего
значения функции на отрезке нужно:
- найти производную функции, найти стационарные
точки (решаем уравнение, приравнивая производную
к нулю) - среди полученных стационарных точек выбрать те,
которые принадлежат отрезку - найти значение в стационарных точках и в концах
отрезка, то естьи
.
- среди полученных значений выбрать наибольшее
или наименьшее.
Записать схему нахождения наибольшего и
наименьшего значения функции на отрезке в
тетради (учитель оформляет схему на доске):
Пусть
непрерывна на
и дифференцируема. Тогда, для нахождения или
:
- Находим
находим
- Проверяем принадлежность
отрезку
- Находим
,
,
.
- Среди полученных значений выбираем
или
.
- Записываем ответ (Акцентировать внимание, что в
ответе должно быть записано либо целое число,
либо конечная десятичная дробь).
Пример № 1. Найти наименьшее значение функции
на отрезке
. (Учитель
совместно с учащимися записывает решение на
доске последовательно проговаривая каждый пункт
алгоритма).
Решение:
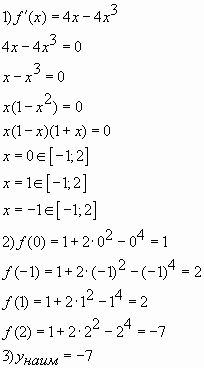
Ответ:
Пример № 2. Найти наибольшее значение
функции на
отрезке
Решение:
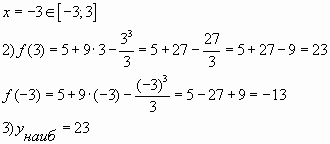
Ответ: 23
Пример № 3. Найдите наименьшее значение
функции на
отрезке .
Решение:
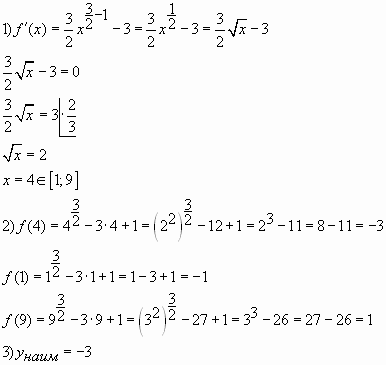
Ответ: -3
Пример № 4. Найдите наибольшее
значение функции на отрезке
.
Решение:
Упростим функцию
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найти наибольшее значение функции
на отрезке
Урок № 2. “Нахождение наибольшего и
наименьшего значения функций и
на отрезке
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма
нахождения наибольшего и наименьшего значения
функции на отрезке; - продолжить формирования навыка применения
этого алгоритма при решении второго типа задач
экзаменационных вариантов ЕГЭ; - продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения в
необходимом темпе читать и писать, анализировать
условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - содействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм. умение
слушать товарищей; - содействовать профилактике утомляемости
школьников.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Проверка домашнего задания. Фронтальная
проверка домашнего задания. Если у большинства
учащихся возникли вопросы, разобрать на доске
решение конкретного задания, если лишь у
некоторых, объяснить в индивидуальном порядке,
предварительно схематично обговорив решение у
доски.
III. Актуализация знаний. Повторить еще раз
алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке с оформлением схемы
на доске.
Повторить следующие формулы для дальнейшего
изучения материала:
,
,
Решить на повторение примеры (1 учащийся пишет
решение на доске с комментариями по решению,
остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает
решение учитель)
Пример № 1. Найти наименьшее значение
функции на
отрезке
Решение
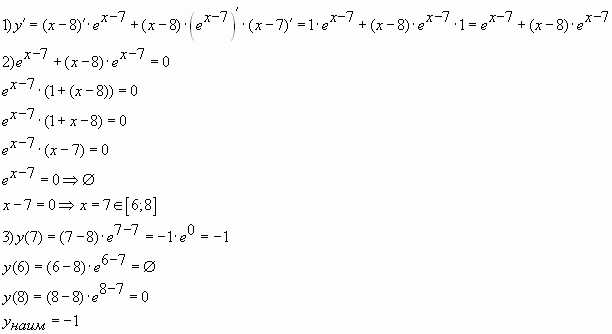
Ответ: —1
Пример № 2. Найти наименьшее значение
функции на
отрезке
Решение. Преобразуем и упростим функцию , используя
свойство логарифмов
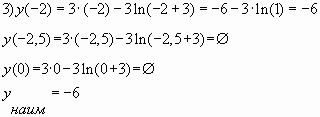
Ответ: -6
V. Закрепление материала (самостоятельное
решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции
на отрезке
Решение.
Ответ: 51
Пример № 4. Найти наименьшее значение функции
на отрезке
Решение.
(, так как
)
Ответ: 4
Пример № 5. Найти наименьшее значение функции
на отрезке
Решение
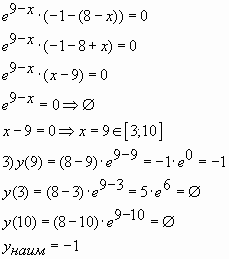
Ответ: -1
Пример № 6. Найти наибольшее значение функции
на отрезке
Решение:
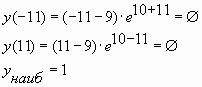
Ответ: 1
Пример № 7: Найдите наибольшее значение
функции на
отрезке
Решение
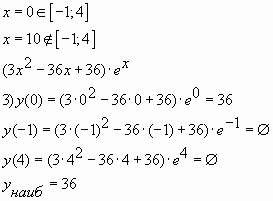
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Проговорить основные алгоритмы решения тех
примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
Воскресенье, 18 декабря, 2011
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x2 – 36x + 81 = 0, значит x2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
- y(8) = 8 · (8-9)2+23 = 31;
- y(9) = 9 · (9-9)2+23 = 23;
- y(13) = 13 · (13-9)2+23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции:
.
Решение: действуем по алгоритму нахождения наибольшего значения функции:
- Область определения функции задается неравенством:
, которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.
- Производная функции равна:
,
область определения которой также не ограничена, поскольку по указанной выше причине x2 – 6x + 10 > 0, и знаменатель дроби нигде не обращается в ноль: D(y’) = R. - Нули производной: 2x — 6 = 0, откуда x = 3 (одна точка, подозрительная на экстремум).
- Отмечаем область определения функции и точки, подозрительные на экстремум, на числовой прямой, определяем знаки производной в получившихся промежутках:
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
- Находим это значение:
.
Итак, наибольшее значение функции равно -1. Ответ: -1.
Репетитор по математике
Сергей Валерьевич
Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).
- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).
- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f
3) Стационарные точки: х = 1; х = 2.

4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим.=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х,
Тогда второе число —
Следовательно,
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)
x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
государственное
образовательное учреждение дополнительного профессионального образования
(повышения квалификации) специалистов «Кузбасский региональный институт
повышения квалификации и переподготовки работников образования»
Факультет повышения квалификации
Кафедра естественнонаучных и математических дисциплин
Решение заданий на нахождение
наибольших и наименьших значений и точек экстремума функции
(методические рекомендации).
Итоговая работа
Срок обучения с 01. 03 2016
г. по 18.03. 2016 г.
Исполнитель:
Сипкова Елена Васильевна,
учитель математики
МОУ Белогорская средняя общеобразовательная школа
(lenasipkova@mail.ru)
Кемерово 2016
Содержание
Введение ……………………………………………………………………………………………..3
1. Методические рекомендации
обучения учащихся решению заданий
по нахождению
наибольшего и наименьшего значения функции с
помощью
производной………………………………………………………5
2. Методические рекомендации
обучения учащихся решению заданий вычислению точек экстремума……………..……………………………..24
Заключение…………………………………………………………………………41
Литература………………………………………………………………… ………42
Приложения………………………………………………….. ……………………………..43
Введение
Содержание
разделов курса, составляющих начала математического анализа вызывает
затруднение у многих обучающихся
Однако, все
обучающиеся должны знать определение производной, основные правила
дифференцирования и формулы производных элементарных функций, понимать
геометрический смысл производной, знать уравнение касательной.
Первоначально
происходит формирование начальных умений находить производные элементарных
функций на основе определения производной.
В дальнейшем все
обучающиеся должны овладеть правилами дифференцирования суммы, произведения и
частного двух функций, вынесения постоянного множителя за знак производной.
В результате
изучения темы у обучающихся должны быть сформированы умения находить
производные элементарных функций.
После усвоения
обучающимися таблиц производных элементарных функций и правил дифференцирования
происходит знакомство с геометрическим смыслом производной, бучение составлению
уравнений касательной к графику функции в заданной точке.
Очень важно знать
всем обучающимся, что с помощью производной можно аналитически установить много
важных свойств функции. Все обучающиеся должны по графику функции выявлять ее
промежутки возрастания и убывания. Находить интервалы монотонности функции,
заданной аналитически.
В ходе изучения
темы необходимо все знать определения точек максимума и минимума, стационарных
и критических точек; уметь применять необходимые и достаточные условия
экстремума для нахождения точек экстремума функции.
Следующей целью
ставиться научиться строить график функции. С помощью производной, применять
производную к нахождению наибольшего и наименьшего значения функций, решать
прикладные задачи на «Экстремум»
Задания на
выполнение производной стали традиционными на ЕГЭ по математике. Они
предназначены для формирования устойчивых навыков решения задач на исследование
функций с применением производной.
Эти задания, по
статистике ЕГЭ прошлых лет, относятся к наиболее проблемным для обучающихся,
поэтому целью своей работы я взяла «алгоритмизацию» процессов обучения по
данной теме.
Воспользовавшись
методическими указаниями обучающиеся сэкономят время для решения задач.
Основная цель моей
работы – повысить уровень математического образования выпускников, что дает им
возможность остановиться на решении не только доступных задач, но и интересных
новых заданий.
В работе приведены
задачи с готовым решением, однако обучающиеся рекомендуют решать задачи
самостоятельно и сравнивать собственное решение с приведенным в работе.
1.
Методические
рекомендации обучения учащихся решению заданий по нахождению наибольшего и
наименьшего значения функции с помощью производной
Формирование
умения решать задачи на нахождение наибольших и наименьших значений – одна из
самых важных целей изучения математического анализа в школе. Решение задач
этого типа, основанное на применении производной, имеет большую прикладную
направленность.
Пусть функция y = f (x) непрерывна на отрезке [a; b]. В этом случае, как известно, она
принимает как наибольшее, так и наименьшее значения на этом отрезке. Во многих
прикладных вопросах важно найти те точки отрезка [a; b], которым отвечают наибольшее и
наименьшее значения функции.
При решении этой
задачи возможны два случая:
1) либо наибольшее (наименьшее) значение
функции достигается внутри отрезка, и тогда эти значения окажутся в числе
экстремумов функции;
2) либо наибольшее (наименьшее) значение
достигается на концах отрезка [a; b].
Итак, чтобы найти
наибольшее и наименьшее значения непрерывной на отрезке функции y = f (x), достаточно:
1. Найти все критические точки,
принадлежащие [a; b], и вычислить значения функции в
этих точках.
2. Вычислить значения функции на концах
отрезка [a; b], то есть найти f (a) и f (b).
3. Сравнить полученные результаты:
наибольшее из найденных значений является наибольшим значением функции на
отрезке [a; b]; аналогично, наименьшее из
найденных значений является наименьшим значение функции на этом отрезке.
Замечание 1. При нахождении критических
точек можно использовать соображения геометрического характера, изобразив
схематически график функции.
Замечание 2. Отыскание наибольшего и
наименьшего значений функции можно упростить, если воспользоваться следующими
свойствами непрерывных функций:
1)
если
функция y = f (x) на
отрезке [a; b] непрерывна и возрастает, то m = f (a) и M = f (b);
2)
если
функция y = f (x) на
отрезке [a; b] непрерывна и убывает, то m = f (b) и M = f (a);
3)
если
функция y = f (x),
непрерывная на отрезке [a; b], имеет на этом отрезке только одну
точку максимума x0 (и ни одной точки минимума), то
наибольшее значение на данном отрезке есть M = f (x0);
4)
если
функция y = f (x),
непрерывная на отрезке [a; b], имеет на этом отрезке только одну
точку минимума x0 (и ни одной точки максимума), то
наименьшее значение на данном отрезке есть m = f (x0).
Алгоритм решения задач на нахождение наибольшего или
наименьшего значения функции:
Если
в задаче требуется найти максимальное или минимальное значение
функции f(x) на отрезке [a; b], выполняем следующие
действия:
1.
Найти производную функции: f ‘(x).
2.
Решить уравнение f»(x) = 0. Если корней нет,
пропускаем третий шаг и переходим сразу к четвертому.
3.
Из полученного набора корней вычеркнуть все, что лежит
за пределами отрезка [a; b]. Оставшиеся числа обозначим x1, x2, …, xn —
их, как правило, будет немного.
4.
Подставим концы отрезка [a; b] и точки x1, x2, …, xn
в исходную функцию. Получим набор чисел f(a), f(b), f(x1), f(x2), …, f(xn),
из которого выбираем наибольше или наименьшее значение —
это и будет ответ.
Небольшое
пояснение по поводу вычеркивания корней, когда они совпадают
с концами отрезка. Их тоже можно вычеркнуть, поскольку
на четвертом шаге концы отрезка все равно подставляются
в функцию — даже если уравнение
f
‘(x) = 0 не имело решений.
Также следует внимательно
читать условие задачи. Когда требуется найти значение функции (максимальное
или минимальное), концы отрезка и точки x1, x2, …, xn
подставляются именно в функцию, а не в ее производную.
Задача 1. Найти наибольшее значение функции
y = x3 + 3x2 − 9x – 7
на отрезке [−5; 0].
Решение. Для начала найдем производную: y’ = (x3 + 3x2 − 9x − 7)’ =
3x2 + 6x − 9.
Затем решаем уравнение: y’ = 0 ⇒ 3x2 + 6x − 9 = 0 ⇒ … ⇒
x = −3; x = 1.
Вычеркиваем корень x = 1, потому что
он не принадлежит отрезку [−5; 0].
Осталось вычислить значение функции на концах отрезка
и в точке x = −3:
y(−5) = (−5)3 + 4·(−5)2 − 9·(−5) − 7 = −12;
y(−3) = (−3)3 + 4·(−3)2 − 9·(−3) − 7 = 20;
y(0) = 03 + 4·02 − 9·0 − 7 = −7.
Очевидно, наибольшее значение равно 20 — оно достигается
в точке x = −3.
Ответ: 20
Задача 2. Найти наибольшее и
наименьшее значения функции
f (x) = 2x3 – 6x + 5 на отрезке .
Решение. 1. Находим критические
точки, принадлежащие :
f¢ (x) = 6x2 – 6 = 6(x2 – 1), 6(x2 – 1) = 0, x1 = –1, x2 = 1.
Вычислим значения
функции в этих точках:
f (–1) = 2 × (–1)3 – 6 × (–1) + 5 = 9; f (1) = 2 × 13 – 6 × 1 + 5 = 1.
2. Вычислим
значения функции на концах отрезка:
3. Таким образом, наибольшее значение
данной функции на рассматриваемом отрезке есть f (–1) = 9, а наименьшее
Ответ: f (–1) = 9,
Дробно –
рациональные функции.
Задача 3. Найдите
наименьшее значение функции  на отрезке [1; 9].
на отрезке [1; 9].
Решение: Найдём производную данной
функции: . Приведём полученное выражение к общему
знаменателю и разложим числитель на множители: 
Отрезку [1; 9]
принадлежит точка х=6, в которой производная меняет знак с минуса на
плюс. Таким образом , точка х=6 является точкой минимума и единственной
точкой экстремума на данном отрезке. Значит, своего наименьшего значения на
данном отрезке функция достигает именно в этой точке. Найдём наименьшее
значение:
Ответ: 12.
Задача 4. Найдите
наименьшее значение функции на отрезке: у = на отрезке
[1;14].
Решение. Заметим, что функция не определена в точке 0.
Берем производную дроби:
Приравниваем
производную к нулю и отыскиваем корни:
Один из корней нас не интересует, так как промежутку не
принадлежит, а во второй точке производная меняет знак с отрицательного на
положительный. То есть функция имеет минимум в данной точке. Определим ее
минимальное значение:

Целые рациональные функции
Задача 5. Найдите наибольшее значение
функции на
отрезке .
Решение. Найдём производную заданной функции:
Найдем нули
производной:
Указанному в
условии интервалу принадлежит точка х = –1.
Вычисляем значения
функции в точках –2, –1 и 0:
Наибольшее
значение функции равно 6.
Ответ: 6
Задача
6. Найдите наибольшее значение функции у = х3 – 6х2 на отрезке
[–3;3].
Решение. Найдём производную заданной функции:
Найдем нули
производной:
Указанному в
условии интервалу принадлежит точка х = 0.
Вычисляем значения
функции в точках –3, 0 и 3:
Наименьшее
значение функции равно 0. Ответ: 0
Задача
7. Найдите наименьшее значение функции у = х3 – 2х2 + х +3 на отрезке [1;4].
Решение. Найдём производную заданной функции:
Найдем нули
производной, решаем квадратное уравнение:
3х2 – 4х + 1 = 0
Получим
корни: х1 =
1 х1 =
1/3.
Указанному в
условии интервалу принадлежит только х = 1.
Найдём значения
функции в точках 1 и 4:
Получили, что
наименьшее значение функции равно 3.
Ответ: 3
Задача
8. Найдите наименьшее
значение функции у = х3 +
2х2 + х + 3 на отрезке
[– 4; –1].
Решение. Найдём производную заданной функции:
Найдем нули
производной, решаем квадратное уравнение:
3х2 + 4х + 1 = 0
Получим корни:
Указанному в
условии интервалу принадлежит корень х = –1.
Находим значения
функции в точках – 4, –1, –1/3 и 1:
Получили, что
наименьшее значение функции равно — 28.
Ответ: — 28.
Рассмотрим способ определения наибольшего и наименьшего значения функций без
производной. Этот подход можно использовать, если с определением производной у
вас большие проблемы. Принцип простой – в функцию подставляем все целые
значения из интервала (дело в том, что во всех подобных прототипах ответом
является целое число).
Задача
9. Найдите наименьшее значение функции у = 7 + 12х – х3 на отрезке [–2;2].
Решение. Подставляем точки от –2 до 2:
у(–2)=7+12 (–2) –
(–2)3 = – 9
у(–1)=7+12 (–1) –
(–1)3 = – 6
у(0)=7+12∙0 – 03 = 7
у(1)=7+12∙1 – 13 = 18
у(2)=7+12∙2 – 23 = 23
Наименьшее
значение равно –9.
Ответ: –9
Задача
10. Найдите наименьшее
значение функции у = х3 -27х на отрезке [0;4].
Решение.
Задача
11. Найдите наименьшее значение функции у = (х –
3)2(х – 6) – 1 на отрезке [4;6].
Решение. Так как интервал дан (при чём он небольшой), то здесь рекомендую
подставить целые значения из него (4, 5 и 6) в функцию:
Наименьшее
значение функции на заданном отрезке равно – 5.
Ответ: – 5
Задача 12. Найдите наибольшее
значение функции у = (х + 6)2(х – 1) – 6
на отрезке [– 9;–2].
Решение. Данную задачу можно решать любым из двух способов. Интервал здесь
маленьким не назовёшь, но и в то же время он невелик. Решим её подстановкой всех
значений из интервала.
Подставим – 9, –
8, – 7, – 6, – 5, – 4, – 3, –2.
Наибольшее
значение функции равно – 6.
Ответ: – 6
Функции, их исследование.
Рассмотрим
задачи, входящие в состав типовых заданий экзамена по математике, связанные
с исследованием функций (где присутствует число е), логарифмические,
показательные, иррациональные и другие. Для того чтобы решать задачи на нахождение наибольшего или
наименьшего значения, задачи на нахождение экстремумов, что производные элементарных функций нужно
знать наизусть, в теме производной без этого никак нельзя. Также необходимо
понимание того, что такое сложная функция, в указанной важно понимать свойства
производной для исследования функций.
Исследование функций с числом «е»
на наибольшее и наименьшее значение.
Решаем такие
задания следующим образом:
1. Находим производную.
2. Находим нули производной.
3. Определяем, какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).
Показательные
функции.
Задача 13. Найдите наименьшее
значение функции ( х – 2)2 ех-2 на отрезке [1 ; 4]
Решение. Сначала найдем производную данной функции, применив
правило для вычисления производной произведения двух функций:
Производная обращается в нуль при х=0; х=2.
Данному промежутку принадлежит единственная точка х=2.
При переходе через эту точку производная функции
меняет знак с минуса на плюс, эта точка является единственной
точкой минимума на данном отрезке и наименьшего значения на этом отрезке
функция достигает именно в этой
точке. Найдем наименьшее значение:
Ответ: 0
Задача 14. Найдите наименьшее значение функции у = (х–17)
ех–16 на отрезке [15;17].
Решение. Мы знаем, что для того, чтобы найти наибольшее или наименьшее
значение функции на отрезке, необходимо вычислить её значение на границах
заданного интервала и в точках, где производная равна нулю. Действуем по
алгоритму:
1. Найдём производную заданной
функции:
2. Найдем нули производной на
заданном отрезке, то есть приравниваем производную к нулю и вычислим корни
уравнения:
Выражение ех-16 не
равно нулю ни при каких х, так как известно, что показательная функция имеет
положительные значения на всей области определения.
3. Определяем,
принадлежит ли найденная точка интервалу.
Точка х = 16
принадлежит интервалу [15;17]. Значит, значение функции будем вычислять в
точках 15, 16 и 17:
*Учтите, что число е
≈ 2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое
выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом,
но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим
на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно посчитать
столбиком для проверки).
4. Делаем вывод.
Таким образом,
наименьшее значение функции равно –1.
Ответ: –1
Ещё один путь
решения (без нахождения производной). Мы знаем, что ответом в задачах
на ЕГЭ в части первой части, должно быть, целое число, либо конечная
десятичная дробь.
Сразу подставляем в
функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и
выбираем наименьшее значение:

Ответ: –1
Задача 15. Найдите наибольшее значение функции у =
(22 – х)ех–21 на отрезке [16;25].
Решение. Найдём производную заданной функции:
Найдем нули производной:
Число ех-21 не
может быть равно нулю, так как степень положительного числа всегда даст в
результате число положительное, значит х = 21.
Полученное значение принадлежит
интервалу [16;25].
Вычислим значения
данной в условии функции в точках 16, 21 и 25:
*То есть на границах
интервала и в точке, где производная обращается в нуль.
Первый результат
меньше единицы (это понятно и без вычислений).
Третий результат так
же меньше единицы (отрицательное число).
Значит наибольшее
значение функции на заданном интервале равно 1.
*Помните, что ответы
с числом е (по требованиям ЕГЭ) не являются верными.
Ответ: 1
Задача 16. Найдите наибольшее
значение функции у = (2х2 – 10х + 10)ех
на
отрезке [–4; 3].
Решение. Необходимо определить значения на границах интервала, и в
точках, где производная обращается в нуль.
Найдём производную
заданной функции:
Найдем нули производной:
Произведение
множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так
как степень положительного числа всегда даст в результате число положительное.
Значит решением являются
корни: х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3],
х=3 совпадает с границей интервала.
Вычисляем значения функции в точках:
– 4, 0 и 3:
Значит наибольшее
значение функции равно 10. Ответ: 10
*Как вы уже поняли,
можно в заданную функцию можно подставить все целые значения х из интервала, и
таким образом найти наибольшее значение функции. Но в данном случае придётся
перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Задача 17. Найдите наименьшее значение функции у = (х +
44)2 е – 44 – х на
отрезке [– 46; –43]
Решение. Найдём производную заданной функции:
Обратите внимание, что результат мы
представили сразу в виде множителей, это будет удобно при вычислении нулей
производной.
Найдем нули производной:
Решением являются
корни: х1= – 44 и х2= – 42.
Заданному интервалу
[– 46;–43] принадлежит только точка х = – 44.
Вычисляем значения
функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке,
где производная равна нулю:
Наименьшее значение
функции равно 0. Ответ:
0
*Как это задание
решить можно быстро?
Учитывая, что
ответом должно быть целое число, видно что значение данной функции будет целым
только при х= – 44 и х= 44.
указанному в условии
интервалу принадлежит х= – 44, вычисляем:
Задача 18. Найти
наибольшее и наименьшее значения функции
f (x) = 5 на отрезке
[4; 40].
Решение. Находим критические точки
функции, лежащие внутри данного отрезка:
Вычисляем
значения функции на концах отрезка и в критической точке: f (4) = 11, f (12) = 13, f (40) = 5. Из полученных значений
выбираем наибольшее и наименьшее:
,
.
Ответ: ,
.
Задача 19. Найти наибольшее значение
функции f (x) = x ln 5 – x ln x на отрезке .
Решение. = ln 5
– ln x – 1 =
при
.
Сравнение значений функции на концах отрезка и в критической точке приводит к
сложным вычислениям. Вместо этого проведем исследование функции на
монотонность. Учитывая непрерывность функции в точке и тот факт, что при
производная положительна, а при
отрицательна, приходим к выводу, что на
промежутке функция возрастает, а на
промежутке убывает. Это и означает, что
значение функции в точке является
наибольшим из всех значений функции на данном отрезке.
Задача 20. Найти наименьшее значение
функции
y = (x – 1) (x – 2) (x – 3) (x – 4) + 3.
Решение. Преобразуем функцию
следующим образом:
y = (x2 – 5 x + 4) (x2 – 5 x + 6) + 3
=
= (x2 – 5 x + 4)2 +
2 (x2 – 5 x + 4) + 1 + 2 = (x2 – 5 x + 5)2 + 2.
Ясно, что
наименьшее значение функции равно 2 и достигается оно при .
Ответ: 2.
Задача 21. Найдите
наибольшее значение функции .
Решение. Данная функция представляет собой выражение,
числитель которой – положительное число, а знаменатель – квадратный трехчлен с
отрицательным дискриминантом.
Следовательно, наибольшее значение данной функции
достигается при наименьшем значении знаменателя при .
Соответственно, .
Ответ: 2.
Задача 22. Найти наибольшее значение
функции f (x) = x ln 5 – x ln x на отрезке .
Решение. = ln 5 – ln x – 1 =
при
.
Сравнение значений функции на концах отрезка и в критической точке приводит к
сложным вычислениям. Вместо этого проведем исследование функции на
монотонность. Учитывая непрерывность функции в точке и тот факт, что при
производная положительна, а при
отрицательна, приходим к выводу, что на
промежутке функция возрастает, а на
промежутке убывает. Это и означает, что
значение функции в точке является
наибольшим из всех значений функции на данном отрезке.
Вычислить
наибольшее ( наименьшее) значение.
Задачи с логарифмами
Задача 23. Найдите
наименьшее значение функции у = 5х – ln (х+5)5 на отрезке
[– 4,5;0].
Необходимо вычислить значение функции на концах интервала, и в
точках экстремума, если таковые имеются на данном интервале, и выбрать
наименьшее из них.
Вычисляем
производную, приравниваем её к нулю, решаем уравнение.
Найдем производную
заданной функции:
Найдем нули
производной на заданном отрезке:
*Дробь равна нулю
тогда, когда числитель равен нулю.
Точка х= –
4 принадлежит заданному интервалу.
Таким образом,
вычисляем значение функции в точках: – 4,5; – 4; 0.
Значения с
логарифмами, которые мы получили, вычислить (или проанализировать) можно. И вы
убедитесь, что наименьшим значением функции на данном отрезке является
«– 20».
Но вычислять их не
обязательно. Почему? Мы знаем, что ответом должно быть либо, целое число, либо
конечная десятичная дробь (это условие ЕГЭ в части В). А значения с
логарифмами: – 22,5 – ln 0,55 и – ln3125
такого ответа не дадут.
Кроме того, убедится
в том, что в точке х=–4 функция приобретает минимальное значение, можно
определив знаки производной на интервалах от (– 5:– 4) и (– 4;+∞).
Теперь информация
для тех, у кого с производной и пониманием того, как решать подобные задачи,
нет трудностей. Как можно обойтись без вычисления производной и без лишних
расчётов?
Итак, если учесть,
что ответом должно быть целое число, либо конечная десятичная дробь, то такое
значение мы можем получить только тогда, когда х будет являться целым числом,
либо целым с конечной десятичной дробью и при этом под знаком логарифма в
скобках у нас будет единица или число е. В противном случае, мы не сможем
получить оговоренное значение. А это возможно только при х = – 4.
Значит, в этой точке
значение функции будет наименьшим, вычислим его:
Ответ: – 20.
Задача 24. Найдите наименьшее
значение функции у = е 2х — 8е х + 9 на
отрезке [0; 2].
Решение. Необходимо определить значения на границах интервала, и в
точках, где производная обращается в нуль.
Найдём производную заданной
функции: у ׳ = (е 2х — 8е х + 9)׳
= 2 е 2 х – 8 е х
Найдем нули производной:
у ׳ = 0 ; 2е 2х – 8 е х =
0; 2 е х
( е х — 4 ) = 0.
е х 0 тогда е х
— 4 = 0 ; е х =
4 ; х = ln 4.
ln 4
[0; 2].
Произведение
множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так
как степень положительного числа всегда даст в результате число положительное.
Значит решением являются
корнь: х = ln 4
Эта точка принадлежат интервалу
[0;2],
Вычисляем значения функции в точках:
0 , ln 4 и 2.
у(
0) = е 2·0 — 8е 0 + 9 = 1 – 8 + 9 =2
у(2)
= е 2·2 — 8е 2 + 9 = е 4 — 8е2
+ 9
у
(ln 4) = е 2ln 4 — 8е ln 4 + 9 = е ln 16 — 8е ln 4 + 9 = 16 – 32 +9
= -7.
Значит наименьшее
значение функции равно — 7. Ответ: — 7.
Функции заданные
вида у = е 2х — 8е х + 9 можно решить
только с помощью производной. При решении получается корень выраженный
через натуральный лагорифм.
Тригонометрические функции
Основная сложность тригонометрических
функций состоит в том, что при решении уравнений возникает
бесконечное множество корней. Например, уравнение sin x = 0
имеет корни x = πn, где n ∈ Z. Ну и как
отмечать их на координатной прямой, если таких чисел бесконечно
много?
Ответ прост: надо
подставлять конкретные значения n. Ведь в задачах B12
с тригонометрическими функциями всегда есть ограничение —
отрезок [a; b]. Поэтому для начала берем n = 0,
а затем увеличиваем n до тех пор, пока соответствующий
корень не «вылетит» за пределы отрезка [a; b]. Аналогично,
уменьшая n, очень скоро получим корень, который меньше нижней границы.
Несложно
показать, что никаких корней, кроме полученных в рассмотренном процессе,
на отрезке [a; b] не существует. Рассмотрим теперь этот
процесс на конкретных примерах.
Задача1. Найти наибольшее значение функции
y = 4tg x − 4x + π − 5
на отрезке [−π/4; π/4].
Решение. Вычисляем производную:
y’ = (4tg x − 4x + π − 5)’ =
4/cos 2x − 4.
Затем решаем
уравнение: y’ = 0 ⇒
4/cos 2x − 4 = 0 ⇒ … ⇒ x = πn, n ∈ Z.
Выделим из этой формулы корни,
подставляя конкретные n, начиная с n = 0:
n = 0 ⇒x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π. Но π > π/4, поэтому
корень x = π и значения n > 1
надо вычеркнуть.
n = −1 ⇒ x = −π. Но π < −π/4, поэтому
x = π и n < −1 тоже вычеркиваем.
Из всего многообразия корней остался лишь
один: x = 0. Поэтому вычисляем значение функции для
x = 0,x = π/4и x = −π/4.
y(0) =4tg 0 − 4·0 + π − 5 =π − 5;y(π/4) =4tg (π/4) − 4·π/4 + π − 5 =1;
y(π/4) =
4tg (−π/4) − 4·(−π/4) + π − 5 =
… = 2π − 9.
Теперь заметим, что
π = 3,14… < 4, поэтому
π − 5 < 4 − 5 < 0
и 2π − 9 < 8 − 9 < 0.
Получается одно положительное число и два отрицательных. Мы ищем
наибольшее — очевидно, это y = 1. Ответ: 1
Заметим, что в последней задаче
можно было и не сравнивать числа между собой. Ведь из чисел
π − 5, 1 и 2π − 9 в бланк ответов может быть
записана лишь единица. Действительно, как написать в бланке, скажем,
число π? А никак. Это важная особенность первой части
ЕГЭ по математике, которая значительно упрощает решение многих задач.
И работает она не только в B12.
Иногда при исследовании функции
возникают уравнения, у которых нет корней. В таком случае задача
становится еще проще, поскольку остается рассмотреть лишь
концы отрезка.
Задача2. Найти наименьшее значение функции
y = 7sin x − 8x + 5
на отрезке [−3π/2; 0].
Решение. Сначала находим производную: y’
= (7sin x − 8x + 5)’ = 7cos x − 8.
Попробуем решить
уравнение: y’ = 0 ⇒
7cos x − 8 = 0 ⇒ cos x = 8/7.
Но значения cos x всегда лежат на отрезке [−1; 1],
а 8/7 > 1. Поэтому корней нет.
Если корней нет,
то и вычеркивать ничего не надо. Переходим к последнему
шагу — вычисляем значение функции:
y(−3π/2) = 7sin (−3π/2) − 8·(−3π/2) + 5 =
… = 12π + 12;
y(0) = 7sin 0 − 8·0 + 5 = 5.
Поскольку
число 12π + 12 в бланк ответов не записать, остается
лишь y = 5.
Ответ: 5
Задача3. Найдите
наименьшее значение функции y = 5cosx – 6x + 4
на отрезке [–3П/2; 0].
Найдём производную заданной функции:
Найдем нули производной на заданном отрезке:
Известно, что – 1 ≤ sin x ≤ 1, то есть уравнение не
имеет решения.
Это означает, что в пределах заданного интервала нет точек
минимума и максимума. Производная будет отрицательна при всех значениях
переменной. Почему?
Если учесть, что – 1≤sinx≤ 1, то получаем
– 1≤sinx≤1 => 5
≥ –5sinx≥ –5 => –1 ≥ –5sinx–6 ≥ –11
то есть значение выражения (производной) «–5cosx – 6» лежит в
пределах от – 11 до – 1 включительно.
Следовательно на указанном интервале функция убывает, и наименьшее
значение будет в крайней правой точке, то есть при х = 0. Таким образом,
Ответ: 9
Задача 4.
Найдите наименьшее значение функции y = 7sin x – 8x + 9
на отрезке [–3П/2; 0].
Найдём производную заданной функции:
Найдем нули производной на заданном отрезке:
Известно, что – 1 ≤ cos x ≤ 1, то есть уравнение не
имеет решения.
Это означает, что в пределах заданного интервала нет точек
минимума и максимума. Производная отрицательна при всех значениях переменной,
значение производной лежит в пределах от – 15 до – 1
включительно.
Значит на указанном интервале функция убывает.
Следовательно наименьшее значение функции на заданном отрезке
будет в правой крайней точке, то есть при х = 0.
Ответ: 9
Задача 5. Найдите наибольшее значение функции
Найдём производную заданной функции:
Найдем нули производной на заданном отрезке:
Точка x = П/6, принадлежит заданному интервалу.
Вычислим значение
функции в точках: 0, П/6, П/2.
Если учесть, что число
Пи равно 3,14 а корень из трёх ≈ 1,73 то значения вычислить
будет не трудно:
Значит наибольшим
значением функции на отрезке будет 12. Данные приближённые значения можно
и не вычислять. Достаточно помнить то, что ответом в задачах части В
является целое число, а там где присутствует неизвлекаемый в целых числах
корень, целое число мы никак не получим.
Ответ: 12
*Примечание. Корень
уравнения мы записали сразу с учётом данного в условии отрезка, поэтому период
косинуса в результате не записан.
Задача 6. Найдите наибольшее
значение функции
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
Значит уравнение не имеет решения, так как – 1 ≤ cos x
≤ 1.
Учитывая данное ограничение, производная на данном отрезке
имеет отрицательное значение:
Следовательно она убывает.
Таким образом, наибольшее значение функции на заданном отрезке
будет в левой крайней точке, то есть при х = – 5П/6.

Задача 7. Найдите наибольшее
значение функции у = 15х – 3 sin x + 5 на отрезке .
Задача
8. Найдите наименьшее значение функции y = 3 + — 5х — 5
cosx на отрезке
.
Задача
9. Найдите наименьшее значение функции y = 3 — + 5х — 5
sinx на отрезке
.
2.
Методические рекомендации обучения учащихся решению заданий вычислению
точек экстремума
Решение задач на
нахождение точек максимума и минимума (точек экстремума) функции
основывается на следующих утверждениях:
Признак
максимума.
Если функция f непрерывна в точке на интервале
на интервале
,
то — точка максимума функции f (упрощенная
формулировка: если в точке производная
меняет знак с плюса на минус, то — точка
максимума).
Признак минимума. Если функция f непрерывна в точке на интервале
на
интервале , то
— точка минимума функции f (упрощенная
формулировка: если в точке производная
меняет знак с минуса на плюс, то – точка
минимума).
Может оказаться
очень полезным следующее свойство непрерывных функций: «Если функция y = f(x)
имеет на промежутке I единственную точку экстремума x0 и эта точка
является точкой минимума, то в ней достигается наименьшее значение функции на
данном промежутке». Аналогичное утверждение справедливо для точки максимума и
наибольшего значения функции.
Например, если
функция y = f(x), непрерывная на отрезке [a;b], имеет на промежутке (a;b)
единственную точку экстремума xо и эта точка является точкой
максимума функции, то наибольшее значение функции на отрезке [a;b] равно f(xо).
Иногда при
решении задач на исследование функций оказывается, что на данном промежутке
точек экстремума нет. Такой ситуации не надо пугаться: она означает, что на
этом промежутке производная принимает значения одного знака, т. е. функция
является монотонной на нем. Остается заметить, что если функция возрастает на
отрезке, то наибольшее значение на нем достигается в правом конце отрезка, а
наименьшее — в левом; если функция убывает на отрезке, то наибольшее значение
на нем достигается в левом конце отрезка, а наименьшее — в правом.
Практические
правила исследования функции на максимум и минимум с помощью производной.
1) Найти производную функции
2) Найти критические точки
функции ,т.е. точки, в которых
обращается в нуль или терпит разрыв.
3) Исследовать знак производной в промежутках, на которые найденные
критические точки делят область определения функции .
При этом критическая точка есть точка
минимума (максимума), если производная меняет знак при переходе через . Если же в соседних промежутках,
разделённых критической точкой , знак
производной не меняется, то в точке функция не
имеет ни максимума, ни минимума.
4) Вычислить значения функции в
точках максимума и минимума.
Рассмотрим примеры:
Пример 1.Найдите точку
максимума функции у = х3 – 48х +17 .
Решение. Найдем производную
заданной функции: у’ = 3х2 — 48 = 3(х2 – 16) = = 3(х — 4)
(х + 4).
Найдем нули
производной: 3 (х — 4) (х + 4) =0 х =4; х= — 4
Определим знаки
производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума
х = — 4.
Ответ: -4
Пример 2. Найдите точку минимума
функции у = (х + 18)ех-18
Решение. 1. Найдём производную заданной функции:
у’ = (х +18)’ ех-18 + (х + 18) (ех-18
)’ = ех-18 + (х + 18) ех-18 = (х + 19)
ех-18
2. Найдем нули
производной:
у’ = 0 (х + 19) ех-18
= 0
Получаем, что х =
–19.
Выражение ех-18 не
равно нулю ни при каких х, так как известно, что показательная функция имеет
положительные значения на всей области определения.
3. Определим знаки
производной функции на интервалах (подставляем любые произвольные значения в
производную) и изобразим на рисунке поведение функции:
у’ (-20) = (-20 + 19) е -20 — 18 = -1 е — 38
у’ (-10) = (-10 + 19) е -10 — 18 = 9 е — 28
В точке х = –19 функция
меняет знак с отрицательного на положительный, значит это искомая точка
минимума.
Ответ: –19
Как решать быстрее
данный тип задач?
Когда мы получили
производную и приравняли её к нулю:
(х +
19) е х–18 = 0
Далее получили, что х = –19. Данное
решение и будет являться ответом задачи т.к. е х–18 0
Пример 3. Найдите
точку максимума функции у = (3х2 – 15х + 15) е7–х.
Решение. Найдём производную заданной функции:
у’ = (3х2 –
15х + 15)’ е7–х + (3х2 – 15х + 15) (е7–х)’
= (6х – 15) е7–х + (3х2 – 15х + + 15) е7–х
( 7 – х)’ = (6х – 15) е7–х + (3х2 – 15х + 15)
е7–х (–1) = (6х – 15) е7–х – – (3х2 –
15х + 15) е7–х = ( (6х – 15) – (3х2 – 15х +
15) ) е7–х = (6х – 15 — 3х2 + + 15х – 15) е7–х
= (– 3х2 + 21х – 30) е7–х = –3 (х –5) (х – 2) е7–х
= 0
Найдем нули производной:
у’ =0 -3 (х -5) (х –
2) е7– х = 0
-3
(х -5) (х – 2) =0 либо е7 – х = 0
Число е7-х не
может быть равно нулю, так как степень положительного числа всегда даст в
результате число положительное.
Решаем – 3
(х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2 .
Определим знаки
производной функции (подставляя любые значения из интервалов в найденную
производную) и изобразим на рисунке поведение функции:
у'(0) = -3 (0 — 5) (0 –
2) е7– 0 = — 30 е70
у'(3) = -3 (3 — 5) (3 –
2) е7– 3 = 6 е40
у'(6) = -3 (6 — 5) (6 –
2) е7– 6 = — 12 е0
В точке х = 5 функция меняет знак с
положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5.
Пример 4. Найдите точку максимума функции у = х2 – 34х
+ 140lnх–10.
Решение. По свойству логарифма выражение, стоящее под его знаком больше
нуля, то есть х > 0.
Функцию будем
рассматривать на интервале (0; +∞).
Найдём производную
заданной функции:
(х2 –
34х +140 ln x -10)’ = 2x -34 +
Найдем нули
производной:
у’ =0 2x -34 +
= 0
2х2 –
34х + 140 = 0
х2 –
17х + 70 = 0
Решая квадратное
уравнение, получим: D = 9 х1 = 10 х2 = 7.
Точка х = 0
не входит в область определения функции и в ней производная не существует.
Отмечаем на числовой оси три точки 0, 7 и 10.
Ось ох разбивается
на интервалы: (0;7), (7;10), (10; +∞).
Определим знаки
производной функции, подставляя произвольные значения из полученных интервалов
в найденную производную, и изобразим на рисунке поведение функции:
у'(5) =2 ·5 -34 +
0
у'(8) =2 ·8 -34 +
0
у'(14) =2 ·14 -34 +
0
Таким образом, в точке х = 7 производная функции меняет знак с
положительного на отрицательный, значит это искомая точка
максимума. Ответ:
7
Пример 5.. Найдите точку максимума
функции .
Решение. Вычислим
производную функции, используем формулу производной показательной и производной
сложной функции:
Найдем нули производной. Известно, что произведение равно нулю
тогда и только тогда, когда хотя бы один из множителей равен нулю, а другие при
этом не теряют смысла. В данном случае:
–30 +
12х – х2 =
0 или –2х + 12 = 0
Решим первое: –30 + 12х – х2 = 0
D= 122 – 4 ·(
-1) ·(- 30) = 144 -120 = 24.
х1 =
= =

; х2
= 

Второе уравнение: –2х + 12 = 0; х = 6
У нас получилось
три точки, в которых производная функции равна нулю. Если записать
приближенно (первые две), то получим: 3,56; 6 и 8,44.
Определим знаки производной на интервалах, которые получаются
разбие-нием числовой оси указанными выше точками. Возьмём точки 0, 5, 7 и 9:
у'(0) = ( — 30 + 12 ·0 – 02) · ln8·(-2·0 +12) = -30 ln8·12 0
функция убывает.
у'(5) = ( — 30 + 12 ·5 – 52) · ln8·(-2·5 +12) = 5 ln8·2 0
функция возрастает.
у'(7) = ( — 30 + 12 ·7 –72) · ln8·(-2·7 +12) = 5 ln8· (-2) 0
функция убывает.
у'(9) = ( — 30 + 12 ·9 –92) · ln8·(-2·9 +12) = -3 ln8· (-2) 0
функция возрастает .
Получили, что в точке х = 6 производная функции меняет свой знак с
положительного на отрицательный, а это означает, что данная точка есть точка
максимума функции.
Ответ: 6
Комментарий:
в данном случае область определения не имеет ограничений, то есть при всех х
функция имеет значение. При вычислении нулей функции получили три точки. Две из
них иррациональны (имеется корень). На основании этого мы уже могли бы сделать
вывод о том, что точка х = 6 это точка максимума, так ответом должно быть целое
число или конечная десятичная дробь. Но, всё же, рекомендую определить знаки
производной на интервалах, чтобы убедиться какая точка является точкой
максимума. В случае, если корни квадратного трёхчлена будут целыми, то это
нужно сделать обязательно.
Если будет стоять
вопрос о нахождении максимального (минимального) значения функции на
определённом интервале, то тут действуйте по стандартному алгоритму (посмотрите
задания на сайте, их достаточно).
В любом случае,
свойства производной для исследования функции, табличные значения производных и
алгоритм нахождения точек максимума (минимума) нужно знать обязательно.
Исследования степенной функции на максимум
и минимум.
Пример 6. Найдите точку максимума функции у = (х – 2)2(х
– 4) + 5.
Решение. Для этого найдём производную, приравняем её к нулю, найдём корни
полученного уравнения:
у’ = ((х – 2)2(х – 4) + 5)’
= ((х –
2)2(х – 4))’ = ((х – 2)2
)(х – 4) +(х – 2)2 (х – 4)’ =
= 2(х – 2) (х – 4) + (х – 2)2 = (х – 2) (2х
– 8 + х – 2) = (х – 2) (3х – 10).
Находим нули
производной:
у’=0 значит (х -2) (3х-10)= 0
х-2=0,
х1 = 2 или 3х-10 =0 , х2 =
Полученные точки
разбивают числовую ость на интервалы.
Посмотрим, как
ведёт себя график функции на этих интервалах. Возьмём значения из них,
подставим их в производную и определим знак:
у’ (0) = (0 -2) (3·0-10) = 20
у’ (3) = (3 -2) (3·3-10) = -1
у’ (4) = (4 -2) (3·4-10) = 4
На интервале
(–∞;2) функция возрастает, на интервале (2;10/3) функция убывает. Значит
х = 2 это точка максимума.
Ответ: х = 2.
Пример 7.Найдите точку минимума функции у = х3+5х2+7х–5.
Решение. Найдём
производную функции:
Найдем нули производной: 3х2 + 10х + 7 = 0. Решая квадратное уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на
эскизе. Подставляем произвольное значение из каждого интервала в
выражение производной:
у(–3)’ = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)’= 3∙(–2)2
+ 10∙(–2) + 7 = –1 < 0
у(0)’= 3∙02 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на
положительный, значит это есть искомая точка минимума.
Ответ: –1
Пример 8. Найдите точку максимума
функции у = 7+12х–х3
Решение. Найдём
производную функции: у’ = (7+12х–х3)‘ = 12 – 3х2
Найдем нули производной:
12 –
3х2 = 0
х2 = 4х1 = –2; х2
= 2
Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на
эскизе. Подставляем произвольное значение из каждого интервала в выражение
производной:
у(–3)’=12
– 3∙(–3)2 = –15 < 0
у(0)’=12
– 3∙02 = 12 > 0
у(3)’=12
– 3∙32 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный,
значит это есть искомая точка максимума.
Ответ: 2.
Для этой же функции точкой минимума является точка х = – 2.
Пример 9. Найдите точку максимума
функции у = 9х2– х3.
Решение. Найдём
производную функции: у’ = (9х2– х3)’= 18х – 3х2
Найдем нули производной:
18х
–3х2 = 0
3х(6 –
х) = 0 х1 = 0; х2= 6.
Определяем знаки производной функции на интервалах и отметим их на
эскизе. Подставляем произвольное значение из каждого интервала в выражение
производной:
у(–1)’=18
(–1) –3 (–1)2 =
–21< 0
у(1)’=18∙1
–3∙12 = 15 > 0
у(7)’=18∙7
–3∙72 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на
отрицательный, значит это есть искомая точка максимума.
Ответ: 6
Для этой же функции точкой минимума является точка х = 0.
Иррациональные функции
Пример 10. Найдите
точку минимума функции у =  — 2х +1
— 2х +1
Решение: . Производная
обращается в ноль при х = 4. В точке х = 4 производная меняет знак с минуса на
плюс. Эта точка является единственной точкой минимума.
Ответ: 4
Пример 11. Найдите точку максимума
функции.
Решение. Сначала
определим, при каких х функция имеет смысл (найдём область определения
функции). Так как подкоренное выражение есть число неотрицательное, то решаем
неравенство:
13 +
6х – х2 ≥ 0
Данные корни разбивают ось х на три интервала.
Проверим при каких значениях х неравенство будет верным. Подставим
из каждого интервала любое значение х в неравенство:
Значит решением неравенства будут являться все значения х
принадлежащие интервалу (включая границы):
*Приближенно полученные
выражения равны:
Область определения данной функции найдена.
Вычислим производную функции. Это сложная функция:
Найдем нули производной:
Дробь равна нулю тогда, когда её числитель равен нулю, значит:
6 –
2х = 0
х = 3
Полученное
значение х входит в область определения и разбивает её на два отрезка.
Определим знаки производной на каждом из них (подставим выборочно любые
значения в выражение производной), например 2 и 4:
Получили, что в точке х = 3 производная функции меняет свой знак с
положительного на отрицательный, а это означает, что данная точка есть точка
максимума.
Ответ: 3
Комментарий:
представленное решение – это полное, математически грамотное решение, то есть
такое как должно быть. Дело в том, что для составления «полной картины», в
первую очередь необходимо найти область определения. Дело в том, можно сразу
находить производную, затем её «нули» и далее установить имеет ли функция
значение при этом х. Затем определить знаки в «соседних» точках и станет
понятно является ли эта точка точкой максимума (или минимума). Да, можно и так.
Пример 12. Найдите точку
максимума функции у = ln(х+5)5 – 5х
Решение. Найдём производную данной функции 
Производная меняет знак в единственной точке х= – 4,причём знак производной в этой точке меняется
с плюса на минус. Следовательно, эта точка является единственной точкой
максимума данной функции.
Пример 13. Найдите точку максимума
функции у =log7(–2 – 12х – х2) + 10.
Решение. Вычислим
производную функции, используем формулу производной логарифма и производной
сложной функции:
Найдем нули производной:
Дробь равна нулю тогда и только тогда, когда её числитель равен
нулю:
– 2х
–12 = 0
х = –
6
Данное значение обращает подлогарифмическое выражение в
положительное:
–2 –
12∙(–6) – (–6)2 = 34
то есть оно принадлежит области определения функции.
Определим знаки производной в «соседних» точках, например возьмем
точки –7 и –5:
Получили, что в точке х = – 6 производная функции меняет свой знак
с положительного на отрицательный, а это означает, что данная точка есть точка
максимума функции.
Ответ: – 6
Комментарий: здесь мы не стали находить область определения.
Сразу вычислили производную и нашли х, при котором производная обращается в
нуль. Затем определили знаки производной на интервалах полученных разбиением
числовой оси точкой х = – 6 и сделали вывод.
Если в подобном задании (с логарифмом) будет стоять вопрос о
вычислении наибольшего (наименьшего) значения функции, то также вычисляйте его
в точке х, полученной при решении f′(х) = 0.
Пример 14. Найдите точку максимума
функции y = (2x –3) cos x – 2sin x + 5
принадлежащую
промежутку (0;/2).
Решение. Найдём производную функции:
у‘ = ((2x –3) cos x – 2sin
x + 5 )’ = ((2x –3) cos x)’ – (2sin x)’ + 5’=
(2x –3)’ cos x + +(2x–3)(cos x)’ – (2sin x)’
+ 5′ = 2 cos x + (-sin x)(2х –3) –2cosx = – sin x (2х–3)
Решаем уравнение:
– sin x (2х –3) = 0
Произведение равно
нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и
другие при этом не теряют смысла. Следовательно:
–sin x =0 или 2х –3 = 0
Решаем уравнение
– sin x = 0: х =
В условии дан
промежуток (0;/2). Ему не принадлежит ни один из полученных корней. *Обратите
внимание, что указанные границы исключены (скобки круглые).
Решаем уравнение:
2х – 3 = 0, получим х = 1,5.
Запишем данный
промежуток в радианах, получим: (0;1,57), так как
Следовательно,
полученное значение принадлежит промежутку (0;/2): 0
Конечно, нам
интуитивно понятно, что полученная точка это и есть точка максимума, и,
казалось бы, в дальнейших вычислениях и рассуждениях нет необходимости. Но
любая задача данного типа должна быть решена до конца по указанному алгоритму.
Это важно!
Полученное
значение х разбивает данный промежуток на два других. Определим знаки
производной функции, подставляя произвольные значения из полученных промежутков
(0;1,5) и (1,5;1,57) в найденную производную, и изобразим на рисунке поведение
функции:
В подобных случаях
необязательно вычислять значения выражений. Важно установить их знаки
(положительный либо отрицательный). Например, мы видим, что выражение:
(3,14/2)
– 3 имеет отрицательный знак
3,14 –
3 имеет положительный знак
В целом
этого достаточно для определения знака выражения.
Таким образом, в
точке х = 1,5 функция меняет знак с положительного на отрицательный. Это
означает, что данная точка является точкой максимума функции на заданном
промежутке.
Ответ: 1,5
Пример 15. Найдите точку минимума функции
y = x3/2 – 3x + 1
Решение. Найдём производную заданной функции:
Найдем нули производной:
Решаем уравнение:
Определим знаки производной функции и
изобразим на рисунке поведение функции. Для этого подставим произвольные
значения из полученных интервалов в производную:
В точке х = 4, производная меняет
знак с отрицательного на положительный, это означает, что данная точка является
точкой минимума.
Ответ: 4

В точке х = 4, производная меняет
знак с положительного на отрицательный, это означает, что данная точка является
точкой максимума.
Ответ: 4
Пример 16. Найдите точку минимума функции у= 4х– ln (х+5)+8
Решение. Сразу
запишем, что х+5>0 (по свойству логарифма), то есть х>–5.
Рассматривать
функцию будем на интервале (– 5;+∞).
Найдём производную
заданной функции:
у’= (4х– ln
(х+5)+8)’ = 4 –
Найдем нули
производной:
у’=0 4 —
= 0; х = — 4 ,75
Точка х
= –5 не входит в область определения функции и в ней производная не
существует. Отмечаем на числовой оси две точки –5 и –4,75. Определим
знаки производной функции, подставляя произвольные значения из интервалов
(–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке
поведение функции:
у’ (- 4,9) = 4 —
; у’ (- 4) = 4 —
;
Таким образом, в точке х= –4,75 производная функции меняет
знак с отрицательного на положительный, значит это искомая точка
минимума. Ответ:
– 4,75
Пример 17.
Найдите точку минимум функции у =
Решение. Найдем производную данной функции:
Определим промежутки знакопостоянства производной, приведя
полученное выражение к общему знаменателю и разложив числитель на множители:
В точке х = 5 производная меняет знак с минуса на
плюс, следовательно, эта точка и является единственной точкой минимума.
Ответ: 5.
Пример18. Найти точку максимума функции
y = sin x − 5x·sin x − 5cos x + 1,
принадлежащую отрезку [−π/3; π/3].
Решение. Вычисляем производную: y’ = (sin x − 5x·sin x − 5cos x + 1)’ =
… = cos x − 5x·cos x =
(1 − 5x)·cos x.
Затем решаем
уравнение: y’ = 0 ⇒
(1 − 5x)·cos x = 0 ⇒ … ⇒ x = 0,2
или x = π/2 + πn, n ∈ Z.
С корнем x = 0,2 все понятно,
а вот формула x = π/2 + πn требует дополнительной
обработки. Будем подставлять разные значения n, начиная с n =
0.
n = 0 ⇒ x = π/2.
Но π/2 > π/3, поэтому корень x = π/2
не входит в исходный отрезок. Кроме того,
чем больше n, тем больше x, поэтому нет смысла
рассматривать n > 0.
n = −1 ⇒
x = − π/2. Но −π/2 < −π/3 — этот корень
тоже придется отбросить. А вместе с ним — и все корни
для n < −1.
Получается, что на отрезке [−π/3; π/3] лежит только
корень x = 0,2. Отметим его вместе со знаками
и границами на координатной прямой:
Чтобы удостовериться,
что справа от x = 0,2 производная действительно
отрицательна, достаточно подставить в y’ значение x = π/4.
Мы же просто отметим, что в точке x = 0,2
производная меняет знак с плюса на минус, а следовательно
это точка максимума.
Ответ: 0,2
Пример
19. Найти точку максимума функции y = (2х – 3)
cos x — 2sin x+5
принадлежащую
отрезку (0; .
Решение: Сначала найдем производную данной функции, применив
правило для вычисления производной произведения двух функций:
На промежутке (0;
производная обращается в нуль
только при х =1,5, поскольку sinx>0 при х (0;
. В точке х =1,5 производная
меняет знак с плюса на минус, эта точка является единственной точкой максимума
на данном промежутке.
Ответ: 1,5
Заключение
При выполнении данной
работы мною были отобраны и проанализированы различные дидактические материалы,
литература, интернет ресурсы по данной теме. В результате которых, были
составлены методические рекомендации к решению заданий 12 с кратким ответом.
Эта работа позволяет учителю подготовить учащихся по данному вопросу, а ученику
успешно справится с заданиями данной группы.
Методика преподавания
школьного курса математики и подготовка к ЕГЭ должна быть ориентирована на
гармонизацию традиционного и инновационного подходов к обучению с применением
современных образовательных технологий, деятельностного подхода в обучении, использования
ресурсов сети Интернет.
При подготовке к ЕГЭ необходимо
использовать интернет-ресурсы:
·
На сайте www.mioo.ru (дистанционные уроки)
·
На сайте www.matheg.ru (открытый банк заданий I части)
А так же печатные издания:
·
Учебники,
имеющие гриф Министерства Образования РФ;
·
Пособия,
рекомендованные ФИПИ и МИОО для подготовки к ЕГЭ
Литература:
При разработке дидактических материалов
использованы ресурсы сети Интернет:
http://www.korolewa-ow.narod.ru/sist_ind.htm
http://www.mathnet.spb.ru/texts.htm
http://www.beluo.ru/
Материалы сайта ФИПИ (http://www.fipi.ru)
КоролеваТ.С.,
СорокинаЛ.В., Новикова Т.В., ЗеленоваЕ.В. и др.
Приложение
1. Найдите
наибольшее значение функции .
2. Найдите
наибольшее значение функции .
3. Найдите
наибольшее значение функции .
4. Найдите наибольшее
значение функции .
5. Найдите
наибольшее значение функции .
6. Найдите
наименьшее значение функции .
7.
Найдите наименьшее значение функции
8.
Найдите точку минимума функции .
9.
Найдите точку минимума функции
10. Найдите
точку максимума функции .
11. Найдите
точку максимума функции
12. Найдите
наибольшее значение функции .
13. Найдите
наибольшее значение функции .
14. Найдите
наименьшее значение функции .
15. Найдите
наименьшее значение функции .
16. Найдите
точку минимума функции
17. Найдите
точку минимума функции .
18. Найдите
точку максимума функции
19. Найдите
точку максимума функции .
20. Найдите
наименьшее значение функции + 19
21. Найдите
наибольшее значение функции =
–
31
22. Найдите
точку максимума функции .
23. Найдите
наибольшее значение функции на
отрезке .
24. Найдите
наибольшее значение функции на
отрезке .
25. Найдите
наибольшее значение функции на
отрезке .
26. Найдите
наименьшее значение функции на
отрезке .
27. Найдите
точку минимума функции .
28. Найдите
точку минимума функции
29. Найдите
точку максимума функции .
30. Найдите
точку максимума функции .
31. Найдите
точку максимума функции
32. Найдите наибольшее
значение функции на отрезке
.
33. Найдите наибольшее
значение функции на отрезке
.
34. Найдите
точку максимума функции .
35. Найдите
наименьшее значение функции на
отрезке .
36. Найдите
точку максимума функции .
37. Найдите
наибольшее значение функции на
отрезке .
38. Найдите
точку минимума функции
39. Найдите
наименьшее значение функции на
отрезке .
40. Найдите
точку минимума функции .
41. Найдите
точку минимума функции .
42. Найдите
точку максимума функции .
43. Найдите
точку минимума функции .
44. Найдите
точку минимума функции .
45. Найдите
точку минимума функции .
46. Найдите
наименьшее значение функции на
отрезке .
47. Найдите
точку минимума функции .
48. Найдите точку минимума
функции .
49. Найдите
наименьшее значение функции на
отрезке .
50. Найдите
точку максимума функции .
51. Найдите
наибольшее значение функции на
отрезке .
52. Найдите
точку максимума функции .
53. Найдите
точку минимума функции .
54. Найдите
наименьшее значение функции на
отрезке .
55. Найдите точку
минимума функции .
56. Найдите
точку максимума функции .
57. Найдите
точку минимума функции
58. Найдите
наименьшее значение функции на
отрезке
59. Найдите
наибольшее значение функции на
отрезке .
60. Найдите
точку минимума функции .
61. Найдите
наименьшее значение функции на
отрезке .
62. Найдите
наибольшее значение функции на
отрезке .
63. Найдите точку минимума
функции .
64. Найдите точку минимума
функции .
65. Найдите наименьшее
значение функции у = на отрезке
.
66. Найдите наименьшее
значение функции у =
на отрезке
.
67. Найдите наибольшее
значение функции у = .
68. Найдите наибольшее
значение функции у = .
69. Найдите
наибольшее значение функции у = .
70. Найдите
наибольшее значение функции .
71. Найдите
наибольшее значение функции .
72. Найдите
наименьшее значение функции .
73. Найдите
наименьшее значение функции .
74. Найдите
точку минимума функции .
75. Найдите
точку минимума функции .
76. Найдите
точку максимума функции .
77. Найдите
точку максимума функции .
78. Найдите наибольшее значение
функции .
79. Найдите
наименьшее значение функции на
отрезке .
80. Найдите
наименьшее значение функции на
отрезке
81. Найдите
наибольшее значение функции на
отрезке .
82. Найдите
наименьшее значение функции на
отрезке
83. Найдите
наименьшее значение функции на
отрезке
84. Найдите
наибольшее значение функции на
отрезке .
85. Найдите
наибольшее значение функции на
отрезке
86. Найдите точку минимума
функции .
87. Найдите точку минимума
функции .
88. Найдите точку минимума функции .
89. Найдите точку минимума
функции .
90. Найдите точку минимума
функции .
91. Найдите точку минимума
функции .
92. Найдите наименьшее
значение функции у = (х — 7)е х — 6 на отрезке
93. Найдите наименьшее
значение функции у = (х2 — 7х — 7)ех — 5 на отрезке
94. Найдите наибольшее
значение функции у = х2 +8.
95. Найдите наибольшее
значение функции у = х2 – 10.
96. Найдите наибольшее
значение функции + 7.
97. Найдите наибольшее
значение функции у = х2 +3.
98. Найдите наименьшее
значение функции + 1.
99. Найдите наименьшее
значение функции — 3.
100. Найдите наибольшее значение
функции .
101. Найдите наибольшее значениефункции .
102.
Найдите точку минимума функции y = 2x2-5x + lnx-3.
103.
Найдите точку максимума функции y = (2x-3) cosx-2sinx +5
принадлежащую промежутку (0;π/2).
104. Найдите наименьшее значение функции на
отрезке
105. Найдите
наименьшее значение функции на
отрезке .
106.
Найдите точку максимума функции
107.
Найдите точку максимума функции .
108.
Найдите точку максимума функции .
109.
Найдите точку максимума функции .
110.
Найдите
наибольшее значение функции на отрезке
.
111.
Найдите наименьшее значение функции на
отрезке .
112.
Найдите наименьшее значение функции на
отрезке .
113.
Найдите наибольшее значение функции на
отрезке .
114.
Найдите наибольшее значение функции на
отрезке .
115.
Найдите наибольшее значение функции на
отрезке .
116.
Найдите наибольшее значение функции на
отрезке
117.
Найдите наименьшее значение функции на
отрезке
118.
Найдите наибольшее значение функции на
отрезке .
119.
Найдите наибольшее значение функции на
отрезке .
120.
Найдите наибольшее значение функции на
отрезке .
121.
Найдите наименьшее значение функции на
отрезке
122.
Найдите наибольшее значение функции на
отрезке
123.
Найдите точку минимума функции .
124.
Найдите точку минимума функции .
125.
Найдите точку минимума функции
126.
Найдите точку максимума функции
127.
Найдите точку максимума функции .
128.
Найдите точку минимума функции
129.
Найдите точку максимума функции .
130.
Найдите точку минимума функции .
131.
Найдите точку минимума функции .
132.
Найдите точку максимума функции .
133.
Найдите точку максимума функции .
134.
Найдите точку минимума функции
135.
Найдите точку минимума функции .
136.
Найдите точку максимума функции, принадлежащую
промежутку .
137.
Найдите точку минимума функции, принадлежащую
промежутку .
138.
Найдите точку максимума функции
139.
Найдите наименьшее значение функции на
отрезке .
140.
Найдите точку минимума функции .
141.
Найдите точку минимума функции .
142.
Найдите наибольшее значение функции на
отрезке .
143.
Найдите наименьшее значение функции на
отрезке
144.
Найдите наименьшее значение функции на
отрезке .
145.
Найдите наибольшее значение функции на
отрезке .
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023

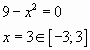
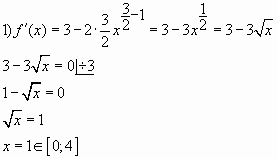
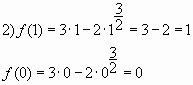
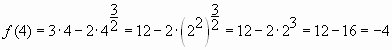
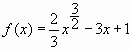 на отрезке
на отрезке 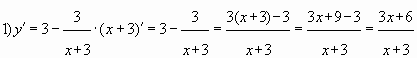
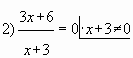
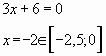
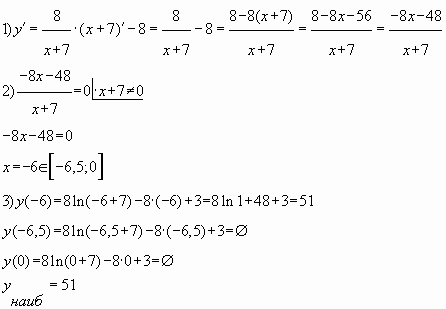
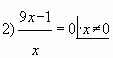
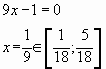
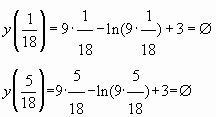
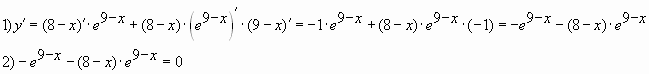
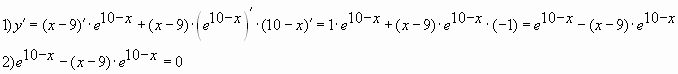
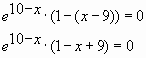
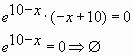
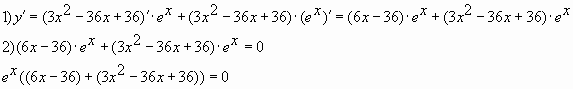
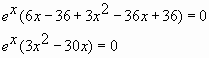
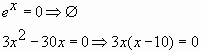
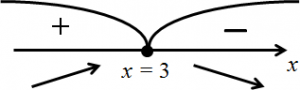 x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.














































































