Медианы, биссектрисы и высоты треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим рассмотрение элементов треугольника – медиан, биссектрис и высот треугольника.
Вначале дадим определение медианы треугольника и рассмотрим три медианы треугольника. Дадим определение биссектрисы треугольника и рассмотрим три биссектрисы треугольника. Дадим определение высоты треугольника и рассмотрим высоты в произвольном треугольнике и в тупом треугольнике. Далее решим ряд задач с использованием этих элементов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
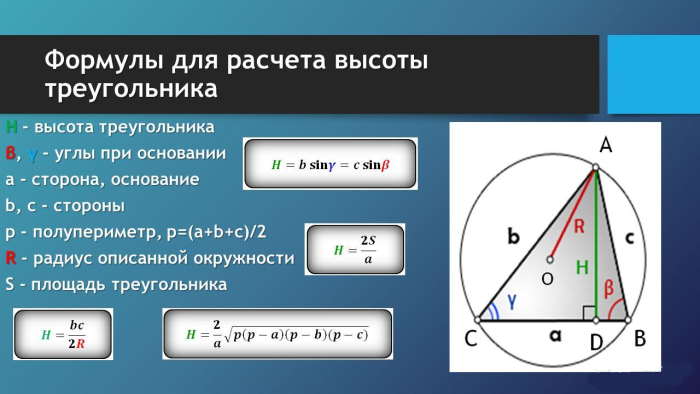
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
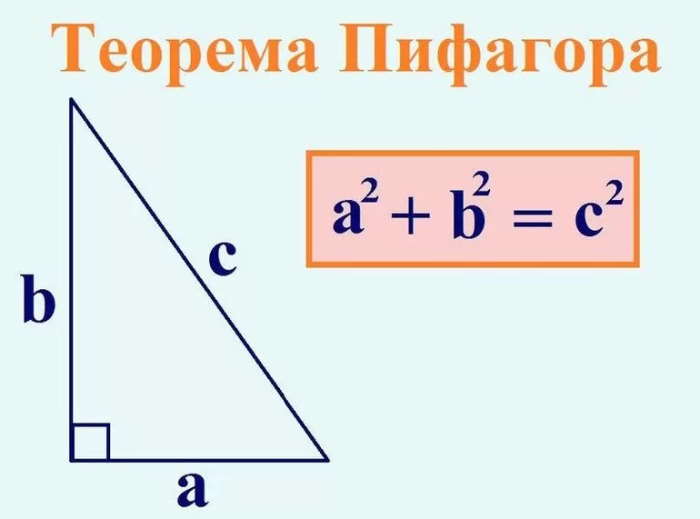
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Как построить высоту треугольника — основные способы
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.
- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
http://nauka.club/matematika/geometriya/kak-postroit-vysotu-treugolnika.html
Содержание материала
- Определение
- Видео
- Свойства равносторонней фигуры
- Высота треугольника по двум сторонам и радиусу описанной окружности
- Свойства высоты в равностороннем треугольнике
- В треугольнике проведены три высоты
- Задача наподобие треугольников
- Высота треугольника по основанию и площади
- Остроугольный треугольник и высота
- Примеры задач
Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.
Видео
Свойства равносторонней фигуры
При решении задач, связанных с нахождением высоты в равностороннем треугольнике, часто приходится использовать его свойства. Зная их, найти нужные параметры будет несложно. Тем более что все они связаны с главной особенностью фигуры — равенством его всех сторон.
Равностороннее тело с тремя углами обладает следующими особенностями:
- в нём все углы одинаковые и равны 60 градусов;
- середина пересечения отрезков, совпадающих с высотой, биссектрисой и медианой, является центром геометрического тела;
- радиус описанной окружности превышает радиус вписанной в 2 раза;
- в равностороннем треугольнике длины всех элементов выражаются через длину стороны.
Эти свойства очевидны. Если начертить треугольник с равными сторонами и вписать его в окружность, за центр можно принять точку O, при этом радиус описанного круга будет OK. Тогда линия, проведённая из неё к вершине, будет радиусом. Пусть конечная точка будет B. Но так как место пересечения является общим и для высот и медиан, из свойства последних можно сделать вывод, что в точке линия делится в отношении 2 к 1. Отсчёт следует вести с вершины треугольника. Значит: OB = 2 * OK.
Из основных формул, которые используются при вычислениях, в первую очередь нужно запомнить:
- радиус описанной окружности: R = (a * √3) / 3;
- диаметр вписанного круга: r = (a * √3) / 6;
- медиана: h = (a * √3) / 2;
- площадь: s = (a2 * √3) / 4;
- периметр: p = 3 * a.
Если рассмотреть треугольник ABC с проведённой высотой BN, можно утверждать, что грань АВ = ВС = АС = AN /2 = NC /2. Так как фигура ABN является копией BNC в зеркальном отражении, разделённые углы у вершины будут одинаковыми, а и их разворот составлять 30 градусов. Из этого следует, что угол A равен 60 градусам, значит, отрезок BN = AB * sin 60 = (AB * √3) / 2.
Зная длину медианы (высоты), вычислить другие параметры треугольника не составит труда. Например, периметр, P = 2 √3 * h; площадь — S = (h * 2) / √3.
При этом замечательным свойством является ещё и то, что ортоцентр одновременно будет в фигуре и центром тяжести (центроидом), поэтому точка пересечения высот и делит отрезок в отношении 2 к 1.
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
 |
(5) |
откуда
 |
(6) |
Далее, из теоремы синусов имеем:
 |
(7) |
Подставляя (6) в (7), получим:
или
 |
(8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
| (small max (b,c) ≤2R < b+c ) | (9) |
Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Проверим сначала условие (9):
| (small max (7,3) ≤2 cdot 4 < 7+3 ) | (10) |
Условие (9) удовлетворяется, следовательно такой треугольник существует. Для нахождения выстоты треугольника воспользуется формулой (8). Имеем:
Ответ: ( small 2frac{5}{8}. )
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
h=a32
где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
h=m=l=32a
где h — высота,
m — медиана,
l — биссектриса,
а — сторона правильного равностороннего треугольника.
В треугольнике проведены три высоты
Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:
В любом треугольнике три высоты или их продолжения пересекаются в одной точке.
Доказывать это утверждение мы здесь, пожалуй, не будем.
Давай просто нарисуем, чтобы понять, как это бывает «высоты или их продолжения».
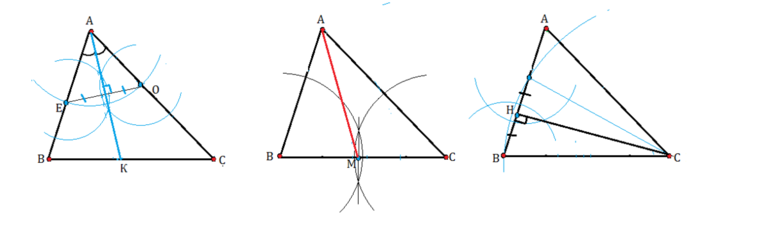
1. Треугольник остроугольный – тогда пересекаются сами высоты:
2. Треугольник тупоугольный – тогда пересекаются продолжения высот:
Что же полезного мы ещё не обсудили?
Задача наподобие треугольников
В прямоугольном треугольнике ABC (угол C = 90) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см
Решение.
Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).
Прямоугольные треугольники — единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.
Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)
Треугольники ABC и CBD подобны. Значит:
AD/DC = DC/BD, то есть
DC2=AD*BD
DC2=9*16
DC=12 см
Высота треугольника по основанию и площади
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

Откуда:
 . . |
(1) |
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Решение:
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ:
Остроугольный треугольник и высота
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.
Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.
И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
Примеры задач
Задача 1 Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2 Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Теги
Определение высоты треугольника
Перед тем как изучать формулы рассмотрим само определение. Это базовая информация, которая позволяет понять значение и предназначение такого показателя.
Высота треугольника — перпендикуляр, который проводится от вершины фигуры к прямой, имеющей противоположную сторону.
Критерии, зависящие от типа треугольника:
-
Внутри геометрической фигуры (подходит для остроугольных).
-
Совпадает с его стороной (подходит для прямоугольных).
-
Проходит вне фигуры (подходит для тупоугольных).
Как найти высоту треугольника
Можно воспользоваться одной из предложенных формул. Наиболее подходящая выбирается, исходя из известных значений. Это поможет не запутаться на середине решения и не пересчитывать по каждой формуле числа, делая из них уравнения. Существует множество выражений, способных в этом помочь. Ниже приведены самые распространенные и простые варианты определения этого показателя.
Через площадь треугольника
Этот способ можно использовать для всех видов фигуры. Чтобы воспользоваться формулой, должны быть известны площадь фигуры со стороной с проведенной высотой. В любой форме перпендикуляры не будут равны, поэтому вычислять возможно лишь одну высоту для одной стороны.
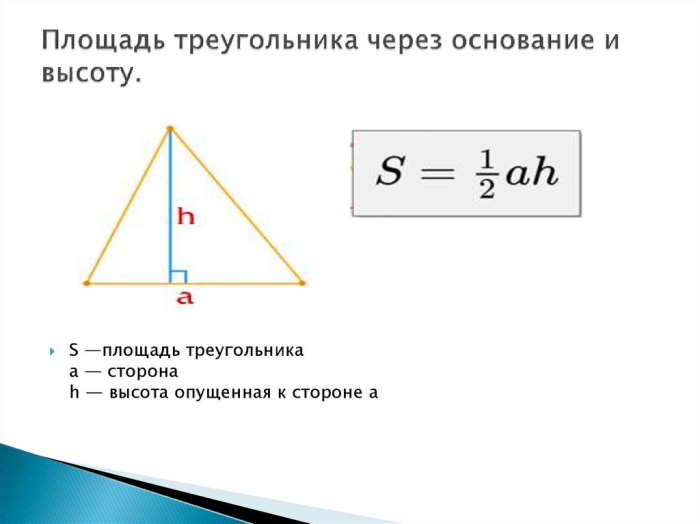
Формула площади треугольника:
S=½∗bh, где b — сторона фигуры, h — проведенная к стороне высота
Таким образом можно выразить перпендикуляр. С этой целью существует следующее выражение:
h=2∗S/b
Пример 1. Чему равна высота равностороннего треугольника АВС, если его площадь составляет 24 см, а длина стороны А составляет одну треть от площади.
Решение:
А=24/3=8 см
h=2∗S/b=2*24/8=6 см
Через теорему Пифагора
Для данного способа хорошо подойдут равнобедренные или равносторонние формы. В случае нахождения высоты равнобедренного треугольника следует знать, где находится основание. Это поможет в определении его боковых сторон, которые в данной форме уравненные и определении высоты, имеющей некоторые свойства:
-
совпадение высоты с биссектрисой и медианой;
-
деление основания пополам.
Формула определения высоты треугольника через теорему Пифагора:
BD=√(BC2−HC2)
Пример 2. Длина катетов прямоугольного треугольника равна 7 см. Вычислите длину его гипотенузы.
Исходя из теоремы Пифагора, длина гипотенузы прямоугольной формы, возведенной в квадрат, равна сумме, полученной в результате сложения квадратов длин его катетов:
х² = 7^2+7^2
Извлекаем квадрат из обеих частей равенства:
x = √(7² + 7²)= √(49+49) = √98 = √49*2 = 7√2=9,89 см
Через тригонометрическую функцию
Такой способ может помочь в решении задачи, если известны как сторона, так и угол при основании. В этом может помочь тригонометрическая функция.
Формула выражения высоты фигуры через тригонометрическую функцию:
BH=BC∗cos(60°)
Пример 3. Дан треугольник АВС. Угол C равен 90°, АС=2,4, sinA=7/25 Найдите AB.
Зная, что sinA=7/25, можно найти cosA. Для этого воспользуемся следующими формулами:
cosA = √1- sin2A = √1 -49/625=24/25
AB = AC/cosA = 4,8:24/25 = 4,8*25/24 = 48/10*25/24 = 5.
Download Article
Download Article
To calculate the area of a triangle you need to know its height. To find the height follow these instructions. You must at least have a base to find the height.
-
1
Recall the formula for the area of a triangle. The formula for the area of a triangle is
A=1/2bh.
[1]
- A = Area of the triangle
- b = Length of the base of the triangle
- h = Height of the base of the triangle
-
2
Look at your triangle and determine which variables you know. You already know the area, so assign that value to A. You should also know the value of one side length; assign that value to «‘b'».
Any side of a triangle can be the base,
regardless of how the triangle is drawn. To visualize this, just imagine rotating the triangle until the known side length is at the bottom.
Example
If you know that the area of a triangle is 20, and one side is 4, then:
A = 20 and b = 4.Advertisement
-
3
Plug your values into the equation A=1/2bh and do the math. First multiply the base (b) by 1/2, then divide the area (A) by the product. The resulting value will be the height of your triangle!
Example
20 = 1/2(4)h Plug the numbers into the equation.
20 = 2h Multiply 4 by 1/2.
10 = h Divide by 2 to find the value for height.
Advertisement
-
1
Recall the properties of an equilateral triangle. An equilateral triangle has three equal sides, and three equal angles that are each 60 degrees. If you
cut an equilateral triangle in half, you will end up with two congruent right triangles.
[2]
- In this example, we will be using an equilateral triangle with side lengths of 8.
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem states that for any right triangle with sides of length a and b, and hypotenuse of length c:
a2 + b2 = c2.
We can use this theorem to find the height of our equilateral triangle![3]
-
3
Break the equilateral triangle in half, and assign values to variables a, b, and c. The hypotenuse c will be equal to the original side length. Side a will be equal to 1/2 the side length, and side b is the height of the triangle that we need to solve.
- Using our example equilateral triangle with sides of 8, c = 8 and a = 4.
-
4
Plug the values into the Pythagorean Theorem and solve for b2.[4]
First square c and a by multiplying each number by itself. Then subtract a2 from c2.Example
42 + b2 = 82 Plug in the values for a and c.
16 + b2 = 64 Square a and c.
b2 = 48 Subtract a2 from c2. -
5
Find the square root of b2 to get the height of your triangle! Use the square root function on your calculator to find Sqrt(2. The answer is the height of your equilateral triangle!
- b = Sqrt (48) = 6.93
Advertisement
-
1
Determine what variables you know. The height of a triangle can be found if you have 2 sides and the angle in between them, or all three sides. We’ll call the sides of the triangle a, b, and c, and the angles, A, B, and C.
- If you have all three sides, you’ll use
Heron’s formula
, and the formula for the area of a triangle.
- If you have two sides and an angle, you’ll use the formula for the area given two angles and a side.
A = 1/2ab(sin C).[5]
- If you have all three sides, you’ll use
-
2
Use Heron’s formula if you have all three sides. Heron’s formula has two parts. First, you must find the variable
s, which is equal to half of the perimeter of the triangle.
This is done with this formula:
s = (a+b+c)/2.[6]
Heron’s Formula Example
For a triangle with sides a = 4, b = 3, and c = 5:
s = (4+3+5)/2
s = (12)/2
s = 6
Then use the second part of Heron’s formula, Area = sqr(s(s-a)(s-b)(s-c). Replace Area in the equation with its equivalent in the area formula: 1/2bh (or 1/2ah or 1/2ch).
Solve for h. For our example triangle this looks like:
1/2(3)h = sqr(6(6-4)(6-3)(6-5).
3/2h = sqr(6(2)(3)(1)
3/2h = sqr(36)
Use a calculator to calculate the square root, which in this case makes it 3/2h = 6.
Therefore, height is equal to 4, using side b as the base. -
3
Use the area given two sides and an angle formula if you have a side and an angle. Replace area in the formula with its equivalent in the area of a triangle formula: 1/2bh. This gives you a formula that looks like 1/2bh = 1/2ab(sin C). This can be simplified to
h = a(sin C)
, thereby eliminating one of the side variables.[7]
Note that angle C and side a are both positioned across from the height that you need to find (both on the right side from it, or both on the left side).Finding Height with 1 Side and 1 Angle Example
For example, with a = 3, and C = 40 degrees, the equation looks like this:
h = 3(sin 40)
Use your calculator to finish the equation, which makes h roughly 1.928.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do I find the area of an equilateral triangle when only the height is given?
H = height, S = side, A = area, B = base. You know that each angle is 60 degrees because it is an equilateral triangle. If you look at one of the triangle halves, H/S = sin 60 degrees because S is the longest side (the hypotenuse) and H is across from the 60 degree angle, so now you can find S. The base of the triangle is S because all the sides are the same, so B = S. Using A = (1/2)*BH, you get A = (1/2)*SH, which you can now find.
-
Question
How do I calculate the height of a right triangle, given only the length of the base and the interior angle at the base?
Look up the tangent of the angle in a trigonometry table. Multiply the tangent by the length of the base.
-
Question
How do I determine the height of a triangle when I know the length of all three sides?
You already know the base, so calculate the area by Heron’s formula. Then, substitute the values you know in the formula. Area=1/2 * base * height or height=2 * Area/base and find your answer.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
References
About This Article
Article SummaryX
If you know the base and area of the triangle, you can divide the base by 2, then divide that by the area to find the height. To find the height of an equilateral triangle, use the Pythagorean Theorem, a^2 + b^2 = c^2. Cut the triangle in half down the middle, so that c is equal to the original side length, a equals half of the original side length, and b is the height. Plug a and c into the equation, squaring both of them. Then subtract a^2 from c^2 and take the square root of the difference to find the height. If you want to learn how to calculate the area if you only know the angles and sides, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,408,639 times.
Reader Success Stories
-
«My Geometry teacher is not the best teacher, and I usually have to look up terms and lessons so I can teach myself…» more
Did this article help you?
Как найти высоту равнобедренного треугольника
Каждому иногда приходится освежить школьные знания, даже если, на первый взгляд, итоговая формула выглядит не сложной. Высоту равнобедренного треугольника легко вывести из теоремы знаменитого математика Пифагора, либо извлечь из формулы Герона.
1
Вычисление высоты равнобедренного треугольника онлайн
Самый простой способ, который не потребует от вас никаких умственных усилий – это нахождение искомой величины с использованием онлайн сервисов. Многие сайты предлагают вычислить высоту равнобедренного треугольника, пользователю лишь потребуется задать первоначальные величины – длины сторон (для равнобедренного – сторону и основание). К примеру, можно воспользоваться этой страницей совершенно бесплатно. Если вы хотите совершить вычисления самостоятельно, переходите к следующему пункту.
2
Формулы для высоты равнобедренного треугольника
Согласно вычислениям из указанных во вступлении теорем, формула для высоты такого треугольника равна корню из разности сторон, каждая из которых возведена в квадрат и поделена на 4. Визуально это выглядит так (где h – искомая высота, а – длина основания треугольника, b – длина его стороны):
Если у вас все еще остались вопросы, послушайте подробное и понятное видео, на котором учитель объясняет, как найти высоту треугольника с равными сторонами.