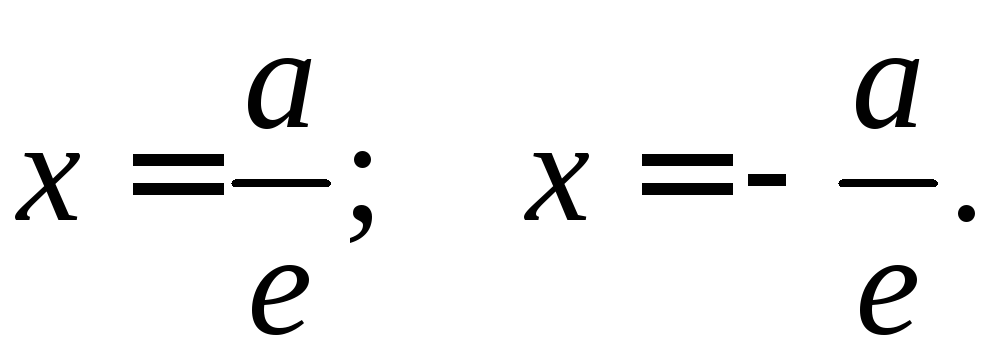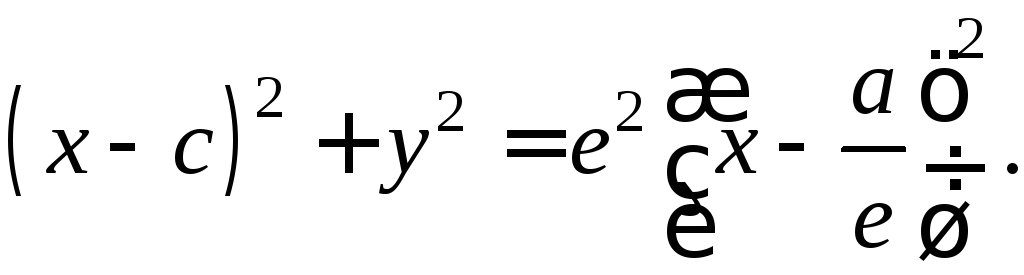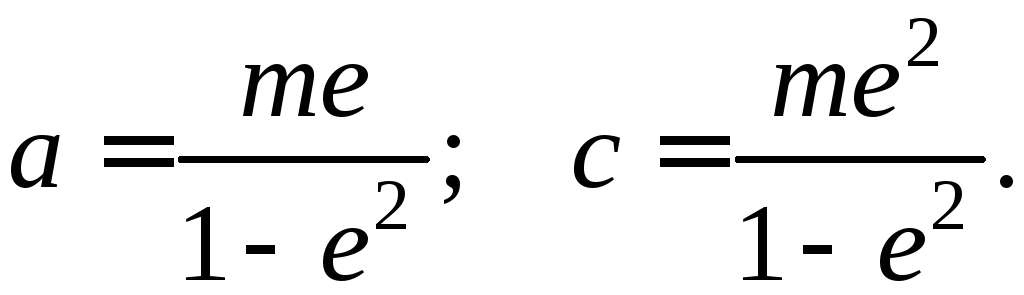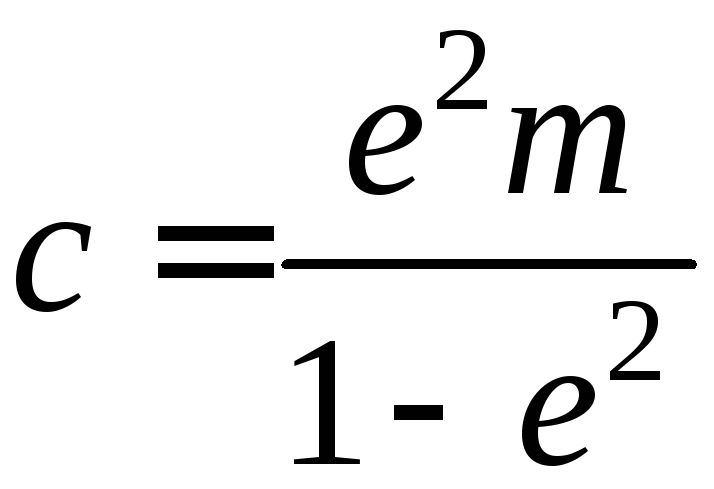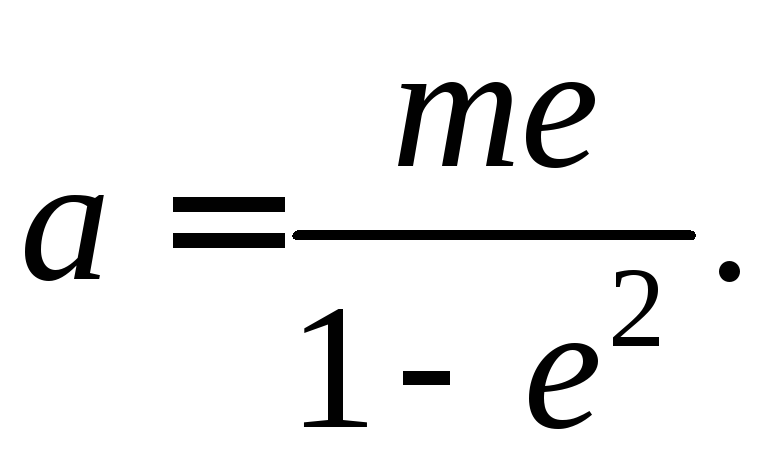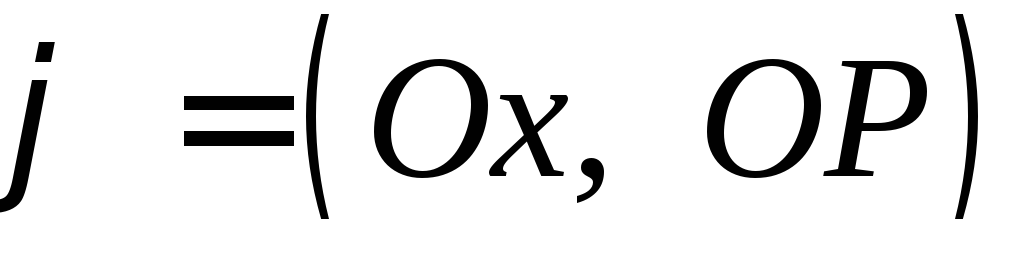Уравнении эллипса как составить уравнение директрисы - Autoru.top

Определение эллипса.

Начать изучение
Фокусы, эксценриситет и директрисы эллипса.

Начать изучение
Уравнение касательной к эллипсу.

Начать изучение

Определение эллипса.

Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1label{ref1}
$$
при условии (a geq b > 0).

Из уравнения eqref{ref1} следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).

Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.

Рис. 8.1. Эллипс

В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_{1}), (M_{2}) и (M_{3}) (рис. 8.1). Следовательно, справедливо следующее утверждение.

Утверждение 1.

Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.

Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^{2}+y^{2}=a^{2}). При каждом (x) таком, что (|x| < a), найдутся две точки эллипса с ординатами (pm b sqrt{1-x^{2}/a^{2}}) и две точки окружности с ординатами (pm a sqrt{1-x^{2}/a^{2}}). Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно (b/a). Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении (b/a) (рис. 8.2).

Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Определение.

Пусть по определению
$$
c^{2}=a^{2}-b^{2}label{ref2}
$$
и (c geq 0).

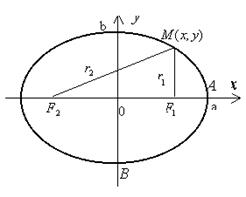
Фокусами называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Определение.

Отношение
$$
varepsilon=frac{c}{a}label{ref3}
$$
называется эксцентриситетом эллипса.

Отметим, что (varepsilon < 1).

Утверждение 2.

Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=a-varepsilon x, r_{2}=|F_{2}M|=a+varepsilon x.label{ref4}
$$

Доказательство.

Очевидно, что (r_{1}^{2}=(x-c)^{2}+y^{2}). Подставим сюда выражение для (y^{2}), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-frac{b^{2}x^{2}}{a^{2}}.nonumber
$$

Учитывая равенство eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+frac{c^{2}x^{2}}{a^{2}}=(a-varepsilon x)^{2}.nonumber
$$
Так как (x leq a) и (varepsilon < 1), отсюда следует, что справедливо первое из равенств eqref{ref4}: (r_{1}=a-varepsilon x). Второе равенство доказывается аналогично.

Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).

Доказательство.

Необходимость. Если мы сложим равенства eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.label{ref5}
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref{ref5}, то есть
$$
sqrt{(x-c)^{2}+y^{2}}=2a-sqrt{(x+c)^{2}+y^{2}}.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=asqrt{(x+c)^{2}+y^{2}}.label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref{ref2}. Мы придем к (b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}), равносильному уравнению эллипса eqref{ref1}.

С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=frac{a}{varepsilon},\ x=-frac{a}{varepsilon}.label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.

Рис. 8.4. Фокусы и директрисы эллипса.

Утверждение 4.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).

Доказательство.

Докажем это предложение для фокуса (F_{2}(-c, 0)). Пусть (M(x, y)) — произвольная точка эллипса. Расстояние от (M) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+frac{a}{varepsilon}|=frac{1}{varepsilon}(varepsilon x+a).nonumber
$$
Из формулы eqref{ref4} мы видим теперь, что (r_{2}/d_{2}=varepsilon).

Обратно, пусть для какой-то точки плоскости (r_{2}/d_{2}=varepsilon), то есть
$$
sqrt{(x+c)^{2}+y^{2}}=varepsilon left(x+frac{a}{varepsilon}right).nonumber
$$
Так как (varepsilon=c/a), это равенство легко приводится к виду eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_{0}(x_{0}, y_{0})) — точка на эллипсе и (y_{0} neq 0). Через (M_{0}) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_{0} > 0) это график (f_{1}(x)=bsqrt{1-x^{2}/a^{2}}), для (y_{0} < 0) — график (f_{2}(x)=-bsqrt{1-x^{2}/a^{2}}). Не уточняя знака (y_{0}), обозначим подходящую функцию (f(x)).) Для нее выполнено тождество
$$
frac{x^{2}}{a^{2}}+frac{(f(x))^{2}}{b^{2}}=1.nonumber
$$
Дифференцируем его по (x):
$$
frac{2x}{a^{2}}+frac{2ff’}{b^{2}}=0.nonumber
$$
Подставляя (x=x_{0}) и (f(x_{0}=y_{0})), находим производную от (f) в точке (x_{0}), равную угловому коэффициенту касательной:
$$
f'(x_{0})=frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}.nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}(x-x_{0}).nonumber
$$
Упрощая это уравнение, учтем, что (b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}), так как (M_{0}) лежит на эллипсе. Результату можно придать вид
$$
frac{xx_{0}}{a^{2}}+frac{yy_{0}}{b^{2}}=1.label{ref8}
$$

При выводе уравнения eqref{ref8} мы исключили вершины эллипса ((a, 0)) и ((-a, 0)), положив (y_{0} neq 0). Для этих точек оно превращается, соответственно, в уравнения (x=a) и (x=-a). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение eqref{ref8} определяет касательную для любой точки (M_{0}(x_{0}, y_{0})) на эллипсе.

Утверждение 5.

Касательная к эллипсу в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Доказательство.

Нам надо сравнить углы (varphi_{1}) и (varphi_{2}), составленные векторами (overrightarrow{F_{1}M_{0}}) и (overrightarrow{F_{2}M_{0}}) с вектором (boldsymbol{n}), перпендикулярным касательной (рис. 8.5). Из уравнения eqref{ref8} находим, что (boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})), и потому
$$
(overrightarrow{F_{1}M_{0}}, boldsymbol{n})=frac{x_{0}}{a^{2}}(x_{0}-c)+frac{y_{0}}{b^{2}}y_{0}=1-frac{x_{0}c}{a^{2}}=frac{a-varepsilon x_{0}}{a}.nonumber
$$
Используя eqref{ref4}, мы получаем отсюда, что (cos varphi_{1}=1/(a|boldsymbol{n}|)). Аналогично находим (cos varphi_{2}=1/(a|boldsymbol{n}|)). Утверждение доказано.

Рис. 8.5.

Источник

Две
прямые, перпендикулярные оси эллипса,
на которой расположены его фокусы, и
отстоящие от центра эллипса на расстоянии

,
где
а
— большая
полуось эллипса, а
е
— его
эксцентриситет, называются директрисами
эллипса.

Окружность,
для которой е
= 0 не имеет директрис

т.е. понятие директрис дается только
для эллипса.

Если
эллипс задан каноническим уравнением,
причем

(т.е. фокусы расположены на оси Ох)
то уравнения директрис имеют вид:

Так как

;
то
,
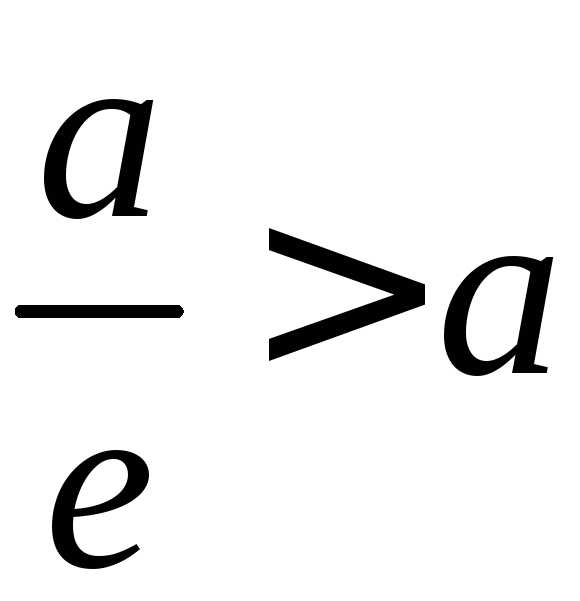
и, значит, директрисы эллипса отстоят
от его центра дальше, чем вершины (см.
рис.). Фокус и директриса эллипса,
расположенные по одну сторону от меньшей
оси эллипса, называются соответствующими
друг другу.

Таким
образом, фокусы
соответствует
директриса
,
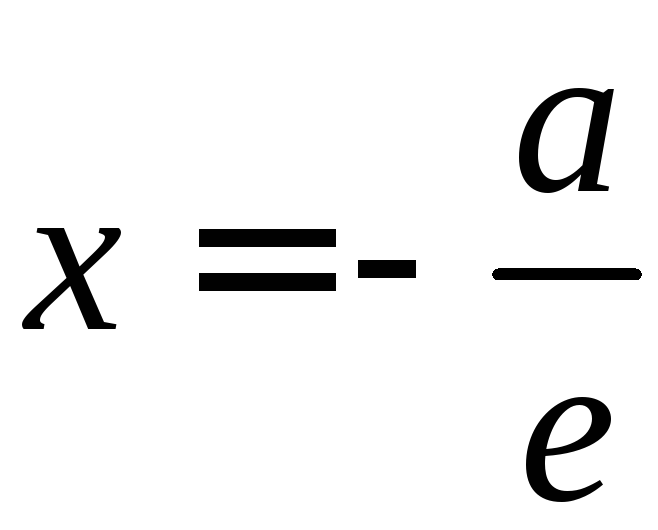
а фокусу
— директриса.

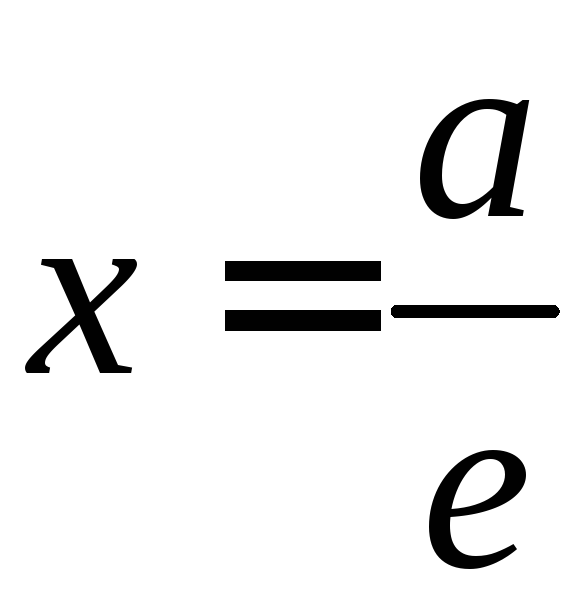
Теорема.
Для того чтобы точка лежала на эллипсе,
необходимо и достаточно, чтобы отношение
расстояния от этой точки до фокуса
эллипса к расстоянию от той же точки до
директрисы, соответствующей рассматриваемому
фокусу, было равно эксцентриситету
эллипса.

Доказательство:
Необходимость. Рассмотрим, например,
фокус
и соответствующую ему директрису.
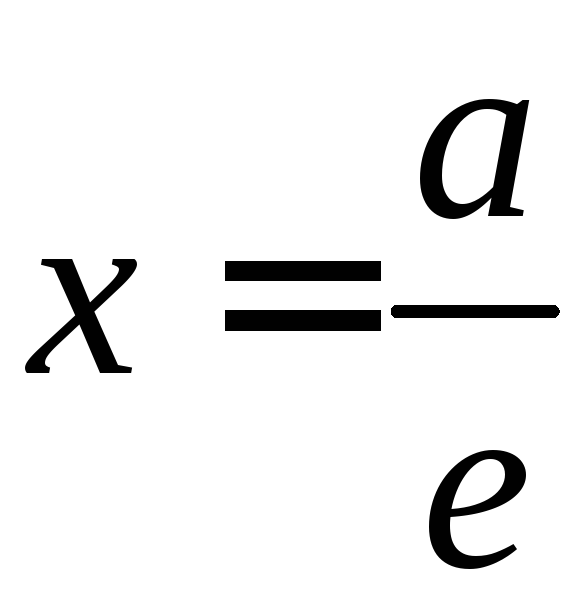
Расстояниеот точкиМ(х,
у)
до

ф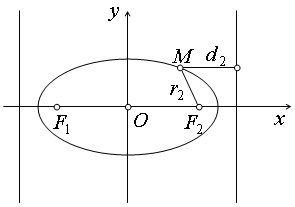окусавычисляется по формуле.

Расстояние
от той же точкиМ(х,
у)
эллипса до прямой
вычисляется по формуле.

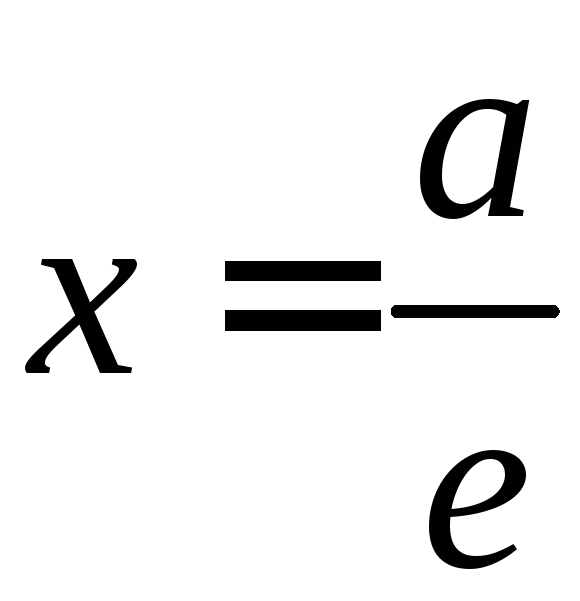
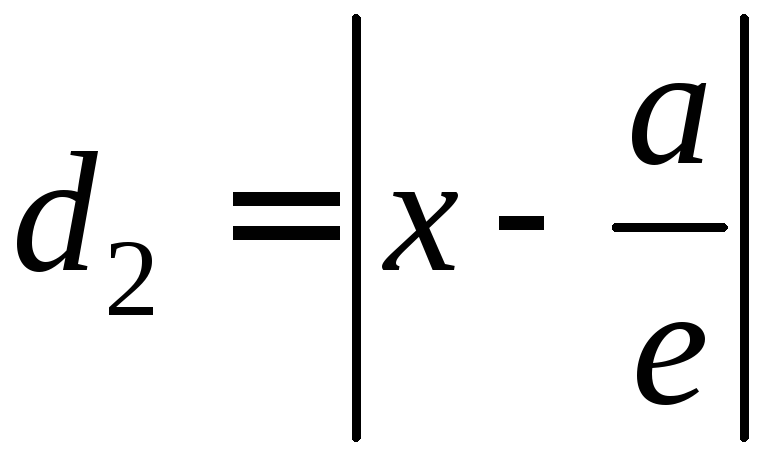
Итак:
.

Отсюда

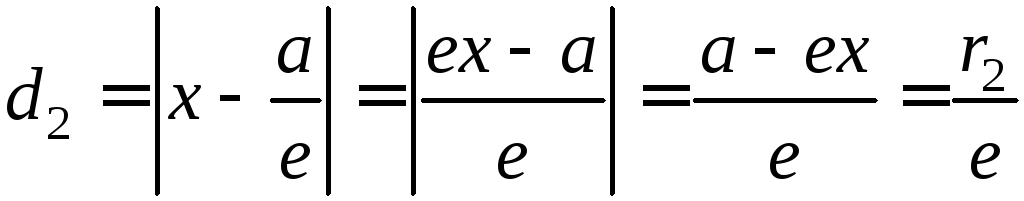
Теорема доказана.

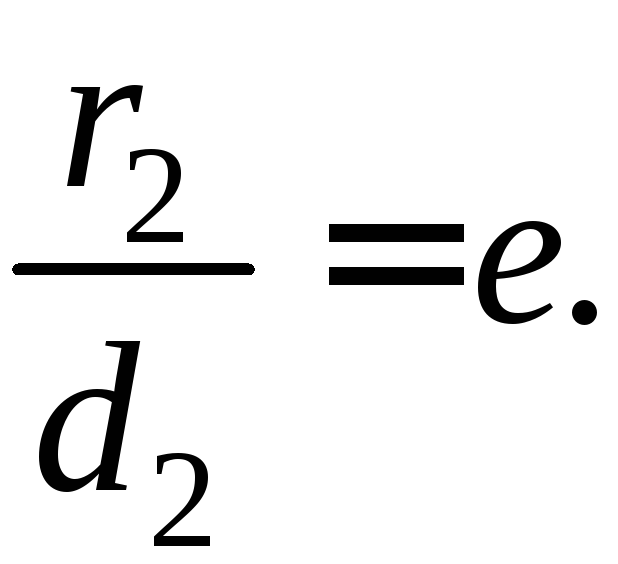
Аналогично
доказывается, что
,
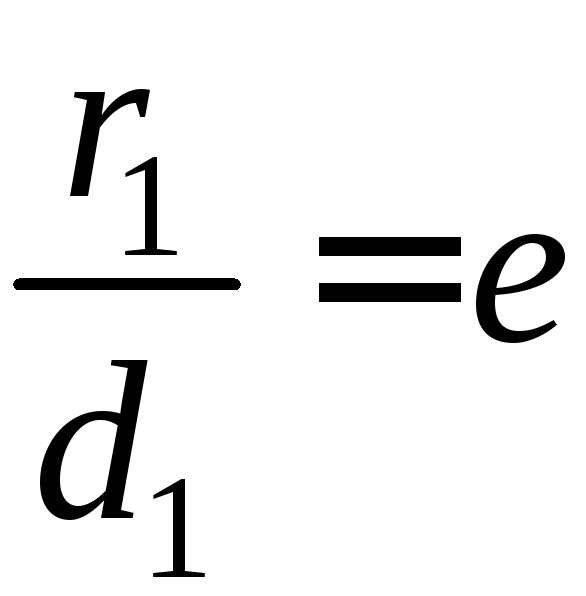
где,
есть расстояние от точкиМ
до фокуса
,
а— расстояние от той же точки до директрисы,
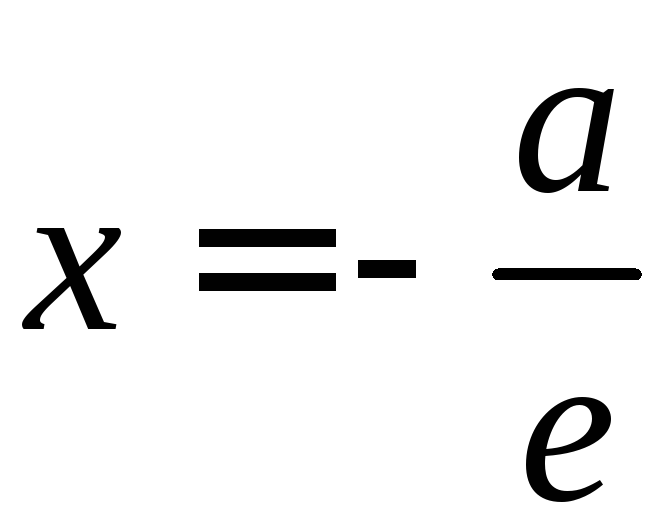
соответствующей фокусу.

Доказательство
достаточности.

Возьмем
каноническое уравнение эллипса, где a
>
b.
Рассмотрим, например, фокус
этого эллипса и соответствующую ему
директрису.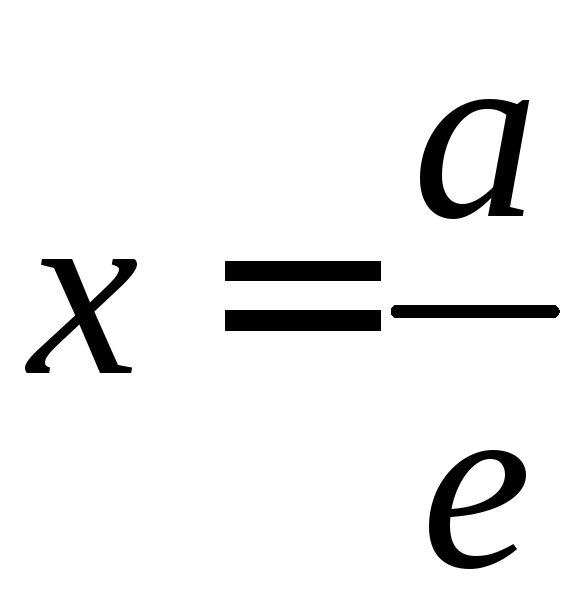

Пусть
М(х,
у)
такая точка, что

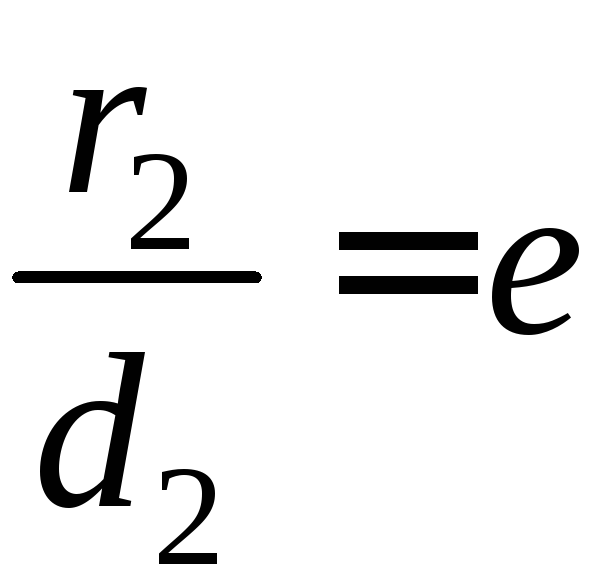
где
— расстояние от точкиМ
до фокуса
,
а— расстояние от точкиМ
до директрисы
.

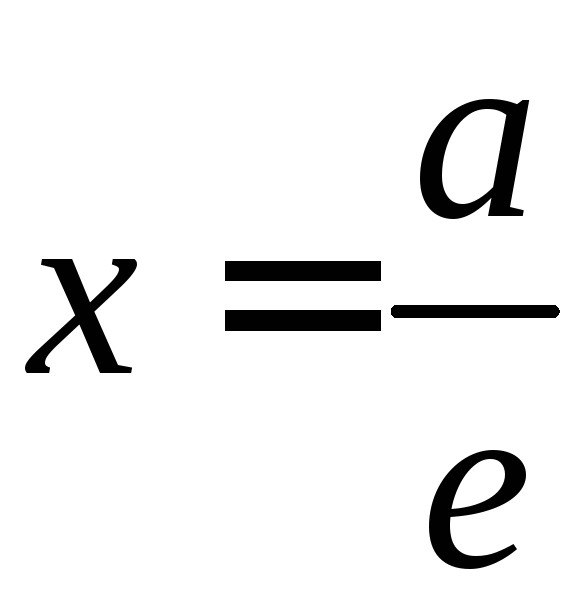
Докажем,
что точка М(х,у)
лежит на эллипсе.

В самом деле, т.к.

;

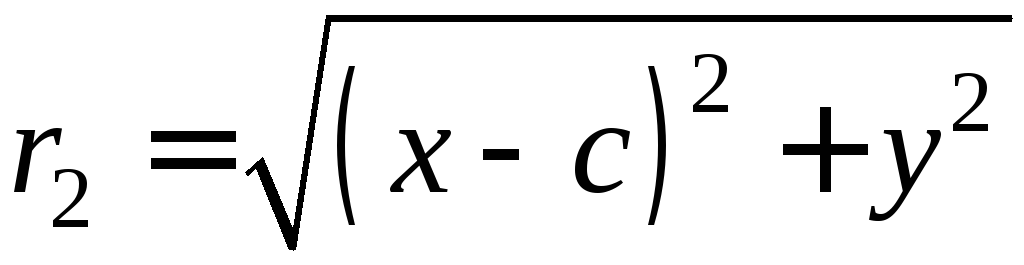
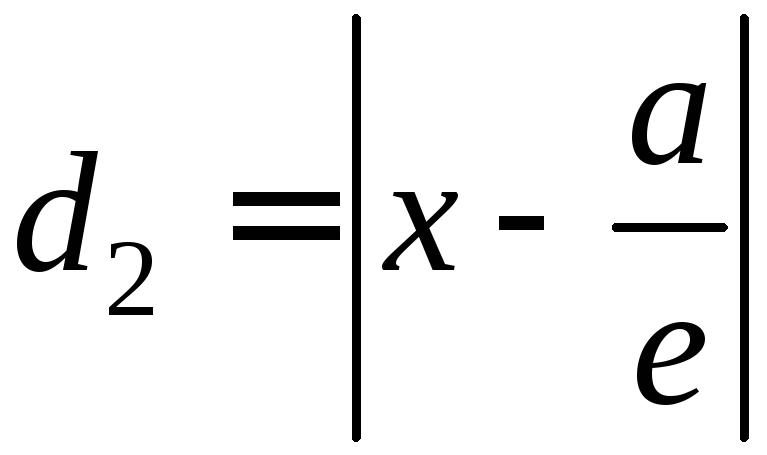
то из соотношения

или
,

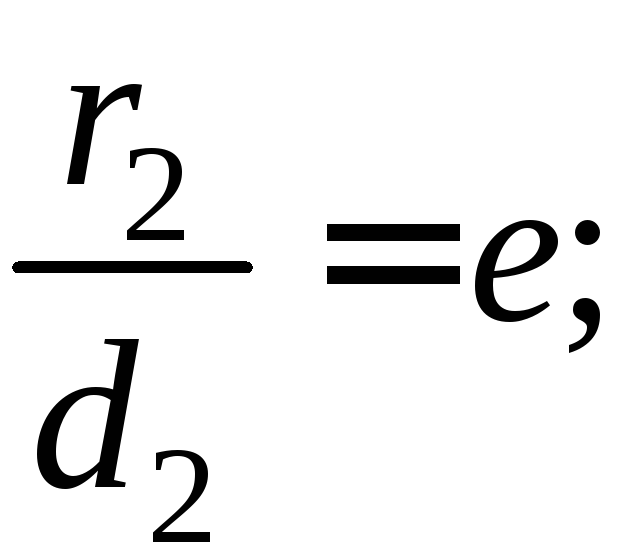
находим:

Упрощая
это уравнение, получим
.
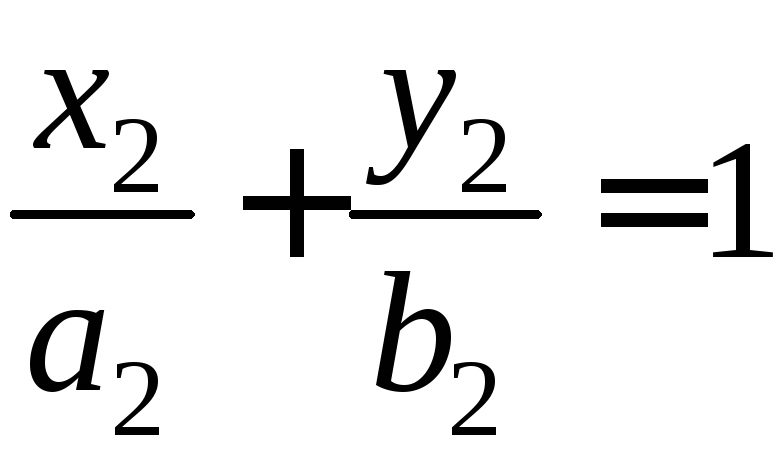
А это означает, что точкаМ(х,
у)
ежит на эллипсе.

Расстояние
m
от фокуса эллипса до его директрисы
равно

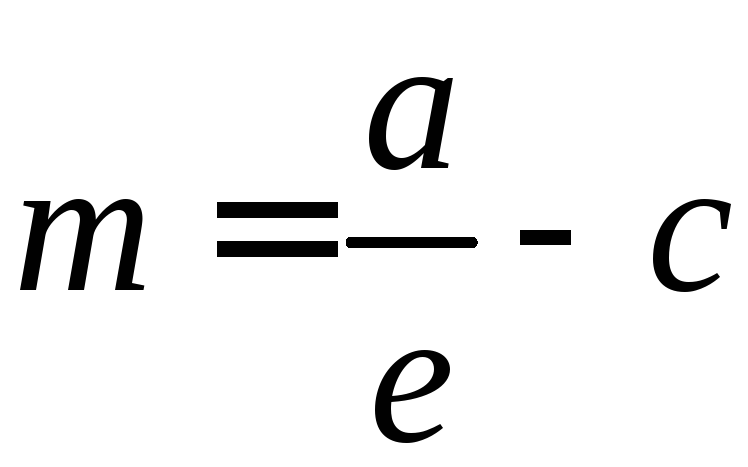
а эксцентриситет
определяется формулой:

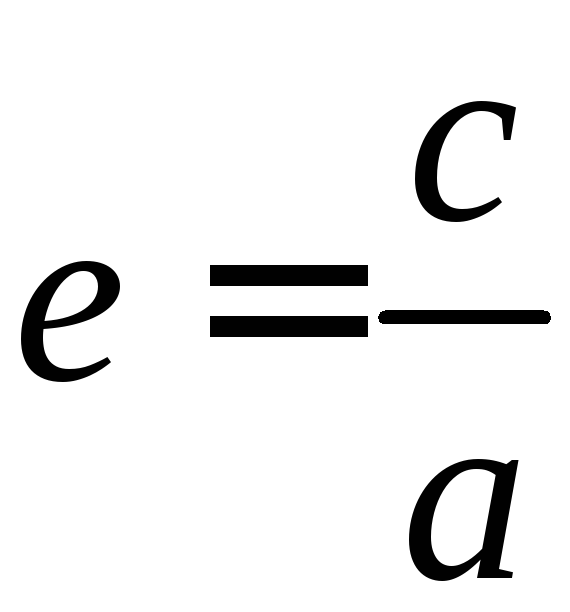
Из
этих соотношений находим

Отсюда
следует, что если на плоскости задана
произвольно точка
,
прямая, не проходящая через эту точку(отстоящая от точкина расстоянии
)
и задано произвольное положительное
число е,
меньшее 1, то существует эллипс, для
которого точка
— фокус, заданная прямая – директриса,
ае
—
эксцентриситет. Центр этого эллипса
находится на расстоянии

от точки
(по одну сторону с точкойот данной прямой), а большая полуось

Отсюда
и из только что доказанной теоремы
следует, что эллипс можно определить
как геометрическое место точек, для
каждой из которых отношение расстояния
от данной точки
к расстоянию до данной прямой,
не проходящей через точку,
равно данному положительному числу,
меньшему 1.

Исключением
является окружность, которая данным
свойством не обладает.

§ 106. Параметрические уравнения эллипса

Пусть
дан эллипс каноническим уравнением
.
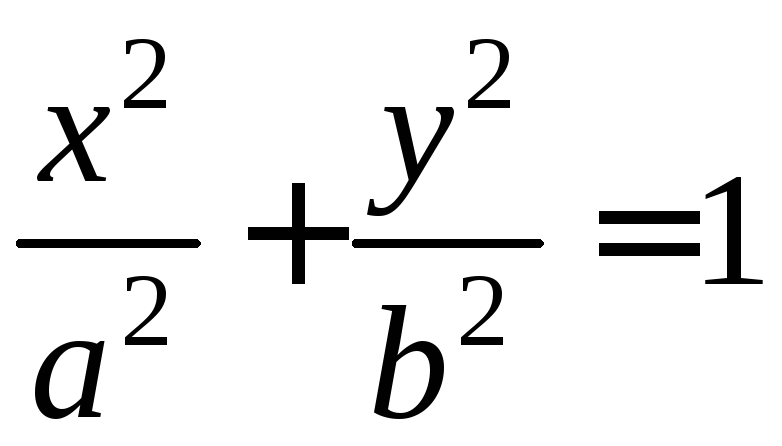
(1)

Рассмотрим
окружность

,
(2)

которая
переходит в данный эллипс в результате
сжатия

(3)

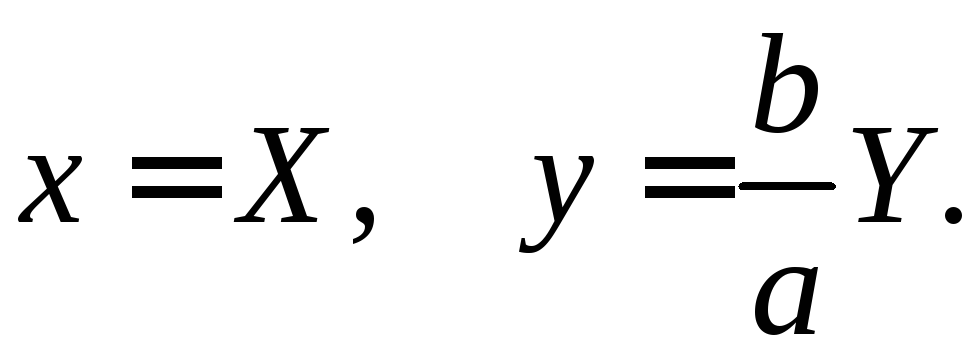
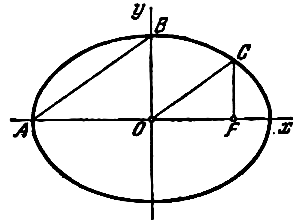
Пусть
М(х,
у)
– произвольная точка данного эллипса,
— ее образ на окружности. Обозначим черезугол от положительного направления осиОх
до луча ОР.

Тогда

и, следовательно,

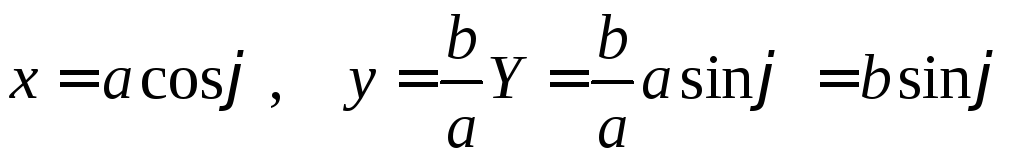
У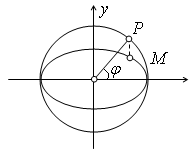равнения

И являются
параметрическими уравнениями эллипса.

Параметр
называется эксцентрическим углом точки
эллипса. Если задана точкаэллипса,
то для нахождениянадо построить
окружность на большей оси эллипса как
на диаметре и через точку М
провести прямую, параллельную малой
оси эллипса.

Точка
пересечения этой прямой с окружностью,
лежащая по ту же сторону от большей оси
эллипса, что и точкаМ,
является прообразом точки М(х,у)
при равномерном сжатии
Угол от осиОх
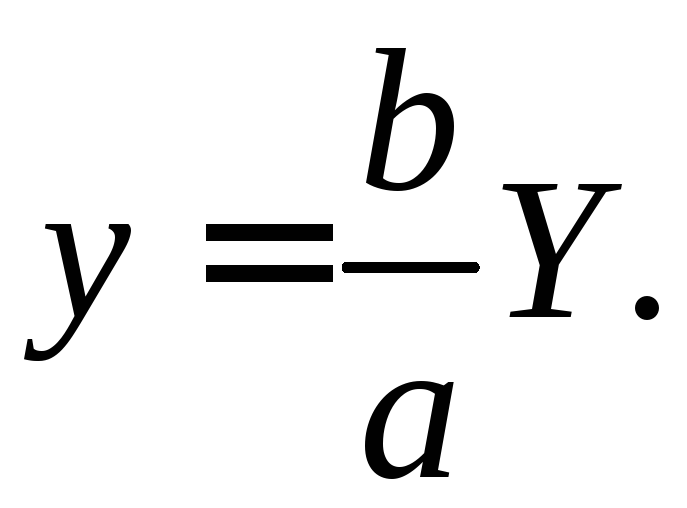
до луча ОР
и являются эксцентрическим углом
,
соответствующим взятой точкиМ
на эллипсе (см. рис.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

444 Составить уравнение эллипса,
фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что: 444.1 его полуоси ранвы 5
и 2; 444.2 его большая ось
равна 10, а расстояние между фокусами 2c=8; 444.3 его малая ось равна
24, а расстояние между фокусами 2c=10; 444.4 расстояние между
его фокусами 2c=6 и эксцентриситет e=3/5. 444.5 его большая ось
равна 20, а эксцентриситет e=3/5. 444.6 его малая ось равна
10, а эксцентриситет e=12/13; 444.7 расстояние между
его директрисами равно 5 и расстояние между
фокусами 2c=4; 444.8 его большая ось
равна 8, а расстояние между директрисами равно 16; 444.9 его малая ось равна
6, а расстояние между директрисами равно 13; 444.10 расстояние между
его директрисами равно 32 и e=1/2. 445 Составить
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что: 445.1 его полуоси равны
соответственно 7 и 2; 445.2 его большая ось
равна 10, а расстояние между фокусами 2c=8; 445.3 расстояние между
его фокусами 2c=24 и эксцентриситет e=12/13. 445.4 его малая ось равна
16, а эксцентриситет e=3/5. 445.5 расстояние между
его фокусами 2c=6 и расстояние между директрисами
равно 50/3; 445.6 расстояние между
его директрисами равно 32/3 и эксцентриситет e=3/4. 446 Определить полуоси
каждого из следующих эллипсов: 446.1

; 446.2

; 446.3

; 446.4

; 446.5

; 446.6

; 446.7

; 446.8

; 446.9

; 446.10

. 447 Дан эллипс

. Найти его полуоси, фокусы,
эксцентриситет, уравнения директрис. 448 Вычислить площадь
четырехугольника, две вершины которого лежат в
фокусах эллипса

, а две другие
совпадают с концами его малой оси. 449 Дан эллипс

. Найти его полуоси, фокусы,
эксцентриситет, уравнения директрис. 450 Вычислить площадь
четырехугольника, две вершины которого лежат в
фокусах эллипса

, две другие лежат с
концами его малой оси. 451 Вычислить
расстояние от фокуса F(c; 0) эллипса

до
односторонней с этим фокусом директрисы. 452 Пользуясь одним
циркулем, построить фокусы эллипса

(считая,
что изображены оси координат и задана масштабная
единица). 453 На эллипсе

найти точку, абсцисса которых равна
–3. 454 Определить, какие
из точек A₁(-2; 3), A₂(2; -2), A₃(2;
-4), A₄(-1; 3), A₅(-4; -3), A₆(3; -1), A₇(3;
-2), A₈(2; 1), A₉(0; 15), A₁₀(0; -16) лежат на эллипсе

, какие
внутри и какие вне его. 455 Установить, какие
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже. 455.1

; 455.2

; 455.3

; 455.4

. 456 Эксцентриситет
эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы. 457 Эксцентриситет
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой. 458 Дана точка М₁(2; -5/3) на эллипсе

; составить
уравнения прямых, на которых лежат фокальные
радиусы точки М₁.
459 Убедившись, что
точка M₁(-4; 2,4) лежит
на эллипсе

, определить фокальные радиусы точки
М₁. 460 Эксцентриситет
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М₁ эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом. 461 Эксцентриситет
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M₁
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой. 462 Определить точки
эллипса

, расстояние которых до
правого фокуса равно 14. 463 Определить точки
эллипса

, расстояние которых до
левого фокуса равно 2,5. 464 Через фокус эллипса

проведен перпендикуляр к его
большой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов. 465 Составить
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны: 465.1 точка М₁(

; 2) эллипса
и его малая полуось b=3; 465.2 точка М₁(2;
-2) эллипса и его большая полуось
a=4; 465.3 точки М₁(4;

) и
М₂(

; 3) эллипса; 465.4 точка М₁(

; -1) эллипса
и его эксцентриситет e=2/3; 465.5 точка М₁(2;
-5/3) эллипса и его эксцентриситет
e=2/3; 465.6 точка М₁(8;
12) эллипса и расстояние r₁=20
от нее до левого фокуса. 465.7 точка М₁(

; 2) эллипса
и расстояние между его директрисами, равное 10. 466 Определить
эксцентриситет e эллипса, если: 466.1 его малая ось видна
из фокусов под углом 60⁰; 466.2 отрезок между
фокусами виден и вершин малой оси под прямым
углом; 466.3 расстояние между
директрисами в три раза больше расстояния между
фокусами; 466.4 отрезок
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
пополам. 467 Через фокус F
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки

будут
параллельны.

468 Составить
уравнение эллипса с полуосями a, b и центром C(x₀, y₀), если
известно, что оси симметрии эллипса параллельны
осям координат. 469 Эллипс касается оси
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям. 470 Точка С(-3; 2)
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям. 471 Установить, что
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис: 471.1

; 471.2

; 471.3

. 472 Установить, какие
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже. 472.1

; 472.2

; 472.3

; 472.4

. 473 Составить
уравнение эллипса, зная, что: 473.1 его большая ось
равна 26 и фокусы суть F₁(-10; 0), F₂(14;0);
473.2 его малая ось равна
2 и фокусы суть F₁(-1; -1), F₂(1;
1);
473.3 его фокусы суть F₁(-2; 3/3), F₂(2; -3/2) и
эксцентриситет e=

.
473.4 его фокусы суть F₁(1; 3), F₂(3; 1) и
расстояние между директрисами равно

.
474 Составить уравнение эллипса, если известны его
эксцентриситет

,
фокус F (-4; 1) и уравнение соответствующей
директрисы

475 Составить
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы

. 476 Точка А(-3; -5) лежит
на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением

. Составить уравнение этого эллипса. 477 Составить
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы

. 478 Точка M₁(2;
-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением

. Составить уравнение этого эллипса. 479 Точка M₁(3;
-1) является концом малой оси
эллипса, фокусы которого лежат на прямой

. Составить
уравнение этого эллипса, зная его эксцентриситет
e=

. 480 Найти точки
пересечения прямой

и эллипса

. 481 Найти точки
пересечения прямой

и эллипса

. 482 Найти точки
пересечения прямой

и эллипса

. 483 Определить, как
расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями: 483.1

; 483.2

; 483.3

. 484 Определить, при
каких начениях m прямая

: 484.1 пересекает эллипс

; 484.2 касается его; 484.3 проходит вне этого
эллипса. 485 Вывести условие,
при котором прямая

касается эллипса

. 486 Составить
уравнение касательной к эллипсу

в его
точке M₁(x₁; y₁). 487 Доказать, что
касательные к эллипсу

, проведенные
в концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр). 488 Составить
уравнения касательных к эллипсу

, параллельных
прямой

. 489 Составить
уравнения касательных к эллипсу

, перпендикулярных
к прямой

. 490 Провести касательные к эллипсу

параллельно
прямой

и вычислить расстояние d между ними. 491 На эллипсе

найти точку М₁,
ближайшую к прямой

, и вычислить расстояние d от точки М₁до
этой прямой. 492 Из точки А(10/3; 5/3)
проведены касательные к эллипсу

. Составить
их уравнения. 493 Из точки С(10; -8)
проведены касательные к эллипсу

. Составить
уравнение хорды, соединяющей точки касания. 494 Из точки Р(-16; 9)
проведены касательные к эллипсу

. Вычислить
расстояние d от точки Р до хорды эллипса,
соединяющей точки касания. 495 Эллипс проходит
через точку А(4; -1) и касается прямой

. Составить
уравнение этого эллипса при условии, что его оси
совпадают с осями координат. 496 Составить
уравнение эллипса, касающегося двух прямых

, при
условии, что его ося совпадают с осями координат. 497 Доказать, чо
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса. 498 Доказать, что
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси. 499 Прямая

касается
эллипса, фокусы которого находятся в точках F₁(-3;
0), F₂(3; 0). Составить
уравнение этого эллипса. 500 Составить
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу

и его малая полуось b=2. 501 Доказать, что
прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F₁M, F₂M и проходит
вне угла F₁MF₂. 502 Из левого фокуса
эллипса

под тупым углом

к оси
Ox направлен луч света. Известно, что

. Дойдя
до эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч. 503 Определить точки
пересечения эллипсов

. 504 Убедившись, что
эллипсы

(

) пересекаются
в четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности. 505 Плоскости

образуют угол

=30⁰. Опредлить
полуоси эллипса, полученного проектированием на
плоскость

окружности радиуса R=10,лежащей на
плоскости

. 506 Эллипс, малая
полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол

между плоскостями, в которых лежат
эллипс и окружность. 507 Направляющей
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом

=30⁰. 508 Направляющей
круглого цилиндра является окружность радиуса R=

. Определить, под каким углом к оси
цилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2. 509 Равномерным
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
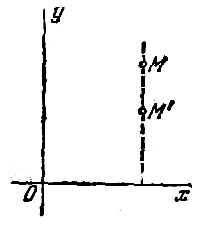
точек плоскости, при котором произвольная точка
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность

, если коэффициент
равномерного сжатия плоскости к оси абсцисс q=4/5.

510 Коэффициент
равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс

. 511 Найти уравнение
линии, в которую преобразуется эллипс

при двух последовательных
равномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7. 512 Определить
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс

преобразуется
в эллипс

. 513 Определить
коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс

преобразуется
в эллипс

. 514 Определить
коэффициенты q₁, q₂ двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс

преобразуется в окружность

Источник

Эллипс: определение, свойства, построение

Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек F_1 , и F_2 есть величина постоянная (2a) , бо́льшая расстояния (2c) между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса.

Фокальное свойство эллипса

Точки F_1 , и F_2 называются фокусами эллипса, расстояние между ними 2c=F_1F_2 — фокусным расстоянием, середина отрезка F_1F_2 — центром эллипса, число — длиной большой оси эллипса (соответственно, число — большой полуосью эллипса). Отрезки F_1M и F_2M , соединяющие произвольную точку эллипса с его фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.

Отношение $e=frac{c}{a}$ называется эксцентриситетом эллипса. Из определения (2a>2c) следует, что 0leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр совпадают, и эллипс является окружностью радиуса (рис.3.36,6).

Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:

$frac{x^2}{a^2}+frac{y^2}{b^2}=1.$

(3.49)

Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Эллипс и его фокальные свойства, эксцентриситет эллипса

Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0),~F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей эллипсу, имеем:

$vline,overrightarrow{F_1M},vline,+vline,overrightarrow{F_2M},vline,=2a.$

Записывая это равенство в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}+sqrt{(x-c)^2+y^2}=2a.$

Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:

$(x+c)^2+y^2=4a^2-4asqrt{(x-c)^2+y^2}+(x-c)^2+y^2~Leftrightarrow ~4asqrt{(x-c)^2+y^2}=4a^2-4cx.$

Разделив на 4, возводим обе части уравнения в квадрат:

a^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^2=a^2(a^2-c^2).

Обозначив $b=sqrt{a^2-c^2}>0$ , получаем b^2x^2+a^2y^2=a^2b^2 . Разделив обе части на a^2b^2ne0 , приходим к каноническому уравнению эллипса:

$frac{x^2}{a^2}+frac{y^2}{b^2}=1.$

Следовательно, выбранная система координат является канонической.

Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку a=b . В этом случае канонической будет любая прямоугольная система координат с началом в точке Oequiv F_1equiv F_2 , a уравнение x^2+y^2=a^2 является уравнением окружности с центром в точке и радиусом, равным .

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.

Директориальное свойство эллипса

Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $frac{a^2}{c}$ от нее. При c=0 , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).

Эллипс с эксцентриситетом 0<e<1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство эллипса). Здесь и — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. F_1,d_1 или F_2,d_2 .

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.37,6) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=ecdot!left(frac{a^2}{c}-xright)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~a^2-c^2=b^2$ , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы $d_1colonfrac{r_1}{rho_1}=e$ .

Эллипс и его директориальное свойство, эксцентриситет эллипса

Уравнение эллипса в полярной системе координат

Построение кривой эллипса по точкам в полярной системе координат

Уравнение эллипса в полярной системе координат F_1rvarphi (рис.3.37,в и 3.37(2)) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$

где $p=frac{b^2}{a}$ фокальный параметр эллипса.

В самом деле, выберем в качестве полюса полярной системы координат левый фокус F_1 эллипса, а в качестве полярной оси — луч F_1F_2 (рис.3.37,в). Тогда для произвольной точки M(r,varphi) , согласно геометрическому определению (фокальному свойству) эллипса, имеем r+MF_2=2a . Выражаем расстояние между точками и F_2(2c,0) (см. пункт 2 замечаний 2.8):

$begin{aligned}F_2M&=sqrt{(2c)^2+r^2-2cdot(2c)cdot rcos(varphi-0)}=\[3pt] &=sqrt{r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2}.end{aligned}$

Следовательно, в координатной форме уравнение эллипса F_1M+F_2M=2a имеет вид

$r+sqrt{r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2}=2cdot a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2-4cdot ccdot rcdotcosvarphi+4cdot c^2~Leftrightarrow~acdot!left(1-frac{c}{a}cdotcosvarphiright)!cdot r=a^2-c^2.$

Выражаем полярный радиус и делаем замену $e=frac{c}{a},~b^2=a^2-c^2,~p=frac{b^2}{a}$ :

$r=frac{a^2-c^2}{acdot(1-ecdotcosvarphi)} quad Leftrightarrow quad r=frac{b^2}{acdot(1-ecdotcosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecdotcosvarphi},$

что и требовалось доказать.

Геометрический смысл коэффициентов в уравнении эллипса

Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение y=0 , находим точки пересечения эллипса с осью абсцисс (с фокальной осью): x=pm a . Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна . Этот отрезок, как отмечено выше, называется большой осью эллипса, а число — большой полуосью эллипса. Подставляя x=0 , получаем y=pm b . Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна . Этот отрезок называется малой осью эллипса, а число — малой полуосью эллипса.

Действительно, $b=sqrt{a^2-c^2}leqslantsqrt{a^2}=a$ , причем равенство b=a получается только в случае c=0 , когда эллипс является окружностью. Отношение $k=frac{b}{a}leqslant1$ называется коэффициентом сжатия эллипса.

Замечания 3.9

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).

2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.

Действительно, пусть в прямоугольной системе координат Oxy уравнение окружности имеет вид x^2+y^2=a^2 . При сжатии к оси абсцисс с коэффициентом 0<kleqslant1 координаты произвольной точки M(x,y) , принадлежащей окружности, изменяются по закону

$begin{cases}x'=x,\y'=kcdot y.end{cases}$

Подставляя в уравнение окружности x=x' и $y=frac{1}{k}y'$ , получаем уравнение для координат образа M'(x',y') точки M(x,y) :

$(x')^2+{left(frac{1}{k}cdot y'right)!}^2=a^2 quad Leftrightarrow quad frac{(x')^2}{a^2}+frac{(y')^2}{k^2cdot a^2}=1 quad Leftrightarrow quad frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=1,$

поскольку b=kcdot a . Это каноническое уравнение эллипса.

3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит эллипсу $frac{x^2}{a^2}+frac{y^2}{b^2}=1$ . то и точки M'(x,-y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат тому же эллипсу.

4. Из уравнения эллипса в полярной системе координат $r=frac{p}{1-ecosvarphi}$ (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

Эксцентриситет, коэффициент сжатия и фокусы эллипса

5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше , тем эллипс более вытянут, а чем ближе к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что $e=frac{c}{a}$ и c^2=a^2-b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2-b^2}{a^2}=1-{left(frac{a}{b}right)!}^2=1-k^2,$

где — коэффициент сжатия эллипса, 0<kleqslant1 . Следовательно, $e=sqrt{1-k^2}$ . Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия и больше эксцентриситет. Для окружности k=1 и e=0 .

6. Уравнение $frac{x^2}{a^2}+frac{y^2}{b^2}=1$ при a<b определяет эллипс, фокусы которого расположены на оси (рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1,~ageqslant b$ определяет эллипс с центром в точке O'(x_0,y_0) , оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).

При a=b=R уравнение (x-x_0)^2+(y-y_0)^2=R^2 описывает окружность радиуса с центром в точке O'(x_0,y_0) .

Параметрическое уравнение эллипса

Параметрическое уравнение эллипса в канонической системе координат имеет вид

$begin{cases}x=acdotcos{t},\ y=bcdotsin{t},end{cases}0leqslant t<2pi.$

Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству cos^2t+sin^2t=1 .

Пример построения эллипса в канонической системе координат

Пример 3.20. Изобразить эллипс $frac{x^2}{2^2}+frac{y^2}{1^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — большая полуось, b=1 — малая полуось эллипса. Строим основной прямоугольник со сторонами 2a=4,~2b=2 с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя x=1 в уравнение эллипса, получаем

$frac{1^2}{2^2}+frac{y^2}{1^2}=1 quad Leftrightarrow quad y^2=frac{3}{4} quad Leftrightarrow quad y=pmfrac{sqrt{3}}{2}.$

Следовательно, точки с координатами $left(1;,frac{sqrt{3}}{2}right)!,~left(1;,-frac{sqrt{3}}{2}right)$ — принадлежат эллипсу.

Вычисляем коэффициент сжатия $k=frac{b}{a}=frac{1}{2}$ ; фокусное расстояние $2c=2sqrt{a^2-b^2}=2sqrt{2^2-1^2}=2sqrt{3}$ ; эксцентриситет $e=frac{c}{a}=frac{sqrt{3}}{2}$ ; фокальный параметр $p=frac{b^2}{a}=frac{1^2}{2}=frac{1}{2}$ . Составляем уравнения директрис: $x=pmfrac{a^2}{c}~Leftrightarrow~x=pmfrac{4}{sqrt{3}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определение

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости и , называемых Фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через . Расстояние между фокусами – .

Если фокусы эллипса совпадают, то он представляет собой окружность.

Расположим эллипс так, чтобы его фокусы лежали на оси абсцисс симметрично относительно оси ординат, то есть (Рис. 2.12.1). Пусть текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:

(2.12.1)

Где – Большая, – Малая полуоси эллипса, . Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (2.12.1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.

Рис. 2.12.1.

Эксцентриситетом эллипса называется число , равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса – (для окружности – ). Отрезки и называются фокальными радиусами точки М и могут быть вычислены по формулам и . Если эллипс определен уравнением (2.12.1) и , то прямые называются Директрисами эллипса (если , то директрисы определяются уравнениями ).

Если центр эллипса перенесен в точку , то его Каноническое уравнение принимает вид

Пример

Дано уравнение эллипса . Вычислить длину осей, координаты фокусов и эксцентриситет эллипса.

Решение

Разделим обе части уравнения на 4225: . Сравнивая полученное уравнение с выражением (3.2.1), заключаем, что , то есть , то есть . Тогда , а .

Пример

Прямые служат директрисами эллипса, малая ось которого равна . Составить уравнение этого эллипса.

Решение

Малая полуось эллипса . Чтобы составить уравнение эллипса нужно знать большую полуось. Имеем: , . Следовательно, . Так как , то . Учитывая, что , получим, что величина удовлетворяет уравнению . Откуда , следовательно . Искомое уравнение принимает вид .