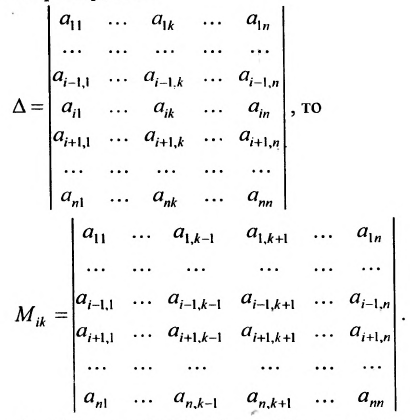
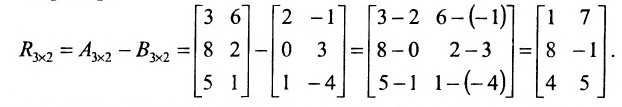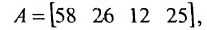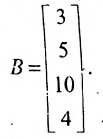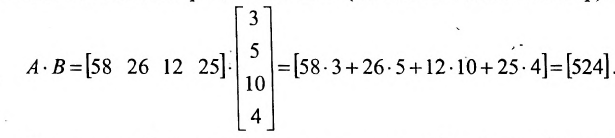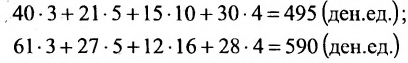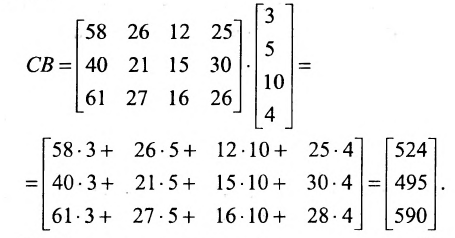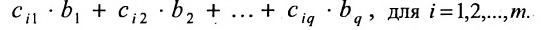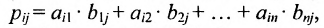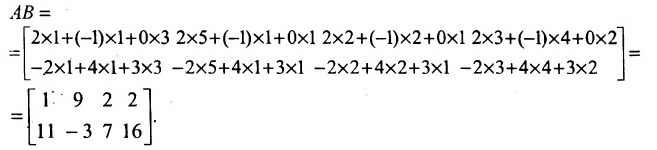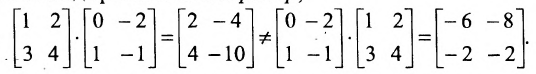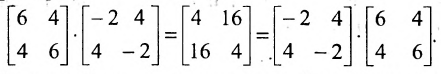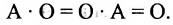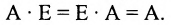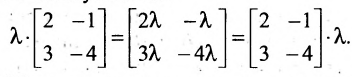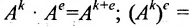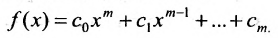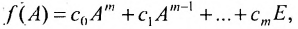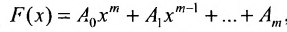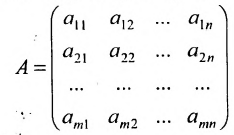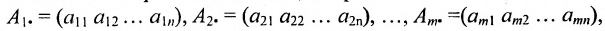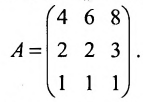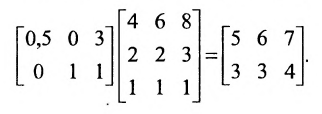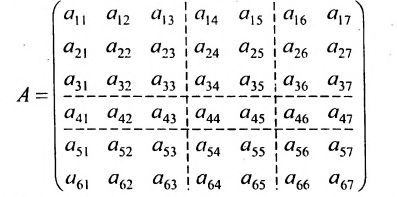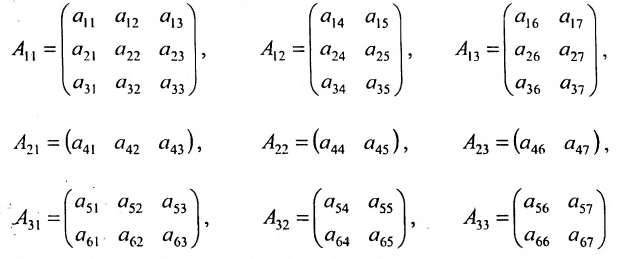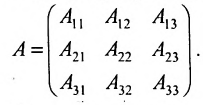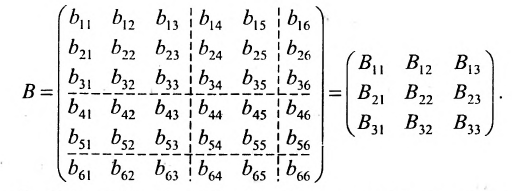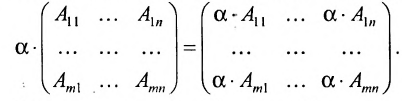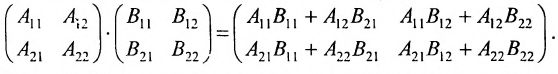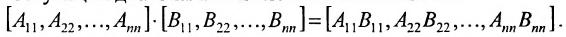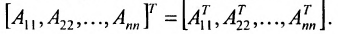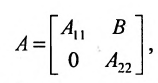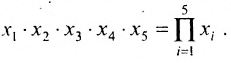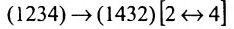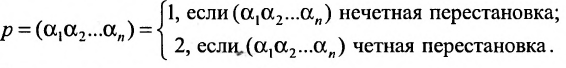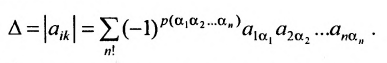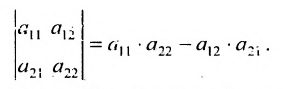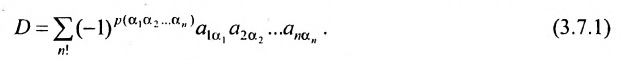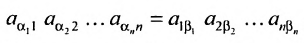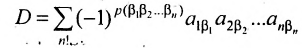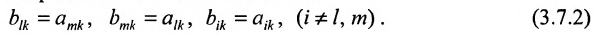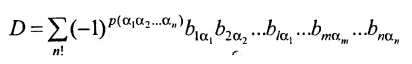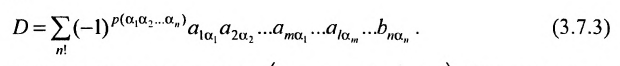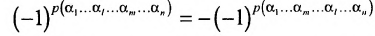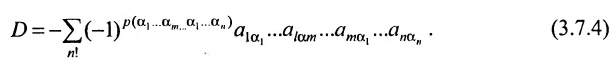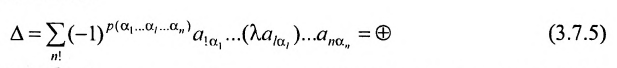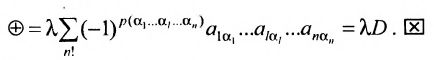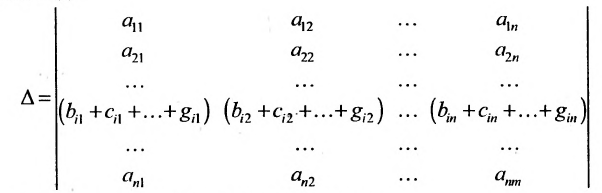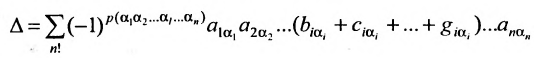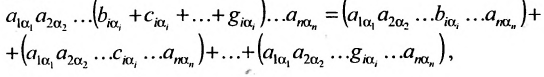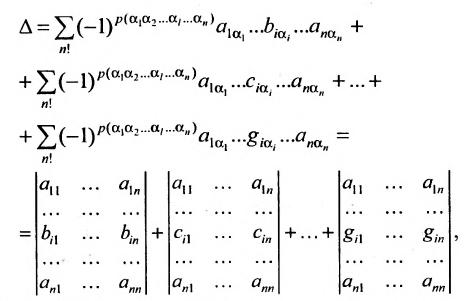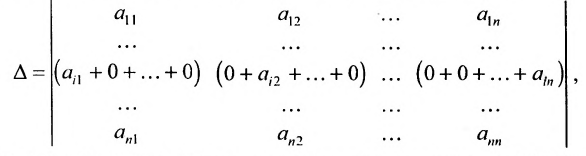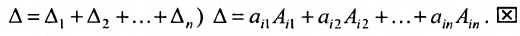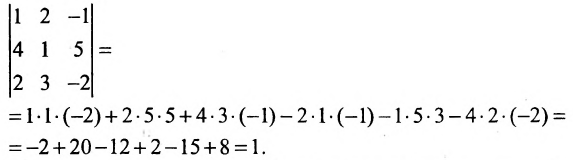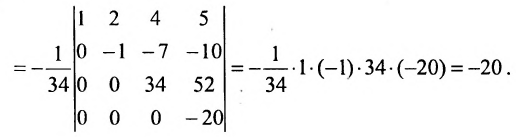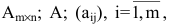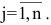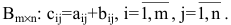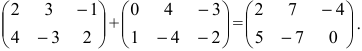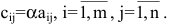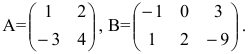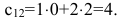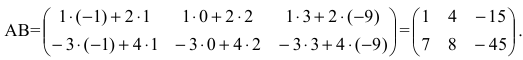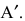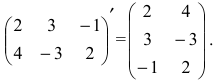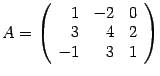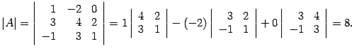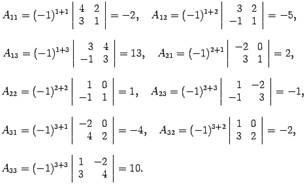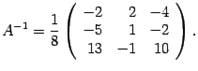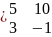Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
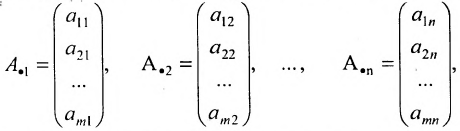
В дальнейшем будем писать матрицу в сокращенном виде
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
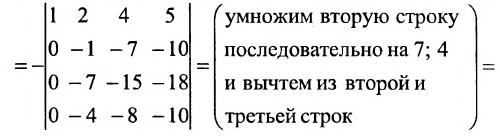
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 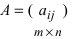
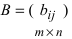
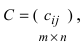
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 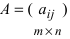
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 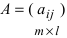
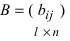
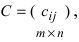
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 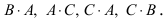
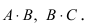
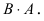
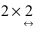
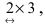
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
Определение: Обратной матрицей к исходной квадратной матрице 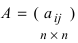
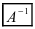
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 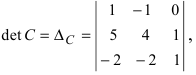
Вычислим алгебраические дополнения всех элементов определителя: 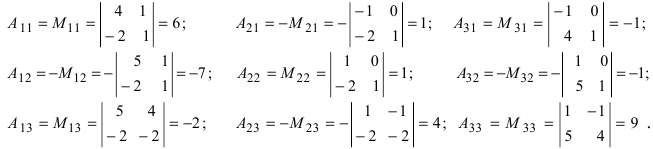
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 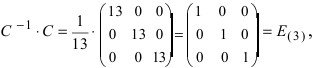
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 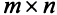
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 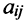
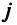
Например, матрица
или, в сокращенной записи,
Например, 
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 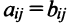
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 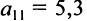
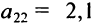
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 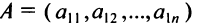
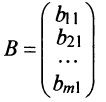
Матрица называется квадратной 
Например, 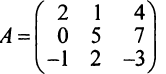
Элементы матрицы 
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
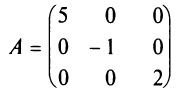
Если у диагональной матрицы 
Например,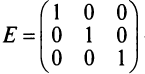
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 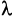
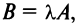
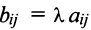
Например, если 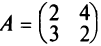
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
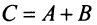
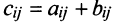
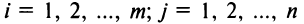
Например,
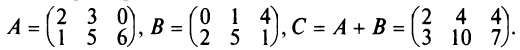
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй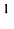
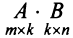
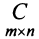
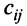

Пример №1
Вычислить произведение матриц 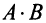
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 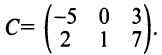
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 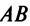
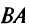
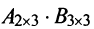
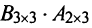
б)Если даже произведения 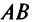
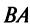
Пример №2
Найти произведения матриц 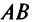
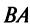
Решение:
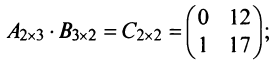
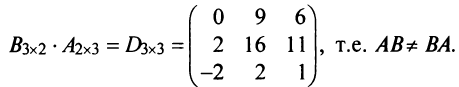
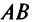
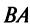
Пример №3
Найти произведения матриц 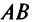
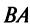
Решение:
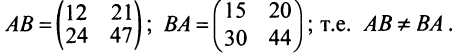
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 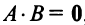
Возведение в степень
Целой положительной степенью 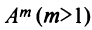
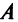
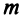
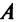
Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 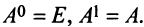
Пример №4
Найти 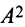
Решение:
Обращаем внимание на то, что из равенства 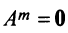
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 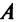
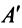
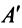
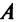
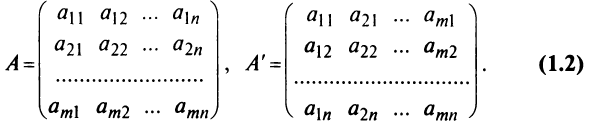
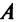
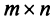
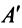
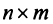
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 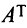
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 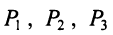
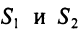
где каждый элемент 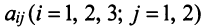
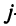
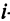
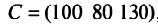
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 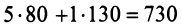
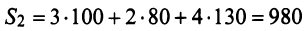
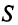
Тогда общая стоимость сырья 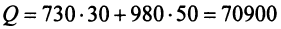
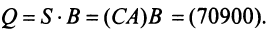
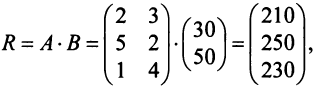
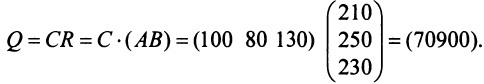
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 
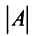
Определителем матрицы первого порядка 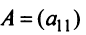
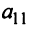
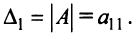
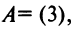
Определителем матрицы второго порядка 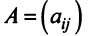
Произведения а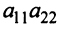
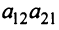
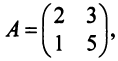
Пусть дана квадратная матрица третьего порядка: 
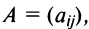
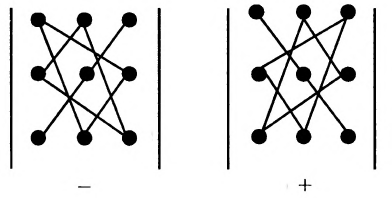
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
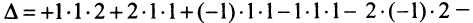
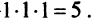
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 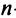
Из общего числа 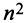
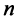
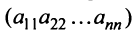
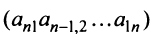
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 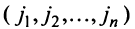
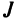
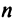

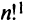
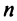
Введем понятие беспорядка, или инверсии, в перестановке 
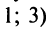
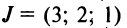
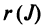
Возвращаясь к наборам (1.5) из элементов матрицы 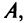
и число 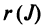
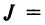
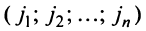
Определение. Определителем квадратной матрицы 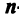
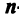
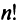
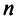
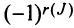
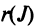
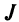
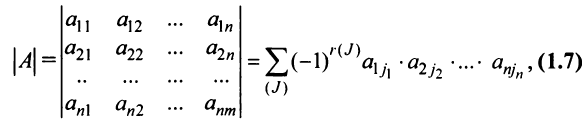
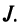
то же число, что и по формуле (1.4).
Заметим, что с ростом 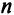
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 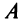
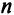
Минором 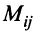
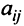
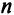
определитель матрицы 
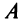
Например, минором элемента 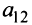
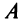
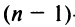
Алгебраическим дополнением 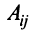
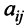
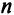
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца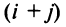
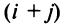
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
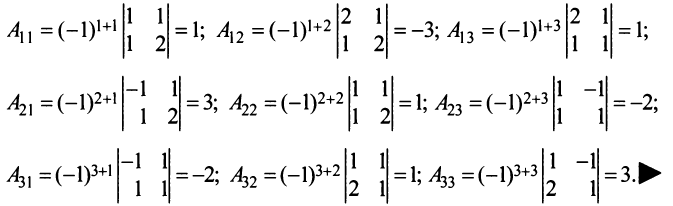
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
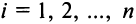
(разложение по элементам 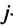
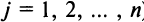

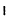
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы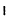
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 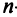
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 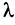
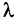
Пусть определитель исходной матрицы равен 
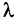
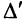
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 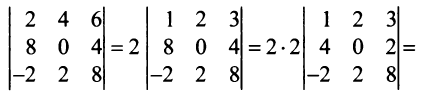
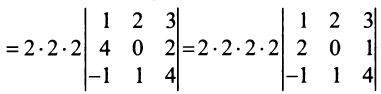
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: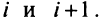


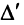
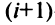
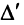
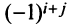
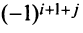
Если переставить не соседние строки, а, скажем, 
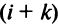

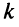
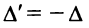
Доказательство для столбцов аналогично.
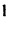
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.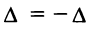
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 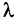
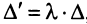

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 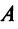
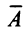
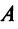
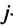

т.е. матрица 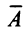
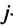
Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
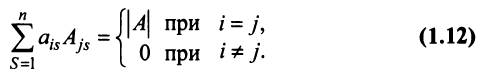
Пусть для определенности к элементам 
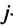
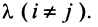
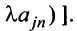

где 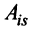

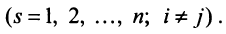
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 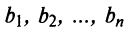
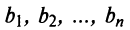
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 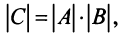
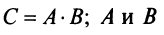
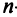
Замечание. Из свойства 10 следует, что даже если 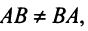
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа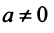
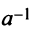
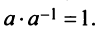
Определение. Матрица 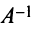
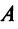
Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 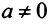
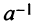

Если определитель матрицы отличен от нуля 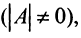
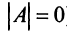
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 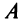

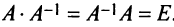
Достаточность. Пусть 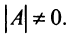
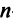

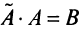
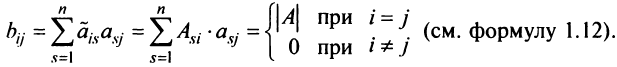
Аналогично доказывается, что произведение 
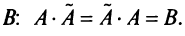
то произведения 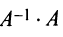
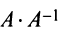
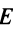
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 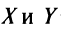
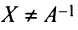
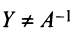

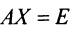
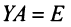

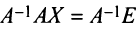
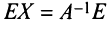
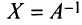

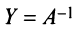
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы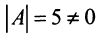


2°. Находим матрицу 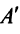

3°. Находим алгебраические дополнения элементов матрицы 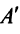
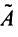
4° . Вычисляем обратную матрицу
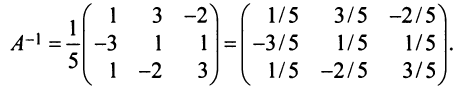
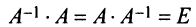
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
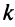
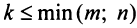
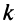

Например, из матрицы 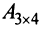
Определение. Рангом матрицы 
Ранг матрицы 
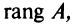
Из определения следует: а) ранг матрицы 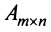
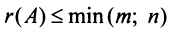
б) 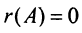
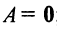
в) для квадратной матрицы 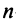

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
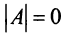

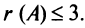
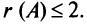
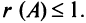

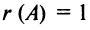
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 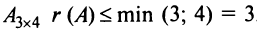
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,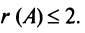
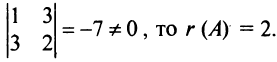
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
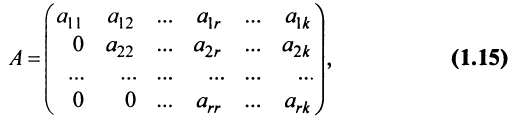
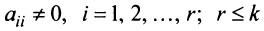
Замечание. Условие 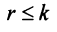
Очевидно, что ранг ступенчатой матрицы равен 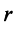
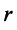
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 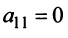
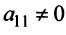
2°. Если 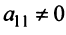
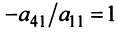
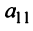
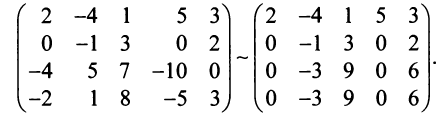

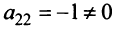
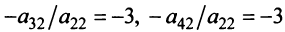
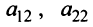
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
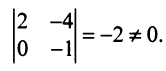
Для рангов матриц справедливы следующие соотношения:
5)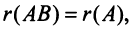
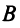
6) 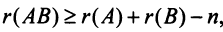
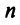

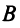
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.
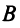

Две строки матрицы называются равными, если равны их соответствующие элементы: 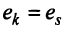
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 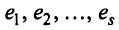
где 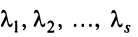
Строки матрицы 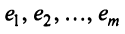
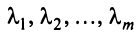
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

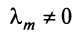
где
Таким образом, строка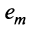
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 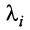
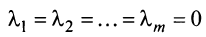
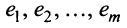
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


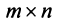
Это означает, что существует отличный от нуля минор 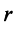
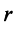
Тогда строки матрицы 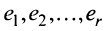
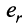
Вычтем из элементов 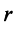
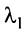
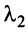
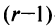
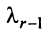

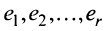
Строки 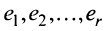
Покажем, что любые 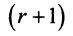
Рассмотрим минор 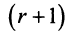
при дополнении рассматриваемого минора элементами еще одной строки 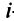
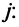
Этот минор равен нулю, так как ранг матрицы равен 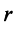
Раскладывая его по элементам последнего (добавленного) столбца, получаем 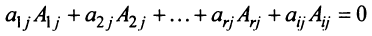
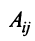

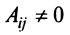
Разделив последнее равенство на 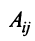
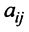
где
Фиксируем значение 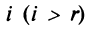
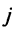
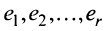
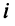
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
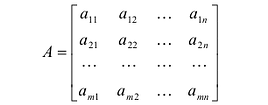
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 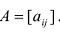
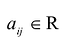
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 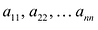
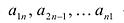
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 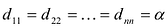
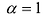
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 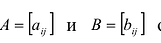
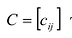
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 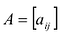
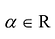
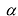
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 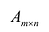
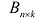
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 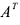
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 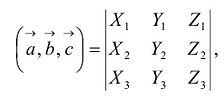
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 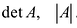
Минором 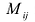
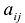
Пример №14
Найти минор 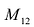
По определению, минор 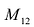
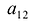
Алгебраическим дополнением элемента 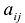
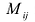
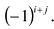
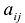
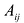
Пример №15
Найти алгебраическое дополнение элемента 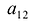
Определителем квадратной матрицы А n-го порядка 
где аи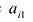
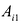
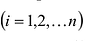
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 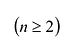
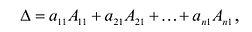
где 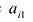
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
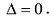
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
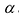
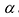
Умножим элементы i-той строки на 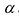
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 

Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 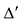

Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 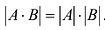
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 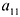
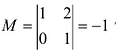
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 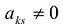
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 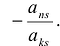
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 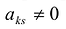
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 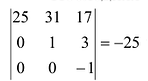
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 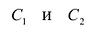
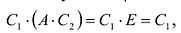
Откуда 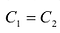
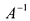
Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 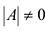
Пусть А имеет обратную матрицу. Тогда 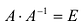
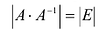
Следовательно, 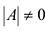
Пусть 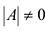
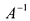
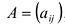
здесь 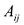
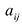
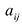
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 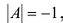
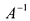
Матрицу 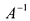
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 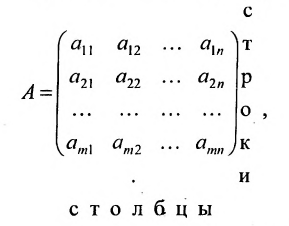
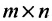
Числа 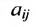
Матрицы удобно обозначать в виде 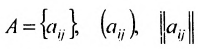
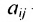
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
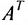
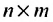
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 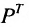
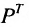
Если, элементы 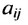
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 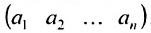
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом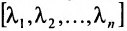
Если в диагональной матрице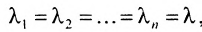
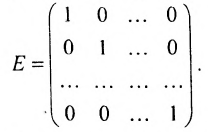
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 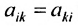
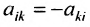
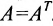
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 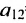
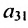
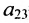
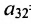
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 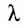
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 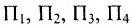
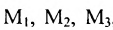
где 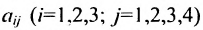
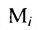
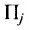
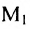
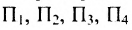
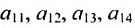
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 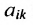
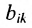
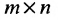
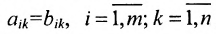
Определение 3.2.1. Суммой матриц А а В размерности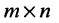
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 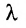
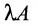
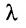
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 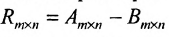
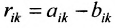
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
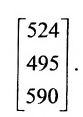
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 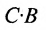
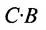
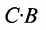
Аналогичным образом определяется произведение матрицы-строки 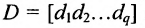
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 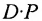
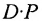
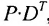
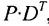
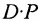
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =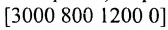
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 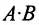
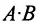
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 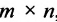
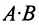
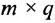
Определение 3.2.4. Произведением матрицы А размерности 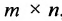
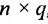
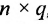
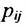
, при 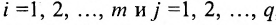
- Заказать решение задач по высшей математике
Пример №22
Пусть 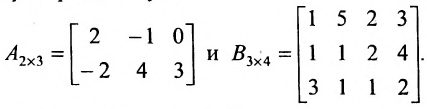
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 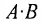
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 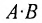
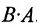
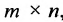
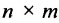
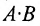
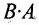
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 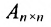
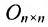
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 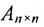
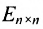
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 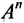
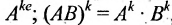
Значением многочлена
с числовыми коэффициентами 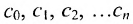
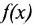
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 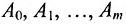
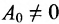
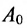
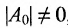
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 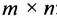
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
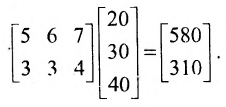
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
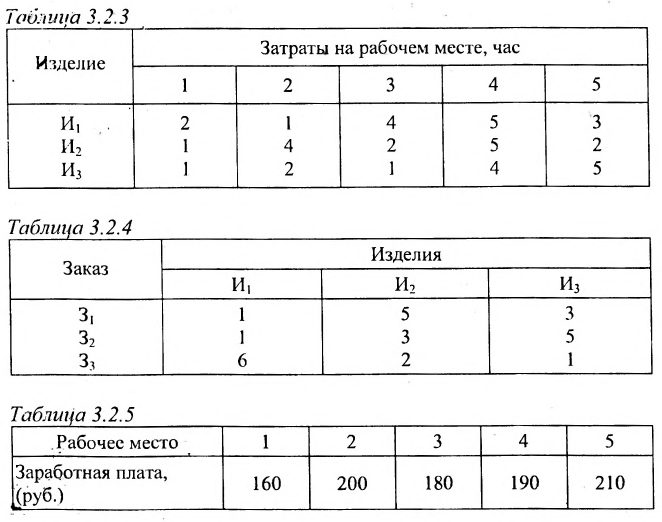
Пример №24
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
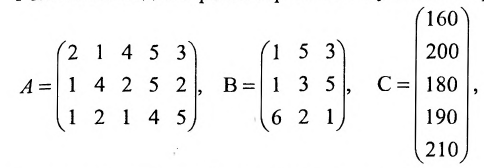
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

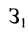
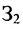
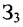
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 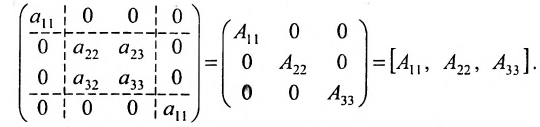
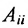
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 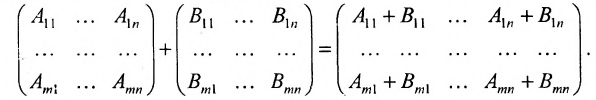
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или
суммирования служит заглавная греческая буква 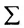
например, сумму 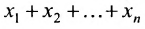
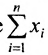
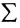
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 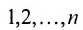
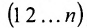
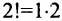
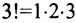
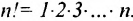
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 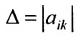
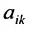
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 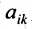
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 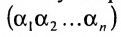
В частности, определителем второго порядка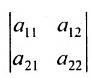
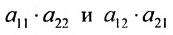
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 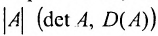
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
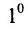
Доказательство. Рассмотрим определитель 
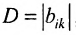
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 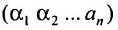
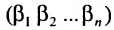
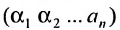
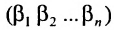
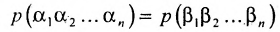
Так как 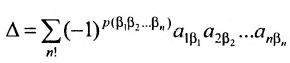
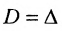
Из свойства 
Доказательство. Рассмотрим определитель 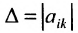
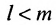
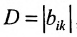

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 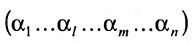
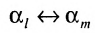
Затем поменяем местами сомножители 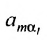
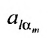
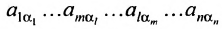
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 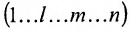
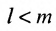
вторых индексов такая же, как и в выражении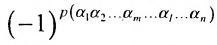
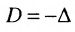
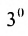
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 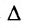
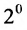
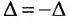
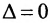
Доказательство. Пусть в определителе 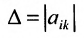
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 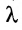
Из свойства 
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 
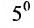
Доказательство. Пусть все элементы 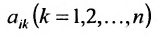

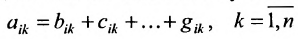
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
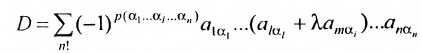
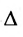
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 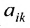

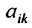
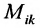
Определение 3.8.1. Минор 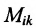
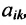
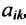

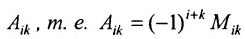
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 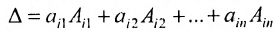
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 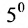
Определитель 
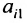
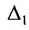

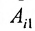
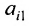
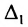
Следовательно,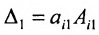
Аналогично 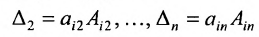
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
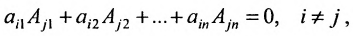
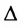
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 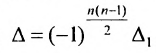
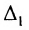
3) Если определитель 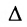
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
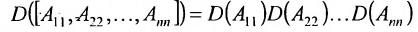
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
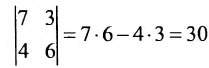
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 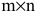
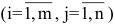
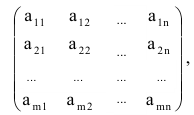
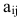
Например, элемент 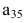
Суммой двух матриц одинакового размера 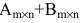
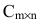
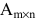
Например,
Произведением матрицы 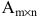
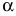
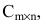
Например,
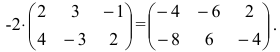
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 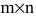
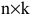
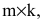
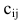
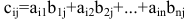
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} — (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Обра́тная
ма́трица —
такая матрица
(А-1),
что их умножение (с любой стороны) даст
в результате единичную матрицу
Свойства
обратной матрицы
Способы
нахождения обратной матрицы
-
Нахождение обратной
матрицы с помощью присоединенной
(АǀЕ) ̴ (ЕǀА-1)
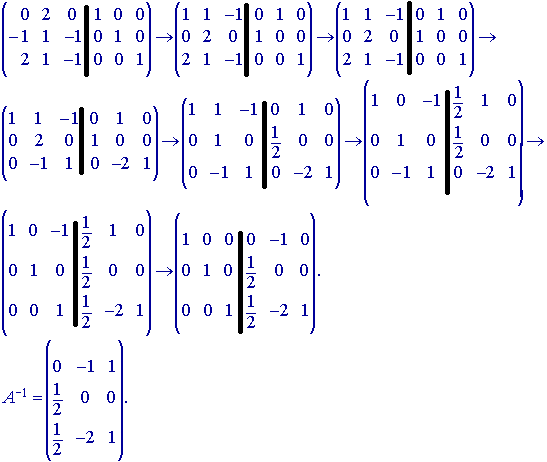
Пример.
С помощью элементарных преобразований
строк найти обратную матрицу к матрице
A.
Определитель
равен –2, следовательно существует
обратная матрица. Припишем к исходной
матрице единичную, и будем преобразовывать
матрицу A, к виду единичной матрицы.
Тогда единичная матрица преобразуется
в обратную к матрице A.
-
Нахождение обратной
матрицы по формуле:
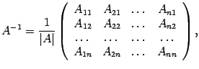
Пример.
Найдите обратную матрицу для
матрицы
Решение.
Находим определитель
Так
как
то
матрица А — невырожденная, и обратная
для нее существует. Находим алгебраические
дополнения:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй — строке:
Полученная
матрица и служит ответом к задаче.
Билет 7. Решение систем линейных уравнений с помощью формул Крамера и с помощью обратной матрицы.
АХ=В
Умножим на А-1
обе части уравнения
А-1 * А * Х = А-1
*В
ЕХ = А-1В
Х
= А-1В
5х1 + 10х2 =
4
3х1 – х2 =
1
А
;
В =
;
Х =

Метод Крамера
(правило Крамера) — способ решения
квадратных систем линейных алгебраических
уравнений (СЛАУ) с ненулевым определителем
основной матрицы (причём для таких
уравнений решение существует и оно
единственно)
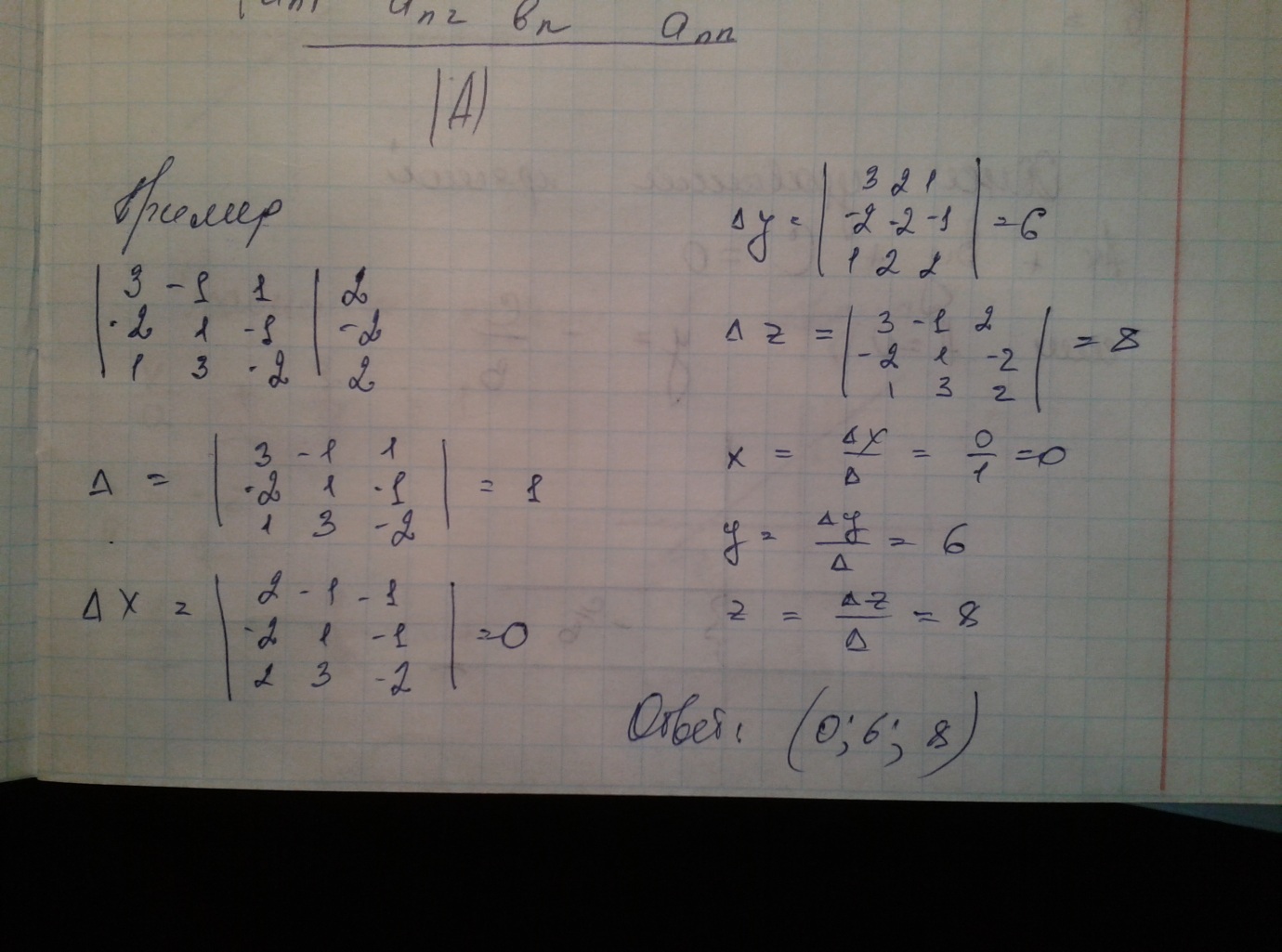
Билет 8. Векторы и линейные операции над ними. Арифметическое n-мерное векторное пространство Rn. Геометрический смысл пространств r2 и r1
Вектором называется
направленный отрезок.
Линейными
операциями
называются операции сложения и
вычитания векторов и умножения
вектора на число.
1. Сумма
векторов
и
находится
по правилу
треугольника
или
по правилу
параллелограмма
— эти
правила равносильны.
Сложение
векторов
коммутативно и ассоциативно:
2.
Разность векторов
можно
определить как сумму
,
т. е. вычитание заменяется прибавлением
противоположного вектора.
Удобно
также правило
треугольника:
векторы
и
откладывают
от общего начала, тогда разность
есть
вектор, начало которого совпадает с
концом
,
а конец — с концом
3.
Произведением
(или
)
вектора
на
действительное число λ называется
вектор
,
коллинеарный вектору
,
имеющий длину, равную
,
и то же направление, что и вектор
,
если λ >
0, и направление, противоположное
направлению вектора
,
если λ <
0.
Так, например,
есть
вектор, имеющий то же направление, что
и вектор
,
а длину, вдвое большую, чем вектор
(рис.
108).
В
случае, когда λ = 0 или
,
произведение
представляет
собой нулевой вектор.
Противоположный
вектор
можно
рассматривать как результат умножения
вектора
на
λ = -1:
.
Очевидно, что
.
Множество
всех векторов размерности n называется
арифметическим n-мерным векторным
пространством и обозначается Rn.
Геометрический смысл
имеют лишь пространства R1, R2, R3 . Для R1 –
это прямая, для R2 – плоскость, для R3 –
трехмерное пространство.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
Содержание
Обратная матрица
Определяется только для квадратных матриц!
Для квадратной матрицы $ A_{} $ матрица $ B_{} $ называется левой обратной, если $ BA=E_{} $, где $ E_{} $ — единичная матрица; для матрицы $ A_{} $ матрица $ C_{} $ называется правой обратной если $ AC=E $.
Т
Теорема. Для того, чтобы существовала левая обратная матрица для матрицы $ A_{} $ необходимо и достаточно, чтобы $ det A_{} ne 0 $. В этом случае, левая обратная матрица будет единственной и совпадает с правой обратной: $ AB=BA=E $.
Доказательство. Необходимость условия $ det A_{} ne 0 $ для существования, например, левой обратной матрицы следует из условия
$$ det (B cdot A)= det E quad iff quad (det B) (det A) =1 . $$
Покажем достаточность. Вычислим все алгебраические дополнения к элементам матрицы $ A_{} $, составим из них новую матрицу порядка $ n_{} $ и транспонируем ее. Полученная матрица
$$
operatorname{adj}(A) =left(left[A_{jk} right]_{jk}^n right)^{top} =
left(
begin{array}{llll}
A_{11} &
A_{21}& dots &
A_{n1} \
A_{12} &
A_{22} & dots &
A_{n2} \
dots & & & dots \
A_{1n} &
A_{2n} & dots &
A_{nn}
end{array}
right)
$$
называется взаимной или союзной матрице1) $ A_{} $ (а также присоединненой к матрице $ A $). Для любой матрицы $ A_{} $ имеет место равенство
$$
A cdot operatorname{adj}(A) =
left(
begin{array}{cccc}
det A & & & \
& det A & & {mathbb O} \
{mathbb O} & & ddots & \
& & & det A
end{array}
right) = det A cdot E .
$$
Справедливость этого факта следует из теории определителей: сумма произведений элементов строки матрицы на их алгебраические дополнения равна определителю матрицы; а на алгебраические
дополнения к элементам любой другой строки — нулю (см. теорему $ 2 $
☞
ЗДЕСЬ ).
При выполнении условия $ det A_{} ne 0 $ можем взять
$$
A^{-1}=frac{ operatorname{adj}(A) }{det A}=
left(
begin{array}{llll}
frac{A_{11}}{det A} &
frac{A_{21}}{det A} & dots &
frac{A_{n1}}{det A} \
&&& \
frac{A_{12}}{det A} &
frac{A_{22}}{det A} & dots &
frac{A_{n2}}{det A} \
&&& \
vdots & & & vdots \
frac{A_{1n}}{det A} &
frac{A_{2n}}{det A} & dots &
frac{A_{nn}}{det A}
end{array}
right) .
$$
Пока что мы получили правую обратную матрицу: доказано, что она удовлетворяет условию $ A C = E_{} $. Проверка того, что полученная матрица будет являться и левой обратной, т.е. удовлетворяет условию $ C A=E $, производится снова с использованием теоремы о сумме произведений элементов столбца матрицы $ A_{} $ на алгебраические дополнения к другому столбцу той же матрицы (см. теорему $ 2 $
☞
ЗДЕСЬ ). Теперь покажем, единственность полученной обратной матрицы. Предположим, что каким-то другим способом найдена еще одна матрица $ C_1 $ обладающая тем же самым свойством $ A C_1 = E $. Домножим это равенство слева на матрицу $ C_{} $:
$$ C(AC_1) = C E . $$
Операция умножения матриц подчиняется ассоциативному закону, поэтому
$$ (CA) C_1 = C , $$
но, по доказанному ранее, $ CA=E_{} $. И мы получили равенство $ C_1 = C $, доказывающее единственность правой обратной матрицы. Аналогично доказывается единственность и левой обратной.
♦
Обратную матрицу к матрице $ A_{} $ обозначают $ A_{}^{-1} $, а сама процедура нахождения такой матрицы называется обращением матрицы $ A_{} $. Матрица, определитель которой отличен от нуля, называется неособенной или невырожденной или обратимой.
Способы построения
1.
Первый способ следует из доказательства предыдущей теоремы. Вычислим все алгебраические дополнения к элементам матрицы $ A_{} $, составим из них новую матрицу порядка $ n_{} $ и транспонируем ее. Полученная матрица
$$
operatorname{adj}(A) =left(left[A_{jk} right]_{jk}^n right)^{top} =
left(
begin{array}{llll}
A_{11} &
A_{21}& dots &
A_{n1} \
A_{12} &
A_{22} & dots &
A_{n2} \
dots & & & dots \
A_{1n} &
A_{2n} & dots &
A_{nn}
end{array}
right)
$$
называется взаимной или союзной матрице $ A_{} $. При условии $ det A_{} ne 0 $ будем иметь:
$$
A^{-1}=frac{operatorname{adj}(A) }{det A}=
left(
begin{array}{llll}
frac{A_{11}}{det A} &
frac{A_{21}}{det A} & dots &
frac{A_{n1}}{det A} \
&&& \
frac{A_{12}}{det A} &
frac{A_{22}}{det A} & dots &
frac{A_{n2}}{det A} \
&&& \
vdots & & & vdots \
frac{A_{1n}}{det A} &
frac{A_{2n}}{det A} & dots &
frac{A_{nn}}{det A}
end{array}
right)
$$
Этот способ вычисления обратной матрицы имеет исключительно теоретическое значение.
П
Пример. Вычислить
$$
left( begin{array}{rrrr}
4&7& 1 &5 \
3 & 4 & 0 &-6 \
-11 & 8 & 2 & 9\
-12 & -10 &0 & 8
end{array}
right)^{-1} .
$$
Решение. Вычисляем определитель этой матрицы: $ det A = -226 ne 0 $. Обратная матрица существует. Вычисляем алгебраические дополнения элементов:
$$
overbrace{left| begin{array}{rrr}
4 & 0 &-6 \
8 & 2 & 9\
-10 &0 & 8
end{array}
right|}^{A_{11}}=-56,
overbrace{-left| begin{array}{rrr}
3 & 0 &-6 \
-11 & 2 & 9\
-12 &0 & 8
end{array}
right|}^{A_{12}}=96,
overbrace{left| begin{array}{rrr}
3 & 4 &-6 \
-11 & 8 & 9\
-12 &-10 & 8
end{array}
right|}^{A_{13}}=-854,
overbrace{-left| begin{array}{rrr}
3 & 4 & 0 \
-11 & 8 & 2 \
-12 & -10 &0
end{array}
right|}^{A_{14}}=36,
$$
$$
A_{21}=-58, A_{22}=164, A_{23}=-1506, A_{24}=118, dots,
A_{44}=58 .
$$
Cоставляем из них матрицу:
$$
left( begin{array}{rrrr}
-56 & 96 & -854 & 36 \
-58 & 164 & -1506 & 118 \
28&-48 & 314& -9 \
-40& 117 & -949 & 58
end{array}
right) .
$$
и не забываем ее транспонировать, а также поделить на определитель!
Ответ.
$$
left( begin{array}{rrrr}
frac{scriptstyle 28}{scriptstyle 113} &
frac{scriptstyle 29}{scriptstyle 113} &
-frac{scriptstyle 14}{scriptstyle 113} &
frac{scriptstyle 20}{scriptstyle 113} \
&&& \
-frac{scriptstyle 48}{scriptstyle 113} &
-frac{scriptstyle 82}{scriptstyle 113} &
frac{scriptstyle 24}{scriptstyle 113} &
-frac{scriptstyle 117}{scriptstyle 226} \
&&& \
frac{scriptstyle 427}{scriptstyle 113} &
frac{scriptstyle 753}{scriptstyle 113} &
-frac{scriptstyle 157}{scriptstyle 113} &
frac{scriptstyle 949}{scriptstyle 226} \
&&& \
-frac{scriptstyle 18}{scriptstyle 113} &
-frac{scriptstyle 59}{scriptstyle 113} &
frac{scriptstyle 9}{scriptstyle 113} &
-frac{scriptstyle 29}{scriptstyle 113}
end{array}
right) .
$$
2.
Второй способ нахождения $ A^{-1}_{} $ часто называют методом Гаусса-Йордана2) или методом приписывания единичной матрицы. Он, фактически, заключается в одновременном решении семейства систем линейных уравнений
$$
AX_1=E_{[1]}, AX_2=E_{[2]},dots, AX_n=E_{[n]}
$$
где $ E_{[1]}, E_{[2]},dots, E_{[n]} $ – столбцы единичной матрицы:
$$
E_{[1]}=left(
begin{array}{c}
1 \ 0 \ 0 \ vdots \ 0
end{array}
right),
E_{[2]}=left(
begin{array}{c}
0 \ 1 \ 0 \ vdots \ 0
end{array}
right),dots,
E_{[n]}=left(
begin{array}{c}
0 \ 0 \ 0 \ vdots \ 1
end{array}
right),
$$
Левые части этих систем одинаковы, поэтому метод исключения переменных Гаусса, примененный к одной, будет действителен и для другой — различия будут проявляться лишь в правых частях. Строго формальное обоснование метода следующее. Рассмотрим систему линейных уравнений относительно неизвестных $ x_1,dots,x_n,y_1,dots,y_n $:
$$ AX=Y . $$
Здесь $ X=(x_1,dots,x_n)^{top}, Y=(y_1,dots,y_n)^{top} $. Если $ A_{}^{-1} $ существует, то эту систему можно разрешить относительно столбца переменных $ X_{} $:
$$ X=A^{-1}Y . $$
С другой стороны, перепишем ту же систему в матричном виде:
$$AX=Y quad iff quad AX=EY quad iff quad left[A mid E right] left(begin{array}{r} X \ -Y
end{array} right)= mathbb O_{2ntimes 1} ; $$
здесь $ E_{} $ — единичная матрица порядка $ n_{} $. Элементарными преобразованиями над строками
матрицы $ left[A mid E right] $ добиваемся того, чтобы в левой ее половине возникла единичная матрица: $ left[E mid Q right] $ (этого всегда можно добиться при условии $ det A_{}ne 0 $). Поскольку элементарные преобразования приводят систему линейных уравнений к эквивалентной ей системе (т.е. имеющей то же множество решений), то
$$
left[A mid E right] left(begin{array}{r} X \ -Y
end{array} right)= mathbb O quad iff quad left[E mid Q right] left(begin{array}{r} X \ -Y
end{array} right)= mathbb O quad iff quad X=QY .
$$
Сравнивая два представления решений системы, приходим к равенству
$$ A^{-1}Y = QY $$
справедливому для любого столбца $ Y_{} $. Выбираем $ Y_{} $ из множества столбцов единичной матрицы, получаем:
$$ A^{-1}E_{[1]}= QE_{[1]}, A^{-1}E_{[2]}= QE_{[2]},dots, A^{-1}E_{[n]}= QE_{[n]} quad iff quad A^{-1}E=QE quad iff quad A^{-1}=Q . $$
Алгоритм обращения матрицы посредством приписыванием к ней единичной
1.
Осуществляем конкатенацию матриц $ A $ и единичной матрицы $ E $ того же порядка: формируем расширенную $ ntimes 2n_{} $-матрицу $ left[A mid E right] $.
2.
Элементарными преобразованиями строк расширенной матрицы, добиваемся, чтобы в левой ее половине получилась единичная матрица.
3.
Если это удается сделать, то матрица, получившаяся в правой половине и будет $ A_{}^{-1} $. Если это сделать невозможно, то $ det A_{}=0 $, т.е. $ A_{}^{-1} $ не существует.
П
Пример. Вычислить
$$
left( begin{array}{rrr}
4& 5 &1 \
1 & 3 &-2 \
3 & 1 & 2
end{array}
right)^{-1}
$$
приписыванием единичной матрицы.
Решение. $$left(begin{array}{rrr|rrr}
4& 5 &1&1&0&0\
1 & 3 &-2&0&1&0\
3 & 1 & 2&0&0&1
end{array}right)to
left(begin{array}{rrr|rrr}
1 & 3 &-2&0&1&0\
4& 5 &1&1&0&0\
3 & 1 & 2&0&0&1
end{array}right) to
$$
$$
to
left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-7&9&1&-4&0\
0&-8&8&0&-3&1
end{array}right)
to left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-8&8&0&-3&1\
0&-7&9&1&-4&0
end{array}right)
to
$$
$$
to left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-1&1&0&-3/8& 1/8\
0&-7&9&1&-4&0
end{array}right)to
left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-1&1&0&-3/8& 1/8\
0&0&2&1&-11/8&-7/8
end{array}right)
to
$$
$$
to left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-1&1&0&-3/8& 1/8\
0&0&1&1/2&-11/16&
-7/16
end{array}right)to
$$
$$
to
left(begin{array}{rrr|rrr}
1&3&-2&0&1&0\
0&-1&0&-1/2& 5/16& 9/16\
0&0&1&1/2&-11/16&-7/16
end{array}right)to
$$
$$
to left(begin{array}{rrr|rrr}
1&0&0&-1/2& 9/16 &13/16\
0&1&0&1/2&-5/16& -9/16\
0&0&1&1/2&-11/16&-7/16
end{array}right) .
$$
Ответ. $$
left( begin{array}{rrr}
-1/2& 9/16 & 13/16 \
1/2&-5/16 & -9/16 \
1/2&-11/16 &-7/16
end{array}
right)
$$
?
Алгоритм шифрования Rijndael, используемый в мобильной телефонии, имеет в одной из стадий следующее преобразование
байтов
$$
begin{pmatrix}
y_0 \ y_1 \ y_2 \ y_3 \ y_4 \ y_5 \ y_6 \ y_7
end{pmatrix}
=
begin{pmatrix}
1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \
1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \
1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \
1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \
0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \
0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \
0 & 0 & 0 & 1 & 1 & 1 & 1 & 1
end{pmatrix}
begin{pmatrix}
x_0 \ x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \ x_7
end{pmatrix}
+
begin{pmatrix}
1 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1
end{pmatrix}
pmod{2}
$$
Найти обратное преобразование.
Ответ
☞
ЗДЕСЬ.
3.
Этот способ основан на теореме Гамильтона-Кэли. Если найден характеристический полином матрицы $ A_{} $:
$$ det(A-lambda E)equiv (-1)^n (lambda^n + a_1 lambda^{n-1} + dots + a_{n-1}lambda + a_n ) , $$
то при условии $ a_n ne 0 $ матрица $ A_{} $ обратима и
$$ A^{-1}= — frac{1}{a_n} left( A^{n-1}+a_1 A^{n-2} + dots + a_{n-1} E right) , $$
т.е. $ A^{-1} $ может быть вычислена посредством возведения в степень матрицы $ A_{} $.
Свойства операции обращения
Если в левой части каждого каждого из следующих равенств операции определены, то равенства справедливы:
1.
$ (A^{-1})^{-1}=A_{} $;
2.
$ (Acdot B)^{-1} = B^{-1}A_{}^{-1} $;
3.
$ (A_{}^{top})^{-1}=(A^{-1})^{top} $;
4.
$ det (A^{-1}) = (det A)^{-1} $.
Использование для решения систем линейных уравнений
Рассмотрим систему линейных уравнений с квадратной матрицей $ A $, т.е. такую, у которой число уравнений совпадает с числом неизвестных:
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2\
ldots& & ldots \
a_{n1}x_1 +a_{n2}x_2+ldots+a_{nn}x_n &=&b_n
end{array}right. quad iff quad AX={mathcal B}
$$
Теорема Крамера утверждает, что такая система имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $ det A ne 0 $. Это же условие является необходимым и достаточным и для существования обратной матрицы $ A^{-1} $. Но тогда решение системы можно записать в матричной форме:
$$
X=A^{-1} {mathcal B} ,
$$
и такое представление бывает удобно в тех задачах, в которых требуется решить семейства систем с одинаковой матрицей $ A $, но различными столбцами правых частей $ {mathcal B} $. Как соотносятся формулы Крамера и только что полученная формула? — Для пояснения, распишем первую компоненту решения, воспользовавшись представлением обратной матрицы по способу
1
( см.
☞
ЗДЕСЬ ). Имеем:
$$
x_1 = frac{A_{11}}{det A} b_1 + frac{A_{21}}{det A} b_2 + dots + frac{A_{n1}}{det A} b_n
$$
Но полученное выражение совпадает с разложением определителя
$$
frac{1}{det A}
left|
begin{array}{rrrr}
b_{1} & a_{12} & dots & a_{1n} \
b_{2} & a_{22} & dots & a_{2n} \
dots &&& dots \
b_{n} & a_{n2} & dots & a_{nn}
end{array}
right|
$$
по первому столбцу, т.е. мы получили первую из формул Крамера.
Обратные к конкретным типам матриц
Обратная к
1.
треугольной матрице (верхней или нижней), если существует, то будет треугольной матрицей (того же типа);
2.
симметричной матрице, если существует, то будет симметричной матрицей;
3.
кососимметричной матрице нечетного порядка не существует, а в случае четного порядка, если существует, то будет кососимметричной матрицей;
4.
ортогональной матрице $ Q_{} $ всегда существует и получается транспонированием матрицы: $ Q^{-1} = Q^{top} $.
5.
квадратной матрице Вандермонда
$$ left(
begin{array}{llll}
1& 1& ldots& 1\
x_1& x_2& ldots& x_n\
x_1^2& x_2^2& ldots& x_n^2\
vdots& vdots& & vdots \
x_1^{n-1}& x_2^{n-1}& ldots& x_n^{n-1}
end{array}
right) $$
существует тогда и только тогда, когда все $ x_1,dots,x_n $ различны. Выражение
☞
ЗДЕСЬ.
В некоторых приложениях важно по виду матрицы быстро определить существует ли у нее обратная — без непосредственного нахождения этой обратной. Для некоторых типов матриц можно получить «вычислительно дешевые» критерии отличия их определителей от нуля.
Следующая теорема основана на связи определителя матрицы с ее собственными числами.
Т
Теорема. Матрица $ A_{} $, у которой элементы каждой строки обладают свойством
$$ |a_{jj}|>|a_{j1}|+dots+|a_{j,j-1}|+|a_{j,j+1}|+dots+|a_{jn}| quad npu quad forall jin {1,dots,n} $$
(модуль элемента на главной диагонали больше суммы модулей остальных элементов строки) называется матрицей с диагональным доминированием (преобладанием). Такая матрица всегда обратима.
Доказательство следует из того факта, что $ det A_{} ne 0 $ тогда и только тогда, когда в наборе собственных чисел матрицы3) $ A_{} $ нет нулевого (см. следствие к теореме 1
☞
ЗДЕСЬ ). Локализовать собственные числа матрицы можно с помощью теоремы Гершгорина: любое собственное число $ lambda_{} $ матрицы $ A_{} $ должно удовлетворять хотя бы одному неравенству
$$ |lambda — a_{jj}| < sum_{k=1 atop k ne j}^n |a_{jk} | . $$
Геометрический смысл последнего неравенства: число $ lambda_{} $ лежит в круге комплексной плоскости с центром в точке $ a_{jj}^{} $ и радиусом — на основании предположения теоремы — меньшим, чем расстояние от $ 0_{} $ до $ a_{jj} $. Следовательно $ lambda_{} ne 0 $.
♦
Поскольку $ det A_{} = det A^{top} $, то утверждение теоремы будет справедливо и для матриц, у которых диагональное доминирование определяется через неравенства на элементы столбцов.
Обращение блочных матриц
Т
Теорема [Фробениус].4). Пусть имеется блочная квадратная матрица вида
$$
left(
begin{array}{rr}
A & B \
C & D
end{array}
right) quad ,
$$
где матрица $ A_{} $ — квадратная порядка $ k_{} $, а матрица $ D_{} $ — квадратная порядка $ ell_{} $. Тогда
$$left(
begin{array}{rr}
A & B \
C & D
end{array}
right)^{-1}=
left(
begin{array}{cc}
A^{-1} +A^{-1}BK^{-1}CA^{-1} & -A^{-1}BK^{-1} \
-K^{-1}CA^{-1} & K^{-1}
end{array}
right) ,
$$
где матрица
$$ K=D-CA^{-1}B $$
называется шуровским дополнением5) к подматрице $ A_{} $. Здесь предполагается, что матрицы $ A_{} $ и $ K_{} $ — неособенные.
=>
При $ B=mathbb O $
имеем:
$$
left(
begin{array}{rr}
A & mathbb O \
C & D
end{array}
right)^{-1}=
left(
begin{array}{cc}
A^{-1} & mathbb O \
-D^{-1}CA^{-1} & D^{-1}
end{array}
right) ,
$$
если матрицы $ A_{} $ и $ D_{} $ — неособенные.
Доказательство. Будем искать
$$
left(
begin{array}{rr}
A & mathbb O \
C & D
end{array}
right)^{-1}
$$
в виде
$$
left(
begin{array}{rr}
X & Y \
U & V
end{array}
right)_{ntimes n}
$$
при $ ktimes k $-матрице $ X $ и $ elltimes ell $-матрице $ V $. Разбиваем
матричное равенство
$$
left(
begin{array}{rr}
X & Y \
U & V
end{array}
right)
left(
begin{array}{rr}
A & mathbb O \
C & D
end{array}
right)
=left(
begin{array}{rr}
E_k & mathbb O \
mathbb O & E_{ell}
end{array}
right)
$$
на четыре отдельных
$$
begin{array}{cc}
XA+YC=E_k, & YD=mathbb O, \
UA+VC=mathbb O, & VD=E_{ell}
end{array}
quad Rightarrow quad
begin{array}{l}
Y=mathbb O, \
V=D^{-1}.
end{array}
$$
Подставляем полученное в два оставшихся равенства: $ X=A^{-1} $, $ U=-D^{-1}CA^{-1} $.
♦
Теорема Фробениуса имеет, в основном, теоретическое значение — за исключением одного частного случая, когда матрица $ D_{} $ имеет порядок 1, т.е. является числом. Пусть, например, уже найдена обратная матрица для матрицы
$$ A =
left(
begin{array}{llll}
a_{11} & dots & a_{1n} \
a_{21} & dots & a_{2n} \
vdots & & vdots \
a_{n1} & dots & a_{nn}
end{array}
right)
$$
порядка $ n_{} $ и ставится задача нахождения обратной матрицы для окаймляющей ее матрицы
$$
left(
begin{array}{rr}
A & B \
C & D
end{array}
right) =
left(
begin{array}{llll}
a_{11} & dots & a_{1n} & a_{1,n+1} \
a_{21} & dots & a_{2n} & a_{2,n+1} \
vdots & && vdots \
a_{n1} & dots & a_{nn} & a_{n,n+1} \
a_{n+1,1} & dots & a_{n+1,n} & a_{n+1,n+1}
end{array}
right)
$$
порядка $ n+1_{} $. Тогда из теоремы следует:
$$
left(
begin{array}{rr}
A & B \
C & D
end{array}
right)^{-1}=
frac{1}{kappa}
left(
begin{array}{cc}
A^{-1}(kappa E+BCA^{-1}) & -A^{-1}B \
-CA^{-1} & 1
end{array}
right) ;
$$
здесь $ E_{} $ — единичная матрица порядка $ n_{} $, а число
$$
kappa=a_{n+1,n+1}-CA^{-1}B=underbrace{a_{n+1,n+1}}_D-underbrace{left( a_{n+1,1} , dots , a_{n+1,n} right)}_CA^{-1}
underbrace{left(begin{array}{l}
a_{1,n+1} \
a_{2,n+1} \
vdots \
a_{n,n+1}
end{array}
right)}_B
$$
очевидно связано с определителем новой матрицы:
$$
detleft(
begin{array}{rr}
A & B \
C & D
end{array}
right)= kappa det A .
$$
Этот метод обращения матрицы известен в литературе как метод окаймления, он подробно изложен в [1].
?
Найти обратную матрицу для матрицы Фробениуса
$$
{mathfrak F}=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
dots& &&&ddots & & dots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
Решение и ответ
☞
ЗДЕСЬ
Обращение «возмущенных» матриц
Довольно часто ставится задача нахождения обратной к матрице $ A+B_{} $ при условии, что известна матрица $ A^{-1} $ и доступна некоторая дополнительная информация о «возмущении» — о матрице $ B_{} $.
Следующий результат формулируем только для случая вещественных матриц, хотя существует его обобщение для комплексных.
Т
Теорема [Шерман, Моррисон]. [3]. Пусть матрицы
$$ A_{ntimes n}, U_{ntimes p}, W_{ptimes p}, V_{ntimes p} $$
таковы, что существуют $ A^{-1}, W^{-1} $ и $ (W^{-1}+V^{top} A^{-1} U)^{-1} $. Тогда существует $ (A+UWV^{top})^{-1} $ и
$$ (A+UWV^{top})^{-1} = A^{-1}- A^{-1}UY^{-1}V^{top} A^{-1} quad npu quad Y=W^{-1}+V^{top}A^{-1}U . $$
Особенно полезен этот результат для случая возмущения матрицы $ A_{} $ посредством матриц одноранговых:
=>
Если $ {u=(u_1,dots,u_n), v=(v_1,dots,v_n)} subset mathbb R^n $, то
$$ (A+u^{top}v)^{-1} = A^{-1}- frac{1}{1+vA^{-1}u^{top}} A^{-1} u^{top} v A^{-1} . $$
П
Вычислить $ (A+B)^{-1} $ для
$$ A=left(begin{array}{rrr}
-7 & 22 & — 55 \
-94 & 87 & -56 \
0 & -62 & 97
end{array} right),
B=left(begin{array}{rrr}
1 & 1 & 2 \
0 & 1 & 1 \
-1 & 0 & -1
end{array} right) ,
$$
если известно, что
$$
A^{-1} = frac{1}{154713}
left(begin{array}{rrr}
-4967 & -1276 & — 3553 \
-9118 & 679 & -4778 \
-5828 & 434 & -1459
end{array} right) .
$$
Решение. Имеем: $ operatorname{rank} (B) =2 $ и, следовательно, матрица $ B_{} $ может быть представлена в виде суммы двух матриц ранга $ 1_{} $:
$$
B=
underbrace{left(begin{array}{rrr}
0 & 1 & 1 \
0 & 1 & 1 \
0 & 0 & 0
end{array} right)}_{=B_1} +
underbrace{left(begin{array}{rrr}
1 & 0 & 1 \
0 & 0 & 0 \
-1 & 0 & -1
end{array} right)}_{=B_2}= {underbrace{(1,1,0)}_{=u_1}}^{top}
underbrace{(0,1,1)}_{=v_1} + {underbrace{(1,0,-1)}_{=u_2}}^{top} underbrace{(1,0,1)}_{=v_2} .
$$
Будем производить обращение матрицы $ A+B $ по схеме:
$$ A+B = (underbrace{(A+B_1)}_{A_1}+B_2)^{-1} . $$
На основании следствия к теореме имеем последовательно:
$$ A_1^{-1}=(A+B_1)^{-1}=A^{-1}- frac{1}{1+v_1A^{-1}u_1^{top}} A^{-1} B_1 A^{-1}=
$$
$$
=frac{1}{140880}
left(begin{array}{rrr}
-5126 & -1117 &-3487\
-9118 & 679 & -4691\
-5828 & 434 & -1546
end{array} right) ;
$$
$$
(A+B)^{-1}=(A_1+B_2)^{-1}=A_1^{-1}- frac{1}{1+v_2A_1^{-1}u_2^{top}} A_1^{-1} B_2 A_1^{-1}=
$$
$$
=frac{1}{134959}
left(begin{array}{rrr}
-5038 & -1078 & -3399 \
-9079 & 629 & -4652 \
-5916 & 395 & -1634
end{array} right) .
$$
♦
Этот прием вычисления обратной матрицы формализуется в методе пополнения [1]: последовательно находятся обратные матрицы
к матрицам последовательности
$$ A_0=E,A_1,dots,A_n=A, $$
в которой $ A_{k-1} $ отличается от $ A_k $ заменой $ k $-й строки матрицы $ A_{k-1} $ на $ k $-ю строку матрицы $ A $.
Используется в модифицированном симплекс-методе, в котором на каждом шаге требуется вычислять обратную матрицу для матрицы, которая отличается от матрицы, полученной на предыдущем шаге только в одном столбце [4].
Псевдообратная матрица
Эта матрица определяется не только для квадратной матрицы $ A_{} $.
Пусть сначала матрица $ A_{} $ порядка $ mtimes n_{} $ — вещественная и $ m ge n_{} $ (число строк не меньше числа столбцов).
Если $ operatorname{rank} (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная матрица (Мура-Пенроуза)6) к матрице $ A_{} $ определяется как матрица
$$ A^{+}=(A^{top}A)^{-1} A^{top} . $$
Эта матрица имеет порядок $ n times m_{} $. Матрица $ (A^{top}A)^{-1} $ существует ввиду того факта, что при условии $ operatorname{rank} (A) = n $ будет выполнено $ det (A^{top} A) > 0 $ (см. теорему $ 2 $ в пункте
☞
ТЕОРЕМА БИНЕ-КОШИ или же пункт
☞
СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^{+} cdot A = E_{n} $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_{} $. В случае $ m=n_{} $ псевдообратная матрица совпадает с обратной матрицей: $ A^{+}=A^{-1} $.
П
Пример. Найти псевдообратную матрицу к матрице
$$ A= left( begin{array}{cc}
1 & 0 \
0 & 1 \
1 & 1
end{array}
right) .
$$
Решение.
$$
A^{top}= left( begin{array}{ccc}
1 & 0 & 1 \
0 & 1 & 1
end{array}
right) quad Rightarrow quad A^{top} cdot A =
left( begin{array}{cc}
2 & 1 \
1 & 2
end{array}
right) quad Rightarrow
quad (A^{top} cdot A)^{-1} =
left( begin{array}{cc}
2/3 & -1/3 \
-1/3 & 2/3
end{array}
right)
Rightarrow
$$
$$
Rightarrow A^{+} = (A^{top} cdot A)^{-1} A^{top} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3
end{array}
right) .
$$
При этом
$$
A^{+} cdot A =
left( begin{array}{cc}
1 & 0 \
0 & 1
end{array}
right),quad A cdot A^{+} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3 \
1/3 & 1/3 & 2/3
end{array}
right) ,
$$
т.е. матрица $ A^{+} $ не будет правой обратной для матрицы $ A_{} $.
♦
?
Вычислить псевдообратную матрицу для
$$ mathbf{a)} left( begin{array}{cc}
1 & 0 \
1 & 1 \
1 & 1
end{array}
right) quad ; quad
mathbf{b)}
left( begin{array}{c}
x_1 \
x_2 \
x_3
end{array}
right)
.
$$
Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений. Если $ A^{+} $ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_{} $ находится по формуле $ X= A^{+} mathcal B $ при любом столбце $ mathcal B_{} $.
Верно и обратное: если
$ E_{[1]}, E_{[2]},dots, E_{[m]} $ – столбцы единичной матрицы $ E_m $:
$$
E_{[1]}=left(
begin{array}{c}
1 \ 0 \ 0 \ vdots \ 0
end{array}
right),
E_{[2]}=left(
begin{array}{c}
0 \ 1 \ 0 \ vdots \ 0
end{array}
right),dots,
E_{[m]}=left(
begin{array}{c}
0 \ 0 \ 0 \ vdots \ 1
end{array}
right),
$$
а псевдорешение системы уравнений $ AX=E_{[j]} $ обозначить $ X_{j} $ (оно существует и единственно при условии $ operatorname{rank} (A) = n $), то
$$ A^{+}=left[X_1,X_2,dots,X_m right] . $$
Т
Теорема. Пусть $ A in mathbb R^{mtimes n} $, $ m ge n_{} $ и $ operatorname{rank} (A) = n $. Тогда псевдообратная матрица $ A^{+} $ является решением задачи минимизации
$$ min_{Xin mathbb R^{ntimes m}} ||AX-E_m||^2 $$
где $ || cdot || $ означает евклидову норму (норму Фробениуса) матрицы :
$$ ||[h_{jk}]_{j,k}||^2=sum_{j,k} h_{jk}^2 . $$
При сделанных предположениях решение задачи единственно.
Образно говоря, если уж невозможно найти обратную матрицу для матрицы $ A in mathbb R^{mtimes n} $, давайте найдем хотя бы такую матрицу $ X_{ntimes m} $, чтобы отклонение произведения $ Acdot X $ от единичной матрицы $ E_m $ (вычисленное как квадрат евклидова расстояния между матрицами $ Acdot X $ и $ E_m $) было бы минимальным.
С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай матрицы $ A in mathbb R^{mtimes n} $, у которой число строк меньше числа столбцов: $ m < n_{} $.
Будем искать эту матрицу как решение задачи минимизации
$$ min_{Yin mathbb R^{ntimes m}} ||YA-E_n||^2 , . $$
Пусть $ operatorname{rank} (A) = m $, т.е. строки матрицы линейно независимы. Тогда псевдообратная к матрице $ A_{} $ определяется как матрица
$$ A^{+}= A^{top} (Acdot A^{top})^{-1} . $$
Очевидно, что в этом случае $ Acdot A^{+}=E_m $.
Система линейных уравнений $ AX=mathcal B $ с такой матрицей $ A $ совместна и имеет бесконечное множество решений при произвольном выборе столбца $ mathcal B $. Известна теорема представления общего решения системы в виде суммы частного решения и общего решения однородной системы $ AX=mathbb O_{mtimes 1} $. Этот результат можно переписать в терминах псевдообратной матрицы.
Т
Теорема. Если все строки матрицы $ A in mathbb R^{mtimes n} $ при $ m<n $ линейно независимы, то общее решение системы $ AX=mathcal B $ представимо в виде
$$
X=A^{+} mathcal B + (E_n-A^{+}A)Y quad mbox{при произвольном столбце } Yin mathbb R^n , .
$$
П
Пример. Найти общее решение системы уравнений
$$
left{begin{array}{rrrr}
x_1 & + 2,x_2 & +3, x_3 &=3, \
-x_1 & + x_2 & &=5.
end{array}
right.
$$
Решение. Здесь
$$
A=left( begin{array}{rrr}
1 & 2 & 3 \
-1 & 1 & 0
end{array}
right) Rightarrow Acdot A^{top}=
left( begin{array}{rr}
14 & 1 \
1 & 2
end{array}
right)
Rightarrow left(Acdot A^{top}right)^{-1} =
left( begin{array}{rr}
2/27 & -1/27 \
-1/27 & 14/27
end{array}
right) Rightarrow
$$
$$
Rightarrow
A^{+}= A^{top} (Acdot A^{top})^{-1}=
left( begin{array}{rr}
1/9 & -5/9 \
1/9 & 4/9 \
2/9 &-1/9
end{array}
right) Rightarrow A^{+}mathcal B = left( begin{array}{r}
-22/9 \
23/9 \
1/9
end{array}
right) , A^{+}A=
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3 \
1/3 & 1/3 & 2/3
end{array}
right) Rightarrow
$$
$$
X= left( begin{array}{r}
-22/9 \
23/9 \
1/9
end{array}
right) + frac{1}{3} (y_1+y_2-y_3) left( begin{array}{r}
1 \
1 \
-1
end{array}
right)
$$
Столбец $ [1,,1,-1]^{top} $ составляет фундаментальную систему решений однородной системы
$$
left{begin{array}{rrrr}
x_1 & + 2,x_2 & +3, x_3 &=0, \
-x_1 & + x_2 & &=0.
end{array}
right.
$$
Псевдообратная к произвольной матрицы $ A $ (без ограничения на ее ранг) может быть вычислена с помощью сингулярного разложения
Задачи
Источники
[1]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960, с.187-192
[2]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234
[3]. Gill P.E., Murray W., Wright M.H. Numerical Linear Algebra and Optimization. V.1. Addison-Wesley, NY, 1991
[4]. Таха Х. Введение в исследование операций. Т.1, глава 7. М.Мир. 1985


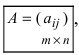
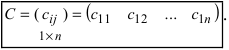
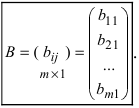
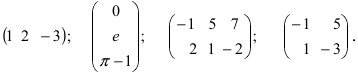


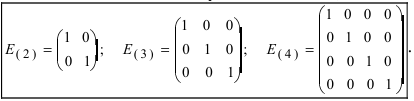
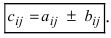
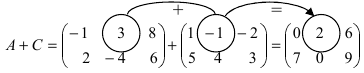
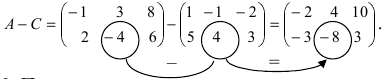

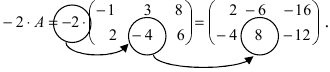
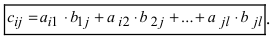
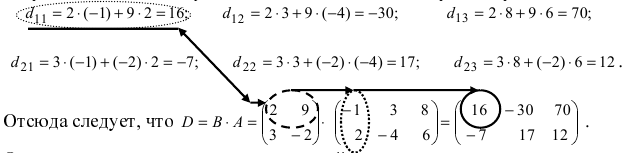
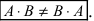
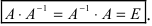
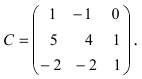
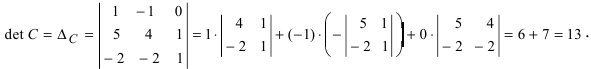
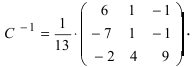
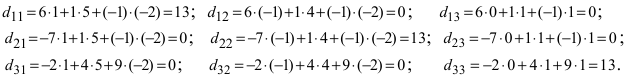
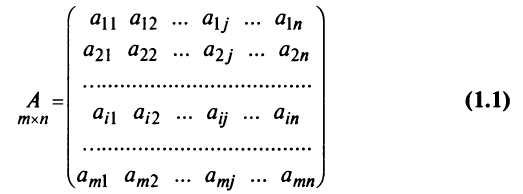
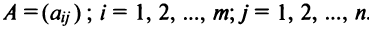

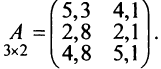
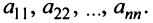

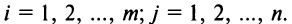
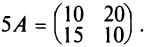
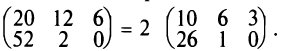
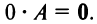
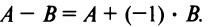
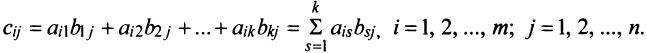

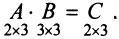
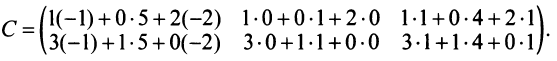
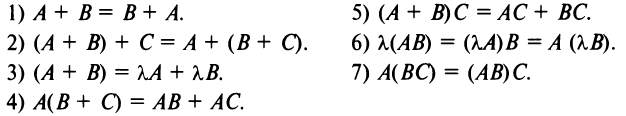
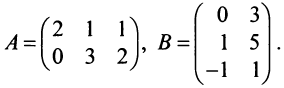
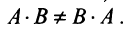
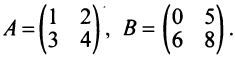
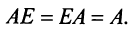
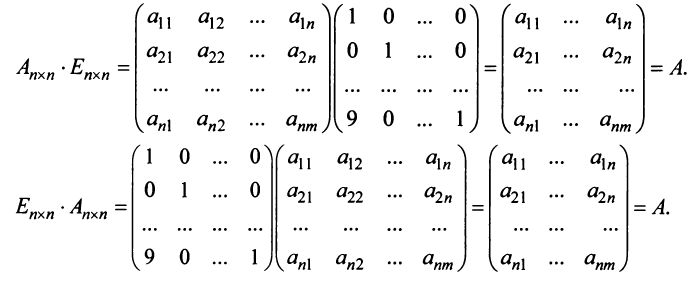
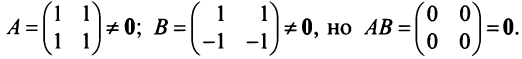
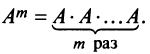
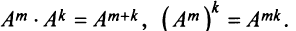
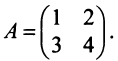
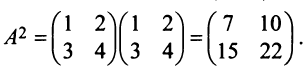
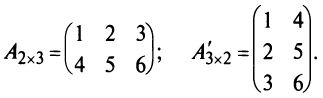

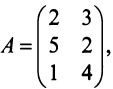
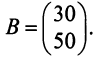
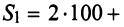
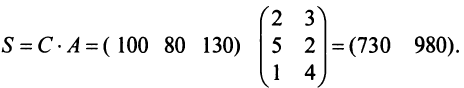

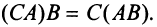

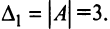
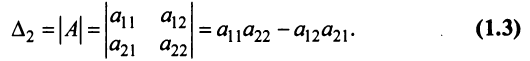
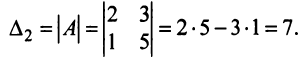
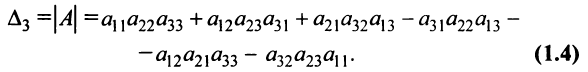

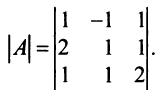


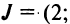

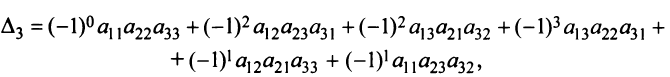

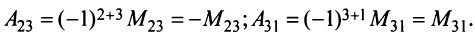
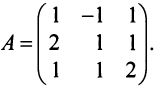
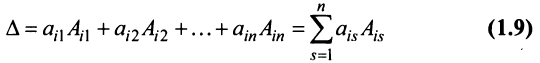
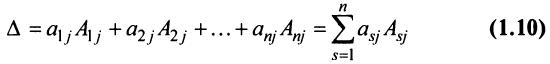
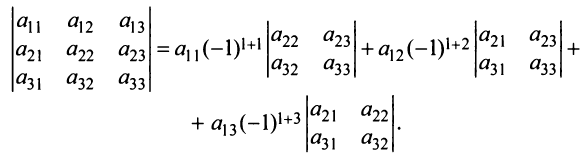

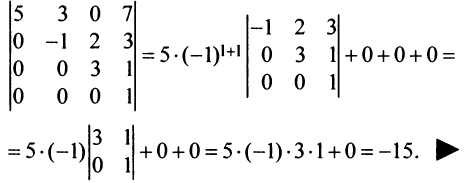
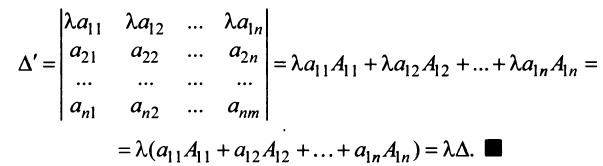
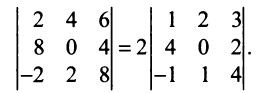
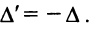

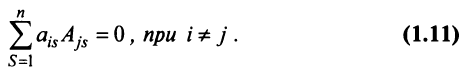
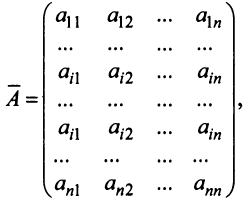
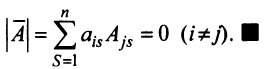
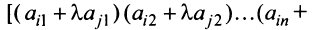
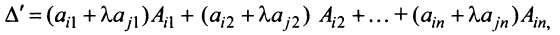
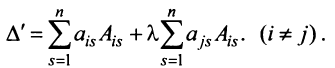
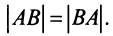
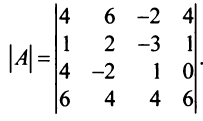
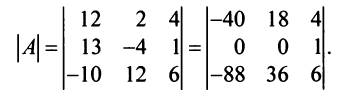
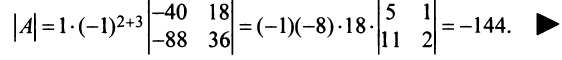

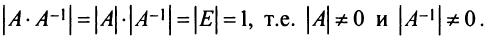
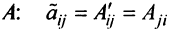
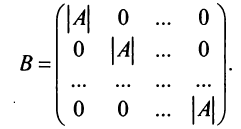
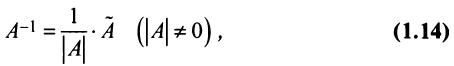

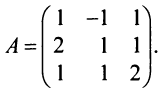
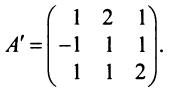
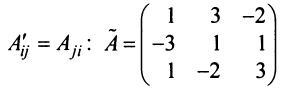
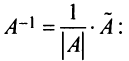
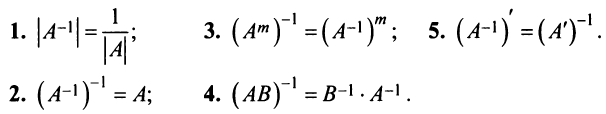
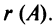
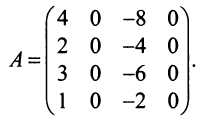

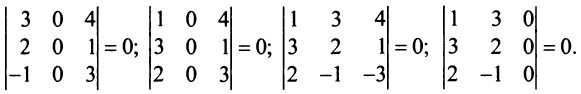

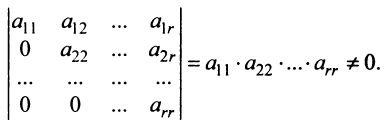
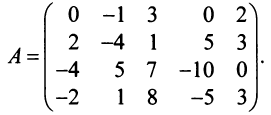
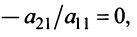
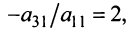
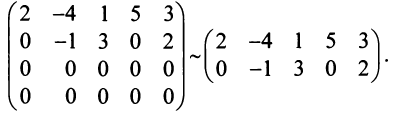

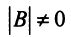
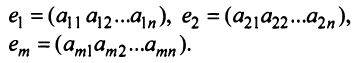
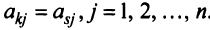
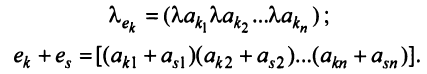
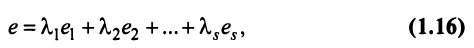
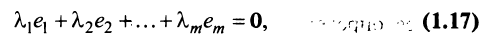
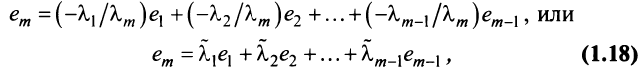
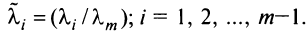


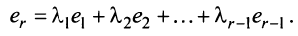


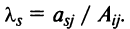
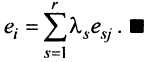
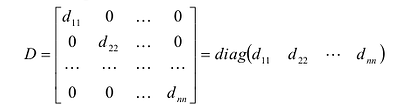
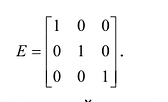
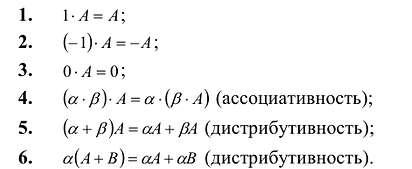
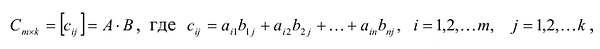
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;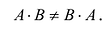
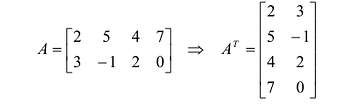
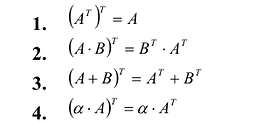
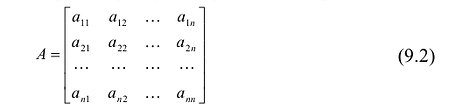
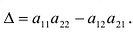
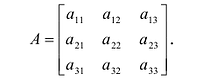
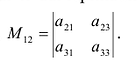
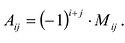
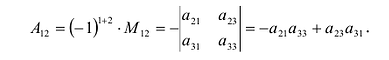
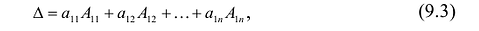
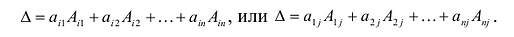
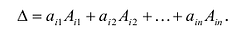
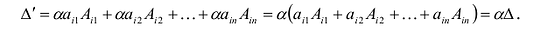
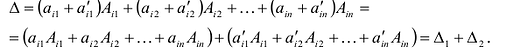

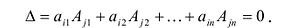
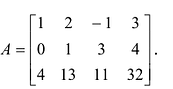

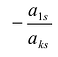 и т.д.;
и т.д.;



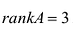
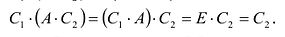
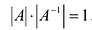
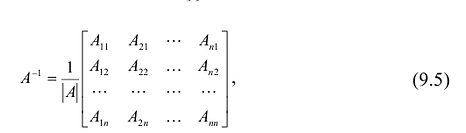
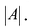

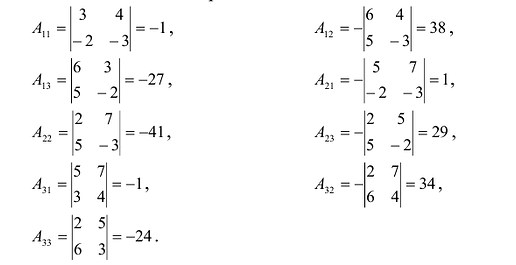
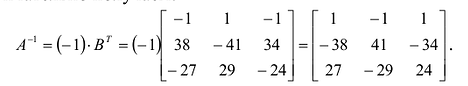
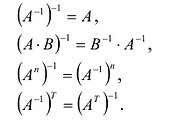


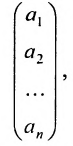
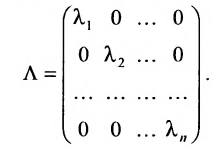
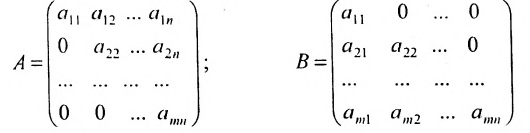

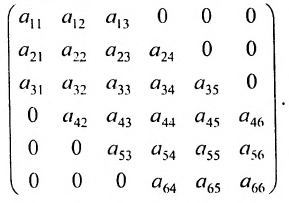
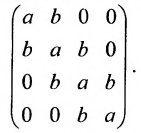




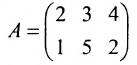

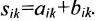
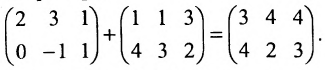
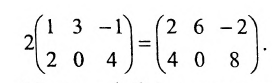
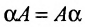 .
.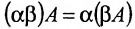 .
.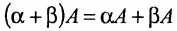 .
.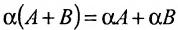 .
.