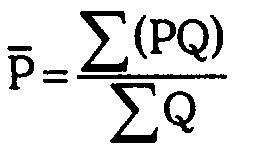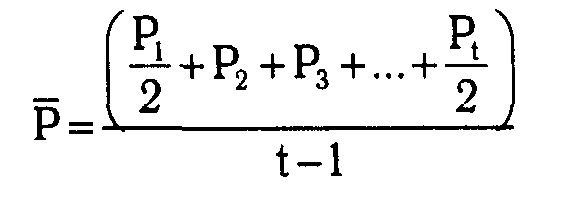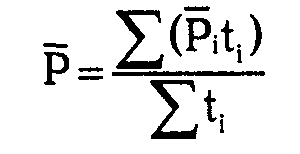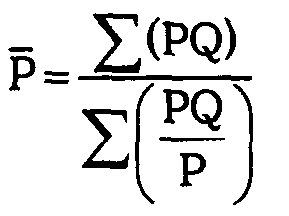С одной стороны, каждый предприниматель имеет право самостоятельно устанавливать цену на свой товар. С другой, корректность цен на продаваемую продукцию могут проверять представители Федеральной налоговой службы. Чаще всего торговые организации сталкиваются с выездным контролем со стороны ФНС.
Российское законодательство допускает такие проверки, если, по мнению налоговиков, стоимость реализуемых продуктов существенно отличается от среднерыночной. Если сотрудники ФНС решат, что ваше предприятие устанавливает некорректные цены, они имеют право доначислить налоги.
Это объясняется тем, что от выбранных предпринимателем принципов ценообразования напрямую зависят платежи в бюджет — не только прямые, но и косвенные. Ведь налоги рассчитываются в зависимости от выручки, дохода, стоимости проданной продукции.
Если по результатам проверки выяснится, что расхождение между установленной вами стоимостью и ценами на аналогичные товары составляет более 20%, налоговая служба имеет право выставить пеню и доначислить налоги. Не имеет значения, продаете вы на 20% дороже или на 20% дешевле — у налоговиков в любом случае возникнут претензии.
Что сделать для того, чтобы у представителей ФНС не было вопросов к ценам на вашу продукцию? Необходимо ориентироваться на среднерыночные цены. При этом есть несколько методов, позволяющих определить среднюю стоимость товара. Вы можете выбрать любой из них, но в большинстве случаев применяется расчет с помощью среднего арифметического. Он самый простой и лучше всего подходит для решения стоящей перед вами задачи.
Определение среднего арифметического
Самый простой вариант — определение цены по рынку с помощью среднего арифметического. Для этого необходимо знать количество продуктов, которые будут учитываться при расчетах, и цену каждого из них
Формула проста: нужно сложить стоимость всех товаров, а полученный результат разделить на их количество. Это и будет показатель, от которого не следует отклоняться более чем на 20% в большую либо меньшую сторону.
Эту методику расчета обычно используют, если нужно определить цену товара в группе других товаров, которые идентичны ему либо являются однородными с ним.
Товары считают идентичными, если их основные признаки полностью одинаковы или напоминают друг друга так, что разницу между ними сложно определить.
Товары называют однородными, если они:
-
имеют схожие параметры;
-
сделаны из похожих компонентов;
-
относятся к одной сфере использования.
Эта формула хорошо работает, если необходимо сравнить ценообразование в пределах одного населенного пункта (региона) или отрезка времени. Если нужно учитывать другие характеристики, например, количество продаж, разные периоды реализации или типы торговых точек, которые различаются между собой, применяются другие методы расчетов.
Средневзвешенная цена
Этой формулой часто пользуются бухгалтеры. Она применяется, когда речь идет о продукции, которая учитывается в простых единицах измерения — килограммах, литрах, метрах и так далее. Также с ней можно работать, если в вашем распоряжении есть информация о продажах однородных товаров, но объемы партий и цены на них различаются.
Для получения результата требуется:
-
умножить количество проданной продукции в натуральном исчислении на стоимость единицы товара в каждой партии, участвующей в расчетах;
-
разделить полученный результат на общее количество реализованной продукции в натуральном исчислении.
Имейте в виду, что средневзвешенная цена не совпадет со стоимостью, определенной как простое среднее арифметическое. Также если в расчетах использовались недорогие товары и однородная им продукция премиум-класса, итог может оказаться заниженным или завышенным в зависимости от объема той или иной ценовой группы.
Эта формула помогает понять, какой тип товара обеспечивает наибольшие продажи и вносит самый весомый вклад в общий товарооборот сети. Чем шире ассортимент, тем более усредненным будет показатель.
Средняя гармоническая формула расчета
Этот метод расчета применяется сравнительно редко. Но в некоторых случаях без него не обойтись, ведь он дает возможность определить ценовую политику, когда вы имеете дело с разнородной продукцией, различающейся по стоимости.
Например, сумма покупки у разных продавцов одна и та же, но при этом вы не знаете количество приобретенной продукции. Если мы попробуем на основе имеющихся данных рассчитать среднее арифметическое, то с высокой вероятностью итоговый показатель получится завышенным.
Оценку, которая ближе к действительности, даст нам формула определения средней гармонической величины.
Последовательность действий будет следующей.
-
Сначала подсчитайте количество покупок, которые будете анализировать. Примем получившееся число за X.
-
Затем разделите единицу, обозначающую каждую конкретную покупку у одного продавца, на цену, по которой приобретен товар, и сложите получившиеся значения. Примем получившийся результат за N.
-
Разделите X на N — это и будет средняя гармоническая величина.
Как найти среднюю цену
Средние величины используются в экономике для удобства расчетов. С их помощью производят вычисления, позволяющие экономить время бухгалтеров за счет применения показателей, отражающих колебания заданных значений с различной степенью точности. Для определения средних цен чаще всего используют формулы средней арифметической, средней арифметической взвешенной и средней гармонической величин.

Инструкция
Самый распространенный вид средней цены — средняя арифметическая. Она используется в случае, когда нужно рассчитать среднее слагаемое в общей совокупности данных. Чтобы найти цену методом средней арифметической, просуммируйте все используемые цены и разделите сумму на их общее количество. Например, вы продали товар, упакованный в коробки. Цены на коробки разные. Общее количество коробок равно 5. Задача — найти среднюю цену одной коробки. Используйте формулу:Цена (ср.ар.) = (10 + 15 + 10 + 25 + 15) / 5 = 15 (руб.).
Когда речь идет о продажах однородного товара по разным ценам и разным количеством партий, очевидно, средняя арифметическая величина не будет отражать реальных цен. В этом случае используйте среднюю арифметическую взвешенную величину. Она позволяет определить цену через отношение общей суммы проданных товаров к их количеству. Например, вы продали разные партии продукции по разным ценам:10 ед. — по 15 руб;15 ед. — по 10 руб;25 ед. — по 20 руб. Задача — найти среднюю цену одной единицы продукции. Определите общий объем продаж:10 × 15 + 15 × 10 + 25 × 20 = 800 (руб.).Общее количество проданных единиц — 50 — известно. Используйте формулу:Цена (ср.ар.вз.) = 800 / 50 = 16 (руб.).
Если же вам нужно рассчитать среднюю цену по разнородному товару различной стоимости, используйте среднюю гармоническую величину. Она тоже рассчитывается как отношение объема реализации к количеству проданных товаров. Однако позволяет учесть разницу в стоимости каждого вида продукции. Например, вы продали три разных партии товаров по разным ценам:Товар А стоимостью 50 руб. за единицу на 500 руб;Товар Б — 40 руб. — на 600 руб;Товар В — 60 руб. — на 1200 руб.Используйте формулу:Цена (ср.гарм.) = (500 + 600 + 1200) / (500/50) + (600/40) + (1200/60) = 51,11 (руб.).
Видео по теме
Источники:
- как найти среднюю арифметическую
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как посчитать среднюю цену товара
Средняя цена на товар или товарную группу — информативный и востребованный показатель при анализе хозяйственной деятельности торговой организации. Особенно он значим в рознице — где различные «манипуляции» с ценами регулярны. Исчисление средних цен в этом сегменте сейчас значительно облегчается благодаря оперативному доступу к первичным данным, которые находятся у заинтересованного лица прямо под рукой — на кассе предприятия.
Формулы средних цен
Средняя цена — показатель, который вычисляется в рамках анализа уровня цен на товар или товары, которые объединены в однотипные товарные группы. При сопоставлении средних цен за те или иные периоды (месяцы, кварталы, годы) можно подсчитать, к примеру, уровень инфляции — если говорить о макроэкономических задачах.
В бизнесе же вычисление средних цен может быть обусловлено, как вариант, подсчетом показателей хозяйственной эффективности — в сопоставлении со средними ценами конкурентов. Если выяснится, что у конкурентов при аналогичных средних ценах рентабельность выше, то значит, что в бизнес-модели исследуемого торгового предприятия что-то не так.
Аналогично средние цены применимы в контексте сравнения эффективности двух или нескольких магазинов одной розничной сети: применение показателя, о котором идет речь, позволит выявить наиболее прибыльную бизнес-модель в рамках соответствующих торговых точек.
При этом есть несколько разновидностей средней цены. К числу наиболее часто применяемых относят нижеследующие.
Простая средняя арифметическая
Вычисляется она по формуле:
СРЕД (ПА) = СУММА (Цi) / СУММА (Оi),
где:
- Цi – цена на товар;
- Оi — объем товара, по которому считается средняя цена.
Простая средняя арифметическая применяется, если в распоряжении есть только 2 даты, на которые установлены анализируемые цены. Например — начало или конец месяца.
Средняя арифметическая взвешенная
Ее формула — следующая:
или простыми словами:
СРЕД (САВ) = СУММА (Ц * О) / СУММА О,
где:
- Ц — средняя цена за единицу товара за период реализации (месяц, квартал);
- О — объем реализованных товаров в тех или иных натуральных показателях (килограммах, литрах и иных) за все периоды реализации (за расчетный период — например, год).
Применяется рассматриваемая разновидность средней цены, если в распоряжении у статиста есть необходимые данные о ценах и объемах проданного товара за достаточно длительный период его реализации.
Средняя хронологическая
Вот ее формула:
или по-другому:
СРЕД (ХРОНОЛОГИЧ) = ((Ц1 / 2 + Ц2 + Ц3 + Ц4 + … + Цt / 2)) / t – 1,
где:
- Ц1, Ц2, Ц3, Цt – цены по состоянию на начало или конец месяца в расчетном периоде;
- t – количество месяцев в определенном периоде.
Рассматриваемая величина применяется, если в распоряжении статиста имеются сведения о ценах по состоянию на даты, между которыми промежутки времени — равные.
Средняя хронологическая взвешенная
Ее формула следующая:
или по-простому:
СРЕД (ХРОНОЛОГ ВЗВЕШ) = СУММА (Цсрi * ti) / СУММА ti,
где:
- Цсрi – средняя цена за расчетный период;
- ti – количество месяцев в расчетном периоде.
Средняя хронологическая взвешенная используется, если есть данные по неравным интервалам времени.
Средняя гармоническая взвешенная
Считается она по нижеследующей формуле:
или другими словами:
СРЕД (ГАРМОНИЧ ВЗВЕШ) = СУММА (Ц * О) / СУММА (Ц * О) / Ц),
где:
- Ц — цена товара за расчетный период;
- О — объем реализованного товара по соответствующей цене за отчетный период.
То есть, Ц * О — выручка за расчетный период по конкретному товару по конкретной цене.
Средняя гармоническая цена — хороша при анализе данных по товарам, реализованным на разных торговых точках за один и тот же период.
Рассмотрим практические примеры использования указанных видов средних цен.
Как рассчитать среднюю цену товара на примерах
Пример 1.
Надо определить среднюю цену 1 кг яблок по ценам реализации, действовавшим в течение года (в каждом из расчетных кварталов). Поскольку период подсчета средней цены — длительный, то будем считать среднюю арифметическую взвешенную цену.
Условимся, что мы продали:
- в 1-м квартале — 5000 кг яблок по цене 100 рублей за 1 кг;
- во 2-м квартале — 6000 кг яблок по цене 120 рублей за 1 кг;
- в 3-м квартале — 7000 кг яблок по цене 140 рублей за 1 кг;
- в 4-м квартале — 8000 кг яблок по цене 150 рублей за 1 кг.
Расчет средней арифметической взвешенной цены для данного примера:
СРЕД (ПА) = (5000 * 100 + 6000 * 120 + 7000 * 140 + 8000 * 150) / (5000 + 6000 + 7000 + 8000) = 130,77 рублей.
Пример 2.
Нужно рассчитать среднюю цену товара за 1-е полугодие, если в распоряжении есть фиксированные цены по состоянию на начало каждого месяца 1-го полугодия. В данном случае подойдет формула средней хронологической цены.
Условимся, что наш товар — груши, и мы устанавливали на них следующие цены:
- по состоянию на 1 января — 100 рублей за 1 кг;
- по состоянию на 1 февраля — 120 рублей за 1 кг;
- по состоянию на 1 марта — 140 рублей за 1 кг;
- по состоянию на 1 апреля — 145 рублей за 1 кг;
- по состоянию на 1 мая — 150 рублей за 1 кг;
- по состоянию на 1 июня — 155 рублей за 1 кг.
При этих условиях расчет средней хронологической цены выглядит так:
СРЕД (ХРОНОЛОГИЧ) = (100 / 2 + 120 + 140 + 145 + 150 + 155 / 2) / 6 — 1 = 136,5 рублей
Пример 3.
Нам надо рассчитать среднюю цену 1 кг яблок, которые реализованы на разных торговых точках. Лучше всего подойдет средняя гармоническая цена. Условимся, что мы продали:
- на точке А яблок на сумму 10 000 рублей по цене 100 рублей за 1 кг яблок;
- на точке Б яблок на сумму 12 000 рублей по цене 120 рублей за 1 кг яблок;
- на точке В яблок на сумму 15 000 рублей по цене 145 рублей за 1 кг яблок;
- на точке Г яблок на сумму 14 000 рублей по цене 150 рублей за 1 кг яблок.
Считаем требуемый показатель:
СРЕД (ГАРМОНИЧ ВЗВЕШ) = (10 000 + 12 000 + 15 000 + 14 000) / (10 000 / 100 + 12 000 / 120 + 15 000 / 145 + 14 000 / 150) = 128,53 рублей
Применение указанных формул потребует наличия исходных данных. Рассмотрим, откуда их может взять современное торговое предприятие.
Где взять показатели для расчета
Сведения по ценам могут быть взяты:
- Из традиционных источников — например, представленных регистрами цен в товароучетной системе.
Эти регистры сообщают статисту точную информацию — но не всегда знакомят его со сведениями о фактической реализации. Отражение таких данных в товароучетной платформе может быть не предусмотрено.
- Из инновационных источников — записей:
- в кассовом модуле товароучетной платформы, которая интегрирована с онлайн-кассой;
- в модуле статистики Оператора фискальных данных.
Сведения фактически о каждом товаре, который отпускается через кассу, входят в состав фискальных данных, которые направляются в ОФД. Многие операторы формируют подробную аналитику по этим данным. В нее включаются, в частности, сведения о ценах по товарам, что были отпущены через онлайн-кассу.
Например, пользователь Яндекс.ОФД может ознакомиться с ценами на реализованные товары, что отражены в фискальных данных, заказав специальный отчет (заказываемый тип отчета — «Товары»). Составление отчета предполагается в привязке к каждой конкретной кассе.
Преимущество обращения к базам ОФД — в том, что там практически безошибочно отражены данные с учетом возвратов (которые, соответственно, снижают выручку — учитываемую, в частности, в формуле средней гармонической взвешенной цены). Дело в том, что во всех случаях возвраты включаются в фискальные данные.
Резюме
Средние цены — показатель, который может применяться как в макроэкономических исследованиях, так и на уровне финансового анализа деятельности отдельно взятого хозяйствующего субъекта. Исчислены они могут быть разными способами — в зависимости от состава вводных данных. Которые статист имеет возможность получить в том числе из отчетности ОФД по онлайн-кассам торгового предприятия.
Выбор показателя для расчета зависит от ваших целей. Например, магазин элитного алкоголя с широким ассортиментом реализует 10% алкогольной продукции и основные продажи 90% составляет недорогой сопутствующий товар (пора бы его закрыть, ну речь не о том). При расчете средней цены на товар мы увидим высокую среднюю цену за счет широкого ассортимента алкоголя. Другими словами, мы как покупатель заходим в магазин и видим все цены, но не учитываем их продажи. При расчете средневзвешенной цены мы увидим низкую цену за счет реализации недорогого товара.
Вывод:
Показатель средней цены необходимо использовать при расчете уровня позиционирования цены для покупателей. Чем шире ассортимент товара, тем более усредненный показатель цены.
Показатель средневзвешенной цены используют при расчете средней цены реализуемого товара. Чем большие продажи у товара, тем больший вклад он оказывает на средневзвешенную цену.
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.