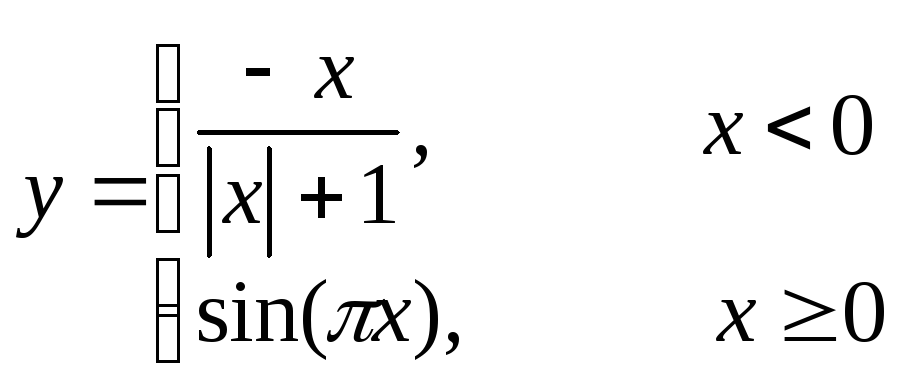Пример
1. ( Функция
одной переменной для шагового аргумента).
Построить
таблицу значений функции
для аргумента x,
изменяющегося от 0 до 1,5 с шагом 0,1.
Построить график функции.
Решение.
Решение
разбивается на два основных этапа:
построение таблицы значений функции и
построение графика функции.
Построение
таблицы
-
Наберем заголовки
столбцов для x
и y
в ячейках A1,
B1. -
Наберем первое
значение x,
равное 0, в ячейку A2. -
Выполним команду
Правка|Заполнить|Прогрессия,
зададим в диалоге Расположение
в столбце,
Арифметическая
прогрессия, Шаг
0,1, Предельное
значение 2.
Заполнятся ячейки A4:A22. -
В ячейку B2
введем формулу: =SIN(4*A2)^2/(A2+1)
и скопируем ее в ячейки B3:B22 -
Выполним
форматирование данных (чисел) и обрамление
таблицы. Фрагмент рабочего листа с
таблицей показан на рис.5.1.
П
остроение
графика функции. Для
построения графика выделим диапазон
данных (ячейки A1:B22)
и построим точечную диаграмму, вид
которой представлен на рис. 5.2.
Рис.
5.1. Таблица значений функции для примера
1
Рис. 5.2. График
(точечная диаграмма) примера 1
Пример
2. (Функция,
заданная различными аналитическими
выражениями (сложная функция)). Построить
таблицу значений и график функции
для аргумента x
, изменяющегося от -2 до 2 с шагом 0,2
Решение
Построение
таблицы.
Решение
выполним
в том же файле, что и предыдущий пример,
но
на новом листе Excel.
Последовательность заполнения ячеек
аналогична примеру 1.
В
ячейку B2
введем формулу:
=ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2))
и скопируем ее в
нижележащие ячейки для всех значений
x
.
П
Рис. 5.4. График
сложной функции
Рис.
5.3. Таблица значений сложной функции
остроение
графика функции также
полностью аналогично построению
предыдущего примера, если заданная
функция непрерывна.
Замечание.
Если функция терпит разрыв при переходе
от одного аналитического выражения к
другому, то нужно построить на одной
диаграмме два графика, каждый из которых
отвечает области непрерывности функции.
В случае разрывной функции можно строить
один график, если выбрать вид графика
из отдельных точек
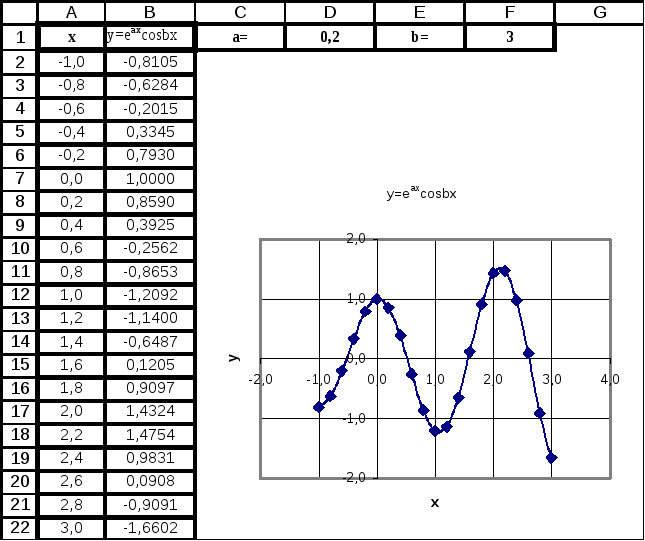
Пример
3. (Функция,
зависящая от параметра). Построить
таблицу значений и график функции
для аргумента x
, изменяющегося
от -1 до 3 с шагом 0,2 при заданных значениях
a
и b.
Решение
-
Введем заголовки
столбцов для x
и y
в ячейки A1,
B1
и значения a,
b
в отдельные ячейки D1,
F1. -
Заполним столбец
A2:A22
значениями x. -
Введем формулу
для y
в ячейку B2
=EXP($D$1*A2)*COS($F$1*A2)
и скопируем ее в ячейки B3:B22.
-
П
Рис. 5.5. Таблица и
график функции, зависящей от параметра
остроим
график аналогично примеру 1 (см. рис.5.5)
Замечание.
Меняя значения параметров, можно получить
совершенно другое поведение функции.
Рекомендуется проанализировать поведение
функции при a>0
и a<0,
а также
рассмотреть уменьшение и увеличение
b.
Пример
4. (Функция,
заданная параметрическими уравнениями).
Вычислить
таблицу значений функции, заданной
параметрическими уравнениями и построить
ее график. В качестве примера рассмотрим
построение окружности.
Параметрические
уравнения окружности рассмотрим для
значений параметра, пробегающих полный
оборот вокруг начала координат:

Построение
таблицы значений функции
-
Перейдем на новый
рабочий лист. -
Зададим заголовки
столбцов t,
x,
y. -
Заполним первый
столбец значениями t,
применив еще один способ задания
аргумента: каждое последующее значение
вычислим через предыдущее, добавляя
шаг. В ячейке D2
вычислим
по формуле =ПИ()/16. В ячейку A2
введем 0, в ячейку A3
введем формулу =A2+$D$2,
которую копируем вниз до значения 2. -
Введем в ячейку
B2
формулу =COS(A2);
в ячейку C2
формулу =SIN(A2) -
Выделим ячейки
B2,
C2
и копируем их для всех значений t
с помощью заполнения. -
Форматируем
таблицу по образцу.
Построение
графика функции
-
Выделим диапазон
B1:C22 -
Вызовем Мастер
диаграмм и
построим точечную диаграмму. В процессе
построения зададим заголовки диаграммы
и осей, уберем легенду, назначим линии
сетки. -
Затем отредактируем
диаграмму: по команде Формат
оси зададим
точность – один знак после запятой, по
команде Формат
области построения укажем
рамку Невидимая. -
Выполним
растяжение-сжатие диаграммы, так чтобы
получилась окружность, а не эллипс.
Результат
построения показан на рис. 5.7.
Рис.
5.7. График функции, заданной параметрическими
уравнениями
Рис.
5.6. Таблица функции, заданной
параметрическими уравнениями
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление значений функции
Онлайн калькулятор поможет найти значения функции в заданном интервале, построить таблицу значений функции онлайн, табулировать функцию.
Вычисляет значения функции одной переменной y для заданных значений переменной x. Функция задается при помощи формулы, пример:
Построить таблицу значений функции f(x)=x/(x+1) на отрезке от 0 до 6 с шагом в единицу.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

In mathematics, a function defines a relationship between an independent variable and a dependent variable. In simple words, a function is a relationship between inputs and outputs in which each input is connected to exactly one output. If every element in set A has exactly one and only one image in set B, then the relation is said to be a function. Every function has a domain and a codomain, where a domain is a set of input values and a codomain, or range, is the set of possible output values for which the function is defined. The domain and codomain of a function are non-empty sets. If there exists a function from A → B and (a, b) ∈ f, then f (a) = b, where “a” is the image of “b” under “f” and “b” is the preimage of “b” under “f” and set A is the domain of the function and set B is its co-domain.
Examples of a function
- The formula for the circumference/perimeter of a circle is P = 2πr, where r is the radius of a circle. We can say that circumference/perimeter (P) is dependent on the radius (r) of the circle. In the language of functions, we say that P is defined as a function of r.
- The area (A) of a square A is a function of its side length. The dependence of A on s is given by A = 4s2.
Table Values of a Function
The table values of a function are referred to as the list of numbers that can be used to substitute for the given variable. By using this variable within the equation or in the other function, it is simple to determine the value of the other variable or the equation’s missing integer. In the table of values of a function, there are two kinds of variables, namely an independent variable and a dependent variable. For any equation of a function, an independent variable is selected independently to determine the value of a dependent variable, which is the output of the given function. The table of values is unique for every function. A graph of the given function can be plotted easily after the determination of the values of the independent and dependent variables. There are many uses and applications for tables of values of a function. These are used in the fields of mathematics, physics, and engineering.
How to make the Table of Values of a Function?
A function is typically represented by f(x), where x is the input, and its general representation is y = f(x).
- Create the table first, then choose a range of input values.
- In the left-hand side column, substitute each input value into the given equation.
- To determine the output value, evaluate the equation in the middle column. (A middle column is optional as the table of values just contains the input (independent variable) and output (dependent variable) pair.)
- Now, note down the output values in the right-hand side column.
Let us solve an example to understand the concept better.
Example: Write the table of the value for the function y = √x.
Here, the input is x and the output is y, where y = √x.
x value
Equation
y = √x
y value
0
y = √0 = 0
0
1
y = √1 = 1
1
4
y = √4 = 2
2
9
y = √9 = 3
3
16
y = √16 = 4
4
25
y = √25 = 5
5
Sample Problems
Problem 1: Write the table of values for the function y = 3x + 5.
Solution:
Here, the input is x and the output is y, where y = 3x + 5.
x value
Equation
y = 3x +5
y value
-2
y = 3(-2) + 5 = -6 + 5 = -1
-1
-1
y = 3(-1) + 5 = -3 + 5 = 2
2
0
y = 3(0) + 5 = 0 + 5 = 5
5
1
y = 3(1) + 5 = 3 + 5 = 8
8
2
y = 3(2) + 5 = 6 + 5 = 11
11
Problem 2: Write the table of values for the function P = 4s, where P is the perimeter of a square and a is its side length.
Solution:
Here, the input is s and the output is P, where P = 4s.
s value
Equation
P = 4s
P value
1
4 × 1 = 4
4
2
4 × 2 = 8
8
3
4 × 3 = 12
12
4
4 × 4 =16
16
5
4 × 5 = 20
20
Problem 3: Write the table of values for the function y = 2x + 3x.
Solution:
Here, the input is x and the output is y, where y = 2x + 3x .
x value
Equation
y = 2x + 3x
y value
-2
y = 2-2 + 3-2 = 1/22 + 1/32 = 1/4 + 1/9 = 13/36 = 0.3611
0.3611
-1
y = 2-1 + 3-1 = 1/2 + 1/3 = 5/6 = 0.834
0.834
0
y = 20 + 30 = 1 + 1 = 2
2
1
y = 21 + 31 = 2 + 3 = 5
5
2
y = 22 + 32 = 4 + 9 = 13
13
3
y = 23 + 33 = 8 + 27 = 35
35
Problem 4: Write the table values for the function y = cos x × sin x.
Solution:
Here, the input is x and the output is y, where y = cos x × sin x.
x value
Equation
y = cos x × sin x
y value
0°
y = cos 0 sin 0 = 1 × 0 = 0
0
30°
y = cos 30 sin 30 = √3/2 × 1/2 = 3/4
√3/4
45°
y = cos 45 sin 45 = 1/√2 × 1/√2 = 1/2
1/2
60°
y = cos 60 sin 60 = 1/2 × √3/2 = 3/4
√3/4
90°
y = cos 90 sin 90 = 0 × 1 = 0
0
180°
y = cos 180 sin 180 = -1 × 0 = 0
0
Problem 5: Write the table values for the function y = x2 – 5x + 6.
Solution:
Here, the input is x and the output is y, where y = x2 – 5x + 6.
x value
Equation
y = x2 – 5x + 6
y value
-3
y = (-3)2 – 5(-3) + 6 = 9 + 15 + 6 = 30
30
-2
y = (-2)2 – 5(-2) + 6 = 4 + 10 + 6 = 20
20
-1
y = (-1)2 – 5(-1) + 6 = 1 + 5 + 6 = 12
12
0
y = 02 – 5(0) + 6 = 0 – 0 + 6 = 6
6
1
y = 12 – 5(1) + 6 = 1 – 5 + 6 = 2
2
2
y = 22 – 5(2) + 6 = 4 – 10 + 6 = 10- 10 = 0
0
3
y = 32 – 5(3) + 6 = 9 – 15 + 6 = 15 – 15 = 0
0
Last Updated :
19 Jul, 2022
Like Article
Save Article
Способы задания функций
«Задать функцию» означает установить правило (закон), с помощью которого по данным значениям независимой переменной (из числа возможных) следует находить соответствующие им значения функции.
Табличный способ
| х | 1 | 2 | 3 | 4 | 5 | 6 |
| у | 2 | 4 | 6 | 8 | 10 | 12 |
При этом способе задания функции в таблицу вносятся значения независимой переменной х и соответствующие им значения зависимой переменной у. Такой способ широко распространен: таблицы логарифмов, корней, степеней чисел.
Основное преимущество табличного способа задания функции — возможность, не проводя дополнительных измерений и вычислений, определить те или другие конкретные значения сразу, если известен аргумент. Недостатком способа является то, что таблица определяет функцию не полностью, а лишь для некоторых значений аргумента: в ней отсутствуют промежуточные значения и в целом их количество ограничено. Также таблица не дает полного представления о характере зависимости функции от изменения аргумента.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Применение табличного способа оправдано в том случае, когда область определения функции является дискретным конечным множеством. В некоторых случаях с помощью интерполяции можно приближенно вычислить значения функции, отсутствующие в таблице и соответствующие промежуточным значениям аргумента.
Графический способ
При графическом способе в системе координат строится график, множество точек которого соответствуют уравнению y=f(x), задающему функцию. Ось абсцисс задает значения аргумента, ось ординат — функции.
Главный недостаток графического способа задания функции заключается в том, что с помощью графика, даже зная численное значение аргумента, невозможно точно определить значение функции. Однако этим способом часто пользуются в физике и технике, так как благодаря своей наглядности он позволяет представить характер заданной функции в целом.
Часто графическое задание функции комбинируют с аналитическим способом, а именно с уравнением, задающим данный график. Такое сочетание позволяет представить функцию наглядно, и при этом точно рассчитать необходимые значения.
Аналитический способ
Аналитический способ состоит в том, что связь между аргументом и функцией выражается с помощью формулы, представляющей собой уравнение. В левой части уравнения находится зависимая переменная у, в правой — выражение, состоящее из независимой переменной х, постоянных, математических операций и известных элементарных функций. Такой способ задания функции очень распространен, так как дает возможность для каждого возможного значения аргумента найти соответствующее ему значение функции точно или с большой точностью.
Зависимость y от x задана явно, если уравнение имеет вид y = f(x).
Если формула выглядит как F(x,y) = 0, то функция задана неявно.
Достоинства этого способа: компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента, возможность применения к данной функции аппарата математического анализа. Недостатком является отсутствие наглядности, которое можно компенсировать построением графика.
Интервальный способ
Функция может быть определена разными формулами на разных интервалах значения аргумента.
Пример 2
(y=left{begin{array}{l}frac{x+1}{x^2+x+2},;x>3\x^2-1,;xleq3end{array}right.)
Параметрический способ
Для выражения функции параметрическим способом вводится дополнительная переменная t, через которую задают значения х и у.
(left{begin{array}{l}у=у(t)\x=x(t)end{array}right.)
Пример 3
(left{begin{array}{l}у=sin t\x=cos3tend{array}right.)
Словесный способ
При выражении функции словесным способом, характер зависимости выражен словами.
Пример 4
Функция (E(x) = [x]) — целая часть числа х.
Такой функцией обозначают наибольшее из целых чисел, которое меньше либо равно x. Если x=а+b, где а — целое число, а b ∈ [0; 1), то [x] = а. Функция E(x) = [x] постоянна на промежутке [a; a+1), и на нем [x] = a.
Пример 3
Функция (y = {x}) — дробная часть числа х.
(y ={x} = x — [x]), где [x] — целая часть числа x. Если x — произвольное число, то его можно представить в виде (x=а+b (а = [x])), где a — целое число и b∈[0; 1), поэтому ({x}=a+b-a=b).
Недостатками данного способа задания функции являются невозможность проведения сложных вычислений и отсутствие наглядности. Главное преимущество — возможность задать те функции, которые сложно выразить аналитически.
Пример решения задачи
Дано: функция задана уравнением (у=х^2+1).
Найти: построить график функции и составить таблицу для целых значений (х∈[0; 5]).
Решение:
| х | 0 | 1 | 2 | 3 | 4 | 5 |
| у | 1 | 2 | 5 | 10 | 17 | 26 |
Задача