Сопряженная функция как найти

В какой области?

[math]u(x,y)=frac{x}{x^2+y^2}[/math]

Условия Коши — Римана:

[math]frac{partial u}{partial x}=frac{partial v}{partial y}hspace{14mm}(1)[/math]
[math]frac{partial u}{partial y}=-frac{partial v}{partial x}hspace{12mm}(2)[/math]

Имеем

[math]frac{partial u}{partial y}=-frac{2xy}{(x^2+y^2)^2}[/math]

Используя (2) получаем

[math]v(x,y)=-intfrac{-2xy}{(x^2+y^2)^2}dx=yintfrac{2x}{(x^2+y^2)^2}dx=-frac{y}{x^2+y^2}+k(y)[/math]

Находим производную [math]v[/math] по [math]y[/math]

[math]frac{partial v}{partial y}=frac{partial}{partial y}left(-frac{y}{x^2+y^2}+k(y)right)=frac{y^2-x^2}{(x^2+y^2)^2}+k'(y)[/math]

и производную [math]u[/math] по [math]x[/math]

[math]frac{partial u}{partial x}=frac{y^2-x^2}{(x^2+y^2)^2}[/math]

Из (1) получаем теперь

[math]frac{y^2-x^2}{(x^2+y^2)^2}=frac{y^2-x^2}{(x^2+y^2)^2}+k'(y)[/math]

Оттуда

[math]k'(y)=0[/math]

следовательно

[math]k(y)=C[/math]

Окончательно получаем

[math]v(x,y)=-frac{y}{x^2+y^2}+C[/math]

Дважды
непрерывно дифференцируемая функция
называетсягармонической
в
области D
плоскости
(Z),
если во всех точках этой области
выполняется равенство

(6).

Отметим,
что уравнение (6) называют уравнением
Лапласа
и коротко записывают

(7).

Две
функции u(x,y)
и v(x,y)
области D
плоскости
(Z)
называются сопряженными
гармоническими функциями
в этой области, если во всех точках этой
области выполняются условия Коши-Римана
,.

Мы
покажем, что действительная и мнимая
части u(x,y),
v(x,y)
в аналитической области D
функции W
= f(Z)
являются сопряженными гармоническими
функциями. Так как у аналитической
функции действительная и мнимая части
удовлетворяют условиям Коши-Римана, то
нам достаточно доказать гармоничность
функций u(x,
y),
v(x,
y)
в области D.

Отметим,
что аналитическая в области D
функция f(Z)
имеет производную всех порядков (без
доказательства). Поэтому действительная
и мнимая части этой функции имеют в
области D
производные всех порядков по всем
переменным, и эти производные непрерывны.
Поэтому в частности будут существовать
все непрерывные производные 1^го
и 2^го
порядка. То есть эти функции будут дважды
непрерывно дифференцируемы.

Воспользуемся
теперь условием Коши-Римана
,.

Продифференцируем
первое равенство по x,
а второе – по y,
и сложим. Получим
(так как смешанные производные, когда
непрерывны, равны). Следовательно,u-гармоническая
функция, аналогично доказывается, что
v
гармоническая функция, следовательно,
u
и v
– сопряженные гармонические функции.

Построение мнимой части аналитической функции по ее действительной части

Пусть
в некоторой области D
плоскости известна действительная
часть u(x,y)
аналитической функции. Требуется
построить ее мнимую часть v(x,y)
в этой области. Как мы знаем
;.

Составим
выражение
.
Очевидно,,
так как(Лапласиян).
Следовательно, выражение
будет полным дифференциалом некоторой
функции.

Пусть
D
– это односвязная область, тогда
криволинейный интеграл
не будет зависеть от формы и пути,
соединяющего точки ()
и (x,y),
принадлежащие D
(лежащие в D)
и, следовательно, будет представлять
собой некоторую функцию
верхнего предела. Как мы знаем из теории
криволинейных интегралов, эта функция
дифференцируема в областиD,
и ее частные производные
исоответственно равныp(x,y),
Q(x,y).
Следовательно, в области D
частные производные функций v(x,y)
и
совпадают. Поэтому эти функции могут
отличаться лишь на константу, следовательно,.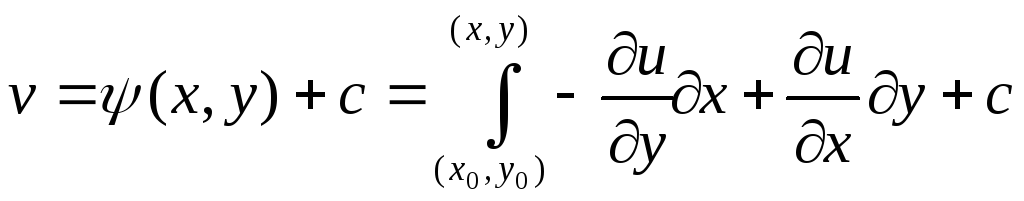
Как видно, мнимая часть аналитической
функции определяется с точностью до
постоянной.

Отметим,
что, если известно значение аналитической
функции W
= f(Z)
в
какой-нибудь одной точке
(),
то мнимая частьv(x,y)
этой функции и, следовательно, сама
аналитическая функция f(Z)
определяется однозначно по действительной
части u(x,y).

В
случае многосвязной области D
криволинейный интегралпредставляет многозначную функцию.
Поэтому мнимая частьv(x,y)
будет также, вообще говоря, многозначной
функцией. Действительная часть по мнимой
части строится аналогичным образом.

Отметим,
что мнимая часть v(x,y)
функции
является действительной частью функции.
Отметим, что мнимая часть по действительной
находится другим способом. Пишут
уравнения;.
Интегрируют одно из равенств (первое
поx)

(1),
затем дифференцируют полученное
равенство по переменной y
.
Отсюда находяти подставляют его в (1).

Пример.

Построить
мнимую часть числа по действительной

;

.
Интегрируем по x.

.
Находим производную по y
и приравниваем

,
и теперь интегрируем
.

Таким
образом,

,
,,,
следовательно,;

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определения

Сопряженная функция

Определение.
Функцией, сопряженной к $$f$$, называется функция, определенная формулой
[
f^*(x^*) = underset{x in X}{text{sup}}left( leftlangle x^*,x rightrangle — f(x) right),
]
где $$x^*$$ — обозначение для аргумента сопряженной функции.

Из определения сопряженной функции вытекает неравенство Юнга-Фенхеля
[
f^*(x^*) + f(x) geqslant leftlangle x, x^* rightrangle ; forall x,x^* in X.
]
Вторая сопряженная функция $$f^{**}$$ определяется по формуле $$f^{**}=(f^*)^*$$.

Пример 1.
Для аффинной функции $$f(x) = leftlangle a,x rightrangle + b$$ сопряженная функция вычисляется по формуле
[
f^*(x^*) =
begin{cases}
-b, &x^* = a;\
+infty, &x^* neq a.
end{cases}
]

Пример 2.
Для произвольной выпуклой функции $$f$$ умножение на положительный скаляр $$lambda gt 0$$ определяется соотношением
[
left( lambda f right)(x) = lambda f(x), ; forall x in X.
]
Непосредственно вычисляется, что
[
left( lambda f right)^*(x^*) equiv lambda f^*(x^*/lambda), ; x^* in X.
]
Пример 3.
Пусть $$M$$ — евклидово пространство, и пусть $$f: M to mathbb{R}$$ — функция $$f(x) = leftlangle a,x rightrangle$$, где $$a in M$$. Поскольку
[
underset{xin M}{text{sup}}left{ leftlangle s,x rightrangle — leftlangle a,x rightrangle right} = underset{xin M}{text{sup}} leftlangle s-a,x rightrangle =
begin{cases}
0, &s = a;\
+infty, &s neq a.
end{cases}
]
для всех $$s in M$$, то сопряженная функция $$f^*$$ — индикаторная функция $$delta_left{ a right}$$ одноэлементного множества $$left{ a right}$$.

Вспомогательная лемма

Лемма.
Пусть функция $$f$$ — выпуклая, замкнутая, собственная. Тогда $$f^*$$ — также собственная функция.

Доказательство

Докажем, что $$f^∗(x^∗) gt -infty$$ $$forall x^∗ in X$$. Возьмем $$x_0 in text{dom} , f neq varnothing$$. Тогда $$f^∗(x^∗) geqslant leftlangle x_0, x^∗rightrangle − f(x_0) gt -infty$$, так как $$f(x_0) lt +infty$$.

Остается доказать существование вектора $$y^∗ in X$$, для которого $$f^∗(y^∗) lt +infty$$.

Очевидно, точка $$(x_0, f(x_0) − 1)$$ не принадлежит замкнутому выпуклому множеству $$text{epi} , f$$. Следовательно, по теореме об отделимости ее можно строго отделить от выпуклого замкнутого множества $$text{epi} , f$$. Поэтому существуют $$y^∗ in X$$ и $$beta in mathbb{R}$$ такие, что
begin{equation}
label{1}
underset{(x,alpha) in text{epi} , f}{text{sup}}left{ betaalpha + leftlangle y^*,x rightrangle right} lt beta (f(x_0) — 1) + leftlangle y^*, x_0 rightrangle.
end{equation}
Докажем, что $$beta lt 0$$. Действительно, предположим обратное. Случай $$beta gt 0$$ невозможен, так как $$(x_0, alpha) in text{epi} , f;$$ $$forall alpha
geqslant f(x_0) neq +infty$$ и, значит, при $$beta gt 0$$ имеет место $$underset{(x_0,alpha) in text{epi} , f}{text{sup}}beta alpha = +infty$$, что противоречит неравенству ($$ref{1}$$).

Пусть теперь $$beta = 0$$. Тогда
[
underset{(x,alpha) in text{epi} , f}{text{sup}} leftlangle y^*, x rightrangle lt leftlangle y^*, x_0 rightrangle,
] хотя
[
(x_0, f(x_0)) in text{epi} , f implies underset{(x,alpha) in text{epi} , f}{text{sup}} leftlangle y^*, x rightrangle geqslant leftlangle y^*, x_0 rightrangle.
]
Полученное противоречие доказывает, что $$beta lt 0$$. Поэтому, в силу положительной однородности неравенства ($$ref{1}$$) по переменной $$(y^∗, beta)$$,
не теряя общности, будем считать, что $$beta = -1$$.

В силу ($$ref{1}$$) имеем
[
f^*(y^*) = underset{x}{text{sup}} left{ -f(x) + leftlangle y^*,x rightrangle right} = underset{(x,alpha) in text{epi} , f}{text{sup}} left{ -alpha + leftlangle y^*,x rightrangle right} lt -(f(x_0) — 1) + leftlangle y^*, x_0 rightrangle implies f^*(y^*) lt +infty.
]
Значит, функция $$f^*$$ является собственной.$$;;blacksquare$$

Теорема Фенхеля-Моро

Теорема.
Пусть функция $$f$$ — выпуклая, замкнутая, собственная. Тогда $$f^{**} = f$$.

Доказательство

Покажем, что $$f^{**} leqslant f$$. В силу неравенства Юнга-Фенхеля $$forall x in X$$ имеем
[
f(x) geqslant leftlangle x, x^* rightrangle — f^*(x^*) ; forall x^* in X implies f(x) geqslant underset{x^*}{text{sup}}left{ leftlangle x, x^* rightrangle — f^*(x^*) right} = f^{**}(x).
]
Остается показать, что $$f^{**} geqslant f$$.
Предположим противное. Тогда существует $$x_0 in X$$, для которого $$f^{∗∗}(x_0) lt f(x_0)$$. Поэтому точка $$(x_0, f^{∗∗}(x_0))$$ строго отделима от выпуклого замкнутого множества $$text{epi} , f$$. Значит, существуют $$y^∗ in X$$ и $$beta in mathbb{R}$$ такие, что
begin{equation}
label{2}
beta f^{**}(x_0) + leftlangle y^*,x_0 rightrangle gt underset{(y,alpha) in text{epi} , f}{text{sup}}left( betaalpha + leftlangle y^*,y rightrangle right).
end{equation}
Докажем, что $$beta lt 0$$. Действительно, случай $$beta gt 0$$ невозможен, что обосновывается так же, как и при доказательстве вспомогательной леммы, с учетом того, что $$text{dom} , f neq varnothing$$.

Пусть теперь $$beta = 0$$. Тогда
[
gamma = leftlangle y^*, x_0 rightrangle — underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle gt 0.
]
В силу леммы функция $$f^*$$ является собственной. Поэтому существует $$y^*_1 in text{dom} , f^* neq varnothing$$. Для $$t gt 0$$ имеем
[
f^*(y^*_1+ty^*) = underset{y in text{dom} , f}{text{sup}} left( leftlangle y^*_1 + ty^*, y rightrangle — f(y) right) leqslant underset{y in text{dom} , f}{text{sup}} left( leftlangle y^*_1, y rightrangle — f(y) right) + t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle = f^*(y^*_1) + t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle.
]
Отсюда в силу неравенства Юнга-Фенхеля для функции $$f^*$$ вытекает
[
f^{**}(x_0) geqslant leftlangle y^*_1 + ty^*, x_0 rightrangle — f^*(y^*_1 + ty^*) geqslant leftlangle y^*_1, x_0 rightrangle + t leftlangle y^*, x_0 rightrangle — f^*(y^*_1) — t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle = leftlangle y^*_1, x_0 rightrangle — f^*(y^*_1) + tgamma, ;forall tgt 0.
]
Получили противоречие, так как $$gamma gt 0$$ и, значит, при больших $$t$$ значение $$tgamma$$ может быть сделано как угодно большим и, следовательно, при достаточно больших $$t gt 0$$ последнее неравенство выполняться не может.

Таким образом, доказано, что $$beta lt 0$$; значит, не теряя общности рассуждений, будем считать, что $$beta = -1$$. В силу неравенства ($$ref{2}$$) имеем
[
-f^{**}(x_0) + leftlangle y^*, x_0 rightrangle gt underset{y in text{dom} , f}{text{sup}} left( -f(y) + leftlangle y^*,y rightrangleright) = f^*(y^*),
]
откуда
[
leftlangle y^*, x_0 rightrangle gt f^*(y^*) + f^{**}(x_0),
]
что противоречит неравенству Юнга–Фенхеля для функции $$f^∗$$. Полученное противоречие доказывает, что $$f^{**} geqslant f$$ и, значит, $$f^{∗∗} = f$$. $$;;blacksquare$$

Приложения теории двойственности

Связь опорной и индикаторной функций множества

Определим опорную функцию множества $$A subset X$$ на $$X$$ соотношением
begin{equation}
label{3}
rho(x^*|A) = underset{y in A}{text{sup}} leftlangle x^*, y rightrangle, x^* in X.
end{equation}
Введем индикаторную функцию следующим образом
[
delta_A(x) =
begin{cases}
0, &x in A;\
+infty, &x notin A.
end{cases}
]
Предложение 1. Пусть $$delta_A(cdot)$$ — индикаторная функция выпуклого замкнутого множества $$A$$. Тогда $$rho^*(cdot|A) = delta_A(cdot)$$.

Доказательство

Функция $$delta_A$$ является выпуклой, замкнутой и собственной. Поэтому по теореме Фенхеля-Моро $$delta_A^{**} = delta_A$$. Кроме того, для произвольного $$x^*$$ имеем
[
delta_A^*(x^*) = underset{x}{text{sup}}left{ leftlangle x, x^* rightrangle — delta_A(x)right} = underset{x in A}{text{sup}} left{ leftlangle x, x^* rightrangle right} = rho(x^*| A).
]
Следовательно, $$delta_A = delta_A^{**} = rho^*(cdot|A)$$. $$;;blacksquare$$

Евклидово расстояние от точки до множества

Для евклидова расстояния
$$d(x,ℳ) = underset{y in ℳ}{text{min}} left| x -y right|$$ от точки $$x$$ до множества $$ℳ$$, $$ℳ in text{conv} ;mathbb{R}^n$$ — выпуклый компакт, справедливы следующие соотношения двойственности
[
d(x,ℳ) = underset{left| l right| leqslant 1}{text{max}} left{ left( l,x right) — rholeft( l|ℳ right) right},
]
[
d^2(x,ℳ) = underset{l}{text{max}} left{ left( l,x right) — rholeft( l|ℳ right) — frac{1}{4} left( l,l right) right},
]
где $$rholeft( l|ℳ right)$$ — опорная функция множества $$ℳ$$.

Покажем справедливость второго соотношения.

Имеем функцию $$varphi(x) = d^2(x,ℳ) = underset{y in ℳ}{text{min}}left( x-y, x-y right)$$. Поскольку функция $$varphi$$ является выпуклой, замкнутой и собственной, по теореме Фенхеля-Моро $$varphi^{**} = varphi$$.

Найдем сопряженную функцию к $$varphi(x)$$
[
varphi^*(l) = underset{x}{text{sup}}left{ left( l,x right) — varphi(x) right} = underset{x}{text{sup}};underset{y in ℳ}{text{max}} left{ left( l,x right) — left( x-y,x-y right)right} = underset{y in ℳ}{text{max}} ;underset{x}{text{sup}} left{ left( l,x right) — left( x-y,x-y right)right} = underset{y in ℳ}{text{max}} left(left( l, frac{l}{2} + y right) — frac{1}{4}left( l,l right)right)= rholeft( l|ℳ right) + frac{1}{4}left( l,l right),
]
откуда, очевидно, следует второе соотношение. $$;;blacksquare$$

Расстояние по Хаусдорфу между двумя компактами

Пусть $$X = mathbb{R}^n$$, $$A$$ и $$B$$ — выпуклые компакты.

Лемма 1.
[
hleft( A, B right) = underset{left| l right| leqslant 1}{text{max}}left| rholeft( l|A right) — rholeft( l|B right)right|,
]
где $$hleft( A, B right)$$ — расстояние по Хаусдорфу между множествами $$A$$ и $$B$$.

Замечание 1. $$dleft( x, B right) = hleft( x, B right) = underset{left| l right| leqslant 1}{text{max}}left| left( l,x right) — rholeft( l|B right)right|$$.

Опорная функция пересечения множеств

Приведем три вспомогательных утверждения без доказательства $$^{[1]}$$.

Лемма 2. Для любых функций $$f_1,{…},f_n$$ имеет место
[
left( f_1 oplus f_2 oplus {…} oplus f_n right)^* = f_1^* + f_2^* + {…} + f_n^*.
]
Предложение 2. Пусть $$f$$ — выпуклая собственная функция и $$X = mathbb{R}^n$$. Тогда ее замыкание $$text{cl} , f$$ также является собственной функцией.

Предложение 3. Для выпуклой функции $$f$$ имеет место
[
(text{cl} , f)^* = f^*.
]

Определим опорную функцию соотношением ($$ref{3}$$).

Предложение 4. Пусть $$A, B$$ — выпуклые ограниченные подмножества $$mathbb{R}^n$$ и $$text{int} , A cap text{int} , B neq varnothing$$. Тогда
[
rholeft( cdot | Acap B right) = text{cl}left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right).
]
Доказательство

Для ограниченного множества опорная функция выпукла и непрерывна на $$mathbb{R}^n$$. Поэтому в силу леммы 2 и предложения 1 для произвольного $$x$$ имеем
[
left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right)^*(x) = rho^*(x| A) + rho^*(x| B) =
delta_A(x) + delta_B(x) = delta_{Acap B}(x) = rho^*( x | Acap B ),
]
откуда в силу предложения 3 имеем
begin{equation}
label{4}
(text{cl} , varphi)^* = rho^*( cdot | Acap B ),
end{equation}
где функция $$varphi$$ определяется соотношением $$varphi(x) = left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right)(x)$$. Здесь мы использовали легко проверяемое свойство индикаторных функций, а именно, что для любых двух множеств $$A, B$$ выполняется $$delta_A + delta_B = delta_{Acap B}$$. Функция $$varphi$$ является собственной, так как она сама не равна тождественно $$+infty$$, и в силу доказанного выше сопряженная к ней функция также не равна тождественно $$+infty$$. Поэтому в силу предложения 2 функция $$text{cl} , varphi$$ также является собственной. Применяя к равенству ($$ref{4}$$) теорему Фенхеля-Моро, имеем $$rholeft( cdot | Acap B right) = text{cl}left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right).$$ $$;;blacksquare$$

Список литературы

1. Арутюнов А. В. «Лекции по выпуклому и многозначному анализу», М.: ФИЗМАТЛИТ, 2014.
2. Востриков И.В. «Лекции по динамическому программированию и процессам управления», 2022.