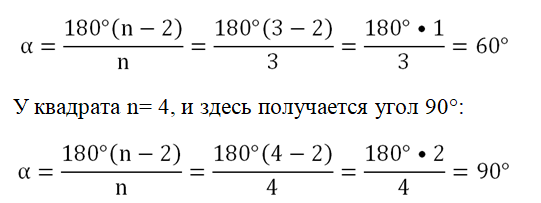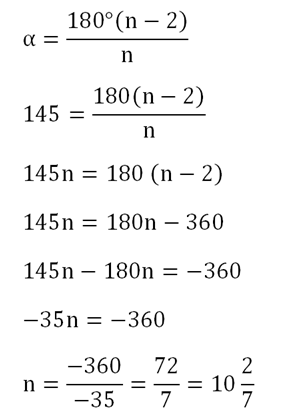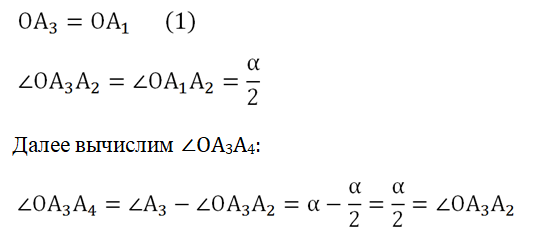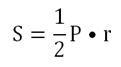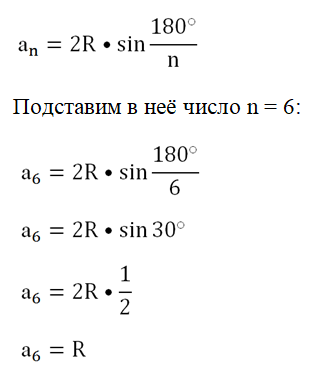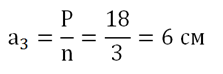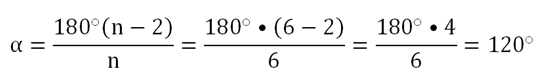| Alpha | Angle of 60° • Perpendicular Bisector • Midpoint • Circle in Square • Rhombus in Rectangle • Circle Center • Inscribed Square |
|---|---|
| Beta | Angle Bisector • Intersection of Angle Bisectors • Angle of 30° • Double Angle • Cut Rectangle • Drop a Perpendicular • Erect a Perpendicular • Tangent to Circle at Point • Circle Tangent to Line • Circle in Rhombus |
| Gamma | Chord Midpoint • Triangle by Angle and Orthocenter • Intersection of Perpendicular Bisectors • Three equal segments — 1 • Circle through Point Tangent to Line • Midpoints of Trapezoid Bases • Angle of 45° • Lozenge • Center of Quadrilateral |
| Delta | Double Segment • Angle of 60° — 2 • Circumscribed Equilateral Triangle • Equilateral Triangle in Circle • Cut Two Rectangles • Square Root of 2 • Square Root of 3 • Angle of 15° • Square by Opposite Midpoints • Square by Adjacent Midpoints • Square by Two Vertices |
| Epsilon | Parallel Line • Parallelogram by Three Vertices • Line Equidistant from Two Points — 1 • Line Equidistant from Two Points — 2 • Hash • Shift Angle • Line Equidistant from Two Lines • Circumscribed Square • Square in Square • Circle Tangent to Square Side • Regular Hexagon |
| Zeta | Point Reflection • Reflection • Copy Segment • Given Angle Bisector • Non-collapsing Compass • Translate Segment • Triangle by Three Sides • Parallelogram • Nine Point Circle • Symmetry of Four Lines • Parallelogram by Three Midpoints |
| Eta | Sum of Areas of Squares • Annulus • Angle of 75° • Line Equidistant from Three Points • Heron’s Problem • Circumscribed Circle • Inscribed Circle • Circle Tangent to Three Lines • Segment by Midpoint • Angle Isosceles • Excircle |
| Theta | Perimeter Bisector • Angle 54° Trisection • Interior Angles • Regular Octagon • Triangle Cleaver • Torricelli Point • Circle Equidistant from Four Points • Octagon from Square • Egyptian Triangle by Side of Length 4 • Chord Parallel to Segment |
| Iota | Minimum Perimeter — 1 • Third Proportional • Harmonic Mean of Trapezoid Bases • Drop a Perpendicular* • Midpoint* • Trisection by Trapezoid Diagonals • Minimum Perimeter — 2 • Harmonic Mean of Segments • Triangle by Angle and Centroid • Triangle Mid-Segment |
| Kappa | Tangent of Circle • Outer Tangent • Inner Tangent • Rotation 90° • Rotation 60° • Segment Trisection • Segment Trisection* • Chord Trisection • Three Circles — 1 • Secant Bisection • Three Circles — 2 • Center of Rotation |
| Lambda | Fourth Proportional • Geometric Mean of Segments • Golden Section • Angle of 54° • Third Parallel Line • Circle in Angle • Geometric Mean of Trapezoid Bases • Regular Pentagon • Point Farthest from Angle Sides • Ratio 1 to 5 |
| Mu | Triangle by Midpoints • Triangle by Side and Centroid • Triangle by Altitude Base Points • Triangle by Tangent Points • Triangle by Excenters • Equilateral Triangle by Centroid and Two Points • Right Triangle by Two Points on Legs • Hypotenuse and Altitude • Hypotenuse and Leg • Isosceles Triangle by Tangent Points |
| Nu | Circle Tangent to Line and Circle • Equilateral Triangle — 2 • Equilateral Triangle on Concentric Circles • Square in Triangle • Point Equidistant from Side of Angle and Point • Circle Through Two Points and Tangent to Line • Inscribed Square — 2 • Line Reflection • Square by Four Points |
| Xi | Rhombus in Triangle • Circle Tangent to Two Circles • Triangle by Tangent Point on Hypotenuse • Parallelogram on Four Lines • Arbelos |
| Omicron | Midpoint* • Copy Circle • Line-Circle Intersection • Three Equal Segments • Tangent to Circle* • Napoleon’s Problem • Drop a Perpendicular** • Line-Circle Intersection* • Circle with Center on Line • Angle of 3° • Mickey Mouse |
| Tutorials | |
| Equilateral Triangle • Intersect Tool • Perpendicular Bisector • Move Tool • Angle Bisector • Perpendicular • Parallel Line • Compass |
Ромб, его свойства. Квадрат, его свойства
Еще одни представители класса параллелограммов — ромб и квадрат.
Параллелограмм, у которого все стороны равны, называется ромбом.
Свойства ромба
Противоположные углы ромба равны.
В ромба сумма углов, прилегающих к одной стороне, равна 180 °. Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Диагонали ромба пересекаются и точкой пересечения делятся пополам.
Признаки ромба
Если в параллелограмме диагонали пересекаются под прямым углом, то этот параллелограмм является ромбом.
Если в параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм является ромбом.
Если в параллелограмме две смежные стороны равны, то этот параллелограмм является ромбом.
Если в четырехугольнике все стороны равны, то этот четырехугольник является ромбом.
Если в параллелограмме одна из диагоналей является биссектрисой его угла, то этот параллелограмм является ромбом.
Если в четырехугольнике диагонали являются биссектрисами его углов и пересекаются под прямым углом, то этот четырехугольник является ромбом.
Это интересно.
Если соединить отрезками середины сторон прямоугольника, то получим ромб.
Если соединить отрезками середины сторон ромба, то получим прямоугольник.
Если у параллелограмма все высоты равны, то этот параллелограмм является ромбом.
Прямоугольник, у которого все стороны равны, называется квадратом.
Свойства квадрата
Все углы квадрата — прямые.
Диагонали квадрата пересекаются и точкой пересечения делятся пополам.
Диагонали квадрата уровне.
Диагонали квадрата пересекаются под прямым углом.
Диагонали квадрата являются биссектрисами его углов.
Признаки квадрата
Если в прямоугольнике диагонали пересекаются под прямым углом, то этот прямоугольник является квадратом.
Если ромба диагонали равны, то этот ромб является квадратом.
Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник является квадратом.
План урока:
Понятие правильного многоугольника
Описанная и вписанная окружности правильного многоугольника
Формулы для правильного многоугольника
Построение правильных многоугольников
Понятие правильного многоугольника
У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.
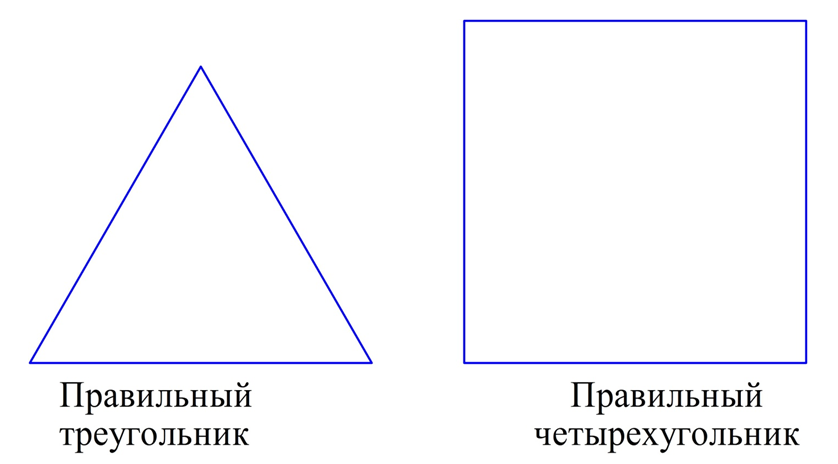
Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.
Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:
Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?
Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:
Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?
Решение. В формулу
Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?
Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.
Ответ: не может.
Описанная и вписанная окружности правильного многоугольника
Докажем важную теорему о правильном многоуг-ке.
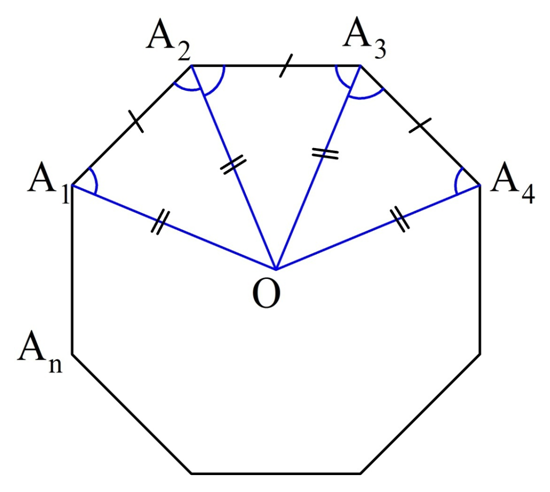
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А1, А2, А3…Аn. Далее проведем биссектрисы углов ∠А1 и ∠А2. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА3, ОА4 и т. д.
∠А1 и ∠А2 одинаковы по определению правильного многоуг-ка:
Из этого факта вытекает два равенства:
Получается, что ОА3 – это также биссектриса ∠А3. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):
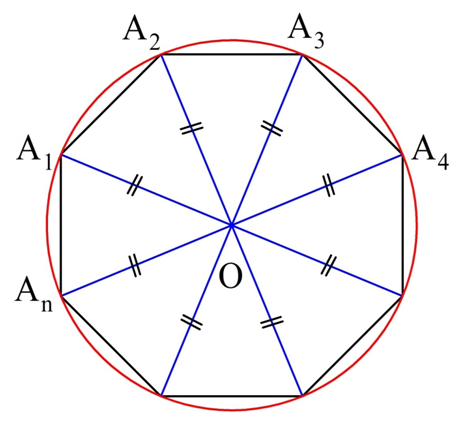
Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А1, А2 и А3, можно провести только одну окружность, ч. т. д.
Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА1А2, ∆ОА2А3, ∆ОА3А4, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН1, ОН2, ОН3… на стороны многоуг-ка.
Так как высоты проведены в равных треуг-ках, то и сами они равны:
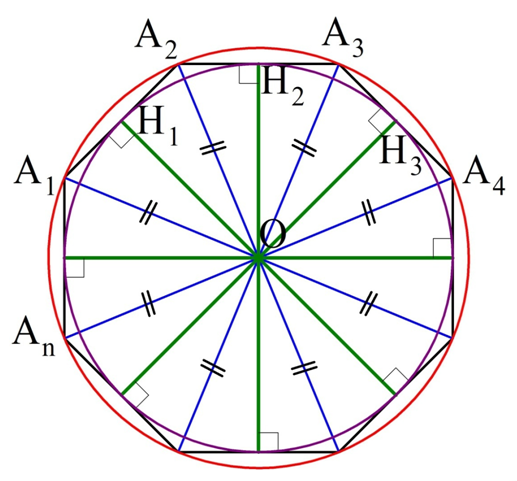
Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН1. Он должен будет пройти и через точки Н2, Н3, … Нn. Причем отрезки ОН1, ОН2, ОН3 окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А1, ∠А2, ∠А3, то есть в точке О. Так как расстояние от О до А1А2 – это отрезок ОН1, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.
Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.
Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН1, ОН2, ОН3,… проведены в равнобедренных треуг-ках∆ОА1А2, ∆ОА2А3, ∆ОА3А4,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н1, Н2, Н3,… – это середины сторон многоуг-ка.
Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?
Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.
Ответ: не могут.
Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.
Формулы для правильного многоугольника
Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой an, где n– число сторон у многоуг-ка. Например a4– это сторона квадрата, a6– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.
Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.
Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:
Теперь можно найти и ∠А1ОН1, рассмотрев ∆А1ОН1:
Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:
С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).
Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.
Решение. Запишем следующую формулу:
Это равенство как раз и надо было доказать в этом задании.
Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.
Решение. Запишем формулу:
Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.
Решение.
Найдем периметр шестиугольника:
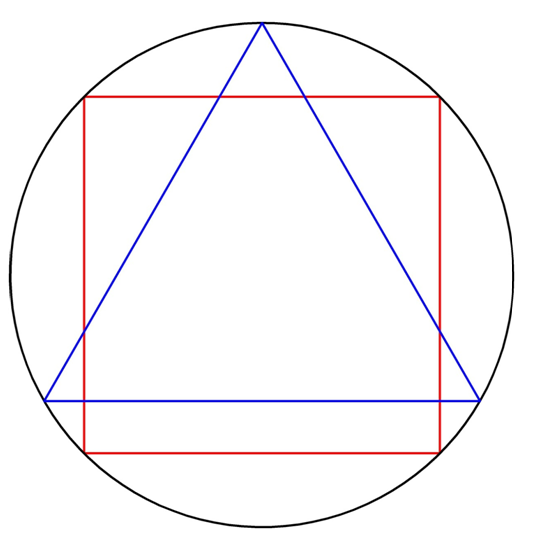
Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?
Решение. Зная периметр треуг-ка, легко найдем и его сторону:
Далее вычисляется радиус описанной около треугольника окружности:
Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?
Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:
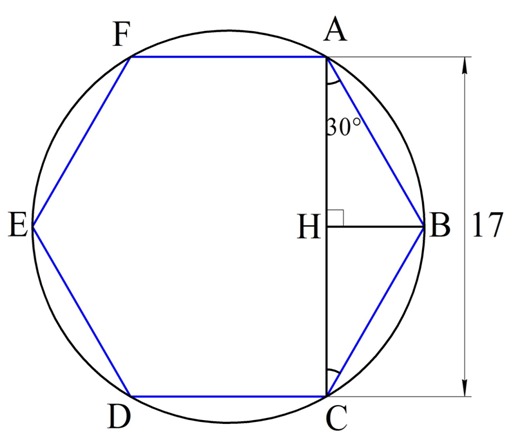
Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:
Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:
AC = 17 мм
∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:
AH = AC/2 = 17/2 = 8,5 мм
Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:
Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.
Ответ: 20 мм.
Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
a6 = R
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.
Пятиугольник, виды, свойства и формулы.
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник, выпуклый и невыпуклый пятиугольник
Правильный многоугольник
Свойства правильного пятиугольника
Построение правильного пятиугольника
Формулы правильного пятиугольника
Правильный пятиугольник в природе, технике и культуре
Пятиугольник, шестиугольник, семиугольник, восьмиугольник
Пятиугольник, выпуклый и невыпуклый пятиугольник:
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).
Пятиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый пятиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 540°.
Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.
Рис. 2. Невыпуклый пятиугольник
Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.
Правильный многоугольник:
Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.
Рис. 3. Правильный пятиугольник
Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.
Свойства правильного пятиугольника:
1. Все стороны правильного пятиугольника равны между собой.
a1 = a2 = a3 = a4= a5.
2. Все углы равны между собой и каждый угол равен 108°.
α1 = α2 = α3 = α4 = α5 = 108°.
Рис. 4. Правильный пятиугольник
3. Сумма внутренних углов правильного пятиугольника равна 540°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.
Рис. 5. Правильный пятиугольник
5. Количество диагоналей правильного пятиугольника равно 5.
Рис. 6. Правильный пятиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр пятиугольника O.
Рис. 7. Правильный пятиугольник
7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Рис. 8. Правильный пятиугольник
8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
a / c ≈ 5 / 8 ≈ 0,618.
Рис. 9. Правильный пятиугольник
Построение правильного пятиугольника:
Метод построения правильного пятиугольника вписыванием его в заданную окружность:
1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.
Формулы правильного пятиугольника:
Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.
Формулы площади правильного пятиугольника:
Формулы высоты правильного пятиугольника:
Формулы стороны правильного пятиугольника:
Формулы диагонали правильного пятиугольника:
Формулы радиуса окружности, вписанной в правильный пятиугольник:
Формулы радиуса окружности, описанной вокруг правильного пятиугольника:
Правильный пятиугольник в природе, технике и культуре:
Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.
Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.
Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Пятиугольник
Шестиугольник
Семиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
9 633
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,660 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,971 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.