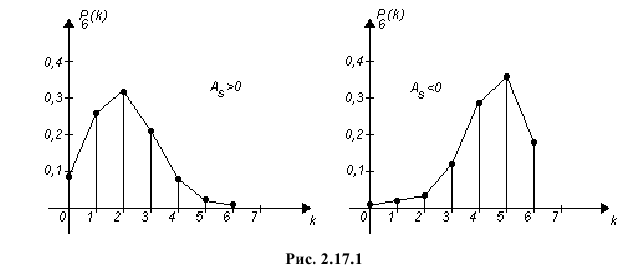
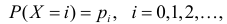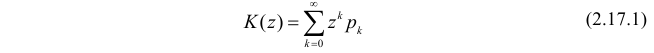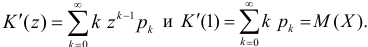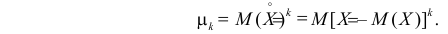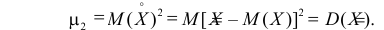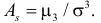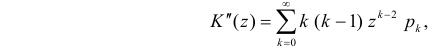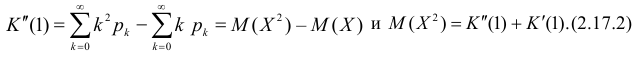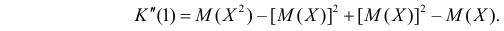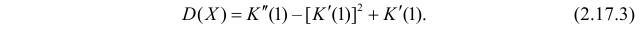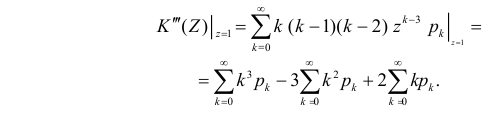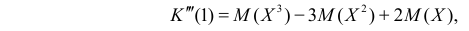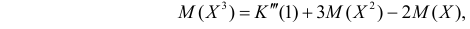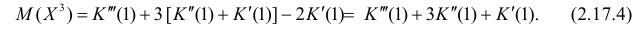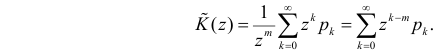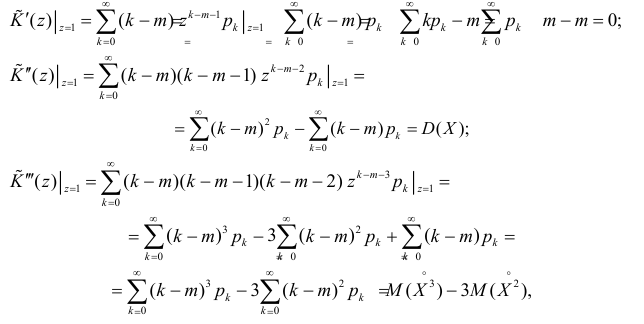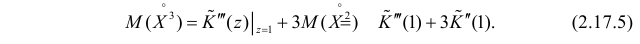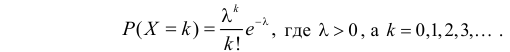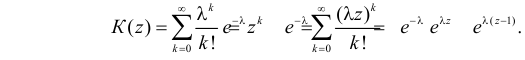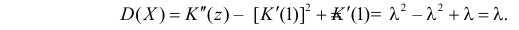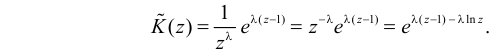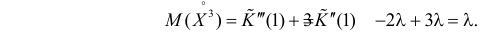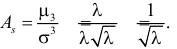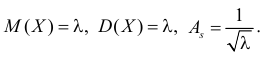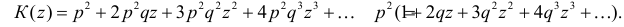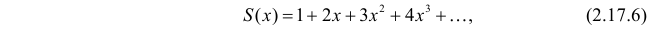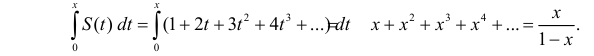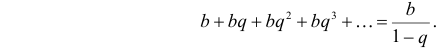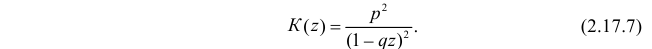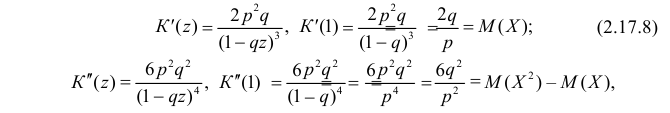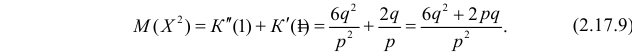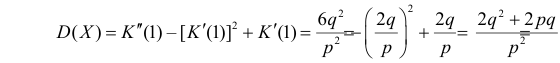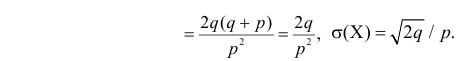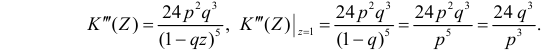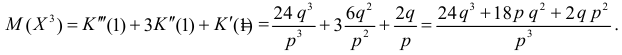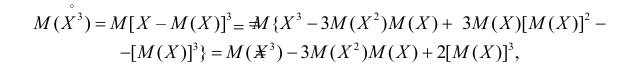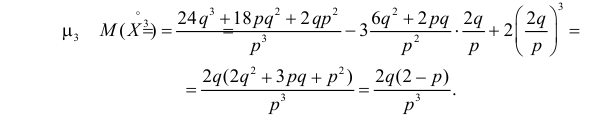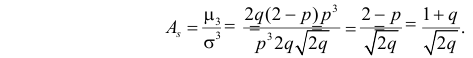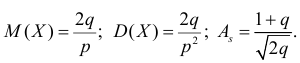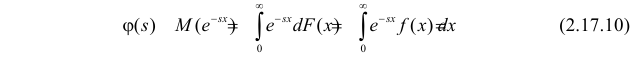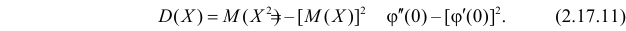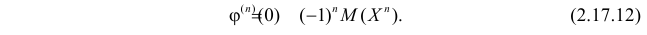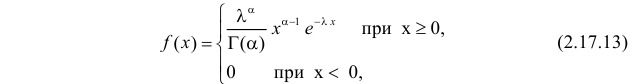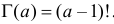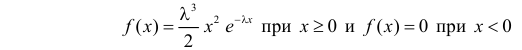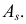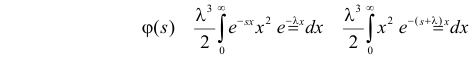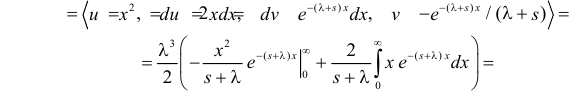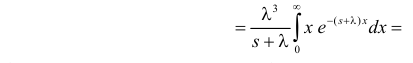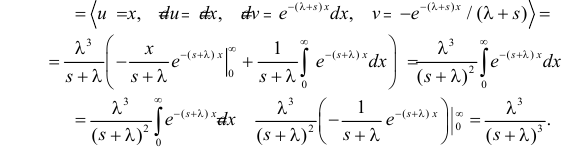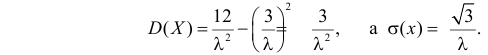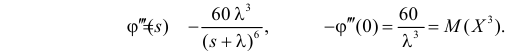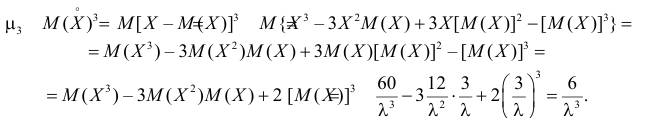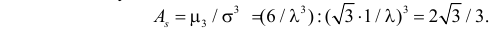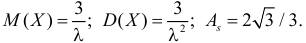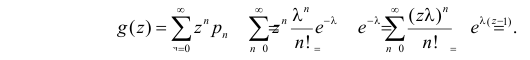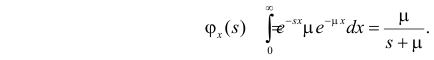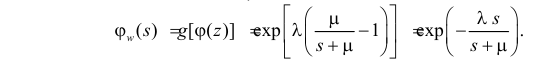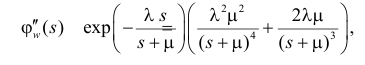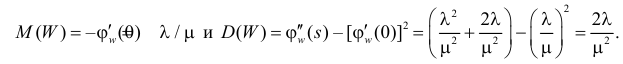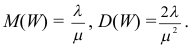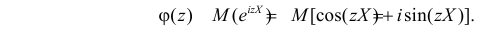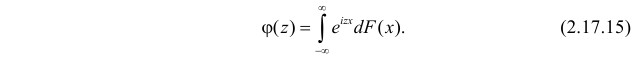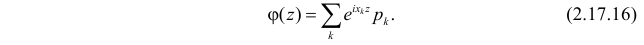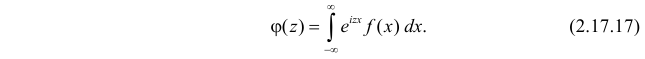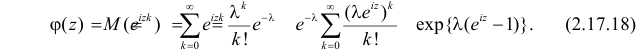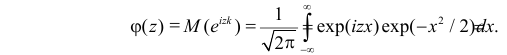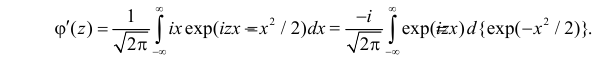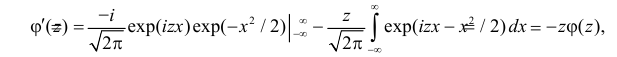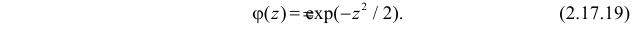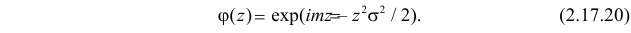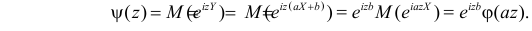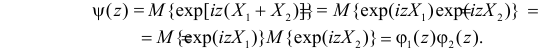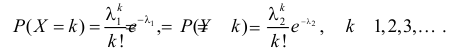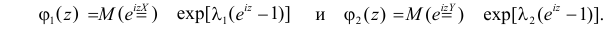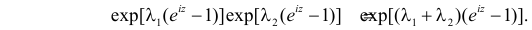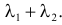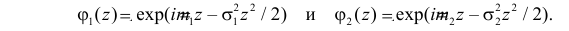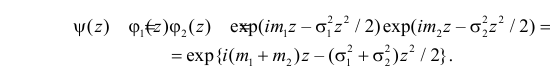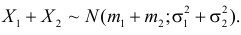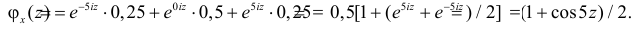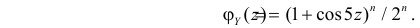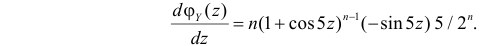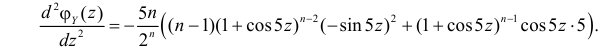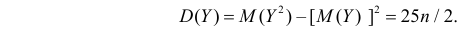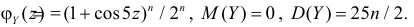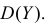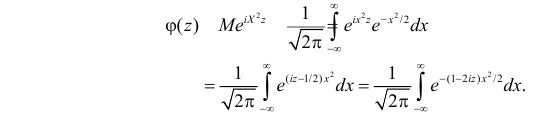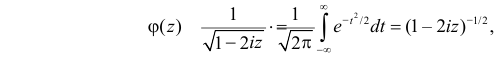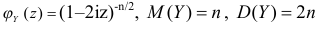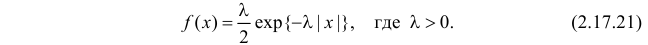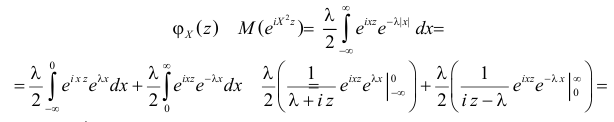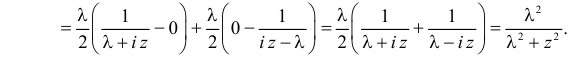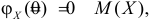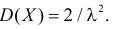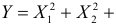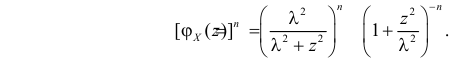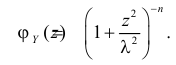Производящие функции:
Пусть дискретная случайная величина Х имеет закон распределения
Функция
называется производящей функцией этого распределения.
Заметим, что
Напомним:
1) Начальным моментом порядка 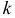
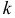
Само математическое ожидание является начальным моментом первого порядка.
2) Центральным моментом 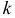
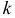
Дисперсия является центральным моментом второго порядка
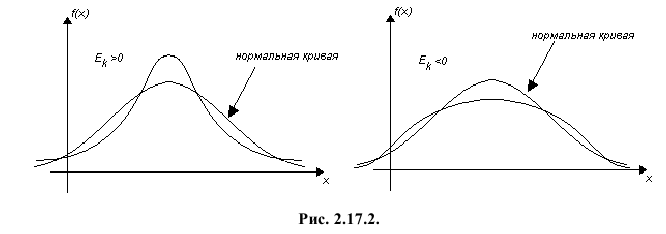
3) Асимметрией распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения случайной величины:
Если распределение симметрично, то 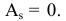
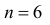
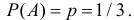
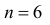
4) Для нормального закона распределения 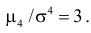
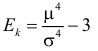
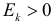
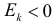
Через производящую функцию можно выразить и другие начальные и центральные моменты случайной величины. Выразим через производящую функцию, например, дисперсию. Так как
то
Сформируем в правой части последнего равенства дисперсию. Для этого прибавим и отнимем квадрат математического ожидания:
Величина 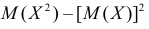
Аналогично
Итак, при z =1 имеем
откуда
а с учетом (2.17.2)
Пусть 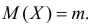
С помощью этой функции можно вычислять сразу центральные моменты случайной величины. Например
откуда
Пример:
Пусть Х имеет пуассоновский закон распределения:
Требуется найти математическое ожидание, дисперсию и коэффициент асимметрии этой случайной величины.
Решение. Производящая функция пуассоновского распределения имеет вид
Заметим, что 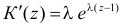

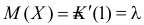
Для вычисления коэффициента асимметрии составим модифицированную производящую функцию. Так как 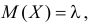
Тогда
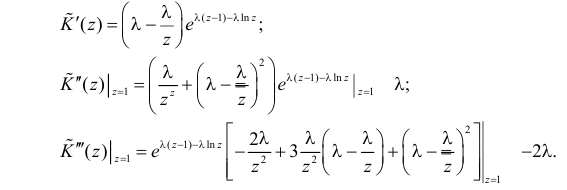
Поэтому по формуле (2.17.5) имеем
В итоге
Ответ.
Пример:
Пусть Х имеет закон распределения
(Это частный случай отрицательного биномиального распределения или распределения Паскаля с параметрами 2 и 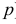
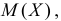
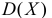
Решение. Составим производящую функцию
Для вычисления суммы ряда в скобке рассмотрим сумму ряда
который абсолютно сходится при 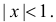
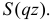
В последней строке мы воспользовались формулой суммы бесконечной убывающей прогрессии:
Отсюда 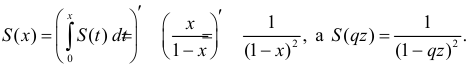
Воспользуемся теперь производящей функцией (2.17.7) для вычисления числовых характеристик случайной величины X:
откуда следует, что
По формуле (2.17.3)
Далее
По формуле (2.17.4) вычисляем
Так как
то с учетом (2.17.8) и (2.17.9) имеем
Учитывая это получаем значение коэффициента асимметрии
Ответ.
Преобразование Лапласа
Для непрерывной и неотрицательной случайной величины роль производящей функции может играть преобразование Лапласа.
Пусть Х – непрерывная, неотрицательная случайная величина с функцией распределения 
называется преобразованием Лапласа для этого распределения. (Фактически роль величины z в формуле (2.17.1) играет величина 
Отметим, что 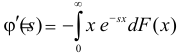
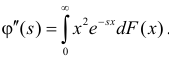
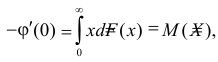
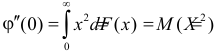
Производная любого порядка от преобразования Лапласа связана с начальными моментами случайной величины соотношением
где 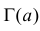
Пример:
Случайная величина X имеет функцию плотности вероятности
(гамма-распределение с параметрами 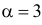
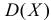
Решение. Соответствующее преобразование Лапласа имеет вид
(интегрируем по частям)
(первое слагаемое в скобке равно нулю, так как 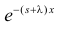
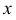
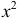
(интегрируем еще раз по частям)
Вычислим начальные моменты распределения:
поэтому
Далее
Вычислим центральный момент третьего порядка:
Поэтому
Ответ.
Пример:
Пусть 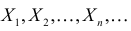
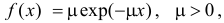
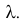
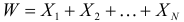
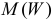
Решение. Производящая функция пуассоновского закона распределения равна
Преобразование Лапласа показательного распределения равно
Поэтому по формуле (2.17.14) имеем
Так как 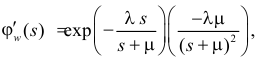
то
Ответ.
Характеристические функции
Замена z на 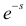
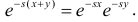
Характеристической функцией 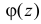
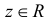
Если 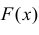
Существование интеграла, определяющего характеристическую функцию, вытекает из непрерывности функции 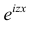
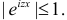
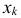
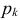
Для непрерывной случайной величины X с функцией плотности вероятности 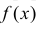
Пример:
Пусть случайная величина X имеет пуассоновский закон распределения, т.е.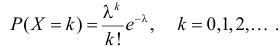
Пример:
Пусть 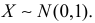
Вместо непосредственного вычисления интеграла, которое требует специальной математической техники, найдем его величину косвенным способом. Заметим, что
Полученный интеграл берем по частям, полагая 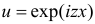
(первое слагаемое равно нулю так как 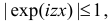
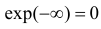
В итоге для искомой характеристической функции получаем уравнение, которое при начальном условии 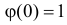
Подобным же образом можно показать, что закон распределения 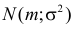
Свойства характеристических функций.
1. 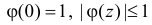
2. Если существует 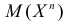
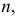
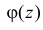
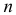
3. Пусть 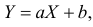
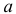
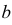
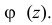
4. Характеристическая функция однозначно определяет распределение случайной величины.
5. Если X1 и X2 – независимые случайные величины, а 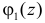
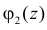
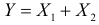
Это следует из того, что в силу независимости слагаемых
Можно показать, что для любого конечного числа независимых случайных величин 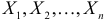
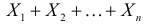
Пример:
Случайные величины X и Y независимы и имеют пуассоновские законы распределения с параметрами 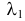
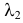
Требуется найти закон распределения случайной величины 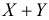
Решение. Согласно формуле (2.17.18) характеристические функции случайных величин X и Y имеют вид:
Сумме независимых случайных величин соответствует произведение характеристических функций слагаемых. Поэтому 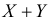
Ответ. 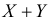
Полученный результат известен как факт устойчивости пуассоновского закона распределения. Этот результат можно обобщить на сумму любого конечного числа пуассоновских случайных величин.
Теорема. Если случайные величины Х1 и Х2 независимы и имеют соответственно нормальные законы распределения 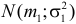
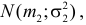
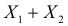
Доказательство. Пусть 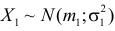
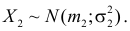
Тогда характеристическая функция суммы 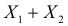
А это и означает, что
Пример:
Случайная величина 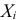
Требуется найти характеристическую функцию этой случайной величины. Используя свойства характеристических функций, найти характеристическую функцию случайной величины 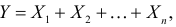
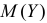
Решение. По формуле (2.17.16)
Поэтому характеристическая функция случайной величины Y имеет вид
Для вычисления 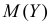
Последнее выражение при 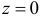
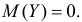
при 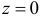
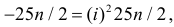
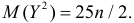
Ответ.
Пример:
Требуется найти характеристическую функцию случайной величины 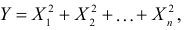
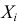
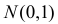
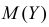
Решение. Найдем сначала характеристическую функцию для 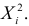
После замены переменных 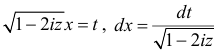
так как 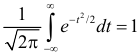
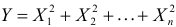
Для вычисления числовых характеристик случайной величины Y найдем сначала первую и вторую производные характеристической функции при
Это означает, что
Ответ.
Пример:
Случайная величина Х имеет функцию плотности вероятности
Требуется найти характеристическую функцию этой случайной величины и ее 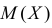
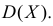
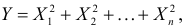
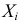
Решение. Найдем сначала характеристическую функцию:
(так как 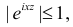
Тогда 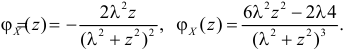
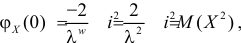
Характеристическая функция случайной величины 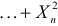
Ответ. 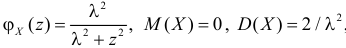
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Центральная предельная теорема
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
| Определение: |
| Производящая функция (англ. generating function) — это формальный степенной ряд вида , порождающий (производящий) последовательность . |
Метод производящих функций был разработан Эйлером в 1750-х годах.
Содержание
- 1 Применение
- 2 Примеры производящих функций
- 3 Примеры решений задач методом производящих функций
- 3.1 Решение рекуррентных соотношений
- 3.2 Расчет дисперсии геометрического распределения
- 3.3 Пример задачи на нахождение производящей функции
- 4 Приложения
- 4.1 Примеры простых производящих функций
- 5 См. также
- 6 Примечания
- 7 Источники информации
Применение
Производящая функция используется для:
- Компактной записи информации о последовательности.
- Нахождения зависимости для последовательности , заданной рекуррентным соотношением. Например, для чисел Фибоначчи.
- Нахождения рекуррентного соотношения для последовательности — вид производящей функции может помочь найти формулу.
- Исследования асимптотического поведения последовательности.
- Доказательства тождеств с последовательностями.
- Решения задачи подсчета объектов в комбинаторике. Например, в доказательстве пентагональной теоремы или в задаче нахождения количества расстановок ладей на доске .
- Вычисления бесконечных сумм.
Примеры производящих функций
Рассмотрим производящие функции для различных комбинаторных последовательностей:
- — производящая функция для разности количества разбиений числа в четное и нечетное число различных слагаемых. Например, коэффициент при равен , потому что существует два разбиения на четное число различных слагаемых и одно на нечетное (). Правильность этого легко осознать, если понять, что каждая скобка представляет какое-то слагаемое и мы можем его взять (второе слагаемое — ) или не взять (первое — ). Эта производящая функция используется в комбинаторном доказательстве пентагональной теоремы.
- — производящая функция для последовательности , где — число разбиений числа на слагаемые.
- — производящая функция для последовательности , где — число разбиений на различные слагаемые.
- — производящая функция для последовательности , где — число разбиений на нечётные слагаемые. С помощью метода производящих функций можно доказать, что производящие функции последовательностей равны, соответственно :
Примеры решений задач методом производящих функций
Решение рекуррентных соотношений
Существует целый класс последовательностей, задаваемых рекуррентным соотношением, например, — числа Фибоначчи или —
числа Каталана. Метод производящих функций позволяет получить выражение для через номер элемента в последовательности в замкнутом виде, то есть в таком виде, что выражение можно вычислить, предполагая, что достаточно мало.
Пусть последовательность удовлетворяет некоторому рекуррентному соотношению. Мы хотим получить выражение для (при ) в замкнутом виде. Алгоритм получения замкнутого выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций состоит из 4 шагов:
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен , то есть количество предшествующих элементов, требуемых для вычисления элемента с номером , равно ):
- Домножить каждую строчку на в соответствующей степени и просуммировать строчки для всех .
- В полученном уравнении привести все суммы к замкнутому виду. Получить уравнение для производящей функции.
- Выразить в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням .
Для демонстрации универсальности метода рассмотрим довольно произвольное рекуррентное соотношение:
Запишем производящую функцию для этой последовательности и преобразуем правую часть:
Для того, чтобы замкнуть последнюю сумму воспользуемся очень важным приемом, который используется при преобразовании производящих функций. Фактически мы имеем дело с последовательностью (в нашем случае последовательность ). Такая последовательность получается путём дифференцирования функции , производящей для , с последующим умножением результата на :
Тогда замкнем последнее слагаемое следующим образом:
Таким образом, наше последнее слагаемое примет вид:
Это уравнение для производящей функции. Из него выражаем :
Разложим знаменатель на множители и разобьём дробь на сумму простых дробей [1]:
Разложим первое слагаемое в ряд, используя расширенные биномиальные коэффициенты [2]:
Расчет дисперсии геометрического распределения
Метод производящих функций также используется для нахождения математического ожидания и дисперсии различных распределений в теории вероятностей. Например, в геометрическом распределении [3] для нахождения дисперсии нужно найти два мат. ожидания:
которые фактически являются производящими функциями последовательностей и :
.
Тогда:
Пример задачи на нахождение производящей функции
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся в и оканчивающихся в . |
Заметим, что для того, чтобы закончить путь в , необходимо совершить равное число шагов вправо и влево. Тогда задача сводится к тому, чтобы выбрать позиций для, например, шагов вправо из всего шагов. Тогда ответом будет сумма от нуля до бесконечности по всех . То есть:
Рассмотрим , где — число Каталана. Тогда, заметим что . Так как , то справедливо равенство:
Мы знаем, что производящая функция для чисел Каталана равна . Найдем .
Соответственно, ответом будет производящая функция вида:
| Задача: |
| Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся и оканчивающихся в и не заходящих в отрицательную полупрямую. |
Заметим, что задача аналогична Правильной скобочной последовательности. Тогда производящей функцией для нашей задачи будет производящая функция для правильной скобочной последовательности, а именно:
Приложения
Примеры простых производящих функций
На последнем шаге приведения производящей функции к замкнутому виду требуется разложить полученные слагаемые в ряд. Для этого можно воспользоваться таблицей основных производящих функций [4].
Все суммы выполняются по переменной от до . Элементы последовательности нумеруются от .
| Последовательность | Производящая функция в виде ряда | Производящая функция в замкнутом виде |
| ( нулей в начале) | ||
| (повторяется через ) | ||
См. также
- Производящая функция Дирихле
Примечания
- ↑ О разложении рациональной функции в ряд
- ↑ Расширенные биномиальные коэффициенты
- ↑ Геометрическое распределение
- ↑ Таблица производящих функций
Источники информации
- Вайнштейн Ф., Разбиение чисел. Журнал «Квант» № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics
Обычная производящая функция — это функция вида
. Разберем на примере, как ее использовать.
Представим, что нам нужно найти, сколькими способами можно составить сумму
. При этом можно использовать по одному элементу из каждого из следующих двух наборов:
и
.
Рассмотрим два многочлена:
— это количество способов составить сумму
с помощью одного элемента из каждого набора.
Например, коэффициент
во втором многочлене равен
. Значит, существует один способ составить сумму из четырех, используя только один элемент из набора.
Теперь рассмотрим произведение многочленов:
В полиномиальном произведении
— количество способов составить сумму из
, когда берется по одному числу из каждого набора.
Разложим произведение:
Коэффициент
равен нулю при
, так как мы не можем получить сумму больше
. Если взять самые большие числа из каждого набора, то получится число
.
То же самое относится и к
. Берем самые маленькие числа из наборов и получаем
.
Когда
, коэффициент равен трем. Это означает, что есть три способа получить число
. Если c помощью формулы дистрибутивности мы развернем произведение полностью, то увидим, что три члена
получаются из произведений:
Производящая функция придает смысл коэффициенту
, но не придает смысла
. Она кодирует числа объектов с помощью формальных степенных рядов — многочленов с бесконечно большим количеством членов.
В разобранном примере можно было просто подсчитать количество способов получения числа 10 путем проверки. Но производящие функции полезны, когда многочлены выражены в более компактной форме — например, с помощью суммы геометрического ряда.
Содержание:
- Примеры с решением
- Биномиальный закон
- Геометрический закон
- Закон Пуассона
Мы видели, что дискретные случайные величины, рассмотренные в предыдущих параграфах, принимали только целые значения 
Определение. Производящей функцией дискретной целочисленной случайной величины 

Поскольку все коэффициенты этого ряда не превосходят 1, то сравнение с геометрической прогрессией показывает, что этот ряд сходится, по крайней мере, для значений 

Теорема 4.4. Производящая функция суммы независимых случайных величин 
Доказательство. Имеем по определению
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Примеры с решением
Пример 4.8.
Найти производящую функцию для биномиального закона.
Решение:
Если вспомнить, что формула Бернулли получается из разложения бинома, то легко сообразить, что
Можно также вспомнить, что случайная величина 



Возможно вам будут полезны данные страницы:
Пример 4.9.
Найти производящую функцию для геометрического закона распределения.
Решение:
Имеем 



Пример 4.10.
Найти производящую функцию для распределения Пуассона.
Решение:
Для пуассоновского закона с параметром 
Поэтому
причем все ряды сходятся для любых значений аргумента 
В качестве следствия получим теорему.
Теорема 4.5. Сумма независимых случайных величин, распределенных по закону Пуассона, распределена по тому же закону.
Доказательство. Пусть 

а производящая функция суммы 
Отсюда видно, что сумма будет распределена по закону Пуассона с параметром 
Зная производящую функцию дискретной случайной величины 
Теорема 4.6. Для дискретной случайной величины 

Доказательство. Дифференцируя почленно ряд (4.22) два раза, имеем
Подставляя 
откуда легко получить формулы (4.25), (4.26).
Комбинируя полученные выражения для производящих функций биномиального, геометрического и пуассоновского законов (4.23), (4.24), (4.25) с формулами (4.26), (4.27), теперь нетрудно найти основные числовые характеристики этих законов.
Биномиальный закон
Из выражения (4.23) для производящей функции получим
Подставляя 

Используя формулы (4.26), (4.27), получим
откуда
Геометрический закон
Дифференцируя два раза производящую функцию, имеем
Отсюда
откуда 
Закон Пуассона
Имеем
поэтому 
Лекции:
- Комбинаторные задачи: пример решения
- Классическое определение вероятности
- Геометрическое определение вероятности
- Элементы комбинаторики
- Действии над событиями
- Количество сочетаний
- Число сочетаний: формула, расчет
- Сочетания с повторениями
- Комбинаторика формулы: основные элементы
- Элементы комбинаторики: примеры решения
Метод
рекуррентных соотношений позволяет
решать многие комбинаторные задачи. Но
в ряде случаев рекуррентные соотношения
трудно составить, а иногда ещё трудней
решить. Часто эти трудности удается
обойти, используя производящие функции.
Понятие производящей функции тесно
связано с понятием бесконечного
степенного ряда.
Здесь
необходимо знать: понятие ряда, сумма
ряда, степенной ряд, сходимость степенных
рядов, свойства сходящихся рядов,
операции над ними. Эти понятия изложены
в любом учебнике по математическому
анализу, и мы их опускаем.
Определение
1: Пусть
дана числовая последовательность:
.
Образуем степенной ряд с этими
коэффициентами:.
Если этот ряд сходится в некоторой
области к функции,
то эту функцию называютпроизводящей
для последовательности чисел
.
Примеры: 1)
Для степенного ряда
,
члены которого можно рассматривать как
геометрическую прогрессию, знаменатель.
Значит, степенной ряд при условиисходится к своей сумме
.
Таким образом, получаем:
,
если.
Значит,
функция
является производящей для последовательности
чисел(коэффициенты степенного ряда).
2) Аналогично
можно получить:
.
Значит,
функция
является производящей для последовательности
чисел.
3)
Из формулы бинома Ньютона следует:
,
т.е.
функция
является производящей для чисел вида
,
где.
С
помощью последней производящей функции
можно доказать некоторые свойства чисел
,
т. е. для биномиальных коэффициентов.
Например:
;
;
(здесь
обе суммы конечны и обрываются, когда
значения
и
станут больше
).
Кроме того:
,
,
.
В
последнем равенстве, если
,
то считают, что.
Поэтомуменяется от
до наименьшего из чисел
,
.
Последнее
равенство можно доказать следующим
образом:
,
.
Отсюда
следует: .
Применяя
в левой части формулу биному Ньютона и
раскрывая скобки в правой части,
приравниваем коэффициенты при одинаковых
степенях
,
получаем требуемую формулу.
В
частном случае, когда
,
получаем равенство:
,
.
Проиллюстрируем
на примерах применение производящих
функций к решению некоторых комбинаторных
задач.
1)
Рассмотрим разбиение числа
на слагаемые, каждое из которых равно
одному из чисел.
При этом слагаемые не повторяются и их
порядок не играет роли.
Для
решения задачи рассмотрим выражение
.
Раскрывая скобки, получим слагаемые
вида,
где– некоторые из чисел
.
Поэтому
встретится
в сумме столько раз, сколькими способами
можно разбить
на слагаемые требуемым образом.
Например,
если надо узнать, сколькими способами
можно заплатить 78 копеек, беря не более
одной монеты каждого достоинства, то
надо составить выражение:
,
раскрыть
скобки и найти коэффициент при слагаемом
.
2)
Если требуется разложить число
на слагаемые
,
каждое из которых может встречаться в
разложении один или несколько раз, тогда
количество слагаемых в скобках
увеличивается.
Например: 1)
Сколькими способами можно заплатить
29 коп., используя монеты по 2 и 5 коп?
Т.е.
надо найти число способов разбить число
29 на слагаемые, равные 2 и 5, причем порядок
слагаемых роли не играет, и каждое
слагаемое может повторяться несколько
раз. Для этого составим выражение:
.
Ясно,
что при раскрытии скобок выражение
войдет в разложение с коэффициентом,
равным числу решений уравнения
.
В частности, коэффициент при
дает ответ на вопрос задачи.
Вместо
раскрытия скобок можно поступить иначе:
составить производящую функцию. Эта
функция представляет собой произведение
двух дробей:
.
Разделив
«уголком» числитель на знаменатель,
находим коэффициент при выражении
.
2)
Поступающий в ВУЗ должен сдать 4 экзамена,
причем для поступления достаточно
набрать 17 балов. Сколькими способами
абитуриент может сдать экзамены, чтобы
поступить в ВУЗ?
Требуется
узнать, сколькими способами можно
представить число 17 в виде суммы 4-х
слагаемых, принимающих значения 3, 4, 5,
причем здесь порядок слагаемых имеет
значение.
Для
решения этой задачи можно взять
производящую функцию
.
При раскрытии скобок каждое слагаемоевстретится столько раз, сколькими
способами можноразбить на сумму 4-х слагаемых, принимающих
значения 3, 4 и 5. При этом встречаются
члены, получаемые друг из друга
перестановкой слагаемых.
В
выражении
можно раскрыть скобки по полиномиальной
теореме, а можно следующим образом:
.
Поэтому
.
.
Перемножая
почленно эти выражения, найдем, что
коэффициент при
равен 16. Значит, разложение можно сделать
16 способами.
Между
производящими функциями и рекуррентными
соотношениями существует тесная связь.
Пусть
— производящая функция для последовательности
чисел.
Это означает, чтоявляется суммой степенного ряда:
.
Пусть
– многочлены, причем
и
,
значит, дробь
– правильная (в противном случае можно
выделить целую часть). Раскладывая дробь
в ряд, получим:
.
Раскрывая
скобки справа и приравнивая коэффициенты
при одинаковых степенях
,
получаем:
При
считаем, что
.
А дальше все соотношения имеют вид:,
где,
т.к.не
имеет членов степени
,
,
…
Таким
образом, коэффициенты ряда
,
,…
удовлетворяют рассмотренному рекуррентному
соотношению. Коэффициенты этого
соотношения зависят только от знаменателя
дроби. Числитель нужен только для
нахождения первых членоврекуррентной
последовательности.
Обратно,
если задано рекуррентное соотношение
и заданы члены
,
то, вычисляя значения,
получим производящую функциюдля последовательности чисел
.
Полученную
алгебраическую дробь можно разлагать
на элементарные дроби и производить
алгебраические преобразования.
Соседние файлы в папке 26-03-2013_00-36-55
- #
- #
- #
- #