Задача. В пятом классе (25) учеников.
всех учащихся класса составляют мальчики.
Сколько мальчиков в классе?
| Вопросы к задаче | Ответы |
| 1. Какая величина принята за целое? |
1. За целое принято количество всех учеников класса |
| 2. Известна ли целая величина? | 2. Целое известно: (25) учеников |
| 3. Какую величину нужно найти? | 3. Количество мальчиков в классе, или часть от целого |
| 4. Как найти величину, которая приходится на 15? |
4. (25 : 5 = 5) учеников |
|
5. Как найти величину, которая приходится на 25 ? |
5. (5 · 2 = 10) мальчиков |
Ответ: в пятом классе (10) мальчиков.
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель
и результат умножить на числитель дроби, которая выражает эту часть.
Пример:
от (39) будет (39 : 3 · 2 = 13 · 2 = 26);
от (60) будет (60 : 4 · 3 = 15 · 3 = 45.)
Правила нахождения
числа по доле и доли по числу.
·
Чтобы
найти число по доле, нужно одну его долю умножить на количество
долей.
1/3 часть=8
Число — ?
Решение: 8·3=24
·
Чтобы
найти долю числа, нужно число разделить на количество равных
долей.
Число-20
1/4 — ?
Решение: 20:4=5
·
Чтобы
найти дробь(часть) от числа, нужно число разделить на знаменатель
и
умножить на числитель дроби.
5/7 — (5- числитель
7-знаменатель)
Число-49
Найти — 5/7
Решение: 49:7·5=35
Ответ: 5/7=35.
Правила
нахождения числа по доле и доли по числу.
·
Чтобы
найти число по доле, нужно одну его долю умножить на количество
долей.
1/3 часть=8
Число — ?
Решение: 8·3=24
·
Чтобы
найти долю числа, нужно число разделить на количество равных
долей.
Число-20
1/4 — ?
Решение: 20:4=5
·
Чтобы
найти дробь(часть) от числа, нужно число разделить на знаменатель
и
умножить на числитель дроби.
5/7 — (5- числитель
7-знаменатель)
Число-49
Найти — 5/7
Решение: 49:7·5=35
Ответ: 5/7=35.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Доли
В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.
Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:
.
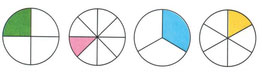
На доли можно разделить окружность:
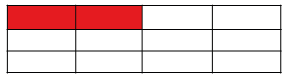
или прямоугольник:
Доля – это каждая из равных частей целого.
Название доли зависит от того, на сколько частей разделили целое.
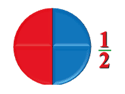
Половина
Половина — это самая известная доля.
Например, яблоко разделили на две части, получилась половина яблока.
Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.
Прочитать такую долю можно как ОДНА ВТОРАЯ.
Треть
Если целое разделили на три части, то получили ТРЕТЬ, третью часть.
Прочитать такую долю можно как ОДНА ТРЕТЬЯ.
Четверть
Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.
Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.
Запись и чтение долей
одна пятая
одна шестая
одна восьмая
Сравнение долей
Для примера сравним две доли: одну шестую и одну третью.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.
Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.
Сравним ещё две доли: одну восьмую и одну четвёртую.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.
Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.
Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.
Правило встречается в следующих упражнениях:
3 класс
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38. ПР 5. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46. Урок 17,
Петерсон, Учебник, часть 1
Страница 94. Урок 41,
Петерсон, Учебник, часть 2
4 класс
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 70,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 53. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 65,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 104,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 10,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 59,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 216,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 82,
Мерзляк, Полонский, Якир, Учебник
Номер 83,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅a / b
= n ⋅ a / b
Пример 1
Найдем5 / 12
от числа 24.
Решение
5 / 12
⋅ 24 =5 ⋅ 24 / 12
=120 / 12
= 10
Пример 2
Найдем4 / 9
от числа 7.
Решение
4 / 9
⋅ 7 =4 ⋅ 7 / 9
=28 / 9
=31 / 9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Видео
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
этой суммы истратили. Сколько денег истратили?
Решение: Чтобы найти 
от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
этой суммы истратили. Сколько денег было истрачено?
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 
длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби 
. Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби 
. Известно, что 
длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 
это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби 
это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
от всего числа. Найдите это число.
Знаменатель дроби 
показывает, что число, которое мы должны найти, разделено на пять частей. Если 
этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти 
(одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби 
20 : 4 = 5
Мы нашли 
от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби 
5 × 5 = 25
Мы нашли 
от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби 
показывает, что общее время приготовления каши разделено на три части. Если 
времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
времени приготовления. Для этого 10 нужно разделить на числитель дроби 
10 мин : 2 = 5 мин
Мы нашли 
времени приготовления каши. 
времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби 
показывает, что общая масса мешка разделена на четыре части. Если 
массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби 
.
30кг : 2 = 15кг
Мы нашли 
массы мешка. 
массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби 
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Регистрация
Ваше имя
Пароль
Хочу получать рассылку рекламных и информационных сообщений.
Нажимая на кнопку «Регистрация», вы подтверждаете свое согласие сусловиями предоставления услуг (пользовательское соглашение) и условиями обработки персональных данных
Теги
Загрузить PDF
Загрузить PDF
Нахождение дроби от числа равнозначно умножению числа на дробь. Описанный метод применим к любому числу (процентам, обыкновенным дробям, смешанным числам, десятичным дробям), но лучше пользоваться им при работе с целыми числами. Чтобы освоить описанный метод, нужно знать операции умножения и деления.
-
1
Запишите задачу. Если в задаче числа представлены словами, запишите их цифрами. Если же в задаче даются цифры, пропустите этот шаг.
- Например: найдите одну третью от семи?
- Если в задаче между двумя числами стоит предлог «от», нужно перемножить эти числа. Таким образом, в нашем примере одну третью нужно умножить на семь.
- Запишите это так: (1/3) x 7.
-
2
Целое число умножьте на числитель. Работая с целым числом, всегда умножайте его на числитель (верхнее число) дроби. Знаменатель не меняется на протяжении всего процесса умножения.[1]
- В нашем примере: (1/3) x 7 = 7/3.
-
3
Полученный результат разделите на знаменатель. Результат умножения разделите на знаменатель (нижнее число) дроби. На данном этапе дробь может быть неправильной, то есть числитель больше знаменателя, или дробь нужно просто сократить.[2]
- В нашем примере после перемножения числа и дроби получилась дробь 7/3. Семь на три не делится нацело, поэтому получится остаток: 7/3 = 2 с остатком 1. Таким образом, в результате получится смешанное число: 21/3
Реклама
-
1
Упростите неправильную дробь. Это дробь, у которой числитель больше знаменателя. Перед тем как написать окончательный ответ, обязательно упростите неправильную дробь, то есть преобразуйте ее в смешанное число. Для этого разделите числитель на знаменатель, а остаток запишите в числителе новой дроби.
- Например: 10/3
- Разделите: 10/3 = 9 с остатком 1.
- Остаток запишите в числителе новой дроби (знаменатель не меняется): 1/3
-
2
Запишите смешанное число. Смешанное число состоит из целой части и дробной части. Это упрощенная форма неправильной дроби. Чтобы записать смешанное число, рядом напишите целое число и дробь, которая получена из остатка.[3]
- Например: 10/3. Разделите 10 на 3: 10/3 = 3 с остатком 1. Смешанное число: 31/3.
-
3
Сократите дробь до наименьших значений числителя и знаменателя. Выполнив умножение, сократите дробь. Для этого разделите числитель и знаменатель на некоторый общий делитель.
- Например, сократите дробь 4/8. Разделите числитель и знаменатель на 4: 4/8 = 1/2.
Реклама
Об этой статье
Эту страницу просматривали 13 418 раз.