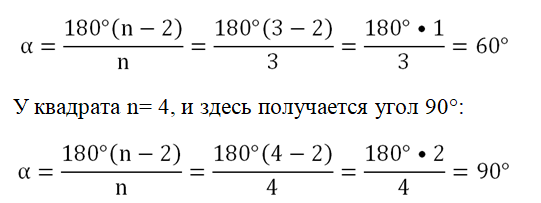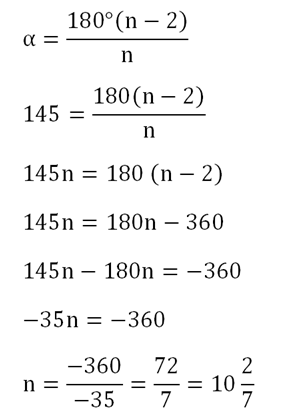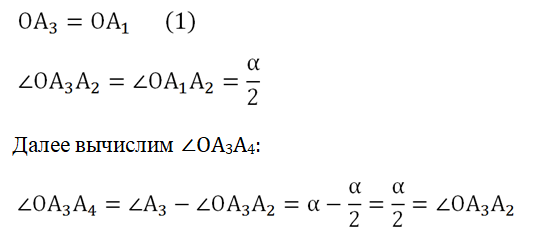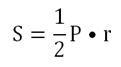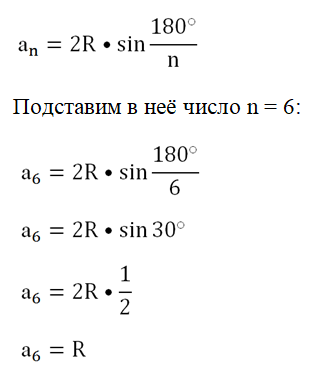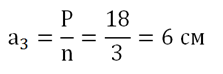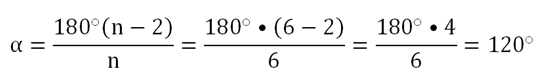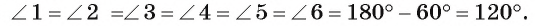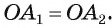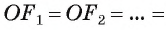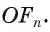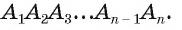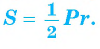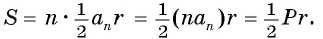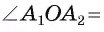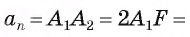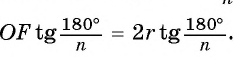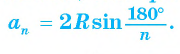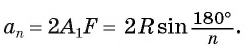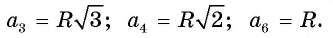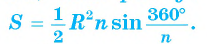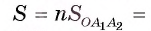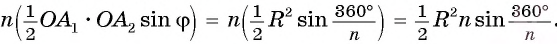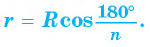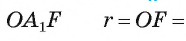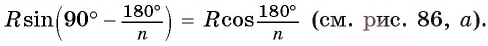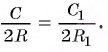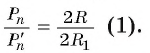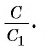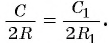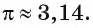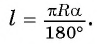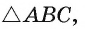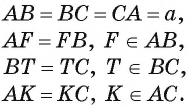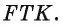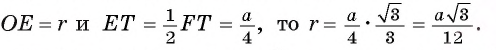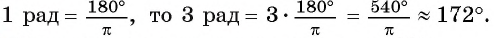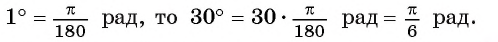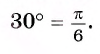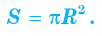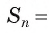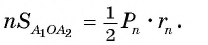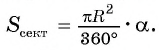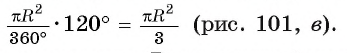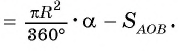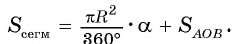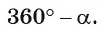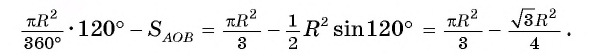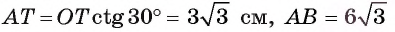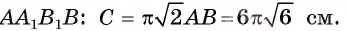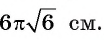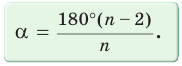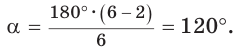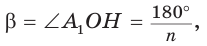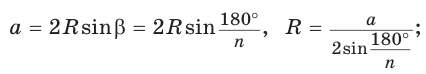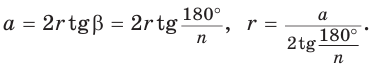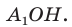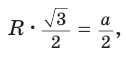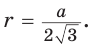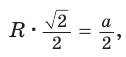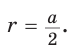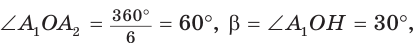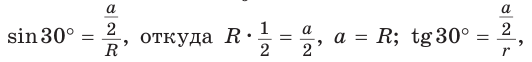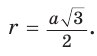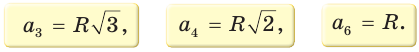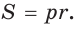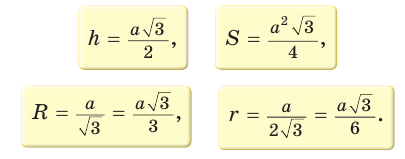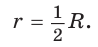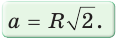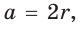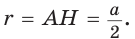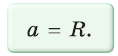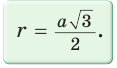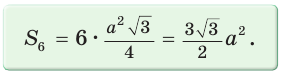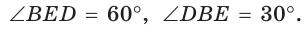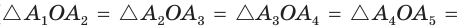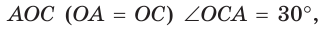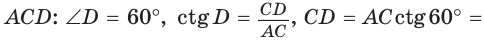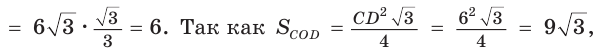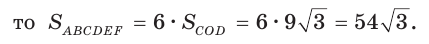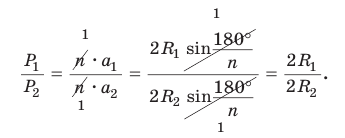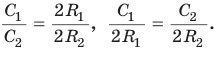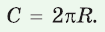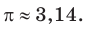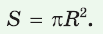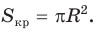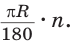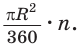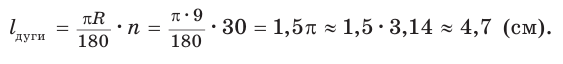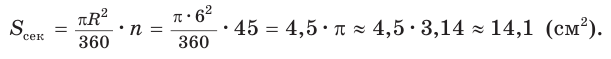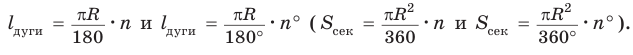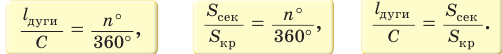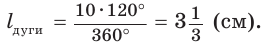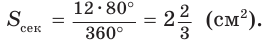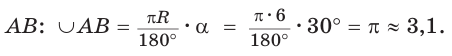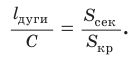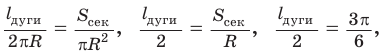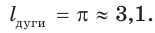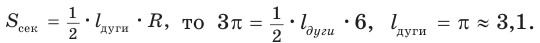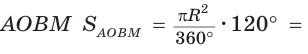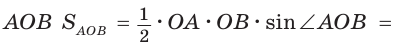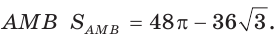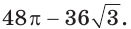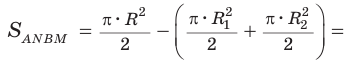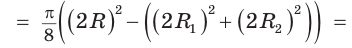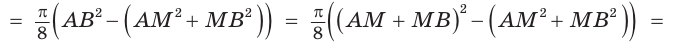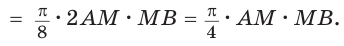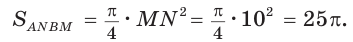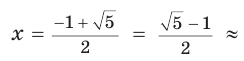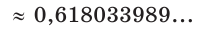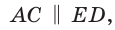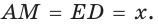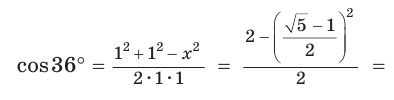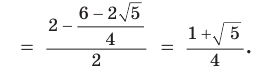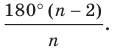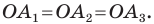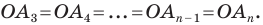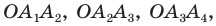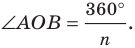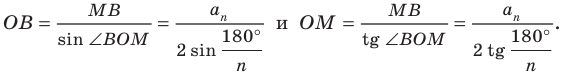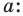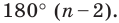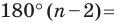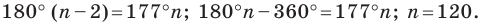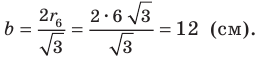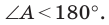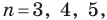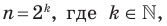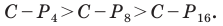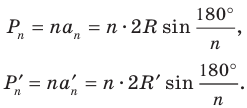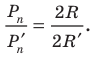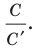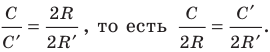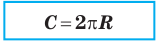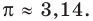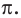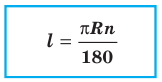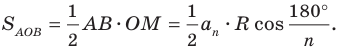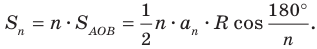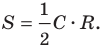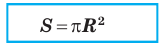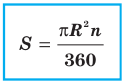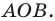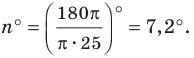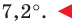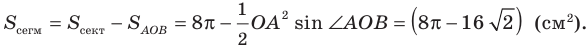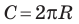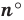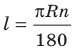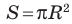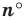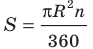План урока:
Понятие правильного многоугольника
Описанная и вписанная окружности правильного многоугольника
Формулы для правильного многоугольника
Построение правильных многоугольников
Понятие правильного многоугольника
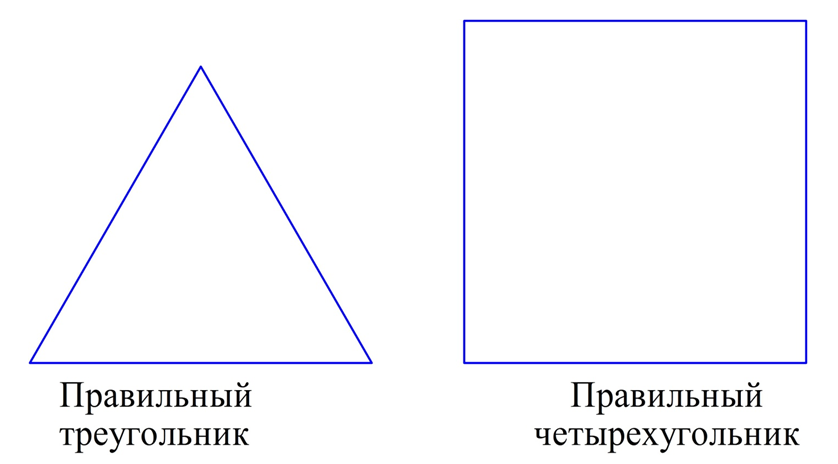
У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.
Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.
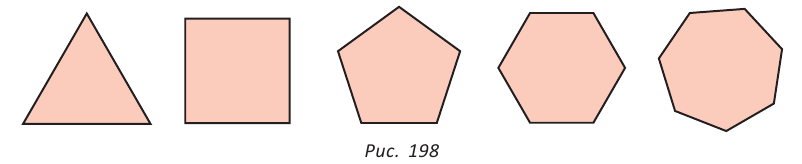
Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:
Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?
Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:
Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?
Решение. В формулу
Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?
Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.
Ответ: не может.
Описанная и вписанная окружности правильного многоугольника
Докажем важную теорему о правильном многоуг-ке.
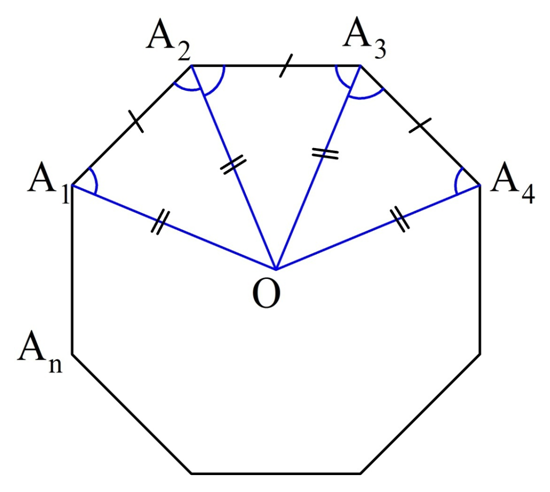
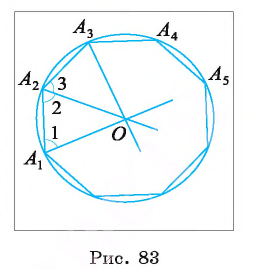
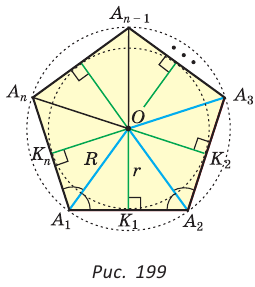
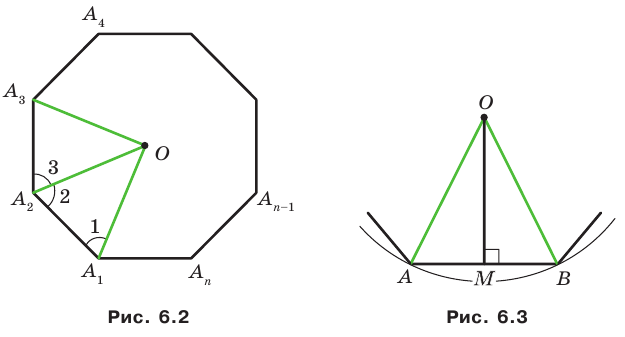
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А1, А2, А3…Аn. Далее проведем биссектрисы углов ∠А1 и ∠А2. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА3, ОА4 и т. д.
∠А1 и ∠А2 одинаковы по определению правильного многоуг-ка:
Из этого факта вытекает два равенства:
Получается, что ОА3 – это также биссектриса ∠А3. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):
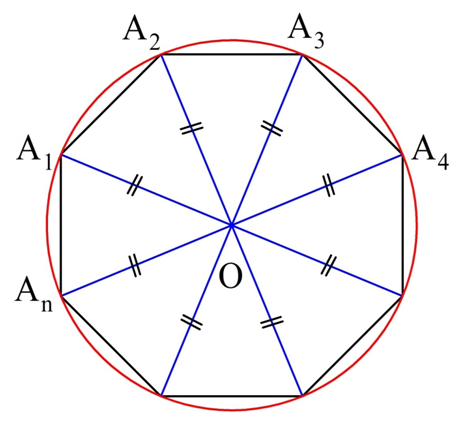
Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А1, А2 и А3, можно провести только одну окружность, ч. т. д.
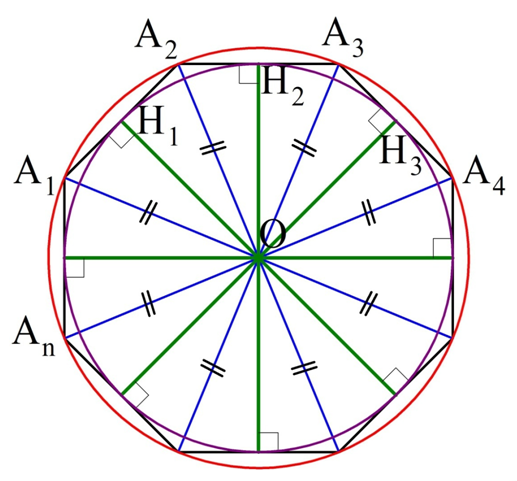
Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА1А2, ∆ОА2А3, ∆ОА3А4, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН1, ОН2, ОН3… на стороны многоуг-ка.
Так как высоты проведены в равных треуг-ках, то и сами они равны:
Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН1. Он должен будет пройти и через точки Н2, Н3, … Нn. Причем отрезки ОН1, ОН2, ОН3 окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А1, ∠А2, ∠А3, то есть в точке О. Так как расстояние от О до А1А2 – это отрезок ОН1, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.
Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.
Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН1, ОН2, ОН3,… проведены в равнобедренных треуг-ках∆ОА1А2, ∆ОА2А3, ∆ОА3А4,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н1, Н2, Н3,… – это середины сторон многоуг-ка.
Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?
Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.
Ответ: не могут.
Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.
Формулы для правильного многоугольника
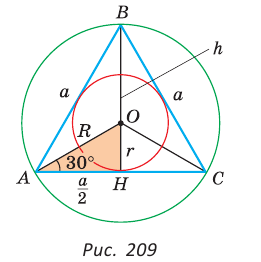
Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой an, где n– число сторон у многоуг-ка. Например a4– это сторона квадрата, a6– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.
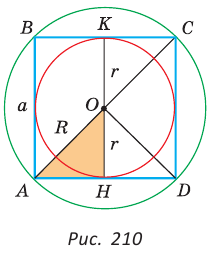
Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.
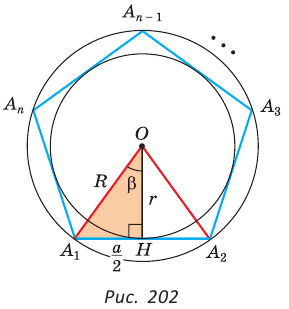
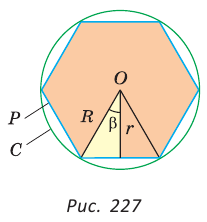
Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:
Теперь можно найти и ∠А1ОН1, рассмотрев ∆А1ОН1:
Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:
С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).
Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.
Решение. Запишем следующую формулу:
Это равенство как раз и надо было доказать в этом задании.
Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.
Решение. Запишем формулу:
Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.
Решение.
Найдем периметр шестиугольника:
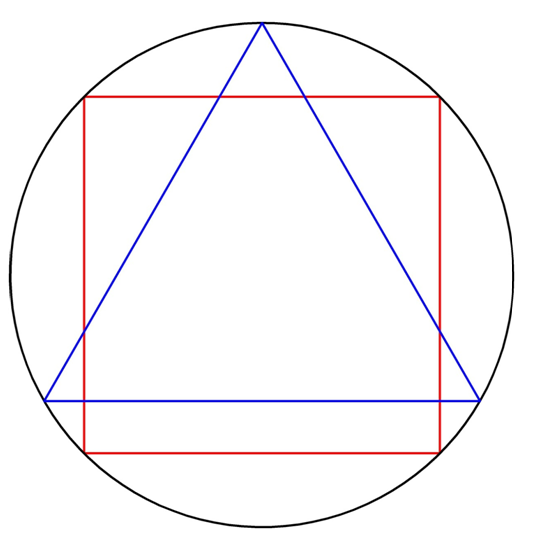
Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?
Решение. Зная периметр треуг-ка, легко найдем и его сторону:
Далее вычисляется радиус описанной около треугольника окружности:
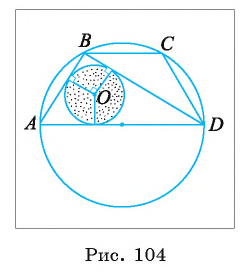
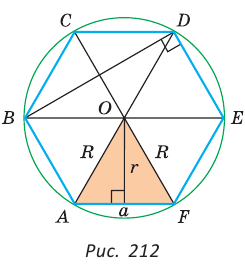
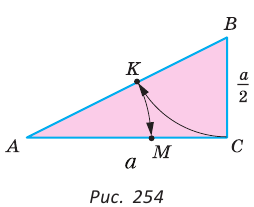
Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?
Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:
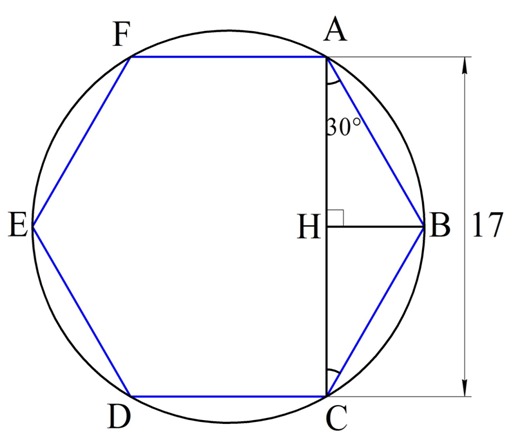
Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:
Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:
AC = 17 мм
∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:
AH = AC/2 = 17/2 = 8,5 мм
Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:
Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.
Ответ: 20 мм.
Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
a6 = R
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.
Содержание:
Вы уже изучили свойства равностороннего треугольника и квадрата. Каждая из этих фигур обладает тем свойством, что у них все углы равны и все стороны равны. Указанные геометрические фигуры служат примерами правильных многоугольников, свойства которых и рассматриваются в данном параграфе.
Определение правильного многоугольника
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
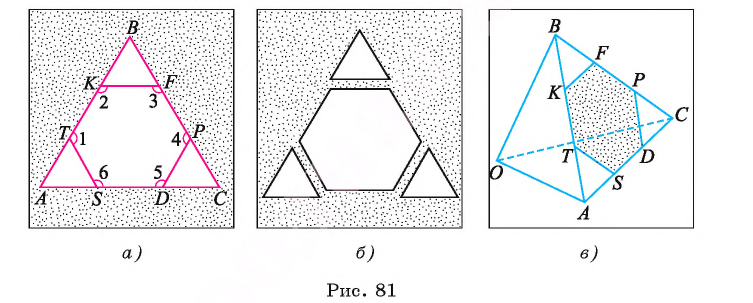
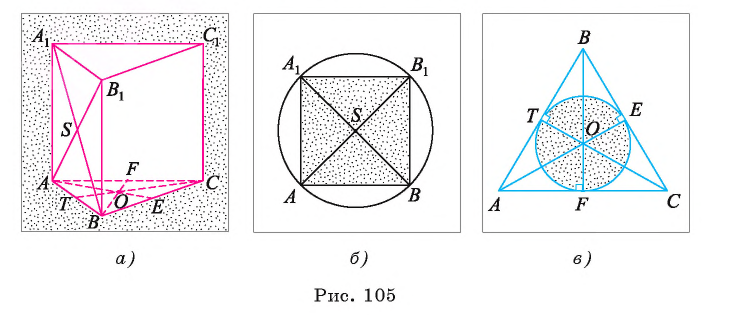
Рассмотрим пример. Пусть ABC — равносторонний треугольник;. Разделим каждую его сторону на три равные части, как показано на рисунке 81, а. Каждый из треугольников ATS, KBF и DPC является равносторонним. Отсюда следует, что
Модель этого правильного многоугольника получится, если от листа бумаги, имеющего форму равностороннего треугольника, отрезать равные части, имеющие форму равносторонних и равных между собой треугольников, как показано на рисунке 81, б.
Если треугольник АБС является гранью тетраэдра ВОАС (тетраэдр — треугольная пирамида, у которой все четыре грани — равные равносторонние треугольники), а каждая пара точек Т, К, F, Р и D, S делит соответственно ребра АВ, ВС и АС на три равные части, то TKFPDS — правильный шестиугольник, лежащий на грани ABC (рис. 81, в).
Ранее, в § 1 главы 1 учебного пособия «Геометрия, 8», была доказана теорема о том, что сумма градусных мер углов любого выпуклого n-угольника равна 180°(n — 2). Из доказанной теоремы и определения правильного n-угольника следует, что градусную меру каждого его угла можно найти по формуле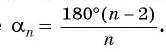
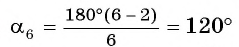
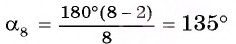
Окружность, описанная около правильного многоугольника
Вы знаете, что около правильного треугольника и правильного четырехугольника можно описать окружность. Теперь изучим вопрос о существовании окружности, описанной около правильного многоугольника.
Определение. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. При этом многоугольник называется вписанным в окружность.
Оказывается, что около любого правильного многоугольника можно описать окружность. Докажем следующую теорему.
Теорема 1 (об окружности, описанной около правильного многоугольника). Около любого правильного многоугольника можно описать единственную окружность.
Доказательство.
I. Докажем, существование окружности.
1) Пусть 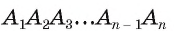
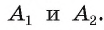
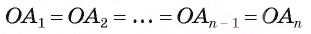
2) Так как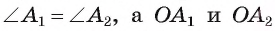
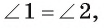
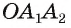
3) Заметим, что треугольник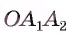
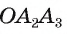
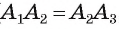
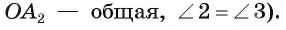
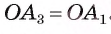
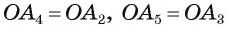
4) Таким образом,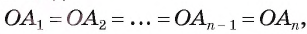
II. Докажем, что описанная окружность единственная.
Пусть существует еще одна окружность со,, которая описана около правильного многоугольника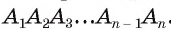
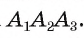
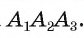
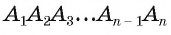
Теорема доказана.
Окружность, вписанная в правильный многоугольник
Известно, что в любой правильный треугольник можно вписать окружность. Рассмотрим вопрос о существовании окружности, вписанной в правильный многоугольник.
Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности. При этом многоугольник называется описанным около окружности.
Докажем, что в любой правильный многоугольник можно вписать окружность.
Теорема 2 (об окружности, вписанной в правильный многоугольник). В любой правильный многоугольник можно вписать единственную окружность.
I. Докажем существование окружности.
1) Пусть 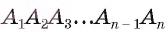
2) Пусть точка О — центр описанной около многоугольника окружности. Теперь проведем высоты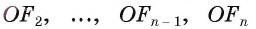
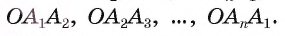
3) Таким образом, окружность 
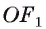
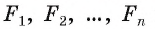
Заметим также, что центр О вписанной в правильный многоугольник окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Подчеркнем, что для правильного многоугольника центр вписанной окружности совпадает с центром, описанной окружности.
II. Докажем, что вписанная окружность единственная.
Предположим, что существует еще одна окружность 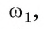
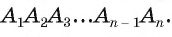
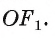
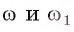
Теорема доказана.
Центром, правильного многоугольника называется центр его вписанной и описанной окружностей.
Выражение элементов n-угольника через радиус вписанной или описанной окружностей
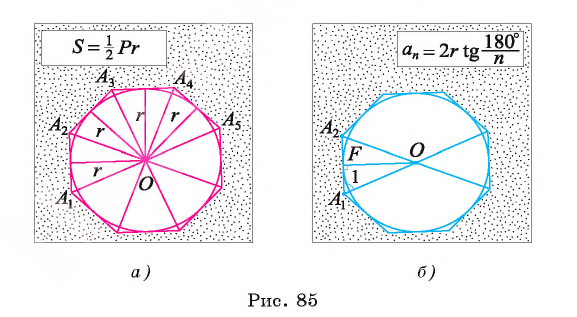
Пусть S — площадь правильного n-угольника, 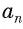
1) Площадь S правильного n-уголъника, описанного около окружности, можно найти, зная периметр Р и радиус г вписанной окружности, по формуле
Соединим центр О правильного многоугольника с его вершинами (рис. 85, а). Тогда многоугольник разбивается на n равных треугольников, площадь каждого из которых равна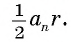
Что и требовалось доказать.
2) Длину стороны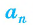
Соединим центр многоугольника с вершинами 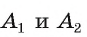
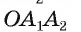
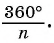
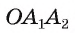
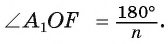
Что и требовалось доказать.
Так как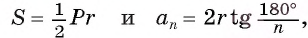
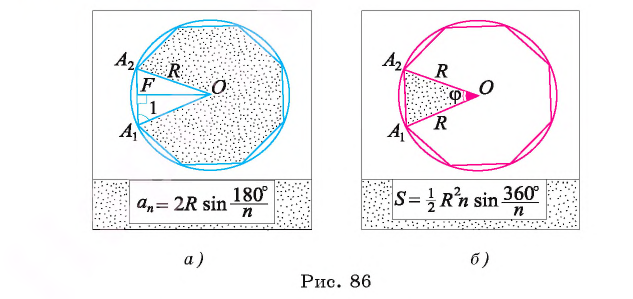
3) Длину стороны аn правильного n-угольника можно найти, зная радиус R описанной окружности, по формуле
Пусть OF — высота равнобедренного треугольника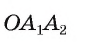
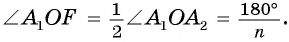
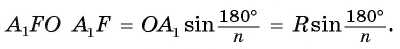
Что и требовалось доказать.
Для правильного треугольника (n = 3), квадрата (n = 4) и правильного шестиугольника, (n = 6) получим соответственно формулы:
4) Площадь S правильного п-угольника можно найти, зная радиус R описанной окружности, по формуле
Соединим вершины правильного /i-угольника с его центром (рис 86, б). Тогда многоугольник разобьется на п равных треугольников. Следовательно,
Что и требовалось доказать.
5) Радиус г вписанной окружности можно найти, зная радиус R описанной окружности, по формуле
В прямоугольном треугольнике
Что и требовалось доказать.
Построение правильных многоугольников
Вопрос о построении правильного треугольника уже рассматривался ранее. Покажем, каким образом можно с помощью циркуля и линейки построить правильный треугольник, вписанный в окружность.
Пример №1
Постройте правильный треугольник, вписанный в данную окружность.
Поиск решения.
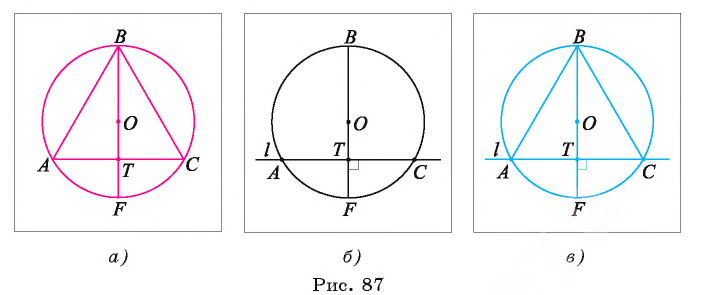
Пусть правильный треугольник ABC вписан в окружность с центром в точке О. Проведем диаметр BF этой окружности, обозначим буквой Т точку пересечения этого диаметра со стороной АС. Тогда положение точки Т на отрезке OF характеризуется равенством ОТ = TF; т. к. центр равностороннего треугольника есть точка пересечения медиан, то 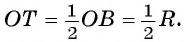
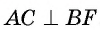
Построение.
1) Проводим диаметр BF окружности и строим точку Т — середину отрезка OF (рис. 87, б).
Строим прямую l, которая проходит через точку Т и перпендикулярна диаметру BF (рис. 87, б).
3) Отметим точки А и С пересечения прямой l с окружностью.
4) Строим отрезки ВА и ВС (рис. 87, в). Треугольник ABC — искомый.
Докажите самостоятельно, что построенный треугольник — правильный.
Пример №2
Постройте правильный шестиугольник, сторона которого равна данному отрезку а.
Поиск решения.
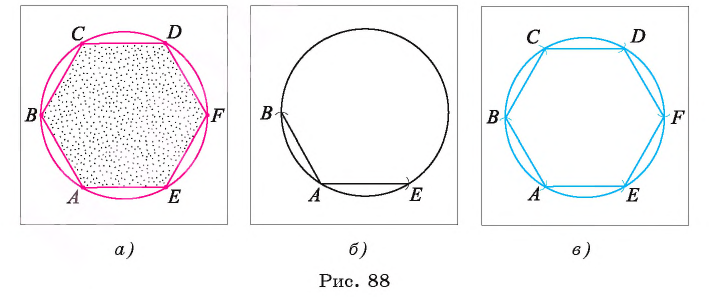
Пусть ABCDFE — правильный шестиугольник, сторона. которого равна а. Рассмотрим, описанную около этого шестиугольника окружность. Известно, что радиус окружности, описанной около правильного шестиугольника, равен его стороне, т. е. R = АВ = ВС = CD = DF = FE = ЕА = a.(рис. 88). Этим можем воспользоваться для построения шестиугольника.
Построение.
1) Строим окружность 
2) Выбираем на этой окружности произвольную точку А и строим окружность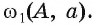
3) Далее строим точку С, которая является одной из точек пересечения окружности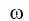
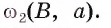
Заметим, что результат задачи 1 позволяет построить правильный шестиугольник, если построен правильный треугольник.
Понятие длины окружности
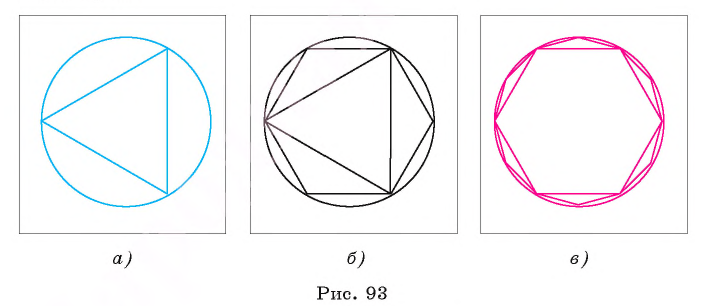
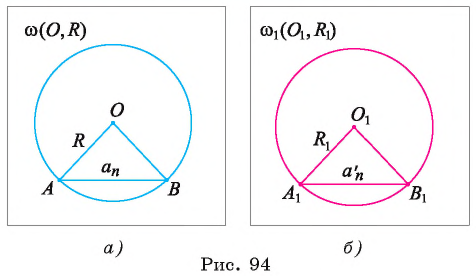
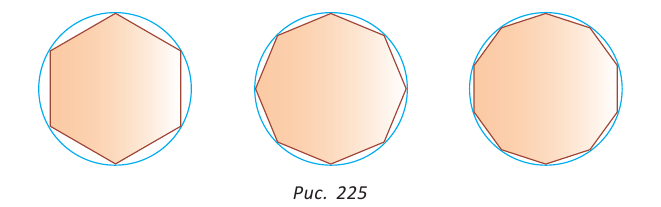
Рассмотрим вопрос о вычислении длины окружности. Пусть в окружность вписан правильный n-угольник. Если число n сторон правильного « угольника, вписанного в окружность, неограниченно возрастает, то геометрическая фигура, образованная его сторонами, все меньше и меньше отличается от окружности (рис. 93, а, б, в). В вузовском курсе математического анализа устанавливается, что существует число, к которому стремятся периметры Р„ правильных n-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется длиной окружности. Таким образом, за длину окружности принимается число, к которому стремятся периметры вписанных в окружность правильных n-угольников при неограниченном увеличении числа их сторон.
Длина окружности зависит от ее радиуса, окружность большего радиуса имеет большую длину. Вместе с тем можно доказать, что отношение длины окружности к ее диаметру есть число постоянное.
2. Теорема об отношении длины окружности к ее диаметру. Докажем теорему, которая характеризует отношение длины окружности к ее диаметру.
Теорема (об отношении длины окружности к ее диаметру).
Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей.
Дано: 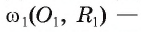
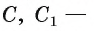
Доказательство.
1) Впишем в каждую из окружностей правильные n-угольники. Пусть длины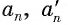
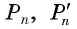
2) Теперь воспользуемся формулой, которой выражается длина стороны правильного п-угольника через радиус описанной окружности. Учитывая эту формулу (глава 3, § 1, п. 3), можем записать равенства 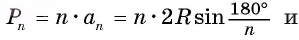
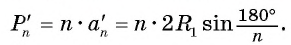
3) Это равенство верно при любом значении n. Будем неограниченно увеличивать число n, тогда периметр 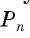
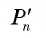
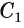
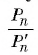
4) Таким образом, 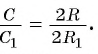
Значит, отношение длины окружности к ее диаметру одно и то же для всех окружностей.
Теорема доказана.
Число, равное отношению длины окружности к ее диаметру, обозначается строчной греческой буквой 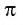
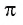
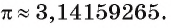
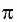
Длина дуги окружности
Для нахождения формулы длины окружности воспользуемся равенством 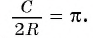
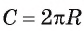
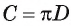
Теперь выведем формулу для вычисления длины I дуги окружности, градусная мера которой равна а. Пусть данная дуга является дугой окружности радиуса R. Так как длина всей окружности равна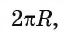
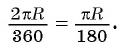
Пример №3
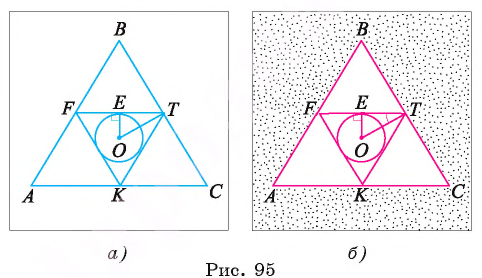
Точки F, Т и К — середины сторон равностороннего треугольника ABC. Найдите длину окружности, вписанной в треугольник FT К, если длина стороны треугольника ABC равна а.
Дано:
Найти: длину окружности, вписанной в треугольник
Решение:
Для нахождения длины окружности можем воспользоваться формулой 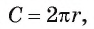
1) Пусть точка О — центр окружности, вписанной в треугольник FTK, а Е — точка касания окружности и стороны FT (рис. 95, а, б).
2) Треугольник FTK является равносторонним, так как 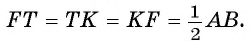
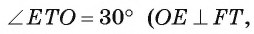
3) В прямоугольном треугольнике 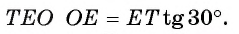
Заметим, что радиус г можно найти и другим способом, воспользовавшись тем, что треугольник FT К подобен треугольнику ABC с коэффициентом подобия
Таким образом, длина окружности
Пример №4
Основанием прямой четырехугольной призмы 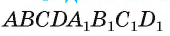
Решение:
Длину С окружности можно найти по формуле 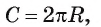
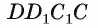
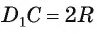
1) По условию длина окружности, описанной около квадрата ABCD, равна 8л см. Диаметр окружности равен диагонали АС, таким образом,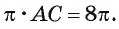
2) Так как четырехугольник ABCD — квадрат, то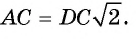
3) По условию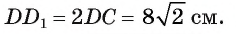
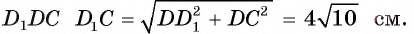
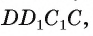
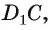
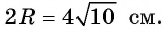
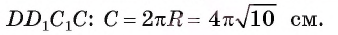
Радианная мера угла
Ранее была определена единица измерения углов — градус. Наряду с ней используется единица измерения углов, которая называется радианом.
Углом в один радиан называется центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Радианная мера угла — это величина угла, выраженная в радианах.
Установим связь между радианной и градусной мерой угла. Углу, градусная мера которого равна 180°, соответствует полуокружность, длина I которой равна 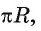
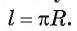
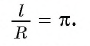
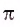
равна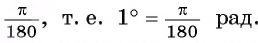
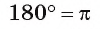
угла в 1 радиан равна 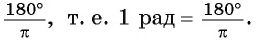
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример №5
Вычислите градусную меру угла 3 рад.
Решение:
Так как
Пример №6
Вычислите радианную меру угла 30°.
Решение:
Так как
При записи радианной меры угла обозначение рад можно
опускать. Например, вместо 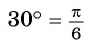
Площадь круга
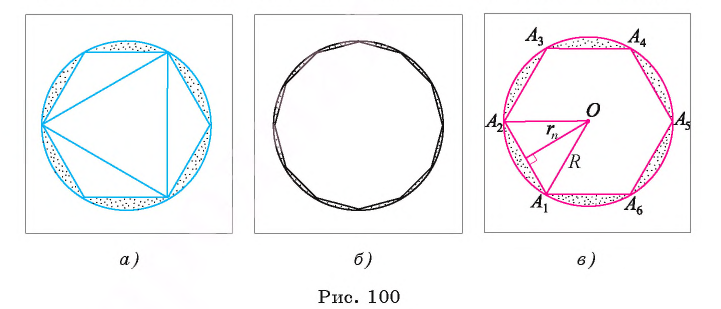
Рассмотрим вопрос о вычислении площади круга. Пусть в окружность, ограничивающую круг, вписан правильный n-угольник. Если число n сторон правильного n-угольника, вписанного в окружность, неограниченно возрастает, то многоугольник все меньше и меньше отличается от круга (рис. 100, а, б). Из результатов, доказывемых в вузовском курсе математического анализа, следует, что существует число, к которому стремятся площади S,, правильных п-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется площадью круга. Таким образом, за площадь круга принимается число, к которому стремятся площади вписанных в окружность, ограничивающую этот круг, правильных n-угольников при неограниченном увеличении числа их сторон.
Теперь докажем следующую теорему.
Теорема (о площади круга). Площадь S круга радиуса R можно вычислить по формуле
1) Пусть дан круг радиуса R и правильный n-угольник 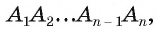
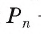
2) При неограниченном увеличении числа n сторон n-угольника радиус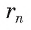
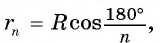
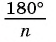
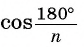
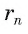
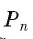
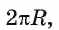
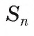
Теорема доказана.
Площадь сектора
Рассмотрим вопрос о вычислении площади части круга, которая называется сектором.
Определение. Сектором называется часть круга, ограниченная дугой окружности и двумя радиусами, соединяющими концы дуги с центром круга.
Дуга окружности, ограничивающая сектор, называется дугой сектора.
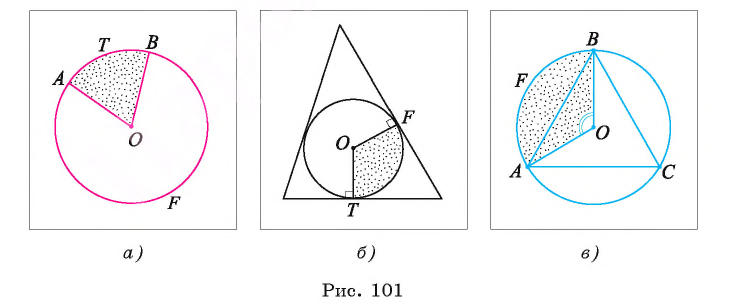
Например, на рисунке 101, а изображены два сектора, дугами которых служат дуги АТ В и AFB. На рисунке 101, б изображены круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соответствующими дугами окружности.
Выведем формулу для вычисления площади S сектора радиуса R, градусная мера дуги которого равна а. Площадь круга радиуса R равна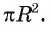
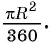
Например, если ABC — равносторонний треугольник, вписанный в круг радиуса R, а точка О — его центр, тогда площадь сектора, ограниченного радиусами ОА, ОБ и дугой AFB, равна
Площадь сегмента
Рассмотрим формулу для нахождения площади фигуры, которая называется сегментом.
Определение. Сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы дуги.
Дуга окружности, ограничивающая сегмент, называется дугой сегмента, а ограничивающая его хорда называется основанием сегмента.
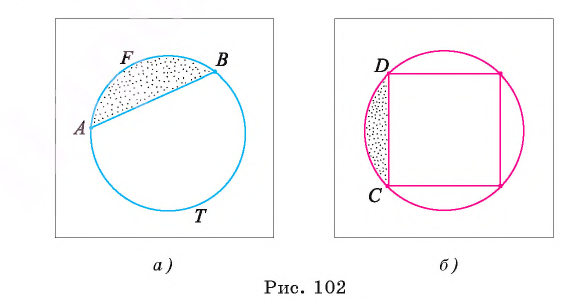
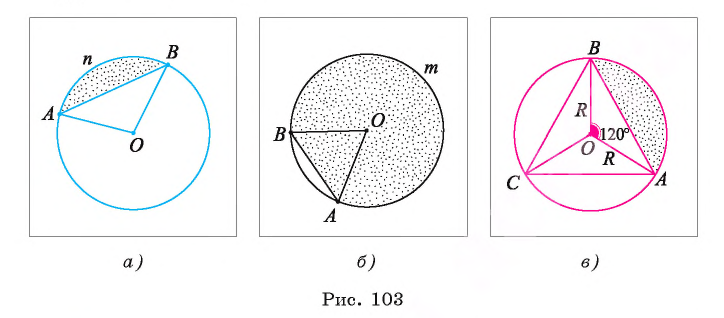
На рисунке 102, а изображены два сегмента, ограниченные хордой АВ и дугами AFB и АТ В. Хорда АВ является основанием для каждого из этих сегментов.
На рисунке 102, б изображены сегменты, ограниченные стороной CD вписанного квадрата и соответствующими дугами окружности.
Выведем формулу для вычисления площади сегмента. Рассмотрим два случая: 1) градусная мера дуги сегмента меньше 180°; 2) градусная мера дуги сегмента больше 180°.
1) Пусть градусная мера дуги АnВ сегмента равна а 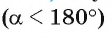
2) Пусть градусная мера дуги АmВ равна а (а > 180°) (рис. 103, б). Тогда площадь этого сегмента равна сумме площади сектора, ограниченного этой дугой и радиусами ОА,OB и площади треугольника, т. е.
Заметим, что площадь этого сегмента можно найти так же, как разность между площадью круга и площадью сегмента с тем же основанием и дугой, градусная мера которой равна
Пусть равносторонний треугольник ABC вписан в крут радиуса R, а точка О — его центр (рис. 103, в). Тогда площадь меньшего сегмента, основанием которого служит сторона АВ треугольника, равна
Пример №7
Диагональ BD равнобедренной трапеции ABCD перпендикулярна боковой стороне, а площадь круга, вписанного в треугольник ABD, равна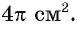
Решение:
Длину С окружности, описанной около трапеции ABCD, можно найти по формуле 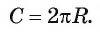
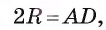
1) Пусть г — радиус круга, вписанного в треугольник ABD. Так как площадь этого круга равна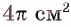
2) Площадь 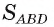
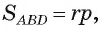
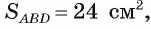
3) Для нахождения длины отрезка AD воспользуемся формулой r=p -AD. Отсюда AD =р — г = 12 — 2 = 10 (см).
4) Теперь длина окружности
Ответ:
Пример №8
Основанием прямой треугольной призмы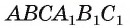
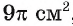
Решение:
По условию задачи каждая боковая грань призмы является квадратом. Длину окружности, описанной около квадрата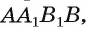
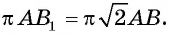
1) Пусть точка О — центр круга, вписанного в равносторонний треугольник ABC, 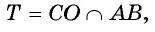
2) Так как площадь круга, вписанного в треугольник ABC, равна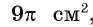
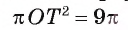
3) В прямоугольном треугольнике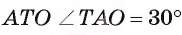
4) Теперь вычислим длину С окружности, описанной около грани
Ответ:
Правильные многоугольники с примерами
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунке 198 изображены правильные треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник. Правильный треугольник — это равносторонний треугольник, а правильный четырехугольник — это квадрат.
Одной из простейших задач является задача нахождения величины внутреннего угла правильного многоугольника. Так как все углы правильного 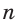
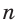
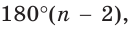
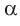
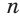
Например, для правильного шестиугольника
Теорема. Около любого правильного многоугольника можно описать окружность, в любой правильный многоугольник можно вписать окружность; центры этих окружностей совпадают.
Доказательство:
В правильном многоугольнике 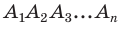
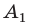
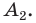
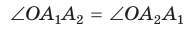
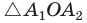
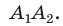
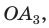
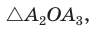
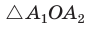
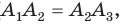
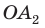
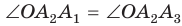
Соединив точку О отрезками с остальными вершинами, получим множество равных равнобедренных треугольников. Отсюда 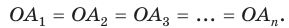
Поэтому окружность с центром О и радиусом 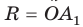
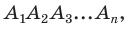
А поскольку высоты указанных равных равнобедренных треугольников, проведенные к их основаниям, равны, т. е. 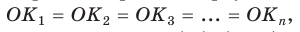
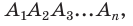
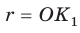
Точка О называется центром правильного 
Формулы радиусов описанной и вписанной окружностей правильного многоугольника
Пусть 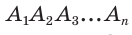
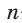
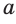
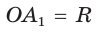
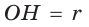
Так как 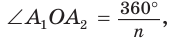
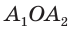
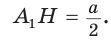
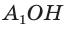
а) 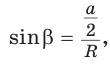
б) 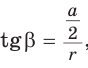
Замечание. Выведенные формулы запоминать не обязательно. Важно помнить способ их получения: решение прямоугольного треугольника
Примеры:
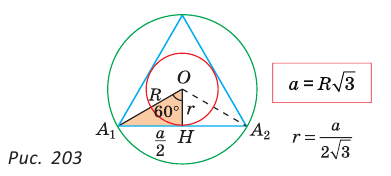
1) Для правильного треугольника (рис. 203) получим:
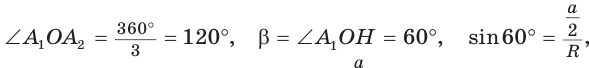
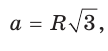
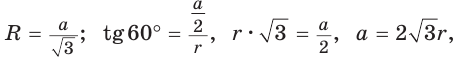
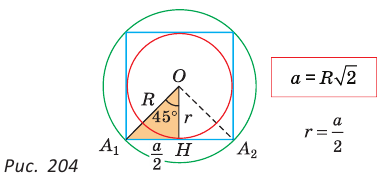
2) Для правильного четырехугольника (рис. 204) получим:
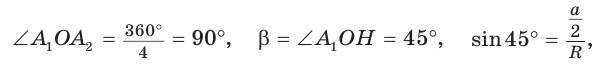
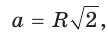
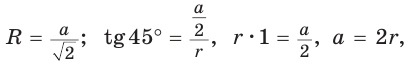
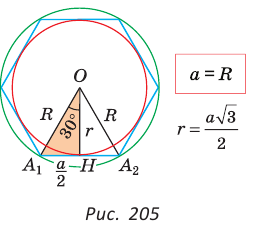
3) Для правильного шестиугольника (рис. 205)
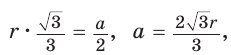
Полезно запомнить формулы, выражающие сторону 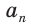
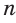
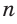
Для нахождения площади правильного 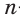
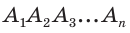
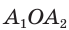
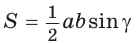
Пример:
Для нахождения радиуса 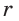
Правильный треугольник
Обобщим информацию о правильном (равностороннем) треугольнике.
Запишем формулы высоты 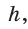
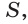
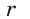
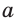
Из 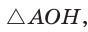
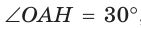
При заданной стороне 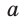
Так как 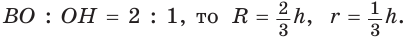
Правильный четырехугольник
Пусть сторона квадрата ABCD равна 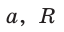
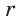
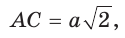
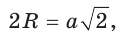
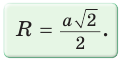
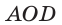
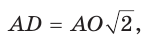
Диаметр КН окружности, вписанной в квадрат, равен длине стороны квадрата, т. е. КН = АВ = а, откуда 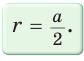
что
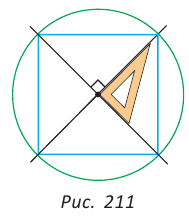
Для построения квадрата, вписанного в данную окружность с заданным центром, можно построить две взаимно перпендикулярные прямые, проходящие через центр окружности (рис. 211). Эти прямые пересекут окружность в вершинах квадрата. Обоснуйте это утверждение. Выполните указанное построение при помощи чертежного треугольника.
Правильный шестиугольник
Рассмотрим правильный 6-угольник ABCDEF со стороной 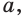
так как ОА = OF = R, 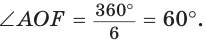
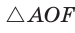
Так как радиус 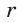
Поскольку 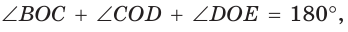
Меньшая (малая) диагональ BD правильного шестиугольника является диагональю ромба BCDO (ВС = CD = DO = ВО — а) с углами, равными 60° и 120°. Откуда 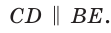
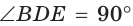
Кроме того, 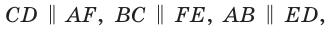
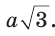
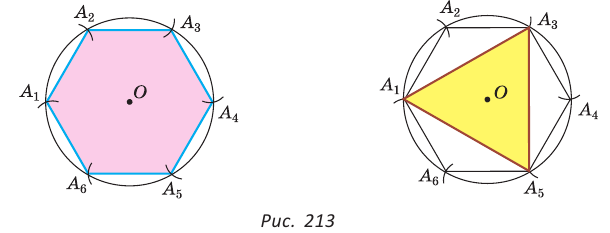
Построим при помощи циркуля и линейки правильный шестиугольник, вписанный в данную окружность с радиусом R (рис. 213, а). Воспользуемся тем, что а = R, где а — сторона правильного шестиугольника.
Одну вершину 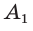
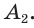
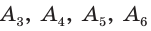
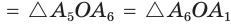
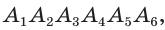
Для построения правильного треугольника, вписанного в данную окружность, достаточно соединить отрезками через одну вершины правильного вписанного шестиугольника (рис. 213, б). Для построения правильного 12-угольника следует разделить дуги 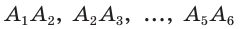
Применяя указанный способ деления дуг пополам, можно с помощью циркуля и линейки построить множество правильных многоугольников.
Так, из правильного 4-угольника можно построить правильный 8-угольник, 16-угольник, и вообще любой правильный 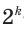
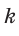
Пример №9
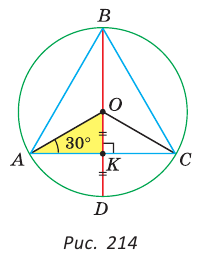
В окружности с центром О проведен диаметр BD, через середину радиуса OD проведена хорда АС, перпендикулярная диаметру BD (рис. 214). Доказать, что 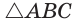
Доказательство:
Так как 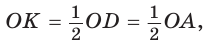
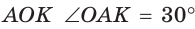
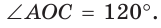
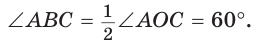
Поэтому АК = КС. Так как в треугольнике АВС высота ВК является и медианой, то он — равнобедренный, АВ = ВС. Отсюда 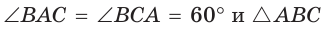
Замечание. Из задачи следует второй способ построения правильного треугольника, вписанного в окружность: строится диаметр BD, через середину радиуса OD проводится хорда АС, перпендикулярная диаметру. Треугольник АВС — правильный.
Пример №10
Дан правильный шестиугольник ABCDEF, диагональ АС равна 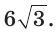
Решение:
Вписанный угол ACD опирается на диаметр АО, поэтому он прямой. Из прямоугольного треугольника
Ответ:
Нахождение длины окружности и площади круга
Длину окружности, сделанной из гибкой проволоки, можно измерить, если проволоку распрямить в отрезок. Еще древние заметили, что отношение длины любой окружности к ее диаметру есть величина постоянная: длина окружности примерно в 3 раза больше диаметра. Вы можете убедиться в этом при помощи нитки и линейки, используя в качестве окружности верхнюю кромку чашки (рис. 224).
Понятно, что периметр правильного многоугольника, вписанного в окружность, будет стремиться к длине окружности при неограниченном увеличении числа его сторон, а площадь этого многоугольника — к площади круга, ограниченного данной окружностью (рис. 225).
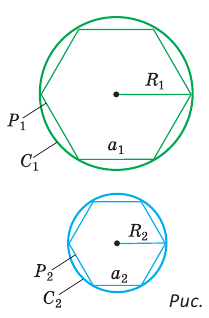
Используя этот факт, выведем уже известные вам формулы длины окружности 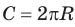
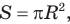
Вначале покажем, что отношение длины любой окружности С к ее диаметру D = 2R есть величина постоянная. Для этого рассмотрим две окружности и два правильных вписанных в них многоугольника с одинаковым числом сторон 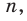
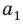
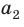
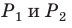
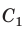
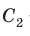
Найдем отношение указанных периметров:
При неограниченном увеличении числа 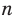
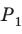
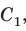
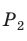
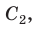
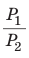
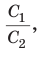
Отсюда следует, что отношение длины окружности к ее диаметру, т. е. . 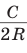
Это отношение обозначается буквой 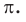
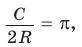
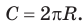
Теорема. Длина окружности радиуса R находится по формуле
Интересно знать. Число 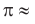
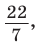
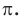
А теперь выведем формулу площади круга.
Теорема. Площадь круга радиуса R находится по формуле
Доказательство:
Рассмотрим некоторую окружность радиуса R и вписанный в нее правильный 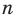
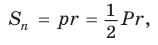
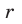
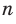
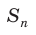
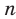
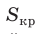
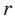
Тогда 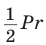
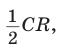
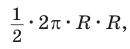
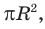
Теорема доказана.
Длина дуги окружности и площадь сектора круга
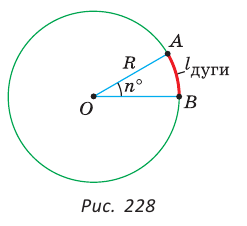
Поскольку длина окружности 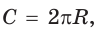
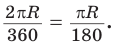
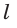
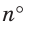
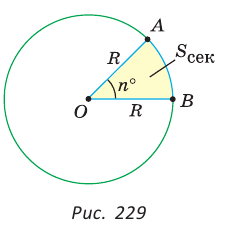
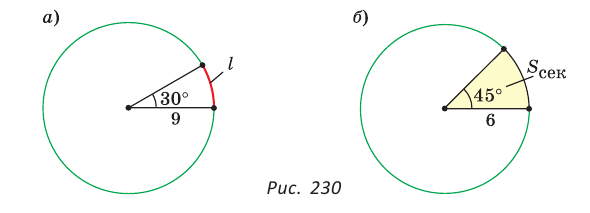
Напомним, что сектором называется часть круга, ограниченная двумя радиусами и дугой, соединяющей концы радиусов (рис. 229). Радиус круга называется радиусом сектора, указанная дуга — дугой сектора, центральный угол между радиусами, ограничивающими сектор, — углом сектора.
Так как площадь круга 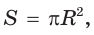
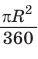
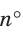
Заметим, что 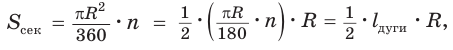
Пример №11
Пусть дана дуга окружности с радиусом 9 см, содержащая 30° (рис. 230, а). Найдем длину дуги:
Пример №12
Пусть угол сектора содержит 45°, а радиус равен 6 см (рис. 230, б). Найдем площадь сектора:
Замечание. При вычислении длины дуги (площади сектора) допустимы обе следующие записи:
Длина дуги и площадь сектора прямо пропорциональны градусной мере дуги и угла сектора. Поэтому длина дуги так относится к длине окружности, как градусная мера дуги относится к градусной мере окружности.
Площадь сектора так относится к площади круга, как градусная мера угла сектора относится к градусной мере полного угла, т. е. справедливы пропорции:
Замечание. В третьей пропорции 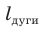
Данные пропорции также позволяют находить длину дуги и площадь сектора. Так, если длина окружности равна 10 см, а градусная мера ее дуги 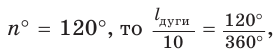
А если площадь круга равна 12 см2 и угол сектора равен 80°, 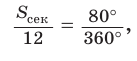
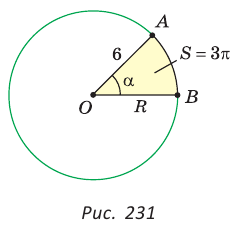
Пример №13
Дан сектор АОВ (рис. 231), радиус которого равен 6, а площадь — 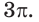
Решение:
Способ 1. Пусть 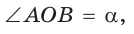
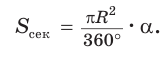
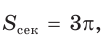
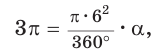
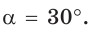
Способ 2. Воспользуемся пропорцией
Тогда
Способ 3. Так как
Ответ: 3,1.
Пример №14
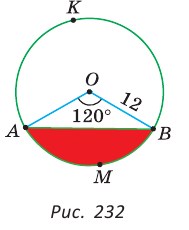
Найти площадь сегмента круга, радиус которого равен 12, если градусная мера дуги этого сегмента равна 120°.
Решение:
Напомним, что сегментом называется часть круга, ограниченная хордой и дугой окружности, которая соединяет концы этой хорды.
Пусть О — центр данной окружности, 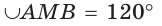
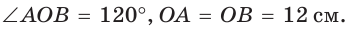
Так как площадь сектора
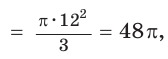
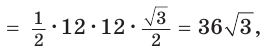
Ответ:
Замечание. Площадь сегмента АКВ (см. рис. 232) можно найти как сумму площадей сектора ОАКВ и треугольника АОВ, либо как разность площади круга и площади сегмента АМВ.
Интересно знать. В 1987 г. был учрежден неофициальный праздник — день числа 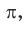
Долгое время математики старались найти как можно большее число знаков числа 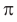
Легко запомнить двенадцать первых знаков числа 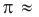
Луночки Гиппократа
Луночками Гиппократа называют серповидные фигуры, ограниченные дугами двух окружностей.
Пример №15
На отрезках АВ, AM и МВ построены полукруги с центрами в точках 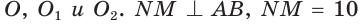
Решение:
Площадь закрашенной фигуры равна разности площадей полукруга с диаметром АВ = 2R и двух полукругов с диаметрами 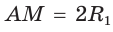
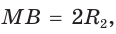
Так как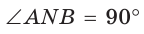
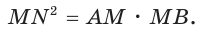
Ответ: 25л.
Золотое сечение
«Золотое сечение», или «божественная пропорция», — так называют математики деление отрезка некоторой точкой на части так, что больший из полученных отрезков является средним пропорциональным (средним геометрическим) между меньшим отрезком и целым. Другими словами, больший отрезок должен так относиться к меньшему, как целый отрезок относится к большему. Если на отрезке АВ отмечена точка М и 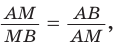
Пусть 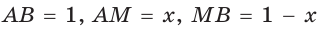
Тогда 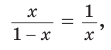
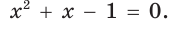
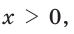
Таким образом, больший отрезок AM составляет приблизительно 62 %, а меньший отрезок МВ — приблизительно 38 % всего отрезка АВ.
Число 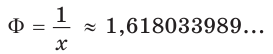
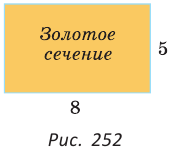
Золотое сечение обладает определенной гармонией, которую человек находит прекрасной. Многие художественные, музыкальные, поэтические произведения, шедевры архитектуры содержат в своей структуре золотое сечение. Опытным путем установлено, что оптимальным человеку кажется прямоугольник, длина и ширина которого находятся в отношении золотого сечения. Физиологи объясняют это тем, что поле зрения человека, т. е. та часть окружающего мира, которую видит человек, представляет собой прямоугольник со сторонами, находящимися в отношении золотого сечения.
Известно, например, что в знаменитой скульптуре Венеры Милосской (рис. 253) — эталоне женской красоты — талия делит фигуру в отношении золотого сечения.
Примечателен один исторический факт. Когда информация о Венере Милосской и золотом сечении была опубликована в одном из популярных журналов начала XX в., то в магазинах поблизости женских гимназий вдруг исчезли портняжные метры. Их раскупили девушки гимназистки, чтобы проверить, насколько их фигура близка к идеалу и какой высоты каблук следует носить, чтобы к нему приблизиться.
Покажем способ деления отрезка в отношении золотого сечения при помощи циркуля и линейки. Пусть дан отрезок, равный 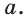
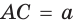
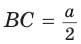
Точка М делит отрезок АС в отношении золотого сечения, т. е. 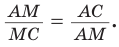
Построение правильного пятиугольника
С давних времен построению правильных многоугольников при помощи циркуля и линейки математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники, а также правильные многоугольники, получаемые удвоением числа их сторон: 6-угольники, 8-угольники, 10-угольники и т. д. Далее дело зашло в тупик: они не могли найти способ построения правильных 7-угольников, 9-угольников, 11-угольников. И только 2000 лет спустя великий немецкий математик XVII в. Карл Гаусс решил эту математическую проблему. Будучи 19-летним юношей, он доказал, что можно построить правильный 17-угольник, а вот 7-угольник, 9-угольник, 11-угольник, 13-угольник циркулем и линейкой построить нельзя. Задача о построении правильного 17-угольника была его первым научным открытием. Несмотря на выдающиеся достижения Гаусса в области математики, этой пер вой своей решенной проблеме он придавал такое значение, что в конце жизни завещал изобразить на могильном камне правильный 17-угольник.
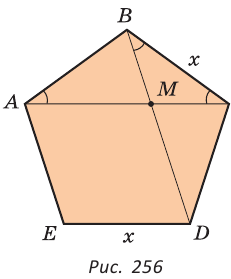
Рассмотрим правильный пятиугольник. Если в нем провести все диагонали (рис. 255), то получится звезда (звездчатый пятиугольник). Звезда была символом школы Пифагора. Замечательно то, что точки пересечения диагоналей пятиугольника делят их в отношении золотого сечения: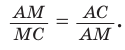
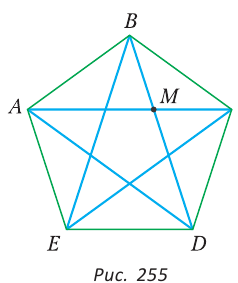
Так как 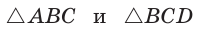
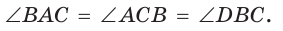
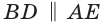
Но ВС = ED = х как стороны пятиугольника. Из подобия треугольников АВС и ВМС (по двум углам) следует 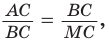
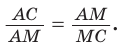
Рассмотрим задачу о построении правильного пятиугольника при помощи циркуля и линейки. Для построения правильного пятиугольника можно взять произвольный отрезок 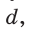
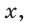
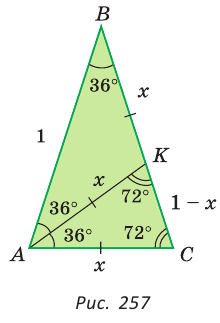
Задача о построении правильного пятиугольника равносильна построению углов, равных 36°, 72°, 108°, а также построению равнобедренного треугольника, биссектриса угла при основании которого разбивает данный треугольник на два равнобедренных. Пусть в треугольнике АВС (рис. 257) 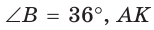
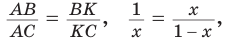
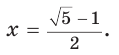
Отметим, что сторона АС треугольника АВС является стороной правильного десятиугольника, вписанного в окружность с радиусом, равным АВ.
Справочный материал по правильным многоугольникам
В этом параграфе вы узнаете, какие многоугольники называют правильными. Изучите свойства правильных многоугольников. Узнаете, как с помощью циркуля и линейки строить некоторые из них.
Научитесь находить радиусы вписанной и описанной окружностей правильного многоугольника, длину дуги окружности, площади сектора и сегмента круга.
Правильные многоугольники и их свойства
Определение. Многоугольник называют правильным, если у него все стороны равны и все углы равны.
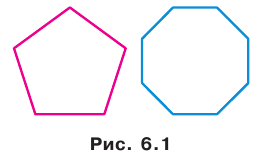
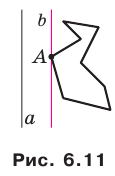
С некоторыми правильными многоугольниками вы уже знакомы: равносторонний треугольник — это правильный треугольник, квадрат — это правильный четырехугольник. На рисунке 6.1 изображены правильные пятиугольник и восьмиугольник.
Ознакомимся с некоторыми свойствами, которыми обладают все правильные 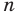
Теорема 6.1. Правильный многоугольник является выпуклым многоугольником.
С доказательством этой теоремы вы можете ознакомиться на с. 61-62.
Каждый угол правильного 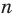
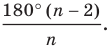
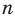
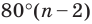
В правильном треугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон. Это точка пересечения биссектрис правильного треугольника. Точка пересечения диагоналей квадрата также обладает аналогичным свойством. То, что в любом правильном многоугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон, подтверждает следующая теорема.
Теорема 6.2. Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.
Доказательство: На рисунке 6.2 изображен правильный 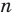
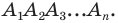
Проведем биссектрисы углов 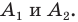
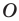
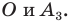
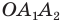
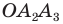
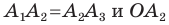
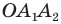
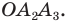
Соединяя точку 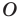
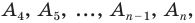
Таким образом, для многоугольника 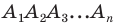
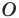
Поскольку равнобедренные треугольники 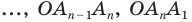
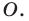
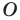
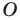
Точку, которая является центром описанной и вписанной окружностей правильного многоугольника, называют центром правильного многоугольника.
На рисунке 6.3 изображен фрагмент правильного 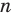
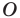
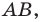
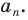
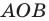
В равнобедренном треугольнике 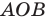
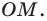
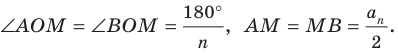
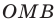
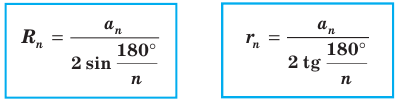
Отрезки 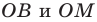
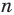
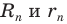
Подставив в эти формулы вместо 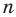
Из полученных результатов следует, что сторона правильного шестиугольника равна радиусу его описанной окружности. Отсюда получаем алгоритм построения правильного шестиугольника: от произвольной точки 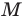
Соединив через одну вершины правильного шестиугольника, получим правильный треугольник (рис. 6.5).
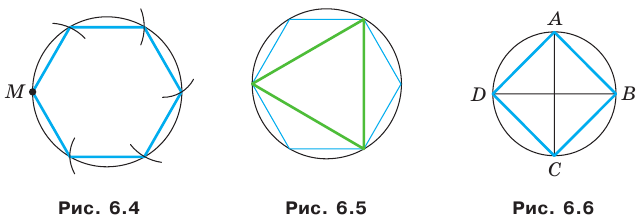
Для построения правильного четырехугольника достаточно в окружности провести два перпендикулярных диаметра 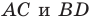
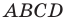
Если уже построен правильный 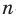
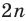
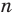
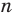
Пример №16
Существует ли правильный многоугольник, угол которого равен: 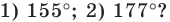
Решение:
1) Пусть 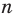
С другой стороны, эта сумма равна 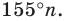
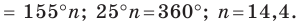
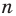
2) Имеем:
Ответ: 1) не существует; 2) существует, это — стодвадцатиугольник.
Пример №17
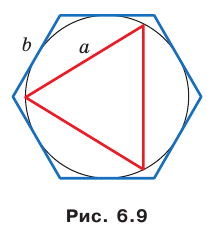
В окружность вписан правильный треугольник со стороной 18 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
Решение:
Радиус окружности, описанной около правильного треугольника, вычисляют по формуле 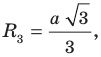
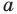
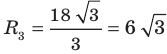
По условию радиус окружности, вписанной в правильный шестиугольник, равен радиусу окружности, описанной около правильного треугольника, то есть 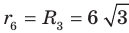
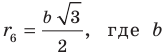
Ответ: 12 см.
О построении правильных n-угольников
Докажем, что любой правильный 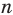
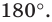
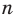
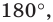
Рассмотрим произвольный многоугольник и прямую 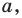
Сравнив длины этих перпендикуляров, мы сможем выбрать вершину многоугольника, наименее удаленную от прямой 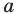
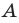
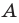
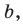
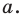
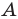
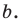
Вы умеете с помощью циркуля и линейки строить правильный 4-угольник, а следовательно, и 8-угольник, 16-угольник, 32-угольник, то есть любой 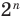
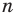
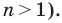
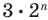
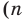
Задачу построения правильных многоугольников с помощью циркуля и линейки изучали еще древнегреческие геометры.
В частности, помимо указанных выше многоугольников, они умели строить правильные 5-угольник и 15-угольник — задачи довольно непростые.
Древние ученые, умевшие строить любой из правильных 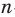
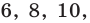
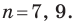
Гаусс доказал, что циркулем и линейкой можно построить правильный 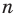
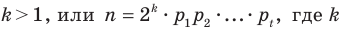
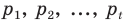
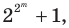
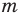
Гаусс придавал своему открытию столь большое значение, что завещал изобразить 17-угольник на своем надгробии. На могильной плите Гаусса этого рисунка нет, однако памятник Гауссу в Браун-швейге стоит на семнадцатиугольном постаменте.
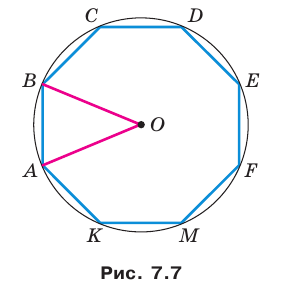
Длина окружности. Площадь круга
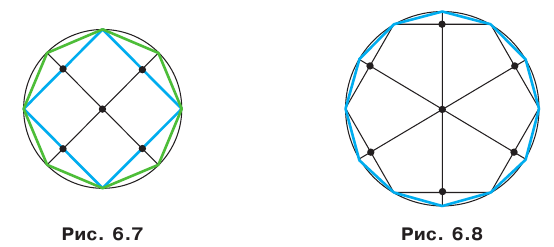
На рисунке 7.1 изображены правильные 4-угольник, 8-угольник и 16-угольник, вписанные в окружность.
Мы видим, что при увеличении количества сторон правильного 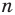
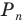
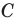
Так, для нашего примера можно записать:
При неограниченном увеличении количества сторон правильного многоугольника его периметр будет как угодно мало отличаться от длины окружности. Это означает, что разность 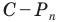
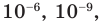
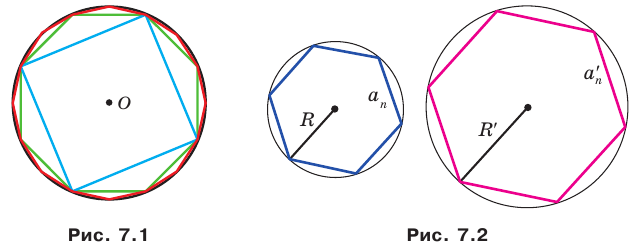
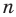
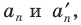
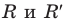
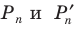
Отсюда
Это равенство справедливо при любом значении 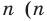
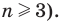
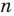
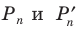
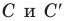
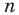
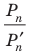
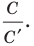
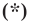
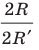
А это возможно только тогда, когда
Последнее равенство означает, что для всех окружностей отношение длины окружности к диаметру является одним и тем же числом.
Из курса математики 6 класса вы знаете, что это число принято обозначать греческой буквой 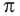
Из равенства 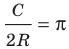
Число 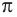
Великий древнегреческий ученый Архимед (III в. до н. э.), выразив через диаметр описанной окружности периметр правильного 96-угольника, установил, что 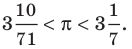
С помощью современных компьютеров и специальных программ можно вычислить число 
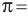
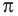
Найдем формулу для вычисления длины дуги окружности с градусной мерой 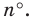
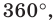
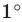
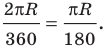
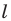
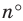
Выведем формулу для вычисления площади круга.
Обратимся снова к рисунку 7.1. Видим, что при увеличении количества сторон правильного 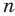
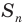
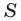
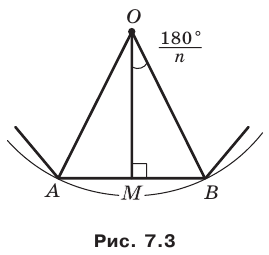
На рисунке 7.3 изображен фрагмент правильного 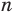
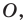
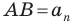
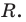
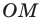
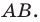
Поскольку радиусы, проведенные в вершины правильного 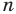
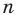
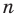
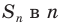
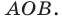
Отсюда
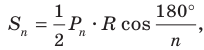
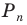
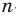
При неограниченном увеличении значения 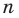
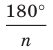
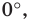
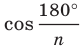
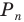
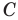
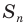
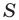
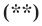
Из этого равенства получаем формулу для нахождения площади круга:
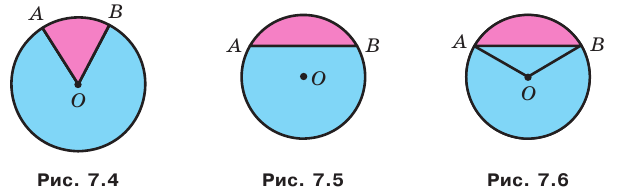
На рисунке 7.4 радиусы 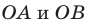
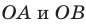
Понятно, что круг радиуса 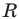
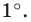
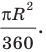
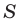
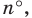
На рисунке 7.5 хорда 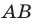
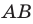
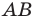
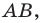
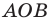
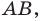
Если хорда 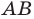
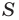
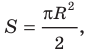
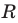
Пример №18
Длина дуги окружности, радиус которой 25 см, равна 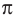
Решение:
Из формулы 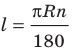
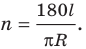
Ответ:
Пример №19
В окружность с центром 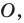
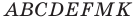
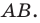
Решение:
Угол 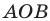
Тогда искомая площадь сектора равна 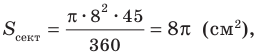
Ответ:
Справочный материал
Правильный многоугольник
Многоугольник называют правильным, если у него все стороны равны и все углы равны.
Свойства правильного многоугольника
Правильный многоугольник является выпуклым многоугольником.
Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.
Формулы для нахождения радиусов описанной и вписанной окружностей правильного многоугольника
Длина окружности
Длина дуги окружности в
Площадь круга
Площадь сектора, содержащего дугу окружности в
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Правильным многоугольником называется выпуклый многоугольник с равными сторонами и равными углами.
а — сторона восьмиугольника,
R — радиус описанной окружности,
r — радиус вписанной окружности.
Сумма внутренних углов правильного n-угольника
180(n-2).
Градусная мера внутреннего угла n-угольника
180(n-2) : n.
Сторона правильного n-ка
Радиус вписанной в правильный многоугольник окружности
Площадь правильного n-ка
УПРАЖНЕНИЯ
1. а) Сумма внутренних углов шестиугольника равна:
1) 360°; 2) 180°; 3) 720°; 4) 540°.
б) Сумма внутренних углов восьмиугольника равна:
1) 360°; 2) 180°; 3) 720°; 4) 1080°.
Решение:
а) По формуле сумма углов шестиугольника равна: 180(6-2)=180*4=720°.
Ответ: 720°.
2. а) Сторона правильного многоугольника равна 5 см, внутренний угол равен 144°. Найдите периметр многоугольника.
а) Сторона правильного многоугольника равна 7 см, внутренний угол равен 150°. Найдите периметр многоугольника.
Решение:
а) 1) Найдем количество сторон многоугольника:
144=180(n — 2):n;
144n=180n-360;
36n=360;
n=10.
2) Найдем периметр десятиугольника: Р=5*10=50 см.
Ответ: 50 см.
3. а) Периметр правильного пятиугольника равен 30 см. Найдите диаметр окружности, описанной вокруг пятиугольника.
б) Диаметр окружности равен 10 см. Найдите периметр вписанного в нее пятиугольника.
Решение:
а) 1) Найдем сторону пятиугольника: 30:5=6 см.
2) Найдем радиус описанной окружности:
a=2R*sin(180°:n);
6=2R*sin (180°:5);
R=3:sin 36°=3:0,588=5,1 см
Ответ: 5,1 см.
4. а) Сумма внутренних углов правильного многоугольника равна 2520°. Найдите количество сторон многоугольника.
б) Сумма внутренних углов правильного многоугольника равна 1800°. Найдите количество сторон многоугольника.
Решение:
а) Найдем количество сторон многоугольника:
2520°= 180°(n-2);
2520°+360°=180°n;
2880°=180°n;
n=16.
Ответ: 16 сторон.
5. а) Радиус окружности, описанной около правильного двенадцатиугольника равен 5 см. Найдите площадь многоугольника.
б) Радиус окружности, описанной около правильного восьмиугольника равен 6 см. Найдите площадь многоугольника.
Решение:
а) Найдем площадь двенадцатиугольника:
S=0.5*R2*n*sin(360°:n)=0,5*25*12*sin30°=75 см2.
Ответ: 75 см2.
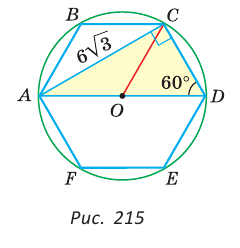
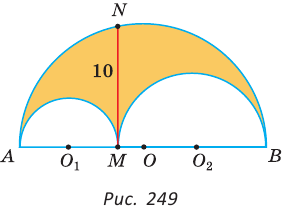
6. Найдите площадь шестиугольника, если известна площадь закрашенной части:
Решение:
а) 1) Найдем длину стороны АВ шестиугольника. Рассмотрим треугольник АВС — равнобедренный (АВ=ВС).
∠АВС=180°(6-2):6=120°.
Площадь треугольника АВС равна 0,5*АВ*ВС*sin120° и равна по условию 48.
2) В правильном шестиугольнике сторона равна радиусу описанной окружности, следовательно R=AB.
3) Найдем площадь шестиугольника:
Ответ: 288 см2.
7. а) Найдите число сторон правильного многоугольника, если его внешний угол при вершине равен 18°.
б) Найдите число сторон правильного многоугольника, если его внешний угол при вершине равен 45°.
Решение:
а) Сумма внешних углов правильного многоугольника равна 360°.
Найдем количество сторон: 360°:18°=20.
Ответ: 20 сторон.
8. Вычислите площадь кольца, если хорда АВ равна:
а) 8 см; б) 10 см.
Решение:
а)
1) ОВ — радиус внешней окружности, ОН — радиус внутренней окружности. Площадь кольца можно найти по формуле: S кольца = S внешней окружности — S внутренней окружности.
S=π *OB2 — π *OH2=π (OB2-OH2).
2) Рассмотрим треугольник АВО — равнобедренный (ОА=ОВ как радиусы). ОН является в треугольнике АВО высотой и медианой, следовательно, АН=НВ=8:2= 4 см.
3) Рассмотрим треугольник ОНВ — прямоугольный: НВ2=ОВ2-ОН2, следовательно
ОВ2-ОН2=16.
4) Найдем площадь кольца:
S=π (OB2-OH2)=16π см2.
Ответ: 16π см2.
9. а) Найдите периметр правильного шестиугольника, если АС=9 см.
б) Найдите площадь правильного шестиугольника, если FA=6 см.
Решение:
а) 1) Найдем угол АВС: 180°(6-4):6=120°.
2) Рассмотрим треугольник АВС — равнобедренный (АВ=ВС как стороны правильного шестиугольника).
∠ВАС=∠ВСА=(180°-120°):2=30°.
По теореме синусов: АС : sin ∠ABC = AB : sin ∠BCA;
AB=AC*sin30°:sin120;
3) Найдем периметр правильного шестиугольника:
Р=6*АВ;
10. Докажите, что в правильном восьмиугольнике площадь закрашенной части равна:
а) четверти площади восьмиугольника; б) половине площади восьмиугольника:
Решение:
а)
1) Проведем биссектрисы углов восьмиугольника, они пересекутся в точке О. Площадь восьмиугольника равна сумме площадей восьми получившихся равных треугольников, т.е. S (ABCDEFKM) =8* S (OEF).
2) Четырехугольник ABEF — параллелограмм (АВ//EF и АВ=EF). Диагонали параллелограмма равны: AE=BF (как диаметры описанной около восьмиугольника окружности), следовательно, ABEF — прямоугольник. Диагонали прямоугольника делят его на четыре равновеликих треугольника.
3) Найдем площадь четырехугольника AFKM:
S (ABEF)= 4* S (OEF).
2*S (AFKM)=S (ABCDEFKM) — S (ABEF) =8* S (OEF)-4* S (OEF)=4* S (OEF).
S (AFKM)=2* S (OEF).
4) Найдем отношение площади восьмиугольника к площади закрашенной части:
S (ABCDEFKM) : S (AFKM) = 8* S (OEF) : (2* S (OEF))=4.
Что и требовалось доказать.
11. Найдите отношение площади сектора ВАС к площади закрашенной фигуры, если ВА=АС и площадь сектора ВАС равна четверти площади круга:
Решение:
а)
1) АВ=АС=2R. Угол ВАС — прямой, т.к. площадь сектора ВАС равна четверти площади круга.
2) Рассмотрим Четырехугольник АО2МО1. Он является ромбом, т.к. все стороны равны радиусу, а т.к. Один их углов равен 90°, то АО2МО1 — квадрат.
3) Найдем площадь сегмента, закрашенного красным цветом:
S=S сектора АО1М — S треугольника АО1М.
S сектора = π*R2*90:360=0,25πR2 см2
S треугольника = 0,5R2 см2.
S сегмента = (0,25π —0,5)R2 см2.
S закрашенной части = 2* S сегмента = 2*(0,25π —0,5)R2 = (0,5π -1)R2 см2.
4) Найдем площадь сектора ВАС:
S сектора = π *(2R)2 *90:360=πR2 см2.
5) Найдем отношение площади сектора ВАС к площади закрашенной части:
πR2 :(0,5π -1)R2 = 2π : (π-2).
Ответ: 2π : (π-2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Чему равна сумма внешних углов пятиугольника?
2. Чему равна площадь восьмиугольника, если площадь закрашенной области равна 20.
3. Периметр правильного четырехугольника равен 20 см. Найдите длину вписанной в него окружности.
4. Сторона АВ правильного многоугольника равна 8 см. О — центр многоугольника, угол АОВ равен 36°. Найдите периметр многоугольника.
5. Периметр правильного восьмиугольника равен 80 см. Найдите его меньшую диагональ.
6. В правильный треугольник вписана окружность и вокруг него описана окружность. Найдите площадь кольца, образованного окружностями, если сторона треугольника равна 8 см.
7. Найдите угол между двумя меньшими диагоналями, выходящими из одной вершины правильного семиугольника.
8. Около окружности описан правильный треугольник, и в нее же вписан правильный шестиугольник. Найдите отношение площадей треугольника и шестиугольника.
9. Выпуклый многоугольник имеет 48 сторон. Найдите число его диагоналей.
10. ABCD — квадрат. Из вершин В и С проведены окружности радиуса АВ. Найдите отношение площади закрашенной фигуры к площади квадрата:
ПРОВЕРЬТЕ СЕБЯ
|
Многоугольник. Окружность. Вариант 1 |
Многоугольник. Окружность. Вариант 2 |
|
1. а3 окружность А3— окружности |
1. и А3— окружности а3 окружность |
|
2. Найти: и |
Найти: и |
|
3. |
3. Найдите |
|
4.Высота |
4. Высота |
|
5. Сторона |
5. Сторона |
|
6. Радиус |
6.Радиус |
|
7. Периметр |
7. Периметр |
|
8. Около |
8. Около |
|
Многоугольник. Окружность. Вариант 1 |
Многоугольник. Окружность. Вариант 2 |
|
2. а3 окружность А3— окружности |
4. и А3— окружности а3 окружность |
|
5. Найти: и |
Найти: и |
|
6. |
3. Найдите |
|
4.Высота |
4. Высота |
|
5. Сторона |
5. Сторона |
|
6. Радиус |
6.Радиус окружности, |
|
7. Периметр |
7. Периметр |
|
8. Около |
8. Около |
Самостоятельная работа. Вариант 1
1. Найдите углы правильного
шестнадцати угольника.
2.
Каждый угол
правильного многоугольника равен 162˚. Найдите число его сторон.
3.
Чему равен
внешний угол правильного восемнадцатиугольника?
4.
Внешний угол
правильного многоугольника равен 15˚. Найдите число его сторон.
5.
Является ли
равнобедренный треугольник с углом при вершине в 60˚правильным? Ответ
обоснуйте.
6. Является ли ромб с равными
диагоналями правильным четырёхугольником? Ответ обоснуйте.
7.
В правильном
шестиугольнике ABCDEF проведены диагонали AC, AD,AE. Найдите площади получившихся
треугольников, если площадь шестиугольника равна 42см2.
Самостоятельная работа. Вариант 2
1. Найдите углы правильного
двенадцатиугольника.
2.
Каждый угол
правильного многоугольника равен 144˚. Найдите число его сторон.
3.
Чему равен
внешний угол правильного пятнадцатиугольника ?
4.
Внешний угол
правильного многоугольника равен 45˚. Найдите число его сторон.
5.
Является ли
равнобедренный треугольник с углом при основании в 60˚правильным? Ответ
обоснуйте.
6.
Является ли
параллелограмм с равными диагоналями правильным четырёхугольником? Ответ
обоснуйте.
7. В правильном шестиугольнике ABCDEF проведены диагонали AC, AD,AE. Найдите площади получившихся
треугольников, если площадь шестиугольника равна 72см2.
Самостоятельная работа. Вариант 3
1. Найдите углы правильного
четырнадцатиугольника.
2. Каждый угол правильного
многоугольника равен 150˚. Найдите число его сторон.
3.
Чему равен
внешний угол правильного восемнадцатиугольника?
4.
Внешний угол
правильного многоугольника равен 40˚. Найдите число его сторон.
5.
Является ли
равнобедренный треугольник с углом при основыании в 60˚правильным? Ответ
обоснуйте.
6.
Является ли
прямоугольник с перпендикулярными диагоналями правильным четырёхугольником?
Ответ обоснуйте.
7. В правильном шестиугольнике ABCDEF проведены диагонали AC, AD,AE. Найдите площади получившихся
треугольников, если площадь шестиугольника равна 66 см2.
«Правильные
многоугольники» 1 ВАРИАНТ
1.Сторона
правильного треугольника равна 36√3.Найдите радиус окружности, описанной
около этого треугольника.
2.Радиус
окружности, описанной около правильного треугольника, равен 36√3. Найдите
сторону этого треугольника.
3.Высота
правильного треугольника равна 90. Найдите радиус окружности, описанной около
треугольника.
4.Радиус
окружности, описанной около правильного треугольника, равен 56. Найдите высоту
этого треугольника.
5.Найдите
радиус окружности, вписанной в правильный треугольник, высота которого равна
132.
6.Радиус
окружности, вписанной в правильный треугольник, равен 29. Найдите высоту этого
треугольника.
7.Сторона
правильного треугольника равна 4√3.Найдите радиус окружности, вписанной в
этот треугольник.
8.Радиус
окружности, вписанной в правильный треугольник, равен √3/2. Найдите
сторону этого треугольника.
«Правильные многоугольники» 2
ВАРИАНТ
1.Сторона
правильного треугольника равна 36√3. Найдите радиус окружности, описанной
около этого треугольника.
2.Радиус
окружности, описанной около правильного треугольника, равен √3. Найдите
сторону этого треугольника.
3.Высота
правильного треугольника равна 123. Найдите радиус окружности, описанной около
этого треугольника.
4.Радиус
окружности, описанной около правильного треугольника равна 18. Найдите высоту этого
треугольника.
5.Найдите
радиус окружности, вписанной в правильный треугольник, высота которого равна
96.
6.Радиус
окружности, вписанной в правильный треугольник, равен 32. Найдите высоту этого
треугольника.
7.Сторона
правильного треугольника равна 17√3. Найдите радиус окружности, вписанной
в этот треугольник.
8.Радиус
окружности, вписанной в правильный треугольник, равен √3/6. Найдите
сторону этого треугольника.
|
Проверочная Вариант |
Проверочная Вариант |
|
1.Найдите |
1. |
|
2.Найдите |
2.Найдите |
|
3.В |
3. |
|
4. |
4. |
|
5. |
5. |
|
6.Найдите |
6.Найдите |
|
7. |
7. |
|
Проверочная Вариант |
Проверочная Вариант |
|
1.Найдите |
1. |
|
2.Найдите |
2.Найдите |
|
3.В |
3. |
|
4. |
4. |
|
5. |
5. |
|
6.Найдите |
6.Найдите |
|
7. |
7. |
Муниципальное бюджетное
общеобразовательное учреждение
«Школа №77»
Научное
общество учащихся
«Правильные
многоугольники и их практическое применение»
Работу выполнила: Зизелева Эльвира
ученица 9 «А» класса
Научный руководитель: Литвинова С.Г.
учитель математики первой категории
Нижний Новгород 2020 год.
Содержание.
Введение……………………………………………………………………..3 Исторические
сведения……………………………………………………………..4
Глава I. Вводные понятия и свойства…………………….………………….5
1.1 Понятия выпуклого
многоугольника, правильного многоугольника, правильного
многогранника………………………………………….…..5
1.2
Теоремы о вписанных и описанных окружностях…………………..6
1.3
Основные формулы связи элементов окружностей и многоугольников
………………………………………………………………………………6
Глава II. Применения правильных многоугольников в практических
задачах.
2.1
Задача
№1.
7
2.2
Задача №2
7
2.3
Задача №3 8
2.4
Задача №4 8
2.5
Задача №5 9
2.6
Задача №6 9
Глава III. Альтернативные способы применения
правильных многоугольников…………………………………………………………….10
Актуальность исследования (Заключение)…………………………………11
Список использованных источников и литературы…………………….…12
Введение
«Все великое – просто»
Замятин Е.И
В нашем мире много необычного и прекрасного.
Нас окружают предметы, формы которых
нас удивляют. Таковыми, например, являются правильные многоугольники и правильные многогранники. Эти
фигуры обладают красотой,
совершенством форм, притягательностью.
С раннего детства мы встречаемся с ними, играя в кубики и развивающие
конструкторы, решая магические квадраты и головоломки Кубика-Рубика и его
разновидностей. Архитекторы, строители и дизайнеры воплощают свои оригинальные
идеи, используя эти фигуры. На
уроках математики изучаются различные геометрические фигуры и их свойства. Но
возникает вопрос: почему именно правильным многоугольникам и многогранникам
уделяется особое внимание? В настоящее время никто не станет отрицать
необходимости популяризации математических знаний. Одним из способов
популяризации является применение правильных многоугольников и правильных многогранников.
Цель исследования: Целью исследования является
сбор и систематизация типов задач, где применяются свойства правильных
многоугольников и показать актуальность этой темы.
Задачи:
1. Сгруппировать блок простейших понятий и теорем, используемых при решении.
2. Показать применение этих теорем
при решении задач.
3. Найти способы более простого и
красивого решения.
Исторические сведения.
Правильные многоугольники известны с древнейших времен. История их изучения
уходит в Древнюю Грецию.
Платон писал о правильных
многоугольниках в своем трактате Тимей, где сопоставил каждую из четырех стихий
правильному многоугольнику. Земля
сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а
огонь — тетраэдру. По поводу пятого элемента, додекаэдра, Платон сделал
смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в
качестве образца»
Евклид дал полное математическое описание
правильных многогранников в последней, XIII книге Начал. Предложения 13—17 этой
книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в
данном порядке. Для каждого многогранника Евклид нашёл отношение диаметра описанной
сферы к длине ребра. В 18-м предложении утверждается, что не существует других
правильных многогранников. Андреас Шпейзер отстаивал точку зрения, что
построение пяти правильных многогранников является главной целью дедуктивной
системы геометрии в том виде, как та была создана греками и канонизирована в
«Началах» Евклида.
А в XVI веке Иоганн Кеплер Иоганн Кеплер пытался
найти связь между пятью известными на тот момент планетами Солнечной системы
(исключая Землю) и правильными многогранниками. В «Тайне мира», опубликованной
в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять
правильных многогранников помещались один в другой и разделялись серией
вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из
планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были
расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним
икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура
Солнечной системы и отношения расстояний между планетами определялись
правильными многогранниками.

кубка Кеплера
Глава I.
Вводные понятия и свойства.
1.1
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой
прямой, проходящей через две его соседние вершины (рис.1)
Правильным многоугольником называется
выпуклый многоугольник, у которого все углы равны и все стороны равны. (рис.2)
Примеров правильного многоугольника
много-треугольник,квадрат,пятиугольник,шестиугольник,восьмиугольник и т.д.


Правильный многогранник-это выпуклый многогранник, состоящий из одинаковых правильных многоугольников
и обладающий пространственной симметрией. (рис.3)


многогранников всего пять: тетраэдр, куб (гексаэдр), октаэдр,
додекаэдр, икосаэдр.
|
Тетраэдр |
|
|
Куб |
|
|
Октаэдр составлен из восьми равносторонних треугольников. |
|
|
Додекаэдр |
|
|
Икосаэдр |
|
1.2. Теорема №1:Около любого правильного многоугольника
можно вписать окружность, и притом только одну.( рис.1)
Теорема №2:В любой правильный многоугольник можно вписать окружность,
и притом только одну.(рис.2)


1.3 Для
правильных многоугольников существуют следующие формулы связи:
Sn=∙P∙r
an=2R∙sin∙
r=R∙cos∙
Из них можно вывести
следующие формулы:
|
a |
r |
R |
S |
Связь между r и R |
|
3 |
|
R√3 |
|
R=2r |
|
4 |
|
R√2 |
a² |
R=r√2 |
|
6 |
|
R |
|
R√3=2r |
|
8 |
|
|
2a²(1+√2) |
|
|
12 |
|
|
3a²(2+√3) |
|
Глава II.
Практические задачи.
2.1 Сечение головки газового вентиля
имеет форму правильного треугольника, сторона которого равна 3 см. Каким должен
быть минимальный диаметр круглого железного стержня, из которого изготавливают
вентиль?
Дано:
△ABC-правильный многоугольник
a3 =3 см
НАЙТИ
d=
?
РЕШЕНИЕ:
a3=R√3 => R= a3/√3
R=3 cм/√3=√3 см
Так как d=2R, то d=2√3 см
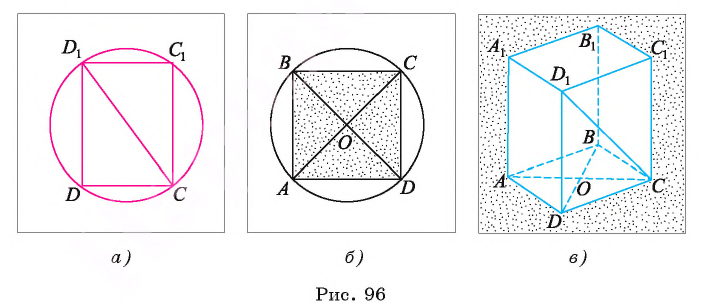
2.2
Расстояние
между параллельными гранями шестигранной головки болта, основание которого
имеет форму правильного шестиугольника, равна 1,5 см. Найдите площадь основания.
ДАНО:
ABCDEF-прав. шестиугольник.
MN=1,5 см.
НАЙТИ: SABCDEF=?
Решение:r=∙MN=
∙1,5 см=
см; r=R∙cos
=>R=r/cos30° =
см/(√3/2) cм=
см; R=a6 ; P=6∙a6=6∙
cм=3√3 см; SABCDEF =
Pr=
∙3√3 cм∙
см =
см
2.3 Из
каких правильных многоугольников одного вида можно сложить паркет?
РЕШЕНИЕ:
Т.к между плитками паркета не должно быть пробелов, то сумма углов
плиток, сходящихся в одной точке, должна быть равна 360º. Значит, угол
правильного многоугольника должен содержать целое число раз в 360º. Углы 60º,
90º,120º содержаться в 360º 6,4,3 раза, т.е целое число раз. Угол 108º и углы
меньше 180º и больше 120º содержать не целое число.
Ответ: Паркет можно сложить из многоугольников с углами
60,90,120,т.е из треугольников(рис.1), квадратов(рис.2) и
шестиугольников(рис.3).
рис.1 
рис.3
2.4 Как положить паркет из : а)правильных восьмиугольников и квадратов; б)правильных двенадцатиугольников
и
треугольников ?

рис.а
рис.б
2.5 Найдите расстояние между центрами смежных отверстий на
разметке, если диаметр окружности равен 250 мм?

Дано: d=250 мм
n =8
Найти:
CB=? (a8 )
Решение:
R=½d=125 см
a8=2Rsin(180/8)=2∙125∙sin22˚30′=95 мм
2.6 в дождевальной установке дождеватели расположены по треугольной схеме , в шахматном порядке. один дождеватель орошает круг радиуса r. При каком максимальном расстоянии d между соседними дождевателями установка будет орошать все поле? Каким должно быть при этом расстояние l между трубопроводами?
Решение:
При наилучшем расположении границы кругов,
орошаемых дождевателями А,В,С, должны, очевидно, пройти через одну точку. В таком случае,r равно радиусу окружности, описанной около △АВС. Поэтому
d=a3=r√3
Из рисунка видно, что l=AD=√(AB²—BD²)=√(d²—)=
=
=
Глава III. Альтернативные способы применения
правильных многоугольников
Применение
правильных многоугольников, правильных многогранников в архитектуре и
строительстве
Александрийский маяк Геометрический сад
Футбольный стадион ,Новосибирск
Применение правильных
многоугольников, правильных многогранников в быту, народных промыслах
Геометрический паркет Лоскутное одеяло
Орнамент
Актуальность
исследования (Заключение).
Математические результаты и методы, полученные
при решении задач о правильных многоугольниках, на протяжении многих веков
стимулировали развитие и становление таких математических дисциплин, как
алгебра, геометрия и теория чисел. На данный
момент полученные знания используются повсеместно, и не только в узких
профессиональных областях — данная тема широко применима в практике.
В старших классах мы продолжим изучение правильных
многогранников, где необходимы свойства правильных
многоугольников. Так же применение правильных
многоугольников и многогранников будет актуально в моей
будущей профессии — дизайнер интерьера и ландшафта.
Список используемых источников и
литературы.
https://school-science.ru/5/7/35614
https://gigabaza.ru/doc/2079.html
Геометрия, 7-9 класс / Атанасян Л.С., Бутузов В.Ф., Кадомцев
С.Б. и др./ Москва « Просвещение» 2015.
Задачи по
планиметрии с практическим содержанием
/ С.С.Варданян
/ Москва. «Просвещение» 1998.