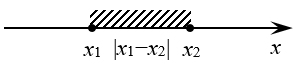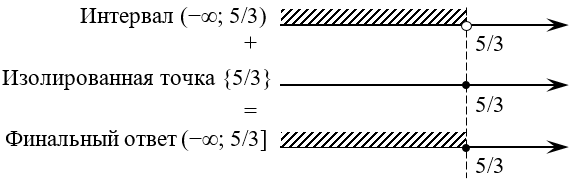Модуль числа как найти уравнение

Как решать уравнения с модулем: основные правила

30 декабря 2016

Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.

Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)

Немного теории

Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.

Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.

Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:

[left| -a right|=left| a right|]

Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.

Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:

[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]

Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.

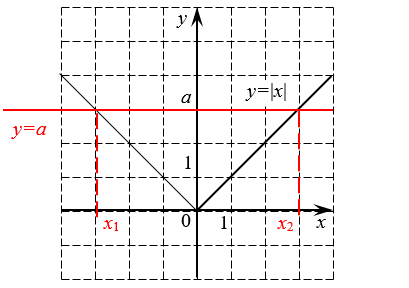
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:

Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)

Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:

Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)

Основная формула

Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?

Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:

[left| x right|=3]

Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:

[left| 3 right|=3]

А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.

Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.

Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:

[left| fleft( x right) right|=a]

Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:

[left| 2x+1 right|=5]

или:

[left| 10x-5 right|=-65]

Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.

А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:

[left| 2x+1 right|=5Rightarrow 2x+1=5]

И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:

[2x+1=5Rightarrow 2x=4Rightarrow x=2]

Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.

Теперь разберём случай отрицательного подмодульного выражения:

[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]

Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:

[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]

Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?

Да, такой алгоритм существует. И сейчас мы его разберём.

Избавление от знака модуля

Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:

[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]

Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого

[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]

Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:

[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]

Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.

Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:

[left| 7-5x right|=13]

Опять раскрываем модуль с плюсом и минусом:

[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]

Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

[left| 3x-2 right|=2x]

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :

[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]

Применительно к нашему уравнению получим:

[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]

Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]

Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

[left| fleft( x right) right|=gleft( x right)]

И решается оно точно так же:

[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]

[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]

[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

[x-{{x}^{3}}ge 0]

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

Уравнения с двумя модулями

До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.

Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:

[left| fleft( x right) right|=left| gleft( x right) right|]

Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.

Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:

[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]

Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.

Давайте попробуем решать вот такую задачу:

[left| 2x+3 right|=left| 2x-7 right|]

Элементарно, Ватсон! Раскрываем модули:

[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]

Рассмотрим отдельно каждый случай:

[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]

В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)

Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:

[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]

Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)

В итоге окончательный ответ: $x=1$.

Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:

[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]

Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:

[{{x}^{2}}-3x+2=pm left( x-1 right)]

Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:

[x-1=pm left( {{x}^{2}}-3x+2 right)]

Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.

Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:

[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]

Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)

В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:

[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]

Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:

[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]

Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:

[{{x}_{1}}=3;quad {{x}_{2}}=1.]

Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)

Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:

[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]

Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:

[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]

Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:

[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]

Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:

[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]

Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)

Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)

Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.

Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.

Итак, уравнение:

[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]

Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)

В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:

[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]

Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:

[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]

А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:

[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]

[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]

Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.

Метод расщепления

Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:

[left| 3x-5 right|=5-3x]

В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:

[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]

Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.

Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:

[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]

Таким образом, наше уравнение превратится в линейное, которое легко решается:

[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]

Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:

[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]

Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(

Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:

[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]

Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:

[5-3x=5-3x]

Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!

А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:

[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]

Другими словами, ответом будет не какое-то отдельное число, а целый интервал:

[xin left( -infty ;frac{5}{3} right)]

Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):

[3x-5=0Rightarrow left| 3x-5 right|=0]

Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:

[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]

Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)

Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:

Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.

Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

1. Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
2. Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
3. Решить исходное уравнение для каждого интервала и объединить полученные ответы.

Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:

Ну и какие тут интервалы? Понятно, что их три:

1. Самый левый: $x lt 1$ — сама единица в интервал не входит;
2. Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
3. Самый правый: $xge 5$ — пятёрка входит только сюда!

Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.

На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.

На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)

Смотрите также:

1. Простейшие уравнения с модулем
2. Уравнение с двумя модулями
3. Сложные выражения с дробями. Порядок действий
4. Сводный тест по задачам B15 (2 вариант)
5. Как решать биквадратное уравнение
6. B4: счетчики на электричество

Одна из самых сложных тем для учащихся  – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля. Итак,  модулем числа a называется само это число, если a неотрицательно и  -a, если  число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее  к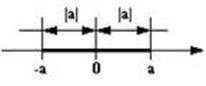оордината. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

                             {±c, если с > 0

 Если |x| = c, то x = {0, если с = 0

                             {нет корней, если с < 0

Примеры:

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

Примеры:

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

x = 2             x = -6

2) |x² – 5| = 11, т.к. 11 > 0, то

x² – 5 = 11 или x² – 5 = -11

x² = 16            x² = -6

x = ± 4             нет корней

3) |x² – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x).

Примеры:

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

              5x ≥ 10  

               x ≥ 2.  

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3x = 9                     7x = 11

x = 3                       x = 11/7

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3  

2) |x – 1| = 1 – x².

1. О.Д.З. 1 – x² ≥ 0. Решим методом интервалов данное неравенство:

             (1 – x)(1 + x) ≥ 0

             -1 ≤ x ≤ 1  

2. Решение:

x – 1 = 1 – x²      или   x – 1 = -(1 – x²)

x² + x – 2 = 0            x² – x = 0

x = -2 или x = 1         x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1. 

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

Пример:

1) |x² – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x² – 5x + 7  = 2x – 5 или x² – 5x +7  = -2x + 5   

x² – 7x + 12  = 0            x² – 3x + 2  = 0

x = 3 или x = 4             x = 2 или x = 1  

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

 x² – 6|x| + 5 = 0. По свойству модуля x² = |x|², поэтому уравнение можно переписать  так:

|x|² – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t² – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1        x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5. 

Рассмотрим еще один пример:

x² + |x| – 2 = 0. По свойству модуля  x² = |x|², поэтому

|x|² + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t² + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2   или |x| = 1

Нет корней     x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

Примеры:

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или  3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5      или     3 + |x + 1| = -5

|x + 1| = 2                       |x + 1| = -8

x + 1 = 2 или x + 1 = -2.   Нет корней.

x = 1            x = -3

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

План урока:

Модуль числа

Решение уравнений с модулем

Уравнения с параметрами

Модуль числа

Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:

|9| = |– 9| = 9

|674| = |– 674| = 674

|2,536| = |– 2,536| = 2,536

Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:

Именно такое определение обычно и применяется в математике.

Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:

Также модуль возникает при извлечении квадратного корня из четной степени числа:

В частности, если n = 1, получим формулу:

Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:

Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:

В результате получилась «галочка».

Пример. Постройте график ф-ции у = |х² – 4х + 3|

Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х² – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:

Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х² – 4х + 3|, надо перевернуть эту часть графика:

Решение уравнений с модулем

Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид

|у(х)| = b

где b – какое-то число, а у(х) – произвольная ф-ция.

Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.

Пример. Найдите корни ур-ния

|125x¹⁰ + 97x⁴– 12,56х³ + 52х² + 1001х – 1234| = – 15

Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.

Ответ: корни отсутствуют.

Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.

Пример. Решите ур-ние

|13х – 52| = 0

Решение.

Ясно, что подмодульное выр-ние равно нулю:

13х – 52 = 0

13х = 52

х = 4

Ответ: 4.

Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:

|b| = b

|– b| = b

То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.

Пример. Решите ур-ние

|х| = 10

Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.

Ответ: 10; (– 10).

Пример. Решите ур-ние

|10х + 5| = 7

Решение. Исходное ур-ние разбивается на два других ур-ния:

10х + 5 = 7 или 10х + 5 = – 7

10х = 2 или 10х = – 12

х = 0,2 или х = – 1,2

Ответ: 0,2; (– 1,2).

Пример. Найдите корни ур-ния

|x²– 2х – 4| = 4

Решение. Снова заменим исходное равенство на два других:

x²– 2х – 4 = 4 или x²– 2х – 4 = – 4

Имеем два квадратных ур-ния. Решим каждое из них:

x²– 2х – 4 = 4

x²– 2х – 8 = 0

D = b²– 4ас = (– 2)² – 4•1•(– = 4 + 32 = 36

х₁ = (2 – 6)/2 = – 2

х₂ = (2 + 6)/2 = 4

Нашли корни (– 2) и 4. Решаем второе ур-ние:

x²– 2х – 4 = – 4

x²– 2х = 0

х(х – 2) = 0

х = 0 или х – 2 = 0

х = 0 или х = 2

Получили ещё два корня: 0 и 2.

Ответ: – 2, 4, 0, 2

Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:

|у(х)| = |g(x)|

Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.

Пример. Решите ур-ние

|x² + 2x– 1| = |х + 1|

Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:

x² + 2x– 1 = х + 1 или x² + 2x– 1 = – (х + 1)

х² + х – 2 = 0 или х² + 3х = 0

Решим 1-ое ур-ние:

х² + х – 2 = 0

D = b²– 4ас = 1² – 4•1•(– 2) = 1 + 8 = 9

х₁ = (1 – 3)/2 = – 1

х₂ = (1 + 3)/2 = 2

Теперь переходим ко 2-омуур-нию:

х² + 3х = 0

х(х + 3) = 0

х = 0 или х + 3 = 0

х = 0 или х = – 3

Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.

Ответ:(– 1), (– 2), 2, 0.

Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.

Пример. Найдите решение уравнения, содержащего модуль:

|х² + 3,5х – 20| = 4,5х

Решение. Рассмотрим два отдельных равенства:

х² + 3,5х – 20 = 4,5х илих² + 3,5х – 20 = – 4,5х

х² – х – 20 = 0 или х² + 8х – 20 = 0

Решим каждое из полученных квадратных ур-ний.

х² – х – 20 = 0

D = b²– 4ас = 1² – 4•1•(– 20) = 1 + 80 = 81

х₁ = (1 – 9)/2 = – 4

х₂ = (1 + 9)/2 = 5

х² + 8х – 20 = 0

D = b²– 4ас = 8² – 4•1•(– 20) = 64 + 80 = 144

х₃ = (– 8 – 12)/2 = – 10

х₄ = (– 8 + 12)/2 = 2

Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:

4,5х ≥ 0

Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.

Ответ: 2 и 5

Мы рассмотрели три случая, когда ур-ние имеет вид:

1. у(х) = b (b– это некоторая константа)
2. |у(х)| = |g(x)|
3. |у(х)| = g(x)

Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.

Пример. Найдите корни ур-ния

|x + 1| + |x– 4| = 6

Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:

Если отметить обе точки на прямой, то они образуют на ней 3 интервала:

Исследуем ур-ние на каждом из полученных промежутков.

Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что

|x + 1| = – (х + 1) = – х – 1

|x– 4| = – (х – 4) = – х + 4

Тогда ур-ние примет вид

|x + 1| + |x– 4| = 6

– х – 1 – х + 4 = 6

–2х = 3

х = – 1,5

Это значение удовлетворяет условию х <– 1, поэтому корень верный.

Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:

|x + 1| = х + 1

|x– 4| = – (х – 4) = – х + 4

Ур-ние примет вид:

|x + 1| + |x– 4| = 6

x + 1 – x+ 4 = 6

5 = 6

Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.

При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому

|x + 1| = х + 1

|x– 4| = х – 4

Исходное ур-ние будет выглядеть так

|x + 1| + |x– 4| = 6

х + 1 + х – 4 = 6

2х = 9

х = 4,5

Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.

Уравнения с параметрами

Изучим ур-ния:

5х = 10

5х = 15

5х = 20

Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.

Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:

5х = v

Решением таких ур-ний будет дробь v/5.

Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.

Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде

ах + b= 0

где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):

ах² + bx + c = 0

Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.

Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.

Пример. Решите ур-ние

х² – 2ах = 0

и найдите его корни при значении параметра а, равном 3.

Решение. Вынесем множитель х за скобки:

х² – 2ах = 0

х(х – 2а) = 0

х = 0 или х – 2а = 0

х = 0 или х = 2а

Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:

при а = 3х = 2•3 = 6

Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.

Пример. Решите ур-ние

р²х – 3рх = р² – 9

Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:

рх(р – 3) = (р – 3)(р + 3)

Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.

Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во

0•х•(0 – 3) = (0 – 3) (3 – 0)

0 = – 9

Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.

Если р – 3 = 0, то есть р = 3, получится следующее

3•х•0 = 0•(3 + 3)

0 = 0

Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.

Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим

В этом случае ур-ние имеет единственный корень.

Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.

Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.

Пример. Сколько корней имеет ур-ние

|х² – 6х + 5| = b

при различных значениях параметра b.

Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х² – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:

х² – 6х + 5 = 0

D = b²– 4ас = (– 6)² – 4•1•5 = 36 + 20 = 16

х₁ = (6 – 4)/2 = 1

х₂ = (6 + 4)/2 = 5

Итак, нули ф-ции – это точки 1 и 5. Найдем координату х₀ вершины параболы по формуле:

х₀ = –b/2a = 6/2 = 3

Подставив х₀ в квадратичную ф-цию найдем координату у₀ вершины параболы:

3² – 6•3 + 5 = 9 – 18 + 5 = – 4

Теперь построим квадратичную ф-цию:

Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:

Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:

При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.

При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.

Если 0 <b< 4, то прямая пересекает график в 4 точках.

При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.

Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.

Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.

Пример. При каком а ур-ние

х⁴ – (а + 2)х² + 3а – 3 = 0

имеет ровно 4 корня?

Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х²:

у² – (а + 2)у + 3а – 3 = 0 (1)

Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у₁ и у₂. Тогда, проводя обратную замену х² = у₁ и х² = у₂, мы получим два разных квадратных ур-ния, корни которых будут равны

Если же хоть один из двух корней, например, у₁, окажется равным нулю, то величины

Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у₁ будет отрицательным числом, то ур-ние

х² = у₁

вовсе не будет иметь решений, и тогда останется не более 2 корней.

Итак, решим ур-ние (1):

у² – (а + 2)у + 3а – 3 = 0

D = b²– 4ас = (– (а + 2))² – 4•1•(3а – 3) = (а + 2)² – 12 а + 12 =

= а² + 4а + 4 – 12а + 12 = а² – 8а + 16 = а² – 2•4•а + 4² = (а – 4)²

Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)² положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.

Извлечем корень из дискриминанта:

Корни ур-ния (1) можно вычислить по формулам:

И у₁, и у₂ должны быть положительными величинами, однако у₁ меньше, чем у₂ (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:

Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство

|а – 4| = а – 4

Тогда имеем

а + 2 – (а – 4) > 0

6> 0

Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.

Если а < 4, то справедливо соотношение

|а – 4| = – (а – 4)

Тогда получится следующее:

а + 2 – |а – 4|> 0

а + 2 – (– (а – 4)) > 0

а + 2 + а – 4 > 0

2а > 2

а > 1

Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение

а > 4

можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).

Ответ: а∊(1; 4)∪(4; + ∞).

Пример. При каких параметрах а у ур-ния

х² – 2(а + 1)х + а² + 2а – 3 = 0

существует два корня, которые принадлежат интервалу (– 5; 5)?

Решение. Данное ур-ние является квадратным. Найдем его дискриминант:

D = b²– 4ас = (– 2(а + 1))² – 4•1•( а² + 2а – 3) = 4(а² + 2а + 1) – 4(а² + 2а – 3) =

= 4(а² + 2а + 1 – а²– 2а + 3) = 4•4 = 16

Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам

Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х₁) был больше – 5, больший (это х₂) – меньше – 5:

Значит, должны выполняться два нер-ва

х₁>– 5и х₂<5

а – 1 >– 5 и а + 3 < 5

а >– 4 и а < 2

Эти два нер-ва выполняются, если а∊(– 4; 2)

Ответ: (– 4; 2)

Уравнения с модулем

Эта статья посвящена приёмам решения уравнений, содержащих переменную под знаком модуля.

Если на экзамене вам попадётся уравнение с модулем, его можно решить, вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда, занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним определение модуля.

Если число x неотрицательное, то модуль x равен самому числу x.

А для отрицательного числа x модуль равен противоположному ему положительному числу -x.

Рассмотрим различные типы уравнений с модулем.

Начнем с простых заданий.

к оглавлению ▴

Слева модуль, справа число

Это самый простой случай. Нам поможет геометрический смысл модуля.

Модуль числа — это расстояние от нуля до данного числа. Очевидно, расстояние не может быть отрицательным. Оно или положительно, или равно нулю. Например, . Другими словами, расстояние от точки -2 до нуля равно 2. Этим мы пользуемся при решении уравнений.

1. Решим уравнение:

Решение:

На числовой прямой есть ровно две точки, расстояние от которых до нуля равно двум. Это точки 2 и -2. Значит, у уравнения есть два решения: и .

Ответ: -2; 2.

2. Решите уравнение:

Решение:

Ответ:

3. Решите уравнение:

Решение:

Мы получили совокупность двух квадратных уравнений. А затем решили отдельно каждое из них.

Вот что мы делали, решая квадратные уравнения:

— применили теорему Виета и нашли корни.

корней нет.

Ответ:

4. Решим уравнение: 

Решение:

Задача похожа на предыдущую.

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение равносильно совокупности двух простых:

или

Второе уравнение не имеет корней. Решения первого: x = 0 и x = 5.

Ответ: 0; 5.

к оглавлению ▴

Слева модуль, справа выражение, зависящее от переменной

Здесь приходится раскрывать модуль по определению. . . или соображать!

5.

Решение:

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.

Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.

Ответ: 1.

6.

Решение:

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения.

Второй случай: x < 3. Снимаем модуль:

Число . больше, чем , и потому не удовлетворяет условию x < 3. Проверим :

Значит, . является корнем исходного уравнения.

Ответ:

7. Решите уравнение: = x.
Если уравнение имеет несколько корней, в ответе запишите меньший корень

Решение:

ОДЗ уравнения: x≠3. Так как в левой части уравнения — неотрицательная величина, должно также выполняться условие Возведем обе части уравнения в квадрат

= x

(разность квадратов),

Так как — это посторонний корень. Уравнение имеет два корня: или

Меньший корень: 1.

Ответ: 1.

8.

Решение:

Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат.

Давайте воспользуемся следующим правилом:

Уравнение вида равносильно совокупности двух систем:

То же самое, но немного по-другому:

Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию

Приступаем. Сначала решаем первое уравнение:

Затем решаем второе уравнение:

Теперь в каждом случае проверяем знак правой части:

Подходят только и .

Ответ:

Еще одно уравнение того же типа.

9. Решите уравнение: .

Это уравнение вида Вспомним, что оно равносильно системе:

Получим:

Решим отдельно каждое уравнение совокупности.

по теореме Виета.

Система примет вид:

Сравним и Для сравнения мы будем использовать вот такой символ:

.

Умножим обе части этого неравенства на 2: .

Прибавим 5 к обеим частям выражения: Обе части выражения неотрицательны, поэтому возведем их в квадрат и сравним квадраты. Очевидно, 17 9. Это значит, что и

Остальные корни, очевидно, меньше, чем -1.

Ответ: .

к оглавлению ▴

Квадратные уравнения с заменой

Замена переменной — универсальный способ решения всевозможных уравнений. И этот способ помогает нам решать квадратные уравнения, содержащие переменную под знаком модуля.

10. Решим уравнение:

Решение:

Поскольку , удобно сделать замену |x| = t. Получаем:

.

Ответ: ±1.

к оглавлению ▴

Модуль равен модулю

Речь идёт об уравнениях вида Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Как мы получили это равенство? Покажем на примере задачи.

11. Решите уравнение:

Решение:

Возведем обе части в квадрат, поскольку они неотрицательны.

Перенесем все в левую часть и воспользуемся формулой разности квадратов:

Ответ:

12. Решим уравнение: .

Решение:

Уравнение равносильно следующей совокупности:

Решим каждое из уравнений совокупности и запишем ответ.

1)

— корни первого квадратного уравнения.

2)

— корни второго квадратного уравнения.

В ответ запишем все 4 корня.

Ответ:

к оглавлению ▴

Два или несколько модулей

13. Решим уравнение:

Решение:

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении).

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются с «плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается с «минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются с «минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Ответ: [1; 2] ∪ {5}.

к оглавлению ▴

Модуль в модуле

14. Решим уравнение:

Решение:

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

2) x ≥ 3. Имеем:

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается с «плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Ответ: 4.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Часто в решении уравнений и неравенств с модулем используется график функции Он строится согласно определению модуля:

.

Для получаем участок графика y = x.

Для  получаем участок графика y = −x. Вот этот график:

15. Решите уравнение:

Решение:

Сделаем замену переменной:

Тогда

Получим:

Мы помним, что

Решим уравнение графически. В левой части — график функции

Построим этот график. Сначала изобразим графики функций (точка минимума (3; 0)) и (точка минимума ( -3; 0)). Можно сказать, что график функции сдвинут относительно графика на 3 единицы вправо, а график — на 3 единицы влево.

И построим график суммы функций и

В точке с абсциссой 3 значение одного из слагаемых равно 0, другое слагаемое равно 6, сумма равна 6.

В точке с абсциссой -3 аналогично.

При х = 0 оба слагаемых равны 3, сумма равна 6.

Легко доказать, что сумма двух линейных функций есть линейная функция.

Поэтому при — получим горизонтальный участок. При x 3 получим луч с угловым коэффициентом, равным 2, а при x — 3 — луч с угловым коэффициентом, равным — 2.

Решения нашего уравнения — все принадлежащие отрезку от до

значит,

Ответ:

Мы рассмотрели все основные типы уравнений с модулями.

Читайте также о том, как решать неравенства с модулем.

Наиболее часто возникают ошибки при решении уранений с модулем. Давайте разберем решение простейших уравнений с модулем. Чтобы решить уранения с модулем, надо знать определение модуля. Модуль обозначает абсолютное значение числа и записывается вертикальными черточками:

(|a|) — читается как модуль числа (a).

Определение модуля:

Пример 2. Решите (|x|=0)

Решение: 

(|x|=0)

(x = 0)

Уравнение имеет один корень

Ответ: (x = 0).