Dilution: It is a process in which the concentration of a solute in the solution is decreased by adding more solvent to the solution. In the dilution process, the concentration of the solution decreases while the volume of the whole solution increased.
The amount of dilute remains constant in the dilution process. (the number of moles is the same before and after dilution).
Why is the (M1V1=M2V2) formula used in the dilution problem, explain?
To understand this equation, we have to focus on the definition of Molarity. “Molarity is defined as the moles of a solute per liters of a solution”.
∴ Molarity = Moles of solute/liters of solution
We can also write it as –
⇒ Moles of solute = (Molarity) × (Liters of solution)
∴ Moles of solute = M × V [∴ M represents molarity and V represents Volume]
In dilution process, the number of moles is the same before and after dilution. That means (M×V) remains same before and after concentration change.
So, according to this, we can write the initial and final conditions as –
⇒ M1V1=M2V2
The above equation represents the dilution equation.
Does M1V1=M2V2 have to be in liters?
The short answer is, It doesn’t matter whether the volumes in the M1V1=M2V2 equation are in liters or not, but it is important to be consistent with the units used. Here’s what you need to consider:
What really matters is –
- The initial and final concentrations must have the same units.
- If your initial concentration is in moles per liter and final concentration should also have the same unit(moles per liter).
- Also, if the concentration is in moles per liter, then, it doesn’t necessary that the volume should also be in liters. But the thing is, the initial volume and final volume must have the same unit.
- Let’s say if V1 is in milliliters then V2 should also be in milliliters, and vice versa, if the given volume is in liters then another volume should also be in liters.
Maintaining consistency in the units used for both concentration and volume will ensure the equation works correctly for solving dilution problems.
How to solve dilution problems using (M1V1=M2V2)?
It’s really easy, all you have to do is rearrange the formula(M1V1=M2V2) according to the question needs and find the value of the unknown one.
In most of the dilution problems, you have to ask to find either the concentration or volume in either the initial side or the final side of the equation.
For example, If in a given problem, the value of M1 is x, for M2, it is y, and for V2, it is z. Now find the value of V1 =?
∴ We have, M1V1=M2V2
Put the given values in the above equation-
⇒ xV1 = yz
∴ V1 = yz/x Answer
That’s how simple it is to solve the problem of dilution using the equation M1V1=M2V2.
Examples of dilution problems using (M1V1=M2V2)?
Let’s take some examples to understand the process of solving dilution problems using the equation (M1V1=M2V2).
| Q1. A solution having a molarity of 6 M and a volume of 4 liters, after the dilution, the volume of the solution becomes 8 liters, then, calculate the molarity of the dilute solution? |
|
Answer – In the given problem, the initial molarity is 6 M, and the initial volume is 4 liters. So, we have, M1 = 6 and V1 = 4 Also, it is given, that after the dilution, the volume of the solution becomes 8 liters. So, V2 = 8 Now we have to find the molarity of the dilute solution which means M2 =? Use the equation, M1V1=M2V2 ∴ M2 = M1V1/V2 = (6 × 4)/8 = 3 ∴ So, the molarity of dilute solution (M2) is 3. Or use the M1V1=M2V2 calculator to solve this problem – |
| Q2. A solution having a molarity of 8 M and a volume of 4 liters. If 2 liters of solvent are added to the solution, calculate the molarity of the final solution? |
|
Answer = Given, M1 = 8, V1 = 4 “If 2 liters of solvent are added to the solution” ∴ V2 = V1 + 2 = 4 + 2 V2 = 6 liters Now we have to find M2. Use the equation, M1V1=M2V2 ∴ M2 = M1V1/V2 = (8 × 4)/6 = 16/3 ∴ M2 = 5.33 Or use the M1V1=M2V2 calculator to solve this problem – |
| Q3. How many mL of a 2.50 M NaOH solution are required to make 525 mL of a 0.150 M NaOH solution? |
|
Answer – In given problem, we have given, M1 = 2.50, M2 = 0.150, V2 = 525 We have to find, V1 =? Use the equation, M1V1=M2V2 ∴ V1 = M2V2/M1 = (0.150 × 525)/2.50 = 31.5 ∴ V1 = 31.5 mL Or use the M1V1=M2V2 calculator to solve this problem – |
| Q4. If 45.0 mL of a 6.00 M HCl solution is diluted to a final volume of 0.250 L, what is the final concentration? |
|
Answer – Given, M1 = 6, V1 = 45 mL Also, the final volume (V2) is 0.250 L, we have to find, M2 =? We have one problem here, in the given question, V1 is in milliliters and V2 is in Liters, so, both have different units. According to the dilution equation concept –
So, what we have to do is convert the milliliter unit to a liter. V1 = 45 mL = 0.045 Liter Now put these values in the dilution equation- ⇒ M1V1=M2V2 ∴ M2 = M1V1/V2 = (6 × 0.045)/0.250 = 1.08 ∴ M2 = 1.08 M Or use the M1V1 = M2V2 calculator to solve this problem – |
Complex problem on (M1V1=M2V2)?
| Determine the mass (g) of calcium nitrate in each milliliter of a solution prepared by diluting 56.0 mL of 0.705 M calcium nitrate to a final volume of 0.100 L. |
|
1) use M1V1 = M2V2: ⇒ (0.705 mol/L) (0.0560 L) = (x) (0.100 L) ∴ x = 0.3948 M 2) moles of Ca(NO3)2 in 1 mL: ∴ 0.3948 mol/L = 0.3948 mol / 1000 mL = 0.0003948 mol/mL 3) Convert moles to grams: ∴ 0.0003948 mol/mL times 164.086 g/mol = 0.0648 g/mL You can check more complex problem on M1V1 = M2V2 here, Dilution problem (chemteam.info) |
FAQ
What does M1V1=M2V2 equation in chemistry represent? |
|
We know, that M1V1=M2V2 represents the dilution equation, that M1 represents initial molarity, M2 represents final molarity, V1 represents initial volume and V2 denotes final volume. |
How can you find initial molarity (M1), initial volume (V1), final molarity (M2), and final volume (V2) using the M1V1=M2V2 equation? |
|
The given equation is- M1V1=M2V2 Now to find the initial molarity (M1), initial volume (V1), final molarity (M2), and final volume (V2) use the formulas given below- ⇒ ⇒ ⇒ ⇒ |
Закон сохранения импульса
Импульсу присуще очень интересное и важное свойство, которым обладают весьма немногие физические величины. Это — свойство сохранения. В чем оно заключается?
Допустим, что два взаимодействующих друг с другом тела, массы которых $m_{1}$ и $m_{2}$, движутся относительно какой-то системы отсчета. Обозначим через $vec{v}_{1}$ и $vec{v}_{2}$ их скорости в какой-то момент времени. В результате взаимодействия скорости тел через некоторое время $t$ изменятся и станут равными $vec{v}_{1}^{ prime}$ и $vec{v}_{2}^{ prime}$. Это означает, что на тела при их взаимодействии действовали соответственно силы $vec{F}_{1}$ и $vec{F}_{2}$, равные:
$vec{F}_{1} = frac{m_{1} vec{v}_{1}^{ prime } — m_{1} vec{v}_{1} }{t}$
и
$vec{F}_{2} = frac{ m_{2} vec{v}_{2}^{ prime} — m_{2} vec{v}_{2} }{t}$.
Согласно третьему закону Ньютона силы $vec{F}_{1}$ и $vec{F}_{2}$ равны по абсолютной величине и противоположны по направлению, т. е.
$vec{F}_{1} = — vec{F}_{2}$.
Следовательно,
$frac{m_{1} vec{v}_{1}^{ prime} — m_{1} vec{v}_{1} }{t} = — frac{ m_{2} vec{v}_{2}^{ prime} — m_{2} vec{v}_{2} }{t}$,
или
$m_{2} vec{v}_{2}^{ prime } — m_{2} vec{v}_{2} = m_{1} vec{v}_{1}^{ prime } — m_{1} vec{v}_{1}$.
Перепишем последнюю формулу в виде
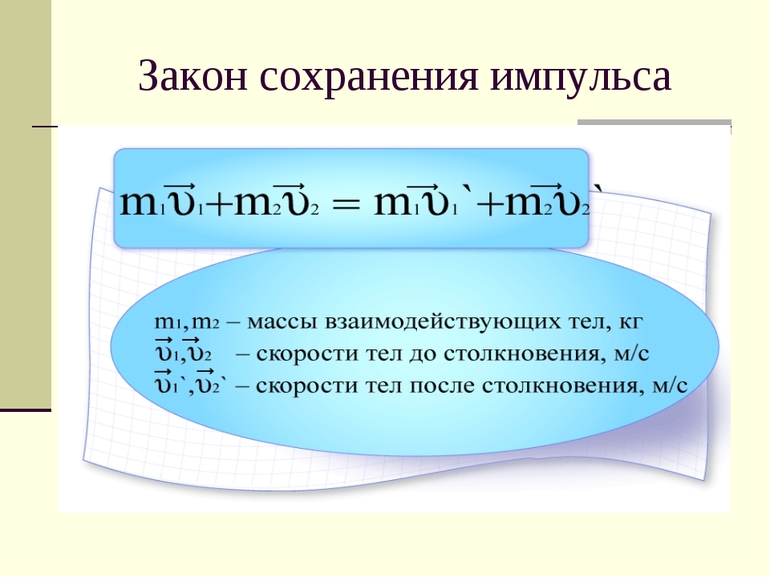
$m_{1} vec{v}_{1} + m_{2} vec{v}_{2} = m_{1} vec{v}_{1}^{ prime } + m_{2} vec{v}_{2}^{ prime}$.
В левой части этого равенства стоит сумма начальных импульсов двух тел, а в правой — сумма импульсов тех же тел через время $t$. Эти суммы равны между собой. Таким образом, хотя импульс каждого из тел при взаимодействии изменяется, их полный импульс, т. е. сумма импульсов обоих тел, остается при этом неизменным. Это и значит, что импульс двух тел при их взаимодействии сохраняется.
Сохранение полного импульса тел при их взаимодействии — один из важнейших законов природы. Можно доказать, и опыт это также подтверждает, что если взаимодействуют не два, а много тел, то геометрическая сумма импульсов всех тел, или, как говорят, системы тел, остается неизменной. Важно только, чтобы эти тела взаимодействовали только друг с другом, чтобы на них не действовали силы со стороны других тел, не входящих в систему (или чтобы эти внешние силы уравновешивались). Такую группу тел, которая не взаимодействует ни с какими другими телами, не входящими в эту группу, называют замкнутой системой. Когда мы до сих пор говорили о взаимодействии двух тел, то тоже имели в виду, что эти тела взаимодействуют только друг с другом, посторонние же тела на них не действуют. Именно для замкнутых систем и справедлив закон сохранения импульса.
Геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Импульс — это векторная величина. Поэтому если векторная сумма импульсов тел сохраняется постоянной, то и сумма проекций этих импульсов на оси координат также остается постоянной. Вследствие этого геометрическое сложение импульсов можно заменить алгебраическим сложением их проекций.
Следующие опыты поясняют закон сохранения импульса.
рис. 1
1. Поставим на рельсы две тележки одинаковой массы т. К торцу одной тележки прикрепим шарик из пластилина. Пусть тележки движутся навстречу друг другу с одинаковыми по абсолютной величине скоростями $v$ (рис. 183). При встрече обе тележки остановятся.
Объяснить результаты опыта легко. До встречи импульс леиой тележки равен $m vec{v}$, а правой тележки $-m vec{v}$ (тележки двигались с противоположно направленными скоростями). Значит, до момента встречи тележек их общий импульс был равен нулю:
$m vec{v} + (- m vec{v}) = 0$.
После соударения тележки остановились. Следовательно, и теперь суммарный импульс обеих тележек равен нулю.
рис. 2
2. Можно повернуть тележки так, чтобы они были обращены друг к другу пружинными буферами (рис. 184). Тогда, повторив опыт, убедимся в том, что после столкновения обе тележки разъедутся в противоположные стороны. При этом взаимодействии скорости тележек изменят свои направления на противоположные, абсолютные же значения скоростей останутся такими же, какими они были до взаимодействия. Если до встречи импульс левой тележки равен $m vec{v}$, а правой $-m vec{v}$, то после встречи импульс левой
тележки равен $-m vec{v}$, а правой $m vec{v}$. Поэтому суммарный импульс обеих тележек равен нулю как до, так и после столкновения, как этого и требует закон сохранения импульса.
Задача 1. Тележка массой 150 кг движется по рельсам со скоростью 3,6 км/ч. По дороге бежит человек массой 75 кг. Приблизившись к тележке, он вскакивает на нее и прекращает бег. После этого тележка остановилась. С какой скоростью бежал человек?
Решение. Так как взаимодействие человека и тележки с землей не влияет на их движение в горизонтальном направлении, можно к этой системе применить закон сохранения импульса. Это значит, что суммарный импульс тележки и человека после взаимодействия должен быть таким же, как и до взаимодействия.
Обозначим массу тележки через $m_{1}$ и ее скорость до взаимодействия через $vec{v}_{1}$, массу человека через $m_{2}$ и его скорость до взаимодействия через $vec{v}_{2}$. Полный импульс системы до взаимодействия равен
$m_{1} vec{v}_{1} + m_{2} vec{v}_{2}$.
В результате взаимодействия тележка и человек остановились. Следовательно, их общий импульс стал равен нулю. Значит, он был равен нулю и до того, как человек вскочил на тележку:
$m_{1} vec{v}_{1} + m_{2} vec{v}_{2} = 0$.
Тележка и человек движутся по одной прямой. Поэтому можно, направив вдоль этой прямой ось координат, вместо векторной суммы импульсов написать алгебраическую сумму их проекций па эту ось:
$m_{1}v_{1} + m_{2}v_{2} = 0$.
Примем направление движения тележки за положительное, тогда
$v_{2} = — frac{m_{1}v_{1} }{m_{2} }$,
или
$v_{2} = — frac{150 кг}{75 кг} cdot 1 frac{м}{сек} = — 2 frac{м}{сек}$.
Знак «минус» указывает на то, что вектор скорости движения человека был направлен противоположно вектору скорости движения тележки.
Задача 2. Железнодорожный вагон массой 30 т, движущийся со скоростью 1,5 м/сек, сцепляется с неподвижным вагоном, масса которого равна 20 т. Какова скорость вагонов после сцепки? (Вагоны находятся на прямолинейном участке пути.)
Решение. Направим координатную ось вдоль железнодорожного пути. Обозначим массу первого (движущегося) вагона через $m_{1}$, массу второго (неподвижного) через $m_{2}$, скорость первого вагона до сцепки через $v_{1}$, а общую скорость обоих вагонов после сцепки через $v$. По закону сохранения импульса полный импульс обоих вагонов до и после сцепки должен быть одинаковым. До сцепки полный импульс (его проекция на ось) обоих вагонов был равен
$m_{1}v_{1}$
а после сцепки
$(m_{1} + m_{2} )v$.
Следовательно,
$m_{1}v_{1} = (m_{1} + m_{2} ) v$.
Отсюда
$v = frac{m_{1}v_{1} }{m_{1} + m_{2} }, v = frac{ 3 cdot 10^{4} кг cdot 1,5 м/сек}{5 cdot 10^{4} кг} = 0,9 м/сек$.
В приведенных задачах мы не знали значений сил взаимодействия между человеком и тележкой или между сцепляющимися вагонами. Но, пользуясь законом сохранения импульса, мы нашли скорости интересующих нас тел. Ясно, что если известны их начальные положения, то, зная их скорости, можно найти положения этих тел в любой момент времени. Вот почему закон сохранения импульса имеет такое большое значение.
Во время эксплуатации различных бытовых приборов мало кто задумывается о том, что в основе многих технических достижений последних лет лежат базовые наработки в области физики, и один из таких — закон сохранения импульса. Применение этого удивительного достижения настоящих изобретателей сопряжено с определёнными познавательными фактами, которые будет интересно узнать тем, кто решил расширить свои знания в области этой науки.
Краткое описание
Импульсом принято называть влияние массы тела на итоговую скорость. На этот случай специалисты разработали следующую формулу: p = m * V. В физике импульс представляет собой некую векторную величину, которая всегда направлена только в одну сторону. Само слово переводится с латинского языка, как «толкать», «двигать». Импульс принято обозначать маленькой буквой р, а вот измеряться он может только в кг*м/с.
Талантливый Рене Декарт был первым человеком, который начал использовать понятие импульс. Он пытался использовать своё открытие как определённую величину, которая заземляет силу. Причина такого подхода Рене весьма очевидна. Измерить единицу силы крайне тяжело, а вот узнать скорость и массу — это задача более простая и выполнимая. Именно поэтому в физике часто говорят, что импульс — это не что другое, как количество движения. Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующий показатель равен нулю.
Чтобы можно было разобраться в том, при каких условиях выполняется закон сохранения импульсов, нужно понять, что это физическое направление лежит в основе такого весьма удивительного явления как реактивное движение. Последнее получило широкое применение не только в технике, но и живой природе. Кальмары, осьминоги и медузы отлично используют реактивное движение, которое позволяет им преодолевать большие расстояния в своём подводном мире.
А вот в технике это физическое явление применяется в самолётах, ракетах и даже космических кораблях. Отдельного внимания заслуживает импульс в релятивистской механике. А всё потому, что законы сохранения механической энергии и импульса применяются для решения задач о движении тел после столкновения.
Ключевые особенности
Активно используемый в современном мире закон о сохранении обычных импульсов является следствием из второго и третьего законов Ньютона. Для лучшего усвоения этой темы лучше рассмотреть характерный пример. Специалистами была взята замкнутая система сразу из двух взаимодействующих между собой тел, которые отобразили при помощи F1 и F2. В третьем законе Ньютона чётко написано, что F2 = -F1. Тела взаимодействуют друг с другом в течение определённого промежутка времени (t).
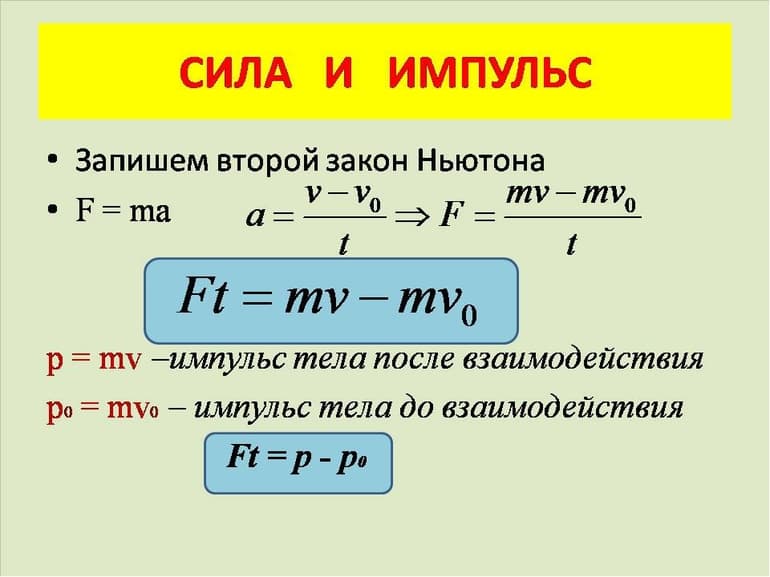
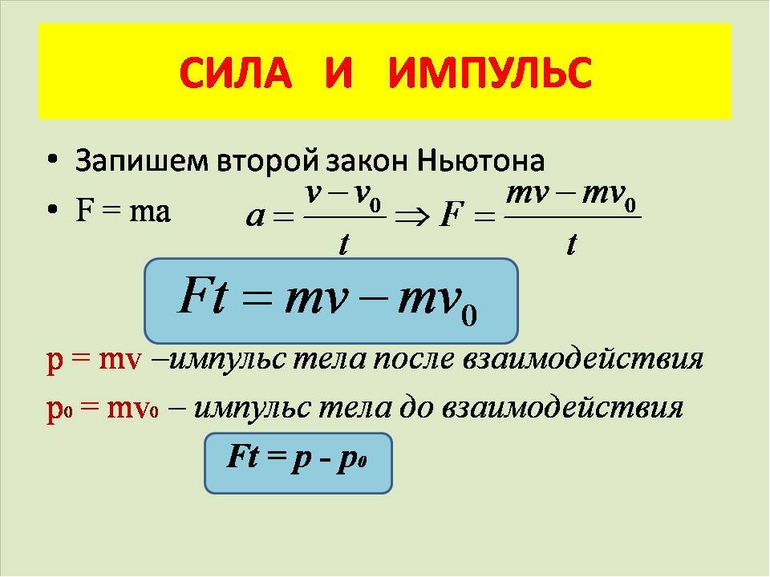
В такой ситуации импульсы сил остаются идентичными по модулю, но противоположными по своему направлению (F1t = -F1t).
Если применить второй закон Ньютона, то в итоге обязательно получиться вот такое математическое выражение: F1t = m1v1 — m1v1; F2t = m1v2 — m1v2. Для отображения реальной скорости тел в конце взаимодействия используются символы v1 и v2. Из этого можно сделать вывод, что соотношение двух тел будет выглядеть следующим образом: m1v1 + m2v2 = m1v1 + m2v2.
Полученный результат позволяет говорить о равенстве (математическая форма записи закона). Это значит, что первоначальный показатель под воздействием какой-либо силы не изменится. Необходимо запомнить, что определение закона сохранения обязательно выполняется и для проекций векторов на координатные оси. Если следовать всем правилам, то можно легко определить суммарный результат в поставленной задаче, а также находить реальную скорость тел, не зная показателей действующих сил.
В качестве примера также можно рассмотреть снаряд, который вылетает из пушки. Эта задача элементарная, но очень познавательная. В роли взаимодействующих тел выступает пушка и снаряд. На первом этапе оба объекта остаются неподвижными. Но при выстреле снаряд приобретает скорость v и летит только вперёд. А вот пушка откатывается в противоположную сторону со скоростью V (происходит отдача, которая может зависеть только от выстрела). В соответствии с законом в проекции на ось можно записать:
- mv-MV=0;
- V=mv/N.
На этом примере можно увидеть, что всё элементарно и просто. При движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. Эту тему активно изучают в 9 классе
Интересные факты
При изучении этой темы нужно понимать, что закон о сохранности импульсов остаётся актуальным исключительно в изолированной/ замкнутой физической системе. В этом случае речь касается той отрасли, где абсолютно все тела тесно взаимодействуют между собой и не реагируют на внешние факторы. Но даже в этом случае действуют свои правила. Лучше представить замкнутую систему, которая состоит из двух физических тел. В этом случае возникают внутренние силы, которые могут характеризоваться определёнными параметрами.
Для первого тела импульс будет равен следующей формуле: Ft = m1v1 — m1v1. В действие снова вступает третий закон Ньютона, описываемый то, что все воздействующие на тела силы равны по своей величине, но противоположны по направлению. А это значит, что для второго тела будет действовать немного другая формула: — Ft = m1v2 — m1v2.
Поиск верного решения происходит путём элементарных вычислений, за счёт чего в итоге получаем математическую формулу закона сохранения импульса: m1v1 + m2v2 = m1v1l + m2v2l. Расшифровка выглядит следующим образом:
- v 1l и v 2l — скорость двух тел;
- p 1 ‘= m 1 · v 1 ‘ — импульс после взаимодействия;
- m 1 и m 2 — масса тел;
- p 2 = m 2 · v 2 — импульс второго тела до взаимодействия;
- v 1 и v 2 — скорость до взаимодействия;
- p 2 ‘= m 2 · v 2 ‘ — после взаимодействия;
- p 1 = m 1 · v 1 — импульс первого тела до взаимодействия.
Для каждого параметра свойственны свои характеристики, но все они тесно связаны между собой. Векторная сумма импульсов тел до их фактического взаимодействия идентична векторной сумме после взаимодействия. Пример: после выстрела из обычного ружья импульс оружия и пули изменится. Но вот итоговая сумма импульсов останется равной.
Более точную формулировку закона дали физики, так как они утверждают, что векторная сумма импульсов всех тел в замкнутой системе представляет собой постоянную величину, но только в том случае, воздействующие внешние силы полностью отсутствуют либо векторная сумма была приравнена к нулю. Безусловно, в природе замкнутых систем не существует. Если внешние силы воздействовали на тела в течение короткого промежутка времени, то в такой ситуации можно оставить всё без изменений, а саму систему рассматривать как замкнутую.
Основополагающие моменты
На нашей планете не существует замкнутых систем. Но если суммарные действия внешних сил меньше минимума (к примеру: во время взрыва), то имеющимся воздействием внешних сил предпочитают пренебрегать, из-за чего система приобретает статус замкнутой. Эксперты также придерживаются того мнения, что если воздействие внешних сил всё же присутствует, но итоговая их сумма проекций на одну из координатных осей равна нулю, то в этом направлении закон сохранения образуемых импульсов остаётся актуальным.
Талантливый учёный Исаак Ньютон в своё время изобрёл действительно отличное приспособление, которое как можно лучше демонстрирует сохранность импульса — маятник (колыбель). Это устройство представляет собой небольшую конструкцию, состоящую из 5 одинаковых металлических шаров, каждый из которых прикреплён к каркасу при помощи двух тросов. Основание имеет своеобразную П-образную форму.
Маятник Ньютона построен таким образом, что первый шар передаёт кинетическую энергию второму шарику, а после этого замирает. На первый взгляд, человек может и не заметить, что следующий шар принимает импульс, так как мы не можем проследить его скорость. Но если хорошо присмотреться, то можно увидеть, как шарик немного «вздрагивает» во время столкновения.
Объясняется это явление тем, что он совершает логическое движение с посланной ему скоростью, но так как итоговое расстояние слишком маленькое, ему просто не удаётся должным образом разогнаться. Но он может передать свой импульс уже третьему шарику и в итоге на время остановиться. Совершенно иная ситуация возникает в случае с последним шаром, так как у него нет возможности выполнить упругий удар и передать свой импульс, из-за чего он просто свободно колеблется.
Сущность реактивного движения
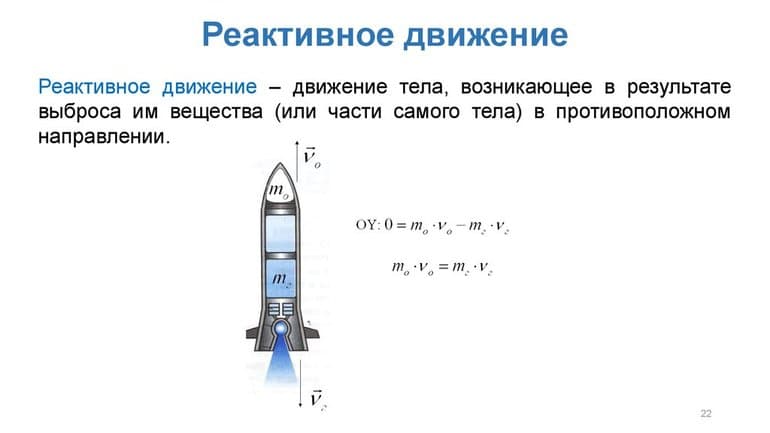
Это физическое явление тоже основано на принципе отдачи. Из сопла реактивного двигателя предварительно нагретые газы выбрасываются наружу со скоростью n. Масса несгоревшего топлива рана m, а вот вес самой ракеты после истечения газов будет обозначаться большой буквой А. В этом случае пример построен на замкнутой системе под названием «ракета-газ».
Из имеющихся данных может легко определяться скорость ракеты С после истечения газов. Все действия происходят в соответствии с формулой: С= mn /А. Ранее рассмотренная формула для пушки с ядром не является актуальной в этом случае, так как она может дать только приблизительные цифры. Всё дело в том, что основная масса газов выходит из специального сопла не сразу, а постепенно.
Масса ракеты в конкретный момент времени (t) равна А, а само устройство движется со скоростью v. В течение определённого промежутка времени ? t из сопел ракеты постепенно выбрасывается газ небольшими порциями с относительной скоростью n. Через некоторое время? t ракета начнёт двигаться со скоростью v +? v. А вот масса устройства станет равной А — ?А. Решение задачи будет выглядеть следующим образом:
- (А-?А)*(v +? v) — импульс ракеты в момент t + ? t.
- ?А*(v + n) — импульс реактивных газов.
- A v = (А−ΔА) ⋅ (v+Δv) + ΔА ⋅ (v+ ? n) — формула, которая соответствует изучаемому закону.
- А Δ v / Δ t = Δ А ⋅ n Δ t (Δ t → 0).
- Aa = − μ u.
В этом случае символом μ μ обозначаем расход задействованного топлива за отведённый промежуток времени. А вот для указания реактивной силы тяги используется сочетание μ u. Направление этой силы максимально совпадает с выбранным направлением движения ракеты. Для расчёта конечной скорости устройства принято использовать формулу: v = nlh (A 0 / A).
Стоит отметить, что
современное ракетостроение шагнуло далеко вперёд, благодаря чему специалисты стремятся развиваться в сторону универсальных многоступенчатых ракет. Своевременный сброс отсеков с уже отработанным топливом позволяет существенно снизить массу агрегата и тем самым максимально оптимизировать дальнейший расход газа для полноценного разгона.
Особенности применения физического явления
Закон сохранения момента импульса весьма удивителен, так как это физическое явление встречается даже в утончённом фигурном катании. А всё дело в том, что раскинув руки в разные стороны и заводя свободную ногу, фигуриста сообщает себе медленное вращение вокруг вертикальной оси. Если резко сгруппироваться, то момент инерции будет снижен, а также произойдёт приращение угловой скорости. Но если ось вращения является свободной, то это не может означать, что в инерциальной системе отсчёта сохраняется прежнее направление угловой скорости.
Если внимательно следить за действиями жонглёра, то в итоге можно заметить, что он передаёт всем подбрасываемым предметам импульс. Только в этом они возвращаются ему в том же положении, которое им было придано изначально. Сохранность импульса важна даже в сфере оружия, так как нарезное орудие даёт большую дальность, нежели гладкоствольное изделие. Выпущенный в один момент артиллерийский снаряд вращается вокруг своей продольной оси, из-за чего его полёт является максимально устойчивым.
Способность сохранять созданный импульс занимает в физике почётное место, так как именно на этом понятии построены фундаментальные законы природы. Если следовать теореме Эмми Нётер, то можно понять, что каждому закону обязательно ставится в соответствие определённая симметрия уравнений, описывающих эту систему. Изучаемый закон эквивалентен однородности пространства. Самый элементарный вывод этого утверждения базируется на применении лагранжева подхода.
§6. Задачи на столкновения и законы сохранения импульса и энергии
В физике под столкновениями понимают процессы взаимодействия между телами (частицами) в широком смысле слова, а не только в буквальном — как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы — тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения) импульсами и энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.
Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль. С такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.
Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.
Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.
Неупругие столкновения
Два куска пластилина массами `m_1` и `m_2`, летящие со скоростями `vecv_1` и `vecv_2` слипаются. Найдите наибольшее `Q_max` и наименьшее количество `Q_min` теплоты, которое может выделиться в результате абсолютно неупругого соударения.
Рассмотрим абсолютно неупругое соударение («слипание») тел, движущихся в ЛСО скоростями `vecv_1` и `vecv_2` соответственно. В процессе абсолютно неупругого соударения импульс системы сохраняется.
`m_1vecv_1+m_2vecv_2=(m_1+m_2)vecv`.
Отсюда находим скорость составного тела
`vecv=(m_1vecv_1+m_2vecv_2)/(m_1+m_2)`.
Закон сохранения энергии принимает вид
`(m_1vecv_1^2)/2+(m_2vecv_2^2)/2=((m_1+m_2)*vecv)/2+Q`.
Из приведенных соотношений находим убыль кинетической энергии
`Q=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(vecv_2-vecv_1)^2`,
здесь `mu=(m_1m_2)/(m_1+m_2)` — приведенная масса системы тел.
Итак, при абсолютно неупругом соударении во внутреннюю энергию переходит кинетическая энергия тела приведенной массы, движущегося с относительной скоростью.
Убыль механической энергии достигает наибольшей величины
`Q_max=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_1+v_2)^2`
при `vecv_1 uarr darr vecv_2`.
Убыль механической энергии будет наименьшей
`Q_min=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_2-v_1)^2`
при `vecv_1 uarr uarr vecv_2`.
Упругие столкновения
На гладкой горизонтальной поверхности лежит гладкая шайба массой `M`. На него налетает гладкая шайба массой `m`, движущийся со скоростью `vec v`. Происходит упругий центральный удар шайб. Найдите скорости `vecv_1` и `vecv_2` шайб после соударения. При каком условии налетающая шайба будет двигаться после соударения в прежнем направлении?
Задачу рассмотрим в ЛСО, ось `Ox` которой направим по линии центров шайб в момент соударения. Внешние силы, действующие на шайбы в процессе соударения, это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно, импульс системы шайб в процессе взаимодействия не изменяется. По закону сохранения импульса `m vec v = m vecv_1 + M vecv_2`.
Переходя к проекциям на ось `Ox`, получаем `mv = mv_(1x) + Mv_2`, здесь учтено, что направление скорости `vecv_1` налетающей шайбы после соударения не известно. По закону сохранения энергии
`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.
Полученные соотношения перепишем в виде
`m(v — v_(1x)) = Mv_2`,
`m(v^2 — v_(1x)^2) = Mv_2^2`.
Разделив второе равенство на первое `(v != v_(1x))`, приходим к линейной системе `v_2 = v + v_(1x)`, `m(v — v_(1x)) = Mv_2`, решение которой имеет вид
`v_(1x) = (m — M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.
Налетающая шайба будет двигаться после соударения в прежнем направлении `(v_(1x) > 0)` при `m > M`, т. е. если масса налетающей шайбы больше массы покоящейся шайбы.
Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности со скоростями `vecv_1` и `vecv_2`. Найдите скорости `vecv_1^’` и `vecv_2^’` шайб после абсолютно упругого нецентрального соударения. Массы шайб `m_1` и `m_2`.
Задачу рассмотрим в ИСО, оси координат `Ox` и `Oy` которой лежат в горизонтальной плоскости, при этом ось `Ox` направлена по линии центров шайб в момент соударения (рис. 16).
В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется
`vecp_1 + vecp_2 = vecp_1^’ + vecp_2^’`,
здесь `vecp_1 = m_1 vecv_1`, `vecp_2 = m_2 vecv_2`, `vecp_1^’ = m_1 vecv_1^’`, `vecp_2^’ = m_2 vecv_2^’` — импульсы шайб до и после соударения.
Так как шайбы идеально гладкие, то в процессе соударения внутренние силы -силы упругого взаимодействия — направлены только по оси `Ox`. Эти силы не изменяют `y`-составляющие импульсов шайб. Тогда из `p_(1y) = p_(1y)^’`, `p_(2y) = p_(2y)^’` находим `y`-составляющие скоростей шайб после соударения
`vecv_(1y)^’ = v_(1y)`, `v_(2y)^’ = v_(2y)`,
т. е. в проекции на ось `Oy` скорости шайб в результате соударения не изменились.
Найдём `x`-составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая энергия
`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x)^’)^2 + (v_(1y)^’)^2))/2 + (m_2 ((v_(2x)^’)^2 + (v_(2y)^’)^2))/2`.
С учётом равенства `y`-составляющих скоростей шайб до и после соударения последнее равенство принимает вид
`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^’)^2)/2 + (m_2 (v_(2x)^’)^2)/2`.
Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось `Ox`
`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^’ + m_2 v_(2x)^’`.
Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе, а по другую — ко второй, и разделить `(v_(1x) != v_(1x)^’)` полученные соотношения. Это приводит к линейному уравнению
`v_(1x) + v_(1x)^’ = v_(2x) + v_(2x)^’`.
Решая систему из двух последних уравнений, находим
`v_(1x)^’ = ((m_1 — m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,
`v_(2x)^’ = (2m_1 v_(1x) + (m_2 — m_1) v_(2x))/(m_1 + m_2)`.
Полученные соотношения для `v_(1x)^’`, `v_(1y)^’` и `v_(2x)^’`, `v_(2y)^’` решают вопрос о проекциях и величинах скоростей шайб после соударения
`v_1^’ = sqrt((v_(1x)^’)^2 + (v_(1y)^’)^2)`, `v_2^’ = sqrt((v_(2x)^’)^2 + (v_(2y)^’)^2)`,
а также об углах `alpha_1` и `alpha_2`, которые векторы скорости `vecv_1^’` и `vecv_2^’` образуют с положительным направлением оси `Ox`:
`bbb»tg» alpha_1 = (v_(1y)^’)/(v_(1x)^’)`, `bbb»tg» alpha_2 = (v_(2y)^’)/(v_(2x)^’)`.
Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц).
Краткое описание
Импульсом принято называть влияние массы тела на итоговую скорость. На этот случай специалисты разработали следующую формулу: p = m * V. В физике импульс представляет собой некую векторную величину, которая всегда направлена только в одну сторону. Само слово переводится с латинского языка, как «толкать», «двигать». Импульс принято обозначать маленькой буквой р, а вот измеряться он может только в кг*м/с.
Талантливый Рене Декарт был первым человеком, который начал использовать понятие импульс. Он пытался использовать своё открытие как определённую величину, которая заземляет силу. Причина такого подхода Рене весьма очевидна. Измерить единицу силы крайне тяжело, а вот узнать скорость и массу — это задача более простая и выполнимая. Именно поэтому в физике часто говорят, что импульс — это не что другое, как количество движения. Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующий показатель равен нулю.
Чтобы можно было разобраться в том, при каких условиях выполняется закон сохранения импульсов, нужно понять, что это физическое направление лежит в основе такого весьма удивительного явления как реактивное движение. Последнее получило широкое применение не только в технике, но и живой природе. Кальмары, осьминоги и медузы отлично используют реактивное движение, которое позволяет им преодолевать большие расстояния в своём подводном мире.
А вот в технике это физическое явление применяется в самолётах, ракетах и даже космических кораблях. Отдельного внимания заслуживает импульс в релятивистской механике. А всё потому, что законы сохранения механической энергии и импульса применяются для решения задач о движении тел после столкновения.
Ключевые особенности
Активно используемый в современном мире закон о сохранении обычных импульсов является следствием из второго и третьего законов Ньютона. Для лучшего усвоения этой темы лучше рассмотреть характерный пример. Специалистами была взята замкнутая система сразу из двух взаимодействующих между собой тел, которые отобразили при помощи F1 и F2. В третьем законе Ньютона чётко написано, что F2 = -F1. Тела взаимодействуют друг с другом в течение определённого промежутка времени (t).
В такой ситуации импульсы сил остаются идентичными по модулю, но противоположными по своему направлению (F1t = -F1t).
Если применить второй закон Ньютона, то в итоге обязательно получиться вот такое математическое выражение: F1t = m1v1 — m1v1; F2t = m1v2 — m1v2. Для отображения реальной скорости тел в конце взаимодействия используются символы v1 и v2. Из этого можно сделать вывод, что соотношение двух тел будет выглядеть следующим образом: m1v1 + m2v2 = m1v1 + m2v2.
Полученный результат позволяет говорить о равенстве (математическая форма записи закона). Это значит, что первоначальный показатель под воздействием какой-либо силы не изменится. Необходимо запомнить, что определение закона сохранения обязательно выполняется и для проекций векторов на координатные оси. Если следовать всем правилам, то можно легко определить суммарный результат в поставленной задаче, а также находить реальную скорость тел, не зная показателей действующих сил.
В качестве примера также можно рассмотреть снаряд, который вылетает из пушки. Эта задача элементарная, но очень познавательная. В роли взаимодействующих тел выступает пушка и снаряд. На первом этапе оба объекта остаются неподвижными. Но при выстреле снаряд приобретает скорость v и летит только вперёд. А вот пушка откатывается в противоположную сторону со скоростью V (происходит отдача, которая может зависеть только от выстрела). В соответствии с законом в проекции на ось можно записать:
- mv-MV=0;
- V=mv/N.
На этом примере можно увидеть, что всё элементарно и просто. При движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. Эту тему активно изучают в 9 классе
Интересные факты
При изучении этой темы нужно понимать, что закон о сохранности импульсов остаётся актуальным исключительно в изолированной/ замкнутой физической системе. В этом случае речь касается той отрасли, где абсолютно все тела тесно взаимодействуют между собой и не реагируют на внешние факторы. Но даже в этом случае действуют свои правила. Лучше представить замкнутую систему, которая состоит из двух физических тел. В этом случае возникают внутренние силы, которые могут характеризоваться определёнными параметрами.
Для первого тела импульс будет равен следующей формуле: Ft = m1v1 — m1v1. В действие снова вступает третий закон Ньютона, описываемый то, что все воздействующие на тела силы равны по своей величине, но противоположны по направлению. А это значит, что для второго тела будет действовать немного другая формула: — Ft = m1v2 — m1v2.
Поиск верного решения происходит путём элементарных вычислений, за счёт чего в итоге получаем математическую формулу закона сохранения импульса: m1v1 + m2v2 = m1v1l + m2v2l. Расшифровка выглядит следующим образом:
- v 1l и v 2l — скорость двух тел;
- p 1 ‘= m 1 · v 1 ‘ — импульс после взаимодействия;
- m 1 и m 2 — масса тел;
- p 2 = m 2 · v 2 — импульс второго тела до взаимодействия;
- v 1 и v 2 — скорость до взаимодействия;
- p 2 ‘= m 2 · v 2 ‘ — после взаимодействия;
- p 1 = m 1 · v 1 — импульс первого тела до взаимодействия.
Для каждого параметра свойственны свои характеристики, но все они тесно связаны между собой. Векторная сумма импульсов тел до их фактического взаимодействия идентична векторной сумме после взаимодействия. Пример: после выстрела из обычного ружья импульс оружия и пули изменится. Но вот итоговая сумма импульсов останется равной.
Более точную формулировку закона дали физики, так как они утверждают, что векторная сумма импульсов всех тел в замкнутой системе представляет собой постоянную величину, но только в том случае, воздействующие внешние силы полностью отсутствуют либо векторная сумма была приравнена к нулю. Безусловно, в природе замкнутых систем не существует. Если внешние силы воздействовали на тела в течение короткого промежутка времени, то в такой ситуации можно оставить всё без изменений, а саму систему рассматривать как замкнутую.
Основополагающие моменты
На нашей планете не существует замкнутых систем. Но если суммарные действия внешних сил меньше минимума (к примеру: во время взрыва), то имеющимся воздействием внешних сил предпочитают пренебрегать, из-за чего система приобретает статус замкнутой. Эксперты также придерживаются того мнения, что если воздействие внешних сил всё же присутствует, но итоговая их сумма проекций на одну из координатных осей равна нулю, то в этом направлении закон сохранения образуемых импульсов остаётся актуальным.
Талантливый учёный Исаак Ньютон в своё время изобрёл действительно отличное приспособление, которое как можно лучше демонстрирует сохранность импульса — маятник (колыбель). Это устройство представляет собой небольшую конструкцию, состоящую из 5 одинаковых металлических шаров, каждый из которых прикреплён к каркасу при помощи двух тросов. Основание имеет своеобразную П-образную форму.
Маятник Ньютона построен таким образом, что первый шар передаёт кинетическую энергию второму шарику, а после этого замирает. На первый взгляд, человек может и не заметить, что следующий шар принимает импульс, так как мы не можем проследить его скорость. Но если хорошо присмотреться, то можно увидеть, как шарик немного «вздрагивает» во время столкновения.
Объясняется это явление тем, что он совершает логическое движение с посланной ему скоростью, но так как итоговое расстояние слишком маленькое, ему просто не удаётся должным образом разогнаться. Но он может передать свой импульс уже третьему шарику и в итоге на время остановиться. Совершенно иная ситуация возникает в случае с последним шаром, так как у него нет возможности выполнить упругий удар и передать свой импульс, из-за чего он просто свободно колеблется.
Сущность реактивного движения
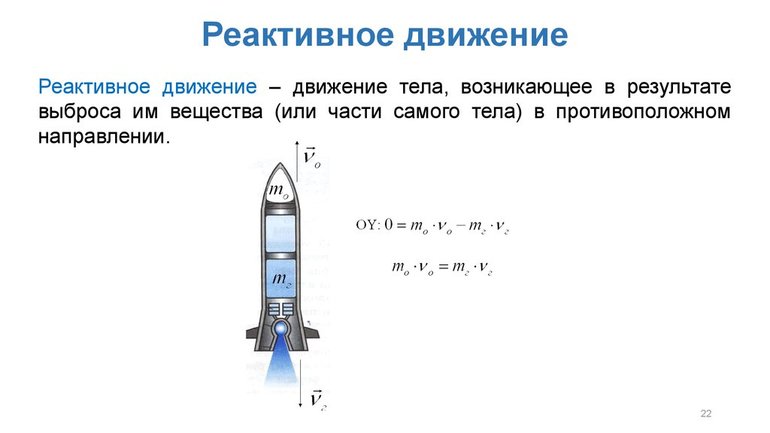
Это физическое явление тоже основано на принципе отдачи. Из сопла реактивного двигателя предварительно нагретые газы выбрасываются наружу со скоростью n. Масса несгоревшего топлива рана m, а вот вес самой ракеты после истечения газов будет обозначаться большой буквой А. В этом случае пример построен на замкнутой системе под названием «ракета-газ».
Из имеющихся данных может легко определяться скорость ракеты С после истечения газов. Все действия происходят в соответствии с формулой: С= mn /А. Ранее рассмотренная формула для пушки с ядром не является актуальной в этом случае, так как она может дать только приблизительные цифры. Всё дело в том, что основная масса газов выходит из специального сопла не сразу, а постепенно.
Масса ракеты в конкретный момент времени (t) равна А, а само устройство движется со скоростью v. В течение определённого промежутка времени ? t из сопел ракеты постепенно выбрасывается газ небольшими порциями с относительной скоростью n. Через некоторое время? t ракета начнёт двигаться со скоростью v +? v. А вот масса устройства станет равной А — ?А. Решение задачи будет выглядеть следующим образом:
- (А-?А)*(v +? v) — импульс ракеты в момент t + ? t.
- ?А*(v + n) — импульс реактивных газов.
- A v = (А−ΔА) ⋅ (v+Δv) + ΔА ⋅ (v+ ? n) — формула, которая соответствует изучаемому закону.
- А Δ v / Δ t = Δ А ⋅ n Δ t (Δ t → 0).
- Aa = − μ u.
В этом случае символом μ μ обозначаем расход задействованного топлива за отведённый промежуток времени. А вот для указания реактивной силы тяги используется сочетание μ u. Направление этой силы максимально совпадает с выбранным направлением движения ракеты. Для расчёта конечной скорости устройства принято использовать формулу: v = nlh (A 0 / A).
Стоит отметить, что
современное ракетостроение шагнуло далеко вперёд, благодаря чему специалисты стремятся развиваться в сторону универсальных многоступенчатых ракет. Своевременный сброс отсеков с уже отработанным топливом позволяет существенно снизить массу агрегата и тем самым максимально оптимизировать дальнейший расход газа для полноценного разгона.
Особенности применения физического явления
Закон сохранения момента импульса весьма удивителен, так как это физическое явление встречается даже в утончённом фигурном катании. А всё дело в том, что раскинув руки в разные стороны и заводя свободную ногу, фигуриста сообщает себе медленное вращение вокруг вертикальной оси. Если резко сгруппироваться, то момент инерции будет снижен, а также произойдёт приращение угловой скорости. Но если ось вращения является свободной, то это не может означать, что в инерциальной системе отсчёта сохраняется прежнее направление угловой скорости.
Если внимательно следить за действиями жонглёра, то в итоге можно заметить, что он передаёт всем подбрасываемым предметам импульс. Только в этом они возвращаются ему в том же положении, которое им было придано изначально. Сохранность импульса важна даже в сфере оружия, так как нарезное орудие даёт большую дальность, нежели гладкоствольное изделие. Выпущенный в один момент артиллерийский снаряд вращается вокруг своей продольной оси, из-за чего его полёт является максимально устойчивым.
Способность сохранять созданный импульс занимает в физике почётное место, так как именно на этом понятии построены фундаментальные законы природы. Если следовать теореме Эмми Нётер, то можно понять, что каждому закону обязательно ставится в соответствие определённая симметрия уравнений, описывающих эту систему. Изучаемый закон эквивалентен однородности пространства. Самый элементарный вывод этого утверждения базируется на применении лагранжева подхода.