17 авг. 2022 г.
читать 2 мин
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например, в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
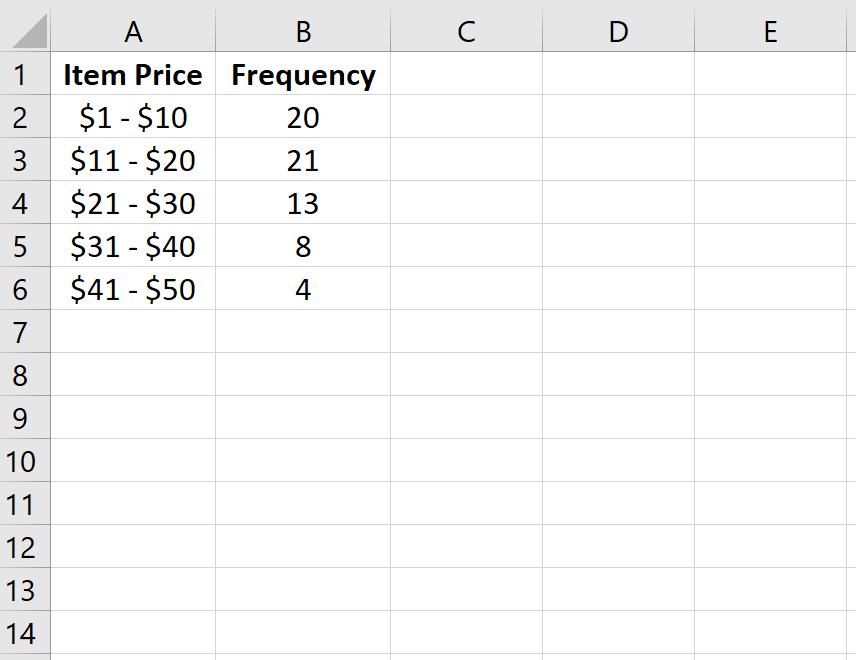
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать совокупную частоту для каждого класса, которая представляет собой просто сумму частот до определенного класса.
| Цена товара | Частота | Накопленная частота | | — | — | — | | $1 – $10 | 20 | 20 | | $11 – $20 | 21 | 41 | | 21 – 30 долларов США | 13 | 54 | | $31 – $40 | 8 | 62 | | $41 — $50 | 4 | 66 |
Например, первая кумулятивная частота просто равна первой частоте 20 .
Вторая кумулятивная частота представляет собой сумму первых двух частот: 20 + 21 = 41 .
Третья кумулятивная частота представляет собой сумму первых трех частот: 20 + 21 + 13 = 54 .
И так далее.
В следующем примере показано, как найти совокупные частоты в Excel.
Пример: кумулятивная частота в Excel
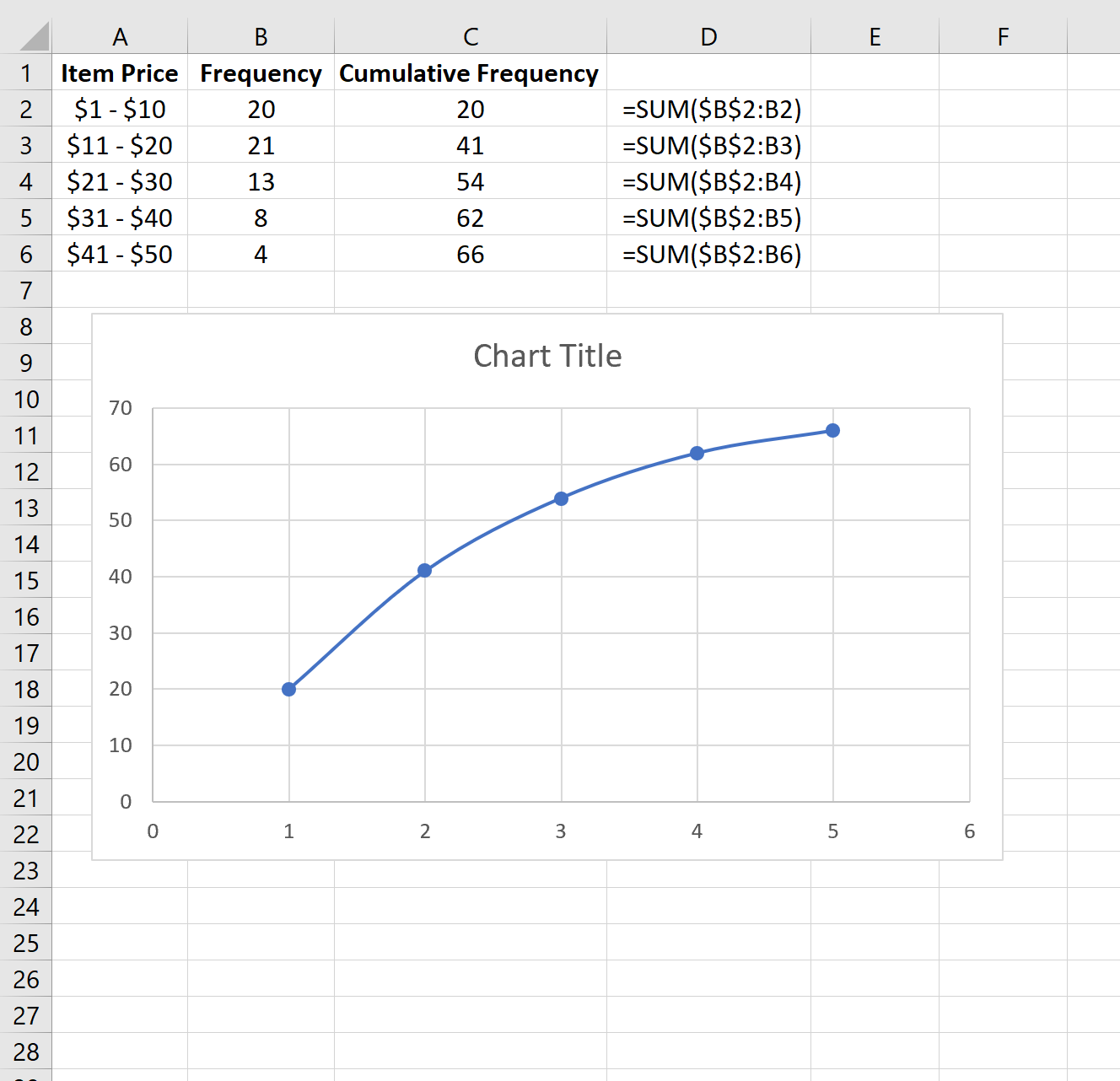
Сначала мы введем класс и частоту в столбцах A и B:
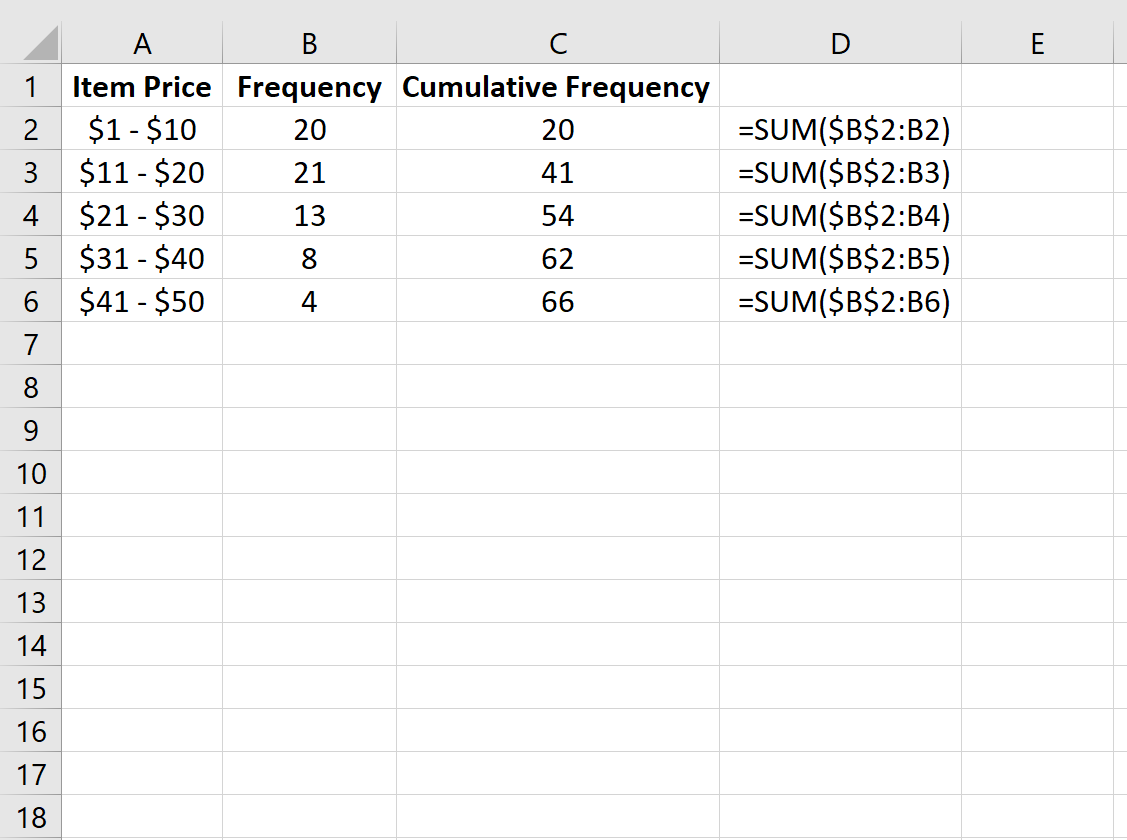
Далее мы рассчитаем совокупную частоту каждого класса в столбце C.
На изображении ниже в столбце D показаны формулы, которые мы использовали:
Мы также можем создать оживальную диаграмму для визуализации кумулятивных частот.
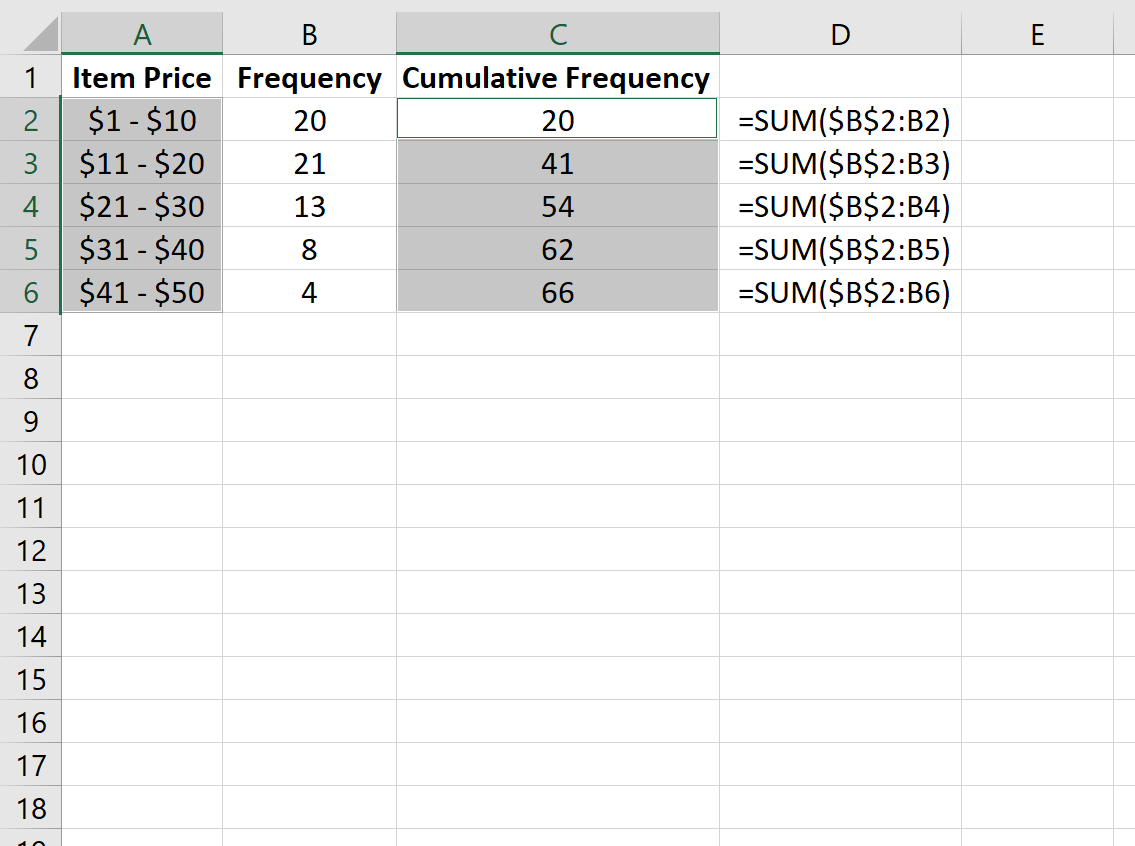
Чтобы создать оживальную диаграмму, удерживайте нажатой клавишу CTRL и выделите столбцы A и C.
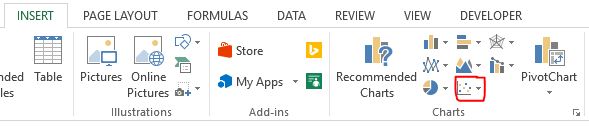
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
На верхней ленте в Excel перейдите на вкладку « Вставка », затем в группу « Диаграммы ». Нажмите Точечная диаграмма , затем нажмите Точечная диаграмма с прямыми линиями и маркерами .
Это автоматически создаст следующий оживальный график:
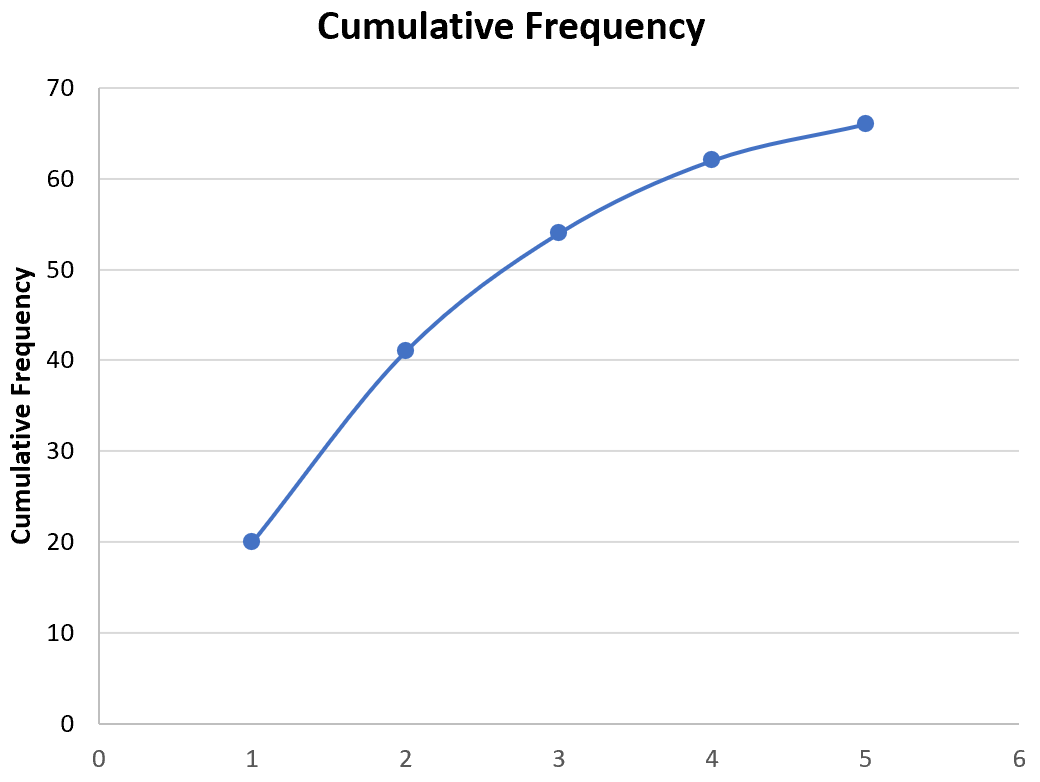
Не стесняйтесь изменять оси и заголовок, чтобы сделать график более эстетичным:
Дополнительные ресурсы
Калькулятор кумулятивной частоты
Как рассчитать относительную частоту в Excel
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Кумулята
Распределение признака
в вариационном ряду по накопленным
частотам (частостям) изображается с
помощью кумуляты.
Кумулята или
кумулятивная кривая в отличие от полигона
строится по накопленным частотам или
частостям. При этом на оси абсцисс
помещают значения признака, а на оси
ординат — накопленные частоты или
частости (рис. 3).
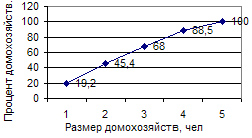
Рис. 6.3.
Кумулята распределения домохозяйств
по размеру
4. Рассчитаем накопленные
частоты:
Наколенная частота первого
интервала рассчитывается следующим
образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для
третьего: 4 + 12 + 8 = 24 и т.д.
|
Размер руб в месяц Xi |
Численность чел. fi |
Накопленные частоты S |
|
до 5000 |
4 |
4 |
|
5000 — 7000 |
12 |
16 |
|
7000 — 10000 |
8 |
24 |
|
10000 — 15000 |
6 |
30 |
|
Итого: |
30 |
— |
При построении кумуляты
накопленная частота (частость)
соответствующего интервала присваивается
его верхней границе:
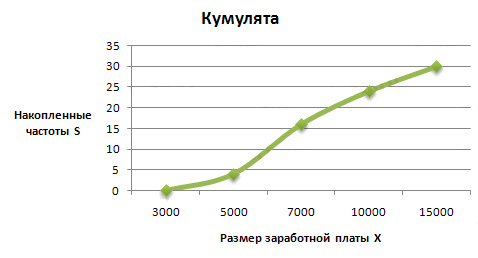
Для
графического изображения дискретного
вариационного ряда применяют полигон
распределения, для построения которого
необходимо соединить прямыми отрезками
точки с координатами
.
Крайние точки полученного графика
соединяют с точками по оси абсцисс,
отстающими на одно деление в принятом
масштабе от минимального и максимального
значений варианта. Полигон может быть
построен и для интервального вариационного
ряда, для этого в качестве координат по
оси абсцисс используют середины
интервалов. Очевидно, что гистограмма
легко может быть преобразована в
полигон распределения, если середины
верхних сторон прямоугольника соединить
отрезками прямых, при этом середины
верхних сторон двух крайних прямоугольников
соединить с осью абсцисс в точках,
отстоящих в принятом масштабе на
величину интервалов от середины первого
и последнего интервалов.
Полигон на рис. 6.1
построен по данным микропереписи
населения России в 1994 г.
|
Домохозяйства, |
одного человека |
двух человек |
трех человек |
5 или более |
всего |
|
Число домохозяйств |
19,2 |
26,2 |
22,6 |
20,5 |
100,0 |

Рис.
3. Распределение домохозяйств по размеру
Условие:
Приводятся данные о распределении 25
работников одного из предприятий по
тарифным разрядам:
4; 2; 4; 6; 5; 6; 4; 1; 3; 1;
2; 5; 2; 6; 3; 1; 2; 3; 4; 5; 4; 6; 2; 3; 4
Задача:
Построить дискретный вариационный ряд
и изобразить его графически в виде
полигона распределения.
Решение:
В
данном примере вариантами является
тарифный разряд работника. Для определения
частот необходимо рассчитать число
работников, имеющих соответствующий
тарифный разряд.
|
Тарифный разряд |
Число работников |
|
1 |
3 |
|
2 |
5 |
|
3 |
4 |
|
4 |
6 |
|
5 |
3 |
|
6 |
4 |
|
Итого: |
25 |
Полигон используется
для дискретных вариационных рядов.
Для
построения полигона распределения (рис
1) по оси абсцисс (X) откладываем
количественные значения варьирующего
признака — варианты, а по оси ординат
— частоты или частости.
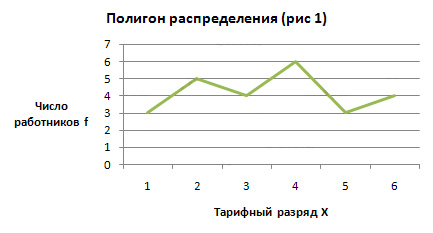
Если
значения признака выражены в виде
интервалов, то такой ряд называется
интервальным.
Интервальные
ряды распределения
изображают графически в виде гистограммы,
кумуляты или огивы.
Огива строится
аналогично кумуляте с той лишь разницей,
что накопленные частоты помещают на
оси абсцисс, а значения признака — на
оси ординат.
Разновидностью
кумуляты является кривая концентрации
или график Лоренца. Для построения
кривой концентрации на обе оси
прямоугольной системы координат
наносится масштабная шкала в процентах
от 0 до 100. При этом на оси абсцисс указывают
накопленные частости, а на оси ординат
— накопленные значения доли (в процентах)
по объему признака.
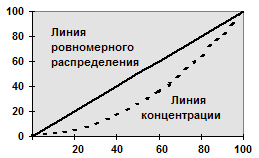
Равномерному
распределению признака соответствует
на графике диагональ квадрата (рис. 4).
При неравномерном распределении график
представляет собой вогнутую кривую в
зависимости от уровня концентрации
признака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Ряды распределения
- Графическое изображение рядов распределения
- Полигон
- Статистическая таблица
- Гистограмма
- Кумулята
- Огива
- содержание
- принципы
- Определения
- оценка вероятности
- Из совокупной частоты
- По рейтинговой методики
- Подгонка вероятностных распределений
- Непрерывные распределения
- Разрывные распределения
- прогнозирование
- неопределенность
- Доверительные интервалы
- период повторения
- Необходимость доверия ремней
- Гистограмма
- Предмет статистики

Ряды распределения
После определения группировочного признака, количества групп и интервалов группировки данные сводки и группировки представляются в виде рядов распределения и оформляются в виде статистических таблиц.
Ряд распределния является одним из видов группировок.
Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.
В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:
- Атрибутивными — называют ряды распределения, построенные по качественными признакам.
- Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.
Вариационный ряд распределения состоит из двух столбцов:
В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются . Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.
Во втором столбце содержится количество конкретных вариант, выраженное через частоты или частости:
Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают . Сумма всех частот равна должна быть равна численности единиц всей совокупности.
Частости ( ) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.
Графическое изображение рядов распределения
Наглядно ряды распределения представляются при помощи графических изображений.
Ряды распределения изображаются в виде:
- Полигона
- Гистограммы
- Кумуляты
- Огивы
Полигон
При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.
Полигон на рис. 6.1 построен по данным микропереписи населения России в 1994 г.
| Домохозяйства, состоящие из: | одного человека | двух человек | трех человек | 5 или более | всего |
| Число домохозяйств в % | 19,2 | 26,2 | 22,6 | 20,5 | 100,0 |
6.1. Распределение домохозяйств по размеру
Условие: Приводятся данные о распределении 25 работников одного из предприятий по тарифным разрядам:
4; 2; 4; 6; 5; 6; 4; 1; 3; 1; 2; 5; 2; 6; 3; 1; 2; 3; 4; 5; 4; 6; 2; 3; 4
Задача: Построить дискретный вариационный ряд и изобразить его графически в виде полигона распределения.
Решение:
В данном примере вариантами является тарифный разряд работника. Для определения частот необходимо рассчитать число работников, имеющих соответствующий тарифный разряд.
| Тарифный разряд Xi |
Число работников fi |
| 1 | 3 |
| 2 | 5 |
| 3 | 4 |
| 4 | 6 |
| 5 | 3 |
| 6 | 4 |
| Итого: | 25 |
Полигон используется для дискретных вариационных рядов.
Для построения полигона распределения (рис 1) по оси абсцисс (X) откладываем количественные значения варьирующего признака — варианты, а по оси ординат — частоты или частости.
Если значения признака выражены в виде интервалов, то такой ряд называется интервальным.
Интервальные ряды распределения изображают графически в виде гистограммы, кумуляты или огивы.
Статистическая таблица
Условие: Приведены данные о размерах вкладов 20 физических лиц в одном банке (тыс.руб) 60; 25; 12; 10; 68; 35; 2; 17; 51; 9; 3; 130; 24; 85; 100; 152; 6; 18; 7; 42.
Задача: Построить интервальный вариационный ряд с равными интервалами.
Решение:
- Исходная совокупность состоит из 20 единиц (N = 20).
- По формуле Стерджесса определим необходимое количество используемых групп: n=1+3,322*lg20=5
- Вычислим величину равного интервала: i=(152 — 2) /5 = 30 тыс.руб
- Расчленим исходную совокупность на 5 групп с величиной интервала в 30 тыс.руб.
- Результаты группировки представим в таблице:
| Размер вкладов тыс.руб Xi |
Число вкладов fi |
Число вкладов в % к итогу Wi |
| 2 — 32 | 11 | 55 |
| 32 — 62 | 4 | 20 |
| 62 — 92 | 2 | 10 |
| 92 — 122 | 1 | 5 |
| 122 — 152 | 2 | 10 |
| Итого: | 20 | 100 |
При такой записи непрерывного признака, когда одна и та же величина встречается дважды (как верхняя граница одного интервала и нижняя граница другого интервала), то эта величина относится к той группе, где эта величина выступает в роли верхней границы.
Гистограмма
Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).
На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.
| Все население | В том числе в возрасте | ||||||||
| до 10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70 и старше | Всего | |
| Численность населения | 12,1 | 15,7 | 13,6 | 16,1 | 15,3 | 10,1 | 9,8 | 7,3 | 100,0 |
Рис. 6.2. Распределение населения России по возрастным группам
Условие: Приводится распределение 30 работников фирмы по размеру месячной заработной платы
| Размер заработной платы руб. в месяц |
Численность работников чел. |
| до 5000 | 4 |
| 5000 — 7000 | 12 |
| 7000 — 10000 | 8 |
| 10000 — 15000 | 6 |
| Итого: | 30 |
Задача: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты.
Решение:
- Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
- Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда.
Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников. - Построим гистограмму:
Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.
Кумулята
Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.
Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости (рис. 6.3).
Рис. 6.3. Кумулята распределения домохозяйств по размеру
4. Рассчитаем накопленные частоты:
Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.
| Размер заработной платы руб в месяц Xi |
Численность работников чел. fi |
Накопленные частоты S |
| до 5000 | 4 | 4 |
| 5000 — 7000 | 12 | 16 |
| 7000 — 10000 | 8 | 24 |
| 10000 — 15000 | 6 | 30 |
| Итого: | 30 | — |
При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:
Огива
Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака.
Равномерному распределению признака соответствует на графике диагональ квадрата (рис. 6.4). При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.
Понятие вариационного ряда. Первым шагом систематизации материалов статистического наблюдения является подсчет числа единиц, обладающих тем или иным признаком. Расположив единицы в порядке возрастания или убывания их количественного признака и подсчитав число единиц с конкретным значением признака, получаем вариационный ряд. Вариационный ряд характеризует распределение единиц определенной статистической совокупности по какому–либо количественному признаку.
Вариационный ряд представляет собой две колонки, в левой колонке приводятся значения варьирующего признака, именуемые вариантами и обозначаемые (x), а в правой – абсолютные числа, показывающие, сколько раз встречается каждый вариант. Показатели этой колонки называются частотами и обозначаются (f).
Схематично вариационный ряд можно представить в виде табл.5.1:
Вид вариационного ряда
В правой колонке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Эти относительные показатели именуют частостями и условно обозначают через 

Варьирующие признаки могут носить разный характер. Варианты одних признаков выражаются в целых числах, например, число комнат в квартире, число изданных книг и т.д. Эти признаки именуют прерывными, или дискретными. Варианты других признаков могут принимать любые значения в определенных пределах, как, например, выполнение плановых заданий, заработная плата и др. Эти признаки называют непрерывными.
Дискретный вариационный ряд. Если варианты вариационного ряда выражены в виде дискретных величин, то такой вариационный ряд называют дискретным, его внешний вид представлен в табл. 5.2:
Распределение студентов по оценкам, полученным на экзамене
Количество студентов (f)
В % к итогу (
Характер распределения в дискретных рядах изображается графически в виде полигона распределения, рис.5.1.
Рис. 5.1. Распределение студентов по оценкам, полученным на экзамене.
Интервальный вариационный ряд. Для непрерывных признаков вариационные ряды строятся интервальные, т.е. значения признака в них выражаются в виде интервалов «от и до». При этом минимальное значение признака в таком интервале именуют нижней границей интервала, а максимальное – верхней границей интервала.
Интервальные вариационные ряды строят как для прерывных признаков (дискретных), так и для варьирующих в большом диапазоне. Интервальные ряды могут быть с равными и неравными интервалами. В экономической практике в большинстве своем применяются неравные интервалы, прогрессивно возрастающие или убывающие. Такая необходимость возникает особенно в тех случаях, когда колеблемость признака осуществляется неравномерно и в больших пределах.
Рассмотрим вид интервального ряда с равными интервалами, табл. 5.3:
Распределение рабочих по выработке
Число рабочих (f)
Кумулятивная частота (f´)
Интервальный ряд распределения графически изображается в виде гистограммы, рис.5.2.
Рис.5.2. Распределение рабочих по выработке
Накопленная (кумулятивная) частота. В практике возникает потребность в преобразовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам. С их помощью можно определить структурные средние, которые облегчают анализ данных ряда распределения.
Накопленные частоты определяются путем последовательного прибавления к частотам (или частостям) первой группы этих показателей последующих групп ряда распределения. Для иллюстрации рядов распределения используются кумуляты и огивы. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумулята), рис.5.3.
Рис. 5.3. Кумулята распределения рабочих по выработке
Если шкалы частот и вариантов поменять местами, т.е. на оси абсцисс отражать накопленные частоты, а на оси ординат – значения вариантов, то кривая, характеризующая изменение частот от группы к группе, будет носит название огивы распределения, рис.5.4.
Рис. 5.4. Огива распределения рабочих по выработке
Вариационные ряды с равными интервалами обеспечивают одно из важнейших требований, предъявляемых к статистическим рядам распределения, обеспечение сравнимости их во времени и пространстве.
Плотность распределения. Однако частоты отдельных неравных интервалов в названных рядах непосредственно не сопоставимы. В подобных случаях для обеспечения необходимой сравнимости исчисляют плотность распределения, т.е. определяют, сколько единиц в каждой группе приходится на единицу величины интервала.
При построении графика распределения вариационного ряда с неравными интервалами высоту прямоугольников определяют пропорционально не частотам, а показателям плотности распределения значений изучаемого признака в соответствующих интервалах.
Составление вариационного ряда и его графическое изображение является первым шагом обработки исходных данных и первой ступенью анализа изучаемой совокупности. Следующим шагом в анализе вариационных рядов является определение основных обобщающих показателей, именуемых характеристиками ряда. Эти характеристики должны дать представление о среднем значении признака у единиц совокупности.
Средняя величина. Средняя величина представляет собой обобщенную характеристику изучаемого признака в исследуемой совокупности, отражающая ее типический уровень в расчете на единицу совокупности в конкретных условиях места и времени.
Средняя величина всегда именованная, имеет ту же размерность, что и признак у отдельных единиц совокупности.
Перед вычислением средних величин необходимо произвести группировку единиц исследуемой совокупности, выделив качественно однородные группы.
Средняя, рассчитанная по совокупности в целом называется общей средней, а для каждой группы – групповыми средними.
Существуют две разновидности средних величин: степенные (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая); структурные (мода, медиана, квартили, децили).
Выбор средней для расчета зависит от цели.
Виды степенных средних и методы их расчета. В практике статистической обработки собранного материала возникают различные задачи, для решения которых требуются различные средние.
Математическая статистика выводит различные средние из формул степенной средней:
где 
Однако вопрос о том, какой вид средней необходимо применить в каждом отдельном случае, разрешается путем конкретного анализа изучаемой совокупности.
Наиболее часто встречающимся в статистике видом средних величин является средняя арифметическая. Она исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
В зависимости от характера исходных данных средняя арифметическая определяется различными способами:
Если данные несгруппированные, то расчет ведется по формуле простой средней величины

Если значение признака встречается несколько раз, то среднюю величину находят по формуле для сгруппированных данных и средняя величина будет называться среднеарифметическая взвешенная.
Расчет средней арифметической в дискретном ряду происходит по формуле 3.4.
Расчет средней арифметической в интервальном ряду. В интервальном вариационном ряду, где за величину признака в каждой группе условно принимается середина интервала, средняя арифметическая может отличаться от средней, рассчитанной по несгруппированным данным. Причем, чем больше величина интервала в группах, тем больше возможные отклонения средней, вычисленной по сгруппированным данным, от средней, рассчитанной по несгруппированным данным.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. А затем рассчитывают среднюю величину по формуле средней арифметической взвешенной.
Свойства средней арифметической. Средняя арифметическая обладает некоторыми свойствами, которые позволяют упрощать вычисления, рассмотрим их.
1. Средняя арифметическая из постоянных чисел равна этому постоянному числу.
Если х = а. Тогда 
2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится.
Если все веса f уменьшить в k раз, то 
3. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю, т.е.
Если 


Если все варианты уменьшить или увеличить на какое- либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же.
Уменьшим все варианты x на a, т.е. x´ = x – a.
Тогда
Среднюю арифметическую первоначального ряда можно получить, прибавляя к уменьшенной средней ранее вычтенное из вариантов числа a, т.е. 
5. Если все варианты уменьшить или увеличить в k раз, то средняя арифметическая нового ряда уменьшится или увеличится во столько же, т.е. в k раз.
Пусть 

Отсюда 
Средняя гармоническая. Средняя гармоническая это величина обратная средней арифметической. Ее используют, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение (М= xf). Средняя гармоническая будет рассчитываться по формуле 3.5
Практическое применение средней гармонической – для расчета некоторых индексов, в частности, индекса цен.
Средняя геометрическая. При применении средней геометрической индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста.
Средняя геометрическая величина используется также для определения равноудаленной величины от максимального и минимального значений признака. Например, страховая компания заключает договоры на оказание услуг автострахования. В зависимости конкретного страхового случая страховая выплата может колебаться от 10000 до 100000 долл. в год. Средняя сумма выплат по страховке составит 
Средняя геометрическая это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии, когда z = 0. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел.
Формулы для расчета следующие


где 

Средняя геометрическая используется в расчетах среднегодовых темпов роста.
Средняя квадратическая. Формула средней квадратической используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения. Так, при расчете показателей вариации среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины.
Средняя квадратическая величина рассчитывается по формуле
В экономических исследованиях средняя квадратическая в измененном виде широко используется при расчете показателей вариации признака, таких как дисперсия, среднее квадратическое отклонение.
Правило мажорантности. Между степенными средними существует следующая зависимость – чем больше показатель степени, тем больше значение средней, табл.5.4:
Соотношение между средними величинами
Соотношение между средними

Все рассмотренные формы степенной средней обладают важным свойством (в отличие от структурных средних) – в формулу определения средней входят все значения ряда т.е. на размеры средней оказывают влияние значение каждого варианта.
С одной стороны, это весьма положительное свойство т.к. в этом случае учитывается действие всех причин, воздействующих на все единицы изучаемой совокупности. С другой стороны, даже одно наблюдение, попавшее в исходные данные случайно, может существенным образом исказить представление об уровне развития изучаемого признака в рассматриваемой совокупности (особенно в коротких рядах).
Квартили и децили. По аналогии с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так, в частности, можно найти значение признака у единиц, делящих ряд на 4 равные части, на 10 и т.п.
Квартили. Варианты, которые делят ранжированный ряд на четыре равные части, называют квартилями.
При этом различают: нижний (или первый) квартиль (Q1) – значение признака у единицы ранжированного ряда, делящей совокупность в соотношении ¼ к ¾ и верхний (или третий) квартиль(Q3) – значение признака у единицы ранжированного ряда, делящий совокупность в соотношении ¾ к ¼.
Второй квартиль, есть медиана Q2 = Ме. Нижний и верхний квартили в интервальном ряду рассчитываются по формуле аналогично медиане.
Для нижнего квартиля 
Для верхнего квартиля 
где 


Интервалы, в которых содержатся Q1 и Q3 определяют по накопленным частотам (или частостям).
Децили. Кроме квартилей рассчитывают децили – варианты, делящие ранжированный ряд на 10 равных частей.
Обозначаются они через D, первый дециль D1 делит ряд в соотношении 1/10 и 9/10, второй D2 – 2/10 и 8/10 и т.д. Вычисляются они по той же схеме, что и медиана и квартили.


И медиана, и квартили, и децили принадлежат к так называемым порядковым статистикам, под которым понимают вариант, занимающий определенное порядковое место в ранжированном ряду.
Накопительный частотный анализ представляет собой анализ частоты встречаемости значений явления меньше , чем заданное значение. Явление может быть по времени или пространственно-зависимый. Накопительная частота также называется частотой непревышения .
Накопительное частотный анализ выполняется , чтобы получить представление о том , как часто определенное явление (особенность) ниже определенного значения. Это может помочь в описании или объяснения ситуации , в которой явление участвует, или в мероприятиях по планированию, например , в защите от наводнений.
Этот статистический метод может быть использован, чтобы увидеть, насколько вероятно событие, как наводнение будет происходить в будущем, основываясь на том, как часто это случалось в прошлом. Он может быть приспособлен, чтобы принести в таких вещах, как изменение климата, вызывая более влажные зимы и сухой лето.
содержание
принципы
Определения
Частотный анализ представляет собой анализ того, как часто, или, как часто, наблюдаемое явление происходит в определенном диапазоне.
Анализ частоты применяется к записи длиной N наблюдаемых данных X 1 , X 2 , X 3 . , , Х Н на переменном явление X . Запись может быть в зависимости от времени (например , количество осадков измеряется в одном месте) или пространственно-зависимой (например , урожайность в области) или иным образом .
Накопленная частота М ХГ опорного значения Xr является частота , с которой наблюдаемые значения Х меньше или равна Xr .
Относительная накопленная частота Fc , может быть рассчитана следующим образом :
где N есть число данных
Кратко это выражение можно записать в виде:
При ХГ = Xmin , где Xmin это уникальное минимальное значение наблюдаемого, было установлено , что Fc = 1 / N , потому что M = 1. С другой стороны, когда ХГ = Xmax , где Xmax является уникальным максимальное значение наблюдается, то обнаружено , что Fc = 1, потому что M = N . Следовательно, когда Fc = 1 это означает , что ХГ является значением , при котором все данные меньше или равна хт .
В процентном отношении уравнение гласит:
оценка вероятности
Из совокупной частоты
Кумулятивная вероятность Рс из X , чтобы быть меньше или равна Xr может быть оценена несколькими способами на основе накопленной частоты M .
Один из способов заключается в использовании относительной накапливаемых частот Fc в качестве оценки.
Другой способ принять во внимание возможность того, что в редких случаях Х может принимать значения больше , чем наблюдаемое максимальное Xmax . Это может быть сделано делением накапливаемых частот M на N + 1 вместо N . Оценка становится:
Там существуют и другие предложения для знаменателя (см Plotting позиции ).
По рейтинговой методики
Оценка вероятности облегчается путем ранжирования данных.
Когда наблюдаемые данные X расположены в порядке возрастания ( Х 1 ≤ Х 2 ≤ Х 3 ≤. ≤ Х Н , минимальный первый и максимальный последний) и Ri представляет ранг номер наблюдения Xi , где adfix я указывает порядковый номер в диапазоне восходящих данных, то кумулятивная вероятность может быть оценена путем:
Когда, с другой стороны, наблюдаемые данные из X расположены в порядке убывания , максимальный первые и минимальная последний, и Rj есть ранг номер наблюдения Xj , кумулятивная вероятность может быть оценена путем:
Подгонка вероятностных распределений
Непрерывные распределения
Для того, чтобы представить кумулятивное распределение частот в виде непрерывного математического уравнения вместо дискретного набора данных, можно попытаться соответствовать кумулятивное распределение частот к известному кумулятивного распределения вероятностей ,.
В случае успеха, известное уравнение достаточно , чтобы сообщить распределение частот и таблицу данных , не требуется. Кроме того, уравнение помогает интерполяции и extrapolation.However, следует соблюдать осторожность с экстраполяцией кумулятивного распределения частот, так как это может быть источником ошибок. Одна из возможных ошибок является то , что распределение частот не соответствует выбранному распределению вероятностей любым больше за пределами диапазона наблюдаемых данных.
Любое уравнение , которое дает значение 1 , когда интегрированному от нижнего предела до верхнего предела , согласившись также с диапазоном данных, может быть использовано в качестве распределения вероятностей для монтажа. Образец вероятностных распределений , которые могут быть использованы , можно найти в вероятностных распределений .
Распределения вероятностей могут быть установлены несколькими способами, например:
- параметрический метод, определение параметров , как среднее значение и стандартное отклонение от X данных с использованием методы моментов , то метод максимального правдоподобия и метод вероятностных взвешенными моментов .
- метод регрессии, линеаризуя распределение вероятностей через преобразование и определение параметров от линейной регрессии преобразованной Pc (полученный из ранжирования) на трансформированных X данных.
Применение обоих типов методов, использующих, например,
часто показывает, что ряд распределений соответствуют скважинам данных и не дает существенно различные результаты, в то время как различия между ними могут быть малы по сравнению с шириной доверительного интервала. Это свидетельствует о том, что это может быть трудно определить, какое распределение дает лучшие результаты.
Разрывные распределения
Иногда можно, чтобы соответствовать один тип распределения вероятностей в нижней части диапазона данных и другого типа в верхней части, разделенные точкой останова, в результате чего улучшается общее нужным.
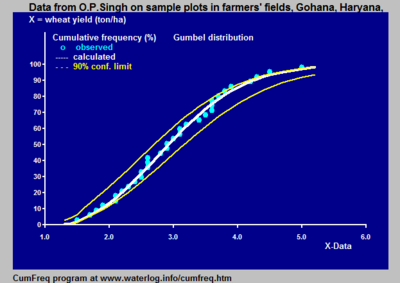
На рисунке приведен пример полезного введения такого прерывистого распределения для данных осадков на севере Перу, где климат подвержен поведению Тихого океана ток Эль — Ниньо . Когда Niño распространяется на юге Эквадора и попадает в океан вдоль побережья Перу, климат в Северном Перу становится тропическим и влажным. Когда Niño не доходит до Перу, климат полузасушливый. По этой причине, более высокие осадки следуют различному распределению частот , чем нижние осадки.
прогнозирование
неопределенность
Когда совокупное распределение частот происходят от записи данных, она может быть поставлена под сомнение , если она может быть использована для предсказания. Например, учитывая распределение стока рек в годы 1950-2000, может это распределение можно использовать для прогнозирования , как часто определенный разряд река будет превышена в годы 2000-50? Ответ : да, при условии , что условия окружающей среды не изменяются. Если условия окружающей среды делают изменения, такие как изменения в инфраструктуре водораздела реки или в структуре осадков из — за климатические изменения, прогнозирование на основе исторических фактов подлежат систематическую ошибку . Даже если нет никаких систематических ошибок, может быть случайной ошибкой , потому что случайно наблюдаемые выбросы в течение 1950 — 2000 может быть выше или ниже , чем обычно, а с другой стороны, выбросы с 2000 по 2050 год может случайно быть ниже или выше , чем обычно. Проблемы вокруг этого были исследованы в книге The Black Swan .
Доверительные интервалы
Теория вероятностей может помочь оценить диапазон , в котором может быть случайная ошибка. В случае кумулятивной частоты есть только две возможности: определенное опорное значение Х превышается или не превышается. Сумма частоты превышений и накопленной частота равна 1 или 100%. Таким образом, биномиальное распределение может быть использовано при оценке спектра случайной ошибки.
В соответствии с обычной теорией, биномиальное распределение можно аппроксимировать и при больших N стандартного отклонения Сд может быть рассчитана следующим образом :
где Рс является кумулятивной вероятностью и N есть число данных. Видно , что стандартное отклонение Сд уменьшает при увеличении числа наблюдений N .
Определение доверительного интервала от ПК позволяет использовать Т-критерий Стьюдента ( т ). Величина т зависит от количества данных и уровня достоверности оценки доверительного интервала. Затем нижний ( L ) и верхней ( U ) доверительные интервалы Pc в симметричном распределении находятся из:
Это известно как интервал Wald . Тем не менее, биномиальное распределение является симметричным только вокруг среднего значения , когда Рс = 0,5, но становится асимметричным и все больше и больше перекоса , когда ПК приближается к 0 или 1. Таким образом, с помощью аппроксимации, Рс и 1- Рса может быть использован в качестве весовых коэффициентов в уступка t.Sd к L и U :
где можно видеть , что эти выражения для Pc = 0,5 такие же , как и предыдущие.
N = 25, Рс = 0,8, Сд = 0,08, доверительный уровень составляет 90%, т = 1,71, L = 0,70, U = 0,85
Таким образом, с 90% уверенностью, было установлено , что 0,70 0,85
пример
- Интервал Wald известно для выполнения плохо.
- Wilson оценка интервал обеспечивает доверительный интервал для биномиальных распределений на основе количественных показателей тестов и имеет более широкий охват выборки см и биномиальное интервал доли доверия для более детального обзора.
- Вместо «Уилсон» набрать интервал «интервал Wald», также может быть использовано при условии, что вес выше факторы.
период повторения
Кумулятивная вероятность Pc также можно назвать вероятность непревышения . Вероятность превышения Пе (также называется функцией выживания ) определяется из:
и указывает на ожидаемое число наблюдений, которые предстоит сделать еще раз , чтобы найти значение переменной в исследовании более чем значение , используемое для T .
Верхний ( Т U ) и нижний ( Т л ) доверительные интервалы возврата периодов могут быть найдены , соответственно , как:
Для экстремальных значений переменной в исследовании, U близка к 1 и небольших изменений в U происходят большие изменения в T U . Таким образом, по оценкам , период возврата экстремальных значений подвергаются большой случайной ошибке. Кроме того, доверительные интервалы, задержать для долгосрочного прогнозирования. Для прогнозов на более короткий период, доверительные интервалы U — L и Т U — T L могут быть на самом деле шире. Вместе с ограниченной достоверностью (менее 100%) , используемой в Т-тесте , это объясняет , почему, например, 100-летний ливень может произойти дважды в течение 10 лет.
Строгое понятие возвратного периода на самом деле имеет смысл только тогда , когда это касается зависящего от времени явления, как точка осадков. Период возврата затем соответствует ожидаемому времени ожидания до тех пор , превышения не происходит снова. Период возврата имеет тот же размер, что и время , для которых каждое наблюдение является репрезентативным. Например, когда наблюдения касаются ежедневных дождей, период возврата выражается в дни, и ежегодно ливни это в годах.
Необходимость доверия ремней
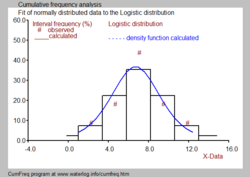
На рисунке показано изменение, которое может произойти при получении образцов в мерном, который следует определенному распределению вероятностей. Данные были предоставлены Бенсоном.
Уверенность пояс вокруг экспериментальной кумулятивной кривой частоты или период возврата дает представление о регионе, в котором истинное распределение может быть найдено.
Кроме того, он уточняет, что экспериментально лучше фитинг распределение вероятностей может отличаться от истинного распределения.
Гистограмма
Наблюдаемые данные могут быть организованы в классах или группах с серийным номером к . Каждая группа имеет нижний предел ( L K ) и верхний предел ( U K ). Когда класс ( к ) содержит м K данные и общее количество данных N , то относительная класса или группы частот определяется из:
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) — результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | — |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).