Утверждение
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
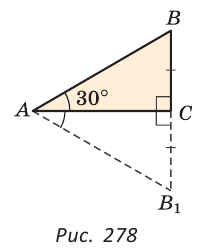
Дано:
∆ ABC,
∠C=90º,
∠A=30º.
Доказать:
Доказательство:
I способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Проведем из вершины прямого угла медиану CF.
Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то
то есть, CF=AF=BF.
Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.
Следовательно, у него углы при основании равны:
∠B=∠BCF=60º.
Так как сумма углов треугольника равна 180º, то в треугольнике BFC
∠BFC =180º -(∠B+∠BCF)=60º.
Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.
Значит, все его стороны равны и
Что и требовалось доказать.
II способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Построим треугольник ADC, равный треугольнику ABC.
В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).
Отсюда, ∠BAD=∠CAD+∠CAB=60º.
Следовательно, в треугольнике ABD все углы равны:
∠BAD=∠D=∠B=60º.
Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.
BC=DC (по построению), поэтому
Что и требовалось доказать.
Преподаватель который помогает студентам и школьникам в учёбе.
Свойство катета прямоугольного треугольника, лежащего против угла в 30°:
Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
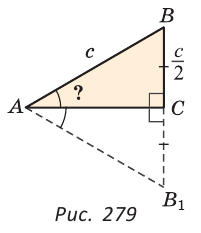
Дано:
Доказать: ВС = 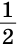
Доказательство:
На луче ВС отложим отрезок СВ1 равный отрезку ВС. Так как 

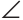

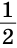
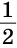
Верно и утверждение, обратное данному. Докажем его.
Теорема. Если в прямоугольном треугольнике катет равен половине гипотенузы, то этот катет лежит против угла в 30°.
Доказательство:
Пусть в треугольнике ABC 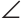
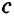
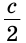
Докажем, что 
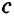


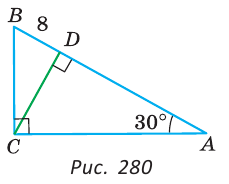
Пример:
В прямоугольном треугольнике ABC, у которого 

Решение:
Так как угол А и угол BCD дополняют угол В до 90°, то 

В прямоугольном треугольнике CDB катет BD лежит против угла в 30°. Поэтому СВ = 2BD = 16 см.
В треугольнике ABC катет ВС лежит против угла в 30°. Поэтому АВ = 2ВС = 32 см.
Отсюда AD=AB-BD = 32 — 8 = 24 (см).
Ответ: 24 см.
Замечание. Мы доказали, что BC = 2BD, AB = 2BC = 4BD, AD = АВ — BD = 3BD, то есть в прямоугольном треугольнике с углом 30° высота делит гипотенузу в отношении 1 : 3.
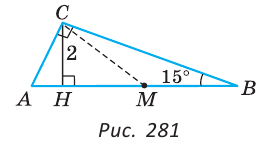
Пример:
Дан прямоугольный треугольник с углом 15°. Высота, проведенная к гипотенузе, равна 2 см. Найти гипотенузу.
Решение:
Пусть в треугольнике ABC 
Нужно найти АВ. Проведем медиану СМ треугольника ABC. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то СМ = MB. Треугольник СМВ — равнобедренный, 


По свойству внешнего угла 


В прямоугольном треугольнике СНМ катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы СМ. Отсюда СМ = 2СН = 4 см, АВ = 2СМ = 8 см.
Ответ: 8 см.
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
- Площадь параллелограмма
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
Содержание
Свойство
Катет прямоугольного треугольника, лежащий напротив угла в
$30^circ$, равен половине гипотенузы.
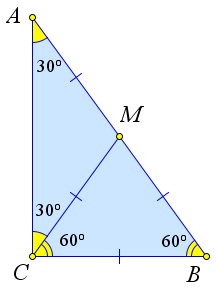
Доказательство
Рассмотрим треугольник $ABC$, в котором $angle C=90^circ, angle A=30^circ$.
Докажем, что $AB=2cdot CB$.
Пусть $CM$ – медиана.
Тогда $CM=MA=MB$, следовательно, $triangle AMC$ и $triangle BMC$ – равнобедренные.
Тогда $angle A=angle ACM$, следовательно, $angle MCB=angle CBM=60^circ$.
Тогда $triangle BCM$ – равносторонний, следовательно, $BC=BM=frac{1}{2}cdot AB$.
Первый признак
Если катет прямоугольного треугольника равен половине гипотенузы, то
угол, противолежащий этому катету, равен $30^circ$.
Доказательство
Рассмотрим прямоугольный треугольник $ABC$, в котором $angle C=90^circ, BC=frac{1}{2}cdot AB$.
Докажем, что $angle A=30^circ$.
Проведем медиану $CM$. Тогда по свойству медианы прямоугольного треугольника $CM = AM = BM$.
Тогда треугольник $CMB$ – равносторонний, а, значит $angle BCM = 60^circ.$
Тогда $angle ACM = 30^circ$.
И поскольку треугольник $ACM$ – равнобедренный, то $angle A = angle ACM = 30^circ.$
Второй признак
Если в треугольнике напротив угла в $30^circ$ лежит сторона, равная
половине другой стороны этого треугольника, то треугольник
прямоугольный.
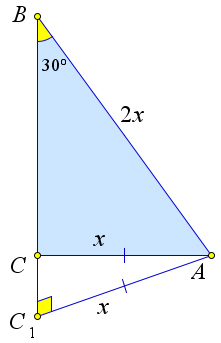
Доказательство
Первый способ.
Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, angle B=30^circ$.
Докажем, что тогда $angle C=90^circ$.
Предположим противное, тогда из точки $B$ можно опустить перпендикуляр $AC_1$ на прямую $CB$.
Треугольник $ABC_1$ – прямоугольный,$angle B=30^circ$, следовательно, $AC_1=x$.
Тогда $triangle CAC_1$ – равнобедренный, и $angle C_1=angle ACC_1=90^circ$, что невозможно.
Значит, $angle C=90^circ.$
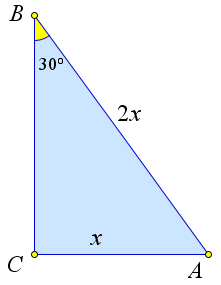
Второй способ.
Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, angle B=30^circ$.
По теореме синусов для $triangle ABC$: $dfrac{x}{sin{30^circ}}=dfrac{2x}{sin{angle C}}$.
Тогда $sin{angle C}=1$, то есть $angle C=90^circ$.
mat:geom:triangle:right
Содержание
Прямоугольный треугольник
Прямоугольный треугольник — треугольник, у которого один из углов – прямой.
Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос», которое означало отвес, перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», — для катетов;
«сторона, стягивающая прямой угол», — для гипотенузы.
В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Мнемоническое правило
Как запомнить где катет, а где гипотенуза, и не перепутать их.
Если сравнить названия сторон прямоугольного треугольника: «катет», «гипотенуза», то видим, что слово «гипотенуза» длиннее слова «катет». Так и в треугольнике: гипотенуза — самая длинная сторона.
Итак, ассоциация: катет — короткое слово, короткая сторона.
Гипотенуза — длинное слово, самая длинная из сторон.
Признаки равенства прямоугольных треугольников:
-
по двум катетам
-
по катету и гипотенузе
-
по катету и прилежащему острому углу
-
по катету и противолежащему острому углу
-
по гипотенузе и остром углу
Признаки подобия прямоугольных треугольников:
-
одному острому углу
-
из пропорциональности двух катетов
-
из пропорциональности катета и гипотенузы
Высота из вершины прямого угла
Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному
Доказательство следует из равенства углов треугольников.
Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике ABC длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной c на отрезки m и n, соответствующие катетам b и a, то
1) $ h^2 = mn $ или $ h = sqrt {mn} $
2) $hc = ab$ или $h = frac {ab} c$
Доказательство следует из подобия треугольников.
Высота есть среднее геометрическое проекций катетов на гипотенузу.
Высота есть произведение катетов, деленное на гипотенузу.
подробнее…
Проще доказать эти соотношения из нахождения косинуса, синуса и тангенса равных острых углов (но для этого нужно знать, что они у равных углов равны, а это вытекает из подобия треугольников. Но запоминается лучше). Для вывода второго соотношения еще можно приравнять площадь треугольника по друм формулам :
половина произведения катетов = половине произведения высоты на гипотенузу
YouTube — Всё про прямоугольный треугольник за 15 минут — Трушин
Сложением двух формул для $sin alpha + sin beta$ получается теорема Пифагора.
Медиана из вершины прямого угла
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы (и наоборот, если медиана равна половине стороны, то эта сторона лежит против прямого угла)
Для доказательства достроить до прямоугольника и посмотреть на диагонали.
Описанная окружность
Центр описанной окружности прямоугольного треугольника совпадает с серединой гипотенузы:

Радиус описанной окружности: $R = frac{c}{2}=m_c$
Катет против угла 30 градусов
Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы

живая модель
Для доказательства достроить до равностороннего треугольника.
Синус, косинус, тангенс, котангенс
В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.
Угол между биссектрисами
Острый угол между биссектрисами острых углов прямоугольного треугольника равен 45°.
легко доказать
· Последние изменения: 2020/02/04 20:29 —
kc
Прямоугольный треугольник и его свойства.
Репетитор по геометрии
+7 916 478 10 32
Прямоугольным треугольником называется треугольник, у которого один из углов равен
90 градусов.
В треугольнике ( ABC ) угол (C ) прямой, то есть он равен 90 градусов.
Треугольник ( ABC ) прямоугольный.
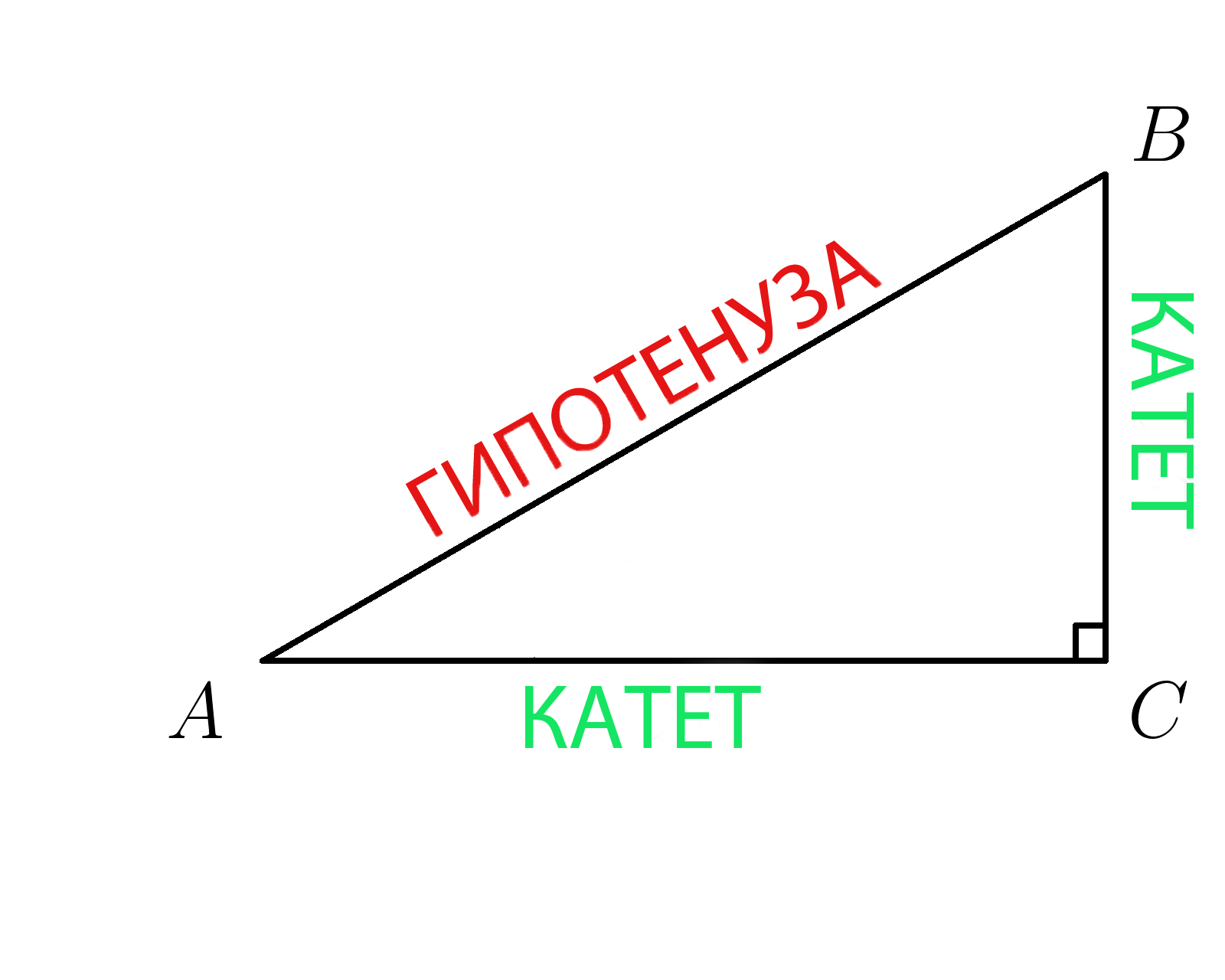
Большая сторона прямоугольного треугольника называется гипотенузой, а две другие катетами.
В прямоугольном треугольнике гипотенуза всегда лежит против прямого угла
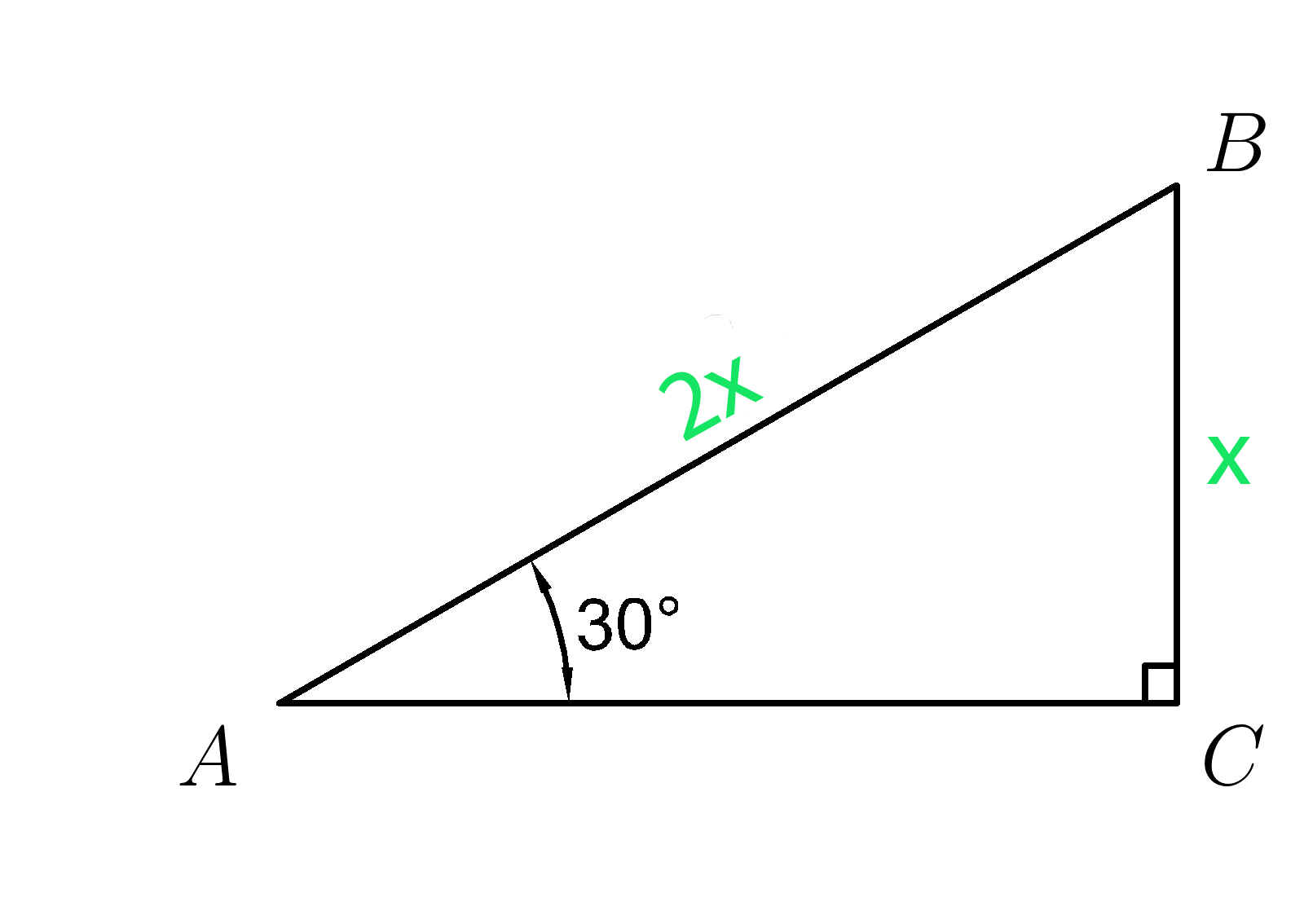
В прямоугольном треугольнике против угла в 30 градусов лежит катет, равный половине гипотенузы
.
В этом треугольнике (ABC ) катет (BC ) в два раза меньше гипотенузы (AB )
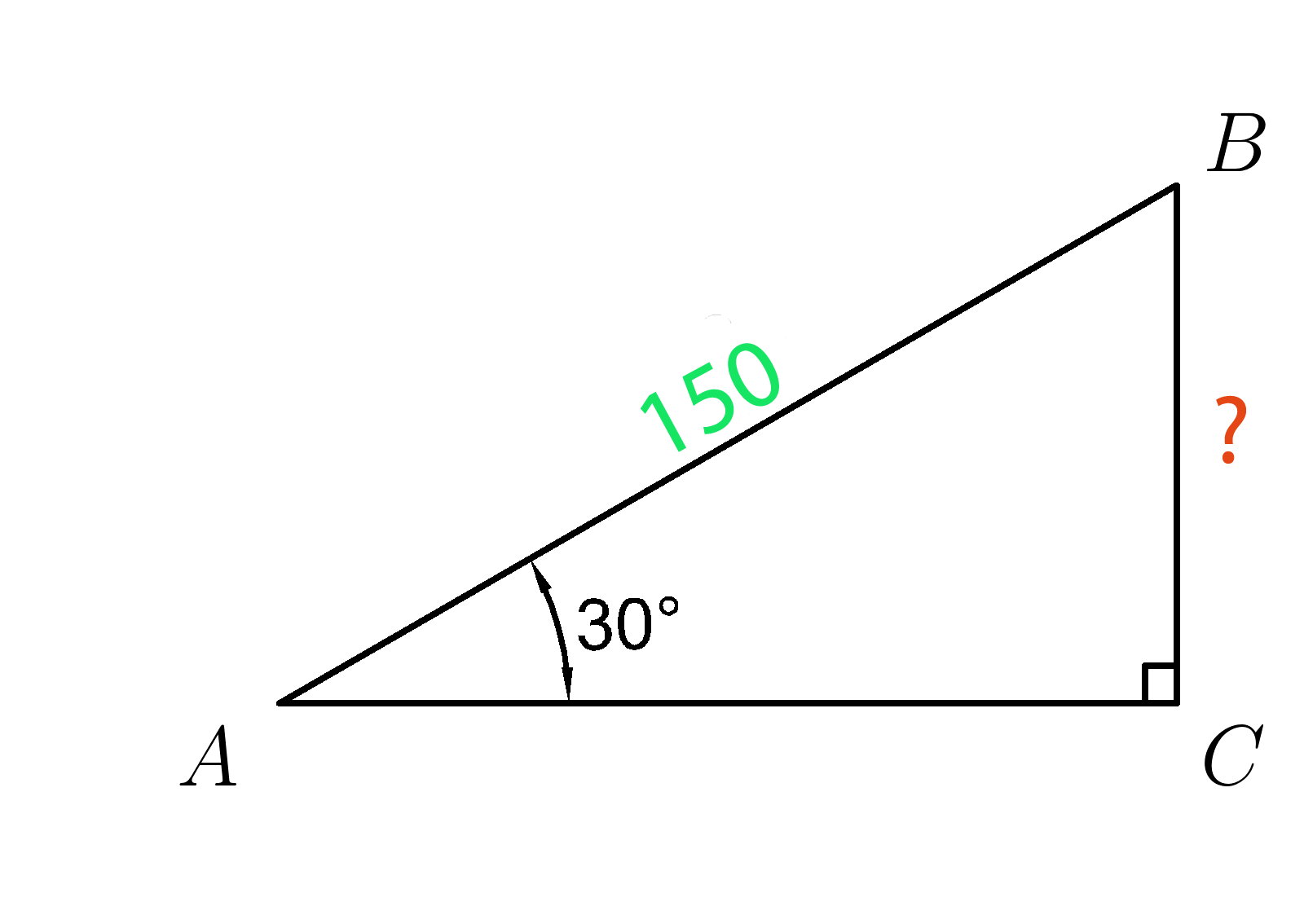
Задача 1
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а гипотенуза (AB=150 см .)
Найдите катет (BC . )
Показать ответ
Показать решение
Видеорешение
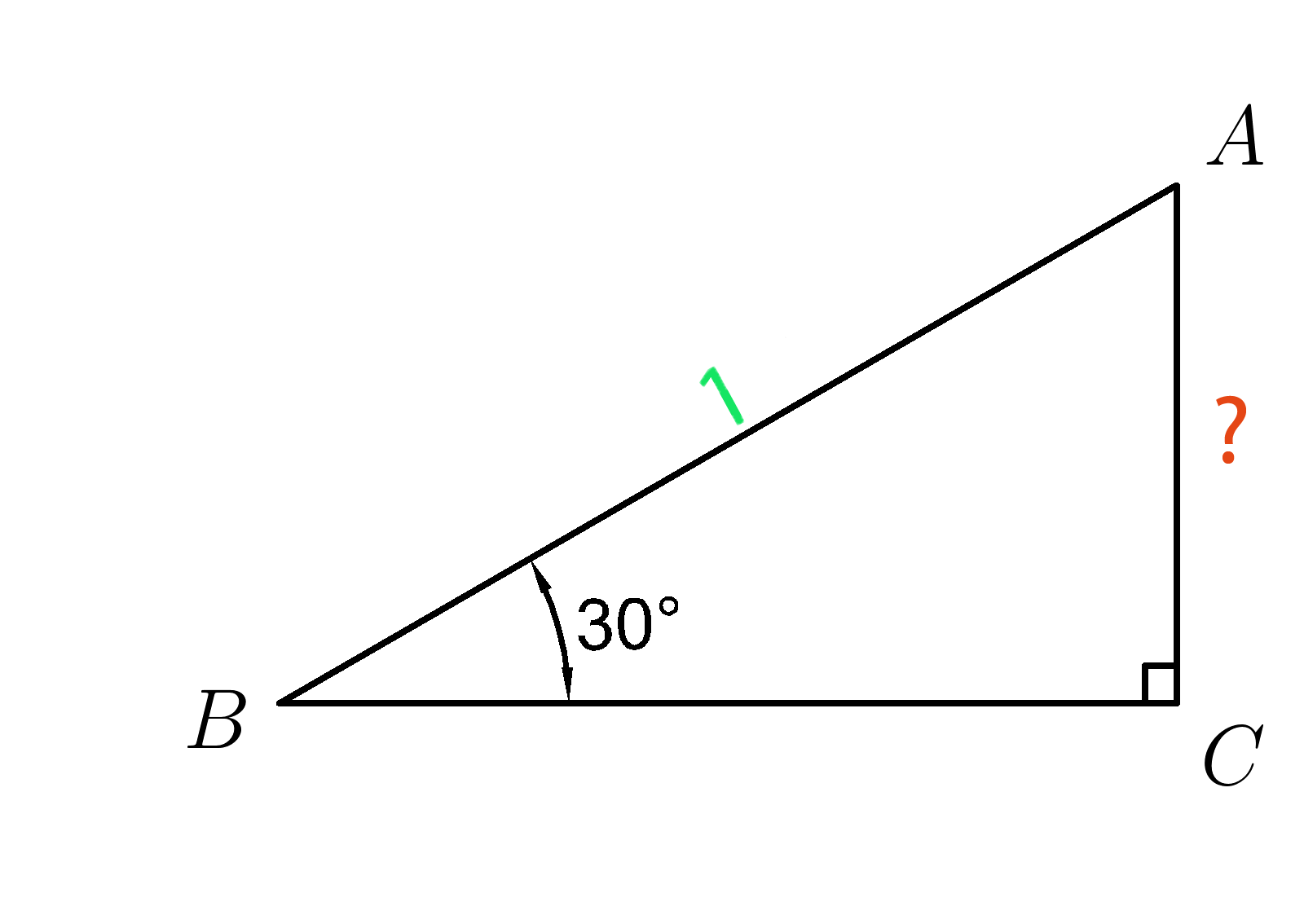
Задача 2.
В прямоугольном треугольнике (ABC ) угол ( B=30^0 ), а гипотенуза (AB=1 .)
Найдите катет (AC . )
Показать ответ
Показать решение
Видеорешение
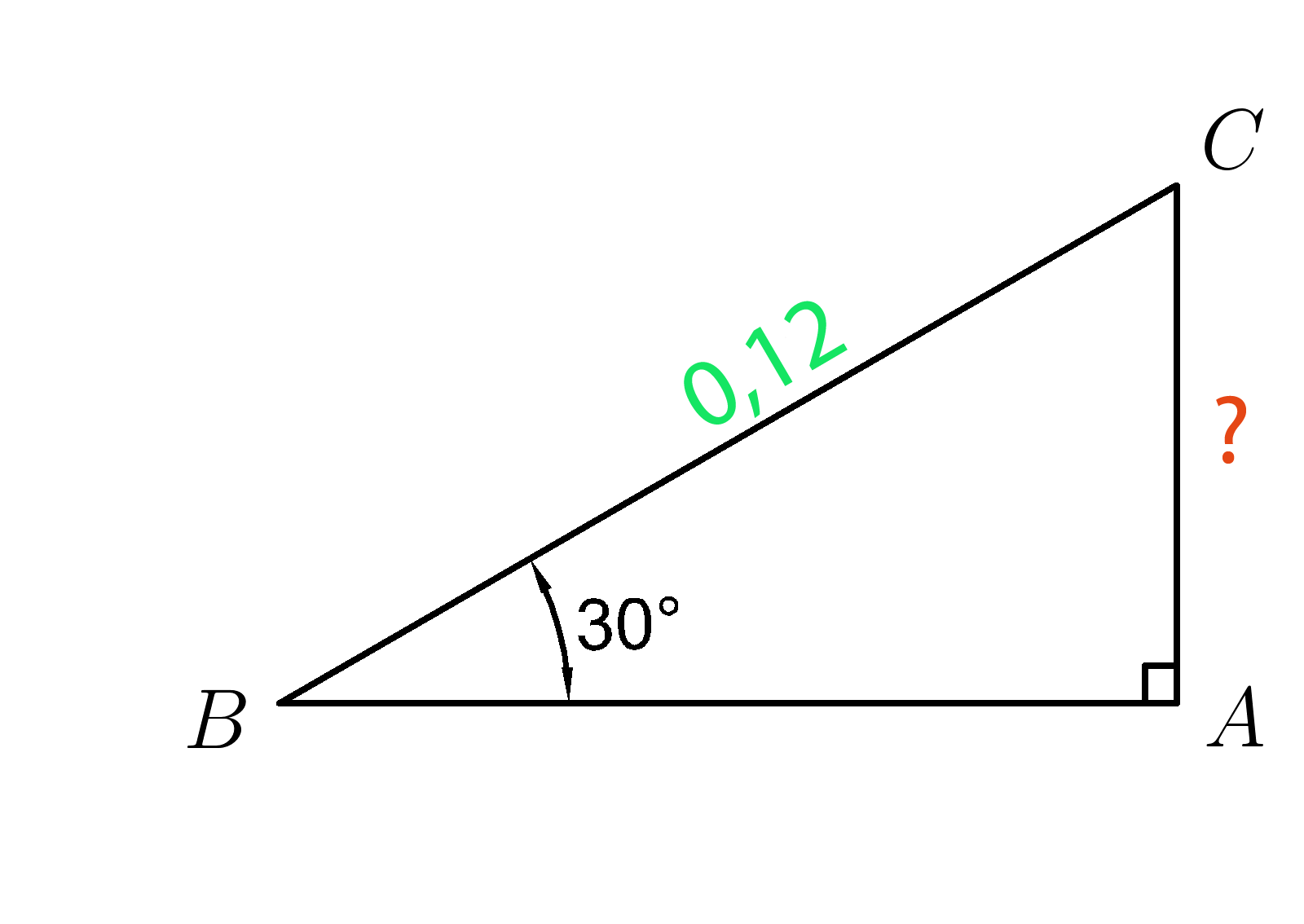
Задача 3.
В прямоугольном треугольнике (ABC ) угол ( B=30^0 ), а гипотенуза (BC=0,12 .)
Найдите катет (AC . )
Показать ответ
Показать решение
Видеорешение
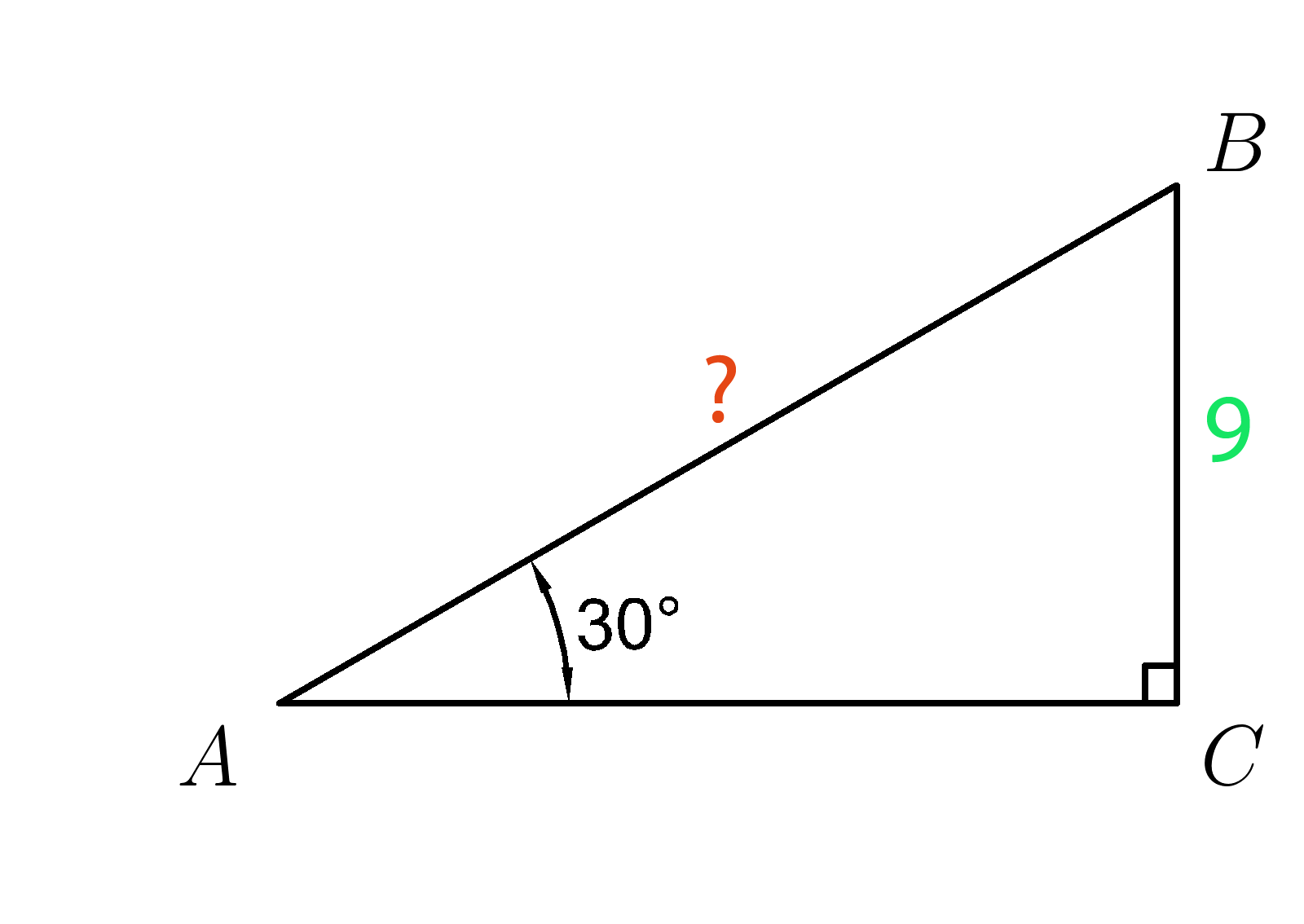
Задача 4.
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а катет (BC=9 .)
Найдите гипотенузу (AB . )
Показать ответ
Показать решение
Видеорешение
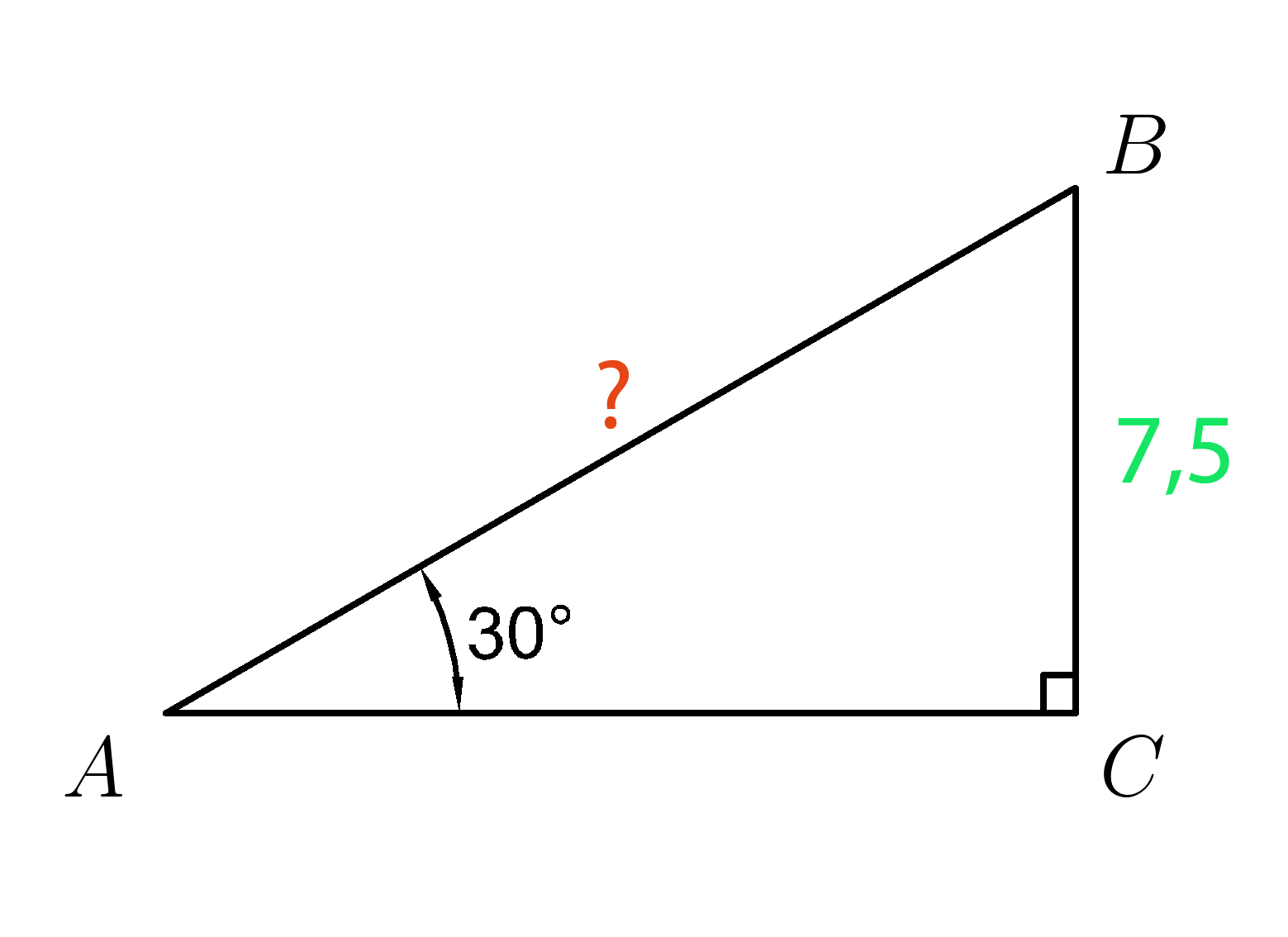
Задача 5.
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а катет (BC=7,5 .)
Найдите гипотенузу (AB . )
Показать ответ
Показать решение
Видеорешение
Задача 6.
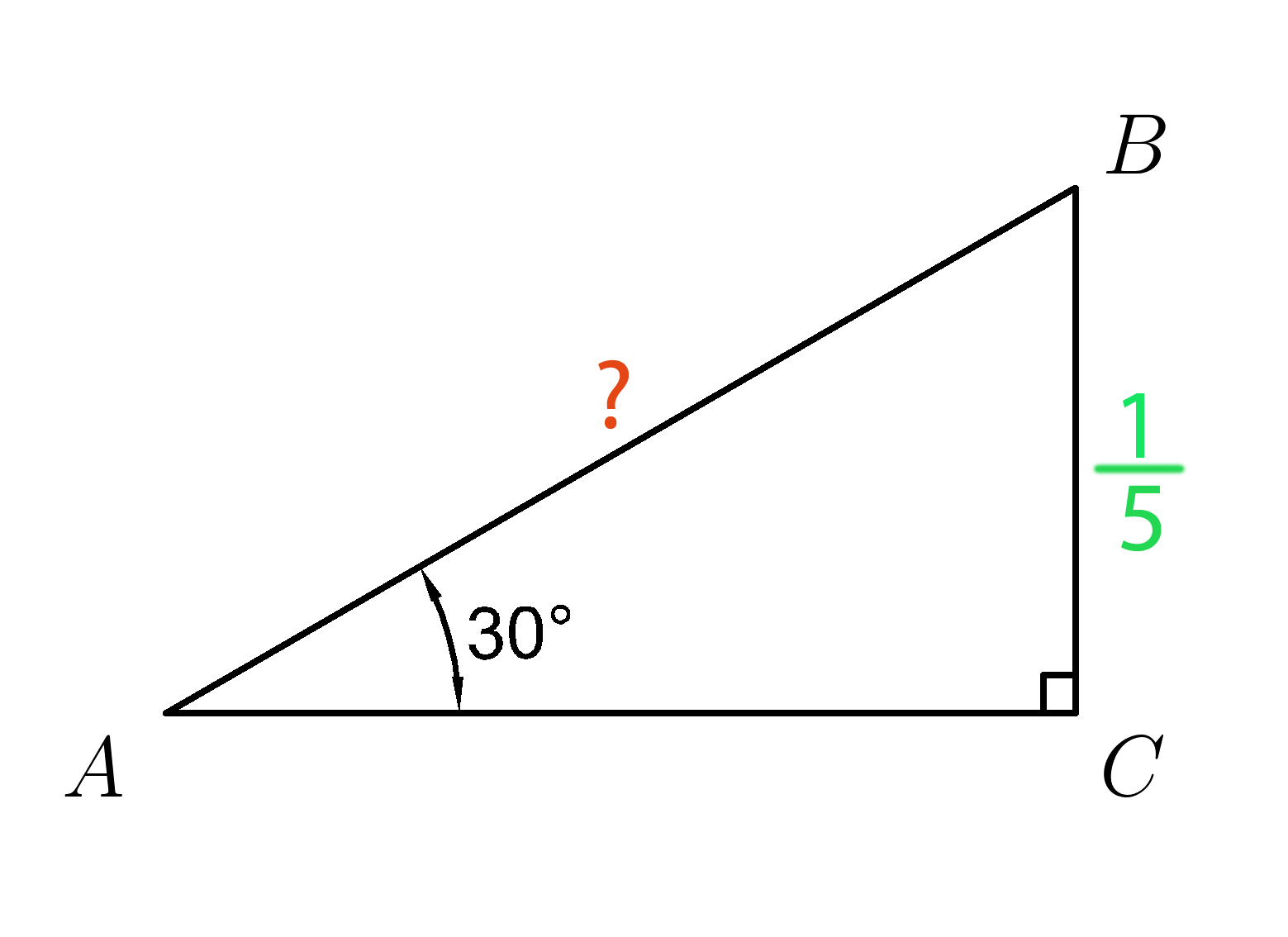
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а катет (BC=dfrac{1}{5} .)
Найдите гипотенузу (AB . )
Показать ответ
Показать решение
Видеорешение
Задача 7.
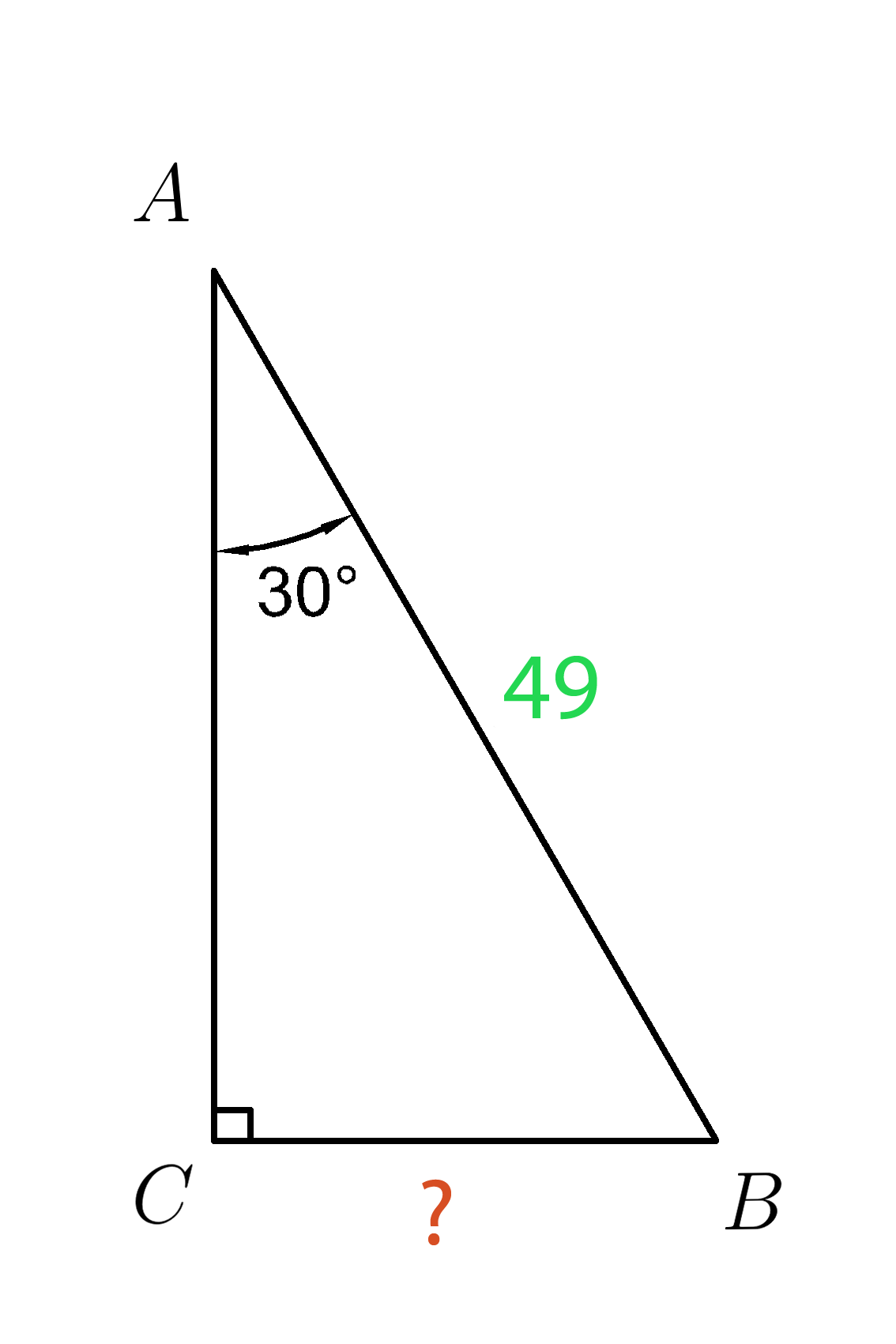
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а гипотенуза (AB=49 .)
Найдите катет (CB . )
Показать ответ
Показать решение
Видеорешение
Задача 8.
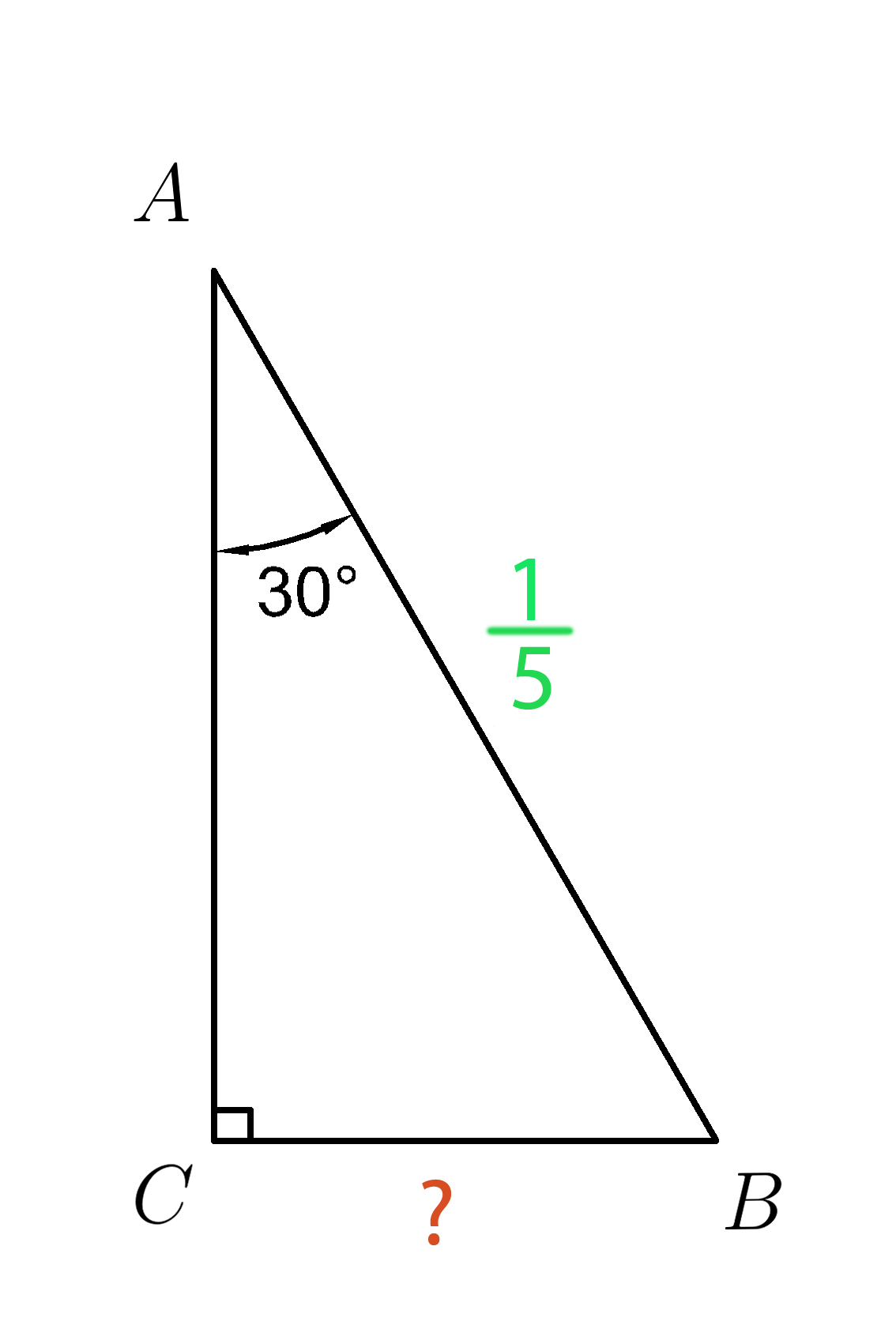
В прямоугольном треугольнике (ABC ) угол ( A=30^0 ), а гипотенуза (AB=dfrac{1}{5} .)
Найдите катет (CB . )
Показать ответ
Показать решение
Видеорешение