Как составить уравнение стороны трапеции - Autoru.top

Задачу можно решить куда легче, если вы введете декартову систему координат, наложите ее на трапецию, приняв за начало координат точку, являющуюся серединой основания трапеции. Далее вы нехитрым способом вычислите координаты всех необходимые точек( с помощью теоремы Пифагора ) и составите уравнения прямых, на которых лежат стороны трапеции.

ссылка

отвечен
23 Окт ’12 20:14

0xFFh
38●1●6

изменен
23 Окт ’12 20:16

10|600
символов нужно
символов осталось

Источник

1 / 1 / 0

Регистрация: 12.12.2014

Сообщений: 61

Написать уравнение сторон равнобедренной трапеции

14.01.2015, 18:25. Показов 10067. Ответов 6

Условие:

Кликните здесь для просмотра всего текста

Написать уравнение сторон равнобедренной трапеции, зная середины ее оснований (1;1), (2;8) и точки
на ее боковых сторонах (4;−3), (− 15;14).

Из этой задачи я смог найти уравнение оснований, зная что нормальный вектор перпендикулярен этим основаниям. А вот как найти уравнения боковых сторон?

3971 / 2950 / 894

Регистрация: 19.11.2012

Сообщений: 6,063

15.01.2015, 07:07

Проще всего так.
1) Проводим срединный перпендикуляр трапеции L: 7х-у-6=0.
2) Строим точки, симметричные заданным, относительно L.
Например, для точки (4,-3) это точка (-3,-2). Значит одна из боковых сторон проходит через две точки (-3,-2) и (-15,14).
3) То же самое для другой боковой стороны.

1 / 1 / 0

Регистрация: 12.12.2014

Сообщений: 61

15.01.2015, 09:08

[ТС]

Идея понятна, но непонятно одно — как вот например вы получили симметричную точку (-3,-2)? Как расчитать её координаты?

3971 / 2950 / 894

Регистрация: 19.11.2012

Сообщений: 6,063

15.01.2015, 09:45

Сообщение от DeStrager

Как расчитать её координаты?

Пусть A — заданная точка, B — симметричная ей относительно прямой L. Тогда вектор AB ортогонален L (первое уравнение), середина отрезка АВ лежит на L (второе уравнение).

1 / 1 / 0

Регистрация: 12.12.2014

Сообщений: 61

15.01.2015, 10:12

[ТС]

Ну ,они оротогональны (AB и L), и как мне из этого получить координаты симметричной точки (-3,-2)?
Может какое то св-во или что то еще есть, я не помню..

3971 / 2950 / 894

Регистрация: 19.11.2012

Сообщений: 6,063

15.01.2015, 14:27

Сообщение от DeStrager

Ну ,они оротогональны (AB и L), и как мне из этого получить координаты симметричной точки (-3,-2)?

Да, уж. Пусть А(4,-3), В(х,у). Тогда АВ=(х-4,у+3). Так как AB и L ортогональны и (1,7) — направляющий вектор L, то
(х-4)+7(у+3)=0. (Это первое уравнение.)

Далее, координаты середины М отрезка АВ равны полусумме координат его концов; отсюда М((х+4)/2,(у-3)/2). Так как М лежит на прямой L, то
7(х+4)/2-(у-3)/2-6=0. (Это второе уравнение.)

Решайте систему для вычисления координат точки В.

6354 / 4062 / 1510

Регистрация: 09.10.2009

Сообщений: 7,550

Записей в блоге: 4

15.01.2015, 14:41

Сообщение от DeStrager

Можно привести формулу в общем виде. Если уравнение прямой задано в общем виде (через нормальный вектор) и есть точка , то нужно знать какую-то точку данной прямой, например, $https://www.cyberforum.ru/cgi-bin/latex.cgi?Mleft(0;-frac{c}{b} right)$ . Тогда точка, симметричная точке А, ищется как $https://www.cyberforum.ru/cgi-bin/latex.cgi?A'=A-2pr_{bar{n}}bar{MA} cdot frac{bar{n}}{left|bar{n} right|}$ .
В вашем случае для прямой и точки берём точку на прямой , тогда $https://www.cyberforum.ru/cgi-bin/latex.cgi?A'=left(-15;14 right)-2frac{left( bar{left(-15;20 right)},bar{left(7;-1 right)}right)}{5 sqrt{2}} cdot frac{bar{left(7;-1 right)}}{5 sqrt{2}}=left(-15;14 right)+5bar{left(7;-1 right)}=left(20;9 right)$ .
P.S. Вообще-то, от точки нельзя отнимать/прибавлять вектор. Если общую формулу записать более канонически, то будет $https://www.cyberforum.ru/cgi-bin/latex.cgi?bar{AA'}=-2pr_{bar{n}}bar{MA} cdot frac{bar{n}}{left|bar{n} right|}$ . Зная начало вектора (А) и найдя сами координаты вектора АА’, легко найти конец A’.

Добавлено через 13 минут
Чтобы не заморачиваться с точкой М на прямой, формулу можно ещё упростить: $https://www.cyberforum.ru/cgi-bin/latex.cgi?A'=A-2 frac{ax_A+by_A+c}{a^2+b^2}bar{left(a;b right)}$

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Как написать уравнение сторон равнобедренной трапеции

Добавлено: 02 окт 2013, 19:38

Начинающий

Зарегистрирован:
02 окт 2013, 19:29
Сообщений: 22
Cпасибо сказано: 3
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Нужна помощь по аналитической геометрии

Как на писать уравнение сторон равнобедренной трапеции, зная середины ее оснований (-1,1) и (1,3) точки на ее боковых сторонах (3,0),(-3,5)?

Вернуться к началу

Zdrastes	Заголовок сообщения: Re: Как на писать уравнение сторон равнобедренной трапеции Добавлено: 02 окт 2013, 21:11
	mad_math писал(а): Вектор, соединяющий середины оснований будет им перпендикулярен. Находите координаты этого вектора и составляете уравнения оснований, как уравнение прямой, проходящей через точку (середина основания) перпендикулярно вектору, соединяющему середины оснований. уравнения оснований составила,не могу найти координаты вектора,соединяющего основания,а следовательно и уравнения боковых сторон,можно поподробнее об этом?
Вернуться к началу

mad_math	Заголовок сообщения: Re: Как написать уравнение сторон равнобедренной трапеции Добавлено: 02 окт 2013, 21:58
	А я-то надеялась, что есть какой-то хитрый ход без использования оси симметрии. Zdrastes писал(а): уравнения оснований составила И что получилось?
Вернуться к началу

Zdrastes	Заголовок сообщения: Re: Как написать уравнение сторон равнобедренной трапеции Добавлено: 02 окт 2013, 22:11
	mad_math писал(а): А я-то надеялась, что есть какой-то хитрый ход без использования оси симметрии. Zdrastes писал(а): уравнения оснований составила И что получилось? y=-x и y=-x-4,но на самом деле,я уже совсем запуталась и не понимаю что делаю,скорее всего это неверно
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Угол наклона боковых сторон равнобедренной трапеции в форуме Начала анализа и Другие разделы школьной математики	neverlucky	5	241	09 янв 2020, 04:48
Как записать уравнение боковых сторон прямоугольной трапеции в форуме Аналитическая геометрия и Векторная алгебра	Root	1	475	15 дек 2013, 16:17
Угол между диогоналями в равнобедренной трапеции в форуме Геометрия	leonidzilb	4	418	29 апр 2015, 22:58
Найти боковую сторону равнобедренной трапеции в форуме Геометрия	wehrwolf	2	478	08 апр 2014, 16:44
Найти длину боковой стороны равнобедренной трапеции в форуме Геометрия	ncux01	1	374	21 дек 2017, 12:12
Даны координаты сторон треугольника, написать уравнение и в форуме Аналитическая геометрия и Векторная алгебра	kity2503	4	572	01 май 2016, 21:16
Написать уравнение сторон треугольника, медианы, высоты и в форуме Геометрия	kity2503	1	752	01 май 2016, 21:14
Построение равнобедренной трапеции — задача на построение в форуме Геометрия	maksim03	15	618	29 апр 2022, 10:25
Написать уравнения сторон треугольника в форуме Аналитическая геометрия и Векторная алгебра	Neyrys	1	324	03 дек 2016, 04:59
Написать уравнения сторон треугольника в форуме Аналитическая геометрия и Векторная алгебра	Iris94	5	575	29 ноя 2018, 08:57

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 7

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

25
Июл 2013

Категория: Справочные материалы

Трапеция. Свойства трапеции

2013-07-25
2016-06-15

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – $k=frac{AD}{BC}.$

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

$S=frac{a+b}{2}cdot h$ или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Автор: egeMax |

комментарий 431

Печать страницы

Источник

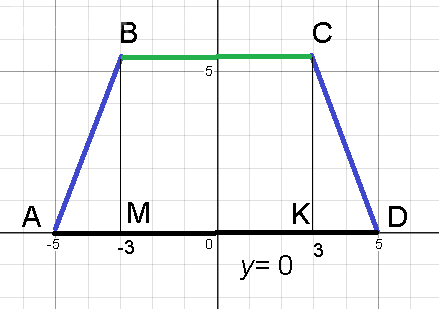
Условие

Записать уравнения прямых, на которых лежат
стороны равнобедренной трапеции, зная, что основания
ее равны 10 и 6, а боковые стороны образуют с большим
основанием угол 60°. Большее основание лежит на оси
абсцисс, а ось симметрии трапеции
на оси ординат.

математика ВУЗ
975

Решение

★

[i]Уравнение прямой [/i]AD:

[b]y=0[/b]

A(-5;0); D(-5;0)

AM=KD=2

BM=CK=2*tg60 ° =2sqrt(3)

BC=6 ⇒

B(-3;2sqrt(3)); C(3;2sqrt(3)) ⇒

[i]Уравнение прямой [/i] BC:

[b]y=2sqrt(3)[/b]

k_(AB)=tg60 ° =sqrt(3)

Уравнение прямой АВ:

y=sqrt(3)x+b

Чтобы найти b подставим координаты точки В

2sqrt(3)=sqrt(3)*(-3)+b

b=5sqrt(3)

[i]Уравнение прямой [/i]АВ:

[b]y=sqrt(3)x+5sqrt(3)[/b]

k_(CD)=tg120 ° =-sqrt(3)

Уравнение прямой CD:

y=-sqrt(3)x+b

Чтобы найти b подставим координаты точки В

2sqrt(3)=-sqrt(3)*(-3)+b

b=-5sqrt(3)

[i]Уравнение прямой [/i]CD:

[b]y=-sqrt(3)x+5sqrt(3)[/b]

Написать комментарий

Источник

Написать уравнение сторон равнобедренной трапеции

Кто сейчас на конференции

Трапеция. Свойства трапеции

Свойства трапеции

Свойства и признаки равнобедренной трапеции

Вписанная окружность

Площадь

Условие

Решение

Написать комментарий

Не пропустите также: