Алгоритмом (algorithm) называют чёткое описание последовательности действий, направленных на решение конкретной задачи. О важности и типах алгоритмических последовательностей сказано уже немало. В этой статье пойдёт речь о способах их представления при записи алгоритмов.
Словесный способ
Словесное описание алгоритма предполагает наличие некого словесного перечня действий. Пример — вам говорят что-то типа следующего: «Вычислите Z при условии, что Z = X + Y, когда X равен 0,89, а Y равен 1,286. Полученное значение Z следует возвести в куб и вычислить корень».
Можно представить ситуацию туристического посещения незнакомого города. Когда вы спрашиваете, как пройти в интересующее место, вам объясняют, что надо через 100 метров повернуть направо, потом пройти прямо, пока не увидите перед собой здание кинотеатра, далее потребуется перейти дорогу, повернуть налево и не сворачивая идти до нужного объекта.
Все эти примеры можно назвать словесным способом представления. У такого способа есть недостаток: отсутствие наглядности выполнения процесса и чёткой формализации объектов алгоритма.
Формульно-словесный способ
При использовании формульно-словесного способа инструкции задаются более чётко. Этот тот случай, когда словесные пояснения сопровождаются перечнем конкретных действий, плюс эти пояснения характеризуются наличием формальных символов и выражений (формул).
Для примера составим формульно-словесный алгоритм вычисления выражения: z=2∙x–(y+6):
• вводим значения х и y;
• находим сумму (y+6);
• находим произведение (2∙x);
• вычисляем z как разность уже полученных выше значений: z=2∙x–(y+6);
• выводим z как результат вычисления выражения.
Это более компактный и лаконичный метод, он нагляднее, но всё же строго формальным не является.
Табличный способ
В случае применения табличного метода алгоритм задаётся в виде входных данных: расчётных форм и таблиц. Способ широко применяется в экономических расчетах. Исходные данные, как и результаты, заносятся в заголовки столбцов используемой таблицы. Простейший пример такого способа представления — та же таблица умножения:
Графический способ
Этот метод ещё называют способом блок-схем. В данной ситуации каждый этап прохождения алгоритма представляется в виде геометрических фигур — так называемых «блоков», причём конкретная форма фигур зависит от выполняемой операции. Существует стандарт, регламентирующий размеры используемых графических блоков, а также их отображение, функции, формы и взаимное расположение. Направление работы алгоритма показывают линии соединения блоков.
Другое название способа — визуальное представление. При проектировании алгоритмов, представленных графически, придерживаются ряда правил:
• в начале алгоритма располагаются блоки ввода значений (входные данные);
• после ввода значений располагаются блоки обработки и блоки условия;
• алгоритм завершается блоками вывода значений, полученных в результате работы алгоритма (выходные данные);
• должен быть лишь один блок начала и один — окончания;
• межблочная связь указывается линиями (направленными либо ненаправленными);
• вычислительные формулы, данные и логические выражения размещаются внутри соответствующих блоков;
• возможно наличие комментариев в виде выносок.
Графический способ представления имеет практическое значение и используется не только в случае программирования. Его применяют при составлении информационных и структурных схем, инфографики и в иных ситуациях, когда нужно обеспечить чёткую визуализацию данных и графически отобразить последовательность расположения объектов алгоритма.
Создание блок-схемы алгоритма — важный и нужный этап решения поставленной задачи. Но при некоторых обстоятельствах этот этап можно считать промежуточным, так как в таком виде описанный алгоритм невозможно выполнить средствами ЭВМ. Зато графический способ представления значительно облегчает процесс дальнейшего создания компьютерной программы. О ней ниже.
Программный способ (текстовая запись)
Программа представляет собой алгоритм, который записан как последовательность команд. Речь идёт о командах, понятных компьютеру, для чего используются различные языки программирования, представляющие собой системы кодирования предписаний с правилами их применения. Языки программирования характеризуются строго определённым синтаксисом, то есть свободное толкование конструкций не допускается.
В случае программного способа представления алгоритмическая последовательность записывается в виде компьютерной программы с высокой степенью формализации. В результате появляется возможность решать прикладные задачи.
Пример — простейший алгоритм сложения 2-ч чисел, который записан средствами языка программирования Qbasic:
О взаимодополнении способов представления
Способы, представленные выше, нередко являются взаимодополняемыми:
— на этапе обсуждения используются словесные и словесно-формульные способы;
— на этапе проектирования рекомендуется использовать графические алгоритмы (графическое представление);
— на этапе проверки возможно табличное описание;
— на этапе непосредственного применения и решения прикладных задач используют текстовую запись, представленную в виде компьютерной программы.
Источники:
• http://csaa.ru/sposoby-predstavlenija-algoritmov-2/;
• https://infourok.ru/konspekt-sposobi-opisaniya-algoritmov-966802.html.
Алгоритмы
имеют несколько форм представления:
словесную, формульно-словесную, табличную,
в виде блок-схем.
Словесная
форма является самой простой и доступной.
Содержание последовательных предписаний
— вычислений задается в произвольной
краткой форме на естественном языке,
не допускающем повторений, неоднозначного
понимания выражений, лишних слов.
Недостаток словесной формы — отсутствие
более или менее строгой формализации
и наглядности вычислительного процесса.
Она не подходит для задач со сложной
логикой и вычислительным процессом и
применима для простых алгоритмов,
отличающихся однократной последовательностью
выполнения предписаний.
Пример:
Записать
алгоритм вычисления y по формуле:
1) умножить x на3;
2) к результату
первого действия прибавить 1;
3) из результата
второго действия извлечь корень;
4) умножить x на x;
5) из результата
четвертого действия вычесть 3;
6)
результат пятого действия разделить
на результат третьего. Полученный
результат считать значением y.
Формульно-словесный
способ основан на задании предписания
алгоритма с использованием математических
формул и словесных пояснений. Формулы
в сочетании с правилами их написания
представляют собой алгоритмический
язык, применимый для задания вычислительных
алгоритмов. Этот способ более нагляден
и компактен по сравнению со словесным.
Однако формула устанавливает
последовательность действий неоднозначно,
т.е. не совсем полно отражаются свойства
детерминированности и определенности.
Пример:
Выражение
задает
объем усеченного конуса. Здесь h-высота,
R и r — соответственно радиусы нижнего и
верхнего основания.
Табличная
форма записи.
Существует несколько типов таблиц.
Первый используется при организации
вычислений по формуле с пооперационной
регистрацией промежуточных результатов.
Разбиение формулы на последовательность
элементарных действий дает последовательность
предписаний. Такая форма наиболее
применима тогда, когда требуется
вычислить несколько значений одного
выражения для различных значений входных
величин.
Пример: Для предыдущей формулы составим табличную запись алгоритма (рис. 3.1)
-
R
r
H
h
1/3h
R2
Rr
r2
R2+Rr+r2
V
Рис.3.1. Табличная
запись алгоритма
Второй тип таблицы
называется решающей
таблицей. В простейшем случае она
включает 4 части: перечень условий,
указатель условий, перечень действий,
указатель действий (рис.3.2).
Перечень
условий содержит все условия, а перечень
действий — все действия, проверка и
выполнение которых необходимы в процессе
решения задачи. Они располагаются одно
за другим; в строке записывается только
одно условие или действие. Правая часть
делится на несколько столбцов, в которых
определяется, какие условия следует
проверить, а какие действия следует
выполнить в результате проверки этих
условий. На пересечении соответствующих
столбцов и строк ставится Y в том случае,
если условие должно выполняться, N — если
нет и «-«, если условие не учитывается.
|
Номер таблицы |
1 |
2 |
3 |
|
k |
||
|
Перечень условий |
Условие 1 |
Y |
N |
Y |
|
N |
Указатель условий |
|
Условие 2 |
— |
Y |
Y |
|
N |
||
|
|
|
|
|
|
|
||
|
Условие |
Y |
— |
Y |
|
— |
||
|
Перечень действий |
Действие 1 |
X |
X |
|
Указатель действий |
||
|
Действие 2 |
X |
|
X |
||||
|
|
|
|
|
|
|
||
|
Действие |
X |
X |
|
X |
Рис.3.2.
Общий вид решающей таблицы
Когда
условие требует выполнения некоторого
действия, то на пересечении соответствующих
столбцов и строк, ставится символ X. В
случае отсутствия действия позиция
остается незаполненной.
Если
условие формируется так, что возможны
два ответа, «да» — «нет» или «Y»
— «N», то таблицы называются таблицами
с ограниченными
входами. Если ответов несколько, то
таблицы называются таблицами с
расширенными
входами. При этом простое условие
записывается так же, как и в таблицах
первого вида, сложные действия
распределяются между столбцами.
Пример:
Алгоритм
поиска HOD в виде решающей таблицы с
расширенными входами показан в таблице
3.2.
Таблица 3.2.
|
Таблица № 0001 |
1 |
2 |
3 |
|
Условие проверки |
a |
a |
а |
|
a |
X |
||
|
b |
X |
||
|
Перейти к началу |
X |
X |
|
|
НОД |
X |
||
|
Конец |
X |
Блок-схемой
называется графическое изображение
алгоритма, дополненное элементами
словесной записи, в котором каждое
предписание алгоритма представляется
в виде геометрического символа, имеющего
определенную конфигурацию в зависимости
от характера выполняемой операций или
отображаемой функций.
Для
однозначного обозначения одинаковых
процедур формы, размеры и правила
оформления определены ГОСТ 19.003-80 «Схема
алгоритмов и программ. Обозначения
условные и графические» и ГОСТ 19.002-80
«Схема алгоритмов и программ. Правила
оформления».
Наиболее
употребительные символы приведены в
табл. 3.3.
При
начертании символов их размеры выбираются
кратными 5, размер (а) равным 10,15,20….
размер (b) составляет b=1,5a.
Табл.
3.3
|
№ п/п |
Название Символа |
Обозначения и размеры |
Отображаемые Функции |
|
1 |
Процесс |
Выполнение |
|
|
2 |
Решение |
Выбор |
|
|
3 |
Модификация |
Выполнение |
|
|
4 |
Типовой процесс |
Вычисления |
|
|
5-6 |
Данные |
Ввод |
|
|
7 |
Документ |
Вывод, |
|
|
8 |
Перфокарта |
Ввод |
|
|
9 |
Процессор (оперативная память) |
Операция |
|
|
10 |
Магнитный диск |
Ввод |
|
|
1 |
Магнитная |
a |
Ввод |
|
1 |
Пуск |
Начало, |
|
|
1 |
Линии |
Указание |
|
|
13 |
Соединитель |
Указание связей |
|
|
|
Межстраничный |
Указание |
Последовательность
выполнения пунктов алгоритма, описываемого
блок-схемой, устанавливается путем
упорядоченного размещения блоков на
схеме и объединение их линиями потока.
Нормальное направление линии потока —
сверху вниз и слева направо. Линии
проводятся строго вертикально и
горизонтально и завершаются на середине
символа. Если направление потока
совпадает с нормальным — стрелки не
ставятся, если в противоположном
направлении — стрелки ставятся. В месте
слияния линии потока ставится точка. В
месте пересечения линии потока точка
не ставится (рис.3.3).
В
символа «Решение» помечаются
символами «да»/»нет»- т.е.
выполняется или не выполняется условие.
Условие записывается внутри символа
(рис.3.4). Содержание надписи внутри
символа или рядом должно быть кратким,
без сокращений, за исключением допустимых
сокращений. Записи представляются так,
чтобы их можно было читать слева направо,
сверху вниз.
Для
удобства нахождения символа задаются
их координаты в виде цифр, букв или цифр
и букв. Они представляются сверху слева
в разрыве контура (рис.3.5).
Б
является исключительно наглядным и
простым способом представления алгоритма.
При этом нет никаких ограничений степени
детализации в его изображении. Если
блок-схема получается очень сложной и
теряет свойства иллюстративности,
вначале составляют укрупненную блок-схему
всего вычислительного процесса, затем
каждый ее блок представляется отдельной
блок-схемой.
Для блок-схем
обязательны следующие правила: каждый
блок имеет только один вход и выполнение
описанных в них действий всегда начинается
с первого; входить в середину блок-схемы
нельзя. Вход в блок-схему обозначается
символом «начало», заканчивается
блок-схема символом «конец».
Соединители
в разрыве линии обозначаются общим
идентификатором, в качестве которого
может использоваться цифра, буква или
буква и цифра (рис.3.6).
М
соединитель маркируется двумя строками
символов: первая строка определяет
лист, вторая является идентификатором
самого соединения (рис.3.7).
В
качестве примера рассмотрим блок-схему
алгоритма Евклида нахождения НОД двух
чисел (рис.3.8).
С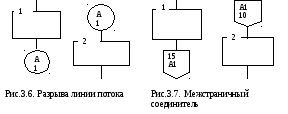
схема записи алгоритма. При операторном
способе записи алгоритма каждое
предписание (процедура) обозначается
определенным символом-оператором.
Операторы записываются построчно в
порядке их выполнения. В зависимости
от своего назначения операторы делятся
на действующие, логические и варьирующие.
Действующие
осуществляют непосредственно
вычислительные и другие преобразующие
операции над информацией.
Логические
описывают условия, от которых зависит
направление решения.
Варьирующие
предусматривают изменение вспомогательных
величин, называемых параметрами. Обычно
параметры являются либо номерами
изменяемых объектов, носящих одинаковые
номера (массивы), либо номерами операторов,
по какой-то причине объединенных в одну
группу.
Полная
последовательность операторов, задающая
весь процесс решения, называется схемой
решения. Операторы на схеме обычно
обозначаются условными (стандартными)
символами. Наиболее употребительными
являются следующие:
Nо — начало процесса;
В — ввод исходных
данных;
D(A) — действующий
(арифметический);
Р — логический;
V — варьирующий;
W — оператор печати
(вывода);
E — оператор останова.
Знаки
переходов имеют вид полускобок с
числовыми индексами. Левыми полускобками
3
5
указывается передача управления. Правая
нижняя полускобка указывает прием
управления 3
5,
она может соответствовать как верхнему,
так и нижнему знакам передачи управления
Соответствие определяется равенством
числовых индексов После логического
оператора могут стоять верхняя и нижняя
полускобка передачи управления. Верхняя
полускобка соответствует » да «,
т.е. выполнению условия. Нижняя полускобка
соответствует невыполнению условия,
т.е. » нет » Р ( а > б ) 3
5.
Операторы
получают номера индексов согласно
порядка их действия. Если оператор
зависит от параметров, например i, j, то
он обозначается так
и т.д. Условие записывается в виде
функции, где в скобках указывается
соответсвующее условие. Варьирующие
изменяют параметры V ( i,j ). Операторная
схема алгоритма Евклида имеет вид:
N0
B1
(a,b)
1
P1(а>b)2
P2(b>a)
3
4 2
D1(а=a-b)
1 3
D2
(b=b-a)1
4
D3(НОД=а(b))W1
E1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
(рекомендуется для учащихся 4-х классов)
Тема занятия: «Табличный способ записи алгоритма на примере задачи о стиральной машине».
Цель занятия:
1. Научить составлять алгоритм в виде таблицы.
2. Развитие логического мышления с помощью поставленной задачи в задании «Стиральная машина».
План занятия:
1. Организационный момент.
2 Повторение понятия «алгоритм».
3. Постановка задачи: наполнить водой стиральную машину.
4. Составление алгоритма заполнения стиральной машины водой в виде таблицы.
5. Игра буддийских монахов на компьютере.
6. Подведение итогов.
На уроке используется цветная таблица «Стиральная машина». На ней изображена стиральная машина, в которой:
1) Слишком мало воды.
2) Слишком много воды.
Таблица, в которой с помощью кнопок (синей и красной) показан порядок действий для наполнения стиральной машины водой (10 л).
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
+3 |
+3 |
+3 |
+3 |
-2 |
№1.
В машину вмещается 10 л воды. У неё есть две кнопки — красная и синяя. Если нажать на красную, то в машину наливается 3 л воды, а если на синюю, то выливается 2 л воды. В какой последовательности надо нажимать на кнопки, чтобы налить полную машину воды?
Учитель: Что произойдёт, если наполнить так, как записано в таблице.
Ученик: При составлении алгоритма допущена ошибка – вариант «слишком много воды».
Учащимся предлагается найти ошибку и объяснить её.
Учитель: Самостоятельно составьте правильный алгоритм в виде такой же таблицы для заполнения стиральной машины водой в тетрадях.
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
+3 |
+3 |
+3 |
-2 |
+3 |
№2.
Учитель: Чем отличаются алгоритмы №1 и №2?
Правильность составления алгоритма проверяем у доски, обсуждая в классе. Отмечаю наиболее активно работавших учащихся.
Игра буддийских монахов – «Ханойская башня».
Давайте поиграем в игру буддийских монахов, установленную на компьютере.
Игра заключается в следующем: на подставке закреплены три стержня. На левый стержень нанизано несколько колец разного размера – внизу самое большое кольцо, на нём поменьше, сверху ещё меньше и т.д. Надо, перемещая по одному кольцу со стержня на стержень, надет все кольца на правый. Как надо перекладывать кольца, если на левом стержне:
1. два кольца
2. три кольца
3. четыре кольца
После выполнения задания предлагается учащимся заполнить таблицу в рабочих тетрадях:
Вариант 1 (два кольца).
|
№ команды |
№ стержня, с которого снимается кольцо |
№ стержня, на который одевается кольцо. |
|
1. 2. |
Вариант 2 (три кольца).
|
№ команды |
№ стержня, с которого снимается кольцо |
№ стержня, на который одевается кольцо. |
|
1. 2. 3. 4. 5. 6. 7. |
Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.
На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.
Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.
Содержание:
- Элементы блок-схем алгоритмов
- Примеры блок-схем
- Нужны ли блок-схемы? Альтернативы
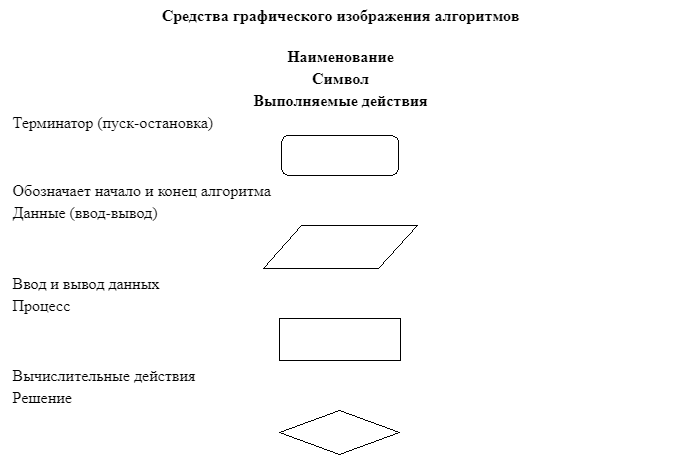
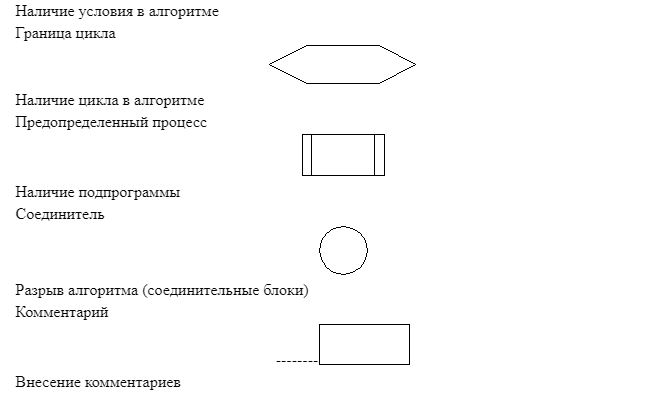
Элементы блок-схем алгоритмов
Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.
Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.
 |
Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора. |
 |
В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях. |
 |
В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций. |
 |
Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной. |
 |
Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями. |
 |
Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while). |
 |
Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком. |
 |
В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно. |
 |
Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией. |
Примеры блок-схем
В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.
Сортировка вставками
Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.
На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.
В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.
На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.
Сортировка пузырьком
Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.
На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.
Сортировка выбором
В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).
На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .
На блоге можно найти другие примеры блок-схем:
- блок-схема проверки правильности расстановки скобок арифметического выражения [2];
- блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].
Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.
Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.
Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.
Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.
Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.
Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.
В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].
В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].
Список использованных источников:
- ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документации».
- Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
- Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
- yEd Graph Editor https://www.yworks.com/products/yed
- Книги: алгоритмы https://pro-prof.com/books-algorithms
- Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
- Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
- Визуальный язык ДРАКОН https://drakon.su/
- Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
- Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.
На практике применяются алгоритмы следующих типов:
Линейные алгоритмы
Это алгоритмы, у которых последовательность операций при исполнении совпадает с порядком их следования в записи алгоритма и не зависит от конкретных значений исходных данных. С помощью таких алгоритмов реализуются задачи типа:
Y = А*Х+В
разветвляющиеся, ветвящиеся алгоритмы. Такие алгоритмы
используются для решения задач, в которых заложена операция выбора одной из формул, в зависимости от заданного
значения переменной. Такие алгоритмы используются при
решение задач, типа:
Y=Ln x, при x>=1
Y=1-x, при x<1
Циклические алгоритмы
Используются в случаях, когда приходится многократно повторять одни и те же действия. Такие алгоритмы используются при решении задач, типа
Y=A-Xn
Для записи алгоритмов обычно используют табличный, словесный и схематичный способы записи.
Табличный способ записи алгоритмов
Табличный способ записи алгоритмов применяется, когда требуется вычислить не одно, а несколько значений одного и того же выражения для различных значений входных величин.
Например, требуется вычислить площадь поверхности цилиндрического тела по формуле:
S=3.14*(D*H+D2 /2)
где D — диаметр, Н — высота.
Табличный алгоритм вычисления площади поверхности тела по указанной формуле представлен в таблице:
| D | H | 3.14*D | 3.14*D2 | 3.14*D2/2 | 3.14*D*H | S |
|---|---|---|---|---|---|---|
| 6 | 4 | 18,84 | 113,04 | 56,52 | 75,36 | 131,88 |
| 5 | 10 | 15,7 | 78,5 | 39,25 | 157 | 196,25 |
| 10 | 12 | 31,4 | 314 | 157 | 376,8 | 533,8 |
Словесный способ записи алгоритмов
Одна из самых распространенных форм представлении алгоритмов — словесная форма. Особенностью словесной представления алгоритма является то, что таким cnocoбом могут быть описаны любые алгоритмы, в том числе и вычислительные.
Опишем последовательность действий для вычислений по формуле:
Y=(6*x+25)/2.
1) Прочитаем заданное значение X;
2) Умножим X на 6;
3) К результату второго действия прибавим 25;
4) Результат третьего действия разделим на 2;
5) Запишем значение результата Y;
6) Конец.
В результате получили словесную запись линейного вычислительного алгоритма.
В приведенном вычислительном алгоритме X является входной величиной (исходным значением, аргументом), а Y выходной величиной (результатом).
В словесной записи алгоритма, если при исполнении текущего предписания не указывается явно номер очередного предписания, происходит автоматический переход к предписанию, следующему за данным в порядке возрастания номеров.
После исполнения предписания с наибольшим номером, процесс выполнения алгоритма заканчивается.
Для удобства рекомендуется заканчивать запись словес о алгоритма специальным предписанием «конец».
При записи вычислительных алгоритмов удобно использовать специальный знак присваивания :=. Этот знак используется для записи специальной операции операции присваивания. Смысл операции присваивания состоит в том, что некоторой переменной, имя которой указывается слева, присваивается значение некоторого выражения, указанного справа.
Например, предписание, вида Y:=X читается так: «переменной Y присвоить значение X». Если X — является формулой, тогда нужно выполнить все действия, предусмотренные формулой и полученный результат (число) присвоить переменной Y.
Операция присваивания может быть обозначена и обычным знаком равенства или стрелками: A:=D*B, A=D*B, A->D*B.
Используя знак операции присваивания и вспомогательные переменные, в которых будут запоминаться промежуточные значения, можно сделать запись приведенного выше словесного алгоритма значительно компактнее:
1) Чтение X;
2) А:= X * 6;
3) В:= А + 25;
4) Y:=B/2;
5) Запись Y;
6) Конец.
После составления словесного алгоритма необходимо провести контроль правильности составления алгоритма. Проверка алгоритма в таблице состоит в том, что выбираются конкретные исходные данные и составленный алгоритм выполняется в строгом соответствии с записанными предписаниями.
Таблица контроля правильности алгоритма вычисления Y=(6*X+25)/2
| Шаги алгоритма | Аргумент X |
Промежуточная величина А | Промежуточная величина B | Результат Y |
Пояснения |
| 1 | 2 | чтение X | |||
| 2 | 12 | ||||
| 3 | 37 | ||||
| 4 | 18.5 | ||||
| 5 | запись 18.5 | ||||
| 6 | остановка |
Важное свойство операции присваивания состоит в том, что одна и та же переменная может находиться и слева и справа от знака присваивания, т.е. можно записать
А := А+В.
Такая запись означает, что к значению переменной А, которое она имела до начала выполнения операции присваивания, прибавляется значение переменной В и полученное в результате значение присваивается переменной А (становится новым значением переменной А). Прежнее значение переменной А при этом пропадает.
Используя это свойство операции присваивания, можно отказаться от использования избыточных промежуточных переменных.
Тогда запись алгоритма вычисления Y будет иметь следующий вид:
1) Чтение X;
2) Y:= X * 6;
3) Y:= Y + 25;
4) Y:=Y/2;
5) Запись Y;
6) Конец.
В приведенном примере можно не использовать ни одной вспомогательной переменной, т.к. для хранения промежуточных результатов достаточно использовать одну переменную Y.
Таблица проверки правильности алгоритма наглядно показывает механизм проведенных присваиваний.
Таблица контроля правильности алгоритма вычисления Y=(6*x+25)/2 без избыточных вспомогательных переменных
| Шаги алгоритма | Аргумент X | Результат Y | Пояснение |
|---|---|---|---|
| 1 | 2 | чтение X | |
| 2 | |||
| 3 | |||
| 4 | 18.5 | ||
| 5 | запись 18.5 | ||
| 6 | остановка |













 1
1 2
2 2
2
 14
14



