Как составить судоку имеющую единственное решение формула

Алгоритм генерации судоку

Доброго времени суток!

Думаю, головоломка Судоку не нуждается в представлении. Многие из нас проводят за её решением достаточно много времени. Например, когда нужно убить время в дороге или просто поворочать мозги, чтобы не сохли. На хабре есть довольно много постов о решении головоломки. Но когда человек решает с десяток, а может и сотню головоломок, то найдётся пытливый ум, который задаст себе вопрос «А как же получается таблица Судоку, имеющая единственное решение? И как можно описать алгоритм для сетки 9×9?».

Приведённый алгоритм является вполне логичным. Но моей задачей было описание и реализация. Обо всём этом написано под катом.

Шаг 1. Взять за основу базовую сетку

Сетка должна подчинятся правилам Судоку. Размещаем в первую строку 1 2… 8 9, в строках ниже смещаем на 3 позиции влево, т.е. 4 5… 2 3 и 7 8… 5 6.
Далее переходя в следующий район по вертикали смещаем на 1 позицию влево предыдущий район.

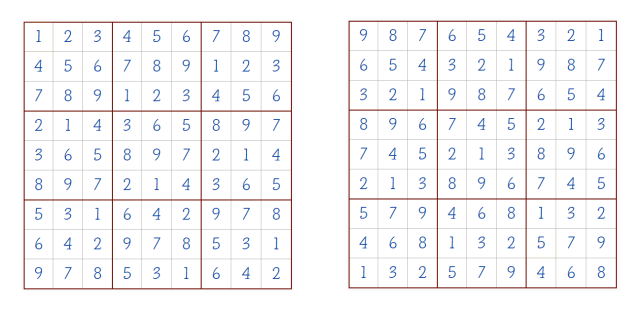
В итоге должна получиться вот такая сетка, её я и назову базовой:

Для реализации создадим класс grid. Заполним его в соответствии с Шагом 1, в котором table — список значений таблицы, метод show — просто наглядный вывод таблицы.

class grid:
	def __init__(self,n = 3):
		"""Generation of the base table"""
		self.n = n
		self.table = [[((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)]
		print "The base table is ready!"

	def __del__(self):
		pass
	
	def show(self):
		for i in range(self.n*self.n):
			print self.table[i]

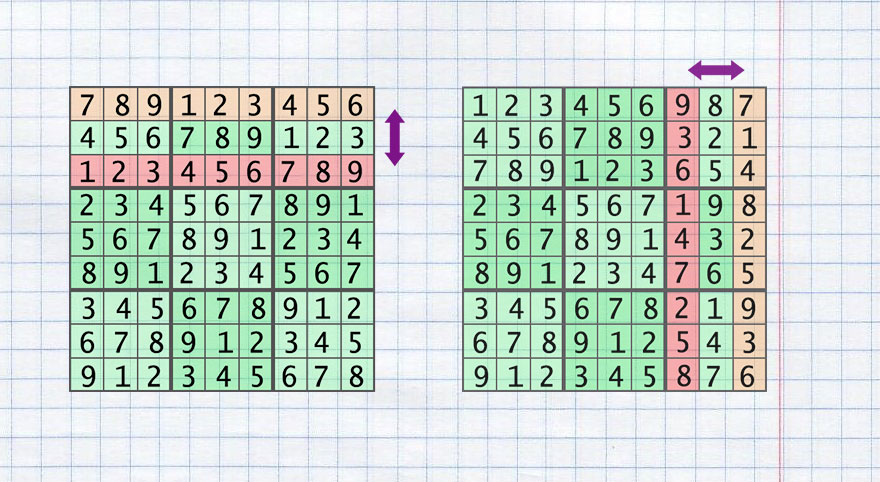
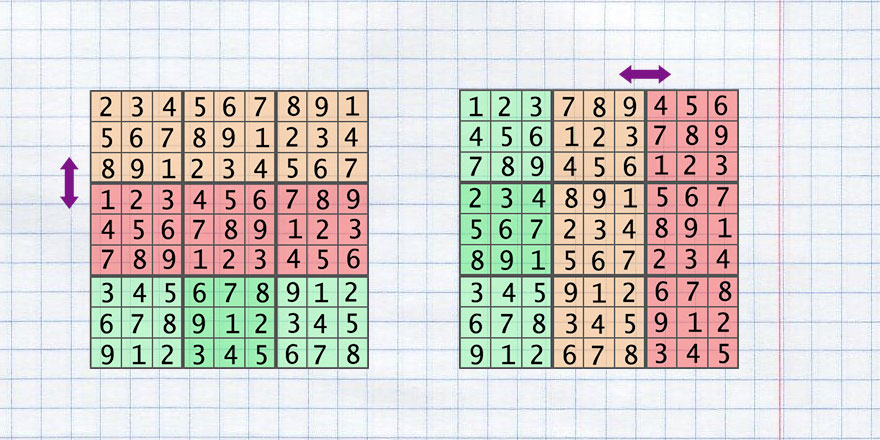
Шаг 2. Перетасовать сетку

Есть несколько видов перестановок, выполнив которые таблица Судоку останется в допустимом состоянии.
К ним относятся:

• Транспонирование всей таблицы — столбцы становятся строками и наоборот (transposing)

• Обмен двух строк в пределах одного района (swap_rows_small)
• Обмен двух столбцов в пределах одного района (swap_colums_small)

• Обмен двух районов по горизонтали (swap_rows_area)
• Обмен двух районов по вертикали (swap_colums_area)

Для каждой из перестановок напишем метод:

transposing

	def transposing(self):
		""" Transposing the whole grid """
		self.table = map(list, zip(*self.table))

swap_rows_small

	def swap_rows_small(self):
		""" Swap the two rows """
		area = random.randrange(0,self.n,1)
		line1 = random.randrange(0,self.n,1)
		#получение случайного района и случайной строки
		N1 = area*self.n + line1
		#номер 1 строки для обмена

		line2 = random.randrange(0,self.n,1)
		while (line1 == line2):
			line2 = random.randrange(0,self.n,1)

		N2 = area*self.n + line2
		#номер 2 строки для обмена

		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]

swap_colums_small

Для обмена столбцов можно поменять строки у транспонированной таблицы:

	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_small(self)
		grid.transposing(self)

swap_rows_area

	def swap_rows_area(self):
		""" Swap the two area horizon """
		area1 = random.randrange(0,self.n,1)
		#получение случайного района

		area2 = random.randrange(0,self.n,1)
		while (area1 == area2):
			area2 = random.randrange(0,self.n,1)

		for i in range(0, self.n):
			N1, N2 = area1*self.n + i, area2*self.n + i
			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]

swap_colums_area

	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_area(self)
		grid.transposing(self)

Может быть есть ещё более сложные преобразования, но, думаю, можно ограничиться этими. Этот каркас инвариантен своей структуре, такие перестановки есть почти тоже самое, что и действия над матрицами относительно определителя или вращение Кубика Рубика.

Теперь, для того чтобы получить случайную комбинацию, достаточно запустить в случайном порядке функции перемешивания. Так и поступим, amt — количество перемешиваний:

	def mix(self,amt = 10):
		mix_func = ['self.transposing()', 
					'self.swap_rows_small()', 
					'self.swap_colums_small()', 
					'self.swap_rows_area()', 
					'self.swap_colums_area()']
		for i in xrange(1, amt):
			id_func = random.randrange(0,len(mix_func),1)
			eval(mix_func[id_func])

base
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[4, 5, 6, 7, 8, 9, 1, 2, 3]
[7, 8, 9, 1, 2, 3, 4, 5, 6]
[2, 3, 4, 5, 6, 7, 8, 9, 1]
[5, 6, 7, 8, 9, 1, 2, 3, 4]
[8, 9, 1, 2, 3, 4, 5, 6, 7]
[3, 4, 5, 6, 7, 8, 9, 1, 2]
[6, 7, 8, 9, 1, 2, 3, 4, 5]
[9, 1, 2, 3, 4, 5, 6, 7, 8]

swap_colums_area
[7, 8, 9, 4, 5, 6, 1, 2, 3]
[1, 2, 3, 7, 8, 9, 4, 5, 6]
[4, 5, 6, 1, 2, 3, 7, 8, 9]
[8, 9, 1, 5, 6, 7, 2, 3, 4]
[2, 3, 4, 8, 9, 1, 5, 6, 7]
[5, 6, 7, 2, 3, 4, 8, 9, 1]
[9, 1, 2, 6, 7, 8, 3, 4, 5]
[3, 4, 5, 9, 1, 2, 6, 7, 8]
[6, 7, 8, 3, 4, 5, 9, 1, 2]

swap_colums_small
[7, 8, 9, 4, 5, 6, 2, 1, 3]
[1, 2, 3, 7, 8, 9, 5, 4, 6]
[4, 5, 6, 1, 2, 3, 8, 7, 9]
[8, 9, 1, 5, 6, 7, 3, 2, 4]
[2, 3, 4, 8, 9, 1, 6, 5, 7]
[5, 6, 7, 2, 3, 4, 9, 8, 1]
[9, 1, 2, 6, 7, 8, 4, 3, 5]
[3, 4, 5, 9, 1, 2, 7, 6, 8]
[6, 7, 8, 3, 4, 5, 1, 9, 2]

swap_colums_small
[7, 8, 9, 4, 5, 6, 1, 2, 3]
[1, 2, 3, 7, 8, 9, 4, 5, 6]
[4, 5, 6, 1, 2, 3, 7, 8, 9]
[8, 9, 1, 5, 6, 7, 2, 3, 4]
[2, 3, 4, 8, 9, 1, 5, 6, 7]
[5, 6, 7, 2, 3, 4, 8, 9, 1]
[9, 1, 2, 6, 7, 8, 3, 4, 5]
[3, 4, 5, 9, 1, 2, 6, 7, 8]
[6, 7, 8, 3, 4, 5, 9, 1, 2]

transposing
[7, 1, 4, 8, 2, 5, 9, 3, 6]
[8, 2, 5, 9, 3, 6, 1, 4, 7]
[9, 3, 6, 1, 4, 7, 2, 5, 8]
[4, 7, 1, 5, 8, 2, 6, 9, 3]
[5, 8, 2, 6, 9, 3, 7, 1, 4]
[6, 9, 3, 7, 1, 4, 8, 2, 5]
[1, 4, 7, 2, 5, 8, 3, 6, 9]
[2, 5, 8, 3, 6, 9, 4, 7, 1]
[3, 6, 9, 4, 7, 1, 5, 8, 2]

swap_colums_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_area
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[3, 6, 9, 4, 7, 1, 2, 8, 5]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]

swap_colums_small
[7, 1, 4, 8, 2, 5, 6, 9, 3]
[8, 2, 5, 9, 3, 6, 7, 1, 4]
[9, 3, 6, 1, 4, 7, 8, 2, 5]
[2, 5, 8, 3, 6, 9, 1, 4, 7]
[1, 4, 7, 2, 5, 8, 9, 3, 6]
[3, 6, 9, 4, 7, 1, 2, 5, 8]
[5, 8, 2, 6, 9, 3, 4, 7, 1]
[4, 7, 1, 5, 8, 2, 3, 6, 9]
[6, 9, 3, 7, 1, 4, 5, 8, 2]

Шаг 3. Удаление клеток

После полученного решения нам необходимо получить задачу (именно в такой последовательности мы можем гарантировать однозначность решения). И это самая сложная часть. Какое количество можно убрать, чтобы гарантировать однозначность решения? Это один из важных факторов, от которого зависит сложность Судоку. Всего в Судоку 81 клетка, обычно считают лёгким когда на поле есть 30-35 «подсказок», средним — 25-30, и сложным — 20-25. Это данные большого набора реальных примеров. Нет никаких законов для сложности. Можно сделать 30-клеточный неразрешимый вариант и 22 клеточный «лёгкий».

• Случайный подход — можно попробовать выкинуть 50-60 клеток наугад, но где вероятность что Судоку можно будет решить? Например, если заполнены 3 строки ( = 27 клеток)
• Случайно с простым ограничением — для примера можно взять некое число N в качестве предела, так что N строк и столбцов могут быть пустыми. Принимая N = 0 — для лёгких уровней, N=1 — средний, N=2 — сложный

Итак, приступим к вычёркиванию ячеек (все варианты равнозначны, поэтому у нас 81 ячейка, которую можно вычеркнуть, поэтому проверим все перебором):

1. Выбрать случайную ячейку N
2. Отметить N просмотренной
3. Удалить N
4. Посчитать решения. Если оно не единственное, то вернуть N обратно

На выходе получится самая сложная из возможных вариантов Судоку для данного перемешивания. Переменная difficult оценивает сложность — количество оставшихся элементов.

flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)]
iterator = 0
difficult = example.n ** 4 #Первоначально все элементы на месте

while iterator < example.n ** 4:
	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку
	if flook[i][j] == 0:	#Если её не смотрели
		iterator += 1
		flook[i][j] = 1 	#Посмотрим

		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много
		example.table[i][j] = 0
		difficult -= 1 #Усложняем, если убрали элемент

		table_solution = []
		for copy_i in range(0, example.n*example.n):
			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список

		i_solution = 0
		for solution in solver.solve_sudoku((example.n, example.n), table_solution):
			i_solution += 1 #Считаем количество решений

		if i_solution != 1: #Если решение не одинственное -- вернуть всё обратно
			example.table[i][j] = temp
			difficult += 1  #Облегчаем

example.show()
print "difficult = ",difficult

# coding=utf-8
import random
import solver

class grid:
	def __init__(self,n = 3):
		""" Generation of the base table """
		self.n = n
		self.table = [[ ((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)]
		print "The base table is ready!"

	def __del__(self):
		pass
	
	def show(self):
		for i in range(self.n*self.n):
			print self.table[i]

	def transposing(self):
		""" Transposing the whole grid """
		self.table = map(list, zip(*self.table))

	def swap_rows_small(self):
		""" Swap the two rows """
		area = random.randrange(0,self.n,1)
		line1 = random.randrange(0,self.n,1)
		#получение случайного района и случайной строки
		N1 = area*self.n + line1
		#номер 1 строки для обмена

		line2 = random.randrange(0,self.n,1)
		#случайная строка, но не та же самая
		while (line1 == line2):
			line2 = random.randrange(0,self.n,1)

		N2 = area*self.n + line2
		#номер 2 строки для обмена

		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]


	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_small(self)
		grid.transposing(self)


	def swap_rows_area(self):
		""" Swap the two area horizon """
		area1 = random.randrange(0,self.n,1)
		#получение случайного района

		area2 = random.randrange(0,self.n,1)
		#ещё район, но не такой же самый
		while (area1 == area2):
			area2 = random.randrange(0,self.n,1)

		for i in range(0, self.n):
			N1, N2 = area1*self.n + i, area2*self.n + i
			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]


	def swap_colums_area(self):
		grid.transposing(self)
		grid.swap_rows_area(self)
		grid.transposing(self)
	
	def mix(self,amt = 10):
		mix_func = ['self.transposing()', 
					'self.swap_rows_small()', 
					'self.swap_colums_small()', 
					'self.swap_rows_area()', 
					'self.swap_colums_area()']
		for i in xrange(1, amt):
			id_func = random.randrange(0,len(mix_func),1)
			eval(mix_func[id_func])

example = grid()
example.mix()

flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)]
iterator = 0
difficult = example.n ** 4 #Первоначально все элементы на месте

example.show() 
print "---------------------------"

while iterator < example.n ** 4:
	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку
	if flook[i][j] == 0:	#Если её не смотрели
		iterator += 1
		flook[i][j] = 1 	#Посмотрим

		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много
		example.table[i][j] = 0
		difficult -= 1 #Усложняем если убрали элемент

		table_solution = []
		for copy_i in range(0, example.n*example.n):
			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список

		i_solution = 0
		for solution in solver.solve_sudoku((example.n, example.n), table_solution):
			i_solution += 1 #Считаем количество решений

		if i_solution != 1: #Если решение не одинственное вернуть всё обратно
			example.table[i][j] = temp
			difficult += 1 # Облегчаем

example.show()
print "difficult = ",difficult

#!/usr/bin/env python3

# Author: Ali Assaf <ali.assaf.mail@gmail.com>
# Copyright: (C) 2010 Ali Assaf
# License: GNU General Public License <http://www.gnu.org/licenses/>

from itertools import product

def solve_sudoku(size, grid):
    """ An efficient Sudoku solver using Algorithm X.

    >>> grid = [
    ...     [5, 3, 0, 0, 7, 0, 0, 0, 0],
    ...     [6, 0, 0, 1, 9, 5, 0, 0, 0],
    ...     [0, 9, 8, 0, 0, 0, 0, 6, 0],
    ...     [8, 0, 0, 0, 6, 0, 0, 0, 3],
    ...     [4, 0, 0, 8, 0, 3, 0, 0, 1],
    ...     [7, 0, 0, 0, 2, 0, 0, 0, 6],
    ...     [0, 6, 0, 0, 0, 0, 2, 8, 0],
    ...     [0, 0, 0, 4, 1, 9, 0, 0, 5],
    ...     [0, 0, 0, 0, 8, 0, 0, 7, 9]]
    >>> for solution in solve_sudoku((3, 3), grid):
    ...     print(*solution, sep='\n')
    [5, 3, 4, 6, 7, 8, 9, 1, 2]
    [6, 7, 2, 1, 9, 5, 3, 4, 8]
    [1, 9, 8, 3, 4, 2, 5, 6, 7]
    [8, 5, 9, 7, 6, 1, 4, 2, 3]
    [4, 2, 6, 8, 5, 3, 7, 9, 1]
    [7, 1, 3, 9, 2, 4, 8, 5, 6]
    [9, 6, 1, 5, 3, 7, 2, 8, 4]
    [2, 8, 7, 4, 1, 9, 6, 3, 5]
    [3, 4, 5, 2, 8, 6, 1, 7, 9]
    """
    R, C = size
    N = R * C
    X = ([("rc", rc) for rc in product(range(N), range(N))] +
         [("rn", rn) for rn in product(range(N), range(1, N + 1))] +
         [("cn", cn) for cn in product(range(N), range(1, N + 1))] +
         [("bn", bn) for bn in product(range(N), range(1, N + 1))])
    Y = dict()
    for r, c, n in product(range(N), range(N), range(1, N + 1)):
        b = (r // R) * R + (c // C) # Box number
        Y[(r, c, n)] = [
            ("rc", (r, c)),
            ("rn", (r, n)),
            ("cn", (c, n)),
            ("bn", (b, n))]
    X, Y = exact_cover(X, Y)
    for i, row in enumerate(grid):
        for j, n in enumerate(row):
            if n:
                select(X, Y, (i, j, n))
    for solution in solve(X, Y, []):
        for (r, c, n) in solution:
            grid[r][c] = n
        yield grid

def exact_cover(X, Y):
    X = {j: set() for j in X}
    for i, row in Y.items():
        for j in row:
            X[j].add(i)
    return X, Y

def solve(X, Y, solution):
    if not X:
        yield list(solution)
    else:
        c = min(X, key=lambda c: len(X[c]))
        for r in list(X[c]):
            solution.append(r)
            cols = select(X, Y, r)
            for s in solve(X, Y, solution):
                yield s
            deselect(X, Y, r, cols)
            solution.pop()

def select(X, Y, r):
    cols = []
    for j in Y[r]:
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].remove(i)
        cols.append(X.pop(j))
    return cols

def deselect(X, Y, r, cols):
    for j in reversed(Y[r]):
        X[j] = cols.pop()
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].add(i)

if __name__ == "__main__":
    import doctest
    doctest.testmod()

The base table is ready!
[5, 4, 6, 8, 7, 9, 2, 1, 3]
[8, 7, 9, 2, 1, 3, 5, 4, 6]
[2, 1, 3, 5, 4, 6, 8, 7, 9]
[6, 5, 7, 9, 8, 1, 3, 2, 4]
[9, 8, 1, 3, 2, 4, 6, 5, 7]
[3, 2, 4, 6, 5, 7, 9, 8, 1]
[7, 6, 8, 1, 9, 2, 4, 3, 5]
[1, 9, 2, 4, 3, 5, 7, 6, 8]
[4, 3, 5, 7, 6, 8, 1, 9, 2]
---------------------------
[0, 0, 6, 0, 0, 0, 0, 0, 0]
[8, 7, 0, 0, 1, 0, 0, 0, 6]
[0, 0, 0, 5, 4, 0, 0, 0, 9]
[6, 0, 0, 0, 8, 1, 3, 0, 4]
[0, 0, 0, 3, 0, 0, 0, 5, 0]
[0, 0, 0, 0, 0, 7, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 9, 0, 4, 0, 0, 0, 0, 8]
[0, 0, 5, 0, 6, 0, 1, 0, 0]
difficult =  22

Скачать в zip

Я уверен, что есть и более сложные подходы в построении таблицы Судоку. Моя цель была достигнута, получился рабочий алгоритм. Теперь мне не нужно искать новые выпуски, я могу их генерировать
В принципе, здесь был приведён частный случай Судоку 9х9. Но нет ограничений для использования его на 16х16 и 25х25.

• Для проверки решения применялся Алгоритм Х и его реализация для Судоку
• Решение Судоку на всех языках http://rosettacode.org/wiki/Sudoku

Если у кого есть лучшие предложения — не стесняйтесь оставить комментарий.
Спасибо за внимание.

Была ли эта статья полезной?

Библиографическое описание:

Евстратов, В. В. Рекурсивный алгоритм решения судоку с проверкой найденного решения на единственность / В. В. Евстратов. — Текст : непосредственный // Молодой ученый. — 2020. — № 51 (341). — С. 8-11. — URL: https://moluch.ru/archive/341/76568/ (дата обращения: 26.05.2023).

В данной статье приводится рекурсивный алгоритм решения судоку (с помощью «грубой силы»). Приводится способ проверки найденного решения на единственность с помощью модификации того же алгоритма. Доказывается, что этот способ работает для любого судоку.

Ключевые слова:



судоку, решение судоку, рекурсия, рекурсивный алгоритм, единственность решения судоку.

Судоку — это незамысловатая головоломка, главной целью которой является заполнение квадрата 9 х 9 ячеек числами от 1 до 9 по специальным правилам. Решение судоку — вид досуга, однако существуют соревнования по его скоростному решению.

Написание программы для автоматического решения судоку является упражнением для программиста, изучающего алгоритмы. В настоящее время существует множество онлайн сервисов, позволяющих подобрать решение для классического судоку [1], [2]. Также, можно найти примеры программ на разных языках программирования, решающие судоку и использующие как «человеческие» методы решения судоку [3], так и алгоритм Х (алгоритм Кнута) для поиска точного покрытия множества [4].

В приведенных выше примерах не учитывается проверка «правильность» поставленной задачи. Напомним, что правильным (валидным) судоку является судоку с такими входными данными, которое имеет одно единственное решение [5].

В данной статье будет рассмотрен алгоритм решения судоку с помощью «грубой силы», т. е. решение полным перебором возможных вариантов решения задачи и показан способ проверки полученного решения на единственность.

Идея алгоритма

Напомним правила классического судоку [5]:

1. Поле головоломки представляет собой квадрат, состоящий из 81 клетки;
2. Часть клеток изначально заполнены числами от 1 до 9 (подсказки);
3. В каждом ряду и столбце любое число от 1 до 9 может встречаться лишь один раз;
4. Кроме того, все поле делится еще на 9 блоков 3×3, в которых цифры от 1 до 9 тоже могут встречаться лишь один раз;
5. Задача заключается в том, чтобы заполнить все клетки цифрами с учетом указанных ограничений.

Нельзя забывать:

1. Валидное судоку должно иметь одно и только одно решение.

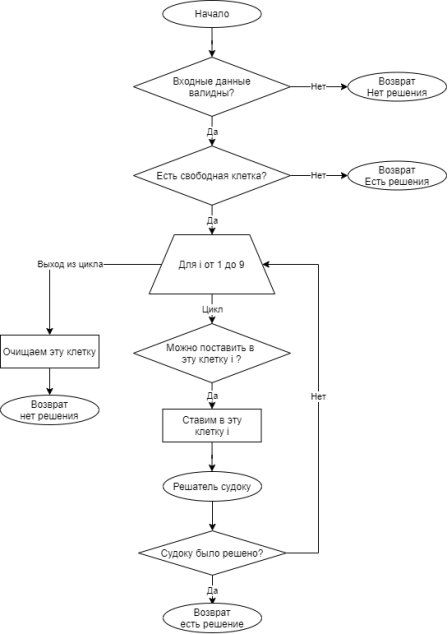
Блок-схема рекурсивного решения судоку без проверки на валидность представлена на рисунке 1. Рекурсивный вызов происходит внутри цикла (овальный блок «решатель судоку»), который вызывает саму эту функцию.

Необходимо понимать, что во время работы этого алгоритма информация о поле головоломки присутствует где-либо в программе (в глобальной переменной или всегда передаётся внутрь по указателю и пр.). Шаги по чтению/записи в это структуру данных в данной блок-схеме опущены, т. к. в общем случае они могут быть разными, и они ухудшают восприятие блок-схемы.

Блок условия «Входные данные валидны?» представляет собой проверку, только на то, что в каждом строке/стобце/блоке числа не повторяются. Обратите внимание, что в данном алгоритме не используются разнообразные методы решения судоку «последний герой», «выбора нет» и прочие [6].

Блок условия «Есть свободная клетка?» проверяет, существует ли на поле свободная клетка, если да, то следующее число мы будем записывать в неё.

Рис. 1. Блок-схема рекурсивного решения судоку

Проверка решения на единственность

Возьмем поле для судоку, которое гарантированно будет иметь больше одного решения (рисунок 2 слева). Рекурсивный алгоритм будет по очереди заполнять клетки этого поля, пока в конце концов не найдет подходящее решение (рисунок 2 справа).

Рис. 2. Судоку с несколькими решениями (слева), процесс работы рекурсивного алгоритма (справа)

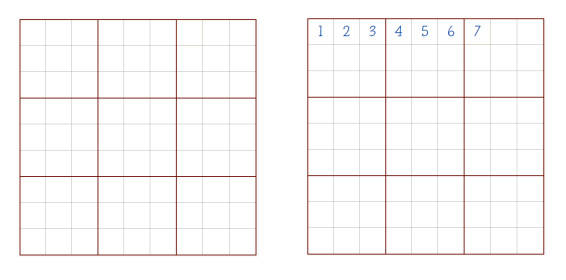
Идея проверки на единственность решения заключается в том, чтобы запустить заполнение поля судоку числами не от 1 до 9, а от 9 до 1. Если после обоих заполнений решения оказались разными, то судоку имеет несколько решений, т. е. исходная задача не валидна. Если решения совпали, то судоку валидно, т. е. имеет ровно одно решение. На рисунке 3 представлено заполнение пустого поля от 1 до 9 и от 9 до 1, наглядная демонстрация, что данное судоку имеет несколько решений.

Рис. 3. «Пустое» судоку заполняется от 1 до 9(слева) и от 9 до 1 (справа)

Доказательство

Поле судоку будем представлять в вдие 81-значного числа. Причем старшинство разрядов должно соответствовать обходу алгоритмом клеток поля судоку. Каждое такое число будем называть полем судоку.

Например, полю на рисунке 3 слева будет соответствовать число

1234567894567891237…8531978531642.

Представим теперь последовательность чисел от 0 до 10^81–1. Числа меньшие 10^80 будем дополнять для удобства незначащими лидирующими нулями:

0000000000…0000000000

0000000000…0000000001

0000000000…0000000002

…

1000000000…0000000000

1000000000…0000000001

…

9999999999…9999999998

9999999999…9999999999

Удалив из этой последовательности все невалидные поля судоку мы получим множество всех возможных решенных судоку.

Наложим на это множество «маску» из нашего изначального поля (пустые клетки — любое число, заполненная клетка должна точно совпасть с соответствующей позицией числа из полученного выше множества). Удалив все поля, несоответствующие маске мы получим множество всех возможных решений нашего судоку. Причем поля (числа) в этом множестве будут отсортированы по возрастанию.

Производя полный перебор путём подстановки в свободные клетки чисел от 1 до 9 мы «продвигаемся» по этой последовательности от меньших чисел к большим. А подставляя числа от 9 до 1 мы «продвигаемся» от больших к меньшим.

Если в множестве возможных решений больше одного элемента, то алгоритм найдет разные ответы: самое «большое» поле-число и самое «маленькое» поле-число. Если в множестве ровно 1 элемент (единственное решение судоку), то эти ответы совпадут.

Примечание по эффективности полного перебора

На первый взгляд может показаться, что рекурсивный полный перебор поиска решения судоку должен занимать очень большое время (10^81 операций, например). Однако, для написанной программы автору не удалось найти примера судоку, который решался бы программой дольше, чем за 1 секунду.

Если убрать проверку судоку на валидность перед запуском основного алгоритма, и попробовать, например, решить судоку, где в первых двух клетках находятся «1», а остальные клетки пустые (очевидно, невалидные входные данные), то действительно, программе требуется значительное время, чтобы понять, что ответа не существует (автор ни разу этого не дождался).

Заключение

Как говорилось ранее, написание программы для решения судоку является упражнением для программиста. Однако, проверка решения на единственность не так очевидна.

Следующим по сложности упражнением может стать проверка единственности решения судоку для более эффективного алгоритма — алгоритма X.

Литература:

1. Решатель судоку. — Программа: веб-сервис — URL: https://sudokus.ru/reshateli/ (дата обращения 10.12.2020)
2. Sudoku solver. — Программа: веб-сервис — URL: https://sudokuonline.ru/resatel-sudoku-onlajn/ (дата обращения 10.12.2020)
3. Решаем судоку на JavaScript. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/113837/ (дата обращения 10.12.2020)
4. Решаем судоку с помощью Алгоритма X. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/462411/ (дата обращения 11.12.2020)
5. Судоку. — Текст: электронный // Википедия свободная энциклопедия. — URL: https://ru.wikipedia.org/wiki/Судоку (дата обращения 10.12.2020)
6. Методы решения судоку. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/173795/ (дата обращения 11.12.2020)

Алгоритм генерации судоку — нужна помощь

06.12.2008, 09:41. Показов 33186. Ответов 2

#include <conio.h>
#include <iostream.h>
#include <stdlib.h>

const int n = 4 ;

void init_ar ( int ar[ n ][ n ] )

{

int i , j ;

    for(i = 1 ; i <= n ; i++ )

        for( j = 1 ; j <= n ; j++ )

        ar[ i ][ j ] = j ;

}

void init_cands( int c1[ n ][ n ] , int c2[ n ][ n ] , int c3[ n ][ n ] )

{

init_ar( c1 ) ;

init_ar( c2 ) ;

init_ar( c3 ) ;

}

void gen_sud( int c11[ n ][ n ],int c22[ n ][ n ],int c33[ n ][ n ],int a[ n ][ n ][ n ] )

{

int z , i , j , k ;

randomize() ;

init_cands( c11 , c22 , c33 ) ;

    for( i = 1 ; i <= 4 ; i++ )

    {

        for( j = 1 ; j <=4 ; j++ )

        {

            if( i <= 2 && j <= 2 )

            k = 1 ;

            if( i <= 2 && j >= 3 )

            k = 2 ;

            if( i >= 3 && j <= 2 )

            k = 3 ;

            if( i >= 3 && j >= 3 )

            k = 4 ;

            z = random( 4 ) + 1 ;

                while( 1 )

                {

                    if( c11 [ i ][ z ] == 0 || c22[ j ][ z ] == 0 || c33[ k ][ z ] == 0 )

                    {

                    z = random( 4 ) + 1 ;

                    }

                else

                {

                c11[ i ][ z ] = 0 ;

                c22[ j ][ z ] = 0 ;

                c33[ k ][ z ] = 0 ;

                a[ i ][ j ][ k ] = z ;

                cout << " " << a[ i ][ j ][ k ] ;

                break ;

                }

                    }

            }

        }

}

void main()

{

clrscr();

int s[n][n][n],str[n][n],stb[n][n],mgrid[n][n];

gen_sud(str,stb,mgrid,s);

getch();

}

#include <conio.h>
#include <stdlib.h>
#include <iostream.h>

int const n=9;

void init(int a[n][n])//inicializacia tablici(prisvaivaem 0)
{
int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
        a[i][j]=0;
}

int unic(int a[n][n],int ci,int cj,int k)//unicalnost v stroke,stolbze i diagonali
{
int i,j,f=0;
    for(i=1;i<=n;i++)
        if(a[i][cj]==k) f++;
            for(j=1;j<=n;j++)
                if(a[ci][j]==k) f++;
    if(ci==cj)
    {
        for(i=1;i<=n;i++)//glavnaia diagonal
            if(a[i][i]==k) f++;
    }
        else
            if(cj==n-ci+1)
            {
                for(i=1;i<=n;i++)//pobochnaia diagonal
                    if(a[i][n-i+1]==k) f++;
            }
return f;
}

void rec(int a[n][n],int i,int j)//recursia dlia zapolnenia tablici
{
int it,jt,fl,num;
    for(it=i;it<=n;it++)
    {
        for(jt=j;jt<=n;jt++)
        {
        num=random(9)+1;
        fl=unic(a,it,jt,num);
                if(fl==0)//esli sovpadenii net
                {
                a[it][jt]=num;
                cout<<" "<<a[it][jt];
                if(jt==9) cout<<"n";
                }
                    else//ecli est sovpadenia, to vozvrashemsia k 
                                                        //predidushei iacheike
                    {
                        if(jt==1&&it>1)
                            rec(a,it-1,jt+8);
                                else
                                rec(a,it,jt-1);
                    }

        }
    }
}

void main()
{
clrscr();
randomize();
int s[n][n];
int i,j;
init(s);
s[1][1]=random(9)+1;
rec(s,1,2);
getch();
}

0

Для тех, кому нравится решать загадки cудоку самостоятельно и неспешно, формула, позволяющая быстро вычислить ответы, может показаться признанием слабости или жульничеством

Но для тех, кому разгадывание судоку стоит слишком больших усилий, это может быть буквально идеальным решением.

Два исследователя разработали математический алгоритм, который позволяет решать судоку очень быстро, без предположений и перебора с возвратом.

Исследователи комплексных сетей Золтан Торожкай и Мария Эркси-Раваз из Университета Нотр-Дама также смогли объяснить, почему некоторые загадки судоку более сложные, чем другие. Единственный недостаток в том, что для того, чтобы понять, что они предлагают, нужна степень доктора математики.

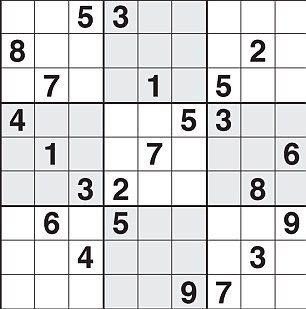
Вы можете решить эту головоломку? Она создана математиком Арто Инкалой, и, как утверждают, это самая сложная судоку в мире. Фото с сайта nature.com

Торожкай и Эркси-Раваз начали анализировать судоку как часть своего исследования теории оптимизации и вычислительной сложности. Они говорят, что большинство любителей судоку используют для решения этих задач подход «грубой силы», основанный на технике предположения. Таким образом, любители судоку вооружаются карандашом и пробуют все возможные комбинации чисел, пока не будет найден правильный ответ. Этот метод неизбежно приведет к успеху, но он трудоемок и занимает много времени.

Вместо этого Торожкай и Эркси-Раваз предложили универсальный аналоговый алгоритм, который абсолютно детерминирован (не использует предположение или перебор) и всегда находит правильное решение задачи, причем довольно быстро.

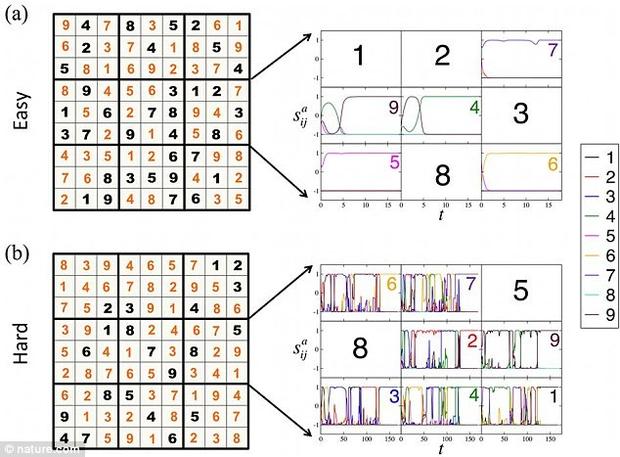
Исследователи использовали «детерминированный аналоговый решатель», чтобы заполнить эту судоку. Фото с сайта nature.com

Исследователи также обнаружили, что время, которое требуется, чтобы решить головоломку с использованием их аналогового алгоритма, коррелируется со степенью сложности задачи, которая оценивается человеком. Это вдохновило их на то, чтобы развивать шкалу ранжирования для трудности загадки или проблемы.

Они создали шкалу от 1 до 4, где 1 – «легко», 2 – «средняя степень сложности», 3 – «сложно», 4 – «очень сложно». Для решения головоломки с рейтингом 2 требуется в среднем в 10 раз больше времени, чем для задачки с рейтингом 1. Согласно этой системе, самая сложная загадка из известных до сих пор имеет рейтинг 3.6; более сложные задачи судоку пока неизвестны.

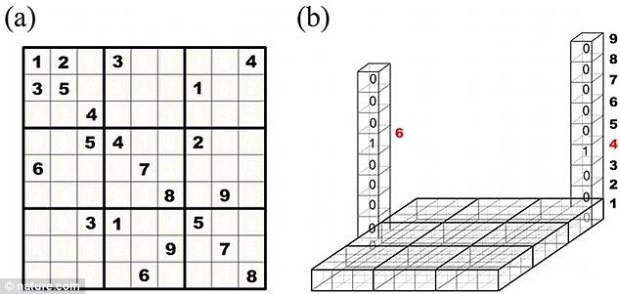
Теория начинается с картографии вероятностей для каждого отдельного квадрата. Фото с сайта nature.com

«Я не интересовался судоку, пока мы не начали работать над более общим классом выполнимости Булевых проблем, – говорит Торожкай. – Так как судоку – часть этого класса, латинский квадрат 9-го порядка оказался для нас хорошим полем для испытаний, так я с ними и познакомился. Меня и многих исследователей, изучающих такие проблемы, захватывает вопрос, как далеко мы, люди, способны зайти в решении судоку, детерминировано, без перебора, который является выбором наугад, и, если догадка не верна, нужно вернуться на шаг или на несколько шагов назад и начать сначала. Наша аналоговая модель решения детерминирована: в динамике нет никакого случайного выбора или возвращения».

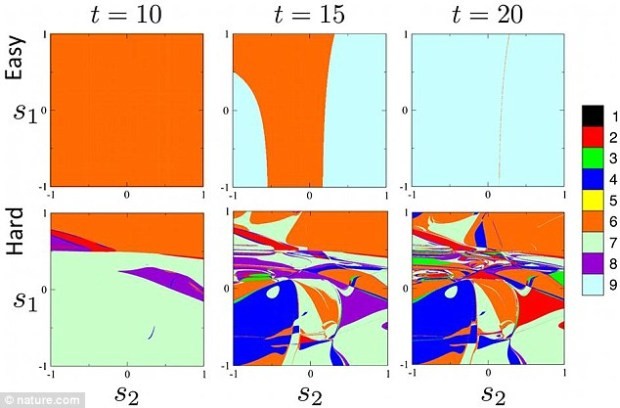
Теория хаоса: степень сложности загадок показывается здесь как хаотическая динамика. Фото с сайта nature.com

Торожкай и Эркси-Раваз полагают, что их аналоговый алгоритм потенциально подходит для применения к решению большого количества разнообразных задач и проблем в промышленности, информатике и вычислительной биологии.

Опыт исследования также сделал Торожкая большим любителем судоку.

«У моей жены и у меня есть несколько приложений судоку на наших iPhone, и мы, должно быть, сыграли уже тысячи раз, соревнуясь за меньшее время на каждом уровне, – говорит он. – Она часто интуитивно видит комбинации паттернов, которых я не замечаю. Я должен их выводить. Для меня становится невозможным решить многие головоломки, которые наша шкала категоризирует как трудные или очень трудные, без того, чтобы записывать вероятности карандашом».

Методология Торожкая и Эркси-Раваз была впервые опубликована в журнале Nature Physics, а затем – в журнале Nature Scientific Reports.