Как составить ранжированный ряд по таблице - Autoru.top

Ранжированный
ряд— это
ряд, в котором все единицы совокупности
располагаются в порядке возрастания
или убывания группировочного признака.
Выбор группировочного признака зависит
от цели данной группировки и
предварительного экономического
анализа.

Имея
данные по 21 хозяйствам Канской
природно-экономической зоны о
среднегодовой заработной плате и ряде
факторов, построим

ранжированный
ряд, т.е. расположим хозяйства в порядке
возрастания группировочного признака.

Ранжированный
ряд хозяйств по уровню заработной платы

В таблице
2.1 представлен ранжированный ряд по
уровню заработной платы.

Таблица
2.1.

№	Название хозяйств	Среднегодовая
п/п		заработная плата, тыс. руб.
1	СПК «Возрождение»	11,6
2	СПК «Майский»	13,53
3	СПК ЗАО «Устьянское»	17,07
4	ООО Агрофирма «Дзержинская»	18,1
5	ООО «Мачинское»	20,23
6	СПК «Восток»	21,79
7	СХПК «Тайнинское»	22,85
8	СПК «Сибиряк»	23,53
9	ЗАО «Восход»	24,13
10	СПК «Георгиевское»	27,86
11	ЗАО «Адвинское»	32,6
12	ЗАО «Племзавод Северное»	34,5
13	СПК «Денисовский»	37,5
14	ЗАО «Арефьевское»	38,99
15	ЗАО «Мокрушенское»	43,32
16	ЗАО «Малкор»	43,53
17	СПК(артель) «Нолобинский»	46,6
18	ЗАО «Болынеуринское»	47,6
19	ООО «Телец»	49,85
20	ЗАО «Камарчагское»	50,66
21	ООО «Шуваево 1»	56,88
22	ГСХУ Учхоз «Миндерлинское»	58,74
23	ОАО «Госсортстанция»	62,5

24	ОАО «Красный Маяк»	64,3
25	СПК «Зыковский»	65,3

Для
наглядности изобразим ранжированный
ряд графически, на оси абцисс запишем
номер хозяйства в ранжированном ряду,
а на оси ординат — величину группировочного
признака, т.е. заработную плату, тыс.
руб. (см. рисунок 2.1).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
10.04.2015628.74 Кб710.doc
#
#
#
10.04.2015613.89 Кб1011.doc
#
10.04.2015408.06 Кб712.doc
#
#
10.04.2015633.34 Кб2013.doc
#
#
10.04.2015602.62 Кб2314.doc
#

Источник

Вариационный ряд может быть:

дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.

Рассмотрим пример построения дискретного вариационного ряда.

Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
Откроем таблицы Excel.

Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.

Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.

Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.

Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Рис.1.2 Пример 1. Построение вариационного ряда

Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Построим полигон:

выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Пример 1. Построение полигона частот

Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel

Следующая тема: Построение интервального вариационного ряда в Excel.

Источник: http://www.reshim.su/blog/variacionnyj_rjad/2014-08-23-500

Как сортировать данные в таблицах Excel (правильный способ)

Итак, нам вручили электронную таблицу Excel с тысячами строк внутри нее и вы понимаете, что все данные в неправильном порядке. Возможно, вам придется сортировать её на основе имен столбцов или путем сортировки данных от большего к меньшему.

На первый взгляд, сортировка данных в Excel задача простая, и приложение, безусловно, упрощает сортировку. Однако, более важно то, как вы можете отсортировать и изменить порядок данных в ваших листах. Вот три метода сортировки данных Excel, о которых вы узнаете в этом уроке:

Сортировка данных всего в несколько кликов
Установка нескольких, ступенчатых правил сортировки, таких как сортировка по алфавиту по состоянию, а затем по всё вместе.
Создать полностью свои настройки сортировки, чтобы отсортировать данные с помощью любого установленного вами правила.

Сортировка данных иногда может казаться опасной; что, если вы отсортируете только один столбец и данные будут смещены? Я покажу вам, как избежать этого. Давайте начнем.

Как сортировать данные в электронной таблице Excel (короткое видео)

Этот скринкаст охватывает несколько методов сортировки ваших данных. Просмотрите этот трехминутный видеоролик, чтобы быстро изучить эти профессиональные техники работы Excel. Мы начнем с простой сортировки и перейдем к более продвинутым методам, чтобы вы всегда смогли отсортировать данные так, как вам нужно.

Читайте дальше пошаговое руководство по сортировке данных в электронных таблицах Excel с использованием простых и передовых методов.

Примеры данных (бесплатная загрузка рабочей книги Excel)

В рамках этого урока я создал книгу, с которой вы можете работать, изучая сортировку данных. Загрузите книгу бесплатно и используйте её во время изучения сортировки в Excel.

1. Простая сортировка в Excel

Сортировка может быть очень простой, всего пара кликов для перестановки данных в ваших таблицах. Давайте узнаем как.

В книге Excel, начните с нажатия на ячейку столбца, который вы хотите отсортировать. Теперь, убедитесь, что вы находитесь на вкладке Главная на ленте Excel’я и найдите кнопку Сортировка и фильтр на самой правой стороне этой панели.

Кнопка Сортировка и фильтр обитает в самой правый части вкладки Главная.

Заметьте, что в вариантах сортировки, вы можете отсортировать текст «А до Я» или «Я до А». Эти простые варианты помогут отсортировать данные в Excel В алфавитном или обратным порядках, в зависимости от того что вы выбрали.

Когда вы сортируете данные в Excel, сортируется вся строка. По сути, выбранный вами столбец будет «ключом», который Excel использует, чтобы решить, как сортировать данные, но каждая строка это запись, которая должна оставаться сгруппированной вместе.

В зависимости от данных, которые вы выбрали, можете произвести сортировку по алфавитному или числовому порядку. Если столбцы содержат числовые данные, вы можете отсортировать в порядке от малого к большому числу, текстовые данные сортируются в алфавитном порядке.

В примере выше, варианты сортировки изменились, потому что я выбрал столбец с цифрами.

Выполнить обычную сортировку на самом деле так просто. Просто кликните по данным, выберите вариант сортировки и Excel перестроит данные в таблице.

Я отсортировал данные в этой таблице на основе клиента всего в несколько кликов.

Дельный совет: попробуйте также сортировать, щелкнув правой кнопкой мыши внутри столбца и выбрав Сортировка, а затем указать способ сортировки исходных данных.

2. Как НЕ нужно сортировать данные в Excel

Не менее важно узнать, о самом опасном способе сортировки данных в Excel, такой метод может испортить ваши исходные данные.

Проблема возникает если в таблице много данных, а вы случайно отсортировали только один столбец данных. Каждая строка с данными в Microsoft Excel действительно похоже на запись, которая должна быть такой же по всей строке.

На изображении ниже, Я раскрасил строки, таким образом опасное место с сортировкой только одного столбца данных, будет выделено.

Я задал цвета строкам в этом примере, чтобы мы могли убедиться, что наши данные отсортированы правильно. Цвета должны проходить полностью через каждую строку без перерывов, если данные сортируются правильно.

Большая ошибка пользователей Excel заключается в выборе только одного столбца при сортировке и выборе неправильного параметра в следующем окне.

Excel даже пытается предупредить нас, показывая окно Обнаруженны данные вне указанного диапазона. Во всплывающем окне можно выбрать автоматически расширить выделенный диапазон (выберите это!) и сортировать в пределах указанного выделения.

Я всегда думал, что варианты, которые дает вам это окно, не совсем ясны. Просто знайте, что вы захотите использовать автоматически расширить выделенный диапазон, чтобы убедиться, что Excel затронет все столбцы при сортировке данных.

Для тестирования давайте посмотрим, что произойдет, если мы выберем один столбец и выберем тип сортировки сортировать в пределах указанного выделения.

Использование вариант сортировать в приделах указанного диапазона сортирует только один столбец данных, который обязательно разрушит вашу исходную электронную таблицу.

На скриншоте ниже вы можете видеть, насколько проблематичен этот тип сортировки. Так как столбец Amount Billed был отсортирован от наименьшего до наибольшего, все остальные столбцы остались на месте. Это означает, что наши данные больше не верны.

Как вы видите из несоответствия цветов, были отсортированы только данные в столбце Amount Billed, поэтому теперь таблица некорректна.

Таким образом, при сортировке данных есть два ключевых «НЕ»:

Не начинайте, выделив один столбец в своей электронной таблице.
Не используйте вариант сортировать в приделах указанного диапазона, если вы работаете не с одним столбцом, убедитесь, что вы расширили выделенный диапазон.

3. Расширенная сортировка данных Excel

До сих пор простая сортировка позволяла нам сортировать данные однотипно. Что, если мы хотим два типа данных в нашей сортировке?

Что, если мы хотим…

Сортировка в алфавитном порядке по состоянию, а затем по области.
Сортировка в алфавитном порядке по имени клиента, а затем по каждому типу проекта, который мы сделали для них.
Сортировка клиентов в список по алфавиту, а затем по количеству для каждого отдельного проекта, от наибольшего до наименьшего.

Ответ на всё это — расширенная сортировка, при которой вы можете установить несколько уровней сортировки данных. Давайте рассмотрим последний пример, используя образцы данных.

Чтобы начать работу, щелкните где-нибудь внутри своих данных и найдите параметр Сортировка и фильтр, а затем выберите Настраиваемая сортировка.

Перейдите к расширенным параметрам сортировки, выбрав Сортировка и фильтр > Настраиваемая сортировка.

В этом окне мы можем добавить несколько уровней сортировки. Начните с нажатия на раскрывающийся список рядом с Сортировка и выберите столбец, который вы хотите отсортировать.

В моем случае я выберу Client в раскрывающемся меню и оставлю значение Сортировка равным Значения, а Порядок — От А до Я. На простом языке это отсортирует электронную таблицу Excel на основе алфавитного порядка.

Теперь давайте нажмем Добавить уровень. Это создаст новую строку в параметрах сортировки и позволит нам добавить второй уровень организации.

Теперь я могу выбрать Amount billed во втором раскрывающемся списке. Комбинация этих двух правил начнется путем сортировки на основе имени клиента, а затем суммы, выставленного счёта за каждый проект.

Вы можете продолжить добавлять столько уровней, сколько хотите в это окно расширенной сортировки. Последовательность строк имеет значение, т.е. вы можете переместить строку вверх для сортировки сначала по выставленному счету, например, а затем по клиенту.

Как только мы нажмем OK, Excel отсортирует таблицу на основе правил, которые мы создали в этом окне.

Совет: Для более продвинутой сортировки попробуйте в раскрывающимся меню Сортировка изменить тип сортировки на расширенные функции, такие как сортировка на основе цвета ячейки.

Расширенная сортировка позволяет создавать два уровня организации данных в вашей таблице. Если сортировки по одному фактору недостаточно, используйте расширенную сортировку, чтобы добавить больше возможностей.

Повторение и продолжение обучения

Сортировка это ещё одно умение, которое нужно держать в готовом виде в своей книге Excel. Когда вам нужно повторно сопоставить данные в электронной таблице, слишком много времени можно потратить для вырезания и вставки строк в определенном порядке, поэтому сортировка является обязательной.

Источник: https://business.tutsplus.com/ru/tutorials/how-to-sort-data-in-excel-spreadsheets—cms-28737

Построить ранжированный ряд пример. Как сделать ранжированный ряд в excel

Задание №1

На основании данных статистического наблюдения, приведенных в таблице построить ранжированный, интервальный и кумулятивный ряды распределения сельскохозяйственных предприятий по факторному признаку, изобразить их графически.

Провести сводку данных. Посредством метода группировок определите зависимость результативного признака в сельскохозяйственных предприятиях от факторного. Построить таблицы и графики зависимости. Вывод.

Решение:

Построение ранжированного ряда распределения предполагает расположение всех вариантов ряда в порядке возрастания изучаемого признака (качества почвы). Проведение сортировки производилось в программе ТП Excel с использованием функции «Сортировка».

Графическое изображение ранжированного ряда распределения

Линия на рис.1 носит название огива Гальтона. Данная огива имеет тенденцию плавного роста с небольшими скачками в некоторых точках. Для преобразования ранжированного ряда в интервальный лучше выполнить разбивку на группы вручную.

Построение интервального ряда распределения предприятий по изучаемому признаку предполагает определение числа групп (интервалов).

Для расчета числа групп воспользуемся формулой:
n=2 , где N-общее число единиц изучаемой совокупности.

n=2 Ig30 = 2,95424251?3.

Величина равного интервала вычисляется по формуле:

i = = = 16,33333

Кумулятивный ряд — это ряд в котором подсчитываются накопленные частоты. Он показывает, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и вычисляется путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Интервальный и кумулятивный ряды
частота — число предприятий в группе;
Удельный вес предприятий в группе — находится по формуле:
(число предприятий в группе*100%)/ m, где m-число экспериментальных данных;
Накопленная
частота — находится по формуле: число предприятий в предедущей группе+частота данной группы.
Гистограмма частот
Кумулята распределения качества почвы
Сводные показатели

№ группы	Число предприятий в группе	Урожайность овощей открытого грунта (всего по группам)	Качество почвы (всего по группам)
II 61,33333-77,33333
III 77,33333-94,1

Средние характеристики групп

№ Группы	Урожайность овощей открытого грунта	Качество почвы
II 61,33333-77,33333
III 77,33333-94,1
В среднем по совокупности

где, столбец «урожайность овощей» находится по формуле: У
У i (в группе)/ число предприятий в группе;
столбец «Качество почвы» находится по формуле: У Х i (в группе)/число предприятий в группе.
Зависимость урожайности овощей открытого грунта от качества почвы.
В рассматриваемом примере можно сделать вывод: с ростом качества почвы увеличивается урожайность овощей открытого грунта, следовательно можно предположить наличие прямой связи между рассматриваемыми параметрами.

Подобные документы

Аналитическая группировка по факторному признаку. Построение вариационного частотного и кумулятивного рядов распределения на основе равно интервальной структурной группировки результативного признака – дивидендов, начисленных по результатам деятельности.контрольная работа , добавлен 07.05.2009 Основные показатели численности населения и его размещения по Калужской области. Построение ранжированного и интервального рядов распределения по одному группировочному факторному признаку. Анализ типических групп по показателям в среднем по совокупности.

Источник: https://netdenegnakino.ru/postroit-ranzhirovannyi-ryad-primer-kak-sdelat-ranzhirovannyi-ryad-v.html

Трюки и хитрости в Excel — Подсветка ряда данных в диаграмме. Часть 1

Всем привет! Друзья, случайно нашел в сети один очень интересный способ видопредставления диаграммы с подсветкой определенного значения. Спешу с вами поделиться этим чудом )) Только не буду выкладывать файлик пример, чтобы вы сами своими руками все сделали, так лучше запомнится. Информации будет много, поэтому разобью ее на три статьи, чтобы не было перегруза. Следите за обновлениями.

Недавно, я писал о том как без применения макросов можно настроить автообновление диаграммы. Если интересно, статью можно почитать здесь Как без формул и макросов сделать автообновление диаграммы?

Сегодня я хочу пошагово показать вам как сделать подсветку или выделить один ряд данных от остальных. Не переключайтесь, будет интересно ))

Шаг 1. Строим таблицу

Для начала составим таблицу. В статье про автообновление я строил таблицу по данным посещения игр на Чемпионате мира по футболу в наших городах. Продолжим с ней работать. В большинстве городов сыграно по 5 матчей, поэтому есть отличный повод сравнить среднюю посещаемость на стадионах. Данные я по прежнему брал с сайта Чемпионат.ком

Шаг 2. Выделяем необходимое значение

Затем в таблицу добавим еще один столбец и назовем его Подсветка. В данном столбце во всех строчках нам необходимо прописать функцию «НД()», которая возвращает значение без аргументов, т.е. создает ошибку.

Но в одной строчке, напротив самого большого значения просто скопируем данные. Цвет шрифта сделал светло серым, чтобы было наглядно понятнее. В нашем случае выделяется стадион «Лужники». У него наибольшая средняя посещаемость.

Не зря все таки на него столько денег потратили…..

Шаг 3. Строим диаграмму

Выделим только три столбца с данными которые необходимо нам отобразить. Затем нужно встать на одну из ячеек таблицы, перейти во вкладку Вставка и выбрать команду Гистограмма. В предложенном списке выберем Гистограмму с группировкой.

В результате у нас получается вот такая диаграмма.

Шаг 4. Делаем подсветку

Теперь самое главное. Для того чтобы выделить наш столбец в диаграмме, кликаем правой кнопкой на выделяющийся ряд данных и выбираем в списке контекстного меню «Формат ряда данных» . Затем в открывшемся окне «параметры ряда данных» в «перекрытии рядов» «с зазором» тянем бегунок вправо до 100%.

Нажимаем закрыть. Всё )) Вот так просто у нас получилось выделить «Лужники» из всех остальных стадионов.

На этом у меня всё. В следующей статье расскажу как подсветить ряд в зависимости от выбранного из списка стадиона. Тоже будет интересно и познавательно! Не пропустите!

Если вам понравился сегодняшний трюк, ставьте лайки и подписывайтесь на канал. Если хотите посмотреть еще уроки загляните в СОДЕРЖАНИЕ, обязательно еще что-нибудь присмотрите )) Спасибо!

Источник: https://zen.yandex.ru/media/id/5a25282b7800192677cc044f/5b3c8d32d75f2900a9562e31

Источник

Варианты для выполнения работы

I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.

В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.

Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.

30,2	51,9	43,1	58,9	34,1	55,2	47,9	43,7	53,2	34,9
47,8	65,7	37,8	68,6	48,4	67,5	27,3	66,1	52,0	55,6
54,1	26,9	53,6	42,5	59,3	44,8	52,8	42,3	55,9	48,1
44,5	69,8	47,3	35,6	70,1	39,5	70,3	33,7	51,8	56,1
28,4	48,7	41,9	58,1	20,4	56,3	46,5	41,8	59,5	38,1
41,4	70,4	31,4	52,5	45,2	52,3	40,2	60,4	27,6	57,4
29,3	53,8	46,3	40,1	50,3	48,9	35,8	61,7	49,2	45,8
45,3	71,5	35,1	57,8	28,1	57,6	49,6	45,5	36,2	63,2
61,9	25,1	65,1	49,7	62,1	46,1	39,9	62,4	50,1	33,1
33,3	49,8	39,8	45,9	37,3	78,0	64,9	28,8	62,5	58,7

Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.

Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.

Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.

Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):

20,4	25,1	26,9	27,3	27,6	28,1	28,4	28,8	29,3	30,2
31,4	33,1	33,3	33,7	34,1	34,9	35,1	35,6	35,8	36,2
37,3	37,8	38,1	39,5	39,8	39,9	40,1	40,2	41,4	41,8
41,9	42,3	42,5	43,1	43,7	44,5	44,8	45,2	45,3	45,5
45,8	45,9	46,1	46,3	46,5	47,3	47,8	47,9	48,1	48,4
48,7	48,9	49,2	49,6	49,7	49,8	50,1	50,3	51,8	51,9
52,0	52,3	52,5	52,8	53,2	53,6	53,8	54,1	55,2	55,6
55,9	56,1	56,3	57,4	57,6	57,8	58,1	58,7	58,9	59,3
59,5	60,4	61,7	61,9	62,1	62,4	62,5	63,2	64,9	65,1
65,7	66,1	67,5	68,6	69,8	70,1	70,3	70,4	71,5	78,0

В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.

Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.

Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.

Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:

где — число групп (классов, интервалов) ряда распределения; n — объем выборки.

Можно также использовать выражение:

При они дают примерно одинаковые результаты.

В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:

Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.

Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:

$[R=x_{max}-x_{min}]$

где — размах вариации,

$x_{max}$ — наибольшее значение варьирующего признака,

$x_{min}$ — наименьшее значение варьирующего признака.

Найдем размах вариации для рассматриваемой задачи:

Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.

$[happrox frac{R}{k}]$

Согласно формуле получаем

$[happrox frac{57,6}{8}=7,2]$

Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:

$[x_1approx x_{min}-frac{h}{2}]$

$[x_1approx 20,4-frac{7,2}{2}=16,8.]$

Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее $x_{min}$ или само значение $x_{min}$ . Далее в табличном виде я покажу оба варианта.

Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто $x_{max}$ .

Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.

Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.

Как и обещал покажу две таблицы построения ряда:

1. Отсчет ведем от $x_{min}$ , т.е. нижняя граница первого интервала совпадает с $x_{min}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
20,4 — 27,6	4	4
27,6 — 34,8	11	15
34,8 — 42	16	31
42 — 49,2	21	52
49,2 — 56,4	21	73
56,4 — 63,6	15	88
63,6 — 70,8	10	98
70,8 — 78	2	100

2. Начало первого интервала определяем с помощью формулы: $x_1approx x_{min}-frac{h}{2}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
16,8 — 24	1	1
24 — 31,2	9	10
31,2 — 38,4	13	23
38,4 — 45,6	17	40
45,6 — 52,8	23	63
52,8 — 60	18	81
60 — 67,2	11	92
67,2 — 74,4	7	99
74,4 — 81,6	1	100

Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.

Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.

Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.

II. Графическая интерпретация вариационных рядов.

№ п/п	Границы интервалов, $[x_{i}; x_{i+1})$	Середины интервалов, $x_{i}^{*}=frac{x_i+x_{i+1}}{2}$	Частоты интервалов,	Относительные частоты $W_i=frac{n_i}{n}$	Плотность относит. частоты $frac{W_i}{h}$	Плотность частоты $frac{n_i}{h}$
1	16,8 — 24	20,4	1	0,01	0,001	0,139
2	24 — 31,2	27,6	9	0,09	0,013	1,250
3	31,2 — 38,4	34,8	13	0,13	0,018	1,806
4	38,4 — 45,6	42	17	0,17	0,024	2,361
5	45,6 — 52,8	49,2	23	0,23	0,032	3,194
6	52,8 — 60	56,4	18	0,18	0,025	2,500
7	60 — 67,2	63,6	11	0,11	0,015	1,528
8	67,2 — 74,4	70,8	7	0,07	0,010	0,972
9	74,4 — 81,6	78	1	0,01	0,001	0,139

Строим графики:

Далее найдем моду вариационного ряда:

$[M_o(X)=x_{M_o}+hfrac{(n_2-n_1)}{(n_2-n_1)+(n_2-n_3)}]$

где

$x_{M_o}$ — начало модального интервала;

— длина частичного интервала (шаг);

n_1 — частота предмодального интервала;

n_2 — частота модального интервала;

— частота послемодального интервала.

Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).

$[M_o(X)=45,6+7,2frac{(23-17)}{(23-17)+(23-18)}=]$

$[=45,6+7,2cdot frac{6}{6+5}=45,6+3,93=49,5]$

Медиана

Для интервального ряда медиана находится по формуле:

$[M_e(X)=x_{M_e}+hfrac{0,5n-S_{M_{e}-1}}{n_{M_e}}]$

где

$x_{M_e}$ — начало медианного интервала;

— длина частичного интервала (шаг);

— объем совокупности;

$S_{M_{e}-1}$ — накопленная частота интервала, предшествующая медианному;

$n_{M_e}$ — частота медианного интервала.

Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).

Получаем,

$[M_e(X)=45,6+7,2frac{0,5cdot 100-40}{23}approx 48,7.]$

III. Расчет сводных характеристик выборки.

Для определения $x_B, D_{B}, sigma_{B}$ составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

$[U_i=frac{(x_i-C)}{h}]$

Произведем расчет условных вариант согласно формуле:

$[U_1=frac{20,4-49,2}{7,2}=-4]$

$[U_2=frac{27,6-49,2}{7,2}=-3]$

$[U_3=frac{34,8-49,2}{7,2}=-2]$

$[U_4=frac{42-49,2}{7,2}=-1]$

$[U_5=frac{49,2-49,2}{7,2}=0]$

$[U_6=frac{56,4-49,2}{7,2}=1]$

$[U_7=frac{63,6-49,2}{7,2}=2]$

$[U_8=frac{70,8-49,2}{7,2}=3]$

$[U_9=frac{78-49,2}{7,2}=4]$

N п/п	Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Условные варианты,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,
1	20,4	1	-4	-4	16	-64	256	9	81
2	27,6	9	-3	-27	81	-243	729	36	144
3	34,8	13	-2	-26	52	-104	208	13	13
4	42	17	-1	-17	17	-17	17	0	0
5	49,2	23	0	0	0	0	0	23	23
6	56,4	18	1	18	18	18	18	72	288
7	63,6	11	2	22	44	88	176	99	891
8	70,8	7	3	21	63	189	567	112	1792
9	78	1	4	4	16	64	256	25	625

Контроль:

$[sum n_i U_i^2 + 2sum n_iU_i+n=sum n_i{(U_i+1)}^2]$

$[sum n_i{(U_i+1)}^2=389]$

Контроль:

$[sum n_i U_i^4 + 4sum n_iU_i^3+6sum n_iU_i^2+4sum n_iU_i+n=sum n_i{(U_i+1)}^4]$

$[sum n_i{(U_i+1)}^4=3857]$

Равенство выполнено, следовательно вычисления произведены верно.

Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:

$[M_1^{*}=frac{sum n_iU_i}{n}=frac{-9}{100}=-0,09;]$

$[M_2^{*}=frac{sum n_iU_i^2}{n}=frac{307}{100}=3,07;]$

$[M_3^{*}=frac{sum n_iU_i^3}{n}=frac{-69}{100}=-0,69;]$

$[M_4^{*}=frac{sum n_iU_i^4}{n}=frac{2227}{100}=22,27.]$

Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :

$[x_{B}=M_1^{*}cdot h+C=-0,09cdot 7,2+49,2=48,552;]$

$[D_{B}=(M_2^{*}-{(M_1^{*})}^2)h^2=(3,07-{(-0,09)}^2){7,2}^2approx 158,73.]$

$[sigma_{B}=sqrt{D_B}=sqrt{158,73}=12,6.]$

Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

$[a_s=frac{m_3}{sigma_B^3}]$

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.

Эксцесс эмпирического распределения определяется равенством:

$[e_k=frac{m_4}{sigma_B^4}-3]$

где — центральный эмпирический момент четвертого порядка.

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Вычисляем центральные эмпирические моменты третьего и четвертого порядков:

$[m_3=(M_3^*-3M_1^*M_2^*+2{(M_1^*)}^3)cdot h^3=51,3;]$

$[m_4=(M_4^*-4M_3^*M_1^*+6M_2^*{(M_1^*)}^2-3{(M_1^*)}^4)cdot h^4=59580,97;]$

Найдем асимметрию и эксцесс:

$[a_s=frac{51,3}{{12,6}^3}=0,026]$

$[e_k=frac{59580,97}{{12,6}^4}-3=-0,635]$

IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона

Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:

$[chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]$

и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы найти критическую точку $chi^2_{kp}(alpha;k)$ , где s — количество интервалов.

Если $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу.

Если $chi^2_{nabl}>chi^2_{kp}$ — нулевую гипотезу отвергают.

Найдем теоретические частоты , для этого составим следующую таблицу.

Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Произведем расчет, $x_{i}^{*}-x_B$	Произведем расчет, $V_i=frac{(x_{i}^{*}-x_B)}{sigma_B}$	Значения функции Гаусса,	Произведем расчет, $frac{nh}{sigma_B}$	Теоретические частоты, $n_i^{'}=57 cdotvarphi(V_i)$
20,4	1	-28,152	-2,23	0,0332	57	2
27,6	9	-20,952	-1,66	0,1006	57	6
34,8	13	-13,752	-1,09	0,2203	57	13
42	17	-6,552	-0,52	0,3485	57	20
49,2	23	0,648	0,05	0,3984	57	23
56,4	18	7,848	0,62	0,3292	57	19
63,6	11	15,048	1,19	0,1965	57	11
70,8	7	22,248	1,77	0,0833	57	5
78	1	29,448	2,34	0,0258	57	1
						$sum n_i^{'}=100$

Вычислим $chi^2_{nabl}$ , для чего составим расчетную таблицу.

		$n_i^{'}$	$n_i-n_i^{'}$	${(n_i-n_i^{'})}^2$	$frac{{(n_i-n_i^{'})}^2}{n_i^'}$		$frac{n_i^2}{n_i^{'}}$
1	1	2	-1	1	0,5	1	0,5
2	9	6	3	9	1,5	81	13,5
3	13	13	0	0	0	169	13
4	17	20	-3	9	0,45	289	14,45
5	23	23	0	0	0	529	23
6	18	19	-1	1	0,05	324	17,05
7	11	11	0	0	0	121	11
8	7	5	2	4	0,8	49	9,8
9	1	1	0	0	0	1	1
	100	100			Наблюдаемое значение критерия, $chi^2_{nabl}=3,30$		103,30

Контроль:

$[sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]$

$[sumfrac{n_i^2}{n_i'}-n=103,3-100=3,3]$

$[sum frac{{(n_i-n_i')}^2}{n_i'}=3,3]$

Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;

По таблице критических точек распределения по уровню значимости и числу степеней свободы k=6 находим $chi^2_{kp}(0,025;6)=14,4.$

Так как $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении sigma генеральной совокупности служит доверительный интервал

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}},]$

где $frac{tsigma}{sqrt{n}}=delta$ — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа (см. приложение 2), при котором $phi(t)=frac{gamma}{2}$ ;

при неизвестном среднем квадратическом отклонении sigma (и объеме выборки n<30)

$[x_B-frac{t_{gamma}cdot S}{sqrt{n}}<a<x_B+frac{t_{gamma}cdot S}{sqrt{n}},]$

$[S=sqrt{frac{n}{n-1}D_B}]$

где S — исправленное выборочное среднее квадратическое отклонение, $t_{gamma}$ находят по таблице приложения по заданным n и .

В нашем примере среднее квадратическое отклонение известно, . А также , , . Поэтому для поиска доверительного интервала используем первую формулу:

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}}]$

Все величины, кроме t, известны. Найдем t из соотношения $phi(t)=frac{0,95}{2}=0,475.$ По таблице приложения находим t=1,96. Подставив t=1,96, , , в формулу, окончательно получим искомый доверительный интервал:

$[48,55-frac{1,96cdot 12,6}{10}<a<48,55+frac{1,96cdot 12,6}{10}]$

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал

(при q<1), (*)

(при q>1),

где q — находят по таблице приложения по заданным n и .

По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив $S=sqrt{frac{n}{n-1}D_B}=sqrt{frac{100}{99}cdot 158,73}approx 12,66, quad quad q=0,143$ в соотношение (*), получим доверительный интервал:

Источник

Содержание

1 Функции ранжирования
- 1.1 Способ 1: функция РАНГ.РВ
2 Способ 2: функция РАНГ.СР
- 2.1 Помогла ли вам эта статья?
3 Сортировка данных
4 Ранжирование данных
- 4.1 Функция РАНГ в Excel
- 4.2 Функции РАНГ.РВ и РАНГ.СР в Excel
- 4.3 Автоматическая сортировка
5 Пример функции РАНГ в Excel
6 Пример функции РАНГ.РВ в Excel
7 Пример функции РАНГ.СР в Excel

При работе с данными часто возникает потребность выяснить, какое место занимает в совокупном перечне по величине тот или иной показатель. В статистике это называется ранжированием. В Excel имеются инструменты, которые позволяют пользователям быстро и легко произвести данную процедуру. Давайте выясним, как ими пользоваться.

Функции ранжирования

Для выполнения ранжирования в Экселе предусмотрены специальные функции. В старых версиях приложения был один оператор, предназначенный для решения этой задачи – РАНГ. В целях совместимости он оставлен в отдельной категории формул и в современных версиях программы, но в них все-таки желательно работать с более новыми аналогами, если есть такая возможность. К ним относятся статистические операторы РАНГ.РВ и РАНГ.СР. О различиях и алгоритме работы с ними мы поговорим далее.

Способ 1: функция РАНГ.РВ

Оператор РАНГ.РВ производит обработку данных и выводит в указанную ячейку порядковый номер заданного аргумента из совокупного списка. Если несколько значений имеют одинаковый уровень, то оператор выводит высший из перечня значений. Если, например, два значения будут иметь одинаковую величину, то им обоим будет присвоен второй номер, а уже следующее по величине значение будет иметь четвертый. Кстати, полностью аналогично поступает и оператор РАНГ в более старых версиях Эксель, так что данные функции можно считать идентичными.

Синтаксис этого оператора записывается следующим образом:

=РАНГ.РВ(число;ссылка;)

Аргументы «число» и «ссылка» являются обязательными, а «порядок» — необязательным. В качестве аргумента «число» нужно ввести ссылку на ту ячейку, где содержится значение, порядковый номер которого нужно узнать. Аргумент «ссылка» содержит адрес всего диапазона, который ранжируется. Аргумент «порядок» может иметь два значения – «0» и «1». В первом случае отсчет порядка идет по убывающей, а во втором – по возрастающей. Если данный аргумент не указан, то он автоматически считается программой равным нулю.

Данную формулу можно записывать вручную, в ту ячейку, где вы хотите, чтобы выводился результат обработки, но для многих пользователей удобнее задавать вводные через окно Мастера функций.

Выделяем на листе ячейку, в которую будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию». Она локализуется слева от строки формул.
Эти действия приводят к тому, что запускается окно Мастера функций. В нем представлены все (за редким исключениям) операторы, которые можно использовать для составления формул в Excel. В категории «Статистические» или «Полный алфавитный перечень» находим наименование «РАНГ.РВ», выделяем его и щелкаем по кнопке «OK».
После указанных выше действий будет активировано окно аргументов функции. В поле «Число» следует ввести адрес той ячейки, данные в которой нужно ранжировать. Это можно сделать вручную, но удобнее выполнить тем способом, о котором пойдет речь ниже. Устанавливаем курсор в поле «Число», а затем просто выделяем нужную ячейку на листе.
После этого её адрес будет занесен в поле. Точно таким же образом заносим данные и в поле «Ссылка», только в этом случае выделяем весь диапазон, в границах которого происходит ранжирование.

Если вы хотите, чтобы ранжирование происходило от меньшего к большему, то в поле «Порядок» следует установить цифру «1». Если же нужно, чтобы порядок распределялся от большего к меньшему (а в подавляющем числе случаев именно это и требуется), то данное поле оставляем пустым.

После того, как все вышеуказанные данные внесены, жмем на кнопку «OK».
После выполнения данных действий в предварительно указанной ячейке будет выведен порядковый номер, который имеет выбранное вами значение среди всего перечня данных.

Если вы желаете проранжировать всю указанную область, то совсем не нужно для каждого показателя вводить отдельную формулу. Прежде всего, делаем адрес в поле «Ссылка» абсолютным. Перед каждым значением координат добавляем знак доллара ($). При этом изменять значения в поле «Число» на абсолютные ни в коем случае не следует, иначе формула будет рассчитываться некорректно.

После этого нужно установить курсор в нижний правый угол ячейки, и дождаться появления маркера заполнения в виде небольшого крестика. Затем зажать левую кнопку мыши и протянуть маркер параллельно вычисляемой области.

Как видим, таким образом, формула скопируется, а ранжирование будет произведено на всем диапазоне данных.

Урок: Мастер функций в Excel

Урок: Абсолютные и относительные ссылки в Excel

Способ 2: функция РАНГ.СР

Второй функцией, которая производит операцию ранжирования в Экселе, является РАНГ.СР. В отличие от функций РАНГ и РАНГ.РВ, при совпадении значений нескольких элементов данный оператор выдает средний уровень. То есть, если два значения имеют равную величину и следуют после значения под номером 1, то им обоим будет присвоен номер 2,5.

Синтаксис РАНГ.СР очень похож на схему предыдущего оператора. Выглядит он так:

=РАНГ.СР(число;ссылка;)

Формулу можно вводить вручную или через Мастер функций. На последнем варианте мы подробнее и остановимся.

Производим выделение ячейки на листе для вывода результата. Таким же образом, как и в предыдущий раз, переходим в Мастер функций через кнопку «Вставить функцию».
После открытия окна Мастера функций выделяем в перечне категории «Статистические» наименование РАНГ.СР и жмем на кнопку «OK».
Активируется окно аргументов. Аргументы у данного оператора точно такие же, как и у функции РАНГ.РВ:
- Число (адрес ячейки содержащей элемент, уровень которого следует определить);
- Ссылка (координаты диапазона, ранжирование внутри которого выполняется);
- Порядок (необязательный аргумент).
Внесение данных в поля происходит точно таким же способом, как и у предыдущего оператора. После того, когда все настройки выполнены, жмем на кнопку «OK».
Как видим, после выполненных действий результат расчета был выведен в ячейку, отмеченную в первом пункте данной инструкции. Сам итог представляет собой место, которое занимает конкретное значение среди других величин диапазона. В отличие от результата РАНГ.РВ, итог оператора РАНГ.СР может иметь дробное значение.
Как и в случае с предыдущей формулой, с помощью изменения ссылок с относительных на абсолютные и маркера выделения, путем автозаполнения можно проранжировать весь диапазон данных. Алгоритм действий точно такой же.

Урок: Другие статистические функции в Microsoft Excel

Урок: Как сделать автозаполнение в Эксель

Как видим, в Экселе существует две функции для определения ранжирования конкретного значения в диапазоне данных: РАНГ.РВ и РАНГ.СР. Для более старых версий программы используется оператор РАНГ, который, по сути, является полным аналогом функции РАНГ.РВ. Главное отличие формул РАНГ.РВ и РАНГ.СР состоит в том, что первая из них указывает наивысший уровень при совпадении значений, а вторая выводит средний показатель в виде десятичной дроби. Это единственное различие между этими операторами, но его нужно учитывать при выборе того, какой именно функцией пользователю лучше воспользоваться.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

Научимся ранжировать числовые данные в Excel с помощью стандартной сортировки, а также функции РАНГ и ее частных случаях (РАНГ.РВ и РАНГ.СР), которые помогут в автоматизации сортировки.

Приветствую всех, дорогие читатели блога TutorExcel.Ru.

Задача ранжирования числовых данных постоянно возникает в работе с целью поиска наибольших или наименьших значений в списке.
В Excel с этой задачей можно справиться 2 способами: стандартным инструментом сортировки и с помощью функций.

Для примера возьмем простую таблицу со списком числовых значений, в которой в дальнейшем и будем ранжировать данные:

Сортировка данных

Начнем с самого простого и доступного варианта — сортировки.

Мы уже частично разбирали как можно структурировать данные с помощью фильтра и сортировки.
Вкратце, для сортировки необходимо выделить диапазон с данными и на панели вкладок выбрать Главная -> Редактирование -> Сортировка и фильтр, а далее указать по какому критерию нужно произвести сортировку.

В данном случае выберем Сортировка по убыванию, где значения будут расположены от большего к меньшему:

Минусом данного способа является изменение структуры исходных данных, так как в процессе сортирования данных строки и столбцы могут меняться местами, что в некоторых случаях неудобно или невозможно сделать.
Также к важным недостаткам этого варианта можно отнести отсутствие возможности автоматизировать сортировку. Поэтому каждый раз при изменении данных сортировку придется делать еще раз.

В качестве решения данной проблемы рассмотрим другой способ ранжирования, который впрочем можно рассматривать и отдельно от решения этой задачи.

Ранжирование данных

При отсутствии возможности изменения структуры документа мы можем создать дополнительный ряд данных, где будут содержаться порядковые номера исходных данных.
Получить эти порядковые номера нам поможет функция РАНГ (а также РАНГ.РВ и РАНГ.СР).

Функция РАНГ в Excel

Синтаксис и описание функции:

РАНГ(число; ссылка; )
Возвращает ранг числа в списке чисел: его порядковый номер относительно других чисел в списке.

Число (обязательный аргумент) — число для которого вычисляется ранг;
Ссылка (обязательный аргумент) — массив или ссылка на массив чисел;
Порядок (необязательный аргумент) — способ упорядочения. Если аргумент равен 0 или не указан, то значение 1 присваивается максимальному элементу в списке (условно говоря, сортируем по убыванию), в ином случае значение 1 присваивается минимальному элементу (сортируем по возрастанию).

Эта функция доступна во всех версиях Excel, однако начиная с Excel 2010 на ее замену добавлены РАНГ.РВ и РАНГ.СР, а РАНГ оставлена для совместимости с Excel 2007, давайте подробнее остановимся на их работе.

Функции РАНГ.РВ и РАНГ.СР в Excel

Синтаксис и описание функций:

РАНГ.РВ(число; ссылка; )
Возвращает ранг числа в списке чисел: его порядковый номер относительно других чисел в списке; если несколько значений имеют одинаковый ранг, возвращается высший ранг из этого набора значений.

РАНГ.СР(число; ссылка; )
Возвращает ранг числа в списке чисел: его порядковый номер относительно других чисел в списке; если несколько значений имеют одинаковый ранг, возвращается средний ранг.

Аргументы у всех трех функций одинаковые, т.е. кардинально они почти не отличаются, есть небольшие различие в деталях.
На примере исходной таблицы посмотрим как работает с данными каждая из функций:

Как мы видим отличие заключаются лишь в типе ранжирования совпадающих элементов данных.

В случае с РАНГ.РВ равным элементам присваивается высший ранг.
В нашем примере категориям Ноутбуки и Мультиварки соответствует одинаковое значение элемента — 710, который является 3 по порядку убывания, соответственно обоим значениям присваивается высший ранг — 3.
Для РАНГ.СР для этих же значений устанавливается их средний ранг, т.е. среднее между 3 и 4 порядковыми номерами — 3,5.

На этом различия между ними заканчиваются, поэтому в зависимости от ваших задач можно использовать ту или иную функцию.
Если нужно отсортировать значения по возрастанию, то в качестве аргумента Порядок нужно указать значение 1:

Автоматическая сортировка

Немного усложним задачу и представим, что нам в дальнейшем нужно составить отсортированную таблицу, которая бы автоматически обновлялась при изменении данных в исходной таблице.

Например, это можно сделать с помощью функции ВПР, или комбинации ИНДЕКС и ПОИСКПОЗ, однако в случае наличия одинаковых значений в списке мы не сможем корректно подтянуть данные и получим ошибку:

В этом случае можно воспользоваться простым приемом в виде небольшой хитрости.
Добавим к каждому значению исходной таблицы не совпадающие случайные числа близкие к нулю, к примеру, я для этих целей использую функции СТРОКА или СТОЛБЕЦ, поделенные на заведомо большую величину.

Этот шаг позволит нам получить различные числа в исходных данных, избежать совпадения рангов и ошибки при подтягивании данных:

Теперь для всех элементов таблицы (даже изначально совпадающих) определен свой индивидуальный ранг отличный от остальных, поэтому ошибок при автоматическом ранжировании данных удастся избежать.

Скачать файл с примером.

Спасибо за внимание!
Если у вас остались вопросы — пишите в комментариях.

Удачи вам и до скорых встреч на страницах блога TutorExcel.Ru!

Для ранжирования данных в Excel применяются статистические функции РАНГ, РАНГ.РВ, РАНГ.СР. Все они возвращают номер числа в ранжированном списке числовых значений. Рассмотрим подробнее синтаксис, примеры.

Функция используется при ранжировании в перечне чисел. То есть позволяет узнать величину числа относительно других числовых значений. Если отсортировать список по возрастанию, то функция вернет позицию числа. Например, в массиве чисел {30;2;26} число 2 будет иметь ранг 1; 26 –2; 30 –3 (как наибольшее значение в списке).

Синтаксис функции:

Число. Для, которого необходимо определить номер в ранжировании.
Ссылка. На массив чисел или диапазон ячеек с числовыми значениями. Если задать в качестве аргумента просто числа, то функция вернет ошибку. Нечисловым значениям номер не присваивается.
Порядок. Способ упорядочения чисел в списке. Варианты: аргумент равен «0» или опущен – значение 1 присваивается максимальному числу в списке (как будто список отсортирован в порядке убывания); аргумент равен любому неравному нулю числу – номер ранжирования 1 присваивается минимальному числу в списке (как будто список отсортирован в порядке возрастания).

Определим ранжирование чисел в списке без повторов:

Аргумент, определяющий способ упорядочения чисел, равен «0». Следовательно, в данной функции номера присваивались значениям от большего к меньшему. Максимальному числу 87 присвоен номер 1.

В третьем столбце приведена формула с рангом по возрастанию.

Определим номера значений в списке, где присутствуют повторяющиеся значения.

Желтым цветом выделены повторяющиеся числа. Для них определяется один и тот же номер. Например, числу 7 во втором столбце присвоен номер 9 (и во второй строке, и в девятой); в третьем столбце – 3. Но ни одно из чисел во втором столбце не будет иметь 10, а в третьем – 4.

Чтобы ранги не повторялись (иногда это мешает пользователю решить поставленную задачу), используется следующая формула:

Для работы функции можно установить пределы. Например, необходимо ранжировать только значения от 0 до 30. Чтобы решить задачу, применим функцию ЕСЛИ (=ЕСЛИ(A2

Серым цветом выделены значения, которые соответствуют заданному условию. Для чисел, которые больше 30, выводится пустая строка.

Пример функции РАНГ.РВ в Excel

В версиях Excel, начиная с 2010 года, появилась функция РАНГ.РВ. Это абсолютный аналог предыдущей функции. Синтаксис такой же. Буквы «РВ» в названии указывают на то, что при обнаружении формулой одинаковых значений функция вернет высший номер ранжирования (то есть первого обнаруженного элемента в перечне равных).

Как видно из примера, данная функция обрабатывает повторяющиеся числа в списке точно так же, как и в обычной формуле. Если необходимо избежать повторений рангов, используем другую формулу (см. выше).

Пример функции РАНГ.СР в Excel

Возвращает номера числового значения в списке (порядковый номер относительно других значений). То есть выполняет ту же задачу. Только при обнаружении идентичных значений возвращает средний показатель.

Вот результат работы функции:

Формула в столбце «по убыванию»: =РАНГ.СР(A2;$A$2:$A$9;0). Так, функция значению 87 присвоила средний номер 1,5.

Допустим, в списке чисел три повторяющихся значения (выделены оранжевым цветом).

Функция присвоила каждому из них ранг 5, что является средним для 4, 5 и 6.

Сравним работу двух функций:

Напомним, что эти две функции работают только в Excel 2010 и выше. В более ранних версиях для этих целей можно задействовать формулу массива.

Скачать примеры функции ранжирования РАНГ в Excel.

Таким образом, все выше описанные примеры позволяют автоматизировать работу по ранжированию данных и составлению рейтинга значений без применения сортировки.

Источник

При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.

При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.

Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.

Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.

Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).

Элементами выборки (x₁ х₂, . х_п) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).

Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.

Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.

Пример 2.1.

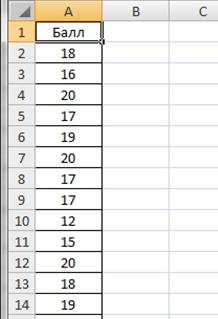
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):

18	16	20	17	19	20	17
17	12	15	20	18	19	18
18	16	18	14	14	17	19
16	14	19	12	15	16	20

Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.

Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).

Рисунок 2.6. Баллы успеваемости студентов

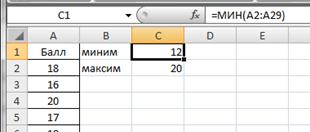
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).

Рисунок 2.7. Минимальный и максимальный балл

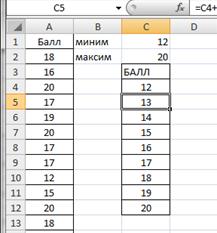
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.

Рисунок 2.8. Значения признака

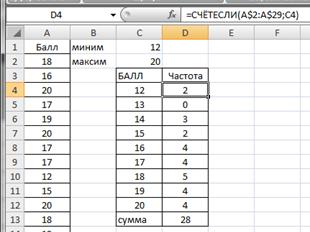
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).

Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.

Рис.2.9. Частоты вариационного ряда

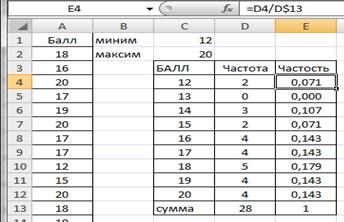
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).

Рисунок 2.10. Частости ряда распределения

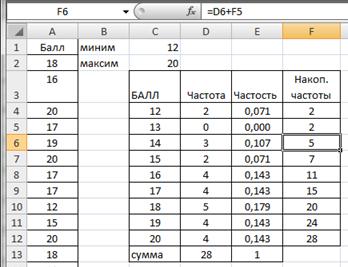
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).

Рисунок 2.11. Накопленные частоты ряда

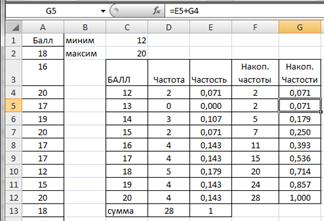
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.

Рисунок 2.12. Накопленные частости ряда

Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.

Рисунок 2.13. Полигон распределения частот

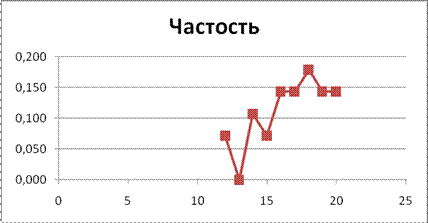
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.

Рисунок 2.14. Полигон распределения частостей

Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).

Рисунок 2.15. Гистограмма распределения частостей

Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.

Рисунок 2.16. Кумулята

Пример 2.2.

В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.

Банковские процентные ставки

№ Банка	Процентная ставка, %
1	20,3
2	17,1
3	14,2
4	11,0
5	17,3
6	19,6
7	20,5
8	23,6
9	14,6
10	17,5
11	20,8
12	13,6
13	24,0
14	17,5
15	15,0
16	21,1
17	17,6
18	15,8
19	18,8
20	22,4
21	16,1
22	17,9
23	21,7
24	18,0
25	16,4
26	26,0
27	18,4
28	16,7
29	12,2
30	13,9

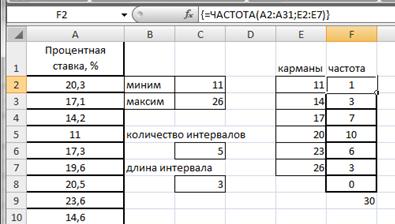
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.

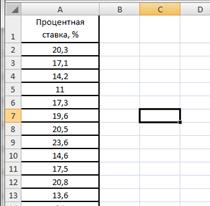
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).

Рисунок 2.17. Процентные ставки банков

Рисунок 2.18. Число интервалов

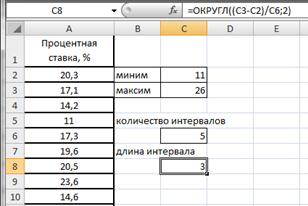
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).

Рисунок 2.19. Длина интервала

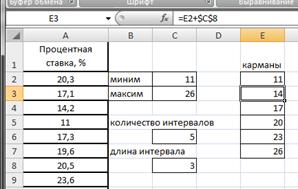
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).

Рисунок 2.20. Границы интервалов

Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.

Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.

Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).

Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.

Рисунок 2.21. Частоты значений признака

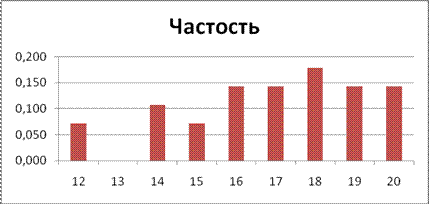
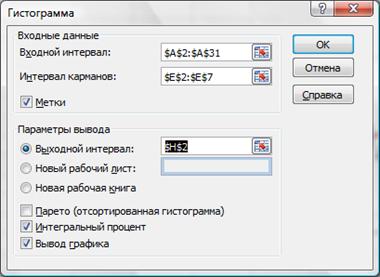
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).

Рисунок 2.22. Построение гистограммы

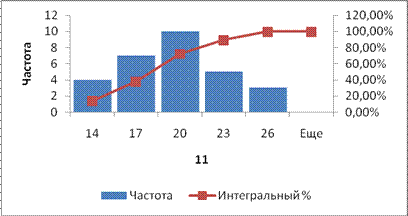
Полученная гистограмма представлена на рис.2.23.

Рис.2.23. Гистограмма частот

Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.

Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав

Вариационный ряд может быть:

– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).

– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.

Рассмотрим пример построения дискретного вариационного ряда.

Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения

Решение .

Алгоритм построения вариационного ряда:

1) Откроем таблицы Excel.

2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.

3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.

4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.

6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Построим полигон:

1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Рис.1.3. Пример 1. Построение полигона частот

В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).

Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.

После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).

Размахом вариации называется число

где х_тах — наибольший вариант;

x min — наименьший вариант.

Сумма всех частот равна определенному числу л, которое называется объемом совокупности:

Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:

Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).

Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.

Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.

Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.

В результате получим дискретный вариационный ряд (табл. 3.10).

Ранжированный ряд успеваемости

Число студентов, л,

Относительная частота, А

В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).

Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).

Рис. 3.13. Контекстное меню строки состояния

Рассмотрим два варианта подсчета частот:

1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.

Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»

В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).

Рис. 3.15. Результаты применения инструмента «Гистограмма)

Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).

В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.

Источник

Как сортировать данные в таблицах Excel (правильный способ)

Как сортировать данные в электронной таблице Excel (короткое видео)

Примеры данных (бесплатная загрузка рабочей книги Excel)

1. Простая сортировка в Excel

2. Как НЕ нужно сортировать данные в Excel

3. Расширенная сортировка данных Excel

Повторение и продолжение обучения

Построить ранжированный ряд пример. Как сделать ранжированный ряд в excel

Подобные документы

Трюки и хитрости в Excel — Подсветка ряда данных в диаграмме. Часть 1

Шаг 1. Строим таблицу

Шаг 2. Выделяем необходимое значение

Шаг 3. Строим диаграмму

Шаг 4. Делаем подсветку

Функции ранжирования

Способ 1: функция РАНГ.РВ

Способ 2: функция РАНГ.СР

Помогла ли вам эта статья?

Сортировка данных

Ранжирование данных

Функция РАНГ в Excel

Функции РАНГ.РВ и РАНГ.СР в Excel

Автоматическая сортировка

Пример функции РАНГ.РВ в Excel

Пример функции РАНГ.СР в Excel

Не пропустите также: