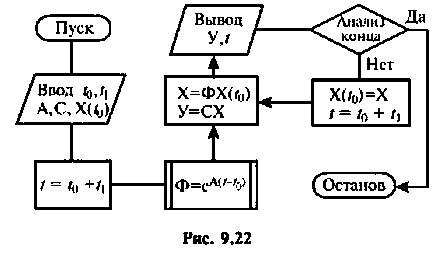
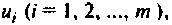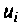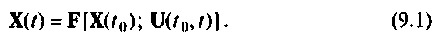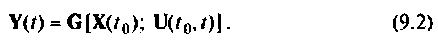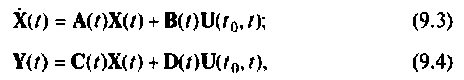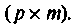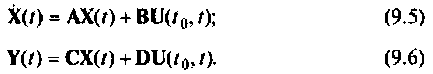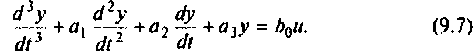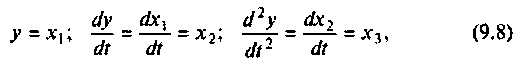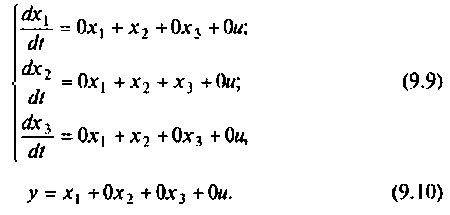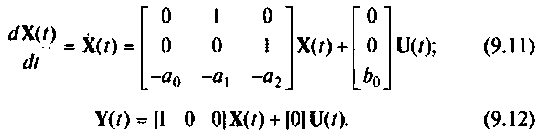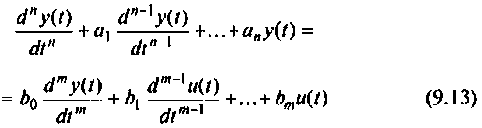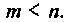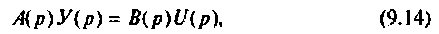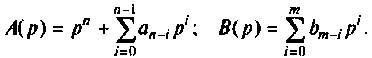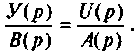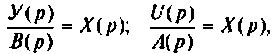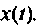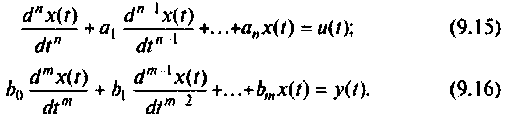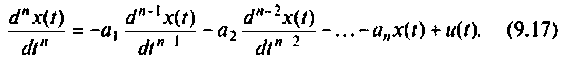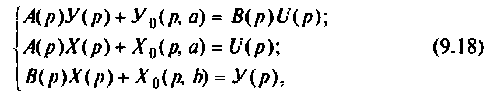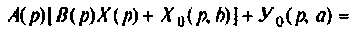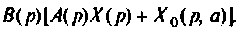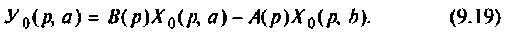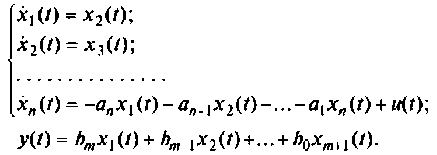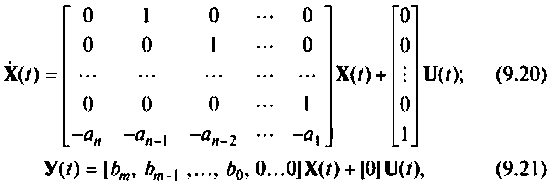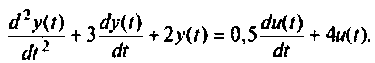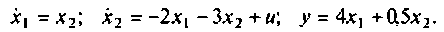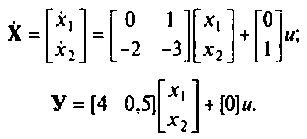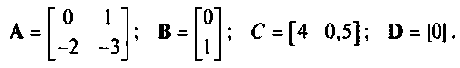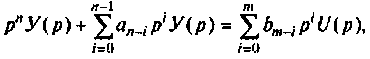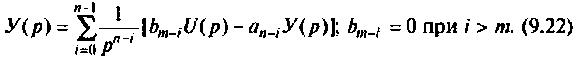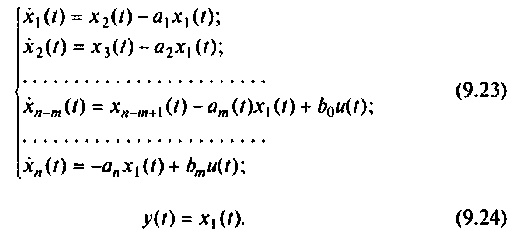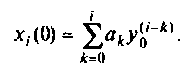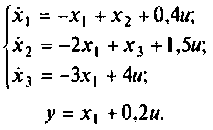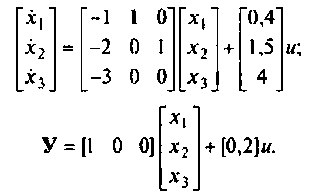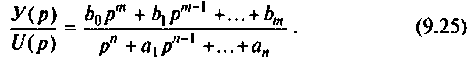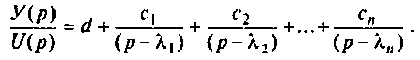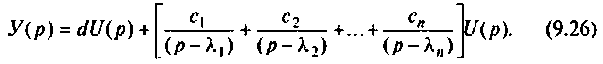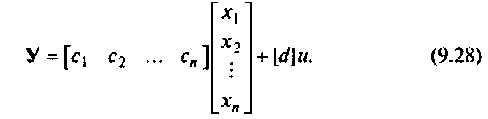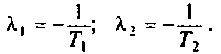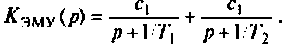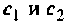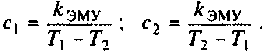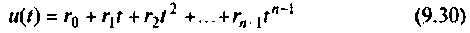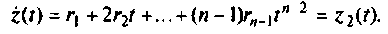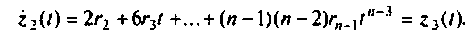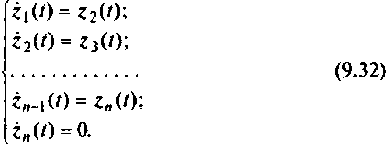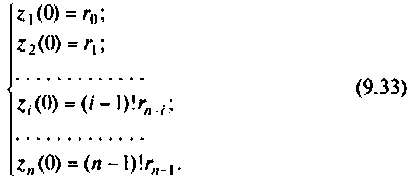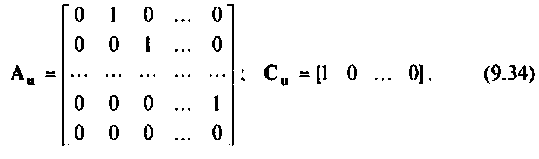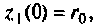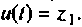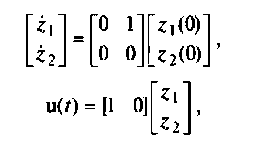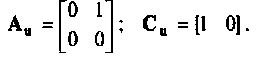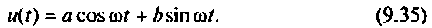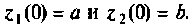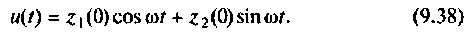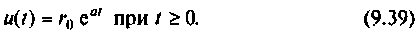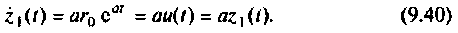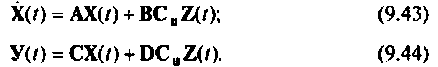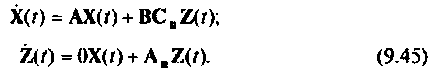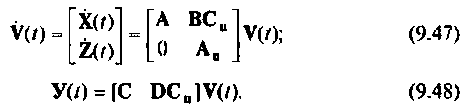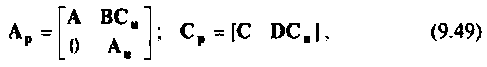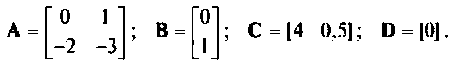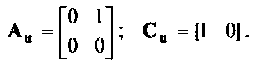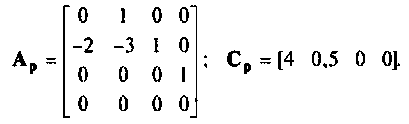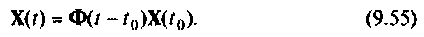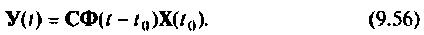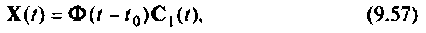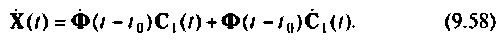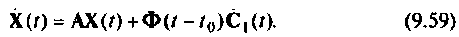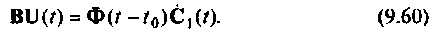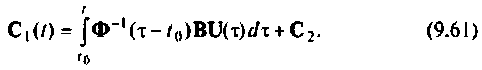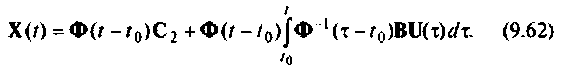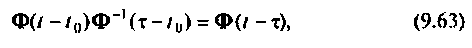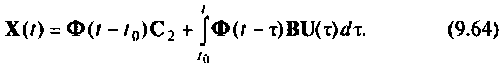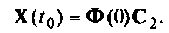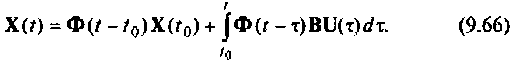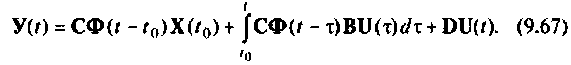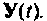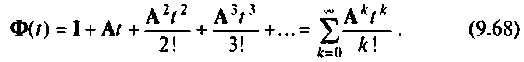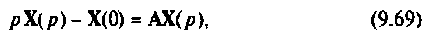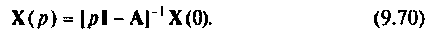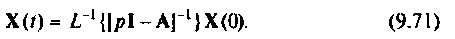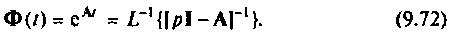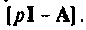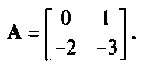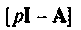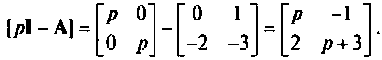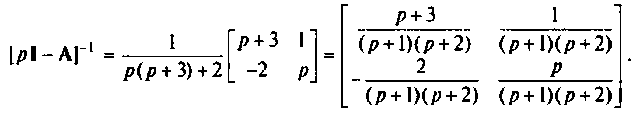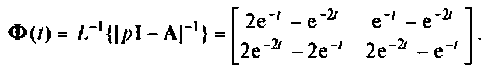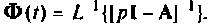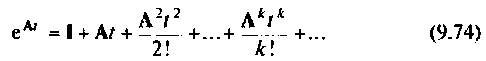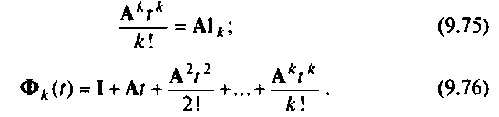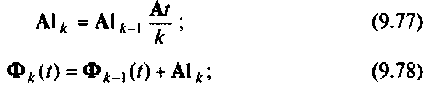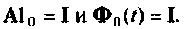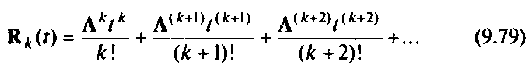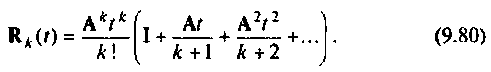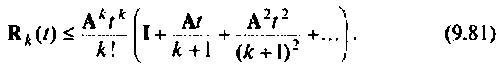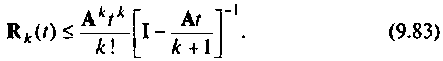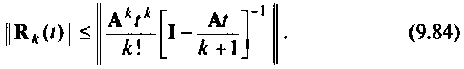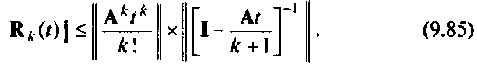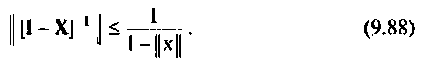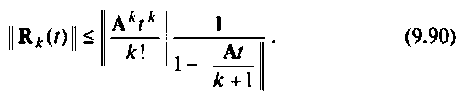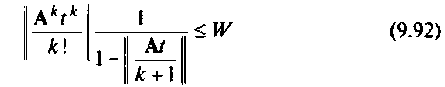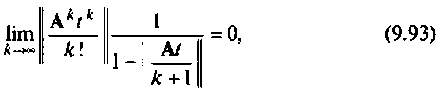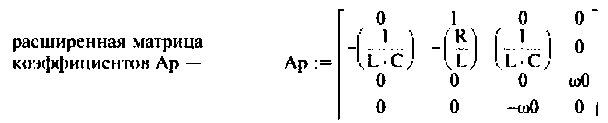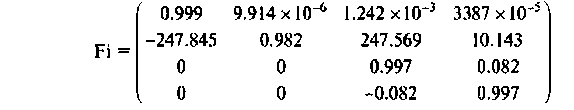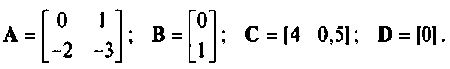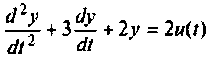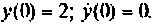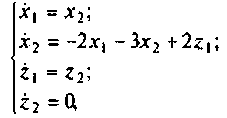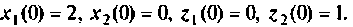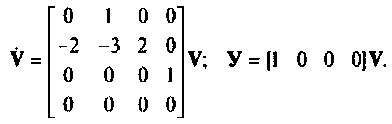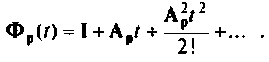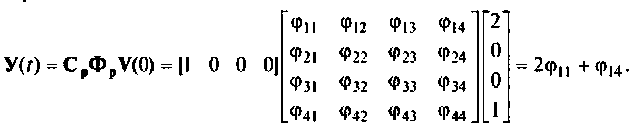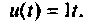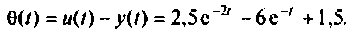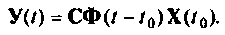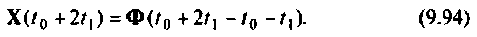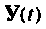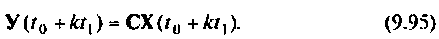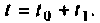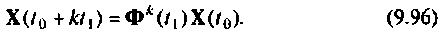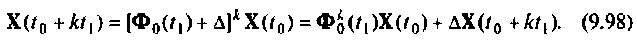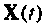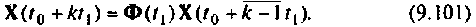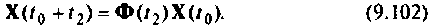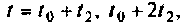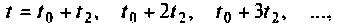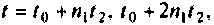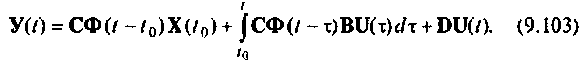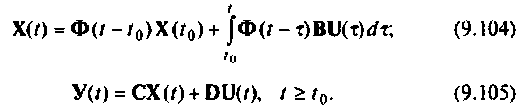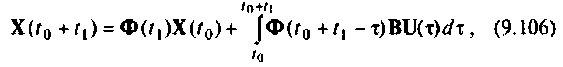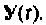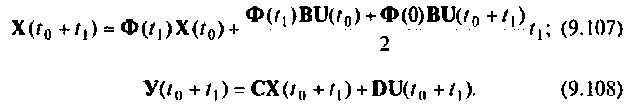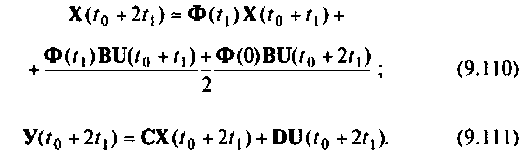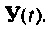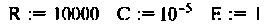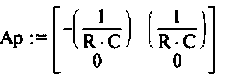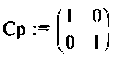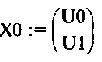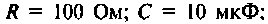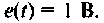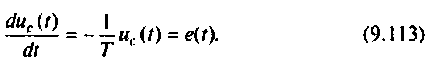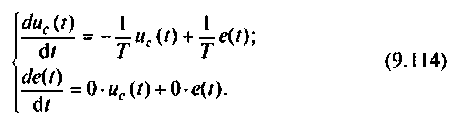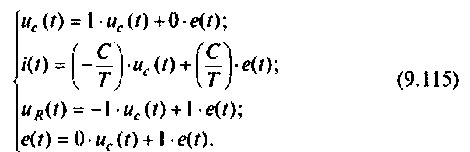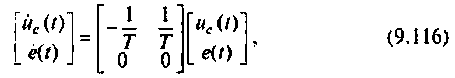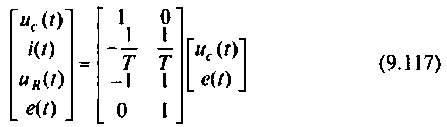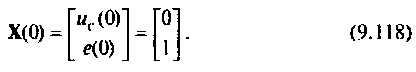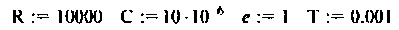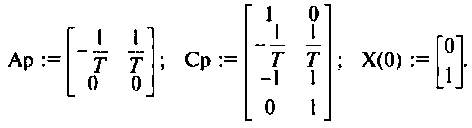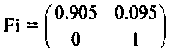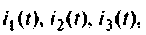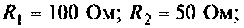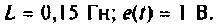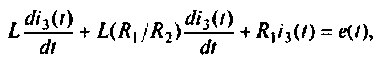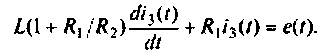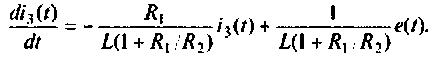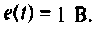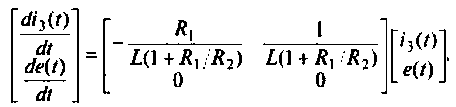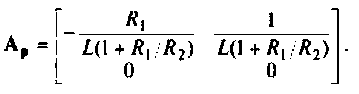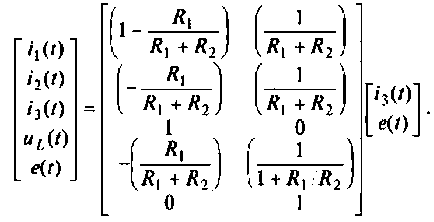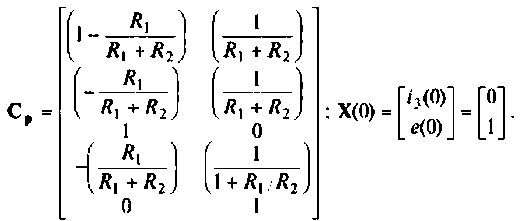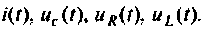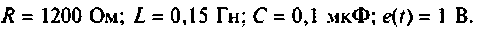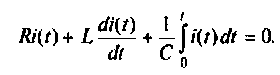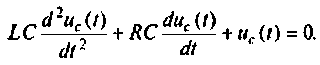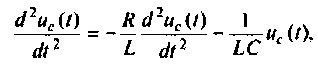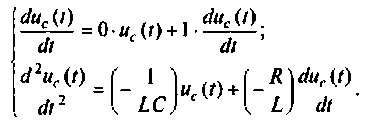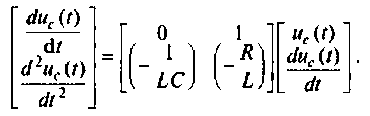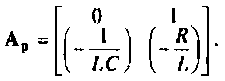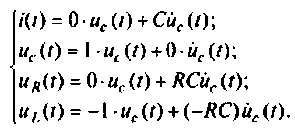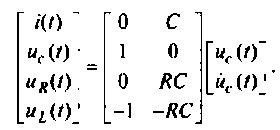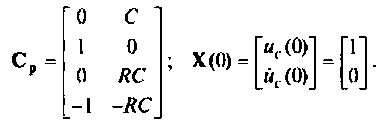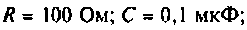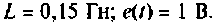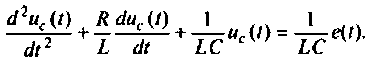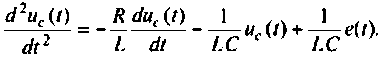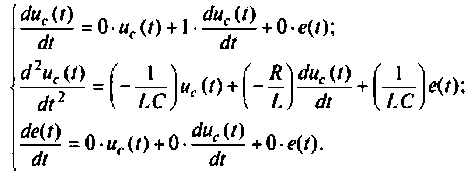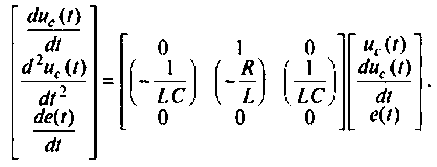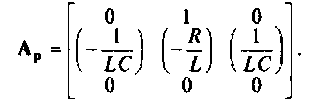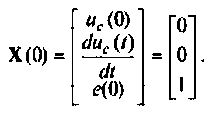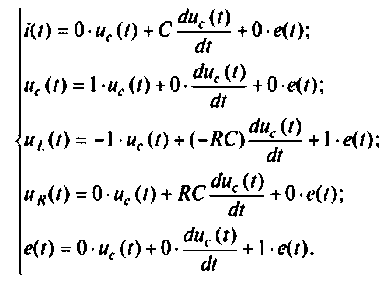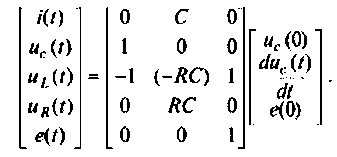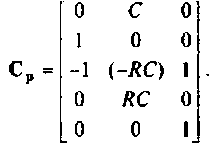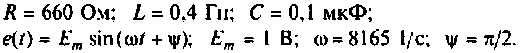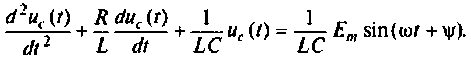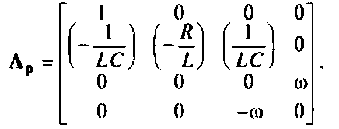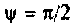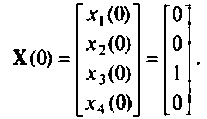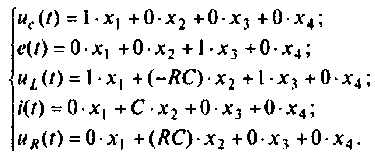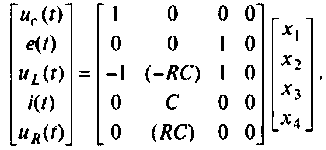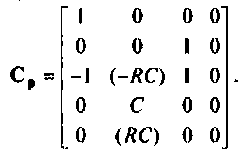Пространство состояний в задачах проектирования систем оптимального управления
Время на прочтение
6 мин
Количество просмотров 18K
Введение
Исследование системы управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа.
Состоянию системы соответствует точка в определённом евклидовом пространстве, а поведение системы во времени характеризуется траекторией, описываемой этой точкой.
При этом математический аппарат включает готовые решения по аналоговому и дискретному LQR и DLQR контролерам, фильтра Калмана, и всё это с применением матриц и векторов, что и позволяет записывать уравнения системы управления в обобщённом виде, получая дополнительную информацию при их решении.
Целью данной публикации является рассмотрение решения задач проектирования систем оптимального управления методом описания пространства состояний с использованием программных средств Python.
Теория кратко
Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:
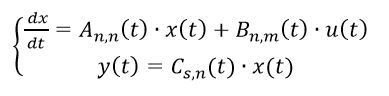
Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным объектом. В противном случае объект будет нестационарным.
При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:

где y(t) – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).
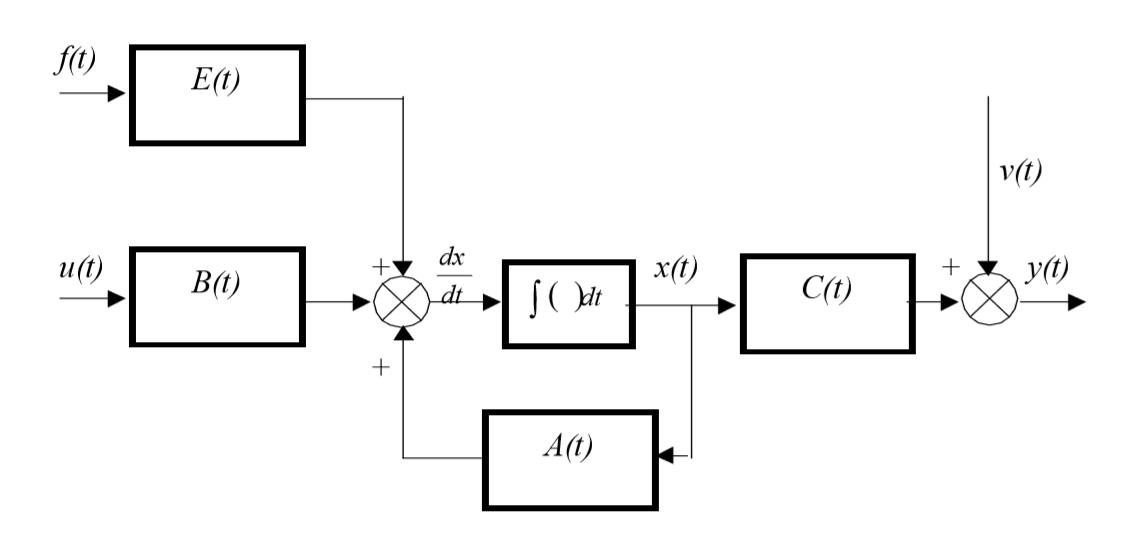
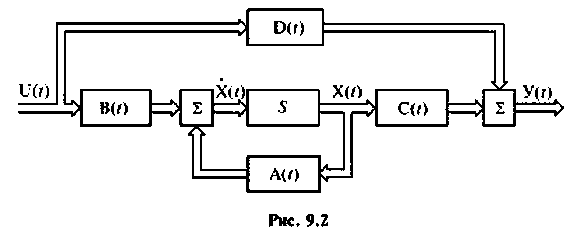
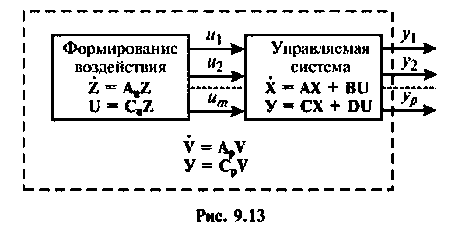
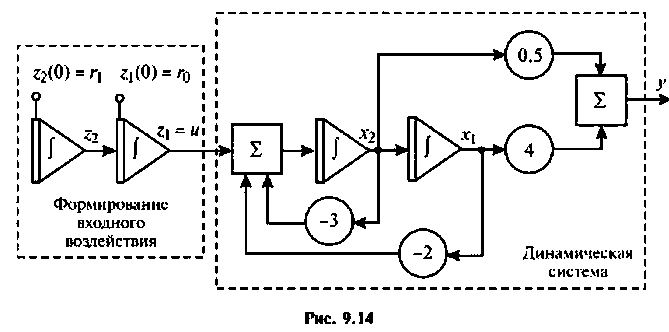
Структура линейной непрерывной системы, реализующая уравнения (1) и (2), приведена на рисунке:
Данная структура соответствует математической модели объекта, построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).
Для примера рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов. Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть так:
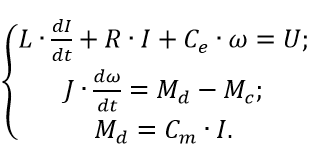
Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе — условия механического равновесия. В качестве обобщенных координат выберем ток якоря I и частоту вращения якоря ω.
Управлением являются напряжение на якоре U, возмущением — момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см (в системе СИ: Cе=См).
Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.
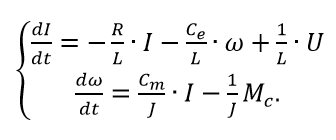
В матричном виде уравнения (4) примут вид (1):
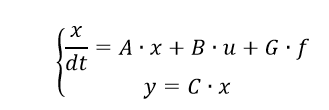
где вектор обобщенных координат 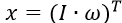
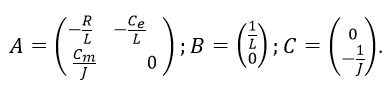
Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде:

а матрица измерений примет вид:
C=(0 1)
Сформируем модель двигателя в Python. Для этого вначале зададим конкретные значения параметров двигателя: U = 110 В; R =0,2 Ом; L = 0,006 Гн; J =0,1 кг/м2;Ce =Cm=1,3 В/С и найдем значения коэффициентом матриц объекта из (6).
Разработка программы формирующей модель двигателя с проверкой матриц на наблюдаемость и управляемость:
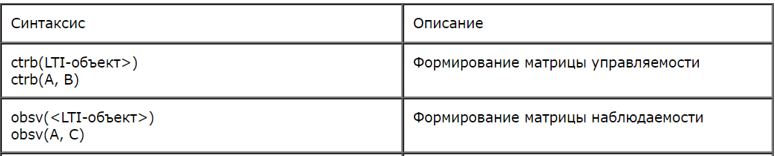
При разработке программы использовалась специальная функция def matrix_rank для определения ранга матрицы и функции, приведенные в таблице:
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from numpy.linalg import svd
from numpy import sum,where
import matplotlib.pyplot as plt
def matrix_rank(a, tol=1e-8):
s = svd(a, compute_uv=0)
return sum( where( s>tol, 1, 0) )
u=110 # Напряжение якоря
J=.1 # Момент инерции
c=1.3; # Конструктивный коэффициент
R=.2; L=.006 # Активное сопротивление и индуктивность якоря
A=matrix([[-R/L ,-c/L],[ c/J ,0]])
print ('Матрица А : n %s'%A)
B=matrix([[1/L],[0]])
print ('Матрица B : n %s '%B)
C=matrix([[0, 1]])
print ('Матрица C : n %s '%C)
D=0
print ('Скаляр D : n %s '%D)
sd=ss(A,B,C,D) #Задание модели объекта в пространстве состояний
wd=tf(sd) # Задание передаточной функции двигателя
print ('Передаточная функция двигателя : n %s '%wd)
a=ctrb(A,B)
print(' Ранг матрицы управляемости : %s'%matrix_rank(a, tol=1e-8))
a=obsv(A,C)
print('Ранг матрицы наблюдаемости: %s'%matrix_rank(a, tol=1e-8))
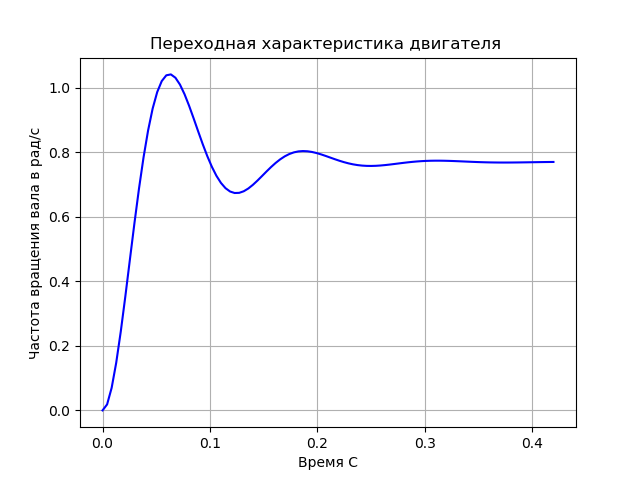
y,x=step(wd) # Построение переходной характеристики
plt.plot(x,y,"b")
plt.title('Переходная характеристика двигателя ')
plt.ylabel('Частота вращения вала в рад/с')
plt.xlabel('Время С')
plt.grid(True)
plt.show()Результаты работы программы:
Матрица А:
[[ -33.33333333 -216.66666667]
[ 13. 0. ]]
Матрица B:
[[166.66666667]
[ 0. ]]
Матрица C:
[[0 1]]
Скаляр D:
0
Передаточная функция двигателя:
2167/(s^2 + 33.33 s + 2817)
Ранг матрицы управляемости: 2
Ранг матрицы наблюдаемости: 2
Выводы:
1. На примере двигателя постоянного тока с независимым магнитным возбуждением рассмотрена методика проектирования управления в пространстве состояний;
2. В результате работы программы получены передаточная функция, переходная характеристика, а так же ранги матриц управляемости и наблюдаемости. Ранги совпадают с размерностями пространства состояний, что подтверждает управляемость и наблюдаемость модели.
Пример проектирования оптимальной системы управления с дискретным dlqr контролером и полной обратной связью
Определения и терминология
Линейно-квадратичный регулятор (англ. Linear quadratic regulator, LQR) — в теории управления один из видов оптимальных регуляторов, использующий квадратичный функционал качества.
Задача, в которой система описывается линейными дифференциальными уравнениями, а показатель качества, представляет собой квадратичный функционал, называется задачей линейно-квадратичного управления.
Широкое распространение получили линейно-квадратичные регуляторы (LQR) и линейно-квадратичные гауссовы регуляторы (LQG).
Приступая к практическому решению задачи всегда нужно помнить об ограничениях
Для синтеза оптимального дискретного регулятора линейных стационарных систем нужна функция численного решения уравнения Беллмана.Такой функции в библиотеке Python Control Systems [1] нет, но можно воспользоваться функцией для решения уравнения Риккати, приведенной в публикации [2]:
def dlqr(A,B,Q,R):
"""Solve the discrete time lqr controller.
x[k+1] = A x[k] + B u[k]
cost = sum x[k].T*Q*x[k] + u[k].T*R*u[k]
"""
#ref Bertsekas, p.151
#first, try to solve the ricatti equation
X = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#compute the LQR gain
K = np.matrix(scipy.linalg.inv(B.T*X*B+R)*(B.T*X*A))
eigVals, eigVecs = scipy.linalg.eig(A-B*K)
return K, X, eigVals
Но нужно ещё учесть ограничения на синтез оптимального регулятора, приведенные в [3]:
- система, определяемая матрицами (A, B) должна быть стабилизируема;
- должны выполняться неравенства S> 0, Q – N/R–N.T>0, пара матриц (Q – N/R–N.T,
A – B/R–B.T) не должна иметь наблюдаемые моды с собственными значениями на
действительной оси.
После копаний в обширной и не однозначной теории, которую, по понятным причинам, я не привожу, задачу удалось решить, и все ответы можно прочитать прямо в комментариях к коду.
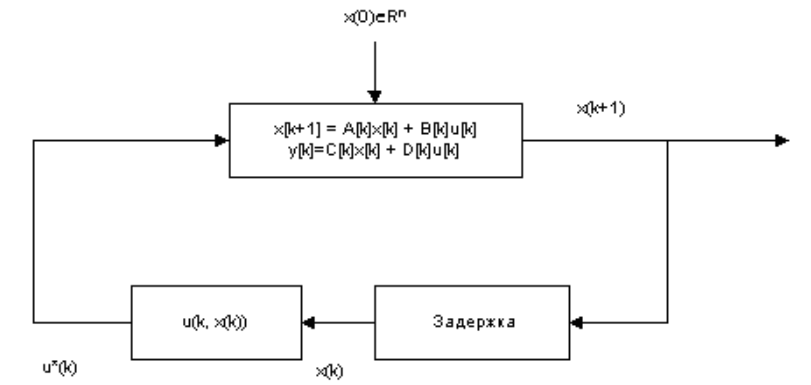
Структурная схема регулятора системы управления с обратной связью по всем переменным состояния изображена на рисунке:
Для каждого начального состояния x0 оптимальный линейный регулятор порождает оптимальное программное управление u*(x, k) и оптимальную траекторию х*(k).
Программа, формирующая модель оптимального управления с dlqr контролером
from numpy import *
import scipy.linalg
import matplotlib.pyplot as plt
def dlqr(A,B,Q,R):
#Дискретное решение матричного уравнения Риккати x[k+1] = A x[k] + B u[k]
P= matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#Дискретный контроллер DLQR
K = matrix(scipy.linalg.inv(B.T*P*B+R)*(B.T*P*A))
E, E1 = scipy.linalg.eig(A-B*K)
return K, P, E
"""Параметры системы"""
A=matrix([[1, 0],[ -2 ,1]])
B=matrix([[1, 0],[1, 0]]).T
"""Параметры качества управления"""
Q=matrix([[0.5, 0],[0, 0.5]])
R=matrix([[0.5,0],[0, 0.5]])
T =100# Время регулирования
SS=0.5# Величина шаг
N =int(T/SS)# Количество шагов
K, P, E=dlqr(A,B,Q,R)#Вычисление параметров контроллера
print("K= n%s"%K)
print("P= n%s"%P)
print("E= n%s"%E)
x = zeros([2, N])
u= zeros([2, N-1])
x [0,0]=2
x [1,0]=1
for i in arange(0,N-2):
u[:, i]= dot(- K,x[:, i])
x[:, i+1]=dot(A,x[:, i])+dot(B,u[:, i])
x1= x[0,:]
x2= x[1,:]
t = arange(0,T,SS)
t1=arange(0.5,T,SS)
plt.subplot(221)
plt.plot(t, x1, 'b')
plt.grid(True)
plt.subplot(222)
plt.plot(t, x2, 'g')
plt.grid(True)
plt.subplot(223)
plt.plot(t1, u[0,:], 'y')
plt.grid(True)
plt.subplot(224)
plt.plot(t1, u[1,:], 'r')
plt.grid(True)
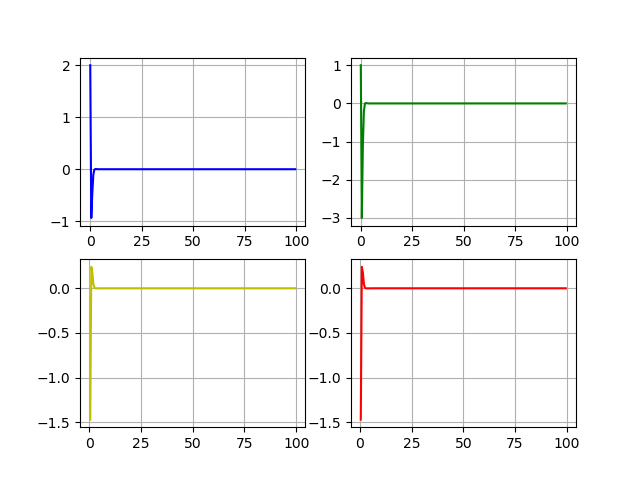
plt.show()
Результаты расчета:
K=
[[ 0.82287566 -0.17712434]
[ 0.82287566 -0.17712434]]
P=
[[ 3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E=
[0.17712434+0.17712434j 0.17712434-0.17712434j]
Динамика состояний и управлений: x1, x2, u1, u2.
Вывод
Отдельные задачи оптимального управления по типу приведенных можно решать средствами Python, комбинируя возможности библиотек Python Control Systems, SciPy,NumPy, что, безусловно, способствует популяризации Python, учитывая, что ранее такие задачи можно было решать только в платных математических пакетах.
Ссылки
- Python Control Systems Library.
- Mark Wilfried Mueller LQR Controllers with Python.
- Е.В.Никульчев. Пособие «Control System Toolbox»
ss
Description
Use ss to create real-valued or complex-valued state-space
models, or to convert dynamic system models to
state-space model form. You can also use ss to create generalized
state-space (genss) models or uncertain state-space
(uss (Robust Control Toolbox)) models.
A state-space model is a mathematical representation of a physical system as a set of
input, output, and state variables related by first-order differential equations. The state
variables define the values of the output variables. The ss model object
can represent SISO or MIMO state-space models in continuous time or discrete time.
In continuous-time, a state-space model is of the following form:
Here, x, u and y
represent the states, inputs and outputs respectively, while A,
B, C and D are the state-space
matrices. The ss object represents a state-space model in MATLAB® storing A, B, C and
D along with other information such as sample time, names and delays
specific to the inputs and outputs.
You can create a state-space model object by either specifying the state, input and output
matrices directly, or by converting a model of another type (such as a transfer function model
tf) to state-space form. For more information, see State-Space Models. You
can use an ss model object to:
-
Perform linear analysis
-
Represent a linear time-invariant (LTI) model to perform control design
-
Combine with other LTI models to represent a more complex system
Creation
Syntax
Description
example
sys = ss(A,B,C,D)
creates a continuous-time state-space model object of the following form:
For instance, consider a plant with Nx states,
Ny outputs, and Nu inputs. The state-space
matrices are:
-
Ais anNx-by-Nxreal-
or complex-valued matrix. -
Bis anNx-by-Nureal-
or complex-valued matrix. -
Cis anNy-by-Nxreal-
or complex-valued matrix. -
Dis anNy-by-Nureal-
or complex-valued matrix.
example
sys = ss(A,B,C,D,ts)
creates the discrete-time state-space model object of the following form with the sample
time ts (in seconds):
To leave the sample time unspecified, set ts to
-1.
example
sys = ss(A,B,C,D,ltiSys)
creates a state-space model with properties such as input and output names, internal
delays and sample time values inherited from the model ltisys.
example
sys = ss(D)
state-space model that represents the static gain, D. The output
state-space model is equivalent to ss([],[],[],D).
example
sys = ss(___,Name,Value)
sets properties of the state-space model using one or more
Name,Value pair arguments for any of the previous input-argument
combinations.
example
sys = ss(ltiSys)
converts the dynamic system model ltiSys to a state-space model. If
ltiSys contains tunable or uncertain elements,
ss uses the current or nominal values for those elements
respectively.
example
sys = ss(ltiSys,component)
converts to ss object form the measured component, the noise
component or both of specified component of an identified linear
time-invariant (LTI) model ltiSys. Use this syntax only when
ltiSys is an identified (LTI) model such as an idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox) or idgrey (System Identification Toolbox) object.
sys = ss(ssSys,'minimal')
returns the minimal state-space realization with no uncontrollable or unobservable
states. This realization is equivalent to minreal(ss(sys)) where
matrix A has the smallest possible dimension.
Conversion to state-space form is not uniquely defined in the SISO case. It is also
not guaranteed to produce a minimal realization in the MIMO case. For more information,
see Recommended Working Representation.
example
sys = ss(ssSys,'explicit')
returns an explicit state-space realization (E = I) of the dynamic
system state-space model ssSys. ss returns an
error if ssSys is improper. For more information on explicit
state-space realization, see State-Space Models.
Input Arguments
expand all
A — State matrix
Nx-by-Nx matrix
State matrix, specified as an Nx-by-Nx
matrix where, Nx is the number of states. This input sets the value
of property A.
B — Input-to-state matrix
Nx-by-Nu matrix
Input-to-state matrix, specified as an
Nx-by-Nu matrix where, Nx
is the number of states and Nu is the number of inputs. This input
sets the value of property B.
C — State-to-output matrix
Ny-by-Nx matrix
State-to-output matrix, specified as an
Ny-by-Nx matrix where, Nx
is the number of states and Ny is the number of outputs. This input
sets the value of property C.
D — Feedthrough matrix
Ny-by-Nu matrix
Feedthrough matrix, specified as an Ny-by-Nu
matrix where, Ny is the number of outputs and Nu
is the number of inputs. This input sets the value of property D.
ts — Sample time
scalar
Sample time, specified as a scalar. For more information, see Ts
property.
ltiSys — Dynamic system to convert to state-space form
dynamic system model | model array
Dynamic system to convert to state-space form, specified as a SISO or MIMO dynamic system model or array of dynamic system
models. Dynamic systems that you can convert include:
-
Continuous-time or discrete-time numeric LTI models, such as
tf,zpk,ss, or
pidmodels. -
Generalized or uncertain LTI models such as
genssoruss(Robust Control Toolbox) models. (Using uncertain models
requires Robust Control Toolbox™ software.)The resulting state-space model assumes
-
current values of the tunable components for tunable control design
blocks. -
nominal model values for uncertain control design blocks.
-
-
Identified LTI models, such as
idtf(System Identification Toolbox),idss(System Identification Toolbox),idproc(System Identification Toolbox),idpoly(System Identification Toolbox), andidgrey(System Identification Toolbox) models. To select the
component of the identified model to convert, specify
component. If you do not specify
component,ssconverts the measured
component of the identified model by default. (Using identified models requires System Identification Toolbox™ software.)
component — Component of identified model
'measured' (default) | 'noise' | 'augmented'
Component of identified model to convert, specified as one of the
following:
-
'measured'— Convert the measured component of
sys. -
'noise'— Convert the noise component of
sys -
'augmented'— Convert both the measured and noise
components ofsys.
component only applies when sys is an
identified LTI model.
For more information on identified LTI models and their measured and noise
components, see Identified LTI Models.
ssSys — Dynamic system model to convert to minimal realization or explicit form
ss model object
Dynamic system model to convert to minimal realization or explicit form, specified
as an ss model object.
Output Arguments
expand all
sys — Output system model
ss model object | genss model object | uss model object
Output system model, returned as:
-
A state-space (
ss) model object, when the inputs
A,B,Cand
Dare numeric matrices or when converting from another
model object type. -
A generalized state-space model (
genss) object, when one
or more of the matricesA,B,
CandDincludes tunable parameters,
such asrealpparameters or generalized
matrices (genmat). For an example, see
Create State-Space Model with Both Fixed and Tunable Parameters. -
An uncertain state-space model (
uss) object, when one or
more of the inputsA,B,
CandDincludes uncertain matrices.
Using uncertain models requires Robust Control Toolbox software.
Properties
expand all
A — State matrix
Nx-by-Nx matrix
State matrix, specified as an Nx-by-Nx matrix
where Nx is the number of states. The state-matrix can be represented
in many ways depending on the desired state-space model realization such as:
-
Model Canonical Form
-
Companion Canonical Form
-
Observable Canonical Form
-
Controllable Canonical Form
For more information, see State-Space Realizations.
B — Input-to-state matrix
Nx-by-Nu matrix
Input-to-state matrix, specified as an
Nx-by-Nu matrix where Nx is
the number of states and Nu is the number of inputs.
C — State-to-output matrix
Ny-by-Nx matrix
State-to-output matrix, specified as an
Ny-by-Nx matrix where Nx is
the number of states and Ny is the number of outputs.
D — Feedthrough matrix
Ny-by-Nu matrix
Feedthrough matrix, specified as an Ny-by-Nu
matrix where Ny is the number of outputs and Nu is
the number of inputs. D is also called as the static gain matrix
which represents the ratio of the output to the input under steady state
condition.
E — Matrix for implicit state-space models
[] (default) | Nx-by-Nx matrix
Matrix for implicit or descriptor state-space models, specified as a
Nx-by-Nx matrix. E is empty
by default, meaning that the state equation is explicit. To specify an implicit state
equation E
dx/dt = Ax +
Bu, set this property to a square matrix of the same size as
A. See dss for more information about creating
descriptor state-space models.
Scaled — Logical value indicating whether scaling is enabled or disabled
0 (default) | 1
Logical value indicating whether scaling is enabled or disabled, specified as either
0 or 1.
When Scaled is set to 0 (disabled), then most
numerical algorithms acting on the state-space model sys
automatically rescale the state vector to improve numerical accuracy. You can prevent
such auto-scaling by setting Scaled to 1
(enabled).
For more information about scaling, see prescale.
StateName — State names
' ' (default) | character vector | cell array of character vectors
State names, specified as one of the following:
-
Character vector — For first-order models, for example,
'velocity' -
Cell array of character vectors — For models with two or more states
StateName is empty ' ' for all states by
default.
StatePath — State path
' ' (default) | character vector | cell array of character vectors
State path to facilitate state block path management in linearization, specified as
one of the following:
-
Character vector — For first-order models
-
Cell array of character vectors — For models with two or more states
StatePath is empty ' ' for all states by
default.
StateUnit — State units
' ' (default) | character vector | cell array of character vectors
State units, specified as one of the following:
-
Character vector — For first-order models, for example,
'm/s' -
Cell array of character vectors — For models with two or more states
Use StateUnit to keep track of the units of each state.
StateUnit has no effect on system behavior.
StateUnit is empty ' ' for all states by
default.
InternalDelay — Internal delays in the model
vector
Internal delays in the model, specified as a vector. Internal delays arise, for
example, when closing feedback loops on systems with delays, or when connecting delayed
systems in series or parallel. For more information about internal delays, see Closing Feedback Loops with Time Delays.
For continuous-time models, internal delays are expressed in the time unit specified
by the TimeUnit property of the model. For discrete-time models,
internal delays are expressed as integer multiples of the sample time
Ts. For example, InternalDelay = 3 means a delay
of three sampling periods.
You can modify the values of internal delays using the property
InternalDelay. However, the number of entries in
sys.InternalDelay cannot change, because it is a structural
property of the model.
InputDelay — Input delay
0 (default) | scalar | Nu-by-1 vector
Input delay for each input channel, specified as one of the following:
-
Scalar — Specify the input delay for a SISO system or the same delay for all inputs of a multi-input system.
-
Nu-by-1 vector — Specify separate input delays for input of a multi-input system, whereNuis the number of inputs.
For continuous-time systems, specify input delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify input delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
OutputDelay — Output delay
0 (default) | scalar | Ny-by-1 vector
Output delay for each output channel, specified as one of the following:
-
Scalar — Specify the output delay for a SISO system or the same delay for all outputs of a multi-output system.
-
Ny-by-1 vector — Specify separate output delays for output of a multi-output system, whereNyis the number of outputs.
For continuous-time systems, specify output delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify output delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Ts — Sample time
0 (default) | positive scalar | -1
Sample time, specified as:
-
0for continuous-time systems. -
A positive scalar representing the sampling period of a discrete-time system. Specify
Tsin the time unit specified by theTimeUnitproperty. -
-1for a discrete-time system with an unspecified sample time.
Note
Changing Ts does not discretize or resample the model. To
convert between continuous-time and discrete-time representations, use c2d and d2c. To change the sample time of a
discrete-time system, use d2d.
TimeUnit — Time variable units
'seconds' (default) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | …
Time variable units, specified as one of the following:
-
'nanoseconds' -
'microseconds' -
'milliseconds' -
'seconds' -
'minutes' -
'hours' -
'days' -
'weeks' -
'months' -
'years'
Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.
InputName — Input channel names
'' (default) | character vector | cell array of character vectors
Input channel names, specified as one of the following:
-
A character vector, for single-input models.
-
A cell array of character vectors, for multi-input models.
-
'', no names specified, for any input channels.
Alternatively, you can assign input names for multi-input models using automatic vector
expansion. For example, if sys is a two-input model, enter the
following:
sys.InputName = 'controls';
The input names automatically expand to {'controls(1)';'controls(2)'}.
You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.
Use InputName to:
-
Identify channels on model display and plots.
-
Extract subsystems of MIMO systems.
-
Specify connection points when interconnecting models.
InputUnit — Input channel units
'' (default) | character vector | cell array of character vectors
Input channel units, specified as one of the following:
-
A character vector, for single-input models.
-
A cell array of character vectors, for multi-input models.
-
'', no units specified, for any input channels.
Use InputUnit to specify input signal units. InputUnit has no effect on system behavior.
InputGroup — Input channel groups
structure
Input channel groups, specified as a structure. Use InputGroup to assign
the input channels of MIMO systems into groups and refer to each group by name. The
field names of InputGroup are the group names and the field values
are the input channels of each group. For example, enter the following to create input
groups named controls and noise that include input
channels 1 and 2, and 3 and
5, respectively.
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
You can then extract the subsystem from the controls inputs to all outputs
using the following.
By default, InputGroup is a structure with no fields.
OutputName — Output channel names
'' (default) | character vector | cell array of character vectors
Output channel names, specified as one of the following:
-
A character vector, for single-output models.
-
A cell array of character vectors, for multi-output models.
-
'', no names specified, for any output channels.
Alternatively, you can assign output names for multi-output models using automatic vector
expansion. For example, if sys is a two-output model, enter the
following.
sys.OutputName = 'measurements';
The output names automatically expand to {'measurements(1)';'measurements(2)'}.
You can also use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.
Use OutputName to:
-
Identify channels on model display and plots.
-
Extract subsystems of MIMO systems.
-
Specify connection points when interconnecting models.
OutputUnit — Output channel units
'' (default) | character vector | cell array of character vectors
Output channel units, specified as one of the following:
-
A character vector, for single-output models.
-
A cell array of character vectors, for multi-output models.
-
'', no units specified, for any output channels.
Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.
OutputGroup — Output channel groups
structure
Output channel groups, specified as a structure. Use OutputGroupto assign
the output channels of MIMO systems into groups and refer to each group by name. The
field names of OutputGroup are the group names and the field values
are the output channels of each group. For example, create output groups named
temperature and measurement that include
output channels 1, and 3 and 5,
respectively.
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
You can then extract the subsystem from all inputs to the measurement
outputs using the following.
By default, OutputGroup is a structure with no fields.
Name — System name
'' (default) | character vector
System name, specified as a character vector. For example, 'system_1'.
Notes — User-specified text
{} (default) | character vector | cell array of character vectors
User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.
UserData — User-specified data
[] (default) | any MATLAB data type
User-specified data that you want to associate with the system, specified as any MATLAB data type.
SamplingGrid — Sampling grid for model arrays
structure array
Sampling grid for model arrays, specified as a structure array.
Use SamplingGrid to track the variable values associated with each model in a model array, including identified linear time-invariant (IDLTI) model arrays.
Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.
For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.
sysarr.SamplingGrid = struct('time',0:10)
Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
When you display M, each entry in the array includes the corresponding zeta and w values.
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...
For model arrays generated by linearizing a Simulink® model at multiple parameter values or operating points, the software populates SamplingGrid automatically with the variable values that correspond to each entry in the array. For instance, the Simulink
Control Design™ commands linearize (Simulink Control Design) and slLinearizer (Simulink Control Design) populate SamplingGrid automatically.
By default, SamplingGrid is a structure with no fields.
Object Functions
The following lists contain a representative subset of the functions you can use with
ss model objects. In general, any function applicable to Dynamic System Models is
applicable to an ss object.
expand all
Linear Analysis
step |
Step response plot of dynamic system; step response data |
impulse |
Impulse response plot of dynamic system; impulse response data |
lsim |
Plot simulated time response of dynamic system to arbitrary inputs; simulated response data |
bode |
Bode plot of frequency response, or magnitude and phase data |
nyquist |
Nyquist plot of frequency response |
nichols |
Nichols chart of frequency response |
bandwidth |
Frequency response bandwidth |
Stability Analysis
pole |
Poles of dynamic system |
zero |
Zeros and gain of SISO dynamic system |
pzplot |
Pole-zero plot of dynamic system model with additional plot customization options |
margin |
Gain margin, phase margin, and crossover frequencies |
Model Transformation
zpk |
Zero-pole-gain model |
tf |
Transfer function model |
c2d |
Convert model from continuous to discrete time |
d2c |
Convert model from discrete to continuous time |
d2d |
Resample discrete-time model |
Model Interconnection
feedback |
Feedback connection of multiple models |
connect |
Block diagram interconnections of dynamic systems |
series |
Series connection of two models |
parallel |
Parallel connection of two models |
Controller Design
pidtune |
PID tuning algorithm for linear plant model |
rlocus |
Root locus plot of dynamic system |
lqr |
Linear-Quadratic Regulator (LQR) design |
lqg |
Linear-Quadratic-Gaussian (LQG) design |
lqi |
Linear-Quadratic-Integral control |
kalman |
Design Kalman filter for state estimation |
Examples
collapse all
SISO State-Space Model
Create the SISO state-space model defined by the following state-space matrices:
A=[-1.5-210]B=[0.50]C=[01]D=0
Specify the A, B, C and D matrices, and create the state-space model.
A = [-1.5,-2;1,0]; B = [0.5;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2
x1 -1.5 -2
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Continuous-time state-space model.
Create Discrete-Time State-Space Model
Create a state-space model with a sample time of 0.25 seconds and the following state-space matrices:
A=[01-5-2]B=[03]C=[01]D=[0]
Specify the state-space matrices.
A = [0 1;-5 -2]; B = [0;3]; C = [0 1]; D = 0;
Specify the sample time.
Create the state-space model.
Continuous-Time MIMO State-Space Model
For this example, consider a cube rotating about its corner with inertia tensor J and a damping force F of 0.2 magnitude. The input to the system is the driving torque while the angular velocities are the outputs. The state-space matrices for the cube are:
A=-J-1F,B=J-1,C=I,D=0,where,J=[8-3-3-38-3-3-38]andF=[0.20000.20000.2]
Specify the A, B, C and D matrices, and create the continuous-time state-space model.
J = [8 -3 -3; -3 8 -3; -3 -3 8]; F = 0.2*eye(3); A = -JF; B = inv(J); C = eye(3); D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2 x3
x1 -0.04545 -0.02727 -0.02727
x2 -0.02727 -0.04545 -0.02727
x3 -0.02727 -0.02727 -0.04545
B =
u1 u2 u3
x1 0.2273 0.1364 0.1364
x2 0.1364 0.2273 0.1364
x3 0.1364 0.1364 0.2273
C =
x1 x2 x3
y1 1 0 0
y2 0 1 0
y3 0 0 1
D =
u1 u2 u3
y1 0 0 0
y2 0 0 0
y3 0 0 0
Continuous-time state-space model.
sys is MIMO since the system contains 3 inputs and 3 outputs observed from matrices C and D. For more information on MIMO state-space models, see MIMO State-Space Models.
Discrete-Time MIMO State-Space Model
Create a state-space model using the following discrete-time, multi-input, multi-output state matrices with sample time ts = 0.2 seconds:
A=[-700-10]B=[5002]C=[1-4-40.5]D=[0-220]
Specify the state-space matrices and create the discrete-time MIMO state-space model.
A = [-7,0;0,-10]; B = [5,0;0,2]; C = [1,-4;-4,0.5]; D = [0,-2;2,0]; ts = 0.2; sys = ss(A,B,C,D,ts)
sys =
A =
x1 x2
x1 -7 0
x2 0 -10
B =
u1 u2
x1 5 0
x2 0 2
C =
x1 x2
y1 1 -4
y2 -4 0.5
D =
u1 u2
y1 0 -2
y2 2 0
Sample time: 0.2 seconds
Discrete-time state-space model.
Specify State and Input Names for State-Space Model
Create state-space matrices and specify sample time.
A = [0 1;-5 -2]; B = [0;3]; C = [0 1]; D = 0; Ts = 0.05;
Create the state-space model, specifying the state and input names using name-value pairs.
sys = ss(A,B,C,D,Ts,'StateName',{'Position' 'Velocity'},... 'InputName','Force');
The number of state and input names must be consistent with the dimensions of A, B, C, and D.
Naming the inputs and outputs can be useful when dealing with response plots for MIMO systems.
Notice the input name Force in the title of the step response plot.
State-Space Model with Inherited Properties
For this example, create a state-space model with the same time and input unit properties inherited from another state-space model. Consider the following state-space models:
A1=[-1.5-210]B1=[0.50]C1=[01]D1=5A2=[7-102]B2=[0.852]C2=[1014]D2=2
First, create a state-space model sys1 with the TimeUnit and InputUnit property set to ‘minutes‘.
A1 = [-1.5,-2;1,0]; B1 = [0.5;0]; C1 = [0,1]; D1 = 5; sys1 = ss(A1,B1,C1,D1,'TimeUnit','minutes','InputUnit','minutes');
Verify that the time and input unit properties of sys1 are set to ‘minutes‘.
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1x2 cell
{'minutes'} {'minutes'}
Create the second state-space model with properties inherited from sys1.
A2 = [7,-1;0,2]; B2 = [0.85;2]; C2 = [10,14]; D2 = 2; sys2 = ss(A2,B2,C2,D2,sys1);
Verify that the time and input units of sys2 have been inherited from sys1.
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1x2 cell
{'minutes'} {'minutes'}
MIMO Static Gain State-Space Model
In this example, you will create a static gain MIMO state-space model.
Consider the following two-input, two-output static gain matrix:
D=[2435]
Specify the gain matrix and create the static gain state-space model.
D = [2,4;3,5]; sys1 = ss(D)
sys1 =
D =
u1 u2
y1 2 4
y2 3 5
Static gain.
Convert Transfer Function to State-Space Model
Compute the state-space model of the following transfer function:
H(s)=[s+1s3+3s2+3s+2s2+3s2+s+1]
Create the transfer function model.
H = [tf([1 1],[1 3 3 2]) ; tf([1 0 3],[1 1 1])];
Convert this model to a state-space model.
Examine the size of the state-space model.
State-space model with 2 outputs, 1 inputs, and 5 states.
The number of states is equal to the cumulative order of the SISO entries in H(s).
To obtain a minimal realization of H(s), enter
sys = ss(H,'minimal');
size(sys)
State-space model with 2 outputs, 1 inputs, and 3 states.
The resulting model has an order of three, which is the minimum number of states needed to represent H(s). To see this number of states, refactor H(s) as the product of a first-order system and a second-order system.
H(s)=[1s+2001][s+1s2+s+1s2+3s2+s+1]
Extract State-Space Models from Identified Model
For this example, extract the measured and noise components of an identified polynomial model into two separate state-space models.
Load the Box-Jenkins polynomial model ltiSys in identifiedModel.mat.
load('identifiedModel.mat','ltiSys');
ltiSys is an identified discrete-time model of the form: y(t)=BFu(t)+CDe(t), where BF represents the measured component and CD the noise component.
Extract the measured and noise components as state-space models.
sysMeas = ss(ltiSys,'measured')
sysMeas =
A =
x1 x2
x1 1.575 -0.6115
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 -0.2851 0.3916
D =
u1
y1 0
Input delays (sampling periods): 2
Sample time: 0.04 seconds
Discrete-time state-space model.
sysNoise = ss(ltiSys,'noise')
sysNoise =
A =
x1 x2 x3
x1 1.026 -0.26 0.3899
x2 1 0 0
x3 0 0.5 0
B =
v@y1
x1 0.25
x2 0
x3 0
C =
x1 x2 x3
y1 0.319 -0.04738 0.07106
D =
v@y1
y1 0.04556
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time state-space model.
The measured component can serve as a plant model, while the noise component can be used as a disturbance model for control system design.
Explicit Realization of Descriptor State-Space Model
Create a descriptor state-space model (E ≠ I).
a = [2 -4; 4 2]; b = [-1; 0.5]; c = [-0.5, -2]; d = [-1]; e = [1 0; -3 0.5]; sysd = dss(a,b,c,d,e);
Compute an explicit realization of the system (E = I).
syse = ss(sysd,'explicit')
syse =
A =
x1 x2
x1 2 -4
x2 20 -20
B =
u1
x1 -1
x2 -5
C =
x1 x2
y1 -0.5 -2
D =
u1
y1 -1
Continuous-time state-space model.
Confirm that the descriptor and explicit realizations have equivalent dynamics.
bodeplot(sysd,syse,'g--')
Create State-Space Model with Both Fixed and Tunable Parameters
This example shows how to create a state-space genss model having both fixed and tunable parameters.
A=[1a+b0ab],B=[-3.01.5],C=[0.30],D=0,
where a and b are tunable parameters, whose initial values are -1 and 3, respectively.
Create the tunable parameters using realp.
a = realp('a',-1); b = realp('b',3);
Define a generalized matrix using algebraic expressions of a and b.
A is a generalized matrix whose Blocks property contains a and b. The initial value of A is [1 2;0 -3], from the initial values of a and b.
Create the fixed-value state-space matrices.
B = [-3.0;1.5]; C = [0.3 0]; D = 0;
Use ss to create the state-space model.
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 2 states, and the following blocks: a: Scalar parameter, 2 occurrences. b: Scalar parameter, 2 occurrences. Type "ss(sys)" to see the current value and "sys.Blocks" to interact with the blocks.
sys is a generalized LTI model (genss) with tunable parameters a and b.
State-Space Model with Input and Output Delay
For this example, consider a SISO state-space model defined by the following state-space matrices:
A=[-1.5-210]B=[0.50]C=[01]D=0
Considering an input delay of 0.5 seconds and an output delay of 2.5 seconds, create a state-space model object to represent the A, B, C and D matrices.
A = [-1.5,-2;1,0]; B = [0.5;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D,'InputDelay',0.5,'OutputDelay',2.5)
sys =
A =
x1 x2
x1 -1.5 -2
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Input delays (seconds): 0.5
Output delays (seconds): 2.5
Continuous-time state-space model.
You can also use the get command to display all the properties of a MATLAB object.
A: [2x2 double]
B: [2x1 double]
C: [0 1]
D: 0
E: []
Scaled: 0
StateName: {2x1 cell}
StatePath: {2x1 cell}
StateUnit: {2x1 cell}
InternalDelay: [0x1 double]
InputDelay: 0.5000
OutputDelay: 2.5000
InputName: {''}
InputUnit: {''}
InputGroup: [1x1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1x1 struct]
Notes: [0x1 string]
UserData: []
Name: ''
Ts: 0
TimeUnit: 'seconds'
SamplingGrid: [1x1 struct]
For more information on specifying time delay for an LTI model, see Specifying Time Delays.
Stability Analysis of State-Space Systems
For this example, consider a state-space system object that represents the following state matrices:
A=[-1.2-1.60100010],B=[100],C=[00.51.3],D=0,State-space matrices
Create a state-space object sys using the ss command.
A = [-1.2,-1.6,0;1,0,0;0,1,0]; B = [1;0;0]; C = [0,0.5,1.3]; D = 0; sys = ss(A,B,C,D);
Next, compute the closed-loop state-space model for a unit negative gain and find the poles of the closed-loop state-space system object sysFeedback.
sysFeedback = feedback(sys,1); P = pole(sysFeedback)
P = 3×1 complex
-0.2305 + 1.3062i
-0.2305 - 1.3062i
-0.7389 + 0.0000i
The feedback loop for unit gain is stable since all poles have negative real parts. Checking the closed-loop poles provides a binary assessment of stability. In practice, it is more useful to know how robust (or fragile) stability is. One indication of robustness is how much the loop gain can change before stability is lost. You can use the root locus plot to estimate the range of k values for which the loop is stable.
Changes in the loop gain are only one aspect of robust stability. In general, imperfect plant modeling means that both gain and phase are not known exactly. Since modeling errors have the most detrimental effect near the gain crossover frequency (frequency where open-loop gain is 0dB), it also matters how much phase variation can be tolerated at this frequency.
You can display the gain and phase margins on a Bode plot as follows.
For a more detailed example, see Assessing Gain and Phase Margins.
Control Design using State-Space Models
For this example, design a 2-DOF PID controller with a target bandwidth of 0.75 rad/s for a system represented by the following matrices:
A=[-0.5-0.110],B=[10],C=[01],D=0.
Create a state-space object sys using the ss command.
A = [-0.5,-0.1;1,0]; B = [1;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2
x1 -0.5 -0.1
x2 1 0
B =
u1
x1 1
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Continuous-time state-space model.
Using the target bandwidth, use pidtune to generate a 2-DOF controller.
wc = 0.75;
C2 = pidtune(sys,'PID2',wc)
C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 0.513, Ki = 0.0975, Kd = 0.577, b = 0.344, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Using the type 'PID2' causes pidtune to generate a 2-DOF controller, represented as a pid2 object. The display confirms this result. The display also shows that pidtune tunes all controller coefficients, including the setpoint weights b and c, to balance performance and robustness.
For interactive PID tuning in the Live Editor, see the Tune PID Controller Live Editor task. This task lets you interactively design a PID controller and automatically generates MATLAB code for your live script.
For interactive PID tuning in a standalone app, use PID Tuner. See PID Controller Design for Fast Reference Tracking for an example of designing a controller using the app.
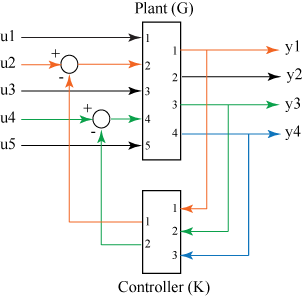
Connect Specific Inputs and Outputs of State-Space Models in a Feedback Loop
Consider a state-space plant G with five inputs and four outputs and a state-space feedback controller K with three inputs and two outputs. The outputs 1, 3, and 4 of the plant G must be connected the controller K inputs, and the controller outputs to inputs 4 and 2 of the plant.
For this example, consider two continuous-time state-space models for both G and K represented by the following set of matrices:
AG=[-30.40.3-0.5-2.8-0.80.20.8-3],BG=[0.400.30.20-0.2-10.1-0.9-0.50.60.90.50.20],CG=[0-0.1-10-0.21.6-0.71.51.2-1.4-0.20],DG=[0000-100.4-0.700.900.30000.20000]
AK=[-0.22.10.7-2.2-0.1-2.2-0.42.3-0.2],BK=[-0.1-2.1-0.3-0.100.6100.8],CK=[-100-0.4-0.20.3],DK=[00000-1.2]
AG = [-3,0.4,0.3;-0.5,-2.8,-0.8;0.2,0.8,-3]; BG = [0.4,0,0.3,0.2,0;-0.2,-1,0.1,-0.9,-0.5;0.6,0.9,0.5,0.2,0]; CG = [0,-0.1,-1;0,-0.2,1.6;-0.7,1.5,1.2;-1.4,-0.2,0]; DG = [0,0,0,0,-1;0,0.4,-0.7,0,0.9;0,0.3,0,0,0;0.2,0,0,0,0]; sysG = ss(AG,BG,CG,DG)
sysG =
A =
x1 x2 x3
x1 -3 0.4 0.3
x2 -0.5 -2.8 -0.8
x3 0.2 0.8 -3
B =
u1 u2 u3 u4 u5
x1 0.4 0 0.3 0.2 0
x2 -0.2 -1 0.1 -0.9 -0.5
x3 0.6 0.9 0.5 0.2 0
C =
x1 x2 x3
y1 0 -0.1 -1
y2 0 -0.2 1.6
y3 -0.7 1.5 1.2
y4 -1.4 -0.2 0
D =
u1 u2 u3 u4 u5
y1 0 0 0 0 -1
y2 0 0.4 -0.7 0 0.9
y3 0 0.3 0 0 0
y4 0.2 0 0 0 0
Continuous-time state-space model.
AK = [-0.2,2.1,0.7;-2.2,-0.1,-2.2;-0.4,2.3,-0.2]; BK = [-0.1,-2.1,-0.3;-0.1,0,0.6;1,0,0.8]; CK = [-1,0,0;-0.4,-0.2,0.3]; DK = [0,0,0;0,0,-1.2]; sysK = ss(AK,BK,CK,DK)
sysK =
A =
x1 x2 x3
x1 -0.2 2.1 0.7
x2 -2.2 -0.1 -2.2
x3 -0.4 2.3 -0.2
B =
u1 u2 u3
x1 -0.1 -2.1 -0.3
x2 -0.1 0 0.6
x3 1 0 0.8
C =
x1 x2 x3
y1 -1 0 0
y2 -0.4 -0.2 0.3
D =
u1 u2 u3
y1 0 0 0
y2 0 0 -1.2
Continuous-time state-space model.
Define the feedout and feedin vectors based on the inputs and outputs to be connected in a feedback loop.
feedin = [4 2]; feedout = [1 3 4]; sys = feedback(sysG,sysK,feedin,feedout,-1)
sys =
A =
x1 x2 x3 x4 x5 x6
x1 -3 0.4 0.3 0.2 0 0
x2 1.18 -2.56 -0.8 -1.3 -0.2 0.3
x3 -1.312 0.584 -3 0.56 0.18 -0.27
x4 2.948 -2.929 -2.42 -0.452 1.974 0.889
x5 -0.84 -0.11 0.1 -2.2 -0.1 -2.2
x6 -1.12 -0.26 -1 -0.4 2.3 -0.2
B =
u1 u2 u3 u4 u5
x1 0.4 0 0.3 0.2 0
x2 -0.44 -1 0.1 -0.9 -0.5
x3 0.816 0.9 0.5 0.2 0
x4 -0.2112 -0.63 0 0 0.1
x5 0.12 0 0 0 0.1
x6 0.16 0 0 0 -1
C =
x1 x2 x3 x4 x5 x6
y1 0 -0.1 -1 0 0 0
y2 -0.672 -0.296 1.6 0.16 0.08 -0.12
y3 -1.204 1.428 1.2 0.12 0.06 -0.09
y4 -1.4 -0.2 0 0 0 0
D =
u1 u2 u3 u4 u5
y1 0 0 0 0 -1
y2 0.096 0.4 -0.7 0 0.9
y3 0.072 0.3 0 0 0
y4 0.2 0 0 0 0
Continuous-time state-space model.
State-space model with 4 outputs, 5 inputs, and 6 states.
sys is the resultant closed loop state-space model obtained by connecting the specified inputs and outputs of G and K.
Version History
Introduced before R2006a
Содержание:
Анализ электрических цепей методом пространства состояний:
Все переменные величины, характеризующие динамическую систему G (рис. 9.1) или имеющие определенное к ней отношение, целесообразно разделить на три группы: 1) входные переменные или входные воздействия
Величины 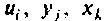
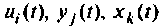
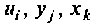
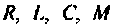
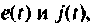
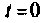
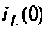
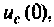
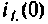
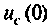
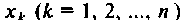
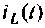
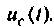
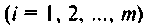
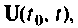
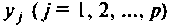
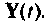
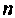
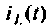
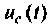
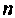
Множество всех значений, которые может принять вектор входа 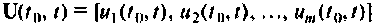
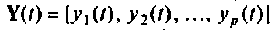
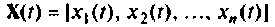
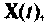
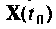
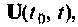
Вектор выхода 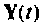
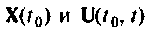
Уравнения (9.1) и (9.2) часто называют уравнениями состояния системы. Для систем, описываемых линейными дифференциальными уравнениями, уравнения состояния (9.1) и (9.2) сводятся к следующим:
где 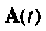
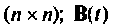
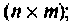
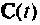
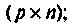
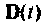
На рис. 9.2 изображена обобщенная схема, динамика которой описывается уравнениями (9.3) и (9.4) [4, 8].
Если система стационарная, то ее динамика описывается уравнениями состояния, матрицы которых имеют элементы, не изменяющиеся во времени, т. е.
Матрица коэффициентов А определяет структуру системы, параметры элементов и их взаимные связи. Динамические свойства системы в основном определяются этой матрицей. Матрица управления В показывает связь управляющих (возмущающих) воздействий 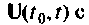
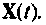
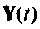
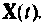
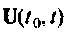
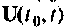
Следует отметить, что уравнения состояния (9.5) и (9.6) — это матричная запись системы линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами, описывающими динамику соответствующей линейной системы а взаимные связи между переменными состояния, входными и выходными величинами.
Уравнения (9.5) и (9.6) принято называть стандартной формой записи уравнений динамики линейных управляемых систем с постоянными параметрами, имеющих произвольную структуру и произвольное число входов и выходов. Стандартная форма отличается компактностью и удобством преобразования. Процедура решения уравнений состояния в конечном итоге сводится к матричным преобразованиям над А, В, С и D, что весьма удобно для программирования на цифровых ЭВМ. Уравнения (9.5) и (9.6) являются исходной информацией при исследовании и проектировании систем управления методом пространства состояний. К такому виду можно привести формы записи уравнений динамики (передаточные функции, дифференциальные уравнения высокого порядка, матричные передаточные функции многомерных систем и т. д.), применяемые в классических методах исследования систем.
Получение уравнений состояния является начальным этапом исследования систем и цепей в современной теории управления.
Методы составления уравнений состояния электрических цепей и динамических систем
Чтобы найти уравнения состояния (9.5) и (9.6), необходимо динамику электрических цепей представить системой дифференциальных уравнений 1-го порядка. В качестве иллюстрации рассмотрим систему третьего порядка, описываемую уравнением
Для записи этого уравнения в векторно-математической форме положим
и тогда вместо уравнения (9.7) с учетом (9.8) получим:
Система уравнений (9.9) совместно с уравнением (9.10) в матричной форме запишется:
Уравнения (9.11) и (9.12) дают конкретный вид матриц А, В, С и D уравнений (9.5) и (9,6).
Приведенный выше метод может с успехом применяться для систем с одним входом и выходом. В многоконтурных системах с несколькими входами и выходами указанная процедура реализуется не так просто поэтому существуют другие способы получения уравнений состояния (9.5) и (9.6).
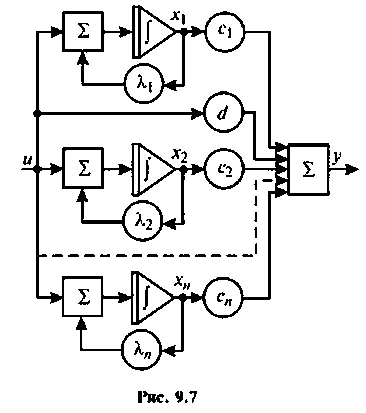
Наиболее распространенным способом получения уравнений состояния исследуемой системы является представление ее в виде схемы системы в переменных состояния. Эта схема составляется из интеграторов, усилителей и суммирующих устройств. Обычно выходы интеграторов выбираются в качестве координат (переменных) состояния системы. Схема в переменных состояния даст наглядную физическую интерпретацию координат системы и описывает их взаимную связь. Схемы непрерывных систем в переменных состояния совпадают со схемами моделирования этих систем на аналоговых вычислительных машинах. Существует много разновидностей схем моделирования для одной и той же системы [8], отсюда и неоднозначность описания системы управления уравнениями состояния.
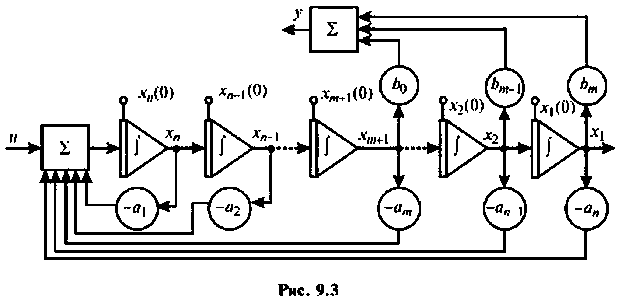
Сначала рассмотрим методы построения схем в переменных состояния для систем с одним входом и выходом, динамика которых описывается дифференциальным уравнением вида
при начальных условиях 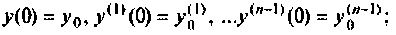
Затем будут показаны некоторые примеры, применяемые при построении схем в переменных состояния для систем более сложной структуры, динамика которых не может быть описана одним уравнением вида (9.13). Конечным результатом построения схем в переменных состояния будет получение уравнений состояния (9.5) и (9.6).
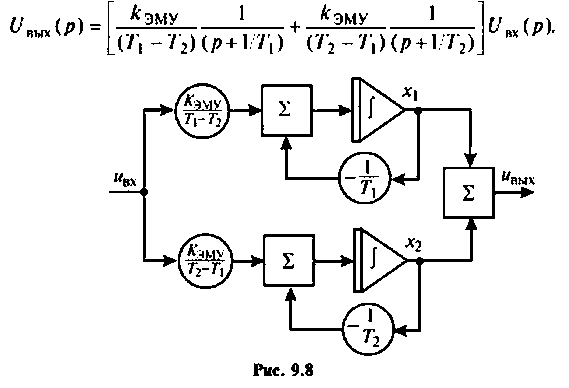
Метод комбинирования производных
Рассмотрим сначала более простой случай, когда начальные условия уравнения (9.13) нулевые. При этом уравнение (9.13) в операторной форме запишется как
где
Представим уравнение (9.14) в виде отношения
Это уравнение заменим следующими двумя:
где 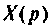
В дифференциальной форме последние два уравнения примут вид
Таким образом, вместо решения уравнения (9.13) можно решить уравнения (9.15) и (9.16). Составим схему решения уравнения (9.15), для этого разрешим его относительно старшей производной:
Предположим, что 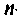
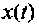
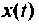
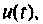
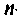
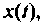
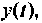
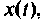
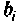
При ненулевых начальных условиях уравнения (9.13) необходимо их перевести в начальные условия (9.15). Предполагая, что уравнения (9.15) и (9.16) эквивалентны (9.13) и при ненулевых начальных условиях, запишем эти уравнения в операторной форме:
где 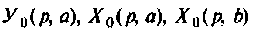
Подставляя 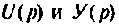
Из этого уравнения находится тождественное равенство, по которому определяются начальные условия уравнения (9.15) по известным начальным условиям (9.13)
Приравнивая коэффициенты при одинаковых степенях р этого равенства, находим начальные условия 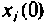
Если в качестве переменных состояния 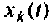
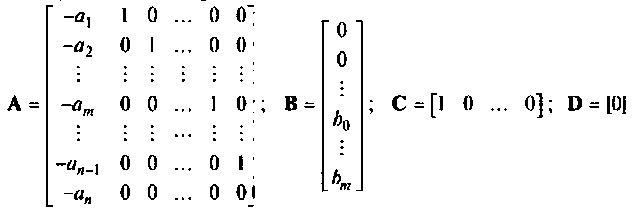
Записывая эту систему уравнений в матричной форме вида (9.5) и (9.6)
получаем конкретный вид матриц А, В, С и D.
Применение этого метода для составления уравнений состояния не требует преобразования уравнения (9.13). Можно непосредственно по виду уравнения (9.13) составлять схему в переменных состояния, так как его коэффициенты являются и коэффициентами схемы в переменных состояния. Пересчет начальных условий происходит по уравнению (9.19).
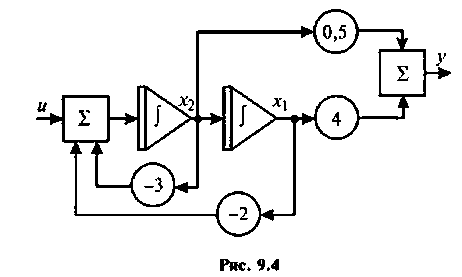
Пример 9.1.
Составить уравнения состояния для системы, динамика которой описывается дифференциальным уравнением
Схема в переменных состояния приведена на рис. 9.4. Из схемы в переменных состояния получаем уравнения:
Эта система уравнений в матричной форме имеет вид:
Следовательно,
Метод последовательного интегрирования
Запишем уравнение (9.13) и операторной форме при нулевых начальных условиях в виде
откуда
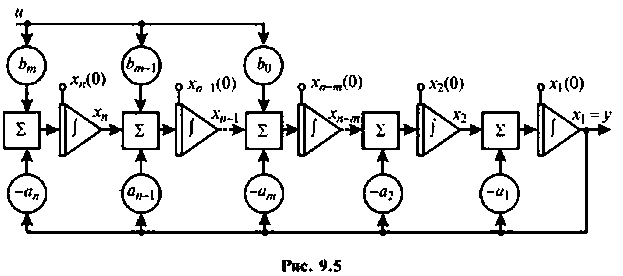
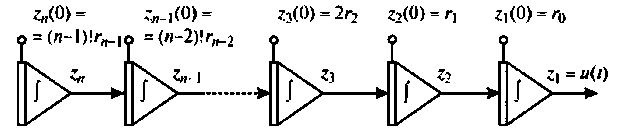
Составим цепочку из 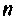
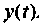
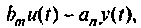
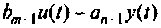
Если снова выбрать в качестве переменных состояния 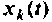
При ненулевых начальных условиях уравнения (9.13) начальные условия интеграторов схемы определяются соотношением [8]
Записывая эту систему уравнений в форме уравнений (9.5) и (9.6), находим матрицы А, В, С и D:
Как и для метода комбинирования производных, коэффициенты уравнения (9.13) являются одновременно и коэффициентами схемы и переменных состояния. Поэтому, зная общую структуру схемы в переменных состояния, можно непосредственно по виду уравнения (9.13) построить соответствующую схему в переменных состояния и найти уравнения состояния в виде (9.5) и (9.6).
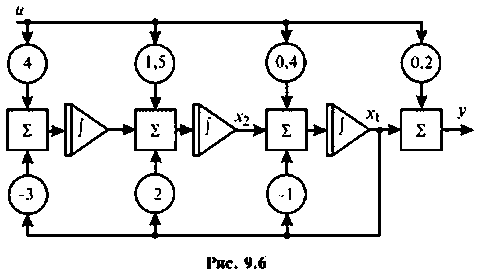
Пример 9.2.
Составить уравнения состояния для системы, описываемой уравнением
Схема а переменных состояния, построенная методом непосредственно интегрирования, показана на рис. 9.6. Из схемы получаем систему уравнений 1-го порядка:
В матричной форме эта система уравнений имеет вид:
Из последних уравнений ясно видны матрицы А, В, С. D.
В примере 9.2 матрица D отлична от нуля. Это имеет место в тех случаях, когда 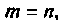
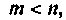
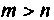
Метод разложения передаточной функции на элементарные дроби
Весьма перспективным для анализа цепей и систем методом пространства состояний является построение схемы в переменных состояния путем разложения передаточной функции на элементарные дроби. Суть его заключается в следующем. Уравнение (9.13) представляется в виде передаточной функции
Разложим эту передаточную функцию на элементарные дроби
Отсюда
Коэффициент d будет отличен от нуля при 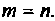
Как видно из выражения (9.27), матрица А является диагональной.
Пример 9.3.
Составим уравнения состояния для электрической цепи второго порядка, передаточная функция которой имеет вид
Полюса этой передаточной функции равны:
Представим передаточную функцию 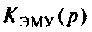
Коэффициенты
Таким образом, необходимо составить схему в переменных состояния для уравнения
Схема в переменных состояния показана на рис. 9.8. Уравнения, связывающие переменные состояния 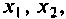
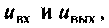
В матричном виде эти уравнения запишем таким образом:
При наличии кратных полюсов передаточной функции (9.25) матрица А будет представлена в канонической форме Жордана [8]. Ниже будет показано, что вычислительная процедура значительно упрощается, если матрица А диагональная или имеет каноническую форму Жордана. Основная трудность получения уравнений состояния вида (9,27) и (9,28) состоит в нахождении полюсов передаточной функции (9.25).
Преобразование неоднородных уравнений состояния в однородные
В результате построения схемы и переменных состояния можно получить уравнения состояния в виде (9.5). Это система неоднородных дифференциальных уравнений первого порядка. Их решение будет содержать две составляющие — свободную и вынужденную. Первая зависит от динамики системы и начального значения вектора переменных состояния 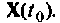
Свободная составляющая определяется решением однородного уравнения
когда вектор входного воздействия 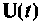
Имеет смысл попытаться преобразовать систему неоднородных уравнений (9.5) в однородную вида (9.29). Цель этого преобразования заключается в том, чтобы получить уравнения состояния системы при наличии внешних воздействий 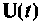
Преобразование системы неоднородных уравнений в однородную можно осуществить в том случае, если вектор внешних воздействий 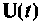
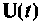
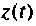
Рассмотрим методику построения схем в переменных состояния для формирования некоторых часто встречающихся входных воздействий
Построение схем в переменных состояния для типовых входных воздействий
Входное воздействие в виде полиномиальной функции:
Полиномиальное входное воздействие описывается функцией
при 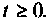
и продифференцируем уравнение (9.31) по t. Тогда
Аналогично
Продолжая этот процесс до тех пор, когда очередная производная будет равно нулю, получим следующую систему уравнений:
Величины 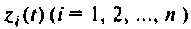
Начальные условия на интеграторах:
Выходом этой системы является заданное входное воздействие, определяемое переменной состояния 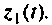
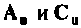
Пример 9.4.
Составить схему в переменных состояния для формирования линейного воздействия 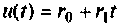
Систему уравнений, решением которой будет линейная функция, получим из выражения (9.32)
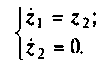
При начальных условиях 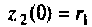
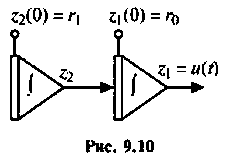
Схема о переменных состояния показана на рис. 9.10,
В матричном виде уравнения состояния схемы (рис. 9.10) будут иметь вид
отсюда матрицы 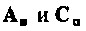
Входное воздействие в виде гармонической функции
В общем случае гармоническое воздействие представляется в виде
Решение дифференциального уравнения
даст гармонический сигнал. Это уравнение может быть записано в виде двух уравнений первого порядка
с начальными условиями
Схема в переменных состояния, которая следует из формул (9.37), показана на рис. 9.11. Сигнал 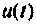
Изменяя начальные условия 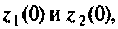
Входное воздействие в виде экспоненциальной функции
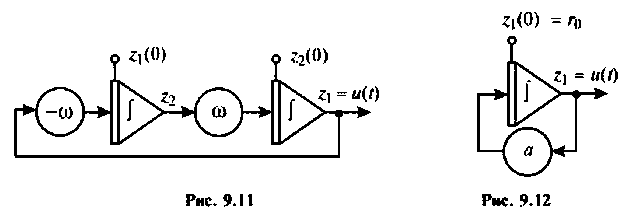
Экспоненциальное входное воздействие описывают функцией
Пусть 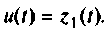
Начальное значение 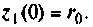
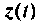
Методика преобразования неоднородных уравнений состояния в однородные
Для преобразования системы неоднородных уравнений (9.5) в однородную (9.29) необходимо вектор 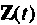
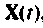
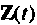
Допустим, что входной вектор 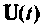
полученных путем построения схемы и переменных состояния дифференциального уравнения, решением которого и является вектор 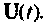
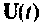
Объединим в одну систему уравнения (9.43) и (9.41)
Обозначим расширенный вектор, включающий как переменные состояния 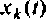
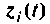
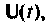
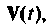
Уравнения (9.43), (9.44) и (9.45) объединим и запишем в виде:
Обозначая
получаем
Матрица 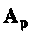
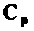
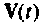
Применение методики преобразования неоднородной системы уравнений состояния в однородную проиллюстрируем на примере.
Пример 9.5.
Найти матрицы 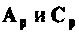
Для линейного воздействия
Подставляя 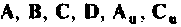
На практике часто пользуются следующим приемом при преобразовании неоднородных уравнений (9,5) и (9.6) в однородные. Составляется расширенная схема в переменных состояния, включающая схемы в переменных состояния входного воздействия и собственно динамической системы. Из этой схемы непосредственно получают расширенные матрицы
Пример 9.6.
Для условий примера 9.5 найти матрицы 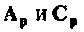
Расширенная схема о переменных состояния показана на рис. 9.14. Из нее получаем:
В матричной форме эту систему уравнений можно записать, если обозначить 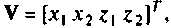
Результаты примеров 9.5 и 9.6 совпадают.
Формы решения уравнений состояния
Рассмотренные методы построения схем в переменных состояния позволяют получить математическое описание динамики линейной стационарной системы и электрической цепи в виде векторно-матричной системы дифференциальных уравнений первого порядка. Рассмотрим решение этих уравнений.
Форма решения однородных уравнений состояния
Если на систему не подаются внешние воздействия, то 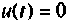
Решение этого уравнения описывает динамику системы за счет ненулевых начальных условий (свободное движение), когда внешние силы равны нулю. Предположим, что движение начинается в момент 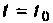
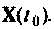
Действительно, если подставить решение (9,53) в (9.52), предварительно взяв производную от (9.53), то получим тождество. Следовательно, (9.53) является решением однородного матричного уравнения (9.52).
Если обозначить
то уравнение (9.53) можно записать как
Выходной вектор системы будет иметь вид
Матрица 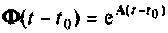
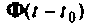
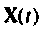
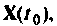
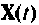
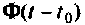
Форма решения неоднородных уравнений состояния
Решение уравнения (9.5) будем искать в форме, аналогичной выражению (9.55). Положим
где 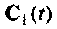
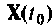
Дифференцируя выражение (9.57) по t, получаем
Учитывая, что 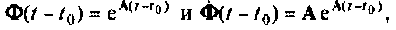
Если выражение (9.57) является решением уравнения (9.5), то величины в правых частях уравнений (9.5) и (9.59) должны быть одинаковыми.
Отсюда
Решая это уравнение относительно 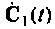
Подставив выражения (9.61) в (9.57), имеем
Учитывая, что
выражение (9.62) примет вид
Постоянную интегрирования 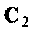
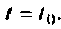
Так как 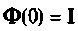
Таким образом,
Вектор выхода 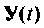
Первое слагаемое выражения (9.67) — составляющая выходного вектора за счет ненулевых начальных условий 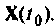
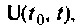
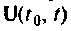
Аналитический подход к вычислению матрицы перехода
Формы решения однородной (9.56) и неоднородной (9.67) систем уравнений состояния содержат матрицу перехода 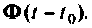
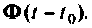
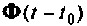
Далее рассматриваются и обосновываются аналитические методы вычисления матрицы перехода 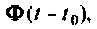
Метод разложения матрицы перехода в бесконечный ряд
Переходная матрица 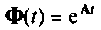
Этот метод наиболее трудоемок, если элементы матрицы 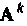
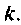
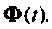
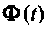
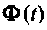
Пример 9.7.
Найти матрицу перехода 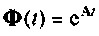
Степени 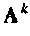
где 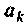
Переходная матрица
Если свернуть бесконечные ряды внутри матрицы 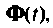
Метод комплексной плоскости
Возьмем преобразование Лапласа от обеих частей уравнения (9.52)
отсюда
Применив к уравнению (9.70) обратное преобразование Лапласа, получим
Сравнивая выражения (9.53) и (9.71), приходим к выводу, что
Основная трудность этого метода состоит в нахождении матрицы, обратной
Пример 9.8.
Найти матрицу перехода 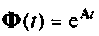
Найдем матрицу
Матрица, обратная 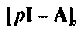
Пользуясь таблицей преобразования Лапласа [26, 28], находим
Рассмотренный метод комплексной плоскости дает возможность проследить физическим смысл матрицы перехода 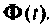
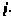
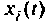
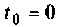
где — элемент матрицы 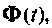
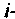
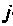
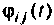
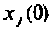
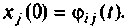
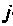
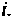
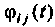
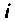
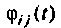
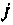
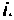
При рассмотрении физического смысла матрицы перехода 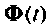
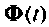
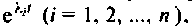
Построение алгоритмов вычисления матрицы перехода
Основой для разработки алгоритмов вычисления матрицы перехода 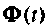
При использовании этого метода для машинного определения матрицы 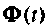
с одновременным их суммированием и, во-вторых, оценка точности вычисления, поскольку ряд (9.74) необходимо ограничивать конечным числом членов.
Алгоритм вычисления бесконечного ряда
При решении этой задачи воспользуемся рекуррентными соотношениями, позволяющими наиболее просто и экономно составить алгоритм вычисления бесконечною ряда (9.74). Обозначим
Тогда
при
Таким образом, вычисление ряда (9.74) состоит из последовательных циклов, в каждом из которых будут использоваться результаты предыдущих вычислений. На рис. 9.15 показана схема алгоритма вычисления 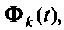
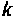
Критерий ограничения бесконечного ряда
Вычисление матрицы перехода с точностью, не хуже заданной, требует способа оценки остаточного члена бесконечного ряда (9.74). Если ряд (9.74) ограничить первыми 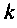
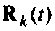
Представим остаточный член (9.79) в следующем виде:
Заменим правую часть ряда (9.80) мажорирующим матричным рядом, где каждый член будет не меньше соответствующего члена ряда (9.80). Тогда вместо (9.80) можно записать
Правая часть этого выражения является матричной геометрической прогрессией с начальным членом 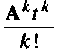
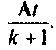
(9.82)
то выражение (9.81) запишется так [8]:
Таким образом, остаточный член матричного ряда (9.74) можно оценивать по матрице в правой части выражения (9.83) при выполнении условия (9.К2). С увеличением 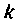
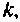
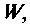
Использование критерия (9.83) для ограничения числа членов бесконечного ряда требует вычисления нормы матрицы, так как
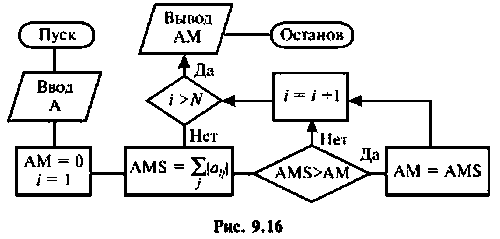
выражение (9.83) справедливо только при выполнении условия (9.82). На рис. 9.16 показана схема алгоритма вычисления нормы произвольной матрицы А. В качестве ее нормы выбрана максимальная сумма абсолютных значений элементов строки матрицы А. Этот алгоритм должен быть составной частью оценки числа членов ряда (9.74).
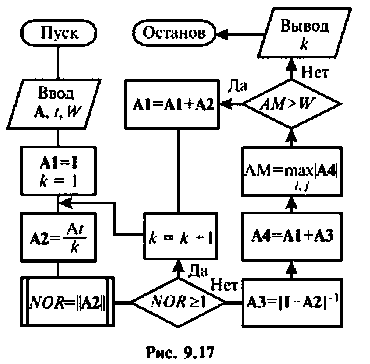
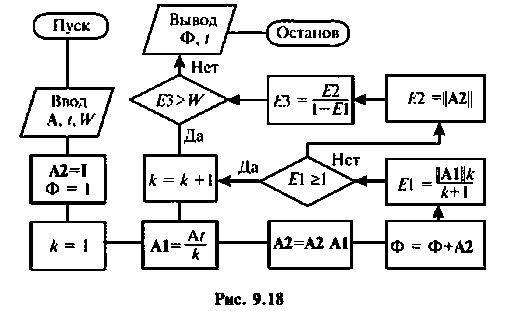
На рис. 9.17 приведена схема алгоритма, но которому можно определить число членов ряда (9.74), обеспечивающих точность вычисления матрицы перехода 
Алгоритм (рис. 9.17) требует достаточно сложной операции обращения матрицы. Целесообразно матричную оценку точности вычисления 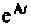
Проведем преобразования правой части критерия (9.84)
Известно [30], что если


Заменяя норму обратной матрицы в выражении (9.85) и учитывая, что
получаем
Рассмотрим построение алгоритма вычисления матрицы перехода 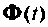
Алгоритм должен содержать цикл по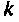
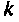
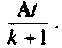
то можно использовать скалярную оценку остаточного члена матричного ряда (9.74). Для этого необходимо определять норму последующего слагаемого ряда (9.74) и при выполнении условия
ограничивать число членов ряда (9.74). Поскольку
всегда найдется такое значение 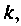
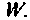
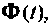
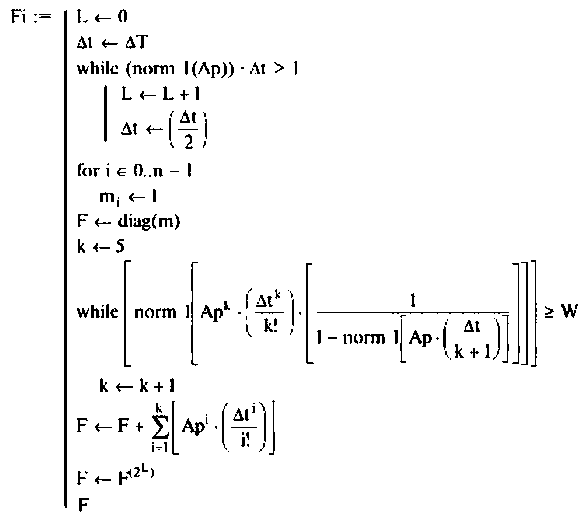
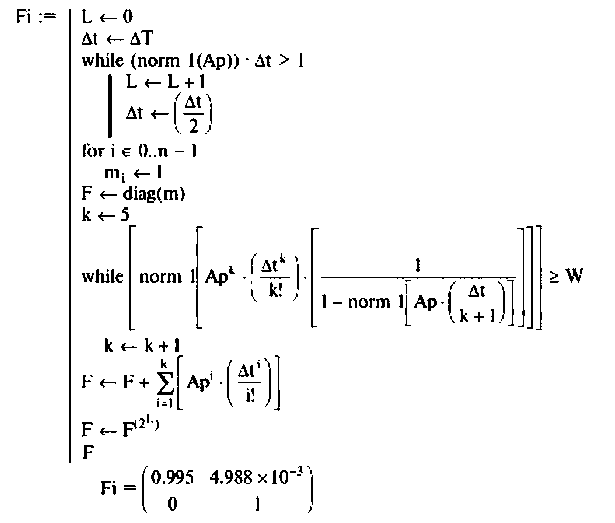
Ниже представлен вариант программы вычисления переходной матрицы в соответствии с алгоритмом (рис. 9.18), составленный в среде Mathcad [43].
Исходные параметры системы (из примера 9.9.5):
Программа вычисления матрицы перехода
Метод разложения 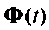
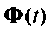
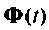
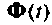
Иногда, особенно при решении задач проектирования, требуется иметь функцию перехода в аналитическом виде, т. е. в виде матрицы, элементами которой являются функции времени. Такой вид 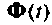
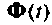
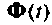
Аналитический подход к решению уравнений состояния
Формы решения уравнений состояния получены в разд. 9.4. Форма решения (9.53) применяется при исследовании как свободного движения системы, так и вынужденного, если входной вектор 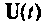
Пример 9.9.
Найти свободное движение системы, схема которой в переменных состояния приведена на рис. 9.4, при начальных условиях 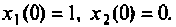
Поскольку требуется исследовать свободное движение, то 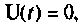
где 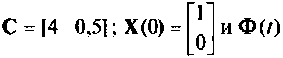
Таким образом
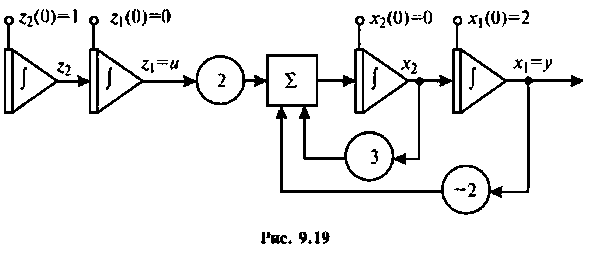
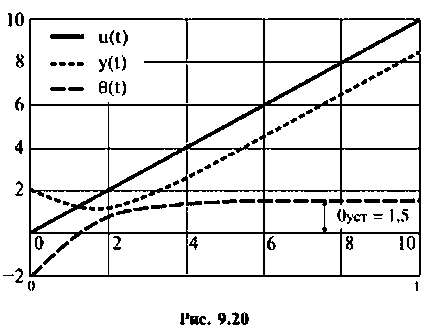
Пример 9.10. Найти реакцию 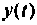
и ошибку 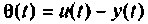
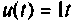
Расширенная схема в переменных состояния показана на рис. 9.19. Уравнения состояния расширенной системы имеют вид
при начальных условиях
Обозначая 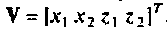
Решение этой системы уравнений можно записать в виде
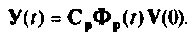
Матрицу перехода представим бесконечным рядом
Степени 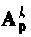
Для нахождения 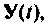
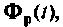
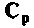
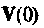
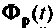
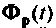
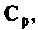
Для определения 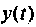
Таким образом,
Входное воздействие 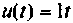
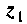
Переменная состояния
Учитывая, что 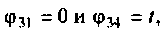
Этот результат очевиден из условия задачи. Ошибка 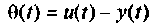
На рис. 9.20 показаны 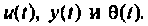
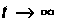
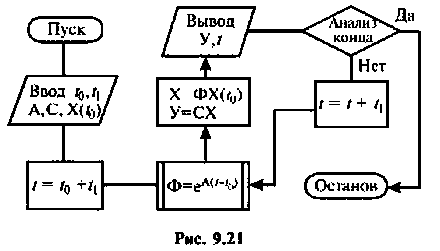
Построение алгоритмов решения уравнений состояния
Рассмотренные примеры показывают основные вычислительные трудности, возникающие при решении задач исследования линейных динамических систем. Более общая форма решения (9.62) требует аналитического интегрирования достаточно сложных функций, особенно если вектор входных воздействий 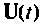
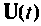
Построение алгоритмов решения однородных уравнений состояния
Простой алгоритм. Выходной вектор 
Построение алгоритма для вычисления 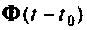
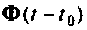
Схема алгоритма решения системы однородных уравнений состояния показана на рис. 9.21. Исходными данными для алгоритма являются матрицы А, С и вектор начальных условий 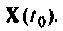
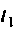
Условный оператор конца счета должен формироваться исходя из решения конкретной задачи.
Итерационный алгоритм. Алгоритм (см. рис. 9.21) имеет один существенный недостаток — обычно шаг 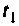

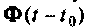
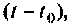
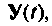
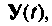
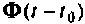
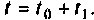
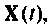
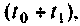
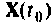
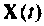
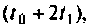
Повторяя этот процесс многократно, получаем последовательность значений вектора переменных состояния 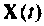
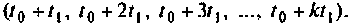
Схема итерационного алгоритма вычисления 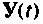
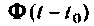
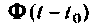
Такое построение алгоритма обусловливает накопление ошибок за счет неточного вычисления 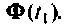
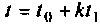
Допустим, что матрица 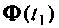
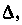
где 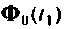
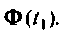
Ошибка 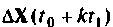
Ошибка 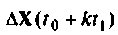
Итерационный алгоритм с компенсацией ошибок. Для компенсации накапливаемых ошибок в итерационном процессе можно применить метод уточнения вектора 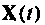
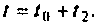
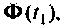
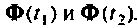
где 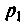
Сначала итерационный процесс использует матрицу 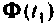
При 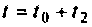
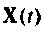
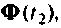
При необходимости можно использовать не одну матрицу 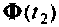
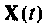
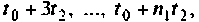
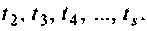
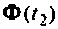
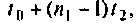
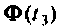
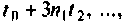
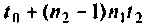
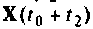
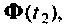
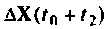
заменяется вектор начальных условий 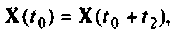
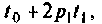

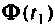
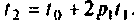
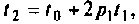
Выбором соотношений между 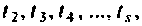
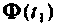
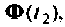
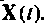
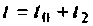
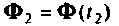
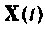
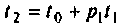
Построение алгоритмов решения неоднородных уравнений состояния
Алгоритмизации подлежит уравнение
Первое его слагаемое отражает свободное движение системы за счет ненулевых начальных условий, второе и третье — определяют вынужденную составляющую решения.
Уравнение (9.103) удобно представить в виде следующих двух уравнений:
Уравнение (9.104) определяет вектор переменных состояния 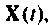
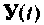
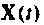
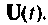
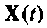
Итерационный алгоритм. Если принять 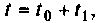
где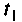
Для вычисления интеграла правой части уравнения (9.106) можно применять различные формулы приближенного вычислении определенных интегралов [4, 29]. Простой и удобной для применения является формула трапеции. Выбором шага дискретности можно обеспечить необходимую точность приближенного вычисления интеграла. Применение более сложных формул (Симпсона, Ньютона-Котеса, Гаусса, Маркова, Чебышева и др.) хотя и дает высокую точность интегрирования, однако затрудняет программирование и понимание построения алгоритма вычисления вектора состояния (9.106). Применение формулы трапеций позволяет выражения (9.106) и (9.105) привести к следующему виду:
Если принять 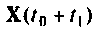
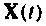
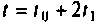
или после применения формулы трапеций
Сравнивая выражения (9.107) и (9.108) с (9.109) и (9.111), видим, что они идентичны по своему виду, за исключением аргументов вектора начальных условий и вектора выходных воздействий. Это дает возможность построить итерационный алгоритм вычисления 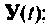
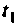
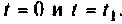
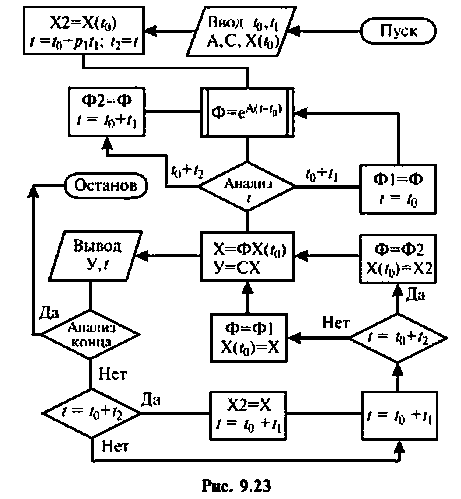
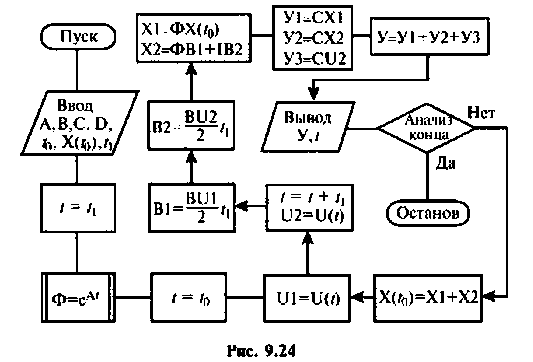
Схема алгоритма показана на рис. 9.24.
Исходными данными для него являются матрицы А, В, С и D. вектор начальных условий 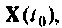
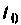
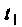
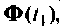
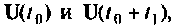
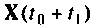
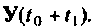
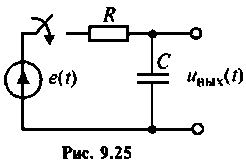
Порядок исследования электрических цепей в среде Mathcad методом пространства состояния
(на примере схемы на рис. 925)
- Составить согласно принципиальной схеме уравнение электрической цепи в дифференциальной форме.
- Составить расширенную схему электрической цепи в переменных состояния.
- Составить в стандартной форме уравнения состояния электрической цепи.
- Экспериментально построить вектор выхода электрической цепи.
Исходные параметры системы уравнений состояния:
Параметры вектора входа:
Исходные параметры электрической цепи:
расширенной матрицы коэффициентов Ар —
расширенной матрицы выхода Ср —
вектора начальных условий —
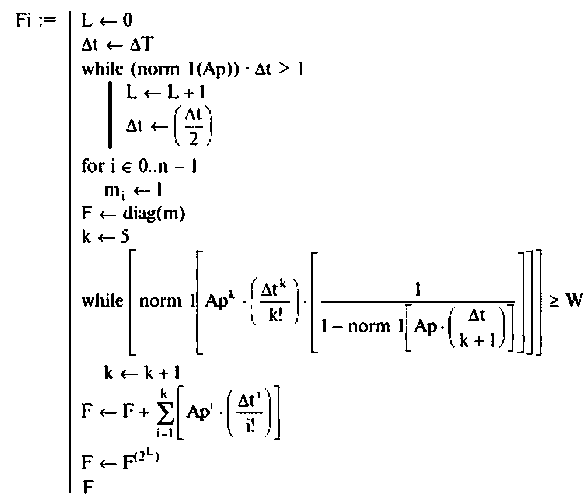
Программа вычисления матрицы перехода
Примеры решения задач
Пример 9.9.1.
Построить методом пространства состояний переходные функции тока 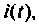
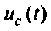
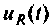
Дано:
Решение
1. Составляем уравнение электрической цепи
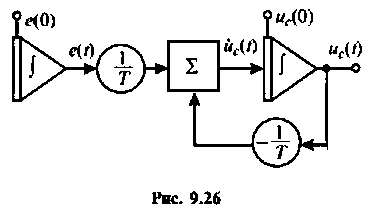
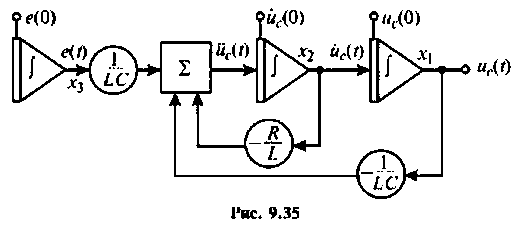
2. Составляем расширенную схему в переменных состояния для составления расширенных уравнений состояния. Уравнение (9.112) представим в виде
Расширенная схема в переменных состояния для решения уравнения (9.113), составленная по методу комбинирования производных, приведена на рис. 9.26.
По схеме в переменных состояния записываем уравнения состояния в виде
В качестве переменных вектора выхода принимаем напряжения 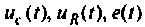
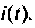
В матричной форме уравнения состояния принимают вид
или 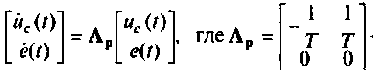
В матричной форме уравнения вектора выхода принимают вид
или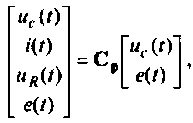
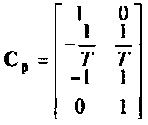
Вектор начальных условий по условию задачи принимает вид
Решение уравнений состояния и формирование вектора выхода проведем в среде Mathcad.
Исходные параметры системы
Параметры электрической цепи
Вводим символьное обозначение матриц:
Программа вычисления матрицы перехода
Матрица перехода при 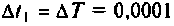
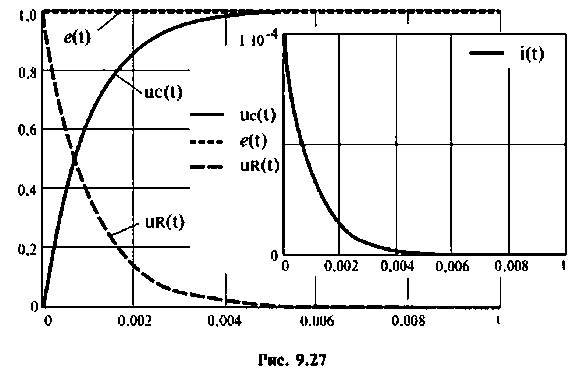
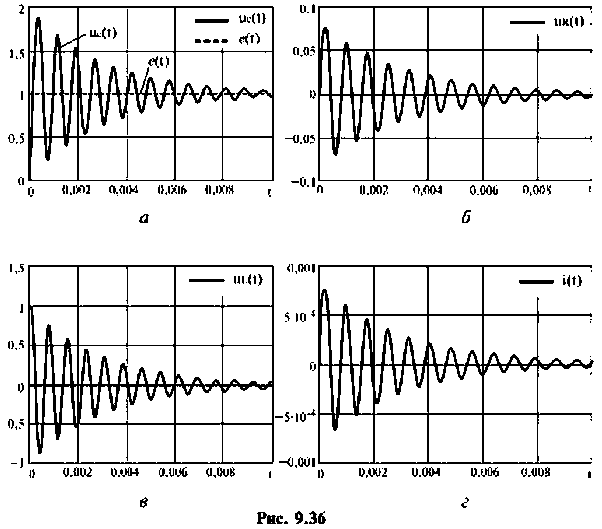
Программа вычисления и построения вектора выхода
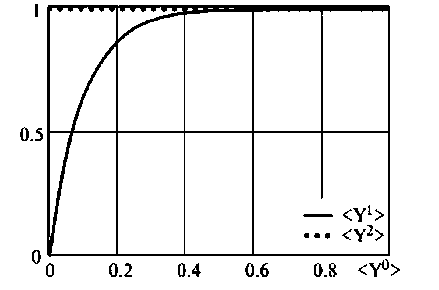
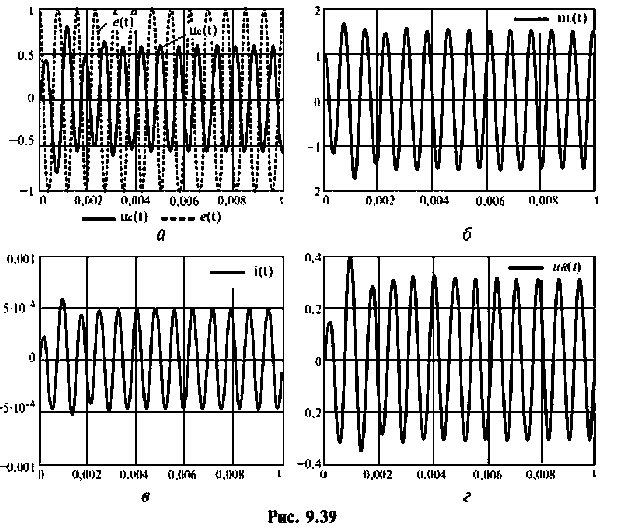
Переменные вектора выхода показаны па рис. 9.27.
Пример 9.9.2.
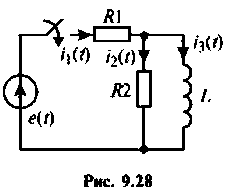
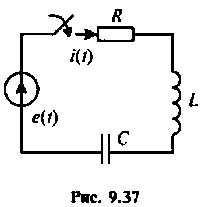
Для электрический цепи (рис. 9.28) после замыкания ключа составить уравнение равновесия, расширенную схему в переменных состояния, уравнения состояния. Решить уравнения состояния в среде Mathcad методом пространства состояний. Вектор выхода сформировать из переменных
Дано:
Решение
1. Составляем уравнение электрического равновесия для цепи в виде
или
2.Составляем расширенную схему в переменных состояния. Уравнение равновесия преобразуем к виду
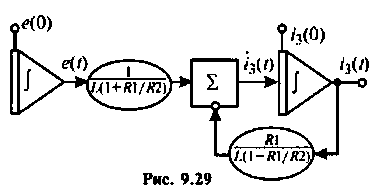
Схема в переменных состояния, составленная по методу комбинирования производных, представлена на рис. 9.29.
3. По виду схемы в переменных состояния составляем уравнения состояния. Схема в переменных состояния содержит два интегратора, следовательно, порядок уравнения 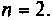
Уравнения состояния в матричной форме принимают вид
Расширенная матрица коэффициентов представляется в виде
4. Уравнения вектора выхода системы в матричной форме имеют вид
Расширенная матрица выхода и вектор начальных условий по условию задачи представлены соответственно в виде:
В среде Mathcad решаем систему уравнений состояния и из переменных состояния формируем вектор выхода электрической цепи.
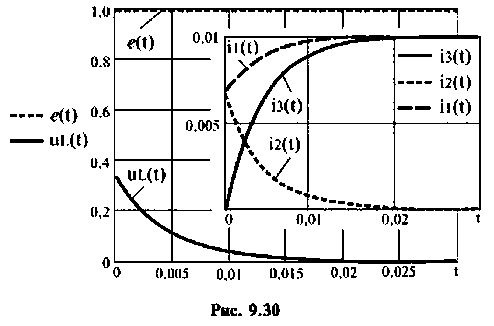
Выходные переменные приведены на рис. 9.30.
Пример 9.9.3.
Для электрической цепи, приведенной на рис.9.31, после замыкания ключа составить уравнение равновесия, расширенную схему в переменных состояния. Решить уравнения состояния в среде Mathcad. Вектор выхода сформировать из переменных состояния:
Дано:
Решение
1.Составляем по второму закону Кирхгофа уравнение электрического равновесия для цепи после ее переключения в виде
Так как 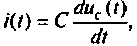
2. Составляем схему электрической цепи в переменных состояния. Так как после переключения внешний источник ЭДС отсутствует, т.е. 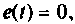
Разрешим уравнение равновесия относительно старшей производной, тогда
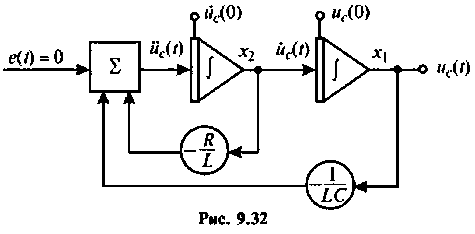
а схема в переменных состояния для решения этого уравнения имеет вид (рис. 9.32).
3. По схеме в переменных состояния (рис. 9.32) составляем уравнения состояния:
или в матричной форме
Матриц коэффициентов определяется выражением
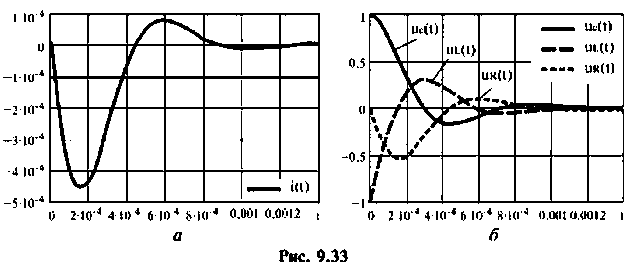
4. Формируем из переменных состояния вектор выхода. Уравнения выхода имеют вид
В матричной форме
Матрица выхода и вектор начальных условий принимают вид:
5.Решение уравнений состояния можно выполнить любым численным методом. На рис. 9.33 приведены переменные вектора выхода, вычисленные методом пространства состояний в среде Mathcad по программе, приведенной в задаче 9.9.1.
Пример 9.9.4.
Задана электрическая цепь (рис.9.34). Требуется составить уравнение равновесия цепи по второму закону Кирхгофа после замыкания ключа и расширенную схему в переменных состояния. Получить и решить уравнения состояния любым численным методом с применением ПЭВМ, сформировать вектор выхода из переменных состояния:
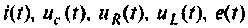
Дано:
Решение
1. Записываем уравнение электрического баланса цепи в виде
2. Составляем расширенную схему в переменных состояния при 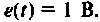
С учетом входного воздействия схема в переменных состояния электрической цепи может быть представлена в виде, приведенном на рис. 9.35.
3. В соответствии со схемой в переменных состояния запишем уравнении состояния электрической цепи
В матричной форме уравнения состояния имеют вид
Расширенная матрица коэффициентов представляется в виде
Вектор начального состояния из условия задачи запишем в виде
4. Определяем уравнения выхода из заданных переменных состояния электрической цепи.
В матричной форме уравнения вектора выхода имеют вид
Матрица коэффициентов выхода
5. Решение уравнений состояния выполняем в среде Mathcad с помощью программы из задачи 9.9.1.
Переменные вектора выхода приведены на рис. 9.36.
Из переменных вектора выхода наглядно видно, что реакция последовательного колебательного контура на единичное воздействие — переходная функция — имеет слабозатухающий колебательный характер.
Пример 9.9.5.
По электрической схеме, представленной на рис.9.37, после замыкания ключа составить уравнение электрического равновесия по второму закону Кирхгофа, расширенную схему в переменных состояния, уравнения состояния и выхода из переменных состояния
Дано:
Решить уравнения состояния одним из численных методов в среде Mathcad и построить графики компонентов вектора выхода.
Решение
1. Записываем уравнение электрического равновесия для электрической цепи
2.Составляем расширению схему в переменных состояния при 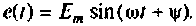
Схема модели гармонического воздействия 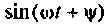
3. Составляем уравнения состояния по схеме в переменных состояния
Запишем уравнения и матричной форме в виде
Расширенная матрица коэффициентов системы имеет вид
Вектор начального состояния системы для
4. Составляем уравнения вектора выхода из переменных состояния
В матричной форме уравнения выхода имеют вид
Расширенная матрица выхода запишется и виде
5. Решение уравнений состояния выполним в среде Mathcad по программе, представленной в задаче 9.9.1. Переменные вектора выхода представлены на рис. 9.39.
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
(Андрей Андреевич Марков (1856-1922) – русский математик, академик)
Определение. Процесс, протекающий в физической системе, называется Марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из K несовместных событий Ai из полной группы. При этом условная вероятность Pij(S) того, что в S –ом испытании наступит событие Aj при условии, что в (S – 1) – ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний.
Независимые испытания являются частным случаем цепи Маркова. События называются Состояниями системы, а испытания – Изменениями состояний системы.
По характеру изменений состояний цепи Маркова можно разделить на две группы.
Определение. Цепью Маркова с дискретным временем Называется цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временем Называется цепь, изменение состояний которой возможно в любые случайные моменты времени.
Определение. Однородной Называется цепь Маркова, если условная вероятность Pij перехода системы из состояния I В состояние J не зависит от номера испытания. Вероятность Pij называется Переходной вероятностью.
Допустим, число состояний конечно и равно K.
Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:
Эта матрица называется Матрицей перехода системы.
Т. к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице.
На основе матрицы перехода системы можно построить так называемый Граф состояний системы, его еще называют Размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.
Пример. По заданной матрице перехода построить граф состояний.
Т. к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.
S1
0,2 0,7
S2 0,4 S4
0,6 0,5
0,1 0,5
S3
На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.
Пусть Pij(N) – вероятность того, что в результате N испытаний система перейдет из состояния I в состояние J, R – некоторое промежуточное состояние между состояниями I И J. Вероятности перехода из одного состояния в другое Pij(1) = Pij.
Тогда вероятность Pij(N) может быть найдена по формуле, называемой Равенством Маркова:
Здесь Т – число шагов (испытаний), за которое система перешла из состояния I В состояние R.
В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности.
Зная переходные вероятности (т. е. зная матрицу перехода Р1), можно найти вероятности перехода из состояния в состояние за два шага Pij(2), т. е. матрицу Р2, зная ее – найти матрицу Р3, и т. д.
Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц).
Тогда в общем виде можно записать:
Вообще то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.
Пример. Задана матрица переходов Р1. Найти матрицу Р3.
Определение. Матрицы, суммы элементов всех строк которых равны единице, называются Стохастическими. Если при некотором П все элементы матрицы Рп не равны нулю, то такая матрица переходов называется Регулярной.
Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через П шагов из любого состояния. Такие цепи Маркова также называются Регулярными.
Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел и матрица Р(¥) имеет вид:
Т. е. матрица состоит из одинаковых строк.
Теперь о величинах Ui. Числа U1, U2, …, Un называются Предельными вероятностями. Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы РТ (транспонированной к матрице Р).
Этот вектор полностью определяется из условий:
Пример. Найдем предельные вероятности для рассмотренного Выше примера.
C учетом того, что U1 + U2 = 1, получаем:
Получаем:
| < Предыдущая |
|---|
Уравнения состояния (8.25) имеют каноническую форму, основная матрица – форму Жордана. Корню кратности k соответствует клетка Жордана размерностью k ´ k . Очевидно, при наличии нескольких кратных корней будем получать соответствующие клетки Жордана для каждого корня.
Пример 8.6. Обратимся к системе управления из примера8.5 и найдем уравнения состояния в канонической форме для разомкнутой системы. Харак-
|
теристическое уравнение |
разомкнутой системыl(0,1l + 1)(0,006l + 1) = 0 |
|
|
имеет три различных корня l1 = 0 , l2 |
= —10 , l3 @ —166,6 . Используя выра- |
|
|
величины bi : b1 = 500 , b2 = —370 , |
||
|
жение bi = (s — li )W(s) |
s = li |
, находим |
b3 = —125 . Таким образом, уравнения состояния в канонической форме для разомкнутой системы имеют вид
|
é0 |
0 |
0 |
ù |
é 500 ù |
y |
= [1,1,1] x . |
|||
|
x& = ê0 |
—10 |
0 |
úx + ê- 370ú e , |
||||||
|
ê |
0 |
ú |
ê |
ú |
|||||
|
ë0 |
—166,6û |
ë—125 |
û |
||||||
|
С учетом уравнения замыкания e = v — y |
нетрудно получить следующие |
||||||||
|
уравнения состояния замкнутой системы: |
|||||||||
|
é- 500 |
— 500 |
— 500 ù |
é 500 ù |
y |
= [1 , 1 , 1 ] x . |
(8.26) |
|||
|
x& = ê 370 |
360 |
370 úx + ê- 370úv, |
|||||||
|
ê |
125 |
ú |
ê |
ú |
|||||
|
ë 125 |
— 41,6û |
ë— 125 |
û |
Сравнивая (8.21) и (8.26), видим, что одна и та же система описывается разными уравнениями состояния, которые эквивалентны между собой.
Пусть линейная САУ описывается следующие уравнениями состояния:
|
x& = Ax + Bv , y = Cx , |
x Î Rn , v Î Rm , |
y Î R p . |
(8.27) |
|||
|
Рассмотрим матричный ряд, который обозначим через e At : |
||||||
|
e At = E + At + |
A2t 2 |
+ |
A3t3 |
+ …, |
(8.28) |
|
|
2! |
||||||
|
3! |
||||||
|
где Е – единичная n ´ n матрица. |
любомt к |
|||||
|
Доказано, что этот ряд абсолютно |
сходится |
при |
некоторой |
n ´ n матрице, обозначенной нами через e At (экспоненциал матрицы).
97
|
Свойства ряда (8.28): |
||||||||||||||
|
1. При t = 0 матрица eAt = E . |
||||||||||||||
|
2. |
d |
At |
A2t 2 |
A3t 3 |
At |
|||||||||
|
e |
= At + |
+ |
+ … = A[E + At + …] = [E + At + …]A = |
Ae |
= |
|||||||||
|
dt |
2! |
3! |
||||||||||||
|
d k |
||||||||||||||
|
= e At A , или в более общем виде |
e At = Ak e At |
= e At Ak . |
||||||||||||
|
t |
dt k |
|||||||||||||
|
3. òe At dt =A—1(e At — E) = (e At — E) A—1 , где A—1 – обратная матрица. |
||||||||||||||
|
0 |
||||||||||||||
|
4. Если A = diag[l1 ,…, ln ], то e At = diag[el1t ,…, elnt ] . |
||||||||||||||
|
Рассмотрим однородное уравнение |
||||||||||||||
|
x& = Ax , |
(8.29) |
|||||||||||||
|
соответствующее |
неоднородному |
дифференциальному |
уравнению |
|||||||||||
|
x& = Ax + Bv, и зададим начальное состояние вектора х(0) при t = 0. |
||||||||||||||
|
Общее решение однородного уравнения (8.29) задается выражением |
||||||||||||||
|
x(t) = e At x(0) . |
(8.30) |
Действительно, подставляя (8.30) в (8.29), с учетом свойства 2 получим тождество, справедливое при любом начальном значении х(0). Это значит, что (8.30) определяет общее решение уравнения (8.29).
Введем обозначение F(t) = e At . Матрицу F(t) размерностью n ´ n будем называть переходной матрицей состояния(в математике ей соответствует фундаментальная матрица), а выражение (8.30) в этом случае будем записывать в виде
Выражение (8.31) можно трактовать как линейное преобразование(переход) начального значения вектора состояниях(0) в текущее значение x(t) в пространстве состояний.
Свойства переходной матрицы состояния:
1.F(0) = E .
2.F(t1 + t2 ) = F(t1) ×F(t2 ) .
3.F—1(t) = F(—t) .
Эти свойства следуют из общих свойств экспоненциала матрицы.
Если известна переходная матрица состояния, то общее решение неоднородного уравнения x& = Ax + Bv записывается в виде (формула Коши):
t
|
x(t) = F(t)x(0) + òF(t — t)Bv(t)dt . |
(8.32) |
|
0 |
98
В силу y = Cx получим выражение для вычисления вектора выхода y(t):
|
t |
|
|
y(t) = CF(t)x(0) + Cò F(t — l)Bv(l)dl . |
(8.33) |
|
0 |
В (8.32), (8.33) первое слагаемое определяет свободную составляющую, обусловленную ненулевым начальным состоянием х(0), а второе – вынужденную составляющую, обусловленную входным сигналом v(t) .
Выражение (8.28) редко употребляется для определения матрицыF(t) , так как в случае произвольной матрицыА элементы матрицы F(t) представляют собой ряды Тейлора при t = 0, пo которым трудно найти исходную функцию в замкнутой форме.
Переходную матрицу состояния обычно находят с помощью операционного исчисления. Применим к (8.29) преобразование Лапласа, тогда получим sX (s) — x(0) = AX (s) , где X (s) = L{x(t)}. Из полученного выражения находим
|
[sE — A]X (s) = x(0) , X (s) = [sE — A]—1 x(0) , где [sE — A]—1 |
– обратная матрица к |
|
матрице [sE — A] . |
|
|
Переходя к оригиналам, имеем |
|
|
x(t) = L—1{[sE — A]—1}x(0) . |
(8.34) |
|
Сравнивая (8.34) с (8.31), приходим к выводу, что |
|
|
F(t) = L—1{[sE — A]—1}. |
(8.35) |
Каждый элемент матрицы [sE — A]—1 есть дробно-рациональная функция переменной s. Знаменатель каждого элемента представляет собой полином n-й степени det(sE — A) , а числитель – полином не выше (n–1)-й степени. Полином det(sE — A) называется характеристическим полиномом системы, а алгебраи-
ческое уравнение n-й степени
|
det[lE — A] = det[ A — lE] = 0 |
(8.36) |
назовем характеристическим уравнением системы.
Применяя к каждому элементу матрицы [sE — A]—1 обратное преобразование Лапласа, получим матрицу F(t) , элементами которой будут некоторые функции времени.
Переходную матрицу состояний можно найти, используя модальную матрицу M. Пусть в уравнении (8.29) матрица А имеет различные собственные
|
значения |
l1 ,…, ln . Тогда в (8.29) |
сделаем замену переменных x = Mz , |
|
где М – |
модальная матрица. В |
результате получим: z& = M —1AMz = |
= diag[l1,…,ln ]z .
Общее решение полученной системы с диагональной матрицей будет таково: z(t) = diag[el1t ,…, el nt ]z(0) . Так как x(t) = Mz(t) , z(0) = M —1x(0) , то
99
|
общее |
решение |
исходного |
уравнения(8.29) |
запишется |
в |
виде |
|||||||
|
x(t) = Mdiag[el1t ,…, elnt ]M —1x(0) . |
|||||||||||||
|
Отсюда следует, что |
|||||||||||||
|
F(t) = Mdiag[el1t ,…, elnt ]M —1 . |
(8.37) |
||||||||||||
|
Пример 8.7. Рассмотрим однородное уравнение в нормальной форме |
|||||||||||||
|
é 0 |
1 ù |
||||||||||||
|
x& = ê |
úx . |
||||||||||||
|
ë— 8 — 6û |
|||||||||||||
|
Собственные |
числа |
матрицы А |
определяются |
из |
решения |
уравнения |
|||||||
|
det[ A — lE] = l2 + 6l + 8 = 0 и будут l1 = —2 , |
l2 = —4 . |
||||||||||||
|
Ищем модальную матрицу М в виде (8.14): |
|||||||||||||
|
é 1 |
1 ù |
é 1 |
1 ù |
1 é- 4 —1ù |
|||||||||
|
M = ê |
ú |
= ê |
ú , M —1 |
= |
ê |
ú . |
|||||||
|
— 2 |
2 |
||||||||||||
|
ël1 |
l2 û |
ë— 2 |
— 4û |
ë |
1 û |
||||||||
|
Находим F(t) |
в соответствии с (8.37): |
|
é |
—2t |
0 |
ù |
é |
2e |
—2t |
— e |
—4t |
||
|
F(t) = M êe |
úM |
—1 = ê |
||||||||
|
ê |
0 e |
—4t |
ú |
ê |
—2t |
—4t |
||||
|
ë— 4e |
+ 4e |
|||||||||
|
ë |
û |
|
1 |
[e—2t — e—4t ]ù |
||||
|
2 |
|||||
|
—2t |
—4t |
ú . |
|||
|
e |
+ 2e |
ú |
|||
|
û |
Можно найти F(t) , используя (8.35). Находим [sE — A] и затем [sE — A]—1 .
|
és |
—1 ù |
é |
s + 6 |
1 |
ù |
|||||||
|
ê |
ú |
|||||||||||
|
, |
[sE — A]—1 |
s |
2 |
+ 6s + 8 |
s |
2 |
+ 6s + 8 |
|||||
|
[sE — A] = ê |
ú |
= ê |
ú . |
|||||||||
|
ë8 s + 6û |
ê- |
8 |
s |
ú |
||||||||
|
2 + 6s + 8 |
||||||||||||
|
ë s |
s2 + 6s + 8û |
Переходя от [sE — A]—1 к оригиналам, найдем выражение для матрицы F(t) , не отличающееся от полученного ранее.
8.7. Передаточная и весовая матрицы
Наряду с переходной матрицей состояния при описании и исследовании линейных многомерных систем находят применение матричные аналоги обычных передаточных функций одномерных систем.
Применим к уравнениям (8.27) преобразование Лапласа, полагая x(0) = 0, тогда получим X (s) = AX (s) + BV (s) , Y (s) = CX (s) или, исключая из уравнений вектор X (s) , получим
100
|
Y (s) = C[sE — A]—1 BV (s) = W (s)V (s) . |
(8.38) |
||
|
Передаточной |
матрицей (матричной |
передаточной |
функцией) |
|
W (s) = C[sE — A]—1 B |
будем называть матрицу |
размерности p ´ m, |
связываю- |
|
щую изображение вектора входа V (s) и вектора выхода Y (s) . |
|||
|
Элементами передаточной матрицы Wij (s) |
являются обычные скалярные |
передаточные функции, связывающие i — й выход Yi (s) с j — м входом V j (s)
при условии, что все остальные входы равны нулю. Передаточная функция Wij (s) есть отношение двух полиномов относительноs. Полином знаменателя
является для всех Wij (s) одним и тем же и равен det[sE — A] (степень его n), а
полиномы числителя будут степени не выше (n – 1).
В уравнении (8.33) будем полагать x(0) = 0 . Внесем матрицу С под знак интеграла и запишем это уравнение в виде
t t
|
y = òCF(t — t)Bv(t)dt = òw(t — t)v(t)dt . |
(8.39) |
|
|
0 |
0 |
|
|
Матрицу w(t) = CF(t)B |
размерностью p ´ m будем называть весовой |
матрицей (импульсной переходной матрицей).
Смысл её такой же, как и у весовой функции скалярной системы. Элементы wij (t) матрицы w(t) являются скалярными весовыми функциями. Если j–й
вход v j (t) = d(t) , а остальные входы равны нулю, то yi (t) = wij (t) . Передаточная и весовая матрицы связаны между собой преобразованием
|
Лапласа |
|
|
W (s) = L{w(t)}, w(t) = L—1{W (s)}. |
(8.40) |
|
Частотные характеристики системы в многомерном случае не нашли ши- |
|
|
рокого применения. Хотя формально сделав вW (s) замену s = jw , |
можно |
ввести аналогичные понятия и рассматривать p ´ m обычных скалярных частотных характеристик Wij ( jw) .
Если уравнения (8.27) описывают одномерную систему, то v, y Î R ,
|
B = col[b ,…,b ] , C = [c ,…,c ]. В этом случае W (s) = C[sE — A]—1 B , w(t) = CФ(t)B |
|||||
|
1 |
n |
1 n |
|||
|
будут скалярными функциями. |
|||||
|
Пример 8.8. Рассмотрим систему, имеющую два входа и один выход: |
|||||
|
x& |
= |
é 0 |
1 ù |
é1 |
3ù |
|
ê |
úx |
+ ê |
úv , y = [1, 1]x , v = col[v1, v2 ] . |
||
|
ë— 8 |
— 6û |
ë1 |
4û |
В примере 8.7 найдена матрица [sE–A]–1. Используя выражение W(s) = C[sE–A]–1B, нетрудно получить передаточную матрицу размерностью1×2
101
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #