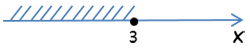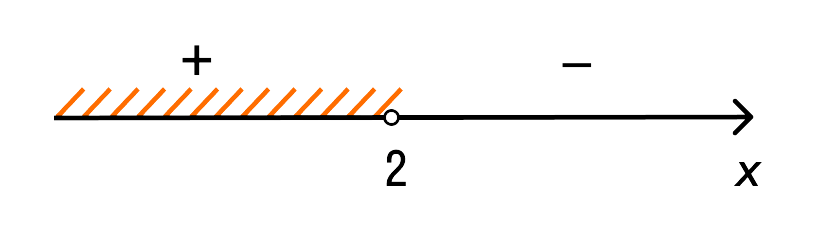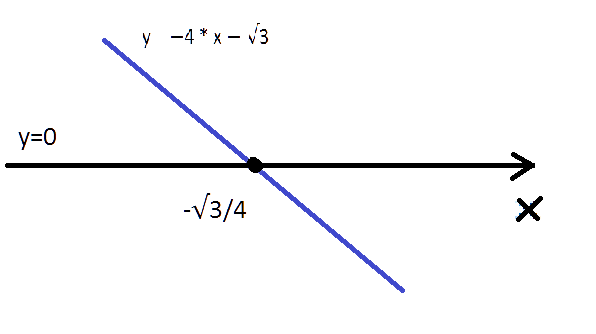Знаки неравенств
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b — любые числа, причем a ≠ 0, x — переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство — получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c — некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Особые случаи при решении линейных неравенств
№3. Решить неравенство
6 x − 1 ≤ 2 ( 3 x − 0,5 ).
№4. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Спасибо за просмотр этого урока! Если у вас остались вопросы, напишите их в комментариях.
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для
сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше |
строгий знак (число на границе не включается) |
| < | меньше |
строгий знак (число на границе не включается) |
| ≥ | больше или равно |
нестрогий знак (число на границе включается) |
| ≤ | меньше или равно |
нестрогий знак (число на границе включается) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство
отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой
знак сравнения: «>», «<»,
«≤» или «≥».
Запомните!
Линейным
неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
x − 6 < 8
Так как в неравенстве «x − 6 < 8»
неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство
Важно!
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное
в первой степени с
коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях,
в неравенствах можно переносить
любой член неравенства из левой части в правую и наоборот.
Запомните!
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на
противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x − 6 < 8
x < 8 + 6
x < 14
Итак, мы получили ответ к неравенству «x < 14». Но что означает такой
ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить,
понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

Запомните!
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу «x < 14» все решения неравенства, то есть область
слева от числа «14».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство
«x − 6 < 8»
даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его
вместо «x» в исходное неравенство «x − 6 < 8».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Важно!
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство
дают верный результат.
Решением неравенства
называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x < 14» можно понимать так: любое число из
заштрихованной области (то есть любое число меньшее
«14») будет являться решением неравенства
«x − 6 < 8».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
2x − 16 > 0
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x − 16 > 0
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x»
стоял коэффициент «1». Для этого достаточно разделить и левую,
и правую часть на число «2».
Запомните!
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2».
Так как «2» —
положительное число, знак неравенства останется прежним.
2x > 16 | (:2)
2x (:2) > 16 (:2)
x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
9 − 3x ≥ 0
Используем правило переноса.
9 − 3x ≥ 0
−3x ≥ −9
Разделим неравенство на «−3».
Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
16 ноября 2021 в 16:44
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Как правильно написать «больше 15» символом? <15 или >15?
0
Спасибо
Ответить
24 ноября 2021 в 12:56
Ответ для Алина Кирщина
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
> 15 Острый конец символа «птичка» > смотрит в сторону меньшего числа
Еще можно запомнить, как что где больше вершин у символа «птички», там большее число находится. У символа > слева две вершины, а справа одна, значит слева находится большее число.
0
Спасибо
Ответить
29 ноября 2021 в 7:32
Ответ для Алина Кирщина
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
>15
0
Спасибо
Ответить
5 марта 2020 в 23:01
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
log3
≤1
0
Спасибо
Ответить
20 августа 2020 в 1:16
Ответ для Лина Недзвецкая
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
0 < (3x − 5)/(x+1) ≤ 3.
(3x − 5)/(x+1) > 0 ⇔ x < − 1 ∪ x > 5/3;
(3x − 5)/(x+1) ≤ 3 ⇔ 8/(x+1) ≥ 0 ⇔ x > − 1.
{(−∞; −1) ∪ (5/3; +∞)} ∩ (−1; +∞) = (5/3; +∞).
0
Спасибо
Ответить
17 июля 2016 в 15:37
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство
2^3-6x<1
0
Спасибо
Ответить
21 сентября 2016 в 13:44
Ответ для Sergey Gurzhiy
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Странно, что для 11класса, но всё же:
23 ? 6x<1
8 ? 6x<1
? 6x< ? 7
x>
1
Спасибо
Ответить
6 июня 2016 в 17:05
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 июня 2016 в 2:49
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть 2x = y > 0.
Неравенство можно записать в виде
? 0.
Откуда y = 2 или 8 ? y < 9.
Стало быть, x = 1 или 3 ? x < log29.
0
Спасибо
Ответить
7 июня 2016 в 13:11
Ответ для Катя Петрова
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1



-Tак как y>0, то сокращаем на y и преобразуем к виду
Учитывая, что y=2x получим x=1 или (3?x<log29) Ответ: (x=1)?(3?x<log2). или так {1?[3;log29)}
0
Спасибо
Ответить
8 июня 2016 в 12:10
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Списывать нехорошо.
0
Спасибо
Ответить
5 мая 2016 в 10:09
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Как решить неравенство (х^2-4х+3)/(х^4-х^6) < или = 0
0
Спасибо
Ответить
8 июня 2016 в 12:28
Ответ для Влада Навдушевич
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
| (x — 1)(x — 3) |
| x4(1 — x)(1 + x) |
? 0.
и метод интервалов.
Ответ: (-oo; -1) U [3; +oo).
0
Спасибо
Ответить
3 августа 2015 в 16:54
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
область решения неравенства (х-4)>3х равна? решить
0
Спасибо
Ответить
31 августа 2016 в 10:31
Ответ для Надие Рахимова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
(x-4)>3x
x-4-3x>0
-4-2x>0
2x+4<0
2x<-4
x<-2
Проверка: Возьмём число меньшее -2, например -3
-3-4>-3 · 3
12>-9 Верно.
Ответ: x<-2
0
Спасибо
Ответить
В статье мы рассмотрим, что собой представляют линейные неравенства с одной переменной и покажем, какими способами их можно решать.
Понятие линейного неравенства
Определение
Линейными неравенствами с одной переменной называются неравенства, которые можно записать в виде формулы ax + b > 0. Вместо «>» могут быть знаки «<» или «≤», «≥». x – неизвестная переменная. a и b – действительные числа.
Линейными неравенствами с одной переменной называют неравенства a*x < c либо a*x > c, в которых x – искомая переменная, а a и c некоторые числа. О том, что коэффициент при x может или не может быть равным нулю, ничего не говорится. Это позволяет строгое неравенство 0*x > c и 0*x < c записать в виде 0*x ≥ c и 0*x ≤ c.
Линейными неравенствами с одной переменой считают неравенства, имеющие вид ax + b < 0, ax + b > 0, ax + b ≥ 0, ax + b ≤ 0. Где a и b являются любыми числами, но a не должно равняться нулю. x – искомая переменная.
Неравенства ax + b > 0 и ax > c считаются равносильными, так как получаются с помощью переноса слагаемого из одной их части в другую. Решения подобных неравенств совпадают.
Примеры линейных неравенств с одной переменной:
- -2x + 4 > 0;
- 3x +1 ≤ 0;
- 2(x-1) < 2x-4;
- 3x+1 ≤ 6-3x
- 3x – 6 > 0.
Как решать линейные неравенства
Решением линейного неравенства называют нахождение всех значений переменной x, при которых оно сохраняет свою силу. Самыми распространёнными и результативными способами, с помощью которых удаётся решить подавляющее большинство линейных неравенств являются метод равносильных преобразований, метод интервалов и графический метод. Рассмотрим каждый из них подробнее.
Решение линейных неравенств с помощью равносильных преобразований
Применительно к нашему случаю равносильными называются следующие преобразования:
- Перенос одного и более членов неравенства из одной части в другую. При этом знак переносимого слагаемого меняется на противоположный. В качестве примеров подобного рода неравенств можно привести
2x − 3 > 6 и 2x > 6 + 3 или 10x – 1 > 3 и 10x > 3 + 1.
- Деление или умножение обеих частей неравенства на одно положительное число. Знак неравенства при этом остаётся тем же. В качестве примеров можно указать
2x > 9 и 10x > 45 или -9x > -15 и -3x > -5.
- Деление или умножение обеих частей неравенства на одно отрицательное число. Знак неравенства при этом нужно сменить на противоположный. Примеры подобных неравенств следующие 5x < -8 и -10x>16 или 9x +12 > 21 и 3x — 4 < -7.
Задачи 1 — 2
Решить: 2x – 9 >3.
Решение: Видно, что коэффициент при x ненулевой. Это значит, описанные выше преобразования применимы.
Переносим свободное слагаемое из левой части в правую и получаем 2x > 3+9, 2x > 12
Разделим обе части на 2. Будем иметь x > 6. Это неравенство равносильно 2x – 9 >3.
Полученное решение можно записать в виде x > 6 либо [(6,+infty)].
Скобки круглые т. к. неравенство строгое.
Ответ: [(6,+infty)].
Решить: -5x – 8 ≥ 12
Решение: Коэффициент при x равен -5 т. е. тоже не нулевой, а значит можно решать дальше. Переносим -8 в правую часть и получаем -5x ≥ 12 + 8, -5x ≥ 20.
Делим обе части на -5. Не забываем, что при этом необходимо будет сменить знак.
x ≤ -4
Решение записываем, как x ≤ -4 или (-∞, -4]. Скобка в конце стоит квадратная т. к. x может быть не только меньше, но и равным 4.
Ответ: (-∞, -4].
Если числовое неравенство b > 0 («<», «≤», «≥») верно, то исходное неравенство будет иметь своё решение при любом из значений x. Если же оно неверно, то у исходного неравенства решений нет вовсе.
Задачи 3 — 4
Решить неравенство: 0*x + 9 > 0.
Решение: Указанное неравенство равносильно 9 > 0.
x при этом может принимать совершенно любые значения.
Решение имеет вид (-∞, ∞).
Ответ: (-∞, ∞).
Решить: 0*x + 3 < 0.
Решение: Данное неравенство сводится к 3 < 0
Оно является неверным, а значит неравенство решений не имеет.
Ответ: решений нет.
У некоторых из читателей возможно появился вопрос, как быть, если и в роли коэффициента при x, и в роли слагаемого выступает ноль. Это неравенства 0*x + 0 < 0, 0*x + 0 > 0, 0*x + 0 ≤ 0, 0*x + 0 ≥ 0. Два первых из них решений не имеют, ведь ноль не может быть больше или меньше самого себя. У двух последних решения есть т. к. любое число равно самому себе, в частности, ноль равен нулю.
Нет времени решать самому?
Наши эксперты помогут!
Решение линейных неравенств методом интервалов
Он может быть использован лишь тогда, когда коэффициент при x не равен нулю. Последовательность действий при использовании указанного метода следующая:
- Находятся нули функции y = ax + b. Для этого, нужно решить уравнение ax + b = 0. При a неравном нулю его решение будет состоять из одного корня x0.
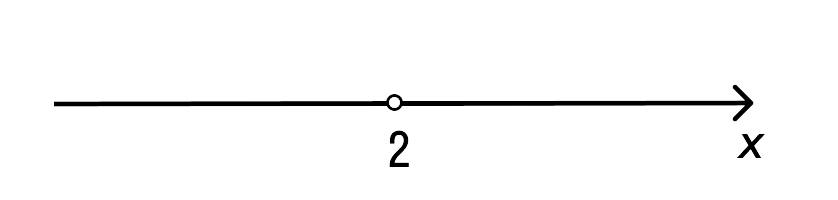
- Строится координатная прямая. На ней изображается точка с координатой x0. При строгом неравенстве точку нужно изобразить выколотой. При нестрогом – закрашенной.
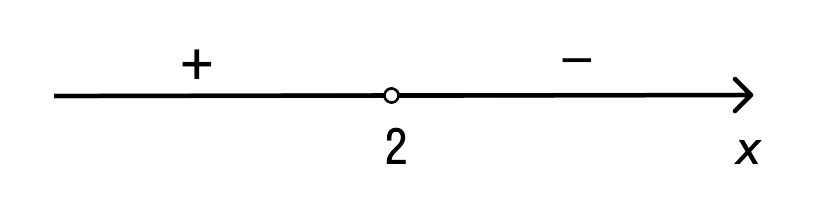
- На промежутках определяются знаки функции y = ax + b. Если решение неравенства имеет знаки > или ≥, то добавляется штриховка над положительным промежутком. Если решение идёт со знаками если < или ≤, штриховка происходит над отрицательным промежутком.
Задача 5
Решить: −6x + 12 > 0 методом интервалов.
Решение:
Действуем в соответствии с алгоритмом. Находим корень уравнения − 6x + 12 = 0.
Делим обе части выражения на -6. Получаем x=2.
Для определения знака на промежутке (−∞, 2) вычисляем функцию y = −6x + 12 при х = 1. Видим, что −6 * 1 + 12
= 6, 6 > 0, т. е. знак положительный. Определяем, какой знак на промежутке (2, + ∞). Для этого в функцию
подставляем х = 3. Получаем
Штрихуем положительный промежуток
Из чертежа ясно, что решение нашего неравенства (−∞, 2) или x < 2.
Ответ: (−∞, 2).
Решение неравенств графическим способом
Главное при пользовании этим методом правильно найти промежутки, которые требуется изобразить на графике.
Действия при пользовании графическим способом следующие:
- При решении ax + b < 0 определяем промежуток, где график будет ниже оси 0x;
- При решении ax + b ≤ 0 определяем промежуток, где график либо ниже 0х, либо совпадает с ней;
- При решении ax + b > 0 определяем промежуток, где график выше оси 0х;
- При решении ax + b ≥ 0 определяем промежуток, где график выше оси 0х или совпадает с ней.
Задача 6
Решить: −4 * x − √3> 0
Коэффициент при x отрицательный, значит наша прямая убывающая. Чтобы определить точки её пересечения с осью 0x нужно решить уравнение −4 * x − √3 = 0
X= -√3/4
Построим график этого линейного неравенства y=0.
Т. к. у решения неравенства знак >, внимание следует обращать на промежуток выше оси 0x.
Он находится левее точки -√3/4.
Видно, что решением неравенства будет (−∞, −√3/4).
Ответ: (−∞, −√3/ 5).
Неравенства, сводящиеся к линейным
При их решении следует использовать такие приёмы, как раскрытие скобок, собирание в левой части неравенства чисел, а в правой переменных, деление обеих частей на коэффициент при x.
Задача 7
Решить: 3x + 2 > 2(x + 3) + x.
Решение: Раскрываем в правой частях скобки 3x + 2 > 2x + 6 + x.
Переносим члены с иксами в одну сторону, без иксов в другую.
3x — 2x — x > 6 – 2
0x > 4
0 > 4
Получаем противоречие, т. е. неравенство решения не имеет.
Ответ: решений нет.
Линейные неравенства – такие неравенства, которые можно привести к одному из видов:
(ax>b), (ax<b), (ax geq b), (ax leq b),
где (a) и (b) любые числа (причем (aneq0)), а (x) — неизвестная переменная.
Проще можно сказать, что это такие неравенства, в которых есть переменная только в первой степени, и она не находится в знаменателе дроби.
Примеры:
(3x>-2)
(frac{3y-4}{5})(leq1)
(5(x-1)-2x>3x-8)
Примеры не линейных неравенств:
(3>-2) – здесь нет переменных, только лишь числа, значит это числовое неравенство
(frac{-14}{(y-3)^{2}-5}) (leq0) – есть переменная в знаменателе, это дробно-рациональное неравенство
(5(x-1)-2x>3x^{2}-8) — есть переменная во второй степени, это квадратное неравенство
Решение линейных неравенств
Решением неравенства будет любое число, подстановка которого вместо переменной сделает неравенство верным. Решить неравенство – значит найти все такие числа.
Например, для неравенства (x-2>0) число (5) будет решением, т.к. при подстановке пятерки вместо икса мы получим верное числовое: (3>0). А вот число (1) решением не будет, так как при подстановке получится неверное числовое неравенство:(-1>0) . Но решением неравенства будут не только пятерка, но и (4), (7), (15), (42), (726) и еще бесконечное множество чисел: любое число, больше двойки.
Поэтому линейные неравенства не решают перебором и подстановкой значений. Вместо этого их с помощью равносильных преобразований приводят к одному из видов:
(x<c), (x>c), (xleqс), (xgeqс), где (с) — любое число
После чего ответ отмечается на числовой оси и записывается в виде промежутка (также называемого интервалом).
Вообще, если вы умеете решать линейные уравнения, то и линейные неравенства вам под силу, потому что процесс решения очень схож. Есть лишь одно важное дополнение:
При умножении или делении неравенства на любое отрицательное число (или выражение) нужно менять знак сравнения на противоположный (почему так – смотри здесь).
Пример. Решить неравенство (2(x+1)-1<7+8x)
Решение:
|
(2(x+1)-1<7+8x) |
Раскроем скобки |
|
|
(2x+2-1<7+8x) |
Перенесем (8x) влево, а (2) и (-1) вправо, не забывая при этом менять знаки |
|
|
(2x-8x<7-2+1) |
Приведем подобные слагаемые |
|
|
(-6x<6) (|:(-6)) |
Поделим обе части неравенства на (-6), не забыв поменять знак сравнения |
|
|
(x>-1) |
Отметим на оси числовой промежуток. Неравенство строгое, поэтому само значение (-1) «выкалываем» и в ответ не берем |
|
|
|
Запишем ответ в виде интервала |
Ответ: (xin(-1;infty))
Особый случай №1: решение неравенства – любое число
В линейных неравенствах возможна ситуация, когда ему в качестве решения пойдет абсолютно любое число – целое, дробное, отрицательное, положительное, ноль… Например, вот такое неравенство (x+2>x) будет верным при любом значении икса. Ну, а как же может быть иначе, ведь слева к иксу прибавили двойку, а справа – нет. Естественно, что слева будет получаться большее число, какой бы икс мы не взяли.
Пример. Решить неравенство (3(2x-1)+5<6x+4)
Решение:
|
(3(2x-1)+5<6x+4) |
Раскроем скобки |
|
|
(6x-3+5<6x+4) |
Приведем подобные слагаемые |
|
|
(6x+2<6x+4) |
Перенесем члены с иксом влево, а числа вправо, не забывая при этом менять знаки |
|
|
(6x-6x<4-2) |
Приведем подобные слагаемые |
|
|
(0<2) |
Получили верное числовое неравенство. Причем оно будет верным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса будет решением |
Ответ: (xin(-infty;infty))
Особый случай №2: неравенство не имеет решений
Возможна и обратная ситуация, когда у линейного неравенства вообще нет решений, то есть никакой икс не сделает его верным. Например, (x-2>x) не будет верным никогда, ведь слева из икса вычитают двойку, а справа – нет. Значит, слева всегда будет меньше, а не больше.
Пример. Решить неравенство (frac{x-5}{2})(>) (frac{3x+2}{6})(-1)
Решение:
|
(frac{x-5}{2})(>) (frac{3x+2}{6})(-1) |
Нам мешают знаменатели. Сразу же избавляемся от них, умножая всё неравенство на общий знаменатель всех дробей, то есть – на 6 |
|
|
(6cdot)(frac{x-5}{2})(>)(6cdot)((frac{3x+2}{6})(-1)()) |
Раскроем скобки |
|
|
(6cdot)(frac{x-5}{2})(>)(6cdot)(frac{3x+2}{6})(-6) |
Сократим то, что можно сократить |
|
|
(3cdot(x-5)>3x+2-6) |
Слева раскроем скобку, а справа приведем подобные слагаемые |
|
|
(3x-15>3x-4) |
Перенесем (3x) влево, а (-15) вправо, меняя знаки |
|
|
(3x-3x>-4+15) |
Вновь приводим подобные слагаемые |
|
|
(0>11) |
Получили неверное числовое неравенство. И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет. |
Ответ: (xinvarnothing)
Смотрите также:
Системы линейных неравенств
Строгие и нестрогие неравенства