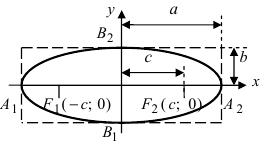
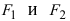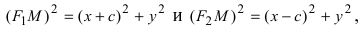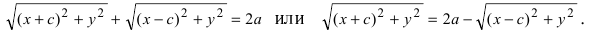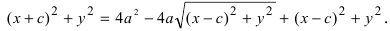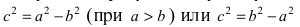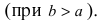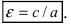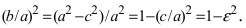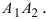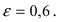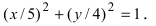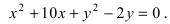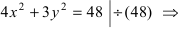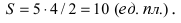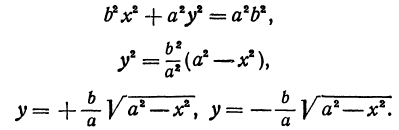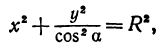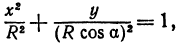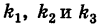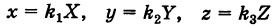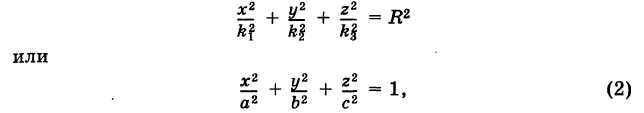Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось 

Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Перифокусное расстояние
Апофокусное расстояние
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса |
 |
| Большая полуось эллипса |
|
8.48528137423857 |
| Малая полуось эллипса |
|
5.656854249492381 |
| Эксцентриситет эллипса |
|
0.8958064164776166 |
| Фокусное/фокальное расстояние |
|
32.2490309931942 |
| Коэффициент сжатия |
|
0.4444444444444444 |
| Координаты первого фокуса F1(x1:y1) |
|
-16.1245154965971 : 0 |
| Координаты второго фокуса F2(x2:y2) |
|
16.1245154965971 : 0 |
| Фокальный параметр |
|
3.5555555555555554 |
| Перифокусное расстояние |
|
1.875484503402901 |
| Апофокусное расстояние |
|
34.1245154965971 |
И еще один пример
Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.
Если мы введем данные в калькулятор получим
 |
| Большая полуось эллипса |
|
5.877538136328849 |
| Малая полуось эллипса |
|
NaN |
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Удачных расчетов!
Глава III. Кривые второго порядка
§ 38. Эллипс.
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости постоянна и больше расстояния между этими точками.
Данные точки называются фокусами эллипса, а расстояние между ними — фокальным расстоянием. С эллипсом человеку приходится иметь дело в самых различных областях его деятельности. Садовник размечает клумбу, ограниченную эллипсом. Художник вычерчивает эллиптический контур для росписи стен или потолка зала. Математик рассчитывает эллиптическую траекторию движения спутника Земли. Наконец, сама Земля, как известно, движется по эллипсу, в одном из фокусов которого находится Солнце.
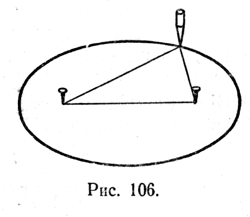
Покажем, как, исходя из определения эллипса, можно разбить эллиптическую клумбу. Забьем в землю два колышка (рис. 106), затем тонкую веревку свяжем в кольцо и наденем веревочное кольцо на оба колышка. Натянув веревку третьим колышком, вычертим им эллипс. Изменяя расстояние между колышками и длину веревки, можно получать эллипсы разных размеров и формы.
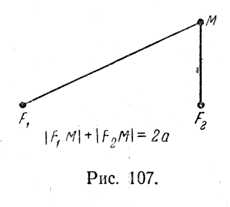
Обозначим фокусы эллипса буквами F1и F2. Пусть фокальное расстояние |F1F2| = 2с. Если М — произвольная точка эллипса (рис. 107), то по определению эллипса сумма
|F1M | + |F2M | постоянна. Обозначив ее через 2а, получим
|F1M | + |F2M | = 2a. (1)
Отметим, что по определению эллипса 2а > 2с, т. е. а > с. Равенство (1) есть уравнение эллипса.
Если точка F1 совпадает с точкой F2, то уравнение эллипса принимает вид
2|F1M| = 2a, т. е. |F1M| = a.
Это уравнение является уравнением окружности радиуса а с центром в точке F1
(F1 = F2). Таким образом, всякая окружность является частным случаем эллипса.
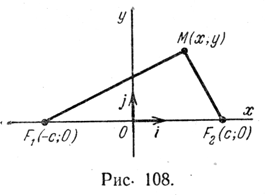
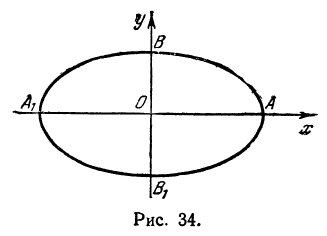
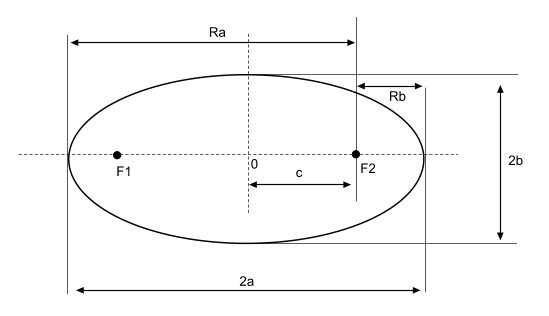
Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса; ось ординат проведем через середину отрезка F1F2 перпендикулярно ему. Тогда фокусами будут точки F1(— с; 0) и F2(c; 0) (рис. 108).
Пусть М(х; у) —любая точка эллипса, тогда
|F1M|= √(x + c)2 + y2 и |F2M|= √(x — c)2 + y2 .
Подставляя найденные значения |F1M| и |F2M| в уравнение (1), получаем
√(x + c)2 + y2 + √(x — c)2 + y2 = 2а. (2)
Уравнение (2) является уравнением эллипса в выбранной системе координат. Это уравнение можно привести к более простому виду. Для этого сначала перенесем второе слагаемое левой части уравнения в правую часть:
√(x + c)2 + y2 = 2а — √(x — c)2 + y2 . (3)
Затем возведем обе части полученного равенства в квадрат:
(x + c)2 + y2 = 4а2 — 4а √(x — c)2 + y2 + (x — c)2 + y2 .
После упрощений получим
√(x — c)2 + y2 = а — c/a х. (4)
Возводя в квадрат обе части уравнения (4), будем иметь
(x — c)2 + y2 = (а — c/a х)2
или
х2 — 2сх + c2 + y2 = a2 — 2сх + c2/a2 х2,
откуда
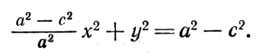
По определению эллипса а > с, поэтому a2 — c2 —-положительное число. Обозначим его через b2, т. е. положим b2 = a2 — c2 . Тогда уравнение (5) примет вид
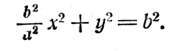
Разделив обе части последнего равенства на b2, получим уравнение
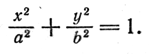
Оно называется каноническим уравнением эллипса. При а = b, т. е. в случае с = 0, уравнение (6) принимает вид
х2 + y2 = a2,
т. е. является каноническим уравнением окружности.
Замечание. Полученное нами уравнение (6) является следствием уравнения (2). Поэтому координаты х и у каждой точки эллипса, заданного уравнением (2), удовлетворяют и уравнению (6). При выводе уравнения (6) мы дважды возводили в квадрат обе части уравнения. Такая операция могла привести к тому, что уравнению (6) удовлетворяли бы не только координаты х и у точек эллипса, но и координаты каких-то точек, не принадлежащих эллипсу (как известно, при возведении в квадрат могут появиться посторонние решения). Покажем, что в данном случае этого не произошло.
Поскольку , то из уравнения (6) следует, что
, т. е. |x| < а. Аналогично заключаем, что |y| < b. Таким образом, все точки М(х; у), координаты которых удовлетворяют уравнению (6), находятся в прямоугольнике |x| < а, |y| < b. Но в прямоугольнике |x| < а, |y| < b нет точек, координаты которых удовлетворяют уравнению (6) и не удовлетворяют уравнению эллипса (2), так как на множестве точек этого прямоугольника при возведении в квадрат не нарушается равносильность из-за неотрицательности обеих частей уравнений (3) и (4). Левые части уравнений (3) и (4) всюду неотрицательны. Покажем, что при |x| < а и |y| < b правые части этих уравнений также неотрицательны. Действительно,
√(x — c)2 + y2 < √(—a — c)2 + b2 = √a2 + 2ac+ c2 + b2 = √2a2 + 2ac < √2a2+2a2 = 2а,
а — c/a х > а — c/a a = а — с > 0.
Итак, уравнения (2) и (6) равносильны.
Задача 1. Написать каноническое уравнение эллипса, проходящего через точку М(5; 0), если фокальное расстояние равно 6.
Так как |F1F2| = 6, то с = 3. Запишем каноническое уравнение эллипса:
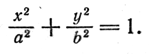
По условию точка М (5; 0) принадлежит эллипсу, следовательно, 25/ a2= 1. откуда
a2 = 25. Из равенства a2 — c2 = b2 находим b2 = 25 — 9 =16. Итак, искомым уравнением эллипса будет уравнение
Задача 2. Доказать, что уравнение 36x2 + 100y2 — 3600 = 0 является уравнением эллипса. Найти координаты фокусов и фокальное расстояние.
Разделив обе части уравнения на 3600, получим
Это уравнение является уравнением эллипса.
Из равенства a2 — c2 = b2 следует, что c2= a2 — b2. Так как a2= 100 и b2= 36, то c2 = 64, откуда с = 8.
Фокусы эллипса будут находиться в точках F1 (—8; 0) и F2(8; 0).
Фокальное расстояние |F1F2| = 16.
Эллипсом называется множество точек
плоскости, сумма расстояний от которых
до двух данных точек
и
этой плоскости, называемых фокусами,
есть величина постоянная, равная
,
,
большая, чем расстояние между фокусами
.
Е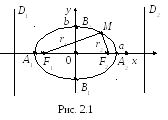
оси координат расположены по отношению
к эллипсу так, как на рис. 2.1, а фокусы
эллипса находятся на оси
на равных расстояниях от начала координат
в точках
и
,
то получится простейшее (каноническое)
уравнение эллипса:
,
(2.2)
где
– большая,
– малая полуось эллипса, причем
,
и
(
– половина расстояния между фокусами)
связаны соотношением
.
Точки
,
.
,
называются вершинами эллипса, оси
симметрии
и
– главными осями, а центр симметрии 0 –
центром эллипса.
Векторы
и
называются фокальными радиус—векторами,
а числа
и
– фокальными радиусами точки
,
принадлежащей эллипсу (в силу определения
эллипса для любой его точки
).
В частном случае
фокусы
и
совпадают с центром, а каноническое
уравнение имеет вид
,
или
,
т. е. описывает окружность радиуса
с центром в начале координат.
Форма эллипса (мера его сжатия)
характеризуется его эксцентриситетом
(;
при
эллипс является окружностью, а т. к.
,
то
).
Прямые
и
,
перпендикулярные главной оси и проходящие
на расстоянии
от центра, называются директрисами
эллипса.
Фокальные радиусы-векторы выражаются
через абсциссу точки эллипса по формулам
и
.
Если центр эллипса с полуосями
и
смещен в точку
,
то его каноническое уравнение имеет
вид
.
(2.3)
Примеры
1. Какую линию определяет уравнение
?
Разделим данное уравнение почленно на
12:
.
Сравнивая полученное уравнение с
уравнением (2.2), заключаем, что оно
определяет эллипс с полуосями
,
.
Найдем фокусы этого эллипса. Так как
,
то
,
.
Следовательно, фокусы эллипса находятся
в точках
,
.
2. Даны координаты точек
,
и радиус окружности
,
центр которой находится в начале
координат. Требуется:
а) составить каноническое уравнение
эллипса, проходящего через данные точки
и
;
б) найти полуоси, фокусы и эксцентриситет
этого эллипса;
в) найти все точки пересечения эллипса
с данной окружностью;
г) построить эллипс и окружность.
Решение.
а) Пусть
– искомое уравнения эллипса. Этому
уравнению должны удовлетворять координаты
данных точек. Следовательно, подставляя
координаты точек, получим
Отсюда находим
,
.
Итак, уравнение эллипса имеет вид
.
б)
,
– соответственно большая и малая полуоси
эллипса. Для эллипса
,
значит
,
откуда
.
Следовательно,
,
– соответственно левый и правый фокусы
эллипса. Эксцентриситет эллипса
.
в) Найдем точки пересечения эллипса с
данной окружностью. Уравнение окружности
.
Решая систему уравнений
получим
,
,
.
Но
,
значит
,
откуда
.
Итак, существуют две точки пересечения
эллипса и окружности
и
.
г) Построить эллипс и окружность.
3. Большая ось эллипса равна 12, а
директрисами его служат прямые
.
Найти уравнение эллипса и его
эксцентриситет.
Решение. По условию
.
Из уравнений директрис
и формулы
находим
.
Тогда
.
Следовательно, искомое уравнение эллипса
есть
,
а эксцентриситет его
.
4. Эллипс касается оси
в точке
и пересекает ось
в точках
и
.
Зная, что оси эллипса параллельны осям
координат, составить его уравнение.
Решение. Будем искать уравнение
эллипса в виде (2.3). Так как эллипс касается
оси
,
то
.
Далее,
,
т. к. прямая
параллельна оси
и отсекает на оси
отрезок
.
Следовательно, уравнение эллипса имеет
вид
.
Полуось
.
В таком случае получим
– уравнение эллипса. Найдем
.
Так как
лежит на эллипсе, то ее координаты
удовлетворяют его уравнению, т. е.
.
Итак, искомое уравнение эллипса
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 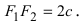
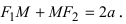
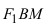
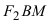
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 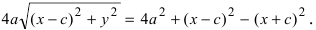
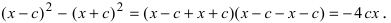
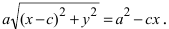
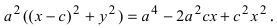
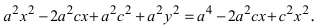
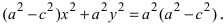
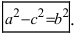
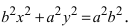
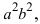
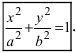
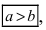
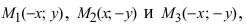
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 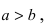
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 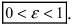
Если 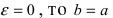
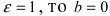
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 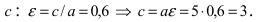
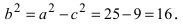
Пример:
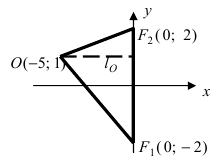
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 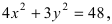
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
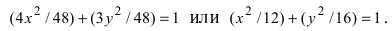
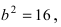
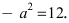
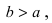
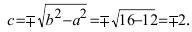
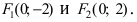
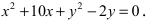
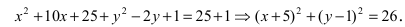
Построим в декартовой системе координат треугольник 
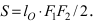
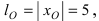
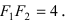
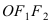
Эллипс в высшей математике
Рассмотрим уравнение
где 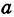
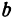
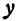
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
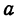

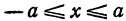
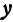
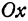
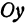
При 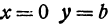
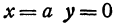
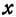

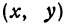
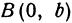
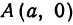
Полученная линия называется эллипсом. Число 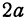
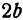
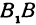
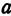
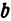
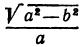
Пример:
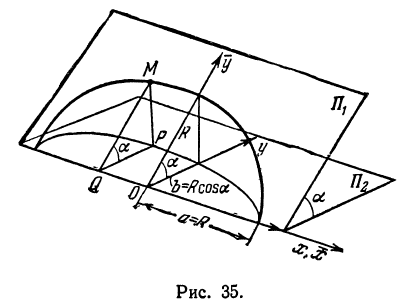
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 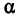
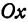
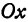
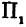
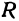
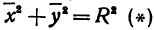
Пусть точка 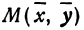
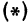
Обозначим проекцию точки 
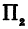
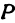
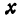
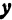


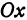
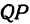
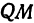
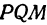
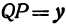
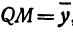
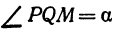
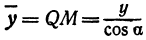


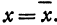
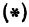
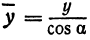
или
а это есть уравнение эллипса с полуосями 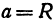
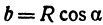
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 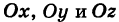
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 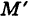
(рис. 206). Отсюда
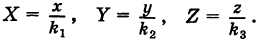
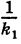
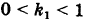
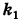
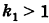
Подставляя эти формулы в уравнение (1), будем иметь
где 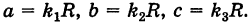
Величины 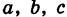
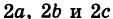
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность





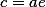


;M_2(3sqrt1.5:sqrt2))