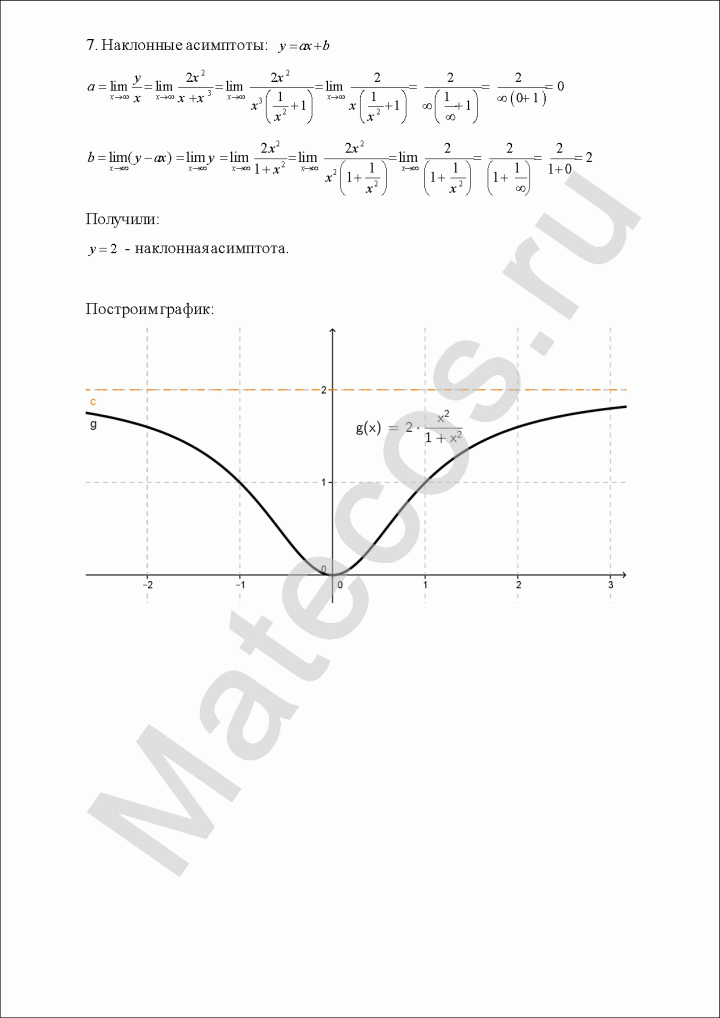
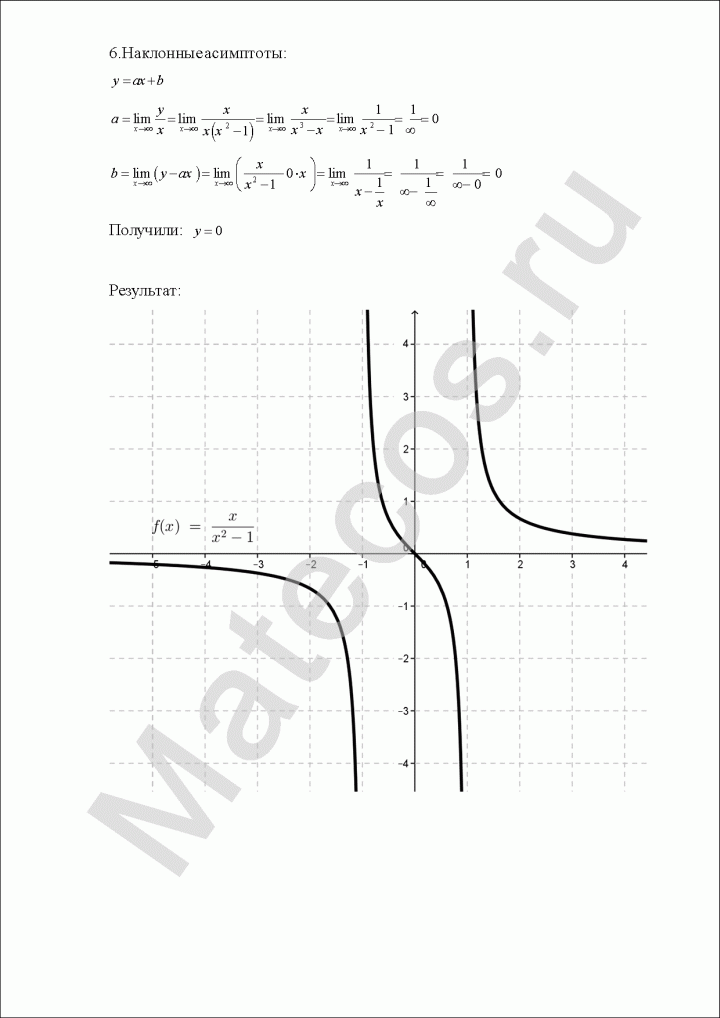
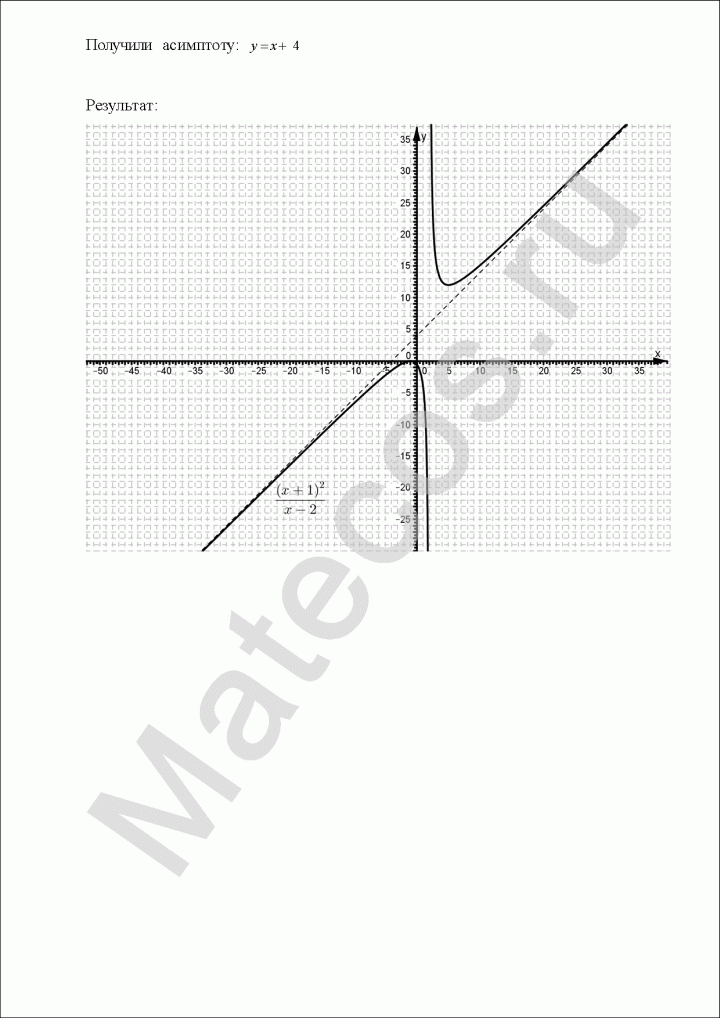
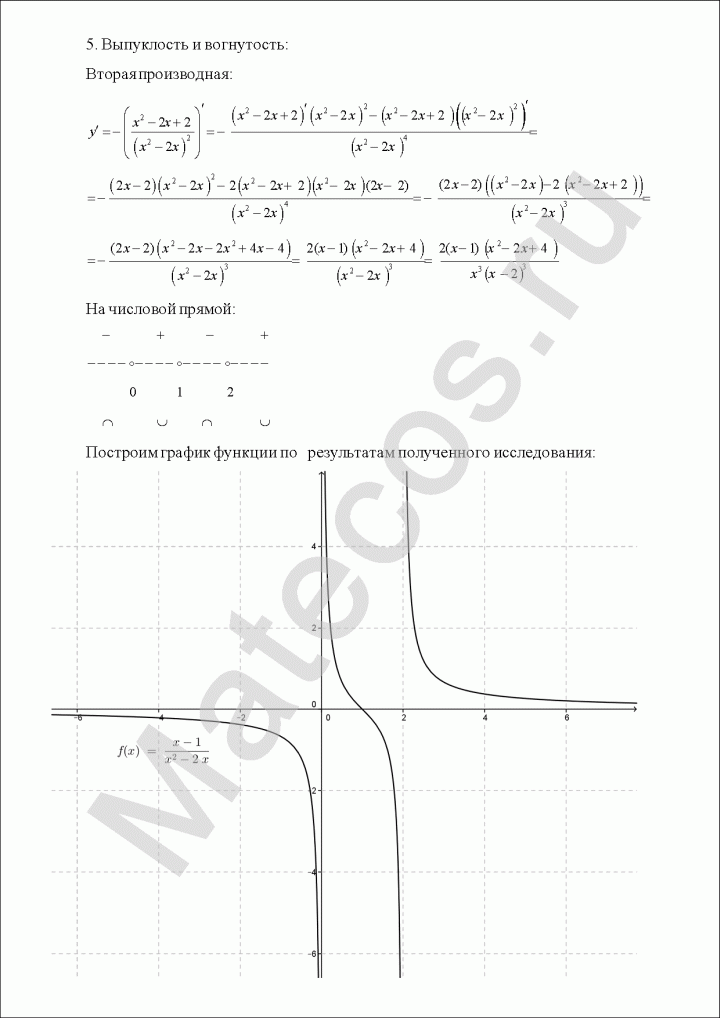
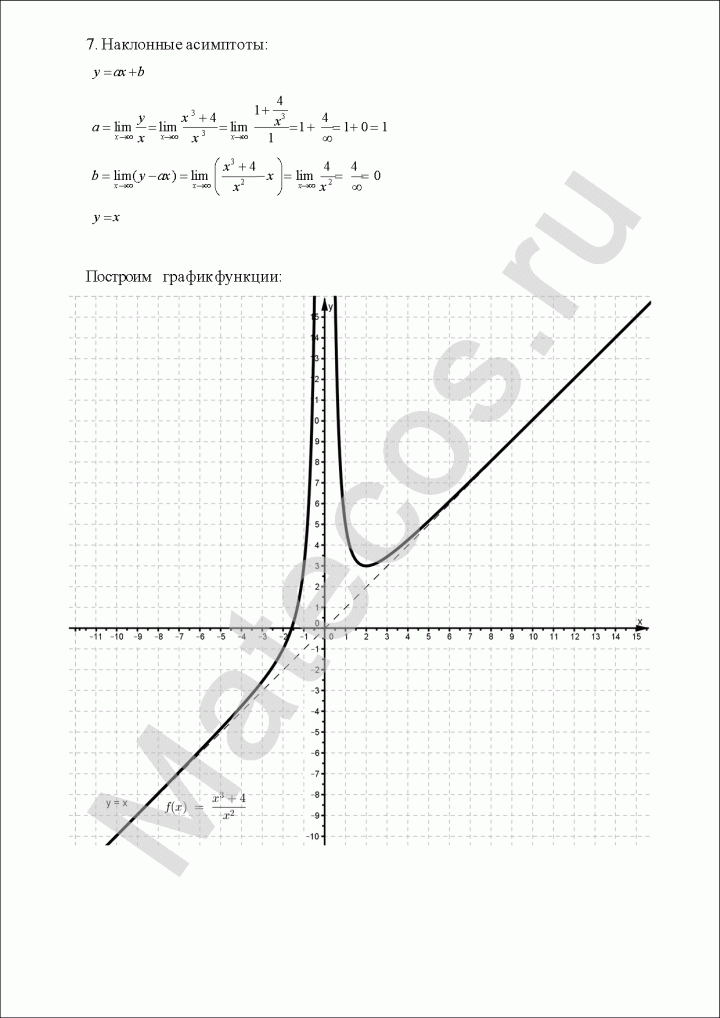
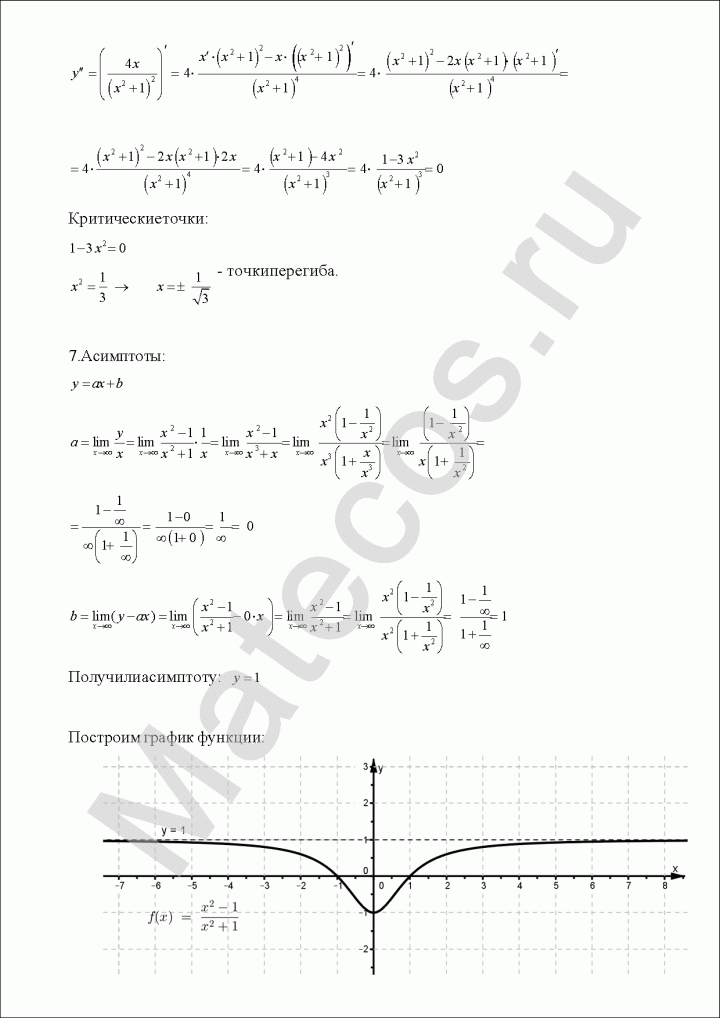
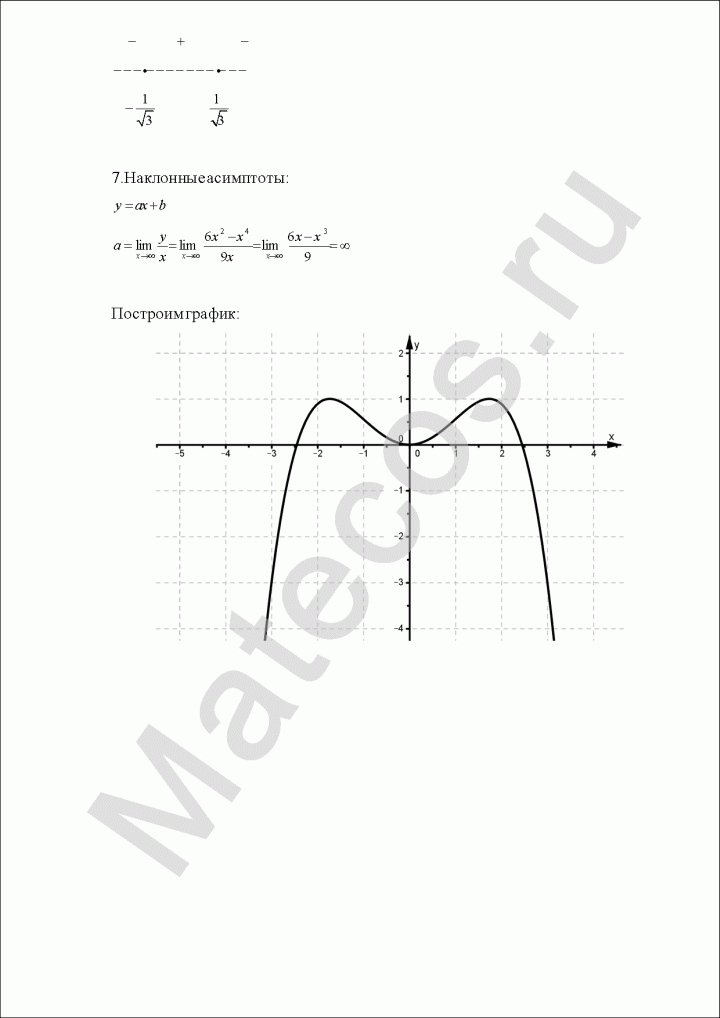
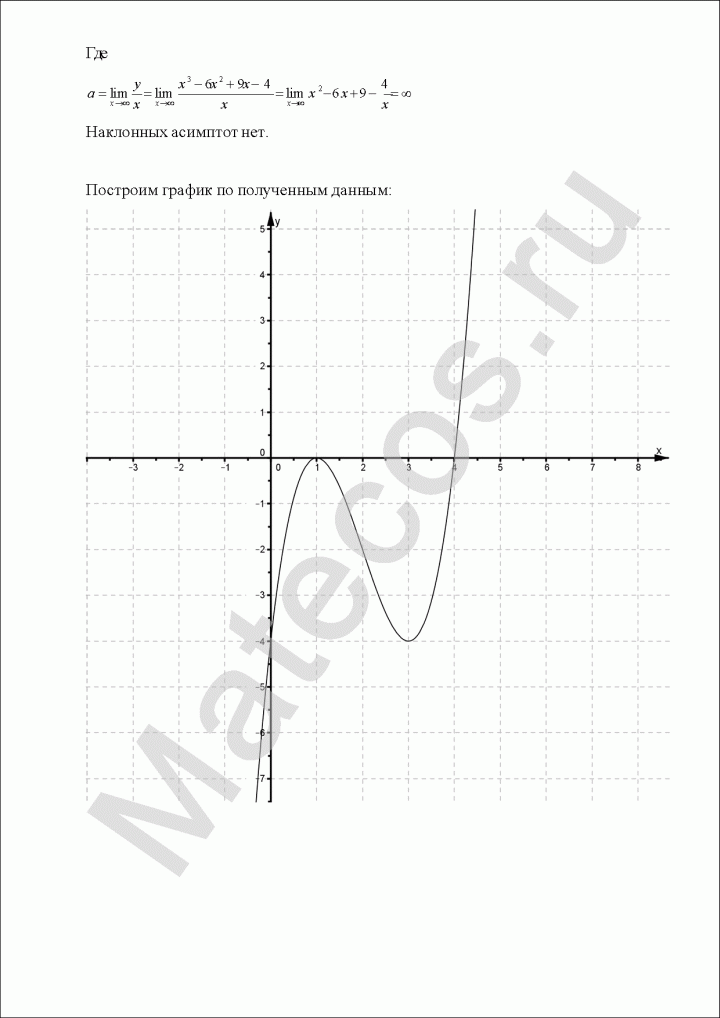
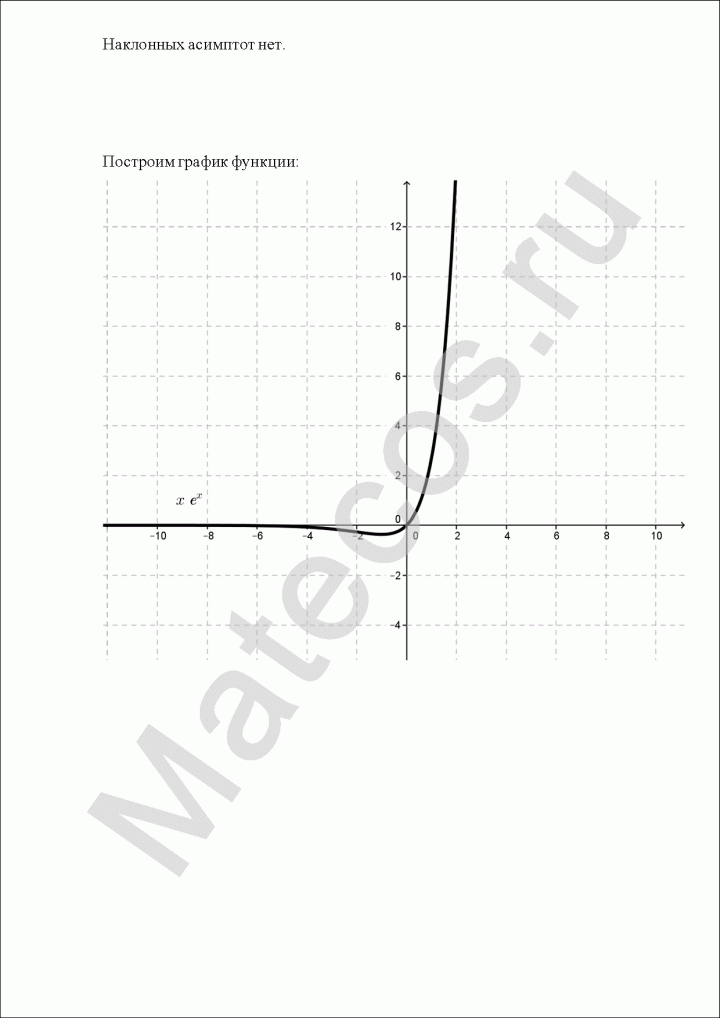
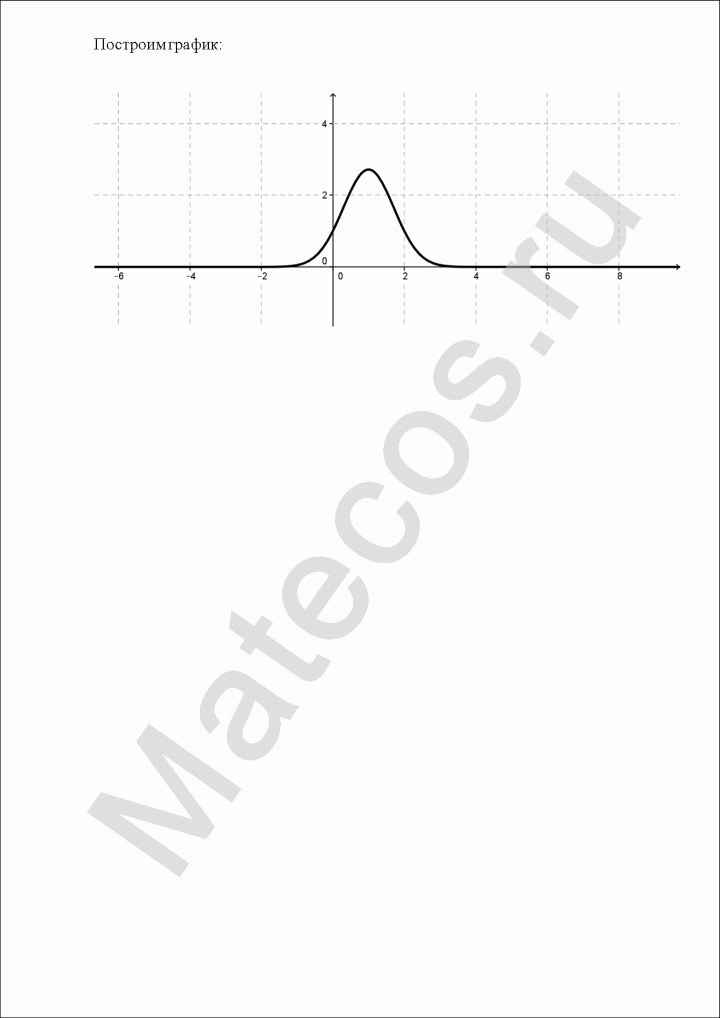
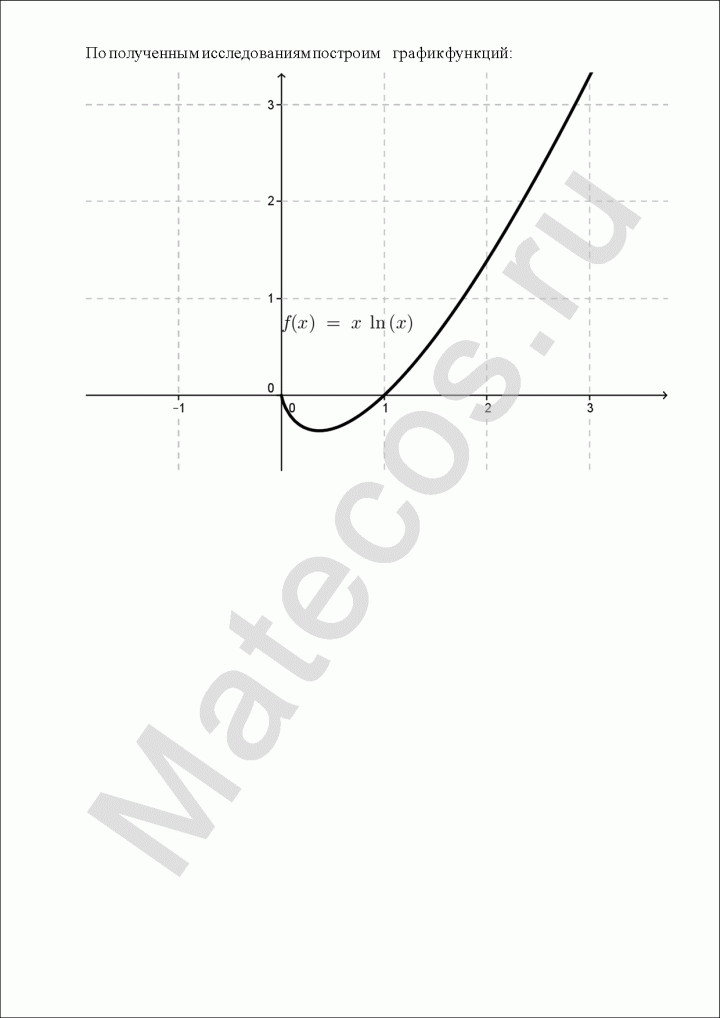
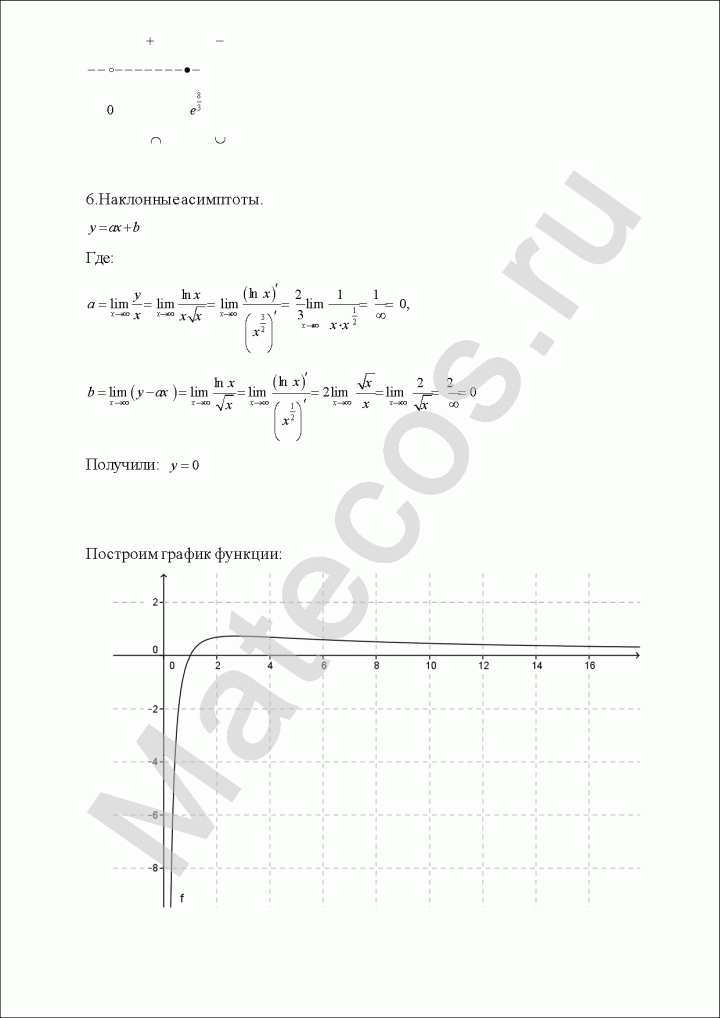
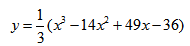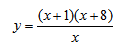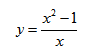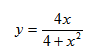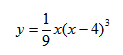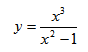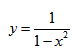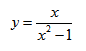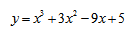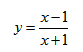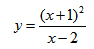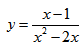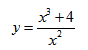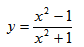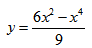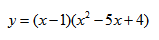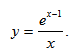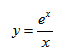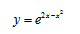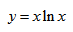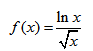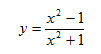Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.
А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
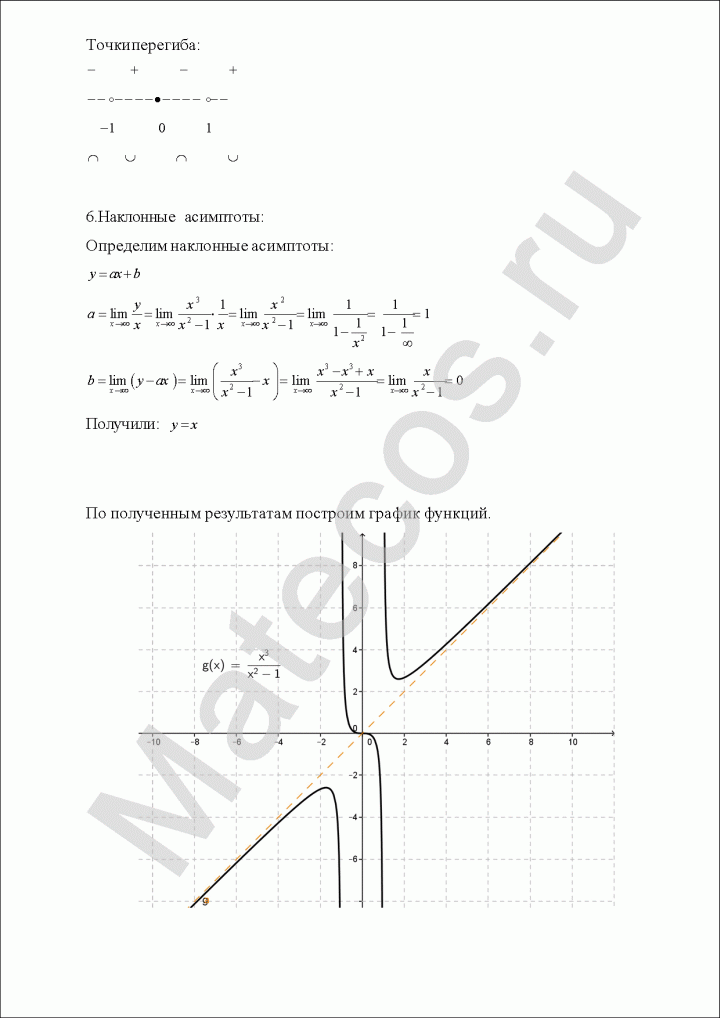
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Спасибо за ваши закладки и рекомендации
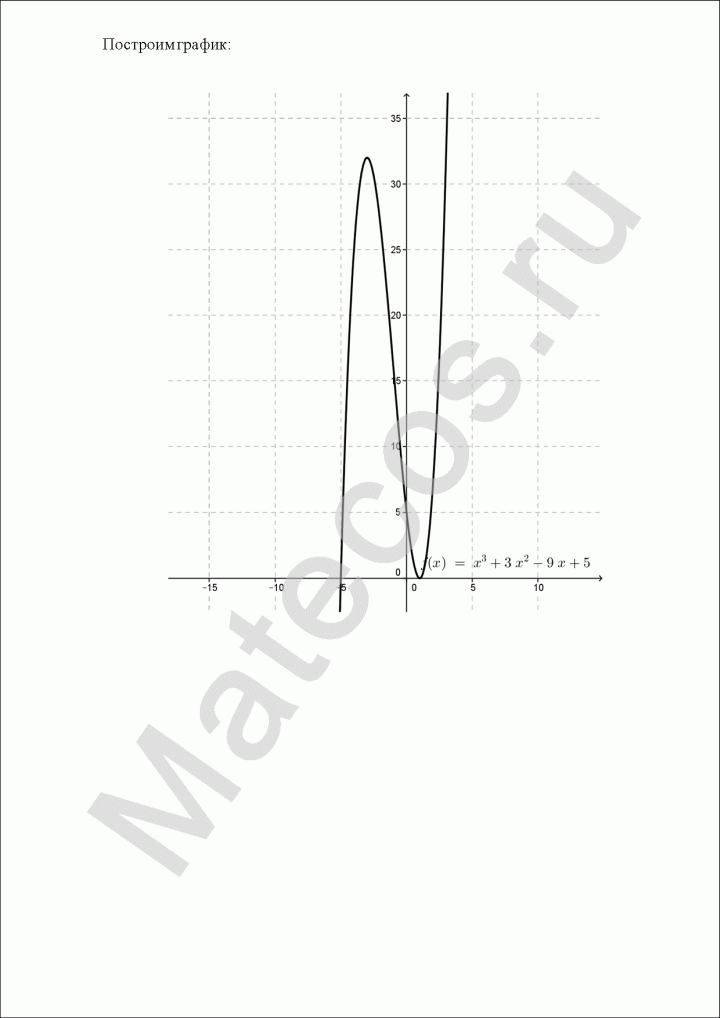
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
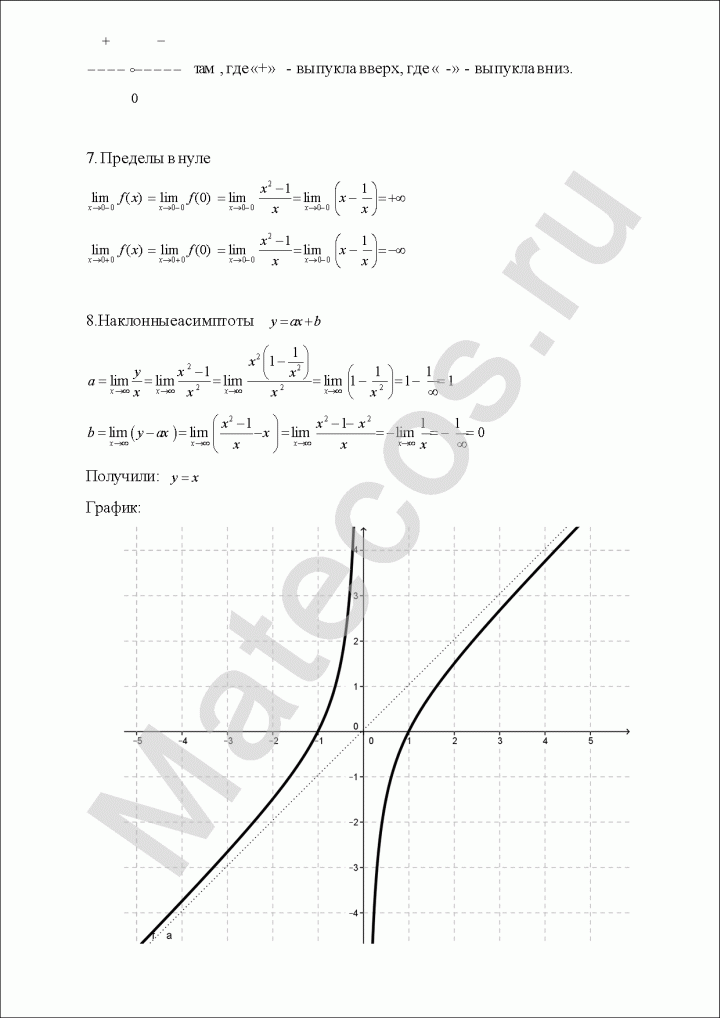
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
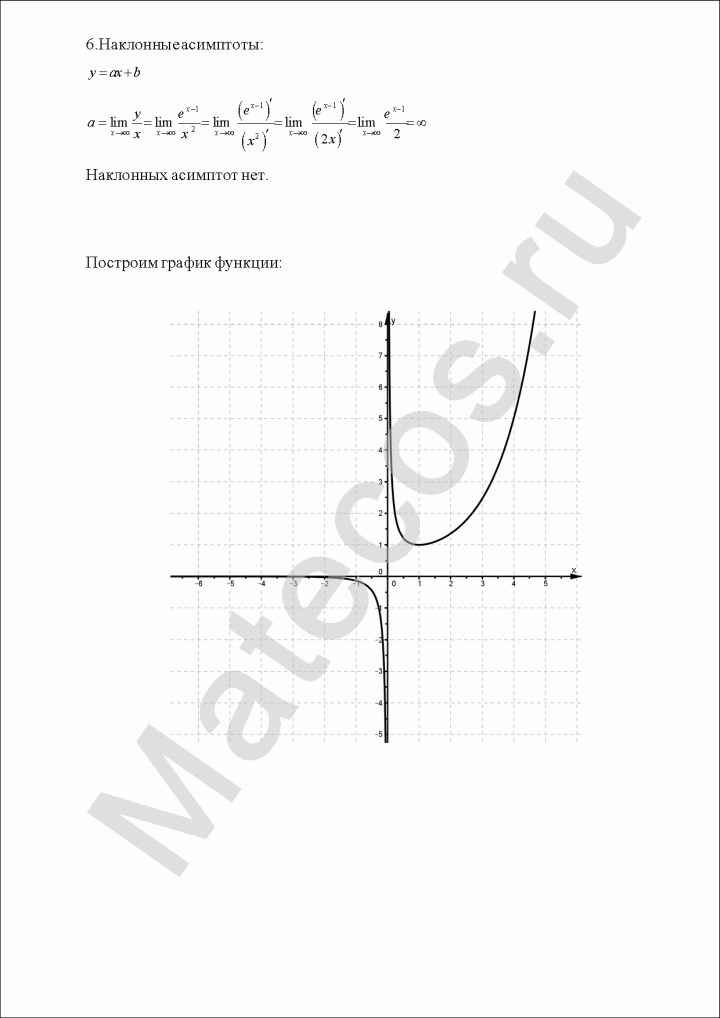
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
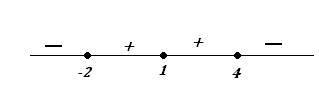
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
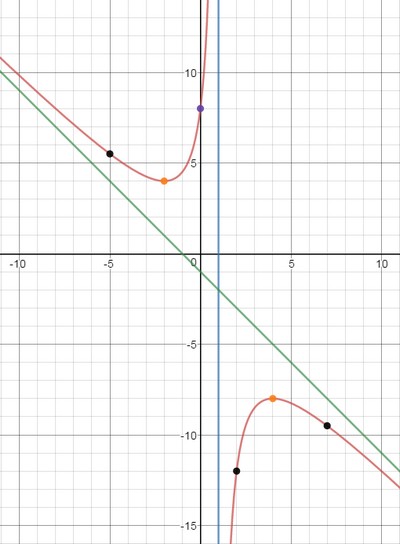
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

.
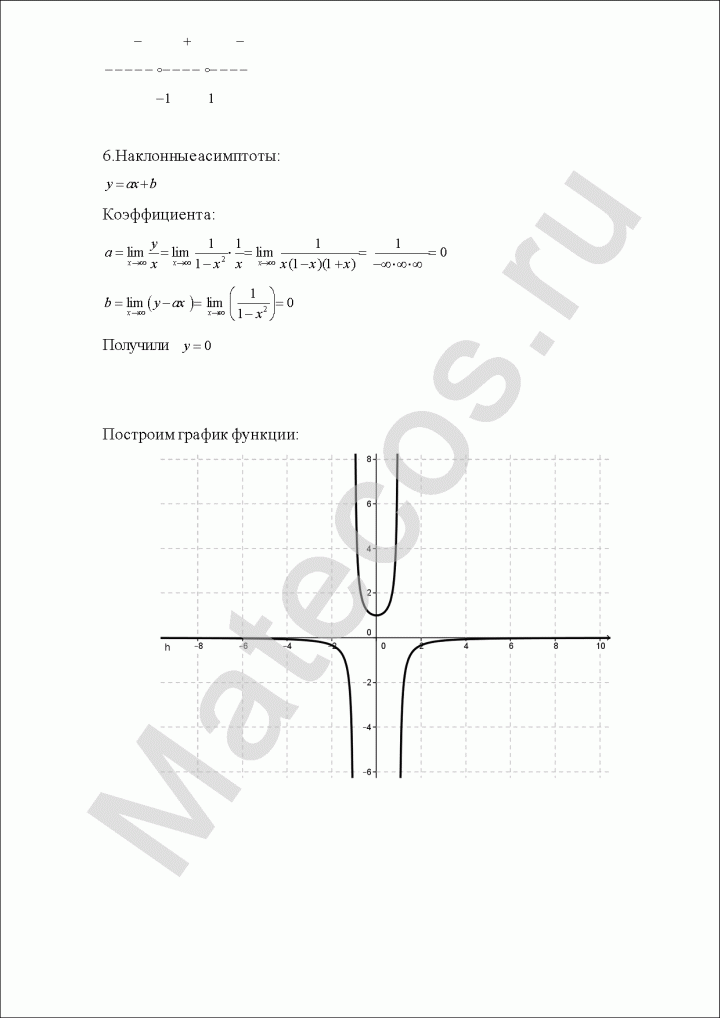
Так как пределы бесконечны, горизонтальных асимптот нет.
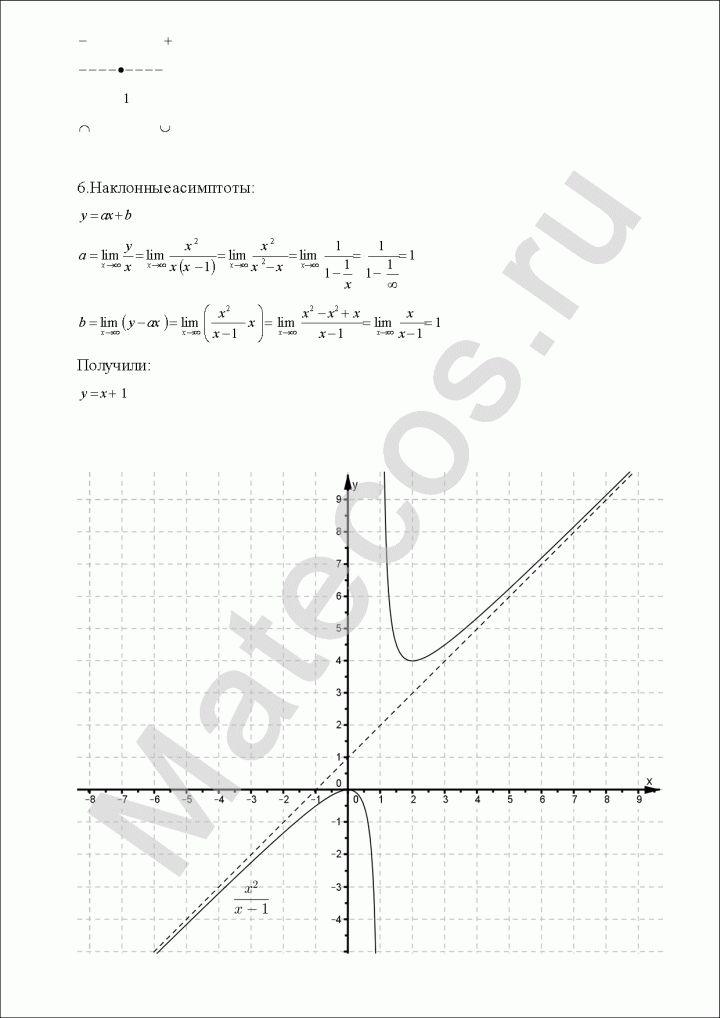
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
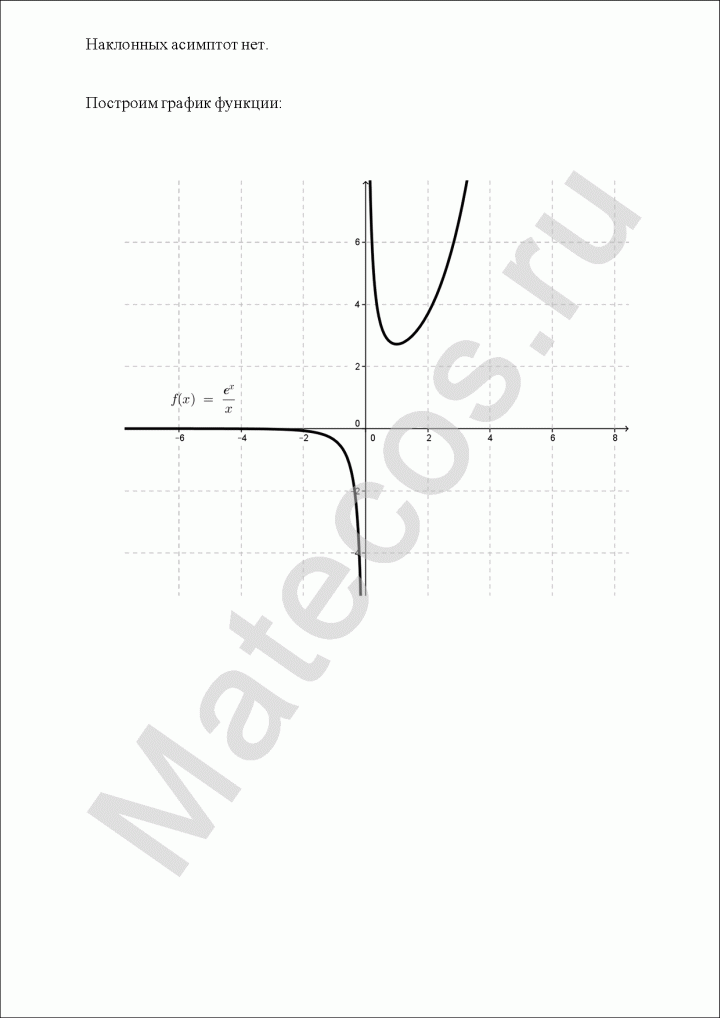
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=frac{x^3-1}{4x^2}.$$
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
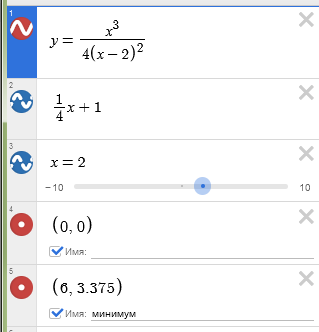
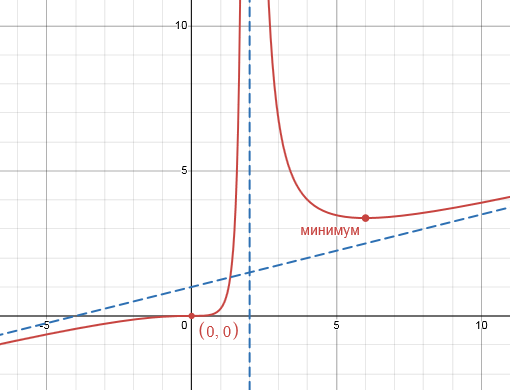
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
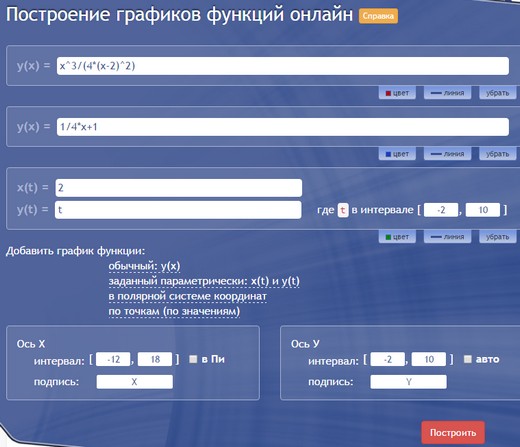
Сайт для построения графиков y(x).ru
y(x).ru
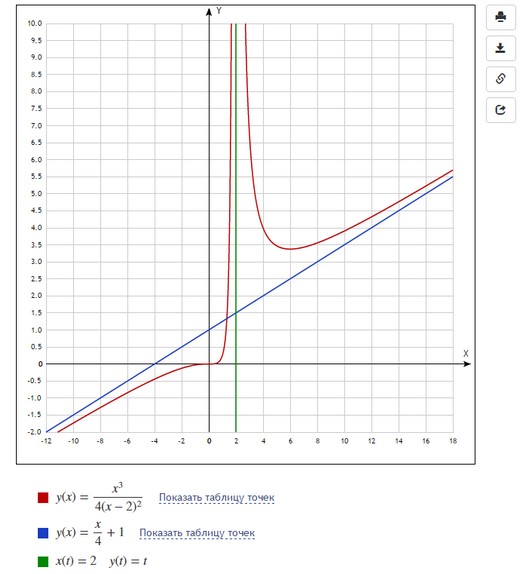
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
И такой график получается в итоге:
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Лучшее спасибо — порекомендовать эту страницу
При
выполнении дипломных работ студенты в
основном становятся участниками
сравнительно небольших по объему научных
тем. Поэтому наиболее удобным и наглядным
является построение ленточного графика
проведения научных работ в форме
диаграммы Ганта.
Диаграмма
Ганта
– горизонтальный ленточный график, на
котором работы по теме представляются
протяженными во времени отрезками,
характеризующимися датами начала и
окончания выполнения данных работ.
Для
удобства построения графика, длительность
каждого из этапов работ из рабочих дней
следует перевести в календарные дни.
Для этого необходимо воспользоваться
следующей формулой:

(5)
где
Ткi–
продолжительность выполнения i-й
работы в календарных днях;
Трi–
продолжительность выполнения i-й
работы в рабочих днях;

коэффициент
календарности.
Коэффициент
календарности определяется по следующей
формуле:

(6)
где

выходных дней в году;

праздничных дней в году.
Рассчитанные
значения в календарных днях по каждой
работе

округлить до целого числа.
Все
рассчитанные значения необходимо свести
в таблицу (табл. 8).
Таблица
8
Временные
показатели проведения научного
исследования
|
Название работы |
Трудоёмкость |
Исполнители |
Длительность работ рабочих |
Длительность работ календарных днях |
||||||||||||||
|
tmin, чел-дни |
tmax, |
чел-дни |
||||||||||||||||
|
Исп.1 |
Исп.2 |
Исп.3 |
Исп.1 |
Исп.2 |
Исп.3 |
Исп.1 |
Исп.2 |
Исп.3 |
Исп.1 |
Исп.2 |
Исп.3 |
Исп.1 |
Исп.2 |
Исп.3 |
Исп.1 |
Исп.2 |
Исп.3 |
|
Примечание:
Варианты
исполнения берутся из раздела 2.
На
основе табл. 8 строится календарный
план-график. График строится для
максимального по длительности исполнения
работ в рамках научно-исследовательского
проекта на основе табл. 9 с разбивкой по
месяцам и декадам (10 дней) за период
времени дипломирования. При этом работы
на графике следует выделить различной
штриховкой в зависимости от исполнителей,
ответственных за ту или иную работу.
Таблица
9
Календарный
план-график проведения НИОКР по теме
|
№ |
Вид |
Исполнители |
кал. |
Продолжительность |
||||||||||||
|
февр. |
март |
апрель |
май |
июнь |
||||||||||||
|
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
||||
|
1 |
Составление |
Руководитель |
4 |
|||||||||||||
|
2 |
Изучение |
Инженер (дипломник) |
28 |
|||||||||||||
|
3 |
Патентный |
Инженер (дипломник) |
6 |
|||||||||||||
|
4 |
Выбор |
Руков., |
4 |
|||||||||||||
|
… |
… |
|||||||||||||||
|
34 |
||||||||||||||||
|
50 |
||||||||||||||||
|
i |
12 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Научные статьи бывают разных размеров и уровней сложности. Не существует единого набора правил, подходящего для каждого проекта, но есть рекомендации, которым вы должны следовать, чтобы не сбиться с пути в течение нескольких недель, пока вы готовитесь, исследуете и пишете. Вы будете выполнять свой проект поэтапно, поэтому вы должны планировать заранее и давать себе достаточно времени для завершения каждого этапа своей работы.
Ваш первый шаг – написать сократить срок сдачи вашей статьи на большом настенном календаре, в планировщике и в электронном календаре.
Планируйте в обратном направлении от этого срока, чтобы определить, когда у вас должна быть завершена работа с библиотекой. Хорошее практическое правило – потратить:
- Пятьдесят процентов своего времени на изучение и чтение.
- Десять процентов вашего времени на сортировку и маркировку ваших исследований
- Сорок процентов вашего времени на написание и форматирование
Содержание
- Временная шкала для Этап исследования и чтения
- График сортировки и маркировки ваших исследований
- График написания и форматирования
Временная шкала для Этап исследования и чтения
- 1 неделя для коротких статей с одним или двумя источниками
- 2-3 недели для статей до десяти страниц
- 2-3 месяца на диссертацию
Важно сразу приступить к работе на первом этапе. В идеальном мире мы бы нашли все источники, необходимые для написания статьи, в ближайшей библиотеке. В реальном мире, однако, мы проводим интернет-запросы и находим несколько прекрасных книг и статей, которые абсолютно необходимы для нашей темы, но обнаруживаем, что их нет в местной библиотеке.
Хорошая новость в том, что вы все еще можете получить ресурсы через межбиблиотечный абонемент. Но на это потребуется время. Это одна из веских причин провести тщательный поиск на раннем этапе с помощью справочного библиотекаря.
Дайте себе время собрать много возможных ресурсов для вашего проекта. Вскоре вы обнаружите, что некоторые из выбранных вами книг и статей на самом деле не предлагают никакой полезной информации по вашей конкретной теме. Вам нужно будет сделать несколько походов в библиотеку. Вы не закончите за одну поездку.
Вы также обнаружите, что найдете дополнительные потенциальные источники в библиографиях ваших первых выбранных вами книг. Иногда наиболее трудоемкой задачей является устранение потенциальных источников.
График сортировки и маркировки ваших исследований
- 1 день для короткой статьи
- 3-5 дней для статей до десяти страниц
- 2-3 недели для диссертации
Вы должны прочитать каждый из ваших источников как минимум дважды. Прочтите свои источники в первый раз, чтобы впитать некоторую информацию и сделать заметки на карточках исследований.
Прочитайте свои источники во второй раз быстрее, просматривая главы и установка флажков для заметок на страницах, содержащих важные моменты, или страницах, содержащих отрывки, которые вы хотите процитировать. Напишите ключевые слова на флажках для заметок.
График написания и форматирования
- Четыре дня для короткой статьи с одним или двумя источниками
- 1-2 недели для статей до десяти страниц
- 1-3 месяца для диссертации
Вы ведь не ожидаете, что с первой попытки напишете хорошую статью, не так ли?
Вы можете ожидать, что предварительно напишите, напишите и перепишите несколько черновиков своей статьи. Вам также придется несколько раз переписать свой тезис, когда ваша статья обретет форму.
Не откладывайте написание какого-либо раздела вашей статьи. – особенно вводный абзац. Для писателей совершенно нормально вернуться и завершить введение после того, как остальная часть статьи будет завершена.
Первые несколько черновиков не обязательно должны иметь идеальные цитаты. Как только вы начнете оттачивать свою работу и приближаетесь к окончательному черновику, вы должны ужесточить свои цитаты. Используйте образец эссе, если вам нужно, просто чтобы уточнить форматирование.
Убедитесь, что ваша библиография содержит все источники, которые вы использовали в своем исследовании.
 |
Для того, чтобы построить график функции необходимо провести полное исследование заданной функции. Затем поэтапно, используя полученные результаты, построить график.Как построить график функции?После краткого описания пунктов исследования, приведем ряд примеров по теме построения графиков функции с полным предварительным исследованием. |
Приведем примерный алгоритм получения необходимых данных.
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале — график расположен выше оси абсцисс. Функция отрицательна — график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна — график функции возрастает, отрицательна — убывает.
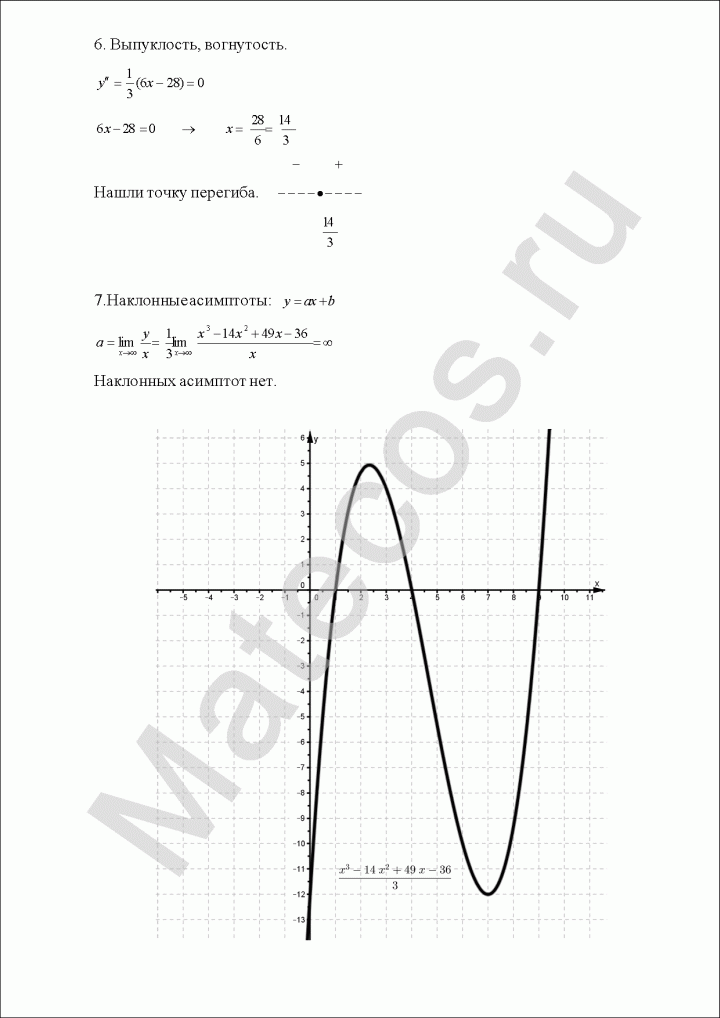
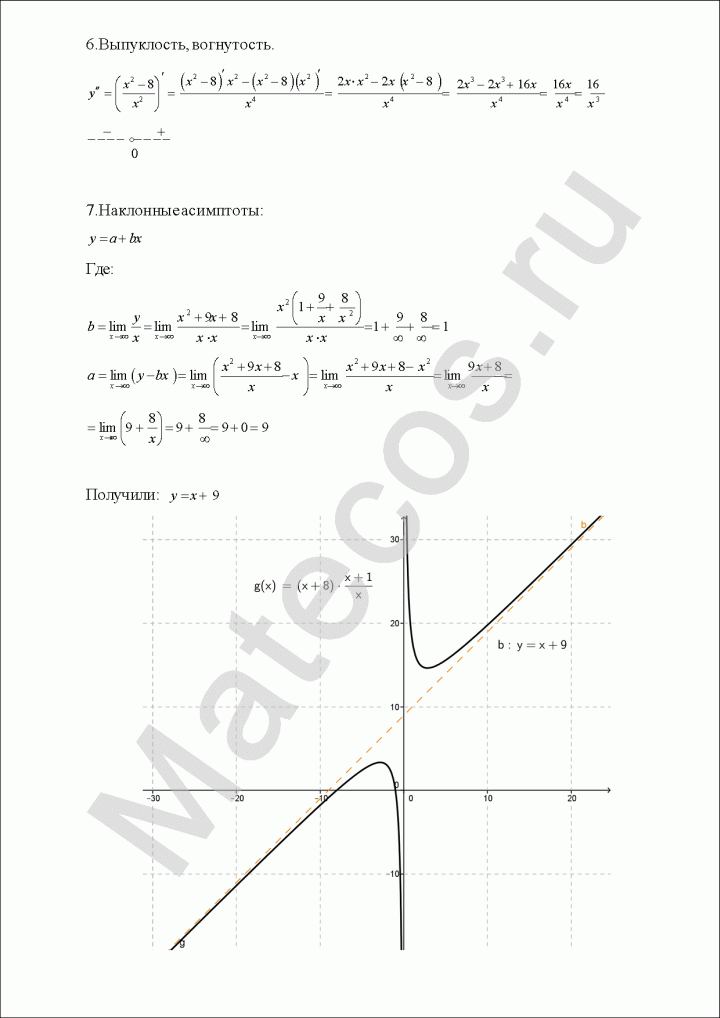
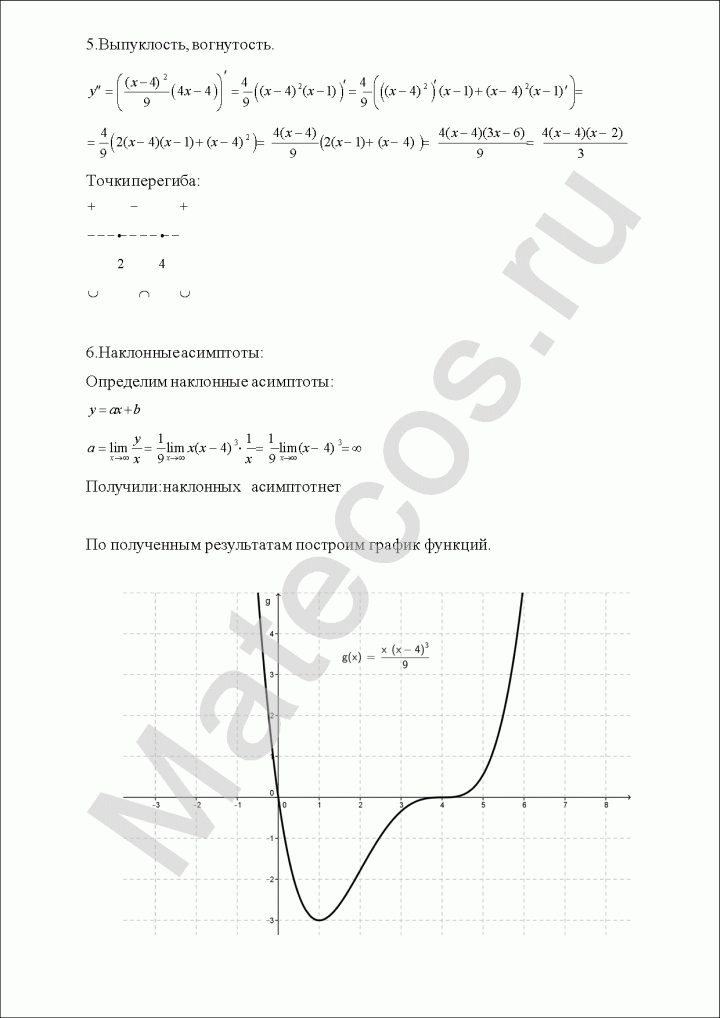
6. Выпуклость, вогнутость.
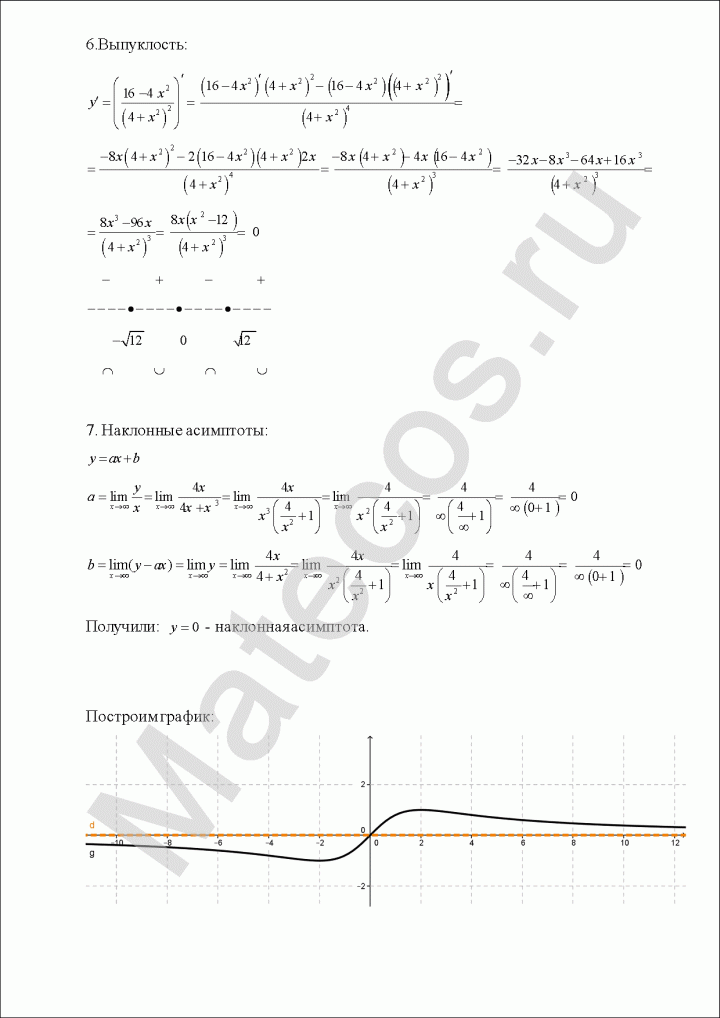
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна — график функции выпукл вверх. Отрицательна — график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №2
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №3
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №4
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №5
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №6
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №7
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №8
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №9
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №10
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №11
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №12
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №13
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №14
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №15
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №16
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №17
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №18
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №19
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №20
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №21
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №22
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №23
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №24
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №25
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №26
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №27
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.

Содержание:
- Схема исследования функции и построение ее графика
- Условия возрастания и убывания функции.
- Экстремумы функции
- Наибольшее и наименьшее значения функции
- Условия выпуклости. Точки перегиба
Схема исследования функции и построение ее графика
График заданной функции можно строить по произвольно взятым точкам. При таком способе можно не обнаружить всех особенностей ее графика.
Проведя предварительно исследования, мы ищем характерные для данного графика точки и тем упрощаем решение задачи о построении графика.
При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы:
Первый этап (использование вида заданной функции).
1) Находим область определения функции, точки разрыва.
2) Исследуем функцию на четность или нечетность, периодичность.
3) Находим асимптоты графика функции.
4) Находим точки пересечения графика функции с осями координат.
Второй этап (использование производной первого порядка).
5) Находим критические точки первого рода, интервалы возрастания и убывания, точки экстремумов и экстремальные значения функции.
Третий этап (использование производной второго порядка).
6) Находим критические точки второго рода, интервалы выпуклости и вогнутости, точки перегиба и значения функции в этих точках.
Четвертый этап. Составим таблицу результатов исследования.
Наносим полученные точки, асимптоты на координатную плоскость и строим график функции с учетом точек разрыва, интервалов возрастания и убывания функций, промежутков выпуклости и вогнутости графика функций.
Пример 1. Исследовать функцию y = x3 – 3x2 и построить ее график.
Решение.
1) Область определения функции: вся числовая ось 
2) Функция ни четная ни нечетная, поскольку y (-x) = -x3 — 3x2, поэтому y (-x) ≠ y (x) ≠ — y (x).
Функции не периодическая.
3) Вертикальных асимптот график не имеет, потому что нет точек разрыва.
Исследуем, имеет ли график наклонные асимптоты y = kx + b:
Наклонных асимптот график также не имеет.
4) Найдем точки пересечения графика функции с осями координат: при x = 0, y = 0; то есть точка O (0; 0);
при y = 0: x3 — 3x2 = 0⇒ x2 (x – 3) = 0⇒ x = 0 и x = 3, то есть точка M (3; 0).
Второй этап.
5) Находим производную первого порядка:
y ‘= 3x2 – 6 x = 3x (x – 2).
Находим критические точки первого рода:
3x (x – 2) = 0, x1 = 0, x2 = 2.
Критические точки разбивают область определения на промежутки (-∞, 0) ∪ (0,2) ∪ (2, ∞) (рис. 19).

Рис. 19. Рис. 20.
Находим знаки производной в этих промежутках:
y’ (3) = 3⋅ 3 (3 – 2) = 9 > 0,
y’ (1) = 3 ⋅ 1 (1 – 2) = –3 < 0,
y’ (1) = 3 (–1) (–1 – 2) = 9 > 0.
Следовательно, функция возрастает на промежутках (–∞; 0) ∪ (2; ∞), убывает на
промежутке (0; 2).
В точке x = 0 функция имеет максимум, ymax = y (0) = 0.
В точке x = 2 функция имеет минимум,
Третий этап.
6) Находим производную второго порядка:
y»= 6 x – 6 = 6 (x – 1). Находим критические точки второго рода: 6 (x — 1) = 0, x = 1 . Критическая точка x = 1 разбивает область определения на промежутки: (-∞, 1) ∪ (1, ∞) (рис. 20). Находим знаки второй производной в этих промежутках:
y» (0) = 6 (0 – 1) = –6 < 0,
y» (2) = 6 (2 – 1) = 6 > 0.
Следовательно, график функции выпуклый на промежутке (-∞, 1), вогнутый на промежутке (1; ∞). Точка x = 1 является точкой перегиба,
7) Составим таблицу, где занесем все результаты исследования.
Найдем еще дополнительно
y (-1) = (-1) 3 – 3 ⋅ (–1) 2 = 4.
Наносим все характерные точки на координатную плоскость и строим график (рис.21).
Рис. 21.
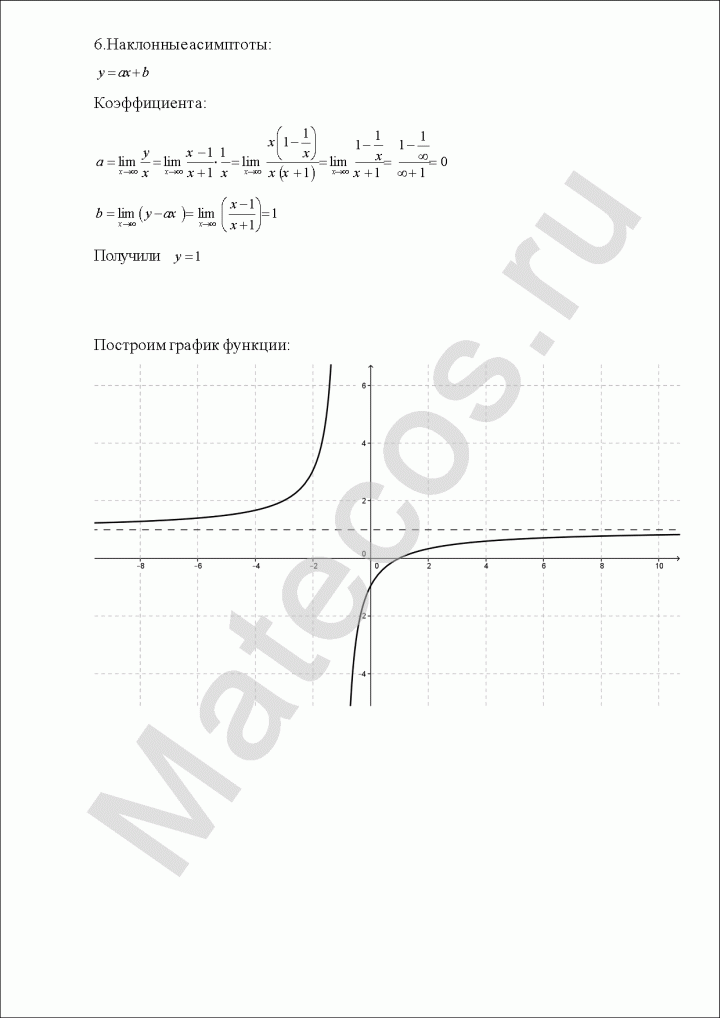
Пример 2. Исследовать функцию
Решение.
Первый этап.
1) Область определения функции (

2) Функция ни четная, ни нечетная, поскольку

Функция непериодическая.
3) Поскольку в точке разрыва x = 2,

то прямая x = 2 — вертикальная асимптота.
Исследуем, имеет ли график наклонные асимптоты y = kx + b:
Итак, y = 0 — горизонтальная асимптота.
4) Найдем точки пересечения графика функции с осями координат: при x = 0, 


Переходим ко второму этапу:
5) Найдем производную первого порядка:
Находим критические точки первого рода:
Учитывая точку x = 2, где производная не существует, разобьем область определения на промежутки (

Следовательно, функция возрастает на промежутке (2; 4), убывает на промежутках (



Рис. 22. Рис. 23
Переходим к третьему этапу:
6) Находим вторую производную:
Найдем критические точки второго рода:

Учитывая точку x = 2, где y» не существует, разбиваем область определения на промежутки: (

Установим знаки второй производной в этих промежутках:
Следовательно, график функции выпуклый на промежутках: (

Имеем точку
Строим график (рис. 24).
Рис. 24.
Условия возрастания и убывания функции.
1) Для того чтобы дифференцируемая на интервале 





2) Для того чтобы дифференцируемая на интервале 





3) Аналогично, достаточным условием строгого убывания дифференцируемой функции 



необходимым и достаточным условием убывания — условие


По этой ссылке вы найдёте полный курс лекций по высшей математике:
Экстремумы функции
1) Точка 



Если для всех 


то точка 

Аналогично, если в некоторой окрестности точки 

то точка 



то точка 
Для краткости слово “локальный” часто опускают и пишут просто “точка минимума” или “точка строгого максимума”.
Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках — ее экстремумами.
2) Необходимые условия экстремума. Если точка 



Эти условия не являются достаточными.
Точки, в которых функция определена, а производная функции равна нулю или не существует, называют критическими точками функции. Экстремумы функции следует искать среди ее критических точек.
3) Достаточные условия строгого экстремума (с использованием первой производной). Пусть функция 








При выполнении условий (1) принято говорить, что производная функции при переходе через точку 
Если же



т. е. если производная при переходе через точку 

4) Условия строгого экстремума (с использованием производных высших порядков). Пусть функция 



то при четном 





В частности, если


то в точке 


Возможно вам будут полезны данные страницы:
Наибольшее и наименьшее значения функции
функции, непрерывной на отрезке, существуют на этом отрезке точка, в которой функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение (теорема Вейерштрасса).
Пусть функция 





Аналогично, если функция 



Условия выпуклости. Точки перегиба
1) Функция 






Геометрический смысл выпуклости вниз функции 

Если при тех же условиях относительно 
то функция 
В том случае, когда при 




Например, функция 
Всякий интервал, на котором функция (строго) выпукла вниз, называется интервалом (строгой) выпуклости вниз этой функции; интервал, на котором функция (строго) выпукла вверх — интервалом (строгой) выпуклости вверх этой функции.
Интервалы выпуклости вверх и интервалы выпуклости вниз называют интервалами выпуклости.
2) Условия выпуклости функции. Для того чтобы функция 



Условие
является достаточным условием строгой выпуклости вниз функции
на интервале
.
Условие (7) не является необходимым для строгой выпуклости. В самом деле, функция 


Аналогично, для функции 

а достаточным условием строгой выпуклости вверх — условие
Пусть функция 





на одном из которых 


3) Пусть функция 








Если 


На рис. 20.2 и рис. 20.3 представлены график функции 




Функция (рис. 20.4)
при переходе через точку 






не меняется (это так называемая точка возврата). При переходе через точку 
меняет направление выпуклости, но точка 
4) Необходимые условия существования точки перегиба. Если точка 



Эти условия не являются достаточными. В самом деле, для функции 

вторая производная в точке 



Точки перегиба функции следует искать среди критических точек ее первой производной.
5) Достаточные условия существования точки перегиба (с использованием второй производной). Пусть функция 









либо



В этом случае принято говорить, что при переходе через точку 
6) Условия существования точки перегиба (с использованием производных высших порядков). Пусть функция 


тогда если 



В частности, если
то 

Примеры с решением
Пример 1.
Найти интервалы возрастания и убывания функции:
1) 
3)
1) Данная функция всюду дифференцируема, причем
Так как 







2) Функция дифференцируема на всей числовой прямой, причем
Так как 



3) Данная функция является четной, поэтому достаточно найти интервалы монотонности при 

получаем



откуда



Таким образом, на интервалах 










Следует обратить внимание на то, что данная функция не является монотонной ни в какой окрестности точки 
Пример 2.
Найти точки экстремума функции 
Функция имеет производную при всех 
Следовательно, у функции может быть только один экстремум в точке 





Пример 3.
Найти экстремумы функции
Так как
то критические точки функции — 




Тот же результат можно получить, используя вторую производную. Так как 




Вычислив значения функций в точках 



Пример 4.
Исследовать на экстремум функцию:
1)
2)
3)
1) Функция определена и дифференцируема при всех 

и находим критические точки: 



переходе через точку 




2) Функция определена и непрерывна при всех 
В точках 












3) Функция дифференцируема при всех 





Поскольку 

Таким образом, первой не равной нулю оказалась производная четного порядка. Следовательно, в точке 


Пример 5.
Исследовать на экстремум функцию 
Функции 


при 



то
Производная 












В некоторой правой окрестности точки 







Лекции:
- Внесение под знак дифференциала: подведение
- Свойства логарифмов
- Линейные дифференциальные уравнения первого порядка
- Скрещивающиеся прямые
- Скалярное призведение двух векторов
- Уравнения касательной и нормали
- Наименьшее значение функции
- Найти угол между прямыми: примеры решения
- Объем шара и его частей
- Производная тангенса



 ,
,
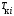 ,
,