to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
В современной школе информатика –
достаточно сложный предмет для усвоения
учащимися. Основное препятствие для
полноценного изучения информатики – нехватка
времени. Мною проанализировано много учебных
планов и методик преподавания информатики и для
общеобразовательных классов, и для профильных с
углубленным изучением информатики. Вывод
неутешителен. Предлагаемые материалы
основываются на гораздо большем годовом
количестве учебных часов, чем то, которым мы
реально располагаем. Следствием расхождения
между рекомендуемым и реальным объемом учебных
часов является невозможность использовать в
процессе обучения какой-то один учебник
информатики. Это неудобно как ученикам, так и
преподавателю. Выходом из этой ситуации является
разработка собственной методики преподавания
информатики с ориентацией на творческую
деятельность учащихся и тестовый контроль,
которая, не уменьшая объем материала, позволяла
бы сократить время на его усвоение учениками и
уложиться в отведенное количество часов.
Основываясь на своем опыте работы с
учащимися старшего звена, я выделила несколько
основных тем, без усвоения которых невозможно
успешное изучение всего курса информатики, и
разработала собственную методику их
преподавания. Я пользуюсь ей уже несколько лет,
что позволяет добиваться хороших результатов в
освоении учениками моего предмета. С методикой
преподавания одной из таких тем я и хочу
познакомить вас.
Секрет могущества ЭВМ – высокая
скорость и большая память. Для записи алгоритмов,
работающих с большими объемами информации, в
алгоритмическом языке существуют специальные
табличные величины (или просто таблицы).
Исполнение многих алгоритмов было бы просто
невозможно, если бы соответствующие объекты не
были каким-либо образом организованы:
упорядочены, классифицированы, занумерованы и
так далее. Итак, нужно уметь организовать не
только действия, но и те объекты, над которыми эти
действия производятся.
Необходимо отметить, что таблицы
(массивы) как основное средство представления
однородной информации неизбежно используются во
всех реальных компьютерных программах. На
табличном принципе основана и архитектура
современных ЭВМ: память машины можно
рассматривать как большой массив байтов, адреса
которых располагаются по возрастанию.
Следовательно, без понимания
информационной сущности таблиц и основных
алгоритмов их обработки невозможно формирование
полноценных представлений о возможностях ЭВМ и
принципах их работы. Для построения сколь-нибудь
сложных и содержательных программ необходимо
уверенное владение общими принципами применения
таблиц и базовыми приемами их
обработки. В данной работе будет рассмотрен ряд
простых алгоритмов, которые используются при
построении более сложных.
Алгоритм вычисления суммы
1. Пусть дан массив A,
состоящий из n элементов: a1,
a2, a3, …, an. Нужно
найти их сумму, т.е. S=a1+a2+a3+…+an.
Нахождение суммы есть
последовательное нахождение суммы по формулам:
S=0 S=S+a2 … S=S+ai S=S+an
S=S+a1 S=S+a3 …
Алгоритм вычисления суммы удобно
организовать циклом, взяв за параметр цикла
переменную i, которая
меняется от 1 до n с шагом 1, и
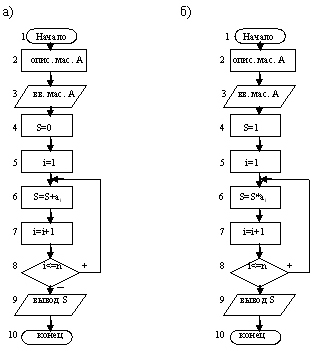
записав в цикле формулу S=S+ai один раз. Схема алгоритма приведена
на рис. 1а.
В схеме блок 4 присваивает S нулевое значение, блок 5 счетчику i
присваивает начальное значение,
блок 6 выполняет накопление суммы, блок 7 изменяет
значение i на 1, блок 8
осуществляет проверку условия повторения цикла.
При выполнении этого условия управление
передается в начало цикла, а при невыполнении –
осуществляется выход из цикла, т.к. при i=n+1 суммировать не нужно. n – в схеме предполагается число, но n может быть и переменной, значение
которой равно числу элементов массива A, которое нужно вводить перед
описанием массива.
При разработке этого алгоритма
учащимся можно предложить изменить схему на
случай, если нужно найти сумму элементов,
расположенных на четных местах в массиве A (Ответ: Блок 5 надо изменить на i=2 и блок 7 на i=i+2)
или задать вопрос – что изменится в схеме на
рис.1а, если суммировать только положительные
элементы массива A? (Ответ:
Перед блоком суммирования 6 нужно поставить блок
проверки элемента массива ai на положительность и, если он
положителен, то его суммировать, а если нет, то
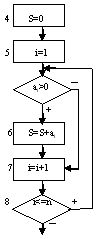
обходить блок суммирования.) Схема алгоритма
будет иметь вид:
При таком тщательном исследовании
схемы алгоритма учащиеся без особых затруднений
ответят на вопрос – что добавить в схеме на
рис.2, чтобы в ней подсчитывалось еще количество
положительных элементов массива?
(Ответ: Надо ввести
переменную k для получения
количества положительных элементов и перед
циклом присвоить ей значение 0. После блока
проверки 7 по пути “+” нужно поставить блок,
содержащий k=k+1, который ведет
счет количества положительных элементов массива
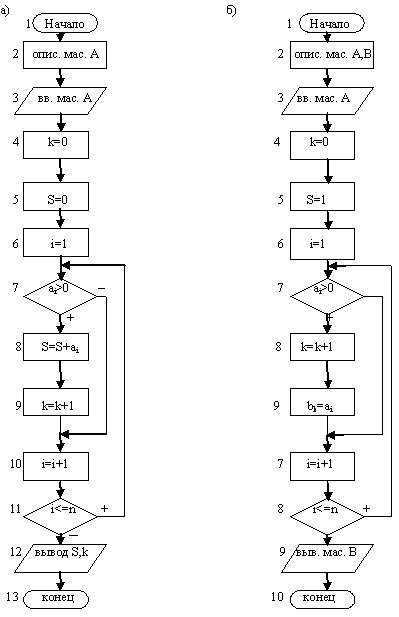
A.) Схема алгоритма приведена
на рис.3а.
Алгоритм вычисления произведения
Этот алгоритм предлагается учащимся
разработать самостоятельно, взяв за основу
алгоритм определения суммы элементов массива
(Рис. 1а). Учащиеся должны не только указать на
изменения блока 6 на S=S*ai
(в S будет направляться
произведение элементов), но и дать четкое
объяснение изменению блока 4 на S=1. Схема алгоритма представлена на
рис.1б.
Алгоритм формирования нового массива
Как положительные элементы массива A сформировать в массив? Обозначим
массив положительных элементов B и по пути “+” после блока 7 поставим
присвоение соответствующему элементу массива B элемент массива A,
т.е. блок, содержимое которого bk=ai.
k будем использовать
как меняющийся индекс нового массива. Необходимо
обратить внимание учащихся на блок 2, в котором
требуется описать массив B,
указав количество его элементов равное
количеству элементов массива A. Схема алгоритма на рис.3б.
Алгоритм определения максимального элемента
Для получения максимального числа
введем переменную M и ей
присвоим значение первого элемента массива a1, а затем необходимо сравнить M с текущим элементом массива ai и если текущий элемент будет больше M, то значение M
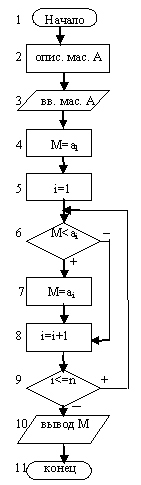
заменить на значение этого элемента. Схема
алгоритма на Рис. 4. Очень важно обратить внимание
учащихся на начальное значение переменной M.
Почему, например нельзя
переменной M присвоить
значение равное нулю? (Ответ: Для массива с
отрицательными значениями элементов максимум не
будет найден.)
Алгоритм упорядочения массива методом
“Пузырька”
Действия по упорядочению некоторых
данных по ключу называются процессом сортировки.
Очевидно, что с отсортированными данными
работать легче и быстрее, чем с произвольно
расположенными. Все применения ЭВМ основаны на
их способности к быстрой и точной обработке
больших объемов информации, а это возможно
только тогда, когда информация однородна и отсортирована.
Существует довольно много различных методов
сортировки, отличающихся друг от друга степенью
эффективности, под которой понимается
количество сравнений и количество обменов,
произведенных в процессе сортировки, время
выполнения и объем
занимаемой ОП. Рассмотрим сортировку методом
“Пузырька”, которая легко описывается в форме
четких алгоритмов и приводит к простой
программной реализации.
Одномерный массив A
из n элементов упорядочим по
возрастанию. При
пузырьковой сортировке элементы массива попарно
сравниваются и более “легкие” элементы как бы
всплывают на поверхность. При реализации
алгоритма возникает проблема в определении
количества шагов сортировки. Для решения этой
задачи воспользуемся известным методом
“расстановки флажков”, благодаря
которому однозначно будет определен момент
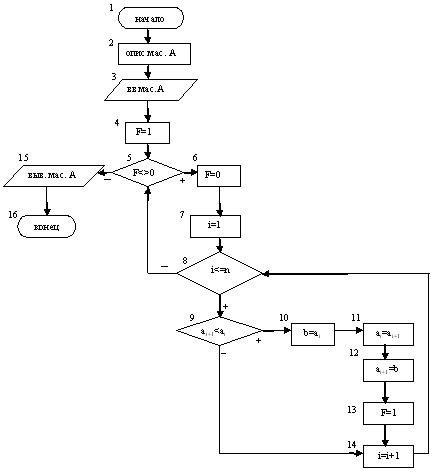
завершения сортировки и выхода из цикла (блок 5).
В качестве “флажка” возьмем числовую
переменную F и присвоим ей
произвольное начальное значение отличное от
нуля (блок 4). Схема алгоритма на рис. 5. По парное
сравнивание элементов и их обмен местами
происходит в блоках 9-12, здесь же изменяется
значение флажка (блок 13). В случае, когда все
элементы массива будут упорядочены, значение F останется равным нулю (блок 6). Блоки
3 и 15 являются укрупненными, т.к. алгоритмы ввода и
вывода элементов массива подробно не описаны на
схеме (Рис. 5).
В помощь учащимся общеобразовательной
школы мною разработано методическое пособие по
алгоритмам обработки массивов данных, в котором
подробно рассматриваются элементарные
алгоритмы, используемые при составлении более
сложных алгоритмов, и прилагается большая
подборка задач.
Задачи “Первые шаги”
- В массиве а1, а2, …, а50
определить количество нулей. - В массиве d1, d2, …, d35
найти сумму чисел, расположенных на нечетных
местах. - В массиве с1, с2
, …, с40
найти произведение отрицательных чисел. - В массиве b1, b2, …, b45
найти сумму отрицательных чисел. - В массиве b1, b2, …, b20
найдите количество «единиц». - Из массива а1, а2
, …, а30
найти произведение чисел, расположенных на
нечетных местах. - В массиве с1, с2
, …, с40
найти сумму чисел больших единицы. - В массиве чисел а1, а2
, …, а50
найти количество чисел меньших единицы. - В массиве с1, с2
, …, с37
найти произведение чисел больших 2. - В массиве а1, а2
, …, а40
найти сумму чисел, расположенных на местах
кратных 3. - В массиве а1, а2
, …, а50
найти произведение чисел меньших или равных 2. - В массиве b1, b2, …, b45
найти количество чисел равных 3,5. - В массиве d1, d2, …, d50
найти сумму чисел равных 4,7. - В массиве b1, b2, …, b30
найти произведение чисел больших
или равных 5. - В массиве с1, с2
, …, с70
найти количество «нулей», стоящих на
нечетных местах. - В массиве b1, b2, …, b65
найти сумму чисел больших или
равных 5. - В массиве d1, d2, …, d30
найти произведение чисел, исключая
первый и последний элемент. - В массиве а1, а2
, …, а35
найти количество «единиц», стоящих на четных
местах. - В массиве чисел а1, а2
, …, а30
найти сумму отрицательных чисел, стоящих на
нечетных местах. - В массиве чисел в1, в2, …, в35
найти произведение чисел больших или равных 2. - В массиве чисел с1, с2, …, с40
найти количество чисел, попавших в интервал [а,
в] - В массиве чисел с1, с2, …, с40
найти сумму чисел, не попавших в
интервал [с, d]. - В массиве чисел в1, в2, …, в45
найти произведение всех ненулевых чисел. - В массиве чисел с1, с2, …, с60 найти
количество нулей стоящих на местах, кратных 4 т.е.
среди чисел с4, с8, …, с60. - В массиве чисел z1, z2, …, z200
найти сумму чисел z5, z10,
…, z200.
Задачи “Джентльменский
набор”.
- Даны три последовательности
чисел а1, а2, …,
a9, b1, b2 …, b9,
с1, с2, …, с9.
Составьте новую последовательность d1, d2,
…, d9, каждый элемент
которой определяется по правилу di =
max (аi, bi, сi), где i=
1,2, …,9. - Найти номер первого нулевого
элемента массива х1, х2, …, х20 и
сумму элементов предшествующих ему. - Даны три последовательности
чисел: а1, а2, …, а8; b1, b2, …, b8; с1, с2
, …, с8.
Составить новую последовательность, в которой
чередовались бы числа всех трех
последовательностей, т.е. d1 = a1; d2=b1;
d3 = c1; d4 = a2; d5 = b2;
d6 = c2. - Известно, что в массиве а1, а2, …, а16
количество отрицательных чисел
равно количеству положительных. Составить новый
массив так, чтобы чередовались положительные и
отрицательные числа. - Найти сумму элементов
последовательности b1, b2, …, b15
, расположенных правее последнего
отрицательного элемента и номер этого элемента. - Дана последовательность чисел с1
, с2, …, с16
. Найти произведение элементов этой
последовательности до первого нулевого и сумму
элементов, расположенных после него. - Из массива с1
, с2, …, с18
получить массив х1
, х2, …, х18
по правилу; х1
= с1, х2
=с3, …, х9
=с17, x10=с18
, х11=с16,
…, x18=с2. - Из данного массива чисел х1
, х2, …, х25
исключить последнее положительное
число. Оставшиеся числа переписать в новый
массив z1, z2, …, z24. - Найти номер первого
положительного элемента массива b1, b2,
…, b15 и сумму элементов,
расположенных правее него. - Все положительные элементы
массива а1, а2
, …, а20,
расположенные правее первого нулевого элемента,
увеличить в два раза. - В массиве х1
, х2, …, х25
поменять местами элементы х1
, х4, х7
, х10, …, х22
с наименьшим из следующий за
ними соответствующей пары элементов. - Из заданного массива а1
, а2, …, а12
, не содержащего нулей, получить
массив b1, b2, …, b12
, приняв в качестве первых его
элементов все положительные элементы массива A
с сохранением порядка их
следования, а в качестве остальных элементов все
отрицательные элементы также с сохранением
порядка их следования. - Дан массив с1
, с2, …, с15, состоящий из нулей и единиц.
Подсчитать количество 0, количество 1 и
количество нулей до первой единицы. - Дан массив чисел х1, х2, …, х22
. Переписать в другой массив из
данного все элементы, расположенные правее
последнего отрицательного элемента, сохраняя
порядок их следования. - По данным числам х, у, z получить массив а1, а2, …, а17
, где а1 = х,
а2 = у, а3 = z,
а каждый следующий элемент
массива определяется как среднее арифметическое
трех предшествующих. - Из заданных массивов а1
, а2, …а8;
b1, b2, …, b12; с1
, с2, …, с6
получить массив d1, d2,
…, d26 в котором
разместить сначала все элементы массива A, затем элементы массива B
и в конце элементы массива C. - В массиве а1
, а2, …, а18 вычислить сумму отрицательных до
последнего нулевого и произведение элементов
расположенных правее него. - В массиве у1, у2, …, у18
элементы с номерами, кратными 4,
заменить среднем арифметическим из трех
предшествующих элементов. - Массивы х1, х2, …, х10
и у1, у2, …, у10
преобразовать по правилу: большее из хi
и уi
принять в качестве нового значения хi
, а меньшее – в качестве нового
значения уi (i = 1,2, …,10). - Все элементы массива а1
, а2, …, а45, начиная с первого по порядку
положительного элемента, уменьшить на 0,5, если
значение элемента превышает 1 и увеличивать на 0,5
в противном случае. - В массиве а1, а2, …, а25
найти произведение первых трех
положительных элементов. - Из десяти последних
отрицательных чисел последовательности t1,
t2, t3, …, t300
сформировать последовательность у1, у2, …, у10. - Если наименьший элемент данной
последовательности х1,
х2, …, х27 больше 0,1 то все отрицательные
элементы последовательности заменить единицей. - Дана последовательность а1, а2, …, а50
. Сформировать последовательность в1, в2, …, в50
следующим образом: в начале
расположить все отрицательные элементы
последовательности, а затем все остальные.
Задачи “Уже
проблемы”
- Дан массив а1, а2,
…, a20. Получить массив
х1+у1
, х2+у2, …, хr+уr
, где элементами массива х1, х2, …, хp
являются отрицательные, а
элементами массива у1, у2
, …, уt
положительные элементы массива A, r = min
(р, t). - Найти номер первого нулевого элемента массива а1, а2, …, а25
и произведение элементов,
расположенных до него, а среди элементов,
расположенных правее первого нулевого, найти
максимальный элемент. - В данном массиве чисел с1, с2, …, с25
поменять местами максимальный элемент с
последним отрицательным элементом. - Из массива х1, х2, …, х25
сформировать два массива; в одном написать числа,
расположенные до минимального элемента массива
х, в другой расположенный правее минимального. - Пять последних элементов последовательности у1,
у2, …, у40 помножить на номер
максимального элемента данной
последовательности. - Из массива а1, а2, …, а30
исключить максимальный элемент. - Среди отрицательных элементов массива х1,
х2, …, х50 найти минимальный и
помножить на него все отрицательные элементы,
стоящие левее этого минимального. - Дана последовательность чисел d1, d2,
…, d50. Найти сумму S1 элементов до
максимального элемента и сумму S2
элементов, расположенных правее него. - В данном массиве чисел а1, а2, …, а25
поменять местами минимальный и максимальный
элементы. - Найти сумму положительных элементов
последовательности d1, d2, …, d40,
расположенных до первого нулевого элемента,
заменить этой суммой минимальный элемент
массива. - Из отрицательных элементов массива х1, х2
…, x30, расположенных левее минимального
элемента, сформировать новый массив. - Из элементов последовательности у1, у2,
…, у25, расположенных между первым нулевым и
максимальным (в предположении, что в массиве есть
положительные числа) (или максимальным и первым
нулевым), сформировать новый массив. - Дан массив чисел а1, а2, …, а50.
Найти сумму элементов массива, стоящих правее
первого положительного элемента, и максимальный
элемент, его номер среди чисел предшествующих
первому положительному. - В массиве у1, у2, …, у25 поменять
местами минимальный элемент с первым
положительным элементом. - Среди элементов последовательности а1, а2,
…, а25 расположенных до первого
отрицательного элемента, найти минимальный
элемент. Из положительных элементов массива,
расположенных правее минимального, сформировать
новый массив. - Три отрицательных элемента массива b1, b2,
…, b25, расположенных правее максимального
помножить на номер максимального элемента. - Дан массив х1, х2, …, х30.
Помножить элементы массива на квадрат его
наименьшего элемента, если хi больше или
равно 0, и на квадрат его наибольшего элемента,
если хi меньше 0. - Дана последовательность t1, t2, …, t20.
Среди положительных элементов найти
максимальный и помножить на него все
положительные элементы последовательности. - Из элементов последовательности с1, с2,
с3 …, с45, стоящих на нечетных местах и
расположенных правее минимального элемента
данной последовательности, сформировать новый
массив d1, d2, … - В массиве чисел х1, х2, …, х17
заменить нулем все отрицательные элементы,
предшествующие его максимальному элементу. - Дана последовательность чисел а1, а2,
…, а25; из положительных элементов данной
последовательности, расположенных до
минимального элемента, сформировать
последовательность р1, p2, p3… - Из массива у1, у2, …, у50
сформировать новый массив в1, в2, в3,
…, в который записать все числа, находящиеся в
массиве у между его максимальным и минимальным
(или минимальным и максимальным) элементами. - Из массива х1, х2, …, х30
получить массив у1, у2, …, уn
состоящий из элементов массива х, расположенных
правее его максимального элемента. - Если наименьший элемент данной
последовательности х1, х2, …, х27
больше 0,1 то все отрицательные элементы
последовательности заменить единицей. - Найти наименьший элемент из элементов
последовательности x1, x2, …, x25,
расположенных до первого отрицательного числа.
Все отрицательные числа, расположенные правее
первого отрицательного, помножить на этот
наименьший. - В последовательности у1, у2, …, у25
найти максимальный элемент из элементов, стоящих
на четных местах. Помножить на него все элементы
данной последовательности, стоящие на нечетных
местах и расположенные правее найденного
максимального.
В
общем случае алгоритм решения задачи
с использованием
массивов выглядит так, как показано
на рис.2. Рассмотрим более подробно шаги
этого алгоритма.
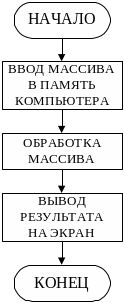
Рис.2
2.2.1. Ввод одномерного массива в память компьютера
При
вводе массива предлагается, что память
для
его размещения уже зарезервирована.
Количество элементов, под которые
зарезервирована
память, обозначим константой LEN.
Тогда LEN
— это максимально возможное для
использования количество элементов
массива (длина массива). В действительности,
при решении большинства
задач количество требуемых элементов
может изменяться от одного запуска
программы
к другому. Поэтому следует предоставить
пользователю возможность заказать
требуемое
ему в данном конкретном случае число
элементов массива, которое обозначим
N.
Таким образом, первым шагом алгоритма
ввода
одномерного массива станет ввод
переменной
N — требуемой длины массива. Напомним,
что N всегда меньше либо равна LEN.
В
языке Паскаль нет средств ввода-вывода
всего
массива целиком, поэтому ввод и вывод
массивов
выполняется поэлементно. Словесно можно
описать шаг ввода одномерного массива
следующим
образом:
ввести
элемент А[1];
ввести
элемент А[2];
….
ввести
элемент А[N].
Т.
о., индекс вводимого элемента изменяется
от 1 до N с
шагом 1. Очевидно, что для реализации
ввода массива необходимо
выбрать структуру цикла. Блок-схема
ввода массива представлена
на рис. 3.

Рис.3
На
языке ТурбоПаскаль ввод одномерного
массива реализуется
следующим фрагментом программы:
Program
ABC;
const
LEN
= 100; {максимальная длина массива}
var
А
: array
[1. .LEN] of real; {объявление массива,
состоящего из 100 вещественных чисел}
i,N
: byte;
{i — индекс, N — требуемая длина массива}
BEGIN
write
(‘Введите длину массива N =’);
readln(N);
for
i:=1 to N do
begin
write(‘A[‘
, i , ‘]=’ );
read
(A [i])
end;
…
END.
В
дальнейшем заголовок и раздел описания
программы приводить не станем. Фрагменты
программ, описанные в примерах, следует
располагать
в требуемом месте раздела исполняемых
операторов приведённой
здесь программы.
2.2.2. Вывод массива на экран
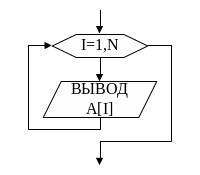
Блок-схема
алгоритма вывода одномерного массива
на экран представлена на рис.4. Она очень
мало отличается от вышеприведённой
блок-схемы алгоритма ввода и построена
на основании
таких же рассуждений. Единственным
принципиальным отличием
является то, что не требуется запрашивать
у пользователя
длину массива, которая к моменту вывода
массива на экран уже
известна.
Фрагмент
программы для вывода одномерного массива
на экран:
…
writeln(‘Массив
А’);
for i:=1 to N do
write (A[ i ]:6:2);
writeln;
…
Рис.4
2.2.3. Подсчёт суммы, произведения, количества элементов одномерного массива, удовлетворяющих заданному условию
Для
нахождения суммы элементов массива
воспользуемся методом накопления. Для
этого заведём
дополнительную переменную S,
к которой поочерёдно станем добавлять
значения элементов
массива. Т.к. при объявлении любой
переменной
на языке ТурбоПаскаль её значение не
определено, необходимо занести в
переменную
S
такое значение, которое не повлияет
на конечный результат суммирования
элементов
массива. Этим значением является 0.
Далее
необходимо к значению переменной S
добавлять элементы массива с номерами
1, 2,
…, N,
т.е. выполнять следующие действия:
S
= S +А[1]
S
= S + A[2]
.
. . . . . . . . . .
S
= S + A[N]
Отсюда
видно, что для вычисления суммы элементов
массива
необходимо использовать цикл, который
будет повторять оператор
S=S+A[i],
где i
поочерёдно принимает значения от 1 до
N с
шагом 1. После завершения N итераций
цикла значение суммы будет
вычислено окончательно и его можно
обработать по условию
задачи, например, вывести на экран.
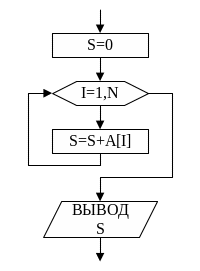
Блок-схема
алгоритма нахождения суммы приведена
на рис.5.
Фрагмент программы записан ниже:
•
• •
S:=0;
for
i:=1 to N do
S:=S+A[i];
writeln(
Сумма
S=’ , S);
•
• •
Рис. 5
В
случае, если необходимо найти сумму
элементов, удовлетворяющих некоторым
условиям (положительные, отрицательные,
четные и т.п.), то в этом случае каждый
элемент массива необходимо будет
сравнивать с некоторым значением,
заданным в условии задачи. На рис.6
представлена блок-схема алгоритма
поиска суммы положительных значений
элементов массива. В этом случае каждый
элемент массива сравнивается с 0, и, если
он больше 0, то он включается в сумму.
Фрагмент
программы
приводится
ниже.
…
S
:= 0;
for i :=1 to N
do
if A[i] > 0
then
S
:= S + A[i];
writeln
(‘S= ‘,S);
…
Рис. 6
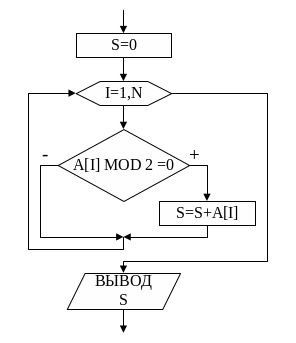
На
рис.7 представлена блок-схема алгоритма
поиска суммы четных элементов массива.
Известно, что четные элементы делятся
на 2 без остатка. В ТР существует
математическая операция MOD,
позволяющая определить остаток от
деления числа а
на некоторое число р:
а MOD
р. Следует заметить, что операнды а
и
р
могут быть только целыми числами.
Например,
4
MOD 2 = 0 ( т.к. 4 – четное число);
5
MOD 2 = 1 ( т.к. 5 – нечетное число);
7
MOD 3 = 1 ( т.к. 7 не кратно 3 ).
Фрагмент
программы приводится ниже.
…
S
:= 0;
for i :=1 to N
do
if A[i] MOD 2 =
0 then
S
:= S + A[i];
writeln
(‘S= ‘,S);
…
Рис. 7
Аналогично
следует вычислять
произведение элементов массива, за
исключением того, что в качестве
начального значения произведения
следует принять 1, т.к. именно
умножение на 1 не повлияет на
искомое произведение.
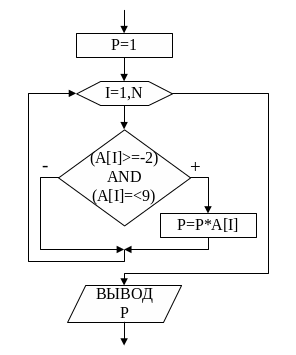
На
рис.8 представлена блок-схема алгоритма
поиска произведения Р элементов массива,
попадающих в интервал от –2 до 9. Фрагмент
программы
приводится
ниже.
…
P
:=1;
for
i:=1 to N do
if
(A[i] >= -2) and (A[i] <= 9) then
P
:= P * A[i];
writeln(‘P=
‘, P);
…
Рис.
8
При
нахождении количества элементов массива
следует воспользоваться
теми же рассуждениями,
что и в ранее рассмотренных случаях.
Обычно требуется подсчитать
количество элементов, удовлетворяющих
некоторым заданным условиям,
например, количество положительных
элементов. Для решения этой задачи
поочерёдно сравним каждый
элемент массива с 0, и при обнаружении
отрицательного увеличим
количество на 1. Когда все элементы
массива закончатся, искомое количество
будет окончательно подсчитано и его
можно обработать
по условию задачи.
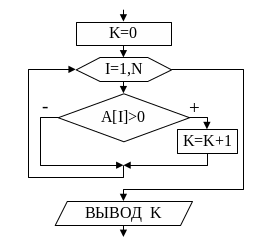
Блок-схема
алгоритма нахождения количества
отрицательных
элементов представлена на рис.9. Фрагмент
программы,
соответствующий этой блок-схеме, приведён
ниже.
К:=0;
for
i:=1
to
N
do
if
A[i]>0 then
K:=K+1;
writeln
( ‘Количество равно’, К);
Рис.9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«Универсальная» блок-схема и 3 типовых алгоритма 
Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) — суммы, количества, произведения, максимума, минимума и т.п.
В картинках не показаны «начало» и «конец», только содержательная часть.
ГОСТовские «перевёртыши» на практике крайне неудобны, классическое изображение с помощью «ромбика» часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла),
а вот значок «цикла с параметром», если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.
I Алгоритм табулирования (составление списка или таблицы)
Алгоритм табулирования (составление списка или таблицы)
Что писать в фигурках вместо цифр?
1. Примем, что управляющая переменная цикла называется x, а здесь зададим её начальное (x1) и конечное (x2) значения, а также шаг изменения dx. Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью «ввод x1,x2,dx«;
2. Обычно внутри значка «цикл с параметром» (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: «для x от x1 до x2 шаг dx» или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;
3. Для очередного x вычислить y=f(x). Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков «расчёт» или условных операторов;
4. Вывести строку таблицы: вывод x, f(x)
II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Вместо цифр в элементах блок-схему указываем:
1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0, количеству k=0, произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);
2. Выполняется как в задаче I;
3. Считаем очередной элемент последовательности y=f(x), с тем же замечанием, что к задаче I;
4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x), количество в виде k=k+1, произведение в виде p=p*f(x). При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;
6. По выходе из цикла выводим найденную величину или величины.
III. Алгоритм поиска максимума или минимума
Блок схема задачи II годится и для этого случая.
1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min, а максимум — max) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -1030, оператор будет иметь вид Max=-1030) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 1030) или первый элемент последовательности;
2-3. Выполняются как в задачах I-II, с теми же замечаниями.
4-5. Для поиска максимума проверяется условие 4 f(x)>max, выполняется действие 5 вида max=f(x), дли минимума проверяется условие 4 f(x)<min и выполняется действие 5 вида min=f(x). С чем сравнивали max или min, то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией «И» либо «ИЛИ» с основным, например, поиск максимального из отрицательных элементов предполагает проверку y<0 and y>max;
6. По выходе из цикла выводим найденную величину или величины.
Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали 
IV. Схема ввода и обработки элементов одномерного массива
Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла «for»). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.
Схема ввода и обработки элементов одномерного массива
V. Реализация алгоритма в кратных (вложенных) циклах
Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:
Блок-схема двойного цикла с параметром
Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки (i) и столбца (j) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.
31.10.2016, 21:46 [10938 просмотров]
Блок-схемы алгоритмов работы с массивами
Используя команды повторения можно коротким алгоритмом описать большой объем действий, необходимых для решения поставленной задачи. Массивы играют аналогичную роль по отношению к данным и позволяют коротким алгоритмом описать действия с огромным объемом информации.
Применение массивов при описании алгоритмов решения практических задач позволяет:
1. записать коротким алгоритмом работу с большим объемом информации;
2. расширить область применимости алгоритма.
Необходимость в применении массивов для описания алгоритмов решения задач возникает, когда при решении задач приходится иметь дело с большим, конечным количеством однотипных упорядоченных по индексам объектов.
Массив– это упорядоченная по индексам, конечная совокупность однотипных объектов, образованных по одному и тому же правилу. Отношение порядка в массиве задается с помощью индексирования элементов массива. Если для индексирования массива используется один индекс, то массив называется одномерным, если два или больше, то многомерным. Для индексации элементов двумерного массива указываются два индекса, первый индекс, как правило, номер строки, второй – номер столбца. Одномерный массив часто называют вектором, двумерный – матрицей.
При работе с массивами, каждому массиву дается имя. Работа с массивом – это работа с элементами массива. Элементу массива дается имя, соответствующее имени массива, и указывается в квадратных или круглых скобках порядковый номер этого элемента в массиве.
Очевидно, чтобы задать массив (таблицу), необходимо:
1. указать, что однотипные объекты объединены в массив (таблицу);
2. указать имя массива (таблицы), начальный и конечный порядковые номера индексов его (её) элементов;
3. указать тип значений элементов массива (таблицы).
При описании массива после имени массива будем в круглых (квадратных) скобках указывать начальный и конечный номера каждого индекса элементов массива через двоеточие. Если массив многомерный, то описание начального и конечного номеров каждого индекса элементов массива разделим запятой. Например, А(1:50) – массив, элементы которого: А(1), А(2), … , А(50); В(1:2,1:3) – массив, элементы которого: 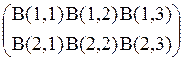
Пример 1. Одномерный массив Осадки (1:365) – количество осадков в течение года.
Пример 2. Двумерный массив Расписание (1:4,1:2) – расписание уроков на 2 дня в 4 классе общеобразовательной школы.
| Дни недели Номер урока | Понедельник | Вторник |
| Математика | Русский язык | |
| Русский язык | Математика | |
| Природоведение | История | |
| Физкультура | Рисование |
Массивы имеют размер и размерность. Размер массива – это количество элементов в данном массиве, размерность – количество индексов, необходимых для однозначного определения места фиксированного элемента массива. Массив примера 1 имеет размерность, равную 1 (одномерный), размер – 365. Массив примера 2 имеет размерность равную 2 (двумерный), размер 2∙4=8. Элемент массива называется переменной с индексом, переменная без индекса – простой переменной. Над элементами массива можно производить те операции, которые допустимы для базового типа.
В качестве типов индексов элементов массива можно использовать целый тип. Индексы могут задаваться константами, переменными и выражениями. Значения переменных и выражений задают номер элемента массива, поэтому их значения должны быть определены при обращении к этому элементу. Элементами массива могут быть значения любого типа данной реализации языка.
Пример 3. Пусть массив A – одномерный массив, имеющий 4 элемента целого типа – integer: -12, 0, 41, -131.
направление изменения индекса

 -12 -12 |
-131 |
Пример 4. Массив Q – двумерный массив, имеющий 3 строки и 4 столбца – 12 элементов вещественного типа – real:
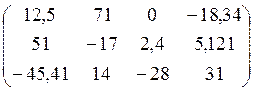
направление изменения второго индекса

| 12,5 | -18,34 | |
| -17 | 2,4 | 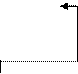 5,121 5,121 |
| -45,41 | -28 |



Решение. Смотри блок-схему алгоритма (задача 21), использована циклическая структура «while P do S».
Произведение можно находить так:
В блок-схеме вместо этой цепочки операторов запишем оператор П:=П×а(k), где k изменяется от 1 до n; k – параметр цикла. Чтобы значение первого произведения было равно a1, следует положить начальное значение П равным 1. Операторы 5-6 составляют тело цикла.
Задача 22. Произведение матриц. Составьте блок-схему нахождения произведения матрицы А на матрицу В:
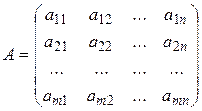
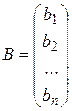
Решение. Смотри блок-схемы 1-3 алгоритма (задача 22).
Смотри блок-схему 1 (задача 22). Произведение матрицы А на матрицу В есть матрица-столбец; обозначим ее С.
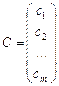
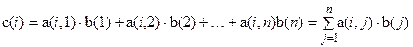
Функциональный блок, вычисляющий величину c(i), обозначим S1. Смотри блок-схему 2 (задача 22).
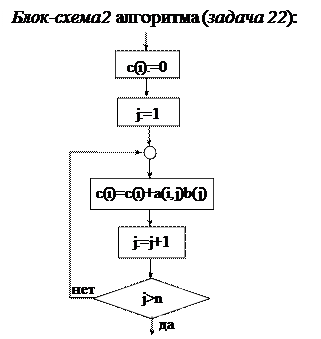
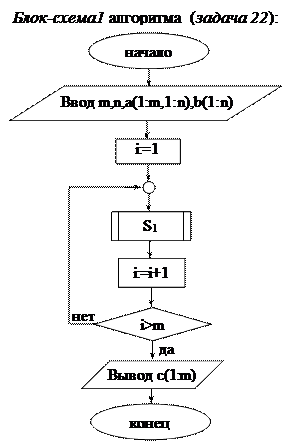
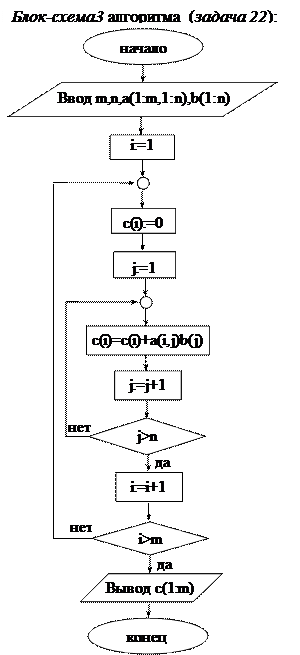
Очевидно, что функциональный блок S1 будет содержать циклическую структуру, например, структуру «repeat S until P».
Подставив детализацию блока S1 (блок-схема 2 (задача 22)) в блок-схему 1 (задача 22), получим одну циклическую структуру внутри другой, вложенные циклы – блок-схема 3(задача 22).
Задача 23. Положительные числа. Дана числовая последовательность a1, a2, … , an. Определите, есть ли среди ai, 1£i£n положительные числа, если да, то переменной K присвойте значение 1, в противном случае – значение 0. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схему алгоритма (задача 23).
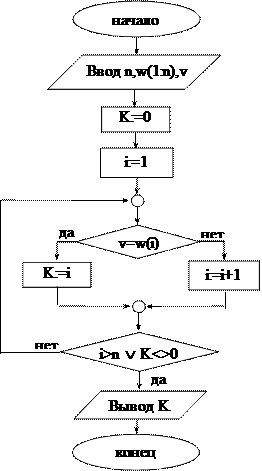
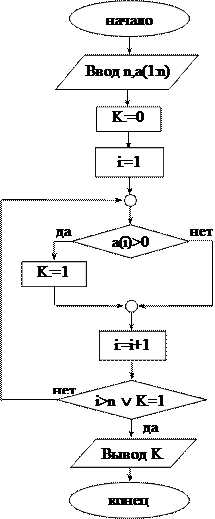
Поскольку положительный элемент может оказаться на i-ом месте, где i 0 – истинно, K получит значение 1. Проверка окончания организована так, что выход из цикла произойдёт или при i>n (положительного элемента нет), K = 0, или при i>n и K = 1 (этот элемент – последний в массиве), или при i n, где i – номер рассматриваемой буквы. Значение переменной K в этом случае равно 0. Если буква v входит в слово, выход из цикла может быть осуществлен раньше, чем i станет больше n, при K<> 0, где K – номер позиции первого вхождения буквы v в слово w.
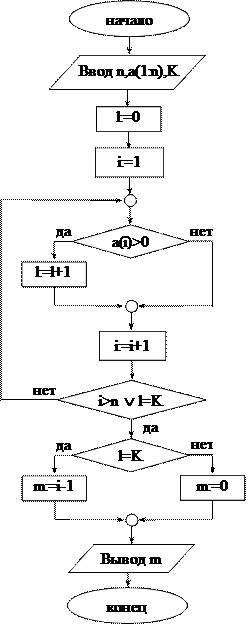
Задача 25.Количество положительных элементов. Дана последовательность чисел a1, a2, … , an. Присвойте переменной m номер K-го положительного элемента этой последовательности. Если в последовательности положительных элементов меньше K, то переменной m присвойте значение 0. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схему алгоритма (задача 25).
Подсчет количества положительных элементов массива организуем с помощью цикла с постусловием. Если положительных элементов нет или их меньше, чем K, выход из цикла осуществим при i>n, m присвоим значение 0. При l = K, где l – число положительных элементов, также реализуем выход из цикла. При этом i получит уже следующее значение. Значит, номер K-го положительного элемента на единицу меньше i.
Задача 26.Сдвиг в массиве. Переставьте вещественные элементы массива A(1:n) таким образом, чтобы они шли в следующем порядке: А(n), А(1), А(2), … , A(n-2), A(n-1), т.е. в массиве произведите сдвиг элементов на одну позицию вправо. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схему алгоритма (задача 26).
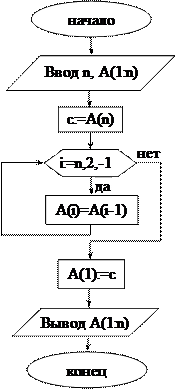
Задача 27.Максимальные элементы массива. Дана последовательность чисел a1, a2, … , an. Найдите количество максимальных элементов последовательности и их номера. Составьте блок-схему решения поставленной задачи.
Решение. Смотри блок-схемы 1-2 алгоритма (задача 27).
В блок-схеме1 алгоритма (задача 27) первый цикл организуем для определения максимального элемента, значение которого присваивается переменной b. Начальное значение b положим равным a1. Второй цикл считает K – количество одинаковых максимальных элементов. Переменная M(K) принимает значение индекса встретившегося максимального элемента. M(K) – числовая последовательность, членами которой являются эти индексы.
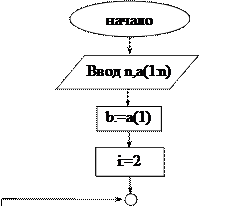
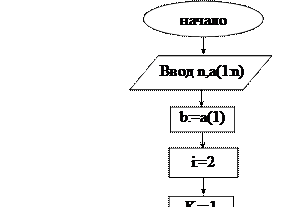
Блок-схема2 алгоритма (задача 27) предполагает в одном цикле на i-ом шаге определение максимального элемента из i рассмотренных, подсчет количества таких элементов и фиксирование их номеров. Если на (i+1)-ом шаге встречается больший элемент, то операторы b:=ai, K:=1, mK:=i зададут новые начальные значения переменных b, K, mK, и все вычисления будут проведены относительно нового большего элемента.
Задача 28. Дружественные числа.Дружественными числами называются два натуральных числа, таких, что каждое из них равно сумме всех натуральных делителей другого, исключая само это другое число. Числа 220 и 284 являются дружественными числами, так как сумма делителей числа 220 – это 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, а сумма делителей числа 284 – это 1 + 2 + 4 + 71 + 142 = 220. Составьте блок-схему алгоритма нахождения дружественных чисел на отрезке [2;n].
Решение. Смотри блок-схему алгоритма (задача 28).
Блок-схема алгоритма (задача 28):


Задача 29.Группировка. Дан массив A(1:n), элементы которого отличны от нуля. Расположите их в таком порядке, чтобы первыми были все положительные элементы, а затем – все отрицательные, причем порядок следования как положительных, так и отрицательных элементов должен сохраняться. При решении задачи нельзя заводить новую таблицу. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схемы 1-2 алгоритма (задача 29).
Для решения поставленной задачи будем перебирать элементы массива с первого по n-ый. Если A(i)>0, никаких изменений в массиве не производим, увеличиваем i на единицу и переходим к исследованию следующего элемента. Если же A(i)
Дата добавления: 2015-01-26 ; просмотров: 63462 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник