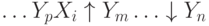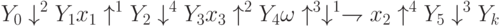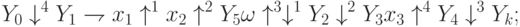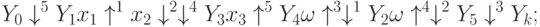Как составить алгоритм логики

Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.

Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.

Содержание:

1. Элементы блок-схем алгоритмов
2. Примеры блок-схем
3. Нужны ли блок-схемы? Альтернативы

Элементы блок-схем алгоритмов

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.

Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.

	Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора.
	В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
	В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций.
	Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной.
	Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями.
	Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
	Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком.
	В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно.
	Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией.

Примеры блок-схем

В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.

Сортировка вставками

Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.

На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.

В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.

На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.

Сортировка пузырьком

Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.

На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.

Сортировка выбором

В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).

На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .

На блоге можно найти другие примеры блок-схем:

• блок-схема проверки правильности расстановки скобок арифметического выражения [2];
• блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].

Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.

Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.

Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.

Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.

Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.

Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.

В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].

В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].

Список использованных источников:

1. ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документа­ции».
2. Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
3. Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
4. yEd Graph Editor https://www.yworks.com/products/yed
5. Книги: алгоритмы https://pro-prof.com/books-algorithms
6. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
7. Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
8. Визуальный язык ДРАКОН https://drakon.su/
9. Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
10. Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.

Операция:
A, B, C, …
или
A1, A2, A3, …
параметры операции:
Aij, Aijk, …
или
A(ij), A(ijk), …
Запись операторов:
линейный алгоритм
разветвленный алгоритм:
логические условия – p, q, r, …
p[f(x1, x2, …, xn)]
ω – тождественно-ложные логические условия
У каждого ЛУ есть ↑(или ↓):
↑i – начало i-ой стрелки (справа от ЛУ)
↓i – конец i-ой стрелки (слева от ЛУ=0)

ЛСА
Пример:
↓2Аp1↑1B↓1p2↑2C
Выполнение ЛСА:
если p1=p2=0, то – АА…А…
если p1=0, p2=1, то – АС
если p1=1, p2=0, то – АВАВ…АВ
если p1=1, p2=1, то – АВС
Пример:
А↓1Вp↑2Сω↑1↓2D
Выполнение ЛСА:
ABCBC…BC…BC BD

p=1 p=0

3.5 Логические схемы алгоритмов

Основное достоинство рассматриваемых ниже логических схем алгоритмов (ЛСА) состоит в том, что, являясь по существу разновидностью языка операторных схем, они допускают запись алгоритма в строчку, что часто является удобным, т.к. появляется возможность исключить процесс рисования, вычерчивания, как это имеет место в ГСА. Важным является также наличие развитой системы преобразований ЛСА и возможности формального перехода к автоматному отображению.

Основными элементами ЛСА являются так же, как и в ГСА, операторы и логические условия.

Основные отличия от ГСА состоят в том, что для указания взаимосвязей между операторами и логическими условиями используются верхние и нижние стрелки.

Логической схемой алгоритма называется строчка, составленная из символов операторов , или и логических условий , а также верхних и нижних стрелок. Иногда верхние и нижние стрелки заменяют на правые и левые полускобки.

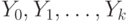
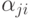
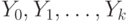
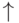
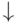
Итак, ЛСА— строчка, составленная из символов операторов , логических условий и верхних и нижних стрелок, причем:

Переход по логическому условию , стоящему в ЛСА

осуществляется так:

Безусловный переход для ясности может быть обозначен дополнительным символом, например .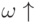

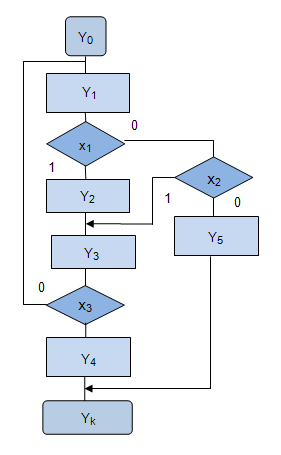
ЛСА для МП, представленной на рис. 3.7 выглядит так:

Правило чтения ЛСА состоит в следующем.

Вначале анализируется элемент ЛСА, следующий непосредственно за оператором 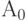. Если рассматриваемым элементом является оператор, то он отмечается (выписывается) и на следующем шаге анализируется стоящий справа элемент (оператор или логическое условие).

Если рассматриваемым элементом является логическое условие 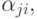производится проверка этого условия;

Анализ ЛСА при соблюдении сформулированных правил приводит через некоторое количество шагов к получению строчки операторов, называемой значением ЛСА при заданной последовательности наборов логических условий.

Пусть задана ЛСА.

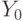
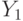
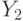
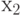
Построим соответствующую ей ГСА. За начальным оператором следует оператор и далее логическое условие . Если логическое условие выполняется, то есть , то следующим оператором выполняется . Если логическое условие не выполняется, то есть , то следующим оператором выполняется , то есть оператор, стоящий за нижней стрелкой с номером 1.

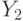
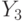
Далее в ЛСА за оператором стоит оператор и . В такой последовательности и изображаем их на ГСА. Далее строим аналогичным образом.

Одной важной особенностью ЛСА является возможность неоднозначной записи одного и того же алгоритма.

Так, ГСА на рис.3.8 может быть описана еще несколькими вариантами ЛСА:

Логическими
принято называть алгоритмы, которые
содержат предписания (операции)
относительно объектов нечисловой
природы. Характерной особенностью
логических алгоритмов является выбор
на каждом шаге по определенным правилам
альтернативной операции, осуществляемой
при переходе к следующему шагу. К
логическим задачам относят многие игры.
Однако выделение логических задач из
класса математических задач достаточно
условно — в большинстве случаев задачи
являются смешанными:
в них присутствуют
и числовые, и логические операции. Так,
машинные алгоритмы игры в шахматы
используют на каждом шаге вычисление
значения некоторой функции, учитывающей
оценку позиции после каждого следующего
хода (точнее, полухода) и стоимость
размена фигур.

Ниже
рассматриваются две задачи, носящие
выраженный логический характер.

1.8.1 Задача “Поиск пути в лабиринте”.

Эта
задача восходит к греческой мифологии,
в которой, в частности описывается
подвиг Тезея, проникшего в лабиринт,
где обитал чудовищ-ный Минотавр,
пожиравший местных красавиц. Тезей
розыскал в лаби-ринте Минотавра и убил
его. Выбраться из лабиринта ему помогла
Ариадна (А), дав ему клубок ниток, один
конец которых держала она сама. По мере
углубления Тезея в лабиринт клубок
разматывался; наматывая потом нитки,
Тезей благополучно вернулся к выходу.

Мы
рассмотрим задачу поиска пути в лабиринте
в общем случае (для класса подобных
задач) и приведем словесное
описание (?)
алгоритма.

Представим
лабиринт в виде конечной системы
площадок, от которых расходятся коридоры,
причем, каждый коридор соединяет две
площадки (будем называть их смежными);
возможно существование таких площадок,
из которых можно пройти только в один
коридор (такие площадки будем называть
тупиками).
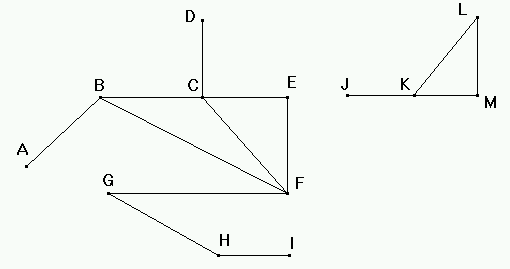
Геометрически лабиринт можно представить
в виде системы точек А, В, С…, изображающих
площадки, и совокупности отрезков АВ,
ВС,…, изображающих коридоры, которые
соединяют определенные пары данных
точек (рис. 1.17). Смежными являются,
например, точки В и С, К и М и т.д., а
тупиковыми — точки А, D,
I, J.

Рис.
1.17. Геометрическое представление
лабиринта

Будем
говорить, что площадка Y достижима
из площадки X , если существует путь от
X к Y через промежуточные коридоры и
площадки . Точнее: либо X и Y — смежные
площадки, либо существует последовательность
площадок X1, X2, … Xn таких, что X и X1, X2 и
Х3 … , и т.д., и, наконец , Xn и Y являются
смежными. Отметим, что если Y достижима
из X, то она достижима и посредством
простого пути
, т.е. такого пути , в котором каждая
площадка (а тем более и каждый коридор)
проходится лишь один раз. Например путь
ABCD
является простым, а путь ABCFECD
— нет.

Тезей
должен был решить задачу: достижима ли
площадка М, на которой находится Минотавр,
из площадки А, на которой находится
Ариадна, или нет. Если да, то к М можно
было добраться по любому пути, то
вернуться к площадке А нужно уже по
простому пути. Поскольку заранее
устройство лабиринта неизвестно, решение
задачи должно быть представлено в виде
общего метода поиска для любого лабиринта
и при любом расположении площадок А и
М, то есть требуется построить алгоритм
поиска пути в лабиринте.

Будем
условно помечать коридоры следующими
красками: непрой-денные ни разу — зеленой,
пройденные один раз — желтой, пройденные
дважды — красной.

Находясь
на начальной площадке, Тезей может
попасть на одну из смежных площадок
посредством одного из следующих двух
ходов:

1. Разматывание
   нити. Прохождение
   от данной площадки по любому зеленому
   коридору до смежной площадки. После
   прохождения этого коридора он считается
   желтым.

2. Наматывание
   нити. Возвращение
   от данной площадки по последнму
   пройденному желтому коридору до смежной
   площадки. При этом нить наматывается
   обратно на клубок, а этот коридор
   становится красным.

Предполагается,
что Тезей делает какие-то пометки,
позволяющие ему впоследствии отличать
красные коридоры от зеленых; желтые
различимы тем, что по ним протянута нить
Ариадны .

Обстановка
на данной площадке характеризуется
признаками:

1. Минотавр.
   Он обнаружен.

2. Петля.
   Через данную площадку уже протянута
   нить Ариадны (иначе: от данной площадки
   расходятся по крайней мере два желтых
   коридора).

3. Зеленая
   улица. От данной
   площадки есть вход по крайней мере в
   один зеленый коридор.

4. Ариадна.
   Она на данной площадке.

5. Особый
   случай. Отсутствие
   всех предыдущих признаков (например,
   тупик).

Признак	Ход
1. Минотавр	Остановка
2. Петля	Наматывание нити
3. Зеленая улица	Разматывание нити
4. Ариадна	Остановка
5. Особый случай	Наматыване нити

Находясь
на некоторой площадке, Тезей делает
очередной ход следующим образом: он
проверяет по порядку номеров в соответствии
с левым столбцом схемы, какой из
перечисленных признаков имеет место;
обнаружив первый такой признак, он (уже
не проверяя остальные признаки) делает
соответствующий ход из правого столбца.
Такие ходы делаются до тех пор, пока не
наступит остановка.

Приведем
(без доказательства) утверждения,
которые являются обоснованием
предложенного метода:

1. При
   любом расположении А и М в лабиринте
   после конечного числа ходов обязательно
   наступит остановка либо на площадке
   Минотавра, либо на площадке Ариадны.

2. Если
   остановка наступила на М, то Минотавр
   достижим. Более того, в этом случае
   нить Ариадны оказывается протянутой
   по простому пути, ведущему от А к М.
   Наматывая нить, Тезей может теперь
   вернуться по этому пути к Ариадне.

3. Если
   остановка наступила на площадке Ариадны,
   то Минотавр не достижим.

Отметим,
что в случае признака “зеленой улицы”
ход не определен однозначно — нарушается
свойство детерминированности алгоритма.
Этот случай легко устраняется, если
ввести дополнительное правило о том,
что при наличии нескольких зеленых
коридоров Тезей обходит площадку по
часовой (против часовой) стрелке, выбирая
очередной коридор. Ясно, что в общем
случае алгоритм основан на перебора
вариантов обхода площадок и коридоров.

Соседние файлы в папке Конспект лекций

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #