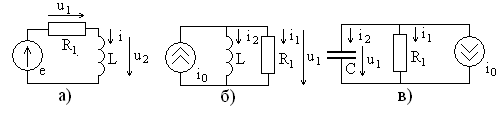
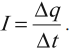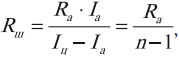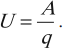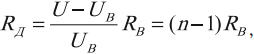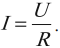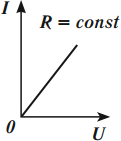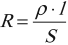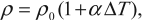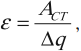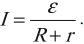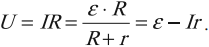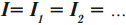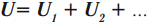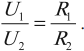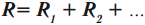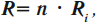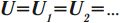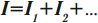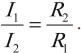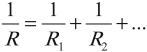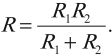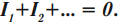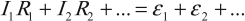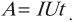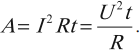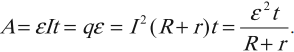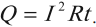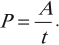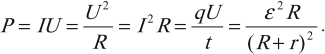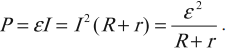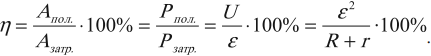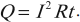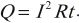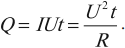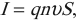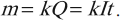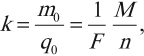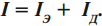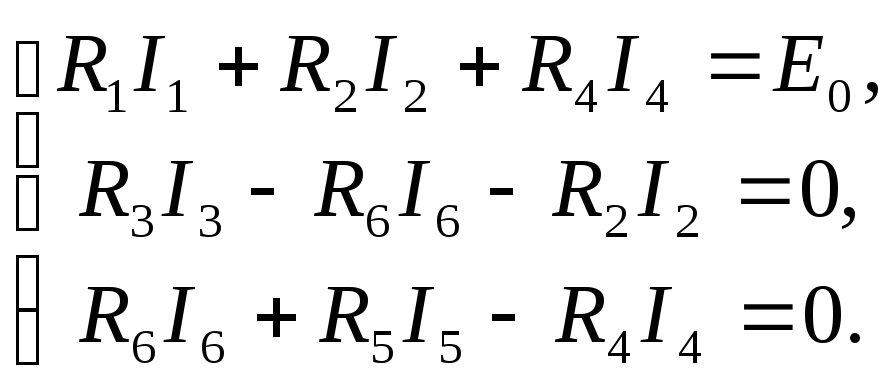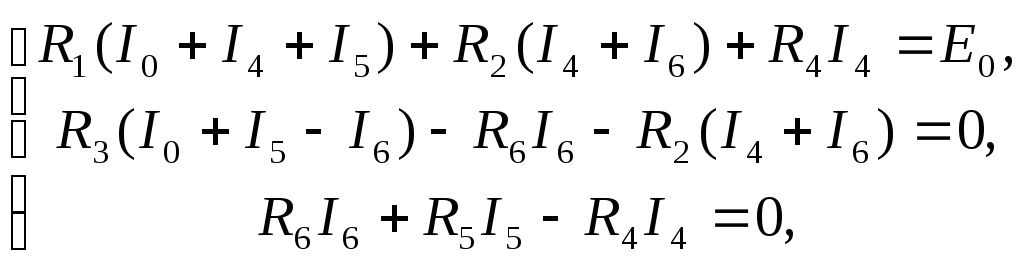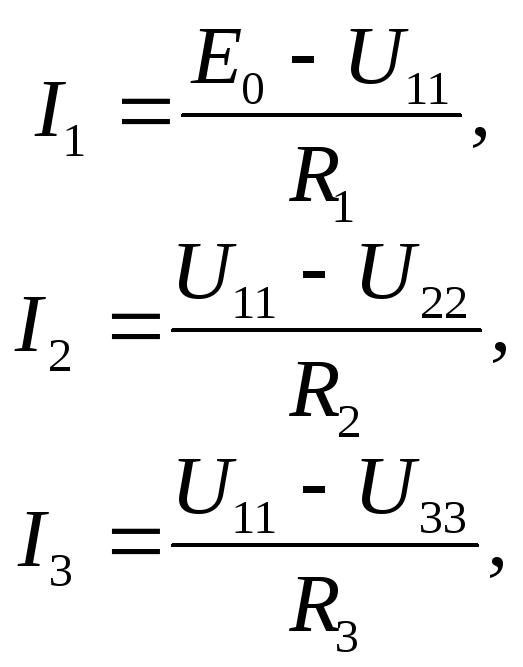Законы постоянного тока
Содержание
- Постоянный электрический ток. Сила тока
- Постоянный электрический ток. Напряжение
- Закон Ома для участка цепи
- Электрическое сопротивление. Удельное сопротивление вещества
- Электродвижущая сила. Внутреннее сопротивление источника тока
- Закон Ома для полной электрической цепи
- Параллельное и последовательное соединение проводников
- Смешанное соединение проводников
- Работа электрического тока. Закон Джоуля–Ленца
- Мощность электрического тока
- Носители свободных электрических зарядов в металлах, жидкостях и газах
- Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
- Основные формулы раздела «Законы постоянного тока»
Постоянный электрический ток. Сила тока
Электрический ток – это упорядоченное движение заряженных частиц.
Условия существования электрического тока в проводнике:
- наличие свободных заряженных частиц;
- наличие электрического поля.
Напряженность электрического поля должна быть постоянной.
Цепь постоянного тока должна быть замкнутой.
Важно!
Тепловое движение заряженных частиц нельзя назвать электрическим током, так как оно беспорядочное.
Электрический ток можно обнаружить по его действиям:
- тепловому – при протекании тока проводник нагревается;
- химическому – изменяется состав вещества при прохождении электрического тока (электролиз);
- магнитному – электрический ток создает магнитное поле.
За направление тока принимают направление движения положительно заряженной частицы.
Сила тока – это скалярная физическая величина, равная отношению заряда, прошедшего через поперечное сечение проводника, ко времени, за которое этот заряд переносится.
Обозначение – ( I ), единица измерения в СИ – ампер (А) (является основной).
Вычисляется по формуле:
Если за одинаковые промежутки времени через поперечное сечение проводника проходит одинаковый заряд, то ток постоянный.
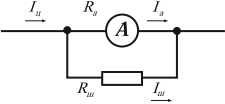
Для измерения силы тока используют амперметр.
Условное обозначение на схемах:
Амперметр – измерительный прибор для определения силы тока в электрической цепи.
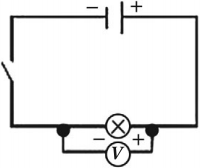
При измерении силы тока амперметр включают в цепь последовательно с тем прибором, силу тока в котором измеряют, и с соблюдением полярности. Клемму амперметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока.
Для того чтобы включение амперметра не влияло на величину измеряемого тока, его сопротивление по сравнению с сопротивлением нагрузки должно быть как можно меньшим. Каждый амперметр рассчитывается на некоторое определенное максимальное значение измеряемой величины. Но возникают ситуации, когда необходимо выполнить измерение силы тока больше предельно допустимого значения силы тока.
Для этого параллельно амперметру присоединяют проводник (шунт), по которому проходит часть измеряемого тока. Значение сопротивления этого проводника рассчитывается так, чтобы сила тока, проходящего через амперметр, не превышала его максимально допустимого значения.
Сопротивление шунта рассчитывается по формуле:
где ( I_ц ) – сила тока в цепи, ( I_а ) – максимально допустимая для данного амперметра сила тока, ( R_а ) – сопротивление амперметра, ( n=frac{I_ц}{I_а} ).
При этом цена деления прибора увеличивается в n раз, а точность измерений во столько же раз уменьшается.
Работающим с электрическими цепями надо знать, что для человеческого организма безопасной считается сила тока до 1 мА. Сила тока больше 100 мА приводит к серьезным поражениям организма.
Постоянный электрический ток. Напряжение
В проводнике, по которому протекает ток, заряды движутся под действием сил электростатического поля. Работу электростатических сил характеризуют разностью потенциалов или напряжением.
Электрическое напряжение – скалярная физическая величина, равная отношению работы по перемещению электрического заряда между двумя точками цепи к величине этого заряда.
Обозначение – ( U ), единица измерения в СИ – вольт (В).
Формула для вычисления:
Напряжение равно разности потенциалов только в том случае, если рассматриваемый участок цепи не содержит источник тока (ЭДС = 0).
Измеряют напряжение вольтметром.
Изображение вольтметра на схеме:
При измерении напряжения вольтметр включают в цепь параллельно с тем прибором, напряжение на котором измеряют, и с соблюдением полярности. Клемму вольтметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока. Для того чтобы включение вольтметра не влияло на измерение напряжения, его сопротивление должно быть большим.
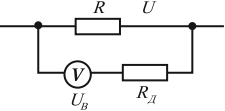
Для измерения напряжения больше, чем допустимое для данного вольтметра, используют добавочное сопротивление – резистор, включаемый последовательно с вольтметром.
Величина добавочного сопротивления рассчитывается по формуле:
где ( U ) – напряжение, которое нужно измерить, ( U_В ) – напряжение, на которое рассчитан вольтметр, ( n=frac{U}{U_В} ), ( R_В ) – сопротивление вольтметра.
При этом цена деления прибора увеличивается в ( n ) раз, а точность измерений во столько же раз уменьшается.
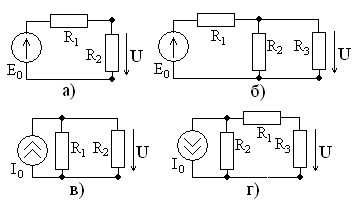
Закон Ома для участка цепи
Взаимосвязь между силой тока, протекающей по проводнику, и напряжением на его концах была экспериментально установлена Г. Омом и носит название закона Ома для участка цепи.
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению:
График зависимости силы тока от напряжения называется вольт-амперной характеристикой. Из закона Ома для участка цепи следует, что при постоянном сопротивлении сила тока прямо пропорциональна напряжению. Следовательно, вольт-амперная характеристика для металлического проводника представляет собой прямую линию, проходящую через начало координат.
Проводник с такими свойствами называется резистором.
Угол наклона графика к оси напряжений зависит от сопротивления проводника. Тангенс угла наклона графика равен проводимости резистора.
Электрическое сопротивление. Удельное сопротивление вещества
Электрическое сопротивление – свойство материала проводника препятствовать прохождению через него электрического тока.
Обозначение – ( R ), единица измерения в СИ – Ом.
Объяснить наличие сопротивления можно на основе строения металлических проводников. Свободные электроны при движении по проводнику встречают на своем пути ионы кристаллической решетки и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Сопротивление различных проводников зависит от материала, из которого они изготовлены, их длины, геометрической формы и температуры. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м2.
Обозначение – ( rho ), единица измерения в СИ – Ом·м.
Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 1,7·10-8 Ом·м, т. е. медный проводник длиной 1 м и сечением 1 м2 обладает сопротивлением 1,7·10-8 Ом. На практике часто используют единицу удельного сопротивления (Ом·мм2)/м.
Электрическое сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника.
Формула для вычисления:
Сопротивление проводника увеличивается с ростом температуры. Удельное сопротивление зависит от температуры:
где ( rho_0 ) – удельное сопротивление при ( T_0 ) = 293 К (20°С), ( Delta T=T-T_0 ), ( alpha ) – температурный коэффициент сопротивления.
Единица измерения температурного коэффициента сопротивления – К-1.
При нагревании увеличивается интенсивность движения частиц вещества. Это создает трудности для направленного движения электронов. Увеличивается число столкновений свободных электронов с ионами кристаллической решетки.
Свойство изменения сопротивления при изменении температуры используется в термометрах сопротивления. Эти приборы могут измерять температуру, основываясь на зависимости сопротивления от температуры. У термометров сопротивления высокая точность измерений.
Электродвижущая сила. Внутреннее сопротивление источника тока
Для создания электрического поля в проводниках используют источник тока. Внутри источника тока происходит перераспределение зарядов, в результате которого на полюсах источника возникает избыток зарядов разных знаков.
Виды источников тока:
- электрофорная машина;
- термопара;
- фотоэлемент;
- аккумулятор;
- гальванический элемент.
Сторонними называются силы неэлектрической природы, действующие внутри источника тока.
Когда проводник соединяют с полюсами источника, то на внешнем участке цепи заряженные частицы движутся под действием электростатической силы. А внутри источника на заряды действуют сторонние и электростатические силы.
Под действием этих сил внутри источника происходит перемещение положительных зарядов от отрицательного полюса источника к положительному. Это перемещение происходит до тех пор, пока сторонние силы не станут равными электростатическим. При переносе заряда эти силы совершают работу. Работа сторонних сил по перемещению заряда компенсирует потери энергии заряженными частицами при их движении по цепи.
Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению положительного заряда к величине этого заряда.
Обозначение – ( varepsilon ), единица измерения в СИ – вольт (В).
Формула для вычисления:
где ( Delta q ) – модуль перенесенного заряда.
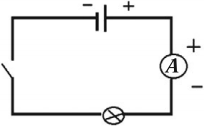
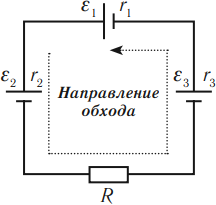
Если электрическая цепь содержит несколько источников тока с ЭДС ( varepsilon_1,varepsilon_2,,…,varepsilon_T ), то суммарная ЭДС ( varepsilon=varepsilon_1+varepsilon_2+…,varepsilon_T ).
ЭДС считается положительной, если направление обхода цепи против часовой стрелки совпадает с переходом внутри источника тока от отрицательного полюса источника к положительному полюсу.
На рисунке: ( varepsilon_1>0,,varepsilon_2<0,,varepsilon_3>0. )
Суммарная ЭДС: ( varepsilon=varepsilon_1-varepsilon_2+varepsilon_3. )
При подключении проводника к полюсам источника тока происходит перераспределение заряда на поверхности проводника, а внутри проводника возникает постоянное электрическое поле. Заряды начинают перемещаться по замкнутой цепи, в которой устанавливается постоянная сила тока.
Сопротивление источника тока называется внутренним сопротивлением.
Обозначение внутреннего сопротивления – ( r ). Единица измерения в СИ – Ом.
Закон Ома для полной электрической цепи
Полная электрическая цепь состоит из источника тока и проводников, представляющих внешнее сопротивление.
Закон Ома для полной электрической цепи
Сила тока в полной цепи прямо пропорциональна ЭДС, действующей в цепи, и обратно пропорциональна полному сопротивлению цепи:
Полное сопротивление – это сумма внутреннего сопротивления источника и сопротивления внешней цепи. Во внешней цепи ток идет по направлению электрического поля, внутри источника тока – против поля.
Напряжение на внешней цепи (падение напряжения):
Если цепь разомкнута, то ток внутри источника не проходит и ( varepsilon=U ).
ЭДС численно равна напряжению на зажимах источника тока (разности потенциалов на полюсах источника).
Сопротивление внешней цепи больше внутреннего сопротивления источника.
Если сопротивление внешней цепи мало ( (R=0) ), то возможно короткое замыкание. Сила тока короткого замыкания: ( I_{кз}=frac{varepsilon}{r} )Возрастание силы тока приводит к резкому увеличению количества теплоты и может стать причиной пожара. Для предотвращения возгорания в электрическую цепь последовательно включают предохранители.
Соединение источников тока
Источники тока можно соединять между собой последовательно и параллельно.
При параллельном соединении положительные полюсы элементов соединяют между собой, отрицательные – между собой. Если ЭДС источников одинаковы, то общая ЭДС ( varepsilon=varepsilon_1 ) (( varepsilon_1 ) – ЭДС одного источника). Величина, обратная общему внутреннему сопротивлению, равна сумме величин, обратных внутренним сопротивлениям элементов: ( frac{1}{r}=frac{1}{r_1}+frac{1}{r_2}+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=frac{r_1}{n} ), ( r_1 ) – сопротивление одного источника, ( n ) – число источников. Сила тока: ( frac{varepsilon}{R+frac{r}{n}} ).
При последовательном соединении положительный полюс источника соединяется с отрицательным полюсом следующего. Общая ЭДС батареи ( varepsilon=varepsilon_1+varepsilon_2+… ), а общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников: ( r=r_1+r_2+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=nr_1 ). Сила тока: ( I=frac{nvarepsilon}{R+nr} ).
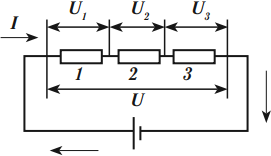
Параллельное и последовательное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
Последовательное соединение проводников
При последовательном соединении начало одного проводника соединяется с концом другого.
При последовательном соединении сила тока во всех проводниках одинакова:
Общее напряжение ( U ) на проводниках равно сумме напряжений на отдельных проводниках:
Напряжение на проводниках прямо пропорционально их сопротивлениям:
Общее сопротивление равно сумме сопротивлений проводников, образующих цепь:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_i ) – сопротивление проводника.
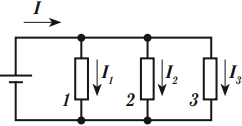
Параллельное соединение проводников
При параллельном соединении проводники подключаются между одной и той же парой точек. Если в этой точке соединяются три и более проводников, то она называется узлом электрической цепи.
При параллельном соединении напряжение на всех проводниках одинаково:
Сумма сил токов, протекающих по проводникам, равна силе тока в неразветвленной цепи:
Это следствие того факта, что в точках разветвления цепи заряды не могут накапливаться.
Силы токов в разветвленных частях цепи обратно пропорциональны их сопротивлениям:
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_1 ) – сопротивление проводника.
Если параллельно соединены два проводника, от общее сопротивление вычисляется по формуле:
Смешанное соединение проводников
Смешанное соединение проводников – соединение, при котором часть проводников соединена последовательно, а часть – параллельно.
Важно!
Чтобы рассчитать общее сопротивление такого участка или найти силу тока и напряжение при таком соединении, нужно:
- разбить его на простые участки с последовательно или параллельно соединенными проводниками;
- найти общее (эквивалентное) сопротивление каждого из этих участков;
- составить эквивалентную схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений;
- рассчитать сопротивление полученной схемы.
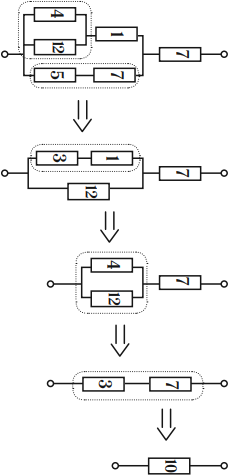
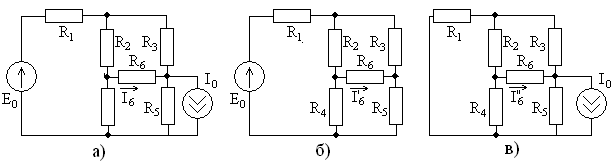
Если в схеме не удается выделить участки с последовательным или параллельным соединением проводников, то можно использовать такое правило: точки с одинаковыми потенциалами можно соединять и разъединять, ток между такими точками не идет.
На рисунке, если ( R_1=R_2,R_4=R_5, ) то потенциалы точек 1 и 2 равны. Резистор ( R_3 ) можно убрать на эквивалентной схеме – ток по нему не идет.
Точки с одинаковыми потенциалами есть в схемах с осью или плоскостью симметрии относительно точек подключения источника тока.
Если схема симметрична относительно оси, проходящей через точки входа и выхода тока, то точки равного потенциала находятся на концах симметричных сопротивлений (по ним идут одинаковые токи).
Если схема симметрична относительно оси, перпендикулярной линии, на которой лежат точки входа и выхода тока, то точки равного потенциала находятся на пересечении этой оси с проводниками.
Если в схеме нет участков с известным видом соединения и нет точек с равным потенциалом, то для расчета таких цепей используют правила Кирхгофа.
Правила Кирхгофа:
- Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
Положительными считают токи, входящие в узел, отрицательными – выходящие из узла.
- В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, имеющихся в контуре:
Порядок расчета цепи:
- выбрать направление токов во всей цепи;
- записать уравнения токов для узлов;
- записать уравнения для выделенных контуров. Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры;
- решить полученную систему уравнений.
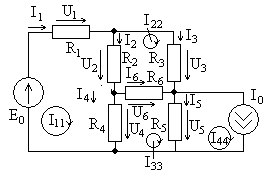
Алгоритм решения задач на определение силы тока, напряжения или сопротивления на участке цепи:
- начертить схему цепи и указать на ней все элементы;
- установить, какие элементы цепи включены последовательно, какие – параллельно;
- расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи;
- используя закон Ома, установить связь между токами, напряжениями и ЭДС;
- если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составить для каждого режима работы цепи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Работа электрического тока. Закон Джоуля–Ленца
Работа тока – работа сил электрического поля, создающего электрический ток.
Работа тока на участке цепи вычисляется по формуле:
Используя формулу закона Ома для участка цепи, можно работу тока вычислить так:
Работа тока в замкнутой цепи находится по формуле:
При протекании постоянного тока по металлическому проводнику электроны сталкиваются с положительными ионами, расположенными в узлах кристаллической решетки. При этом электроны передают им энергию. Это приводит к нагреванию проводника. Количество теплоты, выделяющееся в проводнике за время ( t ), равно:
Эта формула выражает закон Джоуля–Ленца: количество теплоты, выделяющееся при прохождении тока по проводнику, прямо пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.
Мощность электрического тока
Мощность электрического тока равна отношению работы тока ко времени, в течение которого она совершается.
Обозначение – ( P ), единица измерения в СИ – ватт (Вт).
Вычисляется по формуле:
Можно записать еще несколько формул для вычисления мощности электрического тока на участке цепи:
Полная мощность источника тока:
Коэффициент полезного действия источника тока:
При решении задач на тепловое действие тока нужно учитывать следующее:
1. Если на участке есть источник тока, то необходимо использовать для решения формулу закона Джоуля–Ленца:
2. Если сила тока в цепи постоянна, то удобно использовать формулу закона Джоуля–Ленца:
3. Если постоянно напряжение, то формулу:
4. Количество теплоты можно находить, используя формулы термодинамики.
Носители свободных электрических зарядов в металлах, жидкостях и газах
Одним из условий существования электрического тока является наличие свободных заряженных частиц.
Носители электрического тока: в металлах – свободные электроны; в электролитах – положительные и отрицательные ионы; в газах – электроны и положительные ионы; в полупроводниках – электроны и дырки; в вакууме – любые заряженные частицы, но чаще всего это электроны.
Электрический ток в металлах
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. При протекании тока по металлическому проводнику не происходит переноса вещества (опыт Рикке). Это значит, что ионы металла не принимают участия в переносе электрического заряда. Носителями заряда являются частицы одинаковые для всех металлов – электроны.
Сила тока в металлическом проводнике с площадью поперечного сечения ( S ):
где ( q ) – элементарный электрический заряд (заряд электрона), ( n ) – концентрация электронов проводимости, ( v ) – средняя скорость упорядоченного движения электронов.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыты Мандельштама и Папалекси, Стюарта и Толмена). Катушка с большим числом витков проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному гальванометру. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона.
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между положительными ионами, образующими кристаллическую решетку металла.
У некоторых металлов и сплавов обнаружено явление сверхпроводимости. Это явление открыто в 1911 г. Камерлинг-Оннесом. При температурах ниже критической сопротивление проводника становится равным нулю. Значения критической температуры для чистых металлов изменяются в диапазоне от долей кельвина до 30 К. В настоящее время получены вещества с критической температурой 125 К. Сверхпроводящие свойства наблюдаются у ртути, свинца, олова.
Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Явление сверхпроводимости используется для получения сильных магнитных полей
Электрический ток в жидкостях
Жидкости, проводящие электрический ток, называют электролитами. К электролитам относятся водные растворы неорганических кислот, солей и оснований, многие соединения металлов в расплавленном состоянии. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы.
В результате электролитической диссоциации (распада нейтральных молекул на ионы) образуются положительные и отрицательные ионы. При подключении электродов к источнику тока ионы под действием электрического поля начинают упорядоченное движение. Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду).
Электролиз – явление прохождения электрического тока через электролит, сопровождающееся выделением веществ на электродах.
Закон электролиза был экспериментально установлен английским физиком М. Фарадеем в 1833 году.
Масса ( m ) вещества, выделившегося на электроде, прямо пропорциональна заряду ( Q ), прошедшему через электролит:
Величину ( k ) называют электрохимическим эквивалентом.
Электрохимический эквивалент ( k ) равен отношению массы ( m_0 ) иона данного вещества к его заряду ( q_0 ):
где ( M ) – молярная масса вещества, ( n ) – валентность вещества, ( F=eN_A ) – постоянная Фарадея. ( F ) = 96,5·103 Кл/моль.
Постоянная Фарадея численно равна заряду, который нужно пропустить через раствор любого электролита для получения одного моля одновалентного вещества.
Явление электролиза широко применяется в современном промышленном производстве: получение чистых металлов (меди, алюминия), нанесение металлических покрытий (гальваностегия), изготовление копий с матриц (гальванопластика).
Электрический ток в газах
В обычных условиях газы являются диэлектриками, но при определенных условиях газ может стать проводником. Процесс протекания электрического тока через газ называется газовым разрядом. Носители заряда в газе – свободные электроны и ионы. Проводимость в газах смешанная – электронно-ионная.
Свободные носители заряда в газах появляются в процессе ионизации. Ионизация – процесс вырывания электрона из атома. Наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация заряженных частиц.
Ионизацию вызывают нагревание газа, излучение (ультрафиолетовое, рентгеновское или гамма-излучение).
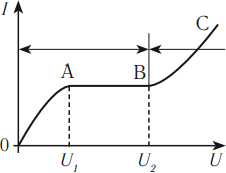
Выделяют два вида разрядов в газе: несамостоятельный и самостоятельный разряды.
Несамостоятельный разряд происходит под действием внешнего ионизатора и прекращается, как только ионизатор перестает действовать. Самостоятельный разряд происходит без действия внешнего ионизатора под действием электрического поля, существующего между электродами. С ростом напряженности электрического поля скорости свободных заряженных частиц растут. Достигая катода, такие частицы выбивают из него электроны (вторичная электронная эмиссия). Эти электроны, разгоняясь полем, вызывают ионизацию других молекул (ионизация электронным ударом). Число заряженных частиц нарастает лавинообразно, и внешний ионизатор не нужен для поддержания тока.
На рисунке участок ОАВ соответствует несамостоятельному разряду, участок ВС – самостоятельному разряду.
Виды самостоятельного разряда:
- тлеющий;
- дуговой;
- коронный;
- искровой.
Тлеющий разряд происходит в разреженном газе при низком давлении. Применяется в газосветных трубках, лампах дневного света, цифровых индикаторах, ртутных лампах низкого давления.
Дуговой разряд – разряд между электродами, нагретыми до высокой температуры при атмосферном или повышенном давлении. Применяется в ртутных лампах высокого давления, при сварке металлов, в электропечах, в источниках света (прожекторах).
Коронный разряд возникает при нормальном и повышенном давлении у заостренных электродов. У острия электрода напряженность электрического поля велика, и в этой области возникает ударная ионизация при атмосферном давлении. Коронный разряд может возникнуть в тонких проводах, находящихся под высоким напряжением. Это приводит к утечке электроэнергии. Применяется в электрофильтрах, громоотводах, счетчике Гейгера–Мюллера.
Искровой разряд – это прерывистый самостоятельный разряд при нормальном или повышенном атмосферном давлении газа в электрическом поле очень большой напряженности. Применяется при обработке металлов. Пример такого разряда в природе – молния.
Плазма – частично или полностью ионизированный газ, в котором плотности отрицательных и положительных зарядов одинаковы. При сильном нагревании любое вещество испаряется, превращается в газ. Если увеличивать температуру и далее, резко усиливается процесс термической ионизации. Молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
В состоянии плазмы находится подавляющая часть вещества Вселенной: звезды, галактические туманности и межзвездная среда. Около Земли плазма существует в виде солнечного ветра и ионосферы. Плазму можно наблюдать в рекламных газовых трубках, кварцевых лампах. За последние годы применение плазмы существенно расширилось. Высокотемпературная плазма (Т ∼ 106–108 К) из смеси дейтерия с тритием используется для осуществления управляемого термоядерного синтеза; низкотемпературная плазма (Т ≤ 105 К) – в различных газоразрядных приборах: газовых лазерах, ионных приборах.
Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
В природе существует большая группа веществ, занимающих промежуточное положение между проводниками и диэлектриками по величине электропроводности.
Полупроводниками называют вещества, удельное сопротивление которых находится в интервале от 10-3 до 107 Ом·м. К типичным полупроводникам относятся германий и кремний, селен, теллур, мышьяк.
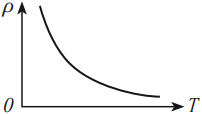
Удельное сопротивление полупроводника зависит от внешних факторов: температуры, освещенности, электрического поля. С ростом температуры удельное сопротивление полупроводника уменьшается. С ростом освещенности также происходит уменьшение сопротивления полупроводника.
Такой ход зависимости удельного сопротивления от температуры ( rho(T) ) показывает, что у полупроводников концентрация свободных носителей заряда не остается постоянной, а увеличивается с ростом температуры. Объясним такую зависимость на примере германия.
Атомы германия на внешней оболочке имеют четыре валентных электрона. В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной, т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум разным атомам. Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах, поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках значительно меньше, чем у металлов. Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.
При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок. Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой восстанавливается электронная связь между атомами германия. Этот процесс называется рекомбинацией. Электронно-дырочные пары могут появляться также при освещении полупроводника за счет энергии электромагнитного излучения. В отсутствие электрического поля электроны проводимости и дырки участвуют в хаотическом тепловом движении.
Если полупроводник поместить в электрическое поле, то в упорядоченном движении участвуют свободные электроны и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток ( I ) в полупроводнике складывается из электронного ( I_Э ) и дырочного ( I_Д ) токов:
Концентрация электронов проводимости в полупроводнике равна концентрации дырок.
Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.
Собственный полупроводник — полупроводник, не содержащий примесей, влияющих на его электропроводность.
При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков.
Важно!
Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.
Примесной проводимостью называют проводимость полупроводников при наличии примесей.
Различают два типа примесной проводимости – электронную и дырочную.
Электронная проводимость
Электронная проводимость возникает при введении в кристалл германия с четырехвалентными атомами пятивалентных атомов (например атомов мышьяка, ( As )).
Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказывается лишним, он легко отрывается от атома мышьяка и становится свободным.
Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки. Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью. В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника.
Основными носителями заряда являются электроны. Концентрация свободных электронов намного больше концентрации дырок. Такая проводимость называется электронной, а полупроводник, обладающий электронной проводимостью, называется полупроводником ( n )-типа.
Дырочная проводимость
Дырочная проводимость возникает при введении в кристалл германия трехвалентных атомов (например атомов индия, ( In )). Атом индия с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия.
Примесь атомов, способных захватывать электроны, называется акцепторной примесью. В результате введения акцепторной примеси в кристалле разрывается множество ковалентных связей и образуются вакантные места – дырки. На эти места могут переходить электроны из соседних ковалентных связей, что приводит к движению дырок по кристаллу.
Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов.
Проводимость такого типа называется дырочной проводимостью. Примесный полупроводник с дырочной проводимостью называется полупроводником p-типа. Основными носителями заряда в полупроводниках p-типа являются дырки.
p-n переход (электронно-дырочный переход) – это область контакта двух полупроводников с разными типами проводимости.
При контакте двух полупроводников n- и p-типов начинается процесс диффузии: дырки из p-области переходят в n-область, а электроны, наоборот, из n-области в p-область. В результате в n-области вблизи зоны контакта уменьшается концентрация электронов и возникает положительно заряженный слой. В p-области уменьшается концентрация дырок и возникает отрицательно заряженный слой. Таким образом, на границе полупроводников образуется двойной электрический слой, поле которого препятствует процессу диффузии электронов и дырок. Пограничная область раздела полупроводников с разными типами проводимости называется запирающим слоем. Объемные заряды этого слоя создают между p- и n-областями запирающее напряжение ( U_З ), приблизительно равное 0,35 В для германиевых n-p-переходов и 0,6 В для кремниевых.
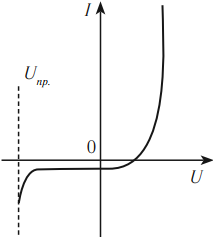
p-n-переход обладает свойством односторонней проводимости. Если полупроводник с p-n-переходом подключен к источнику тока так, что положительный полюс источника соединен с n-областью, а отрицательный – с p-областью, то напряженность поля в запирающем слое возрастает. Дырки в p-области и электроны в n-области будут смещаться от p-n-перехода, увеличивая тем самым концентрации неосновных носителей в запирающем слое. Ток через p-n-переход практически не идет. Напряжение, поданное на p-n-переход, в этом случае называют обратным. Незначительный обратный ток обусловлен только собственной проводимостью полупроводниковых материалов.
Если p-n-переход соединить с источником так, чтобы положительный полюс источника был соединен с p-областью, а отрицательный с n-областью, то напряженность электрического поля в запирающем слое будет уменьшаться, что облегчает переход основных носителей через контактный слой. Дырки из p-области и электроны из n-области, двигаясь навстречу друг другу, будут пересекать p-n-переход, создавая ток в прямом направлении. Сила тока через p-n-переход в этом случае будет возрастать при увеличении напряжения источника.
Способность p-n-перехода пропускать ток практически только в одном направлении используется в приборах, которые называются полупроводниковыми диодами.
Обозначение на схемах полупроводникового диода:
Полупроводниковые диоды изготавливают из кристаллов кремния или германия. Они используются в выпрямителях для преобразования переменного тока в постоянный. Вольт-амперная характеристика полупроводникового диода приведена на рисунке.
Полупроводниковые диоды имеют малые размеры, длительный срок службы, механическую прочность. Существенным недостатком полупроводниковых диодов является зависимость их параметров от температуры.
Основные формулы раздела «Законы постоянного тока»
Законы постоянного тока
3.3 (65%) 64 votes
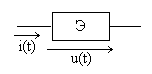
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют
постоянные напряжения и протекают
постоянные токи, то модели реактивных
элементов LиCсущественно упрощаются.
Модель сопротивления
остается прежней и связь между напряжением
и током
определяется законом Ома в виде
.
(3.1)
В идеальной индуктивности мгновенные
значения напряжения и тока связаны
соотношением
.
(3.2)
Аналогично в емкости связь между
мгновенными значениями напряжения и
тока определяется в виде
.
(3.3)
53
Таким образом, в модели цепи постоянного
тока присутствуют только сопротивления
(модели резисторов) и источники сигнала,
а реактивные элементы (индуктивности
и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно
простых цепей с одним источником
сигнала. Он предполагает вычисление
сопротивлений участков цепи, для которых
известна величина тока (или напряжения),
с последующим определением неизвестного
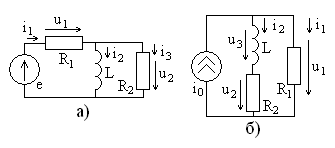
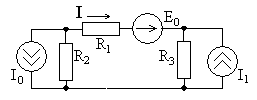
напряжения (или тока). Рассмотрим пример
расчета цепи, схема которой приведена
на рис. 3.1, при токе идеального источникаА
и сопротивленияхОм,
Ом,
Ом.
Необходимо определить токи ветвейи
,
а также напряжения на сопротивлениях,
и
.

ток источника,
тогда можно вычислить сопротивление
цепиотносительно зажимов источника тока
(параллельного соединения сопротивленияи последовательно соединен-
Рис. 3.1. ных
сопротивлений
и
),
.
Тогда напряжение
на источнике тока (на сопротивлении
)
равно
В.
54
Затем можно найти токи ветвей
А,
А.
Полученные результаты можно проверить
с помощью первого закона Кирхгофа в
виде
.
Подставляя вычисленные значения, получимА,
что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти
напряжения на сопротивлениях (величина
уже найдена)
В,
В.
По второму закону Кирхгофа
.
Складывая полученные результаты,
убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе
законов Ома
и Кирхгофа
Общий метод расчета токов и напряжений
в электрической цепи на основе законов
Ома и Кирхгофа пригоден для расчета
сложных цепей с несколькими источниками
сигнала.
Расчет начинается с задания обозначений
и положительных направлений токов и
напряжений для каждого элемента
(сопротивления) цепи.
Система уравнений включает в себя
подсистему компонентных уравнений,
связывающих по закону Ома токи и
напряжения в каждом элементе
(сопротивлении) и подсистему
55
топологических уравнений, построенную
на основе первого и второго законов
Кирхгофа.
Рассмотрим расчет простой цепи из
предыдущего примера, показанной на рис.
3.1, при тех же исходных данных.
Подсистема компонентных уравнений
имеет вид
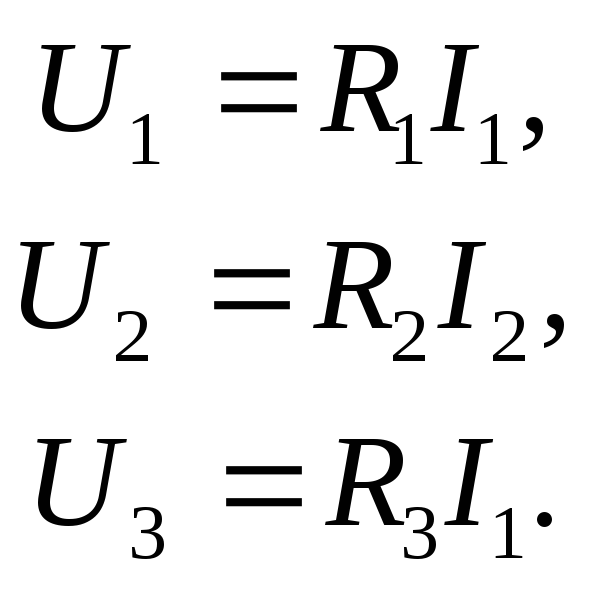
В цепи имеется два узла ()
и две ветви, не содержащие идеальных
источников тока ().
Следовательно, необходимо записать
одно уравнение ()
по первому закону Кирхгофа,
,
(3.5)
и одно уравнение второго закона Кирхгофа
(),
,
(3.6)
которые и образуют подсистему
топологических уравнений.
Уравнения (3.4)-(3.6) являются полной
системой уравнений цепи. Подставляя
(3.4) в (3.6), получим
,
(3.7)
а, объединив (3.5) и (3.7), получим два
уравнения с двумя неизвестными токами
ветвей,
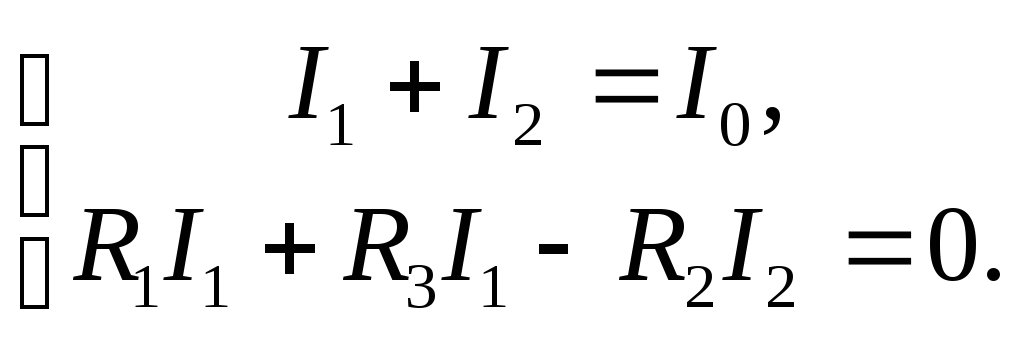
56
Выражая из первого уравнения (3.8) ток
и подставляя его во второе, найдем
значение тока,
А,
(3.9)
а затем найдем
А.
По вычисленным токам ветвей из компонентных
уравнений (3.4) определим напряжения.
Результаты расчета совпадают с полученными
ранее в подразделе 3.2.
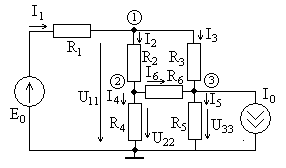
Рассмотрим более сложный пример расчета
цепи в схеме, показанной на рис. 3.2, с
параметрами
Ом,
Ом,
Ом,
Ом,
Ом,
Ом,
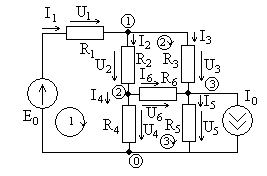
А.
Цепь содержит
узла (их номера указаны в кружках) и
ветвей, не содержащих идеальные источники
тока. Система компонентных уравнений
цепи имеет вид
Рис. 3.2
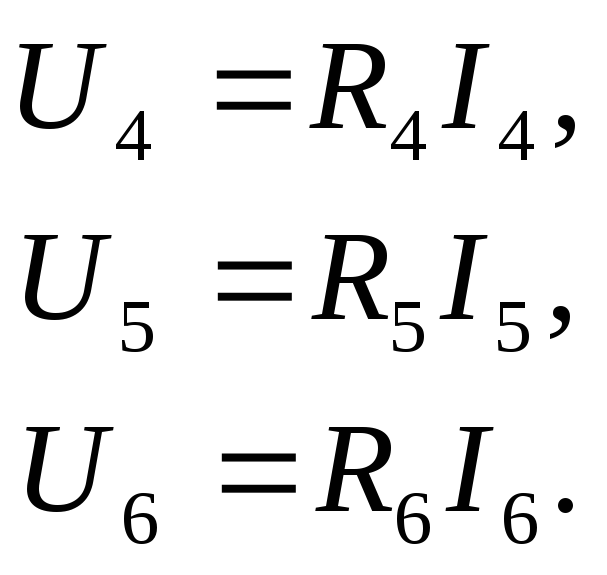
По первому закону Кирхгофа необходимо
записать
уравнения (узел 0 не используется),
57
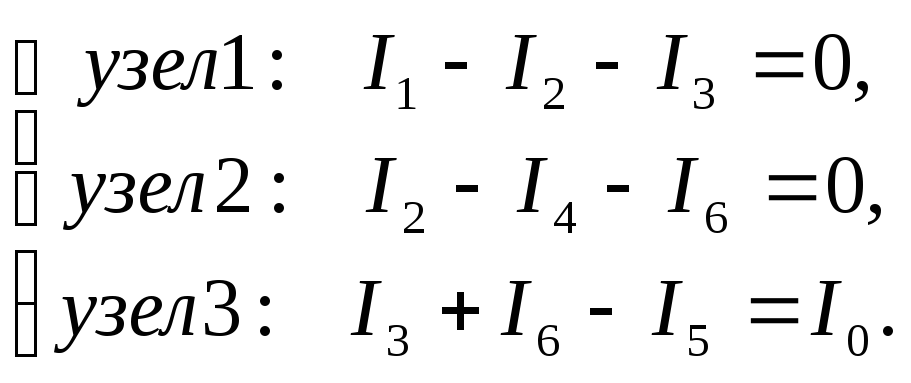
По второму закону Кирхгофа составляется
уравнения для трех независимых контуров,
отмеченных на схеме окружностями со
стрелками (внутри указаны номера
контуров),
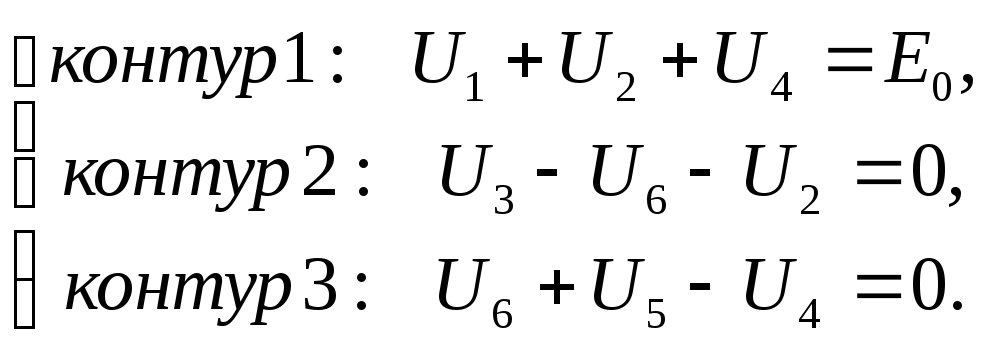
Подставляя (3.11) в (3.13), совместно с (3.12)
получим систему шести
уравнений вида
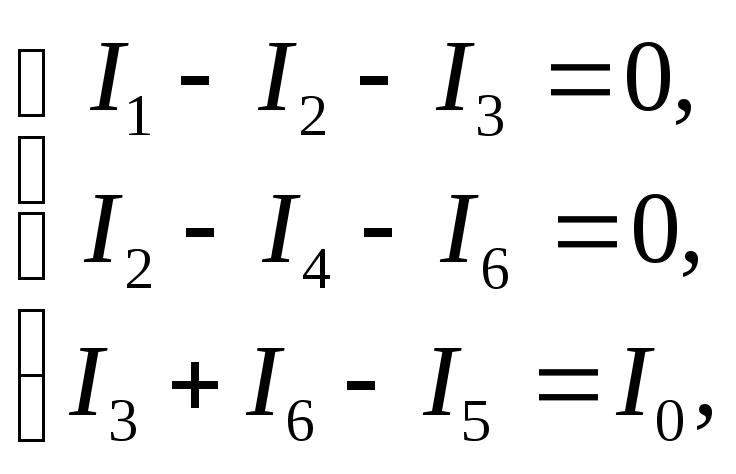
Из второго и третьего уравнений выразим
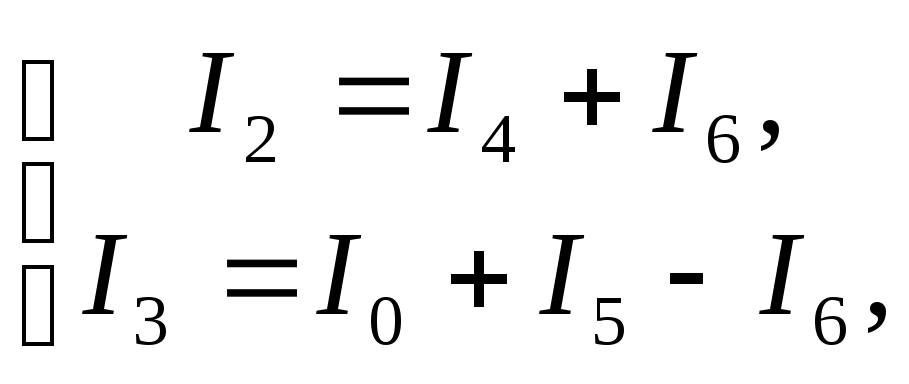
а из первого
,
тогда подставиви
,
получим.
Подставляя токи,
и
в уравнения второго закона Кирхгофа,
запишем систему из трех уравнений
58
которую после приведения подобных
запишем в виде

Обозначим
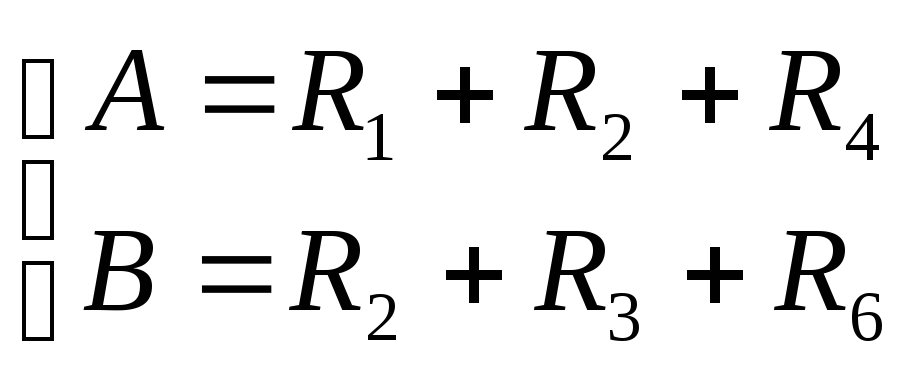
(3.16)
и из третьего уравнения системы (3.15)
запишем
.
(3.17)
Подставляя полученное значение
в первые два уравнения (3.15), получим
систему из двух уравнений вида

Из второго уравнения (3.18) получим
59
,
(3.19)
тогда из первого уравнения найдем ток
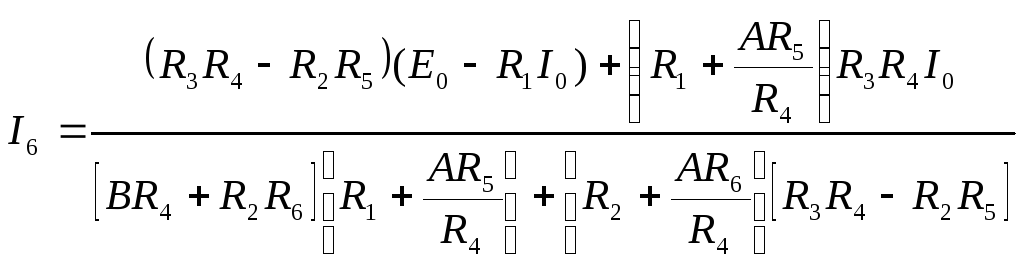
(3.20)
Вычислив
,
из (3.19) найдем,
из (3.17) вычислим,
а затем из уравнений подстановки найдем
токи,
,
.
Как видно, аналитические вычисления
достаточно громоздки, и для численных
расчетов целесообразней использовать
современные программные пакеты, например,
MathCAD2001. Пример программы
показан на рис. 3.3.
Матрица — столбец
содержит значения токов
А,
А,
А.
Остальные
токи вычисляются согласно уравнениям
(3.14) и равны
А,
А,
А.
Вычисленные значения токов совпадают
с полученными по приведенным выше
формулам.
Общий метод расчета цепи по уравнениям
Кирхгофа приводит к необходимости
решения
линейных алгебраических уравнений. При
большом числе ветвейвозникают математические и вычислительные
трудности. Это означает, что целесообразно
искатьметоды расчета, требующие
составления и решения меньшего числа
уравнений.
60
Рис. 3.3
3.4. Метод контурных токов
Метод контурных токов базируется
на уравненияхвторого закона
Кирхгофаи приводит к необходимости
решенияуравнений,
—
число всех ветвей, в том числе и содержащих
идеальные источники тока.
В цепи выбираются
независимых контуров и для каждого
-го
из них вводится кольцевой (замкнутый)
контурный ток(двойная индексация позволяет отличать
кон-
61
турные токи от токов ветвей). Через
контурные токи можно выразить все токи
ветвей и для каждого независимого
контура записать уравнения второго
закона Кирхгофа. Система уравнений
содержит
уравнений, из которых определяются все
контурные токи. По найденным контурным
токам находятся токи или напряжения
ветвей (элементов).
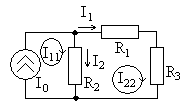
пример цепи на рис. 3.1. На рис 3.4 приведена
схема с указанием обозначений и
положительных направлений двух контурных
токови
(
,
,
).
Рис. 3.4 Через
ветвь
проте-
кает только
контурный ток
и его направление совпадает с
,
поэтому ток ветвиравен
.
(3.21)
В ветви
протекают два контурных тока, ток
совпадает по направлению с
,
а токимеет противоположное направление,
следовательно
.
(3.22)
Для контуров, не содержащих идеальные
источники тока, составляем уравнения
второго закона Кирхгофа с использованием
закона Ома, в данном примере записывается
одно уравнение
.
(3.23)
Если в контур включен идеальный
источник тока, то для него
62
уравнение второго закона Кирхгофа не
составляется, а его контурный ток
равен току источника с учетом их
положительных направлений, в рассматриваемом
случае
.
(3.24)
Тогда система уравнений принимает вид
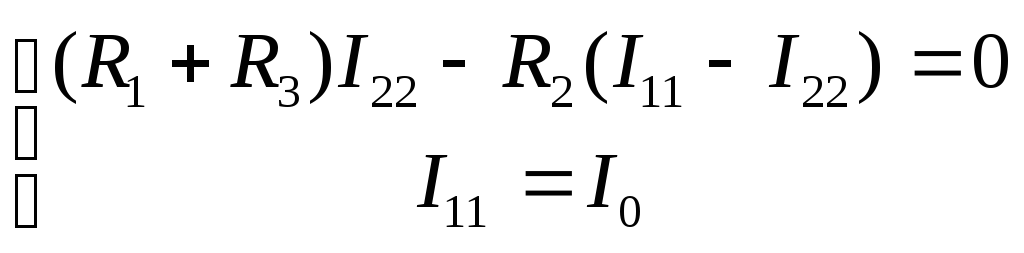
(3.25)
В результате подстановки второго
уравнения в первое получим
,
(3.26)
тогда ток
равен
А,
(3.27)
а ток
А.
Из (3.21)А,
а из (3.22) соответственноА,
что полностью совпадает с полученными
ранее результатами. При необходимости
по найденным значениям токов ветвей по
закону Ома можно вычислить напряжения
на элементах цепи.
Рассмотрим более сложный пример цепи
на рис. 3.2, схема которой с заданными
контурными токами показана на рис. 3.5.
В этом случае число ветвей
,
количество узлов,
тогда число независимых контуров и
уравнений по методу контурных токов
равно.
Для токов ветвей можно записать
63
Рис. 3.5

Первые три контура не содержат идеальных
источников тока, тогда с учетом (3.28) и
использованием закона Ома для них можно
записать уравнения второго закона
Кирхгофа,
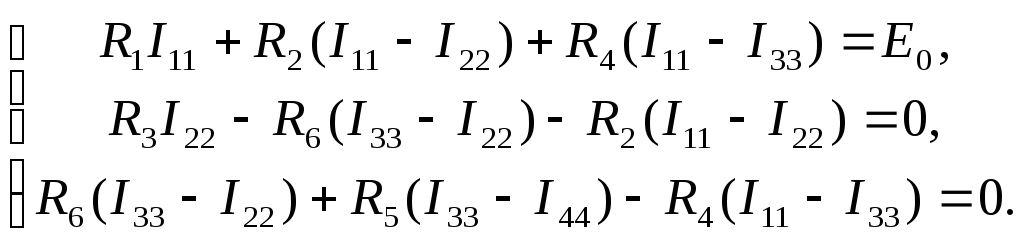
В четвертом контуре присутствует
идеальный источник тока, поэтому для
него уравнение второго закона Кирхгофа
не составляется, а контурный ток равен
току источника (они совпадают по
направлению),
.
(3.30)
Подставляя (3.30) в систему (3.29), после
преобразования получим три уравнения
для контурных токов в виде
64

Систему уравнений (3.31) можно решить
аналитически (например, методом
подстановки – проделайте это),
получив формулы для контурных токов, а
затем из (3.28) определить токи ветвей.
Для численных расчетов удобно использовать
пакет программMathCAD, пример
программы показан на рис. 3.6. Результаты
вычислений совпадают с расчетами,
приведенными на рис. 3.3. Как видно, метод
контурных токов требует составления и
решения меньшего числа уравнений по
сравнению с общим методом расчета по
уравнениям Кирхгофа.
Рис. 3.6
65
3.5. Метод узловых напряжений
Метод узловых напряженийбазируется
на первом законе Кирхгофа, при этом
число уравнений равно.
В цепи выделяются все
узлов и один из них выбирается в качествебазисного, которому присваивается
нулевой потенциал. Потенциалы (напряжения)…
остальных
узлов отсчитываются от базисного, их
положительные направления обычно
выбираются стрелкой в базисный узел.
Через узловые напряжения с использованием
закона Ома и второго закона Кирхгофа
выражаются токи всех ветвей
и для
узлов записываются уравнения первого
закона Кирхгофа.

пример цепи, показанной на рис. 3.1, для
метода узловых напряжений ее схема
показана на рис. 3.7. Нижний узел обозначен
как базисный (для этого используется
символ «земля» — точка нулевого
потенциала), напряжение верхнего узла
относительно базисного обо-
Рис. 3.7 значено как
.
Выразим через
него токи
ветвей
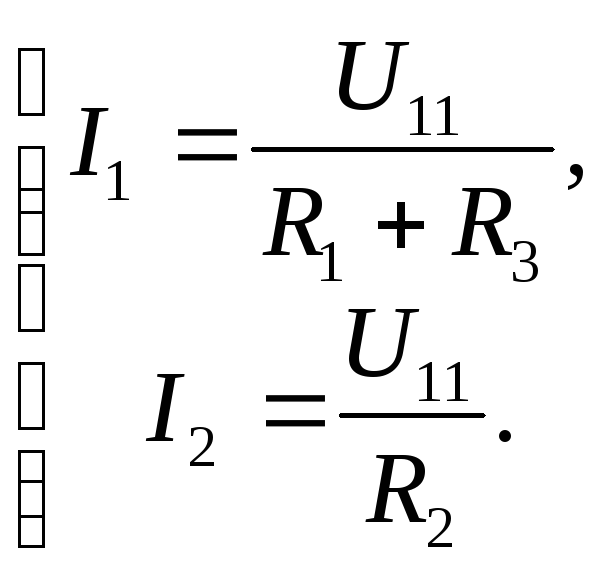
По первому закону Кирхгофа с учетом
(3.32) запишем единственное уравнение
метода узловых напряжений (),
66
.
(3.33)
Решая уравнение, получим
,
(3.34)
а из (3.32) определим токи ветвей
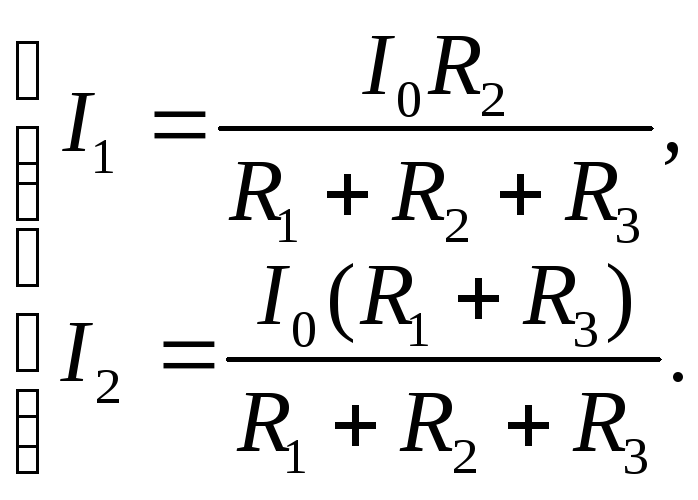
Полученные результаты совпадают с
полученными рассмотренными ранее
методами.
более сложный пример цепи, показанной
на рис. 3.2 при тех же исходных данных, ее
схема показана на рис. 3.8. В цепиузла, нижний выбран базисным, а три
остальные обозначены номерами в кружках.
Введены
положительные на- Рис.
3.8
правления и обозна-
чения узловых напряжений
,
и
.
По Закону Ома с использованием второго
закона Кирхгофа определим токи ветвей,
67
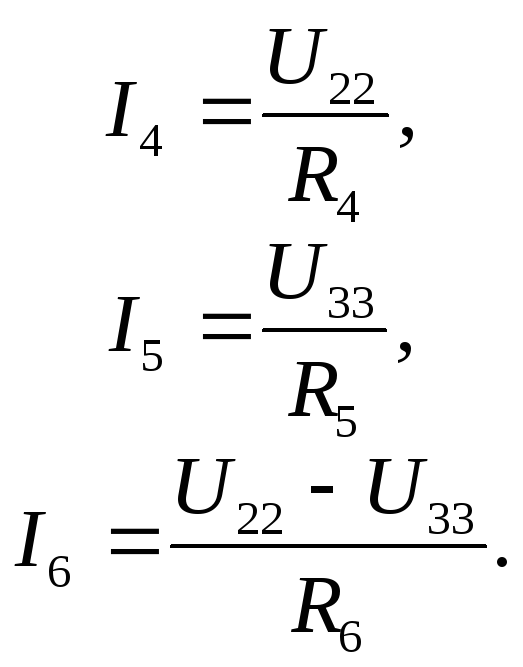
По первому закону Кирхгофа для узлов
с номерами 1, 2 и 3 необходимо составить
три уравнения,
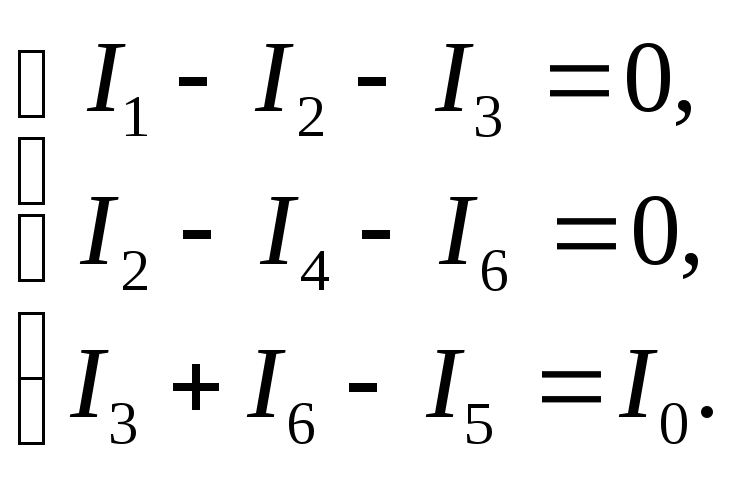
Подставляя (3.36) в (3.37), получим систему
уравнений метода узловых напряжений,

После преобразования и приведения
подобных получим

68
Программа расчета узловых напряжений
и токов ветвей приведена на рис. 3.9. Как
видно, полученные результаты совпадают
с полученными ранее другими методами
расчета.
Проведите аналитический расчет узловых
напряжений, получите формулы для токов
ветвей и вычислите их значения.
Рис. 3.9
69
3.6. Метод наложения
Метод наложениязаключается в
следующем.
Расчет проводится следующим образом.
В цепи, содержащей несколько источников,
поочередно выбирается каждый из них, а
остальные отключаются. При этом образуются
цепи с одним источником, число которых
равно количеству источников в исходной
цепи. В каждой из них проводится расчет
искомого сигнала, а результирующий
сигнал определяется их суммой. В качестве
примера рассмотрим расчет тока
в цепи, показанной на рис. 3.2, ее схема
показана на рис. 3.10а.
Рис. 3.10
70
При выключении идеального источника
тока (его цепь разрывается) получается
цепь, показанная на рис. 3.9б, в которой
любым из рассмотренных методов
определяется ток
.
Затем выключается идеальный источник
напряжения (он заменяется коротким
замыканием) и получается цепь, показанная
на рис. 3.9а, в которой находится ток
.
Искомый токравен
.
Проведите аналитические и численные
расчеты самостоятельно, сравните с
полученными ранее результатами, например,
(3.20).
3.7. Сравнительный анализ методов расчета
Метод расчета, основанный
на законе Ома, пригоден для сравнительно
простых цепей с одним источником. Его
нельзя использовать для анализа цепей
сложной структуры, например, мостового
типа вида рис.3.9.
Общий метод расчета цепи на основе
уравнений законов Ома и Кирхгофа
универсален, но требует составления и
решения системы из
уравнений, которая легко преобразуется
в систему изуравнений. При большом числе ветвей
резко возрастают вычислительные затраты,
особенно при необходимости аналитических
расчетов.
Методы контурных токов и узловых
напряжений более эффективны, так как
приводят к системам с меньшим числом
уравнений, равным соответственно
и
.
При условии
или
(3.40)
метод контурных токов эффективнее, а
иначе целесообразно применять метод
узловых напряжений.
71
Метод наложения удобен, когда при
отключении источников происходит резкое
упрощение цепи.
В системах схемотехнического моделирования
цепей, например, MicroCAPилиOrCADв основном применяют
метод узловых напряжений.
3.8. Задания для самостоятельного решения
Задание 3.1 С помощью
закона Ома определите напряжениев цепях, схемы которых показаны на рис.
3.11 приВ,
мА,
кОм,
кОм,
кОм.
Рис. 3.11
Задание 3.2Общим методом расчета
на основе законов Ома и Кирхгофа
определите токв цепях, схемы которых показаны на рис.
3.11 приВ,
В,
мА,
мА,
кОм,
кОм,
кОм.
Задание 3.3Методами контурных токов,
узловых напряжений и наложения определите
токв цепях, схемы которых показаны на рис.
3.12, параметры цепи возьмите из задания
3.1, сравните полученные результаты.
72
Рис. 3.12
3.4.Методами контурных токов и узловых
напряжений определите токв цепи, схема которой показана на рис.
3.13 приВ,
мА,
мА,
кОм,
кОм,
кОм.
Рис. 3.13
Задание 3.5. Общим методом расчета,
методами контурных токов и узловых
напряжений определите в цепи рис. 3.14
напряжениепри
мА
кОм,
кОм,
кОм,
кОм,
кОм.
Проведите сравнительный анализ
методов расчета.
Рис. 3.14
73
4. ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ
В ЛИНЕЙНЫХ ЦЕПЯХ
4.1. Гармонические ток и напряжение в
элементах цепи
В элементах цепи R,L,
иCвзаимосвязь произвольных
мгновенных значений тока и напряжения
определяется законом Ома, необходимые
соотношения приведены в табл. 1.1.
элементе Э (рис. 4.1) в виде
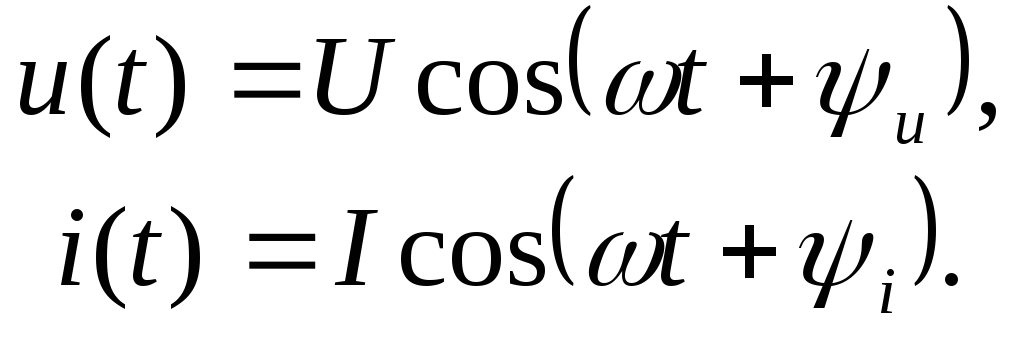
Рис. 4.1
Для сопротивления Rможно записать
.
(4.2)
Сравнивая полученный результат с
выражением для напряжения из (4.1), получим
выражение закона Ома для амплитуд тока
и напряжения.
,
(4.3)
и соотношение для начальных фаз
.
(4.4)
Как видно из (4.3), амплитуды
(и действующие значения) гармонических
тока и напряжения в сопротивлении
связанызаконом Омав классической
формулировке прямой пропорциональности.
74
Начальные фазы тока
и напряжения
в сопротивленииодинаковы, сдвиг
фазмежду напряжением и током равен нулю,
.
(4.5)
Мгновенная мощность (1.6) гармонических
сигналов в сопротивлении равна
,
(4.6)
где
.
Ее зависимость от времени показана на
рис. 4.2. Величинавсегда положительна, то есть
сопротивление толькопотребляет
мощностьот источника сигнала. Это
гармоническая функция времени с
периодом по-
вторения в два раза меньше пе-
Рис. 4.2
риода сигнала.
Средняя мощность (1.8) гармонических
сигналов в сопротивлении определяется
выражением
,
(4.7)
где
и
— действующие значения тока и напряжения,
.
(4.8)
75
Это значение показано пунктирной линией
на временной диаграмме рис. 4.2.
В емкости Cмгновенные значения тока и напряжения
связаны соотношением (табл.1.1)
.
(4.9)
После преобразования тригонометрической
функции к канонической форме гармонического
сигнала получим
.
(4.10)
Сравнивая (4.10) с формулой тока из (4.1),
можно записать
,
(4.11)
.
(4.12)
Введем обозначения
,
(4.13)
,
(4.14)
где
—модуль реактивного сопротивления
емкости (Ом), а—реактивная проводимость емкости
(См=1/Ом). Позднее увидим, что реактивное
сопротивление емкостиотрицательно.
Из (4.11) получим уравнения связи амплитуд
(и действующих значений) гармоническихтока и напряжения в емкости
76
,
(4.15)
которые представляют собой выражение
закона Омадля емкости в классической
формулировке прямой пропорциональности.
Из (4.12) следует, что гармонический ток
в емкости опережает по фазе приложенное
к ней напряжение(напряжение отстает
по фазе от тока) на уголрадиан или 900. Сдвиг фаз между
напряжением и током в емкости равен
.
(4.16)
На рис. 4.3 показаны временные диаграммы
тока и напряжения в емкости. Ток
опережает по фазе напряжение на 900,
что отражается навременной
диаграмме смещением
кривой тока влево на чет-
Рис. 4.3
верть периода.
Мгновенная мощность в емкости из (4.1) и
(4.9) равна
,
а после тригонометрических преобразований
получим
.
(4.17)
Временная диаграмма мгновенной мощности
показана на рис. 4.4
77
мощность электрических сигналов в
емкости может быть положительной
(емкость накапливает энергию электрического
поля) и отрицательной (емкость отдает
во внешнюю цепь ранее накопленную
энергию).Средняя мощность гармонических
сигналов в емкости равна нулю, то
Рис. 4.4 есть емкость
не потребляет мощ-
ность
от гармонического источника.
Для индуктивности Lмгновенные значения тока и напряжения
связаны соотношением закона Ома из
табл.1.1, тогда с учетом выражения для
тока из (4.1) получим
,
а после преобразований
.
(4.18)
Сравнивая (4.18) с выражением для напряжения
(4.1), получим уравнения связи для амплитуд
(действующих значений) тока и напряжения
(4.19)
и их начальных фаз
.
(4.20)
Введем обозначения
78
,
(4.21)
,
(4.22)
где
—реактивное сопротивление индуктивности
(Ом), а—модуль реактивной проводимости
индуктивности (См=1/Ом). Позднее увидим,
что реактивная проводимость индуктивностиотрицательна.
Тогда получим выражения закона Омадля амплитуд (действующих значений)
тока и напряжения в индуктивности
.
(4.23)
Согласно (4.20) гармонический ток в
индуктивности отстает по фазе от
напряжения(напряжение опережает по
фазе ток) на уголрадиан или 900. Сдвиг фаз между
напряжением и током в индуктивности
равен
.
(4.24)
Временные диаграммы тока и напряжения
в индуктивности показаны на рис. 4.5. В
отличие от аналогичных графиков для
емкости на рис. 4.3 ток и напряжение
меняются
местами, кривая напряже-
Рис. 4.5
ния смещена вправо отно-
сительно тока на четверть периода, что
соответствует опережению по фазе на
900.
79
Мгновенная мощность гармонических
сигналов в индуктивности равна
,
(4.25)
а после тригонометрических преобразований
получим
.
(4.26)
Временная диаграмма мгновенной мощности
в индуктивности совпадает с показанной
на рис. 4.4 для емкости.
Средняя мощность гармонических
сигналов в индуктивности (как и в емкости)
равна нулю, то есть индуктивность не
потребляет мощность
от гармонического источника.
В табл. 4.1 приведены сводные результаты
для гармонических сигналов в элементах
цепи.
Таблица 4.1
|
Элемент |
Ток |
Напряжение |
Средняя мощность |
|
R |
|
|
|
|
C |
|
|
|
|
L |
|
|
|
4.2. Средняя мощность гармонических
сигналов в
линейном двухполюснике
Рассмотрим двухполюсник
(ДП) на рис. 4.6, через который протекает
гармонический токи к которому приложе-
80
но напряжение
вила (4.1).
мощность равна
(4.27)
а после тригонометрических преобра-
Рис.4.6
зований получим
.
(4.28)
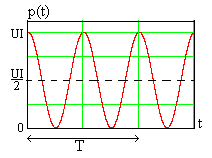
Как видно, мгновенная мощность изменяется
по гармоническому закону с частотой
и содержит постоянную составляющую.
Средняя мощность равна
,
(4.29)
где
— сдвиг фаз между напряжением и током.
Величинуназываюткоэффициентом мощности.
Как видно, потребляемая двухполюсником
мощность определяется амплитудами
(действующими значениями) тока и
напряжения и коэффициентом мощности.
Для максимизации потребляемой мощности
(например, электродвигателем) необходимо
обеспечить условие
,
то есть нулевой сдвиг фаз между напряжением
и током ().
Это означает, что двухполюсник должен
вести себя как сопротивление.
В чисто реактивной цепи, содержащей
только индуктивности и емкости, сдвиг
фаз
,
при этом потребляемая мощность будет
рана нулю при любых амплитудах тока и
81
напряжения.
Полученное выражение (4.29) для средней
мощности полностью согласуется со
значениями
в элементах цепиR,LиC(табл. 4.1), так как в
сопротивлении,
а в индуктивности и емкости.
4.3. Тригонометрический метод расчета
Тригонометрический метод
расчета гармонических токов и напряжений
в линейной цепи базируется на законах
Ома и Кирхгофа для мгновенных значений
сигналов в тригонометрической форме.
качестве примера рассмотрим цепь на
рис. 4.7 при,
В,
рад/с,
,
кОм
инФ.
Обозначим гармонический токв виде
Рис. 4.7
,
(4.30)
тогда с учетом свойств гармонических
напряжений в сопротивлении и емкости
на основе второго закона Кирхгофа
получим
.
(4.31)
82
Левая часть (4.31) может быть преобразована
в тригонометрическую функцию,
,
(4.32)
тогда, уравнивая коэффициенты в правой
и левой частях уравнения, получим
,
(4.33)
.
(4.34)
Из полученных выражений нетрудно
определить амплитуду и начальную фазу
тока в цепи,

.
При найденном токе нетрудно определить
напряжение
на емкости (проведите расчет
самостоятельно).
Как видно, тригонометрический метод
требует суммирования гармонических
функций с неизвестными параметрами,
что приводит к громоздким расчетам,
если число слагаемых функций более
двух. Этот метод применим для расчета
очень простых цепей.
83
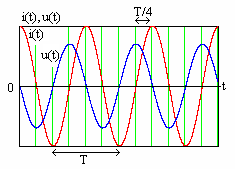
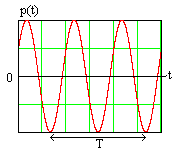
4.4. Векторная диаграмма цепи
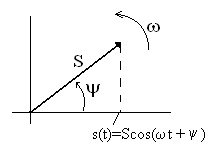
сигналможно представить проекцией на
горизонтальную ось вектора, вращающегося
против часовой стрелки вокруг начала
координат с круговой (угловой) частотой,
как показано на рис. 4.8. Длина (модуль)
вектора равна амплитуде гармонического
сигналаи в момент начала вращения (при
)
угол его наклона к горизонтальной
Рис. 4.8 оси равен
начальной фазе сиг-
нала
(отсчет положительных значений проводится
против часовой стрелки).
Все гармонические токи и напряжения в
цепи с одинаковой частотой, равной
частоте источников сигнала, можно
представить совокупностью синхронно
вращающихся векторов вида рис. 4.8. Так
как все векторы вращаются синхронно и
между ними сохраняются амплитудные и
угловые соотношения, то вращение можно
остановить и рассматривать неподвижную
совокупность векторов. Если вращение
остановлено в момент времени
,
то угол наклона каждого вектора к
горизонтальной оси равен начальной
фазе соответствующего вектору
гармонического сигнала.
84
Для векторного представления гармонических
сигналов выполняются законы Кирхгофав классической формулировке.
В качестве примера рассмотрим векторную
диаграмму цепи, показанной на рис. 4.7.
Результаты ее расчета тригонометрическим
методом приведены в табл. 4.2 (проведите
соответствующие расчеты).
Таблица 4.2
|
Сигнал |
Амплитуда |
Начальная фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
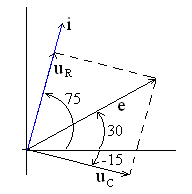
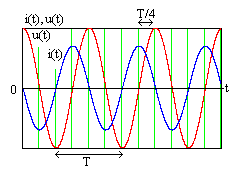
диаграмма цепи приведена на рис. 4.9.
Векторы тока и напряжений построены по
данным табл. 4.2, длина вектора равна
амплитуде сигнала, а угол отклонения
от горизонтальной оси равен начальной
фазе (отсчет положительных значений
угла против часовой стрелки). Вектор
токасовпадает по направлению с вектором
напряженияна сопротивлении, их длины (модули)
не одинаковы, так как масштабы
Рис. 4.9
штабы (например, В/см и мА/см)
токов и напряжений различны (ток и
напряжение не сравнимы между собой).
Напряжение на сопротивлении
опережает по фазе напряжение на емкости
на 900. Это обусловлено тем, что в
85
последовательной цепи рис. 4.7 через
сопротивление и емкость протекает один
и тот же ток, причем напряжение на
сопротивлении совпадает по фазе с током,
а на емкости – отстает по фазе от тока
на 900.
Сумма векторов напряжений на сопротивлении
и емкости в цепи рис. 4.7 по второму закону
Кирхгофа (в векторной форме) равна ЭДС
источника, что и показано на векторной
диаграмме рис. 4.9.
Как видно, векторная диаграмма цепи
может быть построена по результатам
расчета всех гармонических токов и
напряжений. Однако ее можно построить
«качественно» (без знания точных
параметров векторов, но с правильными
соотношениями между ними) и не проводя
численных расчетов.
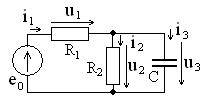
примерRCцепи, показанной
на рис. 4.10, в которой заданы положительные
направления и условные обозначения
всех токов и напряжений.
Прежде всего, необходимо проанализироватьструктуру цепи. В ней присутствует
Рис. 4.10 параллельный
фрагмент (со-
единение
элементов CиR2),
который соединен последовательно с
сопротивлениемR1и источником напряжения.
Тогда построение необходимо начать с
напряжения на параллельном фрагменте,
при этом,
этот вектор проведем произвольно по
модулю и направлению, например,
горизонтально, векторная диаграмма
показана на рис. 4.11.
Ток
совпадает по фазе с напряжениями
,
а токопережает их по фазе на 900.
Соответствующие векторы изображены на
диаграмме рис. 4.11 с произвольной длиной
и указанными угловыми соотношениями
относительно вектора
86
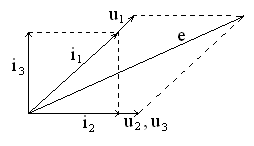
Векторная сумма этих токов по первому
закону Кирхгофа равна току,
то есть этот вектор строится исходя из
векторови
.
Вектор напряженияна сопротивленииR1совпадает по направлению с вектором
токаи имеет произвольную длину, а вектор
ЭДСпо второму закону Кирхгофа Кирхгофа
равен Рис. 4.11
сумме векторов
и
.
На этом построение «качественной»
векторной диаграммы цепи заканчивается.
Если цепь содержит последовательный
фрагмент, входящий в смешанное соединение,
то построение целесообразно начинать
с вектора тока этого фрагмента.
Векторная диаграмма электрической
цепи может использоваться для иллюстрацииамплитудных и фазовых соотношений между
токами и напряжениями, и для формированияаналитических выражений, связывающих
их амплитуды (действующие значения) и
начальные фазы.
Например, для диаграммы рис. 4.11 амплитуды
(действующие значения) токов
,
и
по теореме Пифагора связаны выражением
.
Для других соотношений можно использовать
теорему косинусов (пример приведите
самостоятельно).
Для сложной цепи построение «качественной»
векторной диаграммы требует вдумчивого
подхода при выборе начального вектора
и способов построения остальных векторов.
87
4.5. Особенности расчета цепи с
гармоническими
сигналами
Мгновенные значения токов и напряжений
в электрической цепи связаны между
собой уравнениями законов Ома и Кирхгофа.
Последние предполагают суммирование
гармонических функций времени с
неизвестными амплитудами и начальными
фазами, например, с помощью теоремы
косинусов, а это приводит к громоздким
расчетам даже в относительно простых
цепях.
Существенно упростить расчеты можно,
отказавшись от описания сигналов с
помощью тригонометрических функций
времени и заменив его числами, на
зависящими от времени. На эту возможность
указывает векторная диаграмма цепи,
которая полностью отражает свойства
гармонических сигналов и не зависит от
времени.
Известно, что вектор, выходящий из
начала координат, можно представить
комплексным числом. Таким образом, в
теории электрических цепей при расчете
гармонических процессов возникает
метод комплексных амплитуд.
4.6. Расчет средней (потребляемой) мощности
По результатам расчета гармонических
токов и напряжений можно определить
мощность, потребляемую цепью от источника
сигнала.
В качестве примера используем цепь на
рис. 4.7, результаты расчета приведены в
табл. 4.2. Рассматривая цепь относительно
зажимов источника как двухполюсник,
при амплитуде напряжения
В,
токамА
и сдвиге фаз между ними,
получим
мВт.
88
С другой стороны, в рассматриваемой
цепи емкость не потребляет мощность
гармонического сигнала, и она может
выделяться только в сопротивлении.
Тогда получим
мВт.
Как видно результаты совпадают.
Если в цепи имеется несколько
сопротивлений, то общая потребляемая
цепью мощность будет равна сумме
мощностей, потребляемых каждым
сопротивлением в отдельности.
4.7. Задания для самостоятельного решения
Задание 4.1. Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепей, показанных на рис. 4.12, приВ,
мА,
кОм,
мГн
инФ.
Рис. 4.12
По результатам расчета постройте полные
векторные диаграммы цепей, проверьте
выполнимость законов Кирхгофа.
Задание 4.2.Постройте «качественные»
векторные диаграммы цепей, показанных
на рис. 4.12. Сравните их с расчетными
диаграммами из задания 4.1.
89
Задание 4.3.Определите мощность,
потребляемую от источника сигнала в
цепях, показанных на рис. 4.12. Проведите
расчеты, рассматривая цепь как двухполюсник
или выделив в ней энергопотребляющие
элементы.
Задание 4.4.Постройте «качественные»
полные векторные диаграммы цепей,
показанных на рис. 4.13.
Рис. 4.13
Задание 4.5.Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепи, показанной на рис. 4.10, прикОм,
нФ
иВ.
Постройте полную векторную диаграмму
цепи, сравните ее с приведенной на рис.
4.11. Определите мощность, потребляемую
цепью от источника.
90
На этой странице вы узнаете
- Что общего у электрического тока с водой?
- В чем отличие сопротивления от удельного сопротивления?
- Почему нежелательно использовать телефон, подключенный к зарядке?
- Фамилия какого ученого стоит миллион?
«Все, кина не будет. Электричество кончилось». Наверное, никого не оставит равнодушным популярная фраза из широко известного фильма «Джентльмены удачи». Ведь действительно: бесит, когда сидишь за просмотром любимого сериальчика, вдруг — бамс! Вырубили свет, и зарядки ноута, как назло, не хватило. И не выработаешь электричество в домашних условиях, а жаль… Но вот понять, как оно работает — это мы сможем сделать в статье.

Электрический ток
В наше время трудно себе представить жизнь без электричества. Телевизор не посмотреть, телефон не зарядить, чай не попить… Ни один электроприбор в доме не будет работать без электричества. А объявление об отключении электроэнергии, вызывает тихий ужас.
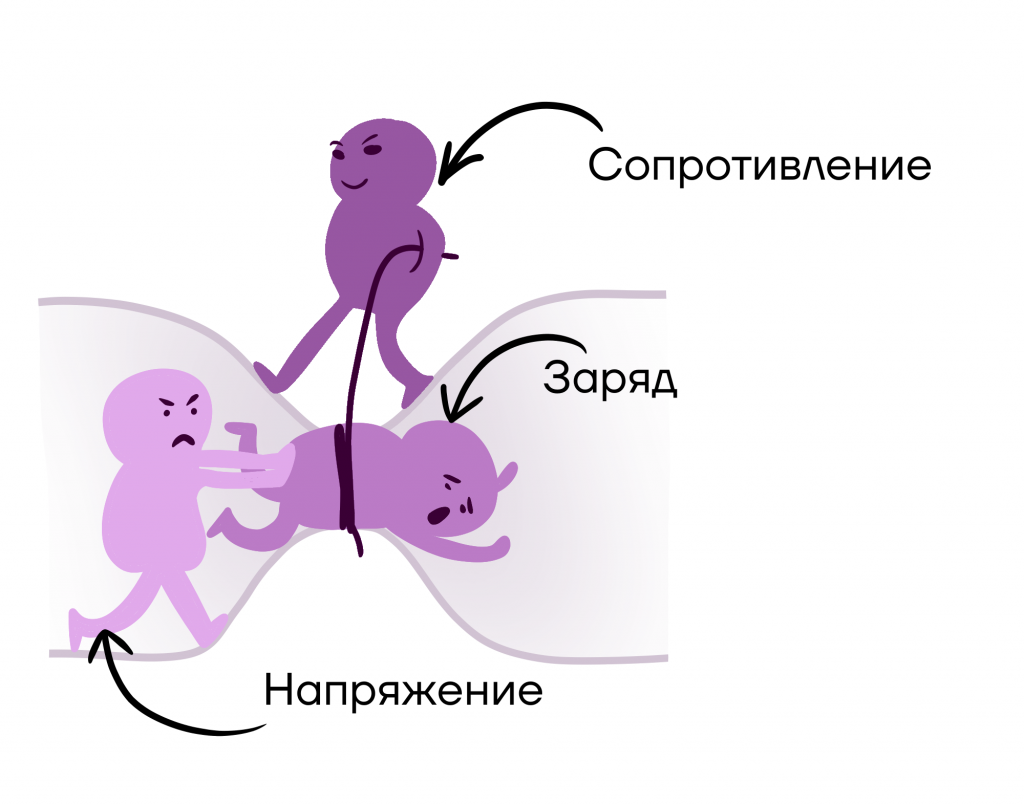
Электричество — это форма энергии, которая существует в виде статических или подвижных электрических зарядов.
Поток. И то и другое представляет собой направленное движение частиц. Из чего состоит вода? Из молекул. Когда эти молекулы движутся в одном направлении, то они образуют поток воды, который течет, например, по трубам.
Так же и электрический ток. Он образуется потоком заряженных частиц, которые движутся по проводам.
Сформулируем определение:
Электрический ток — это упорядоченное движение заряженных частиц.
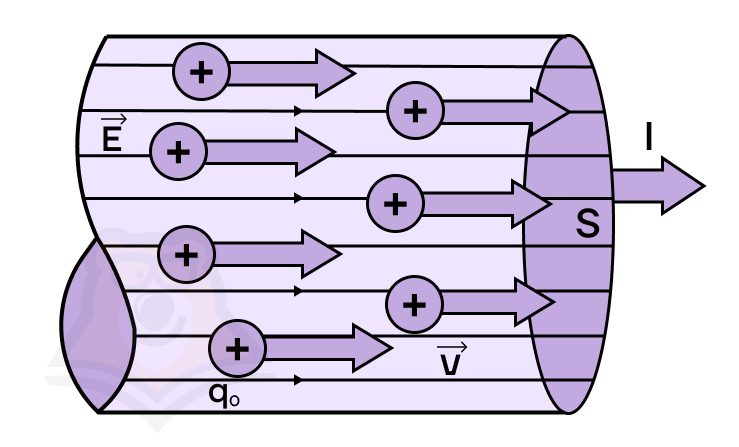
Чтобы электрический ток существовал, необходимо выполнение следующих условий:
- наличие свободных заряженных частиц;
- наличие электрического поля;
- наличие замкнутой электрической цепи.
Основными количественными характеристиками электрического тока являются сила тока и напряжение.
Напряжение
Чтобы внутри цепи существовал электрический ток, цепь должна быть замкнута и между концами участка цепи должно существовать напряжение.
Напряжение — скалярная (не имеющая направления) физическая величина, значение которой равно работе тока на участке цепи, совершаемой при переносе единичного электрического заряда из одной точки в другую.
U — напряжение (В),
A — работа тока на участке цепи (Дж),
q — электрический заряд (Кл).
Единица измерения U — В (Вольт) = (frac{Дж}{Кл})

Электрический ток – результат “труда” множества частиц. Они любят работать – не ленятся перемещаться из одного конца цепи в другой. И чем больше они будут работать, тем большее напряжение получится. Так запоминаем связь напряжения (U) с работой (A).
Услышав слова из известной песни Димы Билана «Это ты, это я, между нами молния, С электрическим разрядом 220 Вольт…» любой физик (и электрик) приобретает новую пару седых волосинок. Такое напряжение очень опасно для человека. Однако, 220 Вольт — это то самое напряжение в наших розетках!
Прибор для измерения напряжения — вольтметр. Он включается в цепь параллельно. Пример подключения представлен на рисунке:
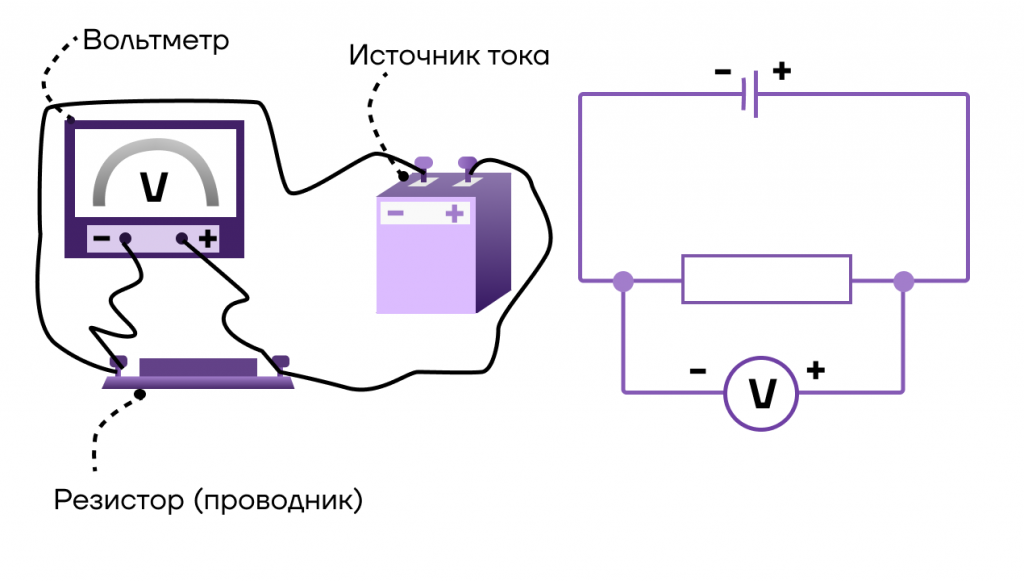
Сила тока
Это еще одна немаловажная характеристика электрического тока.
Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени .
I — сила тока (А),
q — электрический заряд (Кл),
t — время (с).
Единица измерения I — А (ампер) = (frac{Кл}{с}).
Представим, что внутри проводника «бежит» в одном направлении огромное количество заряженных частиц. Так вот, чем больше общий заряд частиц, пробегающих через поперечное сечение проводника за единицу времени, тем больше будет значение силы тока. Это поможет вам запомнить зависимость силы тока (I) от электрического заряда (q).
Прибор для измерения силы тока — амперметр. Он включается в цепь последовательно. Пример подключения представлен на рисунке:
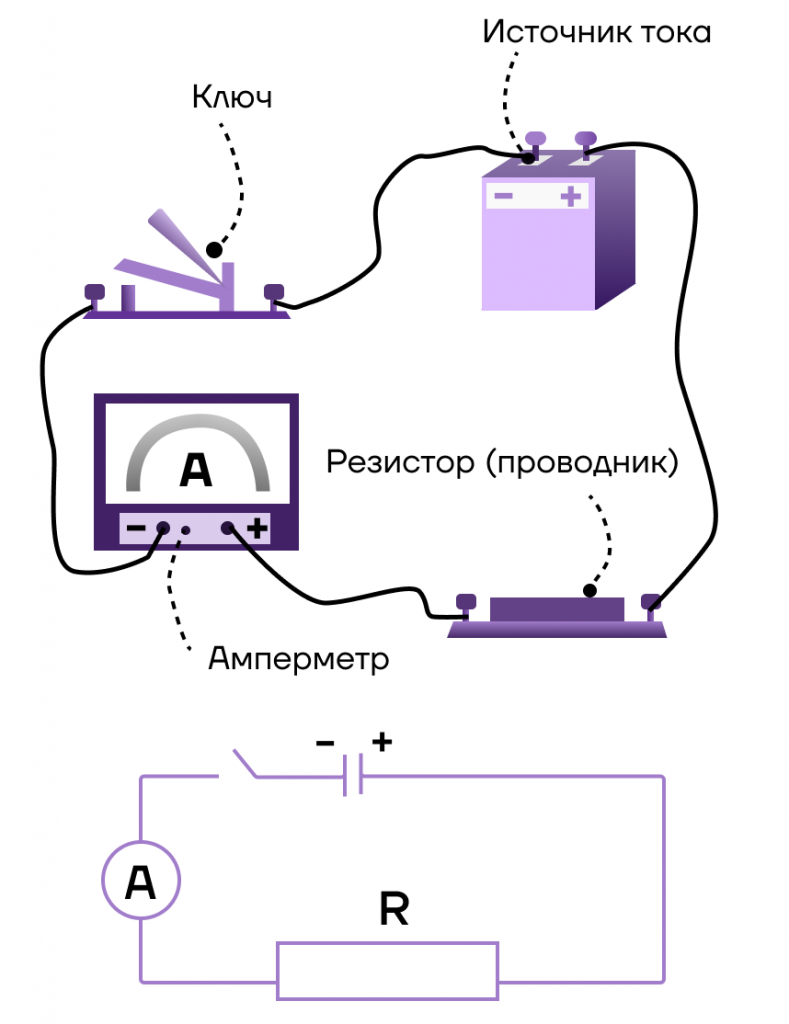
Направление тока совпадает с направлением движения положительно заряженных частиц.
Давайте разберемся, как можно определить направление тока в цепи на примере.
Задача. На рисунке изображена электрическая цепь с источником тока и сопротивлением R. Определите направление тока в данной цепи (по часовой стрелке/против часовой стрелки).
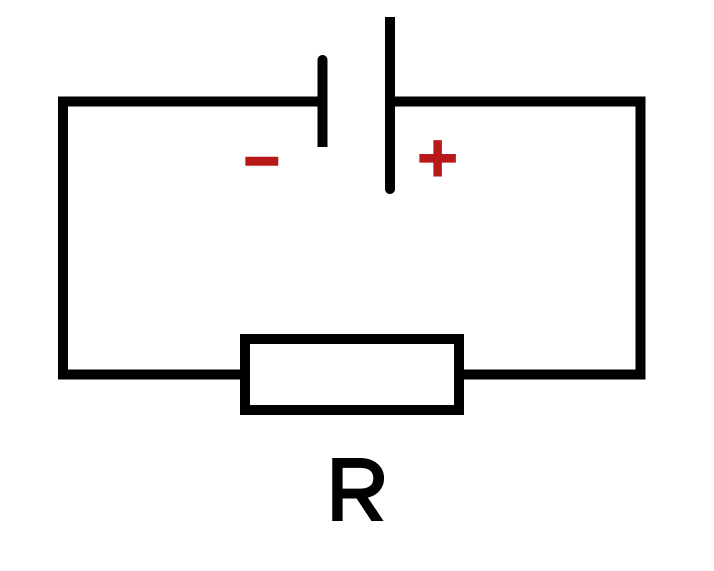
Решение:
Обратите внимание, «большая» пластина реостата расположена справа (именно она и направляет ток), а «маленькая» слева. Положительно заряженные частицы двигаются от катода к аноду (от положительно заряженной пластинки к отрицательно заряженной), а направление тока всегда совпадает с направлением положительно заряженных частиц. Значит, ток в цепи направлен по часовой стрелке.
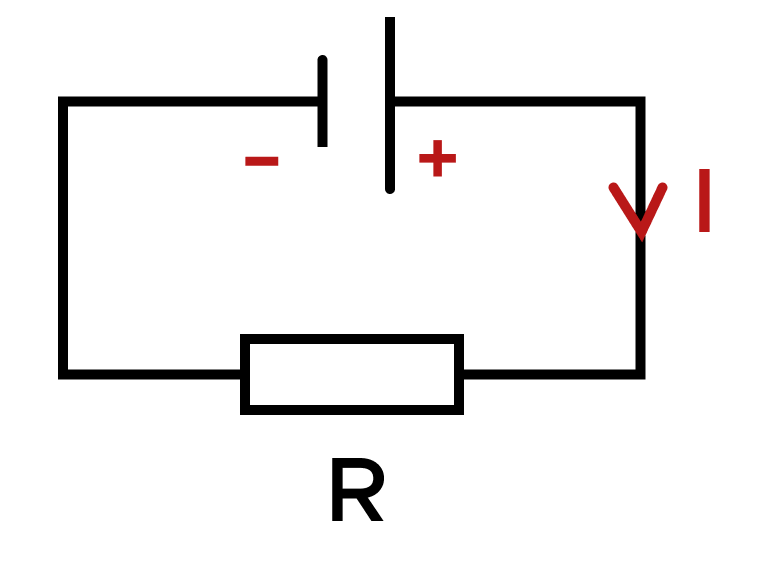
Ответ: по часовой стрелке
Электрическое сопротивление
Оно является электрической характеристикой проводника.
Сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
R — сопротивление (Ом),
p — удельное сопротивление проводника,
l — длина проводника (м),
S — площадь поперечного сечения проводника (мм²).
Единица измерения R — Ом.
Удельное сопротивление проводника (p) можно посмотреть в специальной таблице в справочнике или в интернете. Для каждого материала будет свое значение. Мы приведем для примера лишь фрагмент такой таблицы.
Таблица удельных сопротивлений проводников
| Металл | Удельное сопротивление, Ом * (мм^2)/ м |
| Серебро | 0,0015 |
| Медь | 0,018 |
| Золото | 0,023 |
| Алюминий | 0,029 |
| Вольфрам | 0,055 |
| Железо | 0,098 |
Сопротивление — это внешнее свойство, зависящее от количества присутствующего материала, от геометрических характеристик проводника и от самого материала, из которого сделан проводник.
Удельное сопротивление — это внутреннее свойство проводника, которое не зависит от его размера, а зависит от химического состава вещества и температуры.
Условно можно сказать, что сопротивление — это свойство проводника, а удельное сопротивление — свойство материала.
Получается, что прежде всего на то, каким будет сопротивление, влияют размеры проводника, его форма, материал, из которого он сделан.
Удельное сопротивление проводника зависит также от температуры. Когда температура твердых тел увеличивается, то удельное сопротивление возрастает. А в растворах и расплавах — наоборот, уменьшается. В экзаменационных задачах случаи с изменением удельного сопротивления не рассматриваются, а вот в олимпиадных задачах такое встретить можно.
Давайте поразмышляем: что чему сопротивляется?
Причина электрического сопротивления кроется во взаимодействии зарядов разного знака при протекании тока по проводнику. Это взаимодействие можно сравнить с силой трения, стремящейся остановить движение заряженных частиц.
Чем сильнее взаимодействие свободных электронов с положительными ионами в узлах кристаллической решетки проводника, тем больше сопротивление проводника.
Проводник с определенным постоянным сопротивлением называется резистор.
Вернемся к сравнению электрического тока с водой: как молекулы воды из крана движутся сверху вниз, так и электрический ток имеет определенное направление — от катода к аноду. Электрический заряд условно в нашем примере аналогичен массе воды, а напряжение — напору воды из крана.
Закон Ома
Сила тока, напряжение и сопротивление связаны между собой соотношением, которое называется закон Ома:
I — сила тока (А),
U — напряжение (В),
R — сопротивление (Ом).
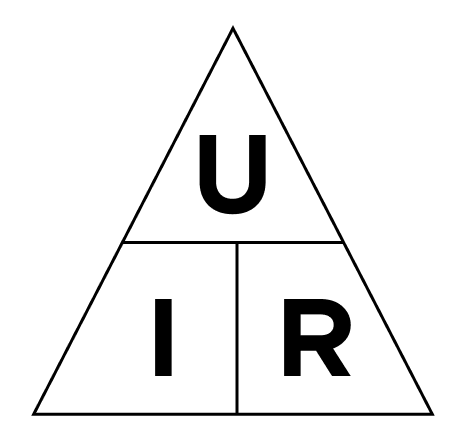
Для упрощенного понимания закона Ома можно использовать данный треугольник. Чтобы вспомнить формулу для нахождения той или иной величины, нужно ее закрыть рукой. Если оставшиеся открытыми величины стоят бок о бок, то они перемножаются друг с другом (U=IR). А если одна величина стоит выше другой, то в таком случае мы делим их друг на друга (I=U/R или R=U/I)
Данный закон справедлив для участка цепи, на который не действуют сторонние силы.
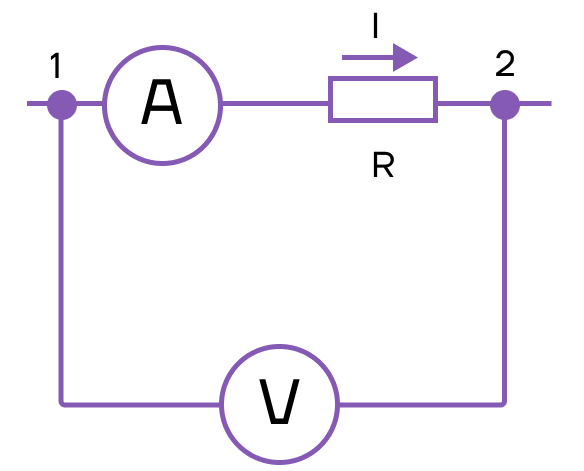
Разберем задачу из контрольно-измерительных материалов ЕГЭ (номер 12).
Ниже на рисунке приведена схема электрической цепи, в которой провода можно считать идеальными. Определите сопротивление резистора, если показания амперметра 0,2 А, а вольтметра — 8 В.
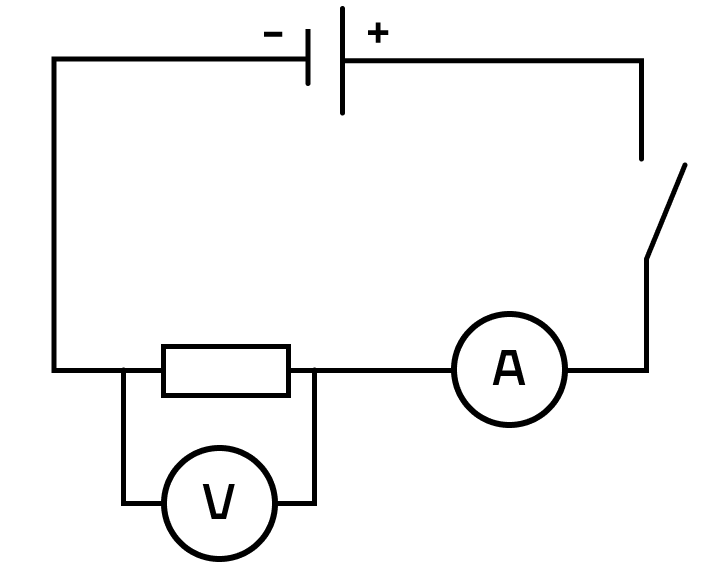
Решение:
Вольтметр подключен параллельно резистору. Следовательно, он показывает напряжение на резисторе U.
Амперметр подключен последовательно. Следовательно, он показывает силу тока I на всей цепи.
Чтобы найти сопротивление на резисторе, воспользуемся законом Ома:
I=(frac{U}{R}), где R — сопротивление резистора.
Выразим R и подставим значения:
R=(frac{U}{I})
R=(frac{8}{0,2})=40 (Ом)
Ответ: 40
Работа и мощность электрического тока
Вернемся к понятию работы. Мы говорили, при перемещении заряда по проводнику электрическое поле совершает работу (А):
A = qU
Если мы выразим заряд из формулы силы тока q=It, то получим, формулу для расчета работы электрического поля (А) при протекании постоянного тока (или просто работа тока):
A — работа электрического тока (Дж),
U — напряжение (В),
I — сила тока (А),
t — время прохождения тока (с).
Единица измерения А — Дж (Джоуль).
В быту ток совершает работу длительное время, поэтому при определении затраченной электрической энергии используют единицу измерения кВт * ч. Киловатт в час — это энергия, которая потребляется устройством мощностью 1 кВт в течении 1 часа. Учитывая, что 1 ч=3600 с, получим:
1 кВт*ч = 1000 Вт * 3600 с = 3600000 Дж = 3600 кДж
Если же работу тока рассчитать за единицу времени, то мы получим мощность постоянного электрического тока.
Мощность — величина, обозначающая интенсивность передачи электрической энергии.
P — мощность (Вт),
A — работа электрического тока (Дж),
t — время прохождения тока (с).
Единица измерения P — Вт (Ватт).
Средняя мощность тока равна:
(P = frac{A}{t} = frac{qU}{t} = IU = frac{U^2}{R} = I^2R)
Теперь мы знаем все про мощность и работу тока, а значит, нужно отработать это на практике. Тем более что такие задачи встречаются в ЕГЭ (номер 12).
Задача.
Какую работу совершит электрический ток в электродвигателе вентилятора за 20 мин., если сила тока в цепи 0,2 А, а напряжение 12 В?
Решение.
Вспомним формулу для работы тока A=U*I*t , где U=12 В — напряжение в электродвигателе, I=0,2 A — сила тока, t=20 мин=1200 с — время.
Все данные нам уже известны, поэтому можем подставить их в формулу для работы тока и получить ответ.
A=12*0,2*1200=2880 Дж
Ответ: 2880 Дж
Мощность электроприбора всегда указывается в документации, прилагающейся к нему. Кроме того, нередко ее пишут на самом приборе. Давайте посмотрим на утюг, или стиральную машину дома. Мы увидим, что утюг имеет мощность 1000 Вт, а обычная энергосберегающая лампочка, всего 40 Вт (на то она и сберегающая). Чем больше мощность прибора, тем больше энергии он будет потреблять. Примеры мощностей различных приборов представлены на рисунке.
Закон Джоуля — Ленца
Теперь же свяжем работу тока и теплоту, которая выделяется на проводнике за некоторое время t.
Когда приборы подключены в сеть, мы можем заметить, что они нагреваются. Очень часто это наблюдается, когда телефон подключен на зарядку, а мы продолжаем по нему звонить, использовать интернет и прочее. Это плохо влияет на телефон: перегрев батареи и корпуса могут быстрее привести девайс в негодность.

Почему так происходит?
Электрический ток оказывает тепловое действие на проводник. Количество теплоты, которое при этом выделяется, будет рассчитываться по закону Джоуля — Ленца:
Количество теплоты, выделяемое за время в проводнике с током, пропорционально произведению квадрата силы тока на этом участке и сопротивления проводника:
Q — количество теплоты (Дж),
I — работа электрического тока (Дж),
R — сопротивление (Ом),
t — время прохождения тока (с).
Единица измерения Q — Дж (Джоуль).
В электронагревательных приборах используются проводники с высоким сопротивлением, что обеспечивает выделение тепла на определенном участке.
Так, проволоку из нихрома (сплав никеля с хромом) применяют в электронагревательных элементах, работающих при температуре до 1000 ℃ (резисторах, например). Нихром относится к классу сплавов с высоким электрическим сопротивлением, что определяет его применение в качестве электрических нагревателей. Этот сплав используется также в печах обжига и сушки и различных аппаратах теплового воздействия, например, в фенах, паяльниках или обогревателях.

Кто первый ввел понятие «электрический ток» в науку? Ответ: Андре-Мари Ампер.
Такой был финальный вопрос (ценой в 1 000 000) в игре «Кто хочет стать миллионером?» от 20 января 2018 г. Но участники не смогли ответить на него, и мечту получить свой миллион не исполнили.

Еще немного про электричество…
- Постоянный электрический ток используется в работе двигателей электротранспорта, схемах автомобилей, электронике и др.
- Электричество есть и в нашем организме. Мышечные клетки сердца при сокращении производят электроэнергию, эти импульсы можно измерить с помощью электрокардиограммы (ЭКГ).
- Бенджамин Франклин (да-да, президент Америки) провел множество опытов в 18 веке и создал громоотвод. Также он является человеком, который вывел закон сохранения электрического заряда.
- В древности люди считали, что, если молния ударила в курган, значит, там зарыто сокровище.
Термины
Источник тока — устройство, разделяющее положительные и отрицательные заряды.
Сторонние силы — силы неэлектрического происхождения, вызывающие разделение зарядов в источнике тока.
Фактчек
- Сила тока — это физическая величина, показывающая, какой заряд переносится через рассматриваемую площадь поперечного сечения за единицу времени: (I = frac{q}{t})
- Напряжение — скалярная физическая величина, равная отношению полной работы кулоновских и сторонних сил А при перемещении положительного заряда на участке цепи к значению этого заряда: (U = frac{A}{q})
- Сопротивление — физическая величина, характеризующая электрические свойства участка цепи: (R = frac{pl}{S})
- Мощность — величина, обозначающая интенсивность передачи электрической энергии: (P = frac{A}{t})
- Закон Ома: сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении и обратно пропорциональна сопротивлению участка при постоянном напряжении: (I = frac{U}{R}).
- Закон Джоуля— Ленца: количество теплоты Q, выделяемое за время t в проводнике с током, пропорционально произведению квадрата силы тока I на этом участке и сопротивления R проводника: Q = I2Rt.
- Работа электрического поля при протекании постоянного тока (или просто работа тока): А = UIt.
Проверь себя
Задание 1.
Упорядоченное движение заряженных частиц — это:
- электрическое поле
- электрический ток
- электрическая мощность
- работа тока
Задание 2.
Удельное сопротивление проводника:
- зависит от температуры
- не зависит от температуры
- зависит от силы протекающего через проводник тока
- не зависит от напряжения
Задание 3.
Формула для расчета силы тока:
- I = Ut
- I = UIt
- I = I2Rt
- (I = frac{q}{t})
Задание 4.
Что такое мощность электрического тока:
- работа за единицу времени
- отношение заряда к единице времени
- произведение силы тока на сопротивление
- тепло, выделяемое на резисторе
Задание 5.
Причина электрического сопротивления:
- во взаимодействии зарядов одинакового знака
- в отсутствии взаимодействия между зарядами
- во взаимодействии зарядов разного знака
- в передаче тепла
Ответы: 1.— 2; 2. — 1; 3.— 4; 4.— 1; 5. — 3.
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Как разными способами найти силу тока
Содержание
- 1 Зачем нужно находить силу тока
- 2 Вычисление тока, если известны мощность и напряжение
- 3 Определение мощности прибора
- 4 Вычисление тока при известных значениях напряжения и сопротивления
- 5 Использование мощности и сопротивления
- 6 Непосредственное измерение силы тока
- 7 Видео по теме
Знание силы тока в электрической цепи является в некоторых случаях необходимым. Ее определяют не только с помощью непосредственного измерения, но и расчетов. В последнем случае нужную информацию можно получить на основе технических характеристик оборудования.
Зависимости между основными электрическими величинами
Зачем нужно находить силу тока
Любое вещество состоит из атомов, которые включают в себя положительно заряженное ядро и вращающиеся вокруг него электроны. При отсутствии электрического поля движение этих частиц является хаотичным. Но как только проводник становится частью электрической цепи, подключённой к источнику питания, электроны начинают двигаться по направлению к положительному полюсу.
Ток проявляется через заряд. Каждый электрон несёт в себе элементарный отрицательный электрический заряд. Сила тока — это количество электронов, проходящих через поперечное сечение проводника за какой-то отрезок времени. Следовательно, можно сделать вывод, что рассматриваемый параметр определяют заряд и время.
Электроток, выраженный через заряд и время
Найти силу тока в проводнике можно только в том случае, когда электрическая цепь подключена к источнику питания. Например, это может быть включение бытового прибора в электросеть с переменным напряжением, равным 220 В. Разным приборам для работы нужна разная мощность. В некоторых случаях даже выключенное оборудование может потреблять небольшое количество электричества, если оставить его вилку в розетке. Поэтому рассчитать силу тока в цепи можно через мощность и напряжение.
Слишком интенсивный электроток способен создавать проблемы. Он может, например, привести к перегреву деталей или к их разрушению. Если большой ток пройдёт через человека, то это нанесет серьёзный вред его здоровью или даже станет опасным для жизни. Для нормального и безопасного функционирования оборудования важно, чтобы электроток соответствовал установленным нормативам. Определение силы тока по мощности и напряжению позволяет проверить, насколько она соответствует требованиям.
Вычисление тока, если известны мощность и напряжение
Есть простой способ, как узнать ток, зная мощность и напряжение. В данном случае рассчитать постоянный ток можно по формуле:
Расчет для переменного тока через мощность усложняется, поскольку его величина и направление постоянно меняются. Это обстоятельство нужно учитывать при расчетах. Если питание однофазное, то используется такая формула:
Чтобы определить силу переменного тока в трехфазной сети, следует воспользоваться формулой:
При рассмотрении переменного тока нужно учитывать не только активную, но и реактивную мощность. Первая связана с активным сопротивлением, а вторая — с реактивным (ёмкостным и индуктивным). Соотношение между различными видами отражается с помощью cos φ.
Косинус угла «фи» обычно указывают в технической документации прибора. Если эту информацию нельзя получить из документации, то в расчетах очень мощных устройств принимают значение 0.8. Для большинства обычных бытовых приборов в вычислениях используют 0.95.
Подставив в формулу, применяемую для определения силы тока на участке цепи, значения напряжения U = 220 В для однофазной цепи и 380 В для трехфазной, а также cos φ = 0.95, получим следующие выражения:
Как видим, сила тока в трехфазной и однофазной сети при одинаковой нагрузке будет разной. В однофазной она втрое больше, чем в трехфазной.
Определение мощности прибора
Перед тем как найти силу электрического тока, нужно определить величину используемой мощности:
- Ее значение должно указываться в технической документации. Однако она не всегда доступна. В частности, документация может быть утеряна.
- На задней панели приборов часто имеется наклейка, на которой приведены важнейшие характеристики устройства. В числе прочих обычно указывают мощность.
Задняя панель прибора с указанием основных данных
- Можно воспользоваться таблицей с указанием средних значений мощности для различных видов устройств.
Мощность разных приборов
При вычислениях необходимо помнить, что пусковая мощность может превышать рабочую. Расчёт силы тока должен учитывать обе этих величины. Когда пусковая мощность вызывает резкое мгновенное увеличение силы тока, оно не должно превышать допустимой величины. Для бытовой техники пусковую мощность указывают редко. Поэтому перед тем как рассчитать силу тока, необходимо обратиться к соответствующим справочникам, чтобы найти определенное значение мощности. Для получения ее точной величины следует провести измерение ваттметром.
Вычисление тока при известных значениях напряжения и сопротивления
Если известно напряжение и сопротивление, то сила тока вычисляется по формуле, вытекающей из закона Ома:
Если известны значения ЭДС, внутреннего сопротивления и нагрузки, то можно найти силу тока, используя закон Ома для полной цепи:
Использование мощности и сопротивления
Как известно, мощность можно находить по формуле.
Применив в данном выражении закон Ома, можно привести его к следующему виду:
Теперь силу тока можно выразить так:
Следовательно, вычислить силу тока можно разными способами.
Непосредственное измерение силы тока
Величину силы тока можно не только рассчитывать, но и измерять, используя такие приборы, как амперметр или мультиметр. Любой из них при измерениях должен стать частью электрической цепи. Поэтому прибор нужно подключать последовательно.
Если нет большой нужды измерять силу тока амперметром, то лучше вычислить этот параметр, используя формулы, даже если для этого придется измерить напряжение. Вольтметром эта процедура осуществляется без разрыва электроцепи, чего нельзя сделать при использовании амперметра.
Также применяется магнитометрический способ. Примером его использования являются токовые клещи. Перед тем как определить силу электротока, их устанавливают так, чтобы они охватывали провод. Поскольку вокруг проводника при протекании тока образуется магнитное поле, которое клещи улавливают, то по его характеристикам прибор определяет силу тока в цепи.