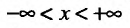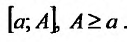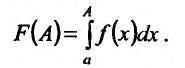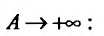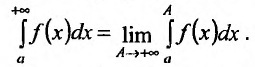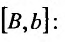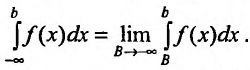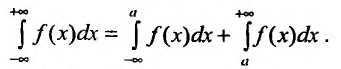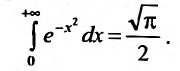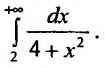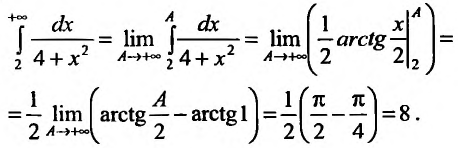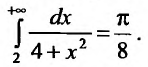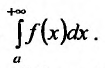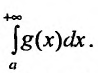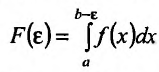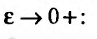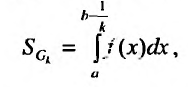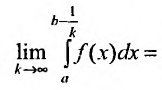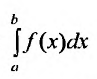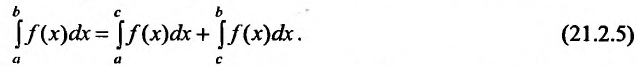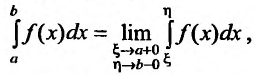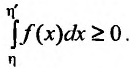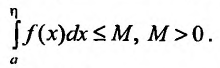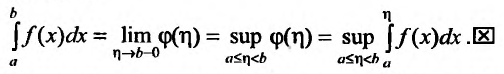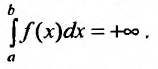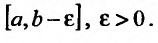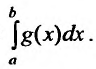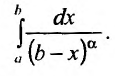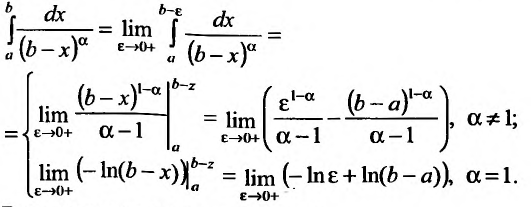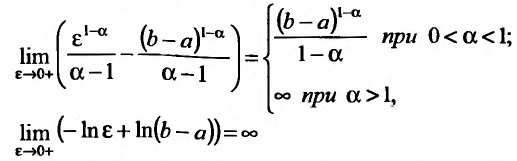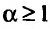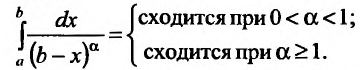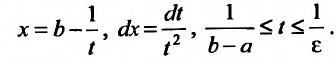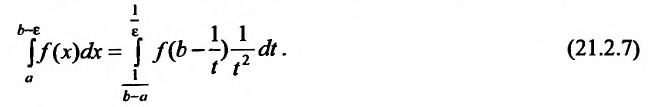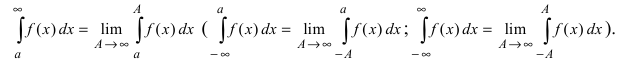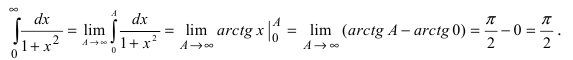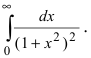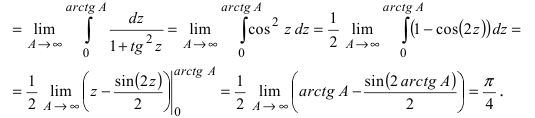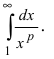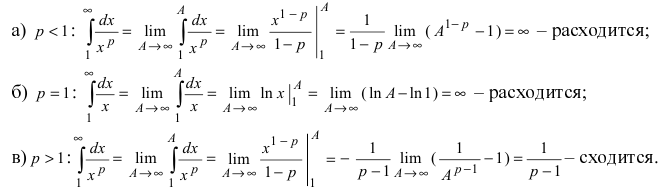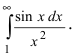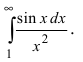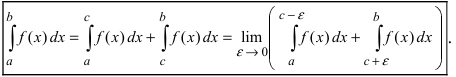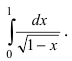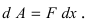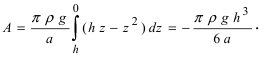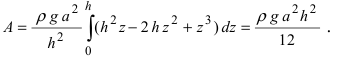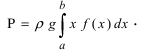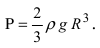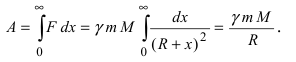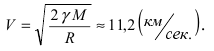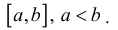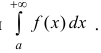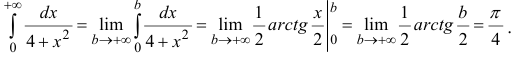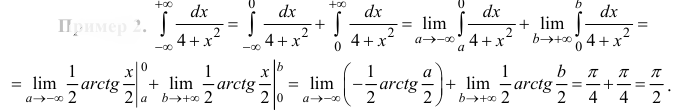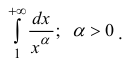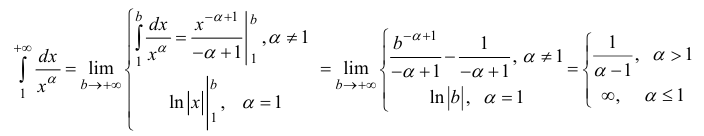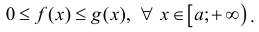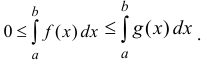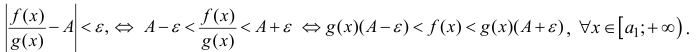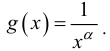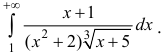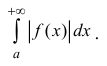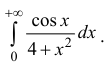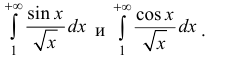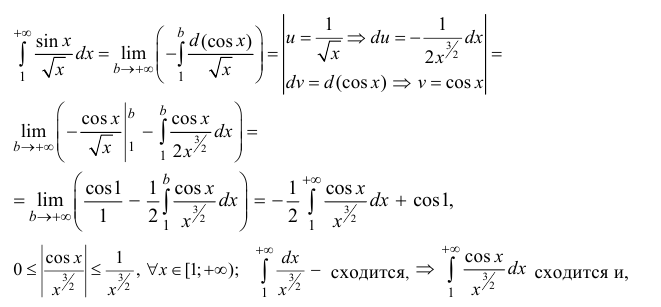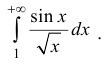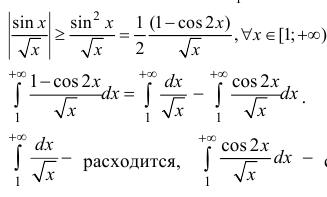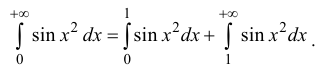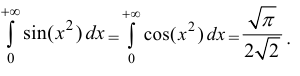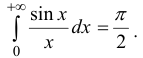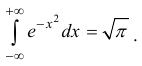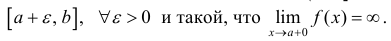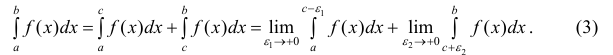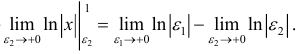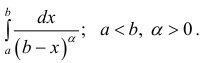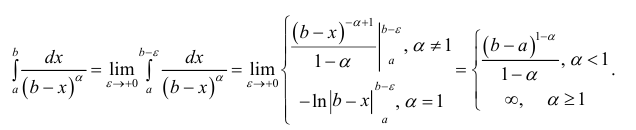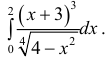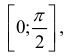Вычисление несобственных интегралов
Для
вычисления несобственных интегралов
существует несколько методов. Мы
ограничимся рассмотрением только двух
видов одномерных несобственных интегралов
и одного из методов их приближенного
вычисления.
Интегралы
с бесконечным пределом интегрирования.
Пусть требуется вычислить приближенное
значение несобственного интеграла
с погрешностью, не превышающей заданного
положительного числа.
Согласно определению,
.
(8.4.9)
Поэтому
в качестве приближенного значения
несобственного интеграла можно выбрать
значение
при достаточно большом значении величиныb.
Осталось найти это значение.
Представим
искомый несобственный интеграл в виде
суммы:
.
(8.4.10)
Выберем
значение величины b
исходя из требования, чтобы
,
(8.4.11)
а
затем используем для вычисления
приближенного значения определенного
интеграла
какую-нибудь квадратурную формулу.
Обозначим черезQ
приближенное значение этого определенного
интеграла, вычисленное с помощью
квадратурной формулы с погрешностью,
не превышающей
.
ТогдаQ
будет также представлять собой и
приближенное значение несобственного
интеграла
с погрешностью,
не превышающей
.
В самом деле,

Пример
1
Требуется
найти приближенное значение несобственного
интеграла
с погрешностью, не превышающей
.
Оценим
сверху левую часть неравенства (8.4.11):

Для
выполнения неравенства (8.4.11) достаточно
потребовать, чтобы выполнялось
неравенство
.
Таким образом, мы можем выбрать.
Осталось вычислитьQ
– приближенное значение определенного
интеграла
с погрешностью, не превышающей
.
Это можно сделать с помощью любой из
квадратурных формул, как показано выше
(мы не будем этого делать). Полученное
значениеQ
можно использовать в качестве искомого
приближенного значения несобственного
интеграла с погрешностью, не превышающей
.
Интегралы от
неограниченных функций.
Пусть имеется функция
,
не ограниченная в окрестности точкии такая, что существует несобственный
интеграл.
Требуется
вычислить приближенное значение
несобственного интеграла
с погрешностью,
не превышающей заданного положительного
числа
.
Согласно
определению,
.
(8.4.13)
Поэтому
в качестве приближенного значения
несобственного интеграла можно выбрать
значение
при значении величиныc,
большем a
и достаточно близком к a.
Осталось найти это значение.
Представим
искомый несобственный интеграл в виде
суммы
.
(8.4.14)
Выберем
значение величины c
исходя из требования, чтобы
,
(8.4.15)
а
затем используем для вычисления
приближенного значения определенного
интеграла
какую-нибудь квадратурную формулу.
Обозначим черезQ
приближенное значение этого определенного
интеграла, вычисленное с помощью
квадратурной формулы с погрешностью,
не превышающей
.
ТогдаQ
будет также представлять собой и
приближенное значение несобственного
интеграла
с погрешностью,
не превышающей
.В самом деле,

Пример
2
Требуется
найти приближенное значение несобственного
интеграла

.
Подынтегральная
функция не ограничена в окрестности
точки
.
Оценим сверху левую часть неравенства
(8.4.15):

Для
выполнения неравенства (8.4.15) достаточно
потребовать, чтобы выполнялось неравенство
.
Таким образом, мы можем выбрать.
Осталось вычислитьQ
– приближенное значение определенного
интеграла
с погрешностью, не превышающей
.
Это можно сделать с помощью любой из
квадратурных формул, как показано выше
(мы не будем этого делать). Полученное
значениеQ
можно использовать в качестве искомого
приближенного значения несобственного
интеграла с погрешностью, не превышающей
.
Соседние файлы в папке ВМ_УЧЕБНИК
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Несобственный интеграл — Основные понятия и теоремы
- Свойства несобственного интеграла
- Несобственные интегралы
- Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
- Интегралы от неограниченных функций (несобственные интегралы II типа)
Несобственный интеграл — Основные понятия и теоремы
Пусть функция 




то его называют несобственным интегралом от функции 


Символ (1.2) также называется несобственным интегралом. Если предел (1.1) существует, то несобственный интеграл называется сходящимся, в противном случае — расходящимся.
Аналогично определяется несобственный интеграл с бесконечным нижним пределом:

Интегралы (1.2) и (1.3) называются несобственными интегралами по неограниченному множеству.
Пусть функция 





называют несобственным интегралом от неограниченной функции и по определению полагают

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Если предел (1.5) существует, то несобственный интеграл (1.4) называется сходящимся, в противном случае — расходящимся.
Аналогично определяется несобственный интеграл по промежутку 
Обозначим через 

Пусть функция 



то его называют несобственным интегралом от функции 


Несобственный интеграл по промежутку 




Несобственные интегралы возникают в задачах на геометрические приложения интегрального исчисления: при вычислении площадей неограниченных фигур; объемов тел и площадей поверхностей вращения, если вращающаяся фигура неограничена.
Пусть функция 


которую назовем неограниченной криволинейной трапецией.
Если несобственный интеграл


Возможно вам будут полезны данные страницы:
Объем тела, образованного вращением фигуры 


Площадь поверхности, полученной вращением непрерывной кривой
вокруг оси 

Формулы (1.10), (1.11), как и формула (1.9), применимы при условии сходимости соответствующих несобственных интегралов.
При решении геометрических задач используются и несобственные интегралы от неограниченных функций.
Свойства несобственного интеграла
1
2.
3. При любом
Свойства 1 и 2 называют линейными, а свойство 3 — аддитивностью.
Теорема 1.1 (о замене переменной в несобственном интеграле). Пусть выполнены следующие условия:
1) непрерывно дифференцируемая и строго монотонная функция 




2) функция 

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

Теорема 1.2 (об интегрировании по частям в несобственном интеграле). Пусть функции 



Тогда интегралы
либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

где
Определенный интеграл считается неуместным, если выполнено хотя бы одно из следующих условий: Поля интеграции бесконечны. Например, бесконечный разрыв. Функция не ограничена вблизи некоторых точек области интегрирования.
Примеры с решением
Вычислить несобственный интеграл или установить его расходимость.
Пример 1.
Решение:
Вычислим несобственный интеграл по определению:
Следовательно, данный интеграл интеграл сходится.
Пример 2.
Решение: По определению несобственного интеграла с бесконечным верхним пределом имеем
Следовательно, данный интеграл интеграл расходится.
Пример 3.
Решение:
По определению несобственного интеграла с бесконечным нижним пределом имеем
Итак, интеграл сходится и равен 1.
Пример 4.
Решение:
Интеграл является несобственным, поскольку верхний предел бесконечен. Рассмотрим два случая.
1). Пусть 
2). Пусть 



Пример 5.
Решение:
Данный интеграл является несобственным, поскольку подынтегральная функция 



Пример 6.
Решение:
Подынтегральная функция
1). Пусть
2). Пусть
Итак, интеграл 

Пример 7.
Решение:
Применим к данному интегралу формулу интегрирования по частям: 
Данный интеграл является несобственным, поскольку
подынтегральная функция 



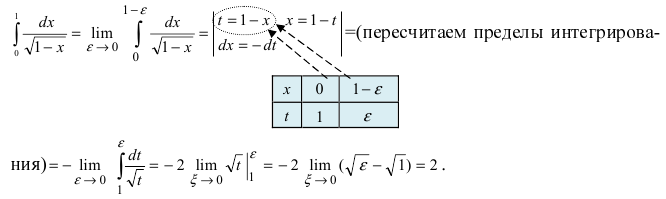
Заметим, что в результате замены переменной несобственный интеграл преобразовался в определенный интеграл от непрерывной функции по отрезку.
Пример 8.
Найти площадь фигуры, ограниченной графиком функции

Решение:
Функция 

Для вычисления интеграла применим формулу (1.13) интегрирования по частям. Положим 




По формуле (1.13) имеем
Пример 9.
Найти объем тела, образованного вращением вокруг оси 

Решение: Функция 

Итак,
Несобственные интегралы
Понятие «несобственные интегралы» связано с нарушением условий теоремы 23.1 о существовании определенного интеграла. В зависимости от того, какая именно условие существования нарушена, рассматривают несобственные интегралы I и II типов.
Различают следующие случаи:
1) вместо конечного отрезка 


2) вместо подынтегральной функции, которая является непрерывной или ограниченной на отрезке интегрирования и имеет конечное число точек разрыва первого рода, рассматривают функцию, имеет на этом отрезке бесконечный разрыв, то есть разрыв второго рода.
Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
Пусть функция 






то есть 
Несобственным интегралом I типа функции 



Если граница 
С учетом формулы Ньютона-Лейбница соотношение (25.1) можно записать так:
где применяется обозначения:
Аналогично определяется несобственный интеграл I типа для случая, когда вместо отрезка интегрирования 
Пусть функция 


Несобственным интегралом I типа функции 


где применяется обозначение
Пусть функция 


Если в соотношении (25.4) обе границы существуют, то несобственный интеграл I типа с бесконечными пределами совпадает.
С учетом формулы Ньютона-Лейбница несобственный интеграл на промежутке
Общий порядок нахождения несобственного интеграла I типа состоит из двух шагов:
1) вычисляем определенный интеграл от 



2) находим границу определенного интеграла при
Под исследованием несобственных интегралов на сходимость понимают установления факта его сходимости или разногласия. Для этого во многих случаях бывает достаточна не вычислять самый интеграл (а он может быть таким, что и «не берется»), а сравнить его с несобственным интегралом, сходимость (или расхождение) которого известна.
Приведем признаки сравнения несобственных интегралов (которые примем без доказательства).
Теорема 25.1. Если функции 





Теорема 25.2. Если функции 




Несобственный интеграл от функции 

В предыдущих теоремах рассматривались несобственные интегралы от неотъемлемых функций. Для знакопеременной функции 
Теорема 25.3. Если несобственный интеграл от модуля заданной функции 
В этом случае несобственный интеграл от 

Рассмотрим некоторые примеры несобственных интегралов I типа. Одним из таких интегралов является интеграл Эйлера-Пуассона:
Этот интеграл нельзя представить в виде конечного числа элементарных функций, поэтому по общему алгоритму проблему вычисления интеграла Эйлера — Пуассона решить невозможно. Докажем, что этот интеграл совпадает, применив теорему 25.1.
Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции 
Рис. 25.1
Сравним функции 





Следовательно, применить теорему 25.1 можно только на промежутке
Исследуем на сходимость интеграл от эталонной функции на
Эталонный интеграл совпадает на промежутке 




В главе 26 будет доказано, что:
При исследовании вопроса о сходимости несобственных интегралов I типа часто в роли эталонного интеграла принимают интеграл вида:
Свойства этого интеграла зависят от значений параметра
Интеграл (25.8) при 
Следовательно, несобственный интеграл от степенной функции 

Исследовать на сходимость несобственный интеграл I типа:
По определению:
Мы доказали, что несобственный интеграл совпадает, поскольку соответствующая граница равна конечном числу.
Исследовать на сходимость несобственный интеграл I типа:
По определению имеем:
Эта граница не существует, поскольку не существует 
Исследовать на сходимость несобственный интеграл I типа:
По определению:
то есть данный интеграл расходится.
Интегралы от неограниченных функций (несобственные интегралы II типа)
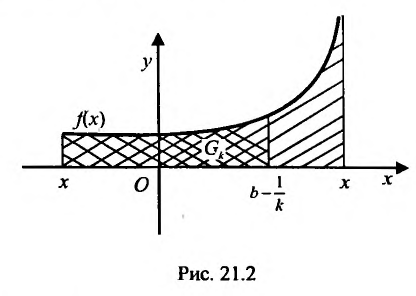
Пусть 





Рис. 25.2
Выберем некоторое положительное число 

Несобственным интегралом II типа от функции 




Аналогично определяют несобственные интегралы II типа для случая, когда особой точкой является верхняя граница отрезка интегрирования:
а также для случая, когда особая точка является внутренней точкой отрезка интегрирования:
Несобственный интеграл II типа называется сходящимся, если существуют конечные границы в правых частях формул (25.10) — (25.12). В противном случае их называют расходящимися.
Порядок исчисления несобственных интегралов II типа принципиально ничем не отличается от порядка определения несобственных интегралов I типа: вычисляют определенный интеграл на конечном отрезке и находят его границу при условии, что 


где
Для первого и второго эталонных интегралов особой точкой является нижняя граница отрезка интегрирования, а для третьего — верхний предел.
Проведем исследование на сходимость первого интеграла с (25.13):
Если 
Следовательно, несобственный интеграл II типа 

Определим, совпадает ли несобственный интеграл
Его подынтегральная функция имеет разрыв второго рода в точке 
Заданный интеграл совпадает, потому соответствующая граница равна конечном числу.
Исследуем на сходимость несобственный интеграл
Подынтегральная функция непрерывна на промежутке 

Если каждый интеграл в правой части совпадает, то выходной интеграл тоже будет совпадать.
Рассмотрим первый интеграл:
Поскольку первый интеграл расходится, то нет необходимости вычислять второй. Окончательно делаем вывод, что заданный несобственный интеграл расходится.
Лекции:
- Определенный интеграл и объем фигур вращения
- Уравнение гиперболы
- Уравнение эллипса
- Степенные ряды
- Случайные события и вероятность
- Свойства пределов функции
- Решение пределов со степенями
- Теория сплайнов примеры решения
- Жорданова форма матрицы
- Скрещивающиеся прямые
Вычислить несобственный интеграл или показать его расходимость.
Пример 1:
Найти значение несобственного интеграла или установить его расходимость.
Решение от преподавателя:
Пример 2:
Вычислить несобственные интегралы или доказать их расходимость.
Решение от преподавателя:
Пример 3:
Вычислить несобственный интеграл или указать его расходимость:
Решение от преподавателя:
Пример 4:
Вычислить несобственный интеграл или доказать его расходимость.
Решение от преподавателя:
Пример 5:
Вычислить несобственный интеграл (или доказать его расходимость):
Решение от преподавателя:
Пример 6:
Вычислить несобственный интеграл или доказать его расходимость:
Решение от преподавателя:
Пример 7:
Вычислить несобственный интеграл (или доказать его расходимость):
Решение от преподавателя:
Пример 8:
Вычислить несобственный интеграл или доказать его расходимость
Решение от преподавателя:
Пример 9:
Вычислить несобственный интеграл с помощью вычетов:
Решение от преподавателя:
Пример 10:
Вычислить несобственные интегралы или доказать их расходимость.
Решение от преподавателя:
Пример 11:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 12:
Вычислить несобственный интеграл или установить его расходимость.
Решение от преподавателя:
Пример 13:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 14:
Вычислить несобственный интеграл или доказать его расходимость
Решение от преподавателя:
Пример 15:
Вычислить несобственный интеграл или доказать его расходимость.
Решение от преподавателя:
Пример 16:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 17:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 18:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 19:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 20:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 21:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 22:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 23:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Содержание:
Несобственные интегралы:
При введении понятия определенного интеграла Римана предполагалось что:
- промежуток интегрирования является конечным;
- подынтегральная функция f(х) является ограниченной.
Обобщим понятие определенного интеграла на два случая, когда:
- промежуток итерирования является бесконечным;
- подынтегральная функция f(x) неограниченна в окрестности некоторых точек отрезка интегрирования.
Несобственные интегралы с бесконечными пределами интегрирования
Обобщим понятие интеграла на случай бесконечных промежутков. На прямой
Рассмотрим для определенности полупрямую 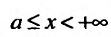
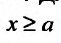
Тогда на отрезке 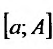
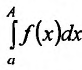
Рассмотрим предел этой функции F(a) при
Определение 21.1.1. Предел (21.1.1) в случае, если он существует, называется несобственным интегралом первого рода от функции f(x) на полупрямой 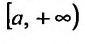
При этом говорят, что несобственный интеграл (21.1.2) сходится, и пишут равенство:
Символ (21.1.2) употребляют и в случае, если предела (21.1.1) не существует, но в этом случае говорят, что несобственный интеграл (21.1.2) расходится.
Аналогично определяется и несобственный интеграл 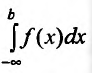
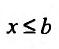
Если для функции f(х) имеют смысл несобственные интегралы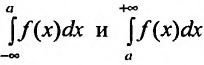
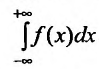
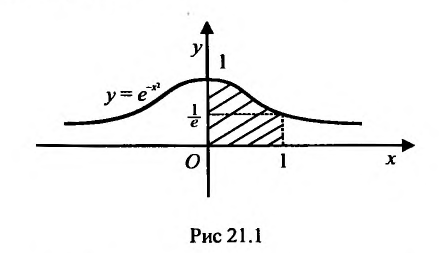
Следует отмстить, что в приложениях важную роль играет интеграл Пуассона:
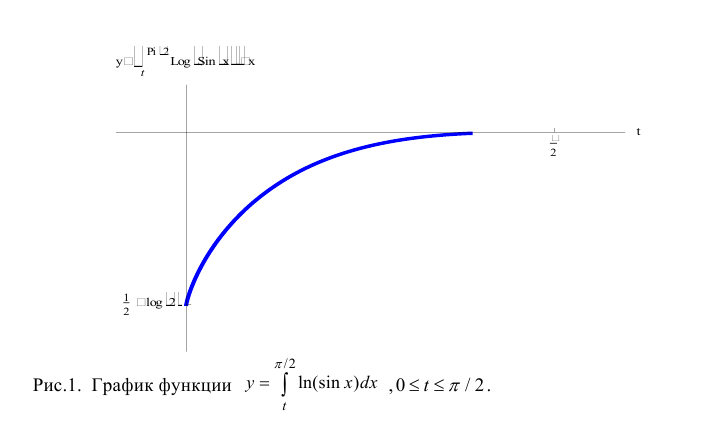
Геометрически, он равен площади неограниченной криволинейной трапеции (см. рис. 21.1)
Пример:
Исследовать сходимость несобственного интеграла
Решение:
Поскольку функция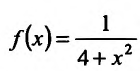
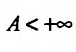
Следовательно, несобственный интеграл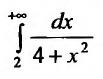
Пример:
Исследовать сходимость несобственного интеграла: 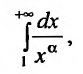
Решение:
Поскольку функция 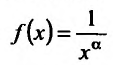
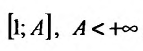
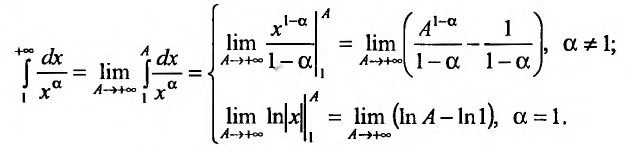
а = 1, то при а > 1 несобственный интеграл 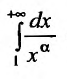
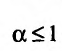
При исследовании сходимости несобственных интегралов целесообразно применять достаточные признаки сходимости.
Предполагая, что функции f(х) и g(x) определены, неотрицательны и интегрируемы по Риману на любом отрезке [а,А],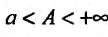
Теорема 21.1.1. Пусть на полупрямой 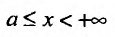
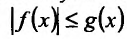
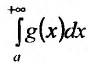
Теорема 21.1.2. Пусть на полупрямой 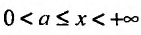
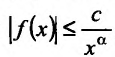
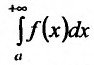
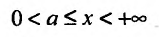
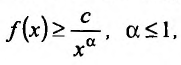
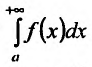
Теорема 21.1.3. Пусть функция f(x) является ограниченной по сравнению с g(x) при 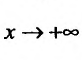
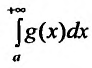
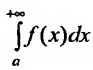
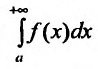
Введем понятие абсолютной и условной сходимости несобственных интегралов.
Несобственный интеграл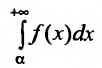
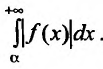
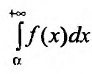
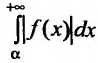
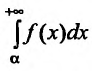
Интегралы от неограниченных функций
Во всех предыдущих рассуждениях мы предполагали, что подынтегральная функция f(х) непрерывна на промежутке интегрирования. Поэтому, если мы хотим, чтобы некоторые неограниченные функции интегрировались в каком-то смысле, то нам нужно обобщить понятие определенного интеграла.
Пусть функция f(x) определена и неограниченна на полуинтервале [а,b), причем она ограничена на любом отрезке 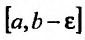
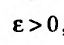
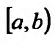
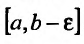
значение которой зависит от 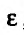
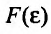
Определение 21.2.1. Правый предел (21.2.1) в случае, если он существует, называется несобственным интегралом второго рода от функции f(х) на отрезке 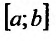
При этом говорят, что несобственный интеграл (21.2.2) сходится, и пишут равенство:
Символ (21.2.2) применяют и в случае, если указанного предела (21.2.3) не существует, но в этом случае говорят, что несобственный интеграл (21.2.3) расходится.
Из определения 21.2.1. следует, что если f(x) > 0 на [a,b), то несобственный интеграл 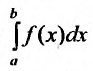
Действительно,
где 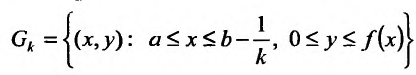
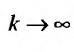
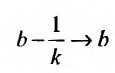
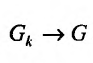
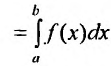
Итак, под несобственным интегралом будем понимать интеграл, определенный формулой (21.2.3).
Аналогично определяется и несобственный интеграл
от функции f(x), определенной на полуинтервале (a,b] и интегрируемой на всех отрезках
Если же функция f(x) определена на интервале (a, b) и если при некотором выборе точки 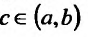
интегралы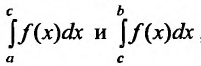
При этом в рассматриваемом случае существование и величина
интеграла 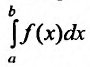
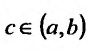
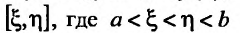
причем переменные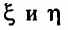
Пример №1
Функция 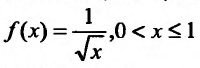
Несобственный же интеграл 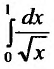
Пример №2
Для функции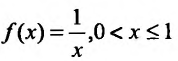
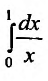
На несобственные интегралы легко переносятся многие свойства интеграла Римана. Так, например, если функция f(x) непрерывна на полуинтервале
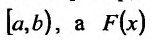
где 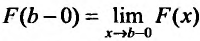
Сформулируем и докажем критерий сходимости несобственных интегралов:
Теорема 21.2.2. Пусть функция f(x) определена и неотрицательна на полуинтервале [a,b). Тогда для того чтобы несобственный интеграл 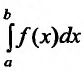
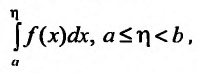
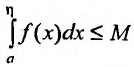
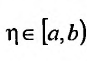
Доказательство. Обозначим через
Если 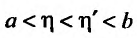
Поэтому справедливо неравенство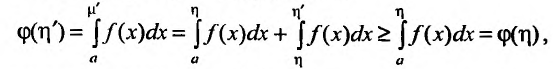
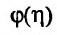
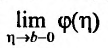
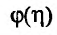
Ясно, что
Из теоремы следует, что для того, чтобы несобственный интеграл 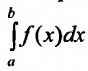
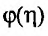
Поэтому когда несобственный интеграл расходится, то пишут:
Сформулируем далее теоремы, которые называются признаками сравнения несобственных интегралов. Для этого предположим, что: 1) функции f(x) и g(x) определены и f(x) > 0, g(x) >0 на 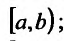
Теорема 21.2.3. Пусть функция f(x) является ограниченной по сравнению с функцией g(x) в некоторой окрестности точки Ь: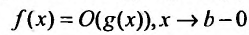
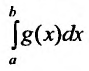
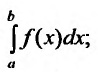
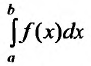
Следствие. Пусть 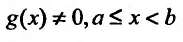
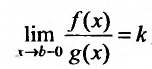
1) если интеграл 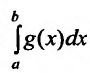
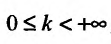
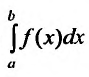
2) если интеграл 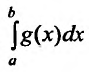
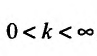
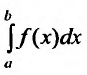
В частности, если 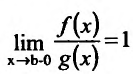
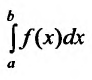
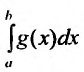
Пример №3
Исследовать сходимость несобственного интеграла:
Решение:
На полуинтервале 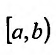
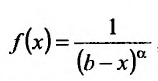
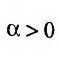
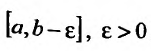
Вычислим полученные пределы:
Следовательно, рассматриваемый несобственный интеграл сходится при 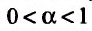
В качестве функции сравнения часто бывает достаточно брать
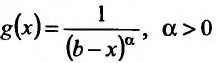
Отметим, что если функция f(x) непрерывна на полуинтервале 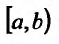
В результате этой замены переменной, получим равенство:
Из этого равенства следует, что если сходится интеграл
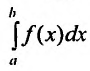
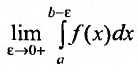
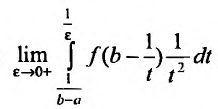
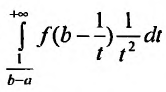
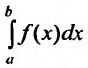
Отмстим, что несобственные интегралы первого рода широко применяются в экономических исследованиях. Так эффективность функционирования розничной торговли; валовой доход (сумму торговых сделок) розничной торговли от реализации товаров и услуг; общая сумма текущих издержек обращения и капиталовложений, сводимых к текущим затратам; совокупная денежная оценка полезности времени, расходуемого населением на приобретение товаров в розничной торговле и др. описывается при помощи несобственных интегралов.
Несобственные интегралы в высшей математике
Определенные интегралы с одним или двумя бесконечными пределами интегрирования от непрерывной на интервале интегрирования функции.(Несобственные интегралы I рода).
Теорема: Пусть функция f(х) непрерывна на интервале 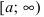
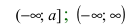
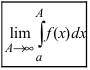
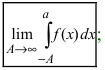
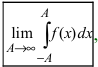
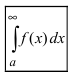
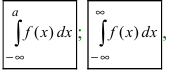
Определение: Определенный интеграл с одним или двумя бесконечными пределами интегрирования от непрерывной на интервале интегрирования функции называется несобственным интегралом I рода
Замечание: Несобственный интеграл I рода вычисляется в смысле главного значения.
В дальнейшем будем изучать только интегралы 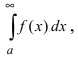
Пример:
Вычислить интеграл
Решение:
Пример:
Вычислить интеграл
Решение:
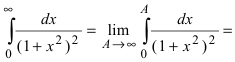
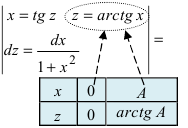
Определение: Несобственный интеграл I рода называется сходящимся, если пределы в указанных выше равенствах конечны, в противном случае несобственный интеграл I рода называется расходящимся.
Пример:
Выяснить сходимость интеграла
Решение:
Рассмотрим возможные случаи:
Следовательно, данный несобственный интеграл расходится при 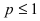
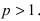
Теорема: Пусть функции f(x) и g(x) непрерывны на интервале 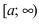
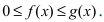
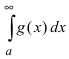
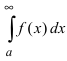
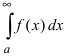
Пример:
Исследовать на сходимость интеграл
Решение:
На интервале 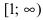
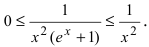
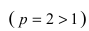
Пример:
Исследовать на сходимость интеграл
Решение:
На интервале 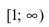
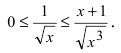
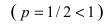
Следствие из теоремы. Если сходится интеграл 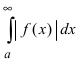
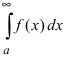
Пример:
Исследовать на сходимость интеграл
Решение:
Так как 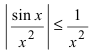
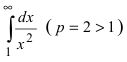
Определенные интегралы с конечными пределами интегрирования от функций, имеющих точки разрыва второго рода на интервале интегрирования. (Несобственные интегралы II рода).
Определение: Если функция f(х) не существует хотя бы в одной точке 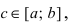
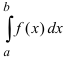
32. Если функция f(х) в точке 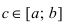
Вычисление определенного интеграла с конечными пределами от разрывной на интервале интегрирования функции производится посредством предельного перехода
Определение: Если приведенные пределы существуют и конечны, то несобственный интеграл II рода называется сходящимся, в противном случае — расходящимся.
Пример:
Вычислить интеграл
Решение:
Рассмотрим признак сходимости несобственных интегралов II рода:
Теорема: Пусть функции f(х) и g(x) непрерывны на интервале 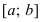
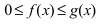
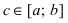
Тогда:
Применение определенного интеграла в науке и технике
1. Работа по сжатию пружины
Пусть тело массой m прикреплено к пружине с коэффициентом упругости k. Требуется вычислить работу, которую совершит сила упругости при растяжении пружины от а до b (Рис. 13):
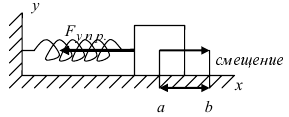
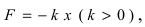
Отсюда находим, что 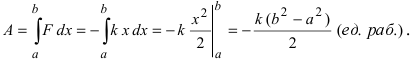
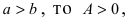
Работа по откачке жидкости из резервуара
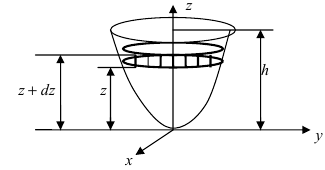
Пусть резервуар представляет собой параболоид вращения и имеет высоту Л. Резервуар заполнен жидкостью с плотностью р. Вычислить работу, которую надо совершить при полной откачке жидкости из резервуара (Рис. 14).
Рис. 14. Вычисление работы по откачке жидкости из параболоида.
Параболоид вращения задается уравнением 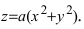
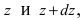
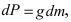
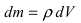
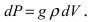
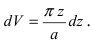
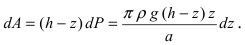
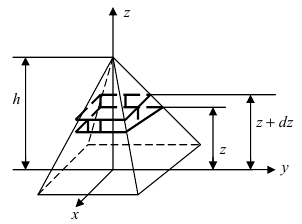
3. Работа по постройке пирамиды
Пусть необходимо построить пирамиду высотой h со стороной основания а из материала с плотностью р . Требуется найти работу по возведению этой пирамиды (Рис. 15, обозначения расставить самостоятельно).
Рис. 15. Вычисление работы по постройке пирамиды.
Для того, чтобы увеличить высоту пирамиды на 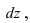
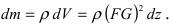
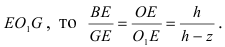
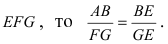
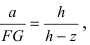
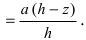
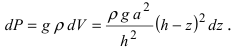
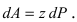
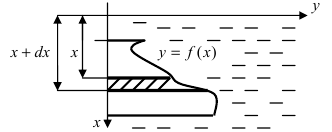
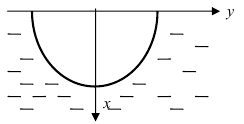
4. Давление жидкости на вертикально погруженную стенку
Пусть в жидкость с плотностью р вертикально погрузили пластину. Требуется вычислить давление, оказываемое со стороны жидкости на пластину (Рис. 16). Давление на глубине х обозначим через Р(х), тогда давление в слое жидкости от х до х + dx будет равно 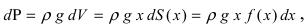
Рис. 16. Вычисление давления жидкости на вертикально погруженную жидкость.
f(x) — функция которая описывает форму пластины. Отсюда находим давление, оказываемое со стороны жидкости на пластину:
- Заказать решение задач по высшей математике
Пример №4
Вычислить давление жидкости на пластину, имеющую форму полуокружности с радиусом R, диаметр которой совпадает с поверхностью (Рис. 17).
Решение:
Рис. 17. Вычисление давления жидкости на пластину, имеющую форму полуокружности с радиусом R.
В данном примере 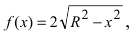
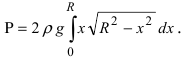
5. Вторая космическая скорость
Известно, что на любое тело массой m, которое находится на высоте х над поверхностью Земли, имеющей массу M и форму шара радиусом R, действует сила притяжения Земли 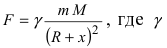
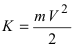
Приравнивая полученное выражение для работы значению кинетической энергии, получим выражение для второй космической скорости
Несобственные интегралы первого рода
Несобственный интеграл первого рода – обобщение понятия интеграла Римана на бесконечный промежуток. Для бесконечного промежутка Δ составить суммы
Римана вида (1) § 24 нельзя.
Определение 1. Пусть функция y=f(x) определена на промежутке 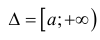
Несобственным интегралом 1-го рода функции y=f(x) на промежутке Δ называется 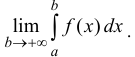
Таким образом:
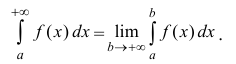
Если предел (1) существует, то интеграл называется сходящимся, в противном случае – расходящимся.
Аналогично:
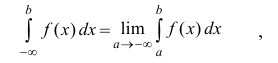
для функции y=f(x), определенной на промежутке 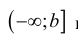
любом конечном промежутке [a b] и 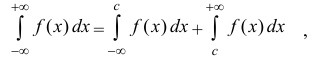
где с – промежуточная точка , и интегралы в правой части формулы (3) вычисляются по формулам (1) и (2).
Пример:
Пример:
Пример:
Исследовать на сходимость
Таким образом, интеграл сходится, если α > 1 и расходится, если α ≤ 1.
Теорема 1 (признак сравнения). Пусть функции 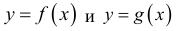
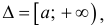
Тогда из сходимости 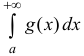
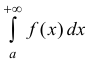
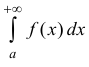
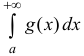
Доказательство следует из неравенства:
Теорема 2 (предельный признак сравнения). Пусть 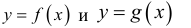
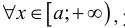
промежутке и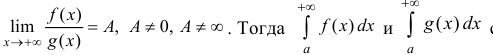
Доказательство. Пусть ε >0 и такое, что A -ε − > 0, тогда из определения предела
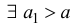
И далее доказательство следует из теоремы 1.
На практике, при исследовании на сходимость по предельному признаку в
качестве g(x) часто используют функцию
Пример:
Исследовать на сходимость интеграл 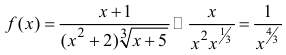
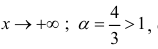
Определение 2. Несобственный интеграл 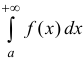
сходящимся, если сходится интеграл
Несобственный интеграл 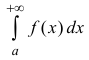
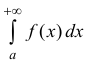
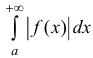
Теорема 3. Пусть 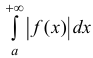
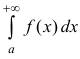
Доказательство. Пусть 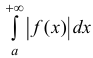
теорему 5 § 3) 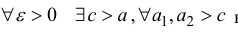
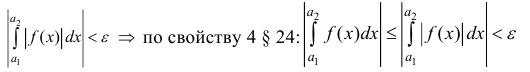
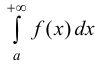
Пример:
Исследовать на абсолютную и условную сходимость
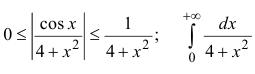
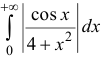
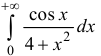
Пример:
Исследовать на абсолютную и условную сходимость интегралы
n.1. Исследуем интегралы на сходимость.
следовательно, сходится
Аналогично: 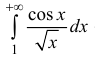
n.2. Исследуем интеграл 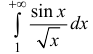
сходится (согласно п. 1), поэтому 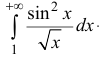
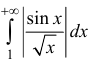
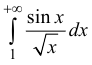
Аналогично: 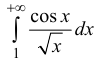
Пример:
Исследовать на абсолютную и условную сходимость интегралы 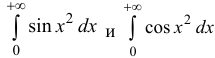
Рассмотрим 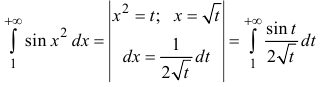
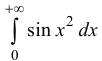
Аналогично 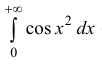
Значения интегралов:
Замечание. Функции 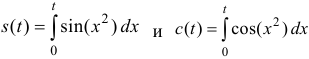
Замечание. Кривая, заданная параметрически в виде: 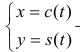
клотоидой (спиралью Корню). Используется при проектировании и строительстве дорог и транспортных развязок (угловое ускорение машины, движущейся по кривой с постоянной скоростью, равно нулю).
Замечание. 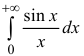
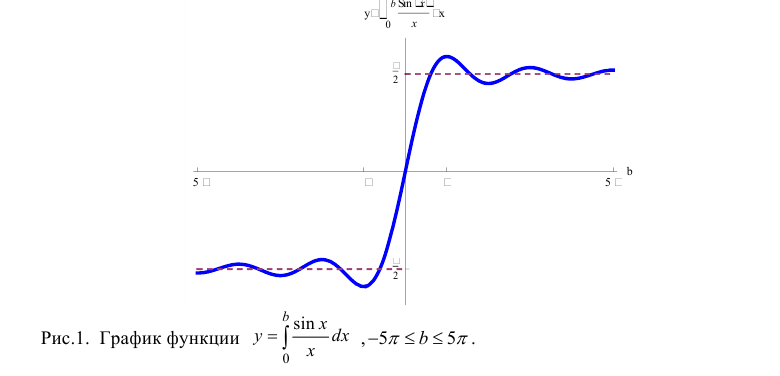
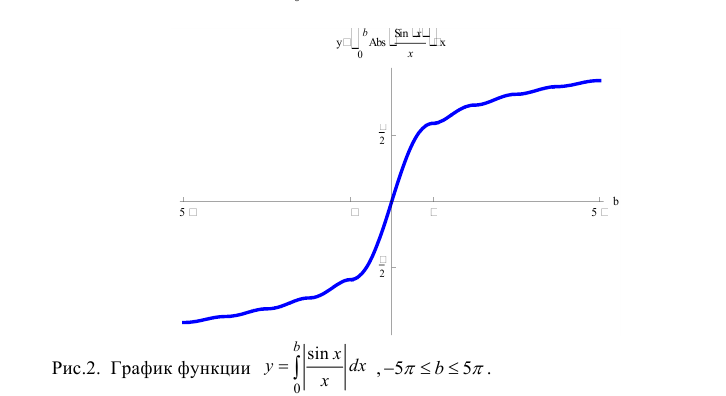
Интегралы Дирихле и Френеля являются примерами интегралов от
функций, первообразные которых не выражаются через элементарные функции.
Еще один такой пример – интеграл Пуассона (Эйлера-Пуассона или Гауссов
интеграл): 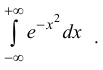
Несобственные интегралы второго рода
Несобственный интеграл второго рода – обобщение понятия интеграла Римана на случай, когда подинтегральная функция – неограниченна. Согласно необходимому условию интегрируемости функции (см. теорему 1 § 24) интегрируемая на промежутке Δ = [a b] функция ограничена на этом промежутке.
Определение 1. а) Пусть функция y=f(x) определена на промежутке Δ = [a b), интегрируема на отрезке 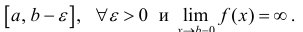
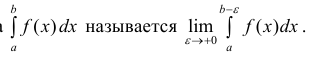
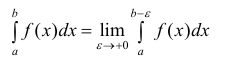
Если предел (1) существует, то интеграл называется сходящимся, в противном случае – расходящимся.
б) Аналогично 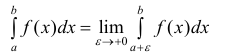
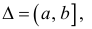
в) Если же 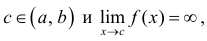
Если хотя бы один из пределов не существует, то интеграл расходится.
Пример №5
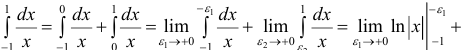
Так как оба предела равны −∞, то интеграл расходится.
Пример №6
Исследовать на сходимость
Таким образом интеграл сходится, если 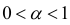
Теорема 1. (признак сравнения). Пусть 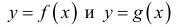
Тогда из сходимости несобственного интеграла 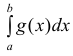
несобственного интеграла 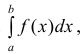
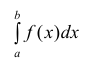
Теорема 2. (предельный признак сравнения). Пусть 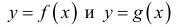
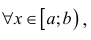
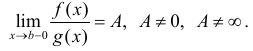
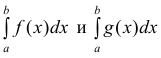
расходятся одновременно.
Доказательство теорем 1 и 2 аналогично доказательству теорем.
На практике, при исследовании на сходимость по предельному признаку в
качестве g (x) часто используют функцию 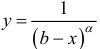
Пример №7
Исследовать на сходимость интеграл
Решение.
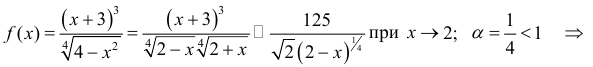
Пример №8
Исследовать на сходимость 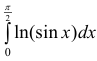
Решение. Проверим сходимость. 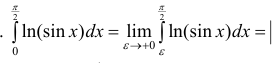
по частям
Таким образом 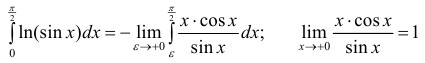
доопределить подинтегральную функцию до непрерывной на отрезок
поэтому интеграл 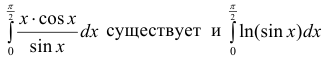
Вычислим интеграл.
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных