В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №10 ЕГЭ.
Что такое функция
Чтение графика функции
Четные и нечетные функции
Периодическая функция
Обратная функция
5 типов элементарных функций и их графики
Преобразование графиков функций
Построение графиков функций
Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 10 в формате ЕГЭ-2021
Линейная функция
Необходимая теория
1. На рисунке изображён график функции . Найдите значение
, при котором
Решение:
Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:
Вычтем из первого уравнения второе:
Уравнение прямой имеет вид:
Найдем, при каком значение функции равно -13,5.
Ответ: -7.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Запишем формулы функций.
Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция
Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции
Вычтем из первого уравнения второе.
тогда
Прямая задается формулой:
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
Ответ: -1,75.
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
Для прямой, расположенной выше, угловой коэффициент равен
Эта прямая проходит через точку (-2; 4), поэтому:
эта прямая задается формулой
Для точки пересечения прямых:
Ответ: -12.
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции Найдите b.
Решение:
На рисунке — квадратичная парабола полученная из графика функции
сдвигом на 1 вправо, то есть
Получим:
Ответ: -2.
5. На рисунке изображен график функции . Найдите с.
Решение:
На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции
на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид
.
Значит, с = 1.
Ответ: 1
6. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:
отсюда
Формула функции имеет вид:
Ответ: 31.
7. На рисунке изображены графики функций и
которые пересекаются в точках А и В. Найдите абсциссу точки В.
Решение:
Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому
График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:
отсюда
Найдем абсциссу точки B. Для точек A и B:
(это абсцисса точки A) или
(это абсцисса точки B).
Ответ: 6.
Степенные функции. Необходимая теория
8. На рисунке изображены графики функций и
, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Решение:
График функции проходит через точку (2; 1); значит,
График функции проходит через точки (2; 1) и (1; -4),
— угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда
Для точек A и B имеем:
Отсюда (абсцисса точки A) или
(абсцисса точки B).
Ответ: -0,2.
9. На рисунке изображён график функции . Найдите f (6,76).
Решение:
Функция задана формулой:
Ее график проходит через точку (4; 5); значит,
Тогда
Ответ: 6,5.
10. На рисунке изображен график функции . Найдите
.
Решение:
График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции:
, а = — 1. Тогда
= 5.
Ответ: 5.
Показательная функция. Необходимая теория
11. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:
Поделим второе уравнение на первое:
Подставим во второе уравнение:
Ответ: 0,25.
12. На рисунке изображен график функции . Найдите
Решение:
График функции проходит через точку
Это значит, что
формула функции имеет вид:
.
Ответ: 2.
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
Отсюда:
Вычтем из второго уравнения первое:
или
— не подходит, так как
(как основание логарифма).
Тогда
Ответ: 4.
14. На рисунке изображен график функции .
Найдите f(0,2).
Решение:
График логарифмической функции на рисунке проходит через точки и
. Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
Формула функции:
Найдем :
Ответ: -7.
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции Найдите
Решение:
График функции сдвинут на 1,5 вверх;
Значит,
Амплитуда
(наибольшее отклонение от среднего значения).
Это график функции Он получен из графика функции
растяжением в 2 раза по вертикали и сдвигом вверх на
.
Ответ:
16. На рисунке изображён график функции
Найдите .
Решение:
На рисунке — график функции Так как
График функции проходит через точку A Подставим
и координаты точки А в формулу функции.
Так как получим:
Ответ: 2.
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения
Решение:
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то
Пользуясь периодичностью функции , период которой T = 4, получим:
Ответ: 5.
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Задача на тему “Графики функций” в едином государственном экзамене по математике профильного уровня появилась только в 2022 году, на данный момент это самая молодая и мало изученная задача на экзамене.
В перечне требований к результатам освоения основной образовательной программы среднего общего образования указано, что для успешного выполнения этой задачи экзаменуемый должен уметь:
- определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций, описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики;
- моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры, а именно – решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;
В перечне элементов содержания, проверяемых на едином государственном экзамене по математике задачей на тему “Графики функций” указаны:
- Линейная функция, её график
- Функция, описывающая обратную пропорциональную зависимость, её график
- Квадратичная функция, её график
- Степенная функция с натуральным показателем, её график
- Тригонометрические функции, их графики
- Показательная функция, её график
- Логарифмическая функция, её график
А также преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей.
Количество заданий по теме графики функций, представленных на сайте fipi.ru [2] в открытом банке задач, на данный момент невелико, поэтому при подготовке к экзамену мы можем дополнительно использовать задачи из сборников, рекомендованных ФИПИ [1], варианты ЕГЭ, тренировочных [3] и диагностических работ этого и прошлого года и собственную фантазию.
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне, 8 минут.
Перейдём к разбору задач. Первая группа из трёх заданий решается подстановкой координат единственной точки в указанную функцию, получением недостающего параметра и вычислением искомого значения.
Задача 1. На рисунке 1 изображён график функции вида 
Рис. 1
Рис. 2
Решение: Координаты точки, указанной на рисунке, (2;1), подставляем в равенство, получаем 


Ответ: 0,2.
Задача 2. На рисунке 2 изображён график функции вида 
Решение: На приведённом рисунке указаны две точки, координаты первой (1;0) не позволяют найти значения параметра a, так как все логарифмические функции данного вида проходят через эту точку. Подставляя в равенство координаты второй точки (2;-1), получаем 



Ответ: 16.
Задача 3. На рисунке 3 изображён график функции вида 
Рис. 3
Решение: На приведённом рисунке указаны две точки, координаты первой (0;1) не позволяют найти значения параметра a, так как все показательные функции данного вида проходят через эту точку.
Подставляя в равенство координаты второй точки (-1;2), получаем 2=a-1 или 


В следующей группе задач будут рассмотрены линейные функции, напомним основные сведения о них.
Линейную функцию можно задать уравнением с угловым коэффициентом y=kx+b, где коэффициент k отвечает за угол наклона α прямой к оси Ox (рис.4).
В случае когда свободный коэффициент b равен нулю, функция превращается в прямую пропорциональность y=kx, если нулю равен угловой коэффициент k, то графиком функции будет горизонтальная прямая y=b (рис.5).
Рис. 4
Рис. 5
Следует напомнить, что существует ещё один способ задания линейной функции, эффективный на ЕГЭ, – это уравнение прямой, проходящей через две точки с координатами (x1;y1) и 
Задача 4. На рисунке 6 изображён график функции вида f(x)=kx+b. Найдите значение f(5).
Рис. 6
Рис. 7
Решение: Способ 1. Определим координаты выделенных точек A(2;1) и B(0;-2). Самым простым способом решения задачи является подстановка координат выделенных точек в функцию и решение полученной системы уравнений 
Способ 2. Построив вспомогательный прямоугольный треугольник (рис.7), проходящий через две выделенные точки, получим, что тангенс угла наклона прямой к оси Ox равен 
Способ 3. Воспользуемся уравнением прямой, проходящей через две точки и подставим в него координаты выделенных точек A(2;1) и B(0;-2), через которые проходит наша прямая. Получим, что 
Задача 6. На рисунке 8 изображён график функции вида f(x)=kx+b. Найдите сумму коэффициентов k и b.
Рис. 8
Решение: Эту задачу опять можно решить подстановкой двух точек в исходную функцию или с помощью уравнения прямой, проходящей через две точки. При решении с помощью нахождения тангенса угла наклона (рис.9) могут возникнуть трудности, связанные с тем, что ученики неверно находят угол α между прямой и осью Ox, путая его со смежным углом β.
Рис. 9


Коэффициент b можно найти, подставив координату одной из точек, например (-1;4), в уравнение 



Задача 7. На рисунке 10 изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.
Рис. 10
Решение: Уравнения линейных функций 

Ответ: 1,25.
Перейдём к задачам на квадратичную функцию.
Задача 8. На рисунке 11 изображён график функции вида 
Рис. 11
Решение: у этой задачи опять существует несколько способов решения, ученикам с минимальным уровнем знаний о квадратичной функции проще будет воспользоваться первым способом, а более продвинутым школьникам – последующими.
Способ 1. Найдём координаты выделенных точек (-3;-2), (-2;-1) и (-1;2) и решим систему, подставив их в уравнение функции. 


Способ 2. Для решения задачи можно использовать значение абсциссы вершины параболы 

Способ 3. Этот способ подойдёт для школьников, которые знакомы с элементарными преобразованиями графиков функций, претендует на высокие баллы за экзамен и хочет потратить на решение задачи минимум времени.
Рис. 12
Введём вспомогательную систему координат с центром в вершине параболы (рис.12) и заметим, что в новой системе координаты точек равны (0;0), (1;1) и (2;4), то есть в новой системе координат эта парабола задаётся уравнением y=x2.
Из этого мы можем сделать вывод, что график искомой функции получается линейными преобразованиями квадратичной функции y=x2, а именно сдвигом на 3 единицы влево и на 2 вниз, то есть искомая функция имеет вид 
Ответ: 7.
Задача 9. На рисунке 13 изображён график функции вида 
Рис. 13
Рис. 14
Решение: Этот номер можно решать подстановкой трёх точек в уравнение функции, а можно опять ввести вспомогательную систему координат (рис.14), в которой у параболы будут два пересечения с осью Ox – точки 2 и 3. Следовательно, квадратичная функция в новой системе координат описывается равенством y=a(x-2)(x-3). Подставив точку (4;2) получим, что a=1. А далее, легко видеть, что искомый график получается из графика y=(x-2)(x-3) сдвигом на 4 по вертикали, то есть уравнение имеет вид y=(x-2)(x-3)-4 или y=x2-5x+2, значит, c=2.
Ответ: 2.
Задача 10. На рисунке 15 изображены графики функций видов f(x)=2x2-5x+5 и g(x)=ax2+bx+c, пересекающиеся в точкаx A и B. Найдите ординату точки B.
Рис. 15
Решение: При решении этой задачи учащиеся сталкиваются с двумя проблемами: не все школьники могут сопоставить функции и их графики, и не все школьники понимают где расположена точка B, так как она не указана на рисунке.
Задача о сопоставлении графиков быстро решается нахождением вершины параболы, заданной уравнением f(x)=2x2-5x+5, абсцисса её вершины 
Для того, чтобы найти точки пересечения двух функций, нужно решить систему уравнений 
Ответ 68.
Задача 11. На рисунке 16 изображён график функции вида f(x)=ax2+bx+c. Найдите произведение абсцисс точек, для которых f(x)=-13.
Рис. 16
Решение: Находим коэффициенты a, b и c для функции y=f(x) и получаем, что f(x)=-x2-8x-14.
Для того, чтобы найти абсциссы точек, при которых f(x)=-13, нужно решить уравнение -x2-8x-14=-13⇔x2+8x+1=0. Произведение корней уравнения находится по теореме Виета и равно 
Ответ: 1.
Успешному решению задач на графики дробно-рациональных функций помогает знание того, что график функции 



Задача 12. На рисунке 17 изображён график функции вида 
Рис. 17
Рис. 18
Решение: Способ 1. График функции 







Способ 2: Введём новую систему координат, так что оси будут направлены вдоль асимптот исходной функции (рис.18).
В этой системе координат наш график является графиком обратной пропорциональности 


График искомой функции получается линейными преобразованиями функции 


Ответ: 1,4.
Задача 13. На рисунке 19 изображён график функции вида 
Рис. 19
Рис. 20
Решение: Способ 1. Найдём координаты точек, через которые проходит график функции, (0;-2), (π;8) и решим систему, подставив их в уравнение функции 

Способ 2. Коэффициент a у искомой функции отвечает за сжатие-растяжение графика функции вдоль оси Oy. Мы видим, что амплитуда у графика, изображённого на рисунке, равна 10 и делаем вывод, что 2|a|=10, то есть a=5 или a=-5, чтобы выбрать нужное значение, заметим, что в точке 0 у изображённой функции достигается минимальной значение, тогда как у обычной функции y=cosx точка 0 является точкой локального максимума, значит, график был не только растянут вдоль оси Oy, но и симметрично отражён относительно оси Ox, а коэффициент a=-5. Последнее преобразование графика – сдвиг на 3 вверх, значит, искомая функция имеет вид 
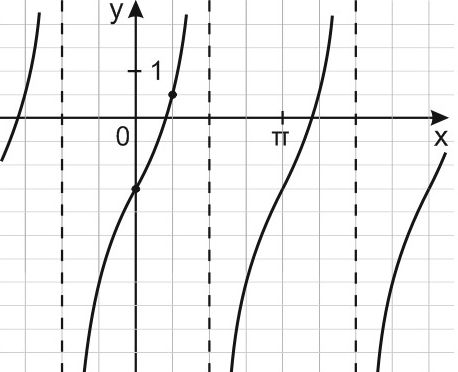
Задача 14. На рисунке 20 изображён график функции вида 

Решение: График искомой функции – синусоида, растянутая в 1,5 раза и сдвинутая на 0,5 вниз, то есть функция имеет вид 

Мы видим, что для успешного решения задач на тему “Графики функций” учащийся должен не только быть знакомым с графиками элементарных функций, а ещё и моделировать реальные ситуации на языке алгебры, составлять уравнения и системы уравнений по условию задачи; исследовать построенные модели с использованием аппарата алгебры, быть знакомым с элементарными преобразованиями графиков функций.
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Комбинированные задачи
Версия для печати и копирования в MS Word
Гиперболы
Версия для печати и копирования в MS Word
1
2
На рисунке изображён график функции
Найдите, при каком значении x значение функции равно 0,8.
3
4
5
На рисунке изображён график функции
Найдите k.
6
На рисунке изображён график функции
Найдите a.
Корни
Версия для печати и копирования в MS Word
Параболы
Версия для печати и копирования в MS Word
1
2
3
4
5
6
7
На рисунке изображены графики функций и
которые пересекаются в точках A и B. Найдите ординату точки B.
8
Тригонометрические функции
Версия для печати и копирования в MS Word
1
На рисунке изображён график функции
Найдите a.
2
На рисунке изображён график функции
Найдите b.
3
На рисунке изображён график функции
Найдите a.
4
На рисунке изображён график функции
Найдите b.
5
На рисунке изображён график функции Найдите a.
6
На рисунке изображён график функции
Найдите b.
Линейные функции
Версия для печати и копирования в MS Word
1
2
3
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
4
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
5
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
6
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Показательные и логарифмические функции
Версия для печати и копирования в MS Word
1
2
3
4
5
6
7
8
9
На рисунке изображен график функции вида
Найдите значение f(4).
10
На рисунке изображён график функции вида
Найдите значение f(16).