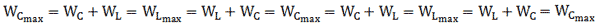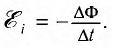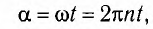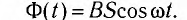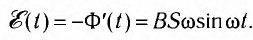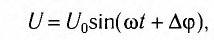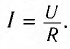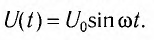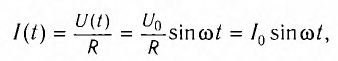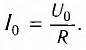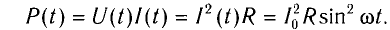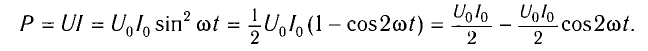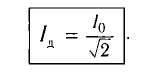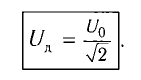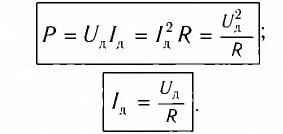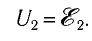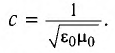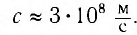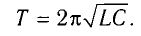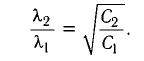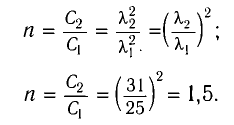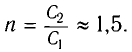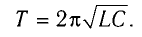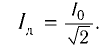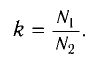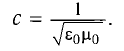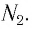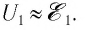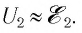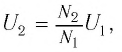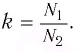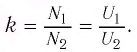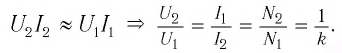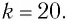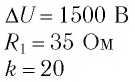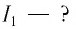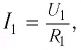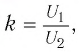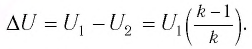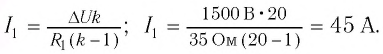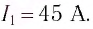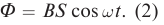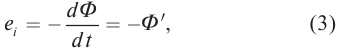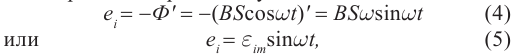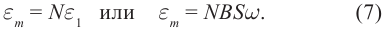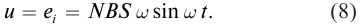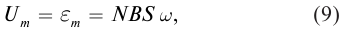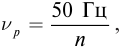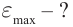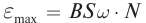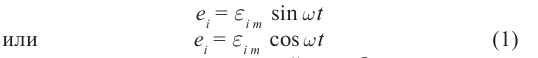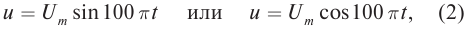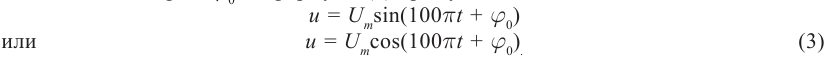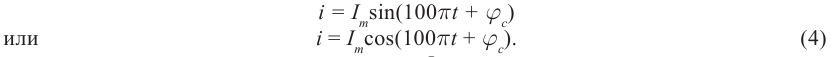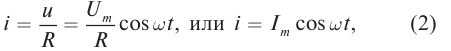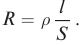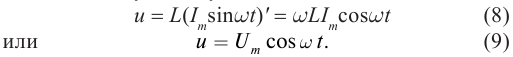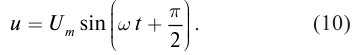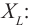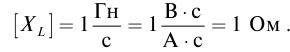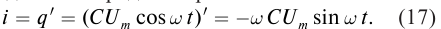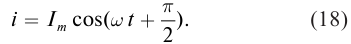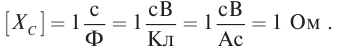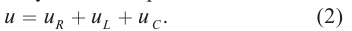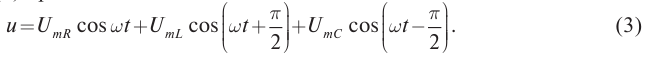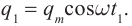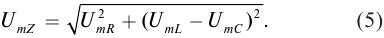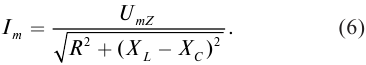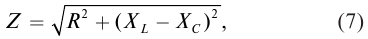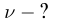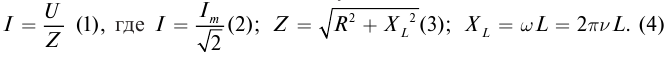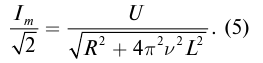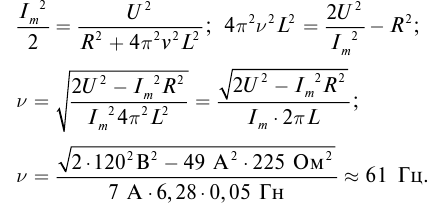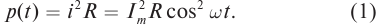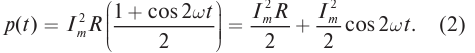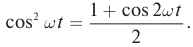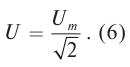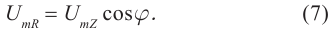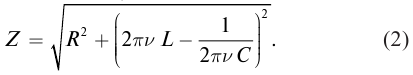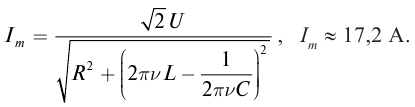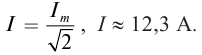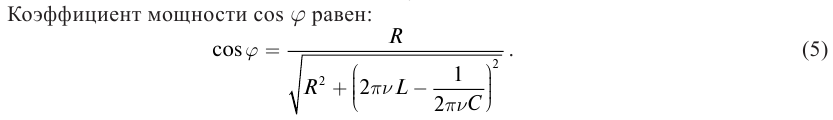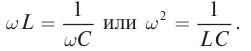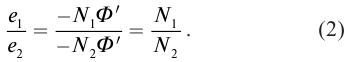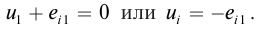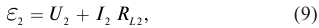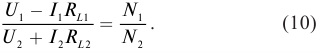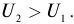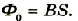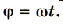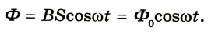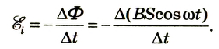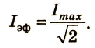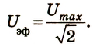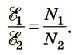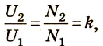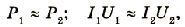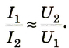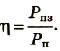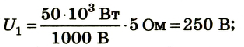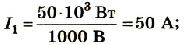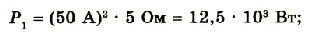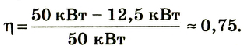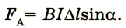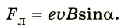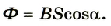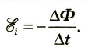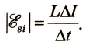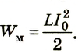Фундаментальной связью в электричестве является зависимость силы тока от напряжения. Благодаря этому закону, экспериментально установленном Омом в 1826 году, созданы различные измерительные приборы. Удалось исследовать физику короткого замыкания. Формулу можно применять для систем, которые зависят от электросопротивления. Пожалуй, разработка любой электрической сети невозможна без использования этого открытия.
Величина силы тока
По определению силой тока называется физическая величина равная величине заряда q, прошедшего через поперечное сечение проводника за время t:
Если сила тока не зависит от времени, то такой электрический ток называется постоянным. Рассмотрим далее именно такой случай, когда ток постоянен. Измерить величину заряда чрезвычайно трудно, поэтому в 1826 г. немецкий физик Георг Ом поступил следующим образом: в электрической цепи, состоящей из источника напряжения (батареи) и сопротивления, он измерял величину тока при разных значениях сопротивления. Затем, не меняя величину сопротивления, он стал изменять параметры источника напряжения, подключая сразу, например, два-три источника. Измеряя величину тока в цепи, он получил зависимости силы тока от напряжения U и от сопротивления R.
Рис. 1. Схема измерений тока и напряжения Георга Ома.
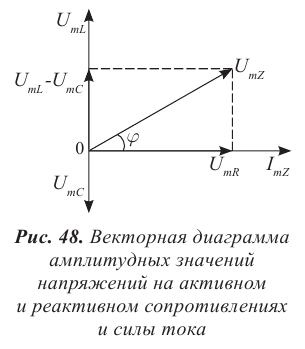
Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.
Закон Ома
В результате проведенных исследований Георг Ом обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I в цепи есть величина постоянная:
где R — электрическое сопротивление. Данная формула называется законом Ома, который до сих пор является основным расчетным инструментом при проектировании электрических и электронных схем.
Если по оси абсцисс отложить значения напряжения, а по оси ординат — значения тока в цепи при данных значениях напряжения, то получится график зависимости силы тока I от напряжения U.
Рис. 2. График зависимости силы тока от напряжения.
Из этого графика видно, что эта зависимость линейная. Угол наклона прямой зависит от величины сопротивления. Чем больше R, тем меньше угол наклона.
Рис. 3. График зависимости силы тока от сопротивления.
Если зафиксировать напряжение U и по оси абсцисс откладывать значения R электрического сопротивления, то из полученного графика видно, что эта зависимость уже нелинейная — с ростом сопротивления поведение тока описывает обратно пропорциональной функцией — гиперболой.
Закон Ома перестает работать при больших величинах тока, так как начинают работать дополнительные эффекты, связанные с тепловым разогревом вещества, ростом температуры. В газах при больших токах возникает пробой, ток растет лавинообразно, отклоняясь от линейного закона.
Вынужденные электромагнитные колебания
Как вы помните, вынужденные колебания
возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.
Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).
Рис. 12. Вынужденные колебания
Если напряжение источника меняется по закону:
то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .
Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс
— резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.
Звоните нам: 8
(бесплатный звонок по России)
+7
(бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео БЕСПЛАТНО
Техническая поддержка: [email protected] (круглосуточно)
Полный онлайн-курс подготовки к ЕГЭ по математике. Структурировано. Четко. Без воды. Сдай ЕГЭ на 100 баллов!
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Единицы измерения
В международной системе единиц СИ единица измерения электрического сопротивления называется “ом” в честь физика Георга Ома. По определению электрическим сопротивлением 1 Ом обладает участок цепи, на котором падает напряжение 1 В при силе тока 1 А.
Единица измерения удельного сопротивления получается производной от единиц величин, входящих в фориулу: сопротивления, длины и площади. То есть в системе СИ получатся, что если R = 1 Ом, S = 1 м 2 , а L = 1 м, то ρ = 1 .
Это и есть единица измерения удельного сопротивления. Но на практике оказалось, что у реальных проводов площади сечений гораздо меньше 1 м 2 . Поэтому было решено при вычислении ρ использовать значение площади S в мм 2 , чтобы итоговое значение имело компактный вид. Тогда получаются более удобные (меньше нулей после запятой) для восприятия числовые значения удельного сопротивления:
Общие сведения
Любое физическое тело состоит из молекул и атомов. Эти частицы взаимодействуют между собой. Они могут притягиваться друг к другу или отталкиваться. В изолированной системе элементарные частицы являются носителями заряда. В спокойном состоянии, то есть когда на тело не оказывается внешнего воздействия, алгебраическая сумма энергии частиц всегда постоянная величина. Это утверждение называется законом сохранения электрического заряда.
Частицы хаотично могут перемещаться по кристаллической решётке, но их движение компенсируется. Поэтому ток не возникает. Но если к телу приложить внешнюю силу, то свободные электроны начинают двигаться в одну сторону. Это упорядоченное движение заряженных частиц и называют электрическим током. Количественно его можно описать через силу.
Упорядочено заряды заставляет двигаться электрическое поле, вдоль линий которого и происходит перемещение. Впервые этот термин ввёл Фарадей. Он сумел выяснить, что вокруг любого носителя существует особый вид материи, влияющий на поведение других частиц. За силовую характеристику электрического поля было взято отношение действующей силы к величине заряда, помещённого в данную точку: E = F / q. Назвали эту характеристику напряжённостью.
Изучение поля позволило экспериментально открыть принцип суперпозиции. То есть установить, что напряжённость поля, созданного системой зарядов, равна геометрической сумме величин, существующих у отдельных носителей: E = Σ E1 + E2 +…+ En. Напряжённость прямо пропорциональна напряжению, которое, в свою очередь, равняется разности потенциалов между двумя точками.
По сути, это работа электрического поля, совершаемая для переноса единичного заряда из одного места в другое: U = A / q = E * d, где d – расстояние между точками. Значение напряжения зависит от нескольких факторов:
- строения тела;
- температуры;
- сопротивления.
Самое большее влияние оказывает последняя величина. Именно она характеризует способность материала препятствовать прохождению тока, то есть определяет проводимость. Сопротивление зависит от длины проводника и его сечения: R = (p * l) / S, где p – параметр обратный удельной проводимости (справочное значение). Он численно равняется сопротивляемости однородного проводника единичной длины и площади сечения.
Что мы узнали?
Итак, мы узнали, что зависимость силы тока в электрической цепи описывается с помощью закона Ома. Сила тока I прямо пропорциональна величине U напряжения, и обратно пропорциональна сопротивлению R.
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн.
Определите модуль среднего значения ЭДС самоиндукции в интервале времени от 10 до 15 с.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока в цепи и индуктивности:
Поскольку в интервале времени от 10 до 15 с ток в цепи не менялся, получаем, что модуль среднего значения ЭДС самоиндукции в этом интервале времени равен нулю.
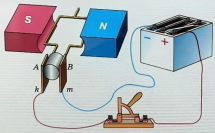
На рисунке изображен момент демонстрационного эксперимента по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится внутри сплошного металлического кольца, но не касается его. Коромысло с металлическими кольцами может свободно вращаться вокруг вертикальной опоры. При выдвижении магнита из кольца влево кольцо будет
1) оставаться неподвижным
2) перемещаться вправо
3) совершать колебания
4) перемещаться вслед за магнитом
При выдвижении магнита из кольца влево магнитный поток от него через кольцо начинает уменьшаться. В кольце возникает индукционный ток. Согласно правилу Ленца, направление тока таково, что создаваемое им магнитное поле препятствует изменению магнитного потока. Поскольку коромысло может свободно вращаться вокруг вертикальной оси, а магнитное поле магнита неоднородно, коромысло начнет двигаться под действием сил Ампера таким образом, чтобы препятствовать изменению магнитного потока, то есть коромысло начнет перемещаться вслед за магнитом.
Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1) :
Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона
. Мы вскоре приведём её более строгий вывод.
Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
Это пробная версия онлайн курса по профильной математике.
Вы получите доступ к 3 темам, которые помогут понять принцип обучения, работу платформы и оценить ведущую курса Анну Малкову.
— 3 темы курса (из 50). — Текстовый учебник с видеопримерами. — Мастер-класс Анны Малковой. — Тренажер для отработки задач.
Регистрируйтесь, это бесплатно!
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных
Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
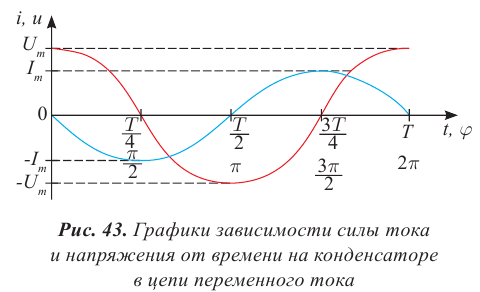
Переменный ток — вынужденные электромагнитные колебания.
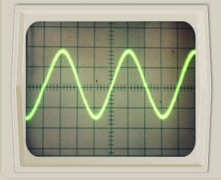
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
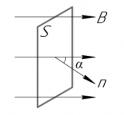
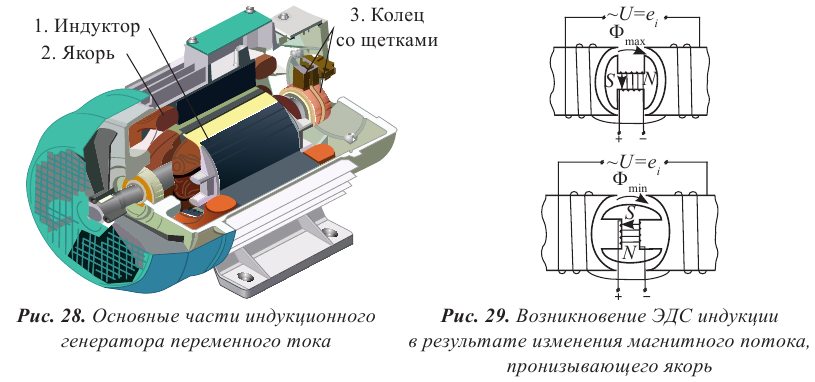
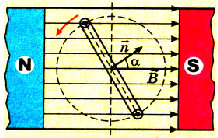
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
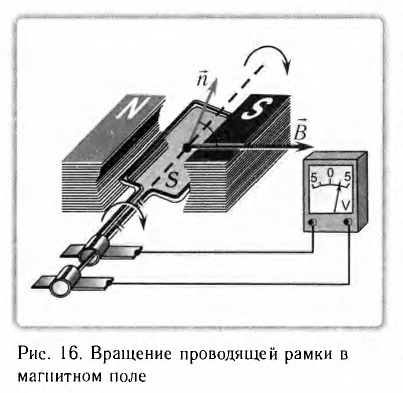
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
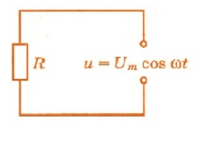
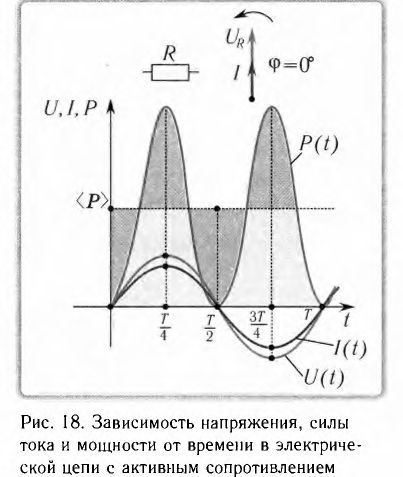
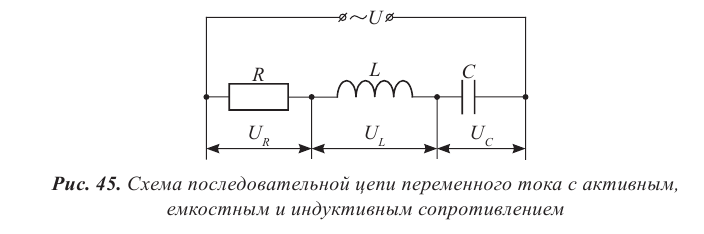
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
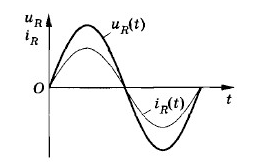
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
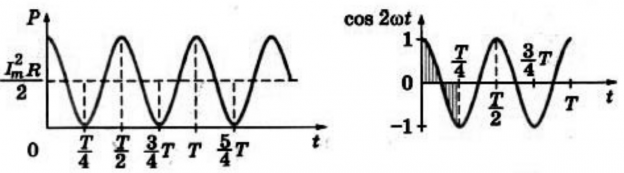
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
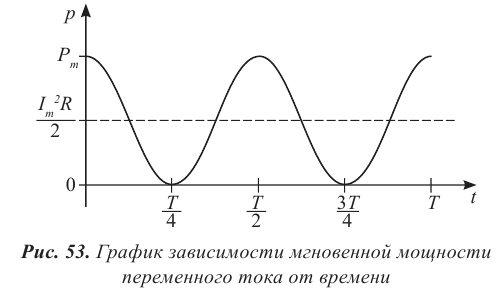
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
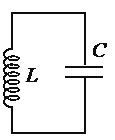
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
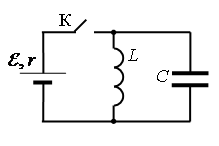
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
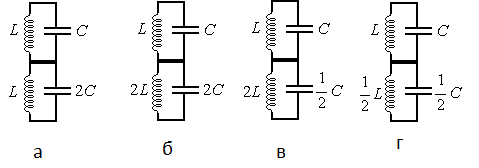
Задание EF18116
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
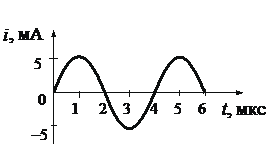
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
Амплитуда силы тока в контуре формула
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.
Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.
Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.
Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.
Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.
Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.
Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.
Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.
Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.
Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).
Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k
величины, характеризующие состояние системы:
величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .
ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид
где q» — вторая производная заряда по времени. Величина
является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.
Одним из решений уравнения (1) является гармоническая функция
Период колебаний в контуре дается формулой (Томсона):
Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.
Фаза определяет состояние колеблющейся системы в любой момент времени t.
Ток в цепи равен производной заряда по времени, его можно выразить
Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу
ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,
где- угол между нормалью к рамке и вектором магнитной индукции .
По закону электромагнитной индукции Фарадея ЭДС индукции равна
где — скорость изменения потока магнитной индукции.
Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции
где — амплитудное значение ЭДС индукции.
2. Если к контуру подключить источник внешней гармонической ЭДС
то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.
При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.
В промышленных цепях переменного тока России принята частота 50 Гц.
Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:
Поэтому количество теплоты, выделится за время Т:
Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:
Отсюда действующее значение тока
Аналогично действующее значение напряжения
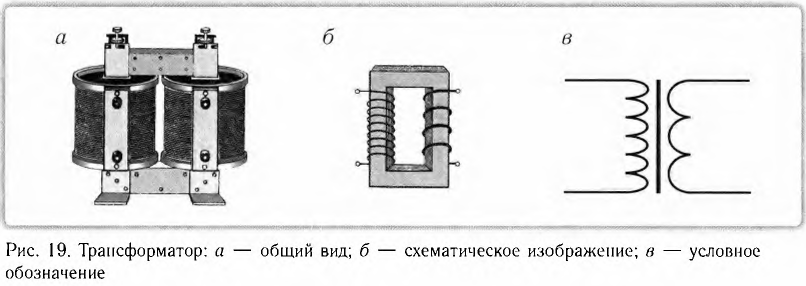
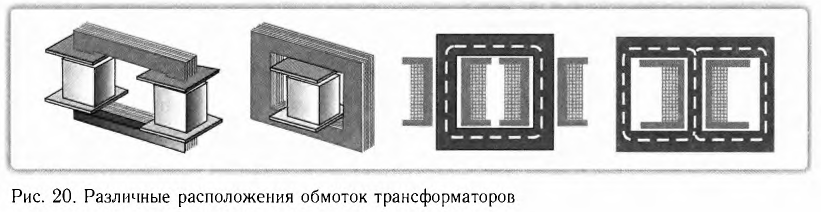
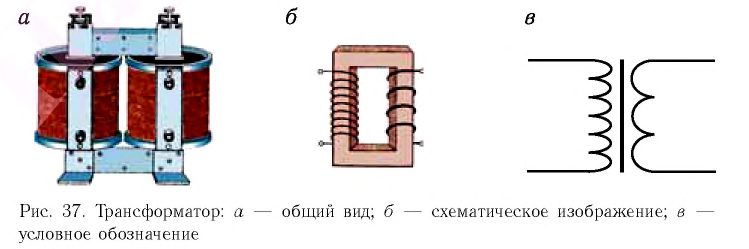
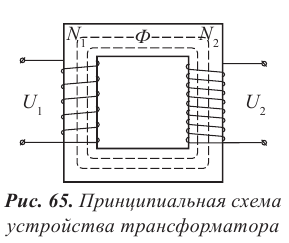
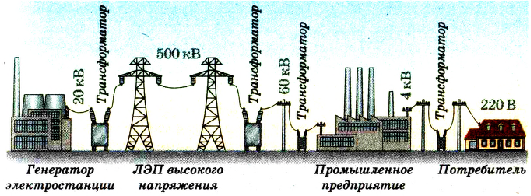
Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.
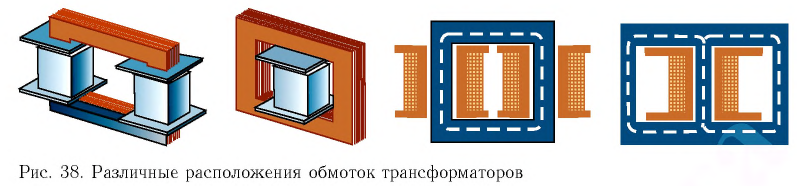
Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.
называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего
Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.
Из уравнения следует, что . Период определим по формуле циклической частоты
Зависимость силы тока от времени имеет вид:
Амплитуда силы тока.
Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:
i=-5000 sin100t
Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым. Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).
Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд +Q , а на другой – заряд —Q . При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией
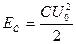
где 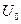
После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения 

(где 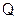

Когда конденсатор полностью разрядится 
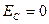


Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q , но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.
Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.
Перезарядка конденсатора до максимального напряжения 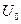
В реальных контурах имеют место следующие потери энергии:
1) тепловые потери, т.к. R ¹ 0;
2) потери в диэлектрике конденсатора;
3) гистерезисные потери в сердечнике катушке;
4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что 
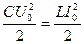
Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.
В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:
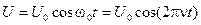
где n — собственная частота колебательного контура, w = 2pn — собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как

Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона
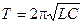
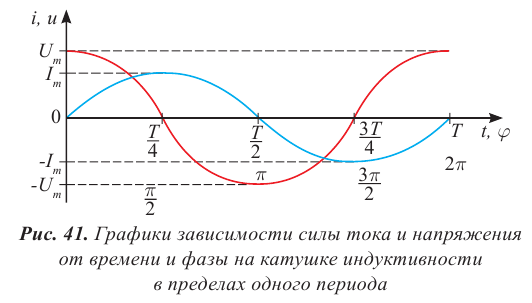
Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на 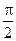
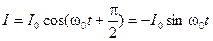
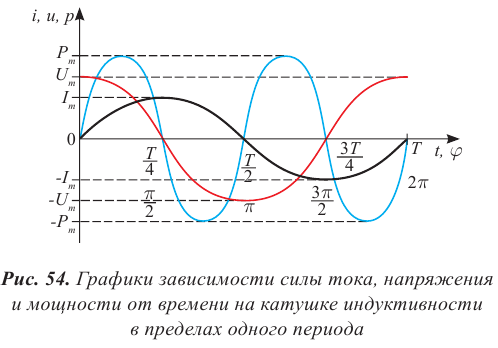
На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.
В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.
Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10034 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением где все величины выражены в СИ. Емкость конденсатора равна Найдите амплитуду силы тока. (Ответ дать в амперах.)
Общий вид зависимости напряжения на конденсаторе в колебательном контуре: где — амплитудное значение напряжения. Сравнивая с находим, что Значение максимального заряда на обкладках конденсатора равно Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением Отсюда находим
Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс — емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.
P. S. Мой способ решения кажется мне более разумным по той причине, что обе формулы даны в учебнике по физике, в отличие от последней формулы в предложенном вами способе решения.
Спасибо. Хороший вариант.
Но использованная в конце формула, конечно же, дается в школьном курсе. Ведь насколько я знаю, в этот момент в школьной физике уже начинают использовать производные. Формула следует из закона изменения заряда со временем при гармонических колебаниях и из того, что ток — это производная от заряда
Уравнение выражает зависимость силы тока от времени
Вопрос по физике:
Уравнение i=0.0001пcos(wt+п/2) выражает зависимость силы тока от времени в колебательном контуре. Чему будет равна энергия на конденсаторе и в катушке индуктивности, если ток в цепи равен 0.0001 А?
1) В конденсаторе энергия минимальна, в катушке максимальна
2) В конденсаторе и катушке энергия распределена поровну
3) В конденсаторе энергия максимальна, в катушке равна нулю
4) В конденсаторе энергия равна нулю, в катушке максимальна
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Очевидно что ответ 4) потому что Iм=0,0001A
в этот момент энергия МП максимальна а энергия ЭП равна нулю.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Уравнение зависимости силы тока от времени
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.
Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.
Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.
Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.
Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.
Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.
Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.
Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.
Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.
Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).
Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k
величины, характеризующие состояние системы:
величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .
ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид
где q» — вторая производная заряда по времени. Величина
является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.
Одним из решений уравнения (1) является гармоническая функция
Период колебаний в контуре дается формулой (Томсона):
Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.
Фаза определяет состояние колеблющейся системы в любой момент времени t.
Ток в цепи равен производной заряда по времени, его можно выразить
Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу
ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,
где- угол между нормалью к рамке и вектором магнитной индукции .
По закону электромагнитной индукции Фарадея ЭДС индукции равна
где — скорость изменения потока магнитной индукции.
Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции
где — амплитудное значение ЭДС индукции.
2. Если к контуру подключить источник внешней гармонической ЭДС
то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.
При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.
В промышленных цепях переменного тока России принята частота 50 Гц.
Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:
Поэтому количество теплоты, выделится за время Т:
Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:
Отсюда действующее значение тока
Аналогично действующее значение напряжения
Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.
Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.
называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего
Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.
Из уравнения следует, что . Период определим по формуле циклической частоты
Зависимость силы тока от времени имеет вид:
Амплитуда силы тока.
Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:
i=-5000 sin100t
Презентация к уроку
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
- Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
- Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.
Тип урока:систематизация и обобщение знаний.
Техническая поддержка урока:
- Демонстрации:
- Плакаты.
- Показ слайдов с помощью информационно – компьютерных технологий.
- Дидактический материал:
- Опорные конспекты с подробными записями на столах.
- Оформление доски:
- Плакат с кратким содержанием опорных конспектов (ОК);
- Плакат – рисунок с изображением колебательного контура;
- Плакат – график зависимости колебаний заряда конденсатора, напряжения между обкладками конденсатора, силы тока в катушке от времени, электрической энергии конденсатора, магнитной энергии катушки от времени.
План урока:
1. Этап повторения пройденного материала. Проверка домашнего задания.
Четыре группы задач по теме:
- Электромагнитные колебания.
- Колебательный контур.
- Свободные колебания. Свободные колебания – затухающие колебания
- Характеристика колебаний.
2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.
Учитель: Темой урока является «Решение задач по теме: «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ»
К доске вызываются 3 ученика для проверки домашнего задания.
– Задания по этой теме можно разделить на четыре группы.
Четыре группы задач по теме:
1. Задачи с использованием общих законов гармонических колебаний.
2. Задачи о свободных колебаниях конкретных колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.
– Мы остановимся на решении задач 1 и 2 групп.
Урок начнем с повторения необходимых понятий для данной группы задач.
Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.
Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.
Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.
Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 10 8 (м/с)
Основные характеристики колебаний
Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u
Схема колебательного контура
Учитель: Что представляют электромагнитные колебания в контуре?
Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.
Задача №1 (д/з)
Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?
Задача № 2 (д/з)
Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.
Задача № 3 (д/з)
Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.
Схема электромагнитных колебаний
Ученик 1 наглядно описывает процессы в колебательном контуре.
Ученик 2 комментирует электромагнитные колебания в контуре, используя графическую зависимость заряда, напряжения. Силы тока, электрической энергии конденсатора, магнитной энергии катушки индуктивности от времени.
Уравнения, описывающие колебательные процессы в контуре:
Обращаем внимание, что колебания силы тока в цепи опережают колебания напряжения между обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы тока по гармоническому закону, необходимо учитывать связь между функциями синуса и косинуса.
Задача № 1.
По графику зависимости силы тока от времени в колебательном контуре определите, какие преобразования энергии происходят в колебательном контуре в интервале времени от 1мкс до 2мкс?
1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.
Задача № 2.
По графику зависимости силы тока от времени в колебательном контуре определите:
а) Сколько раз энергия катушки достигает максимального значения в течение первых 6 мкс после начала отсчета?
б) Сколько раз энергия конденсатора достигает максимального значения в течение первых 6 мкс после начала отсчета?
в) Определите по графику амплитудное значение силы тока, период, циклическую частоту, линейную частоту и напишите уравнение зависимости силы тока от времени.
Задача № 3 (д/з)
Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите, какое преобразование энергии происходит в интервале времени от 0 до 2 мкс?
1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.
Задача № 4 (д/з)
Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.
К доске вызываются 2 ученика
Задача № 5, 6
Задача № 7
Заряд на обкладках конденсатора колебательного контура изменяется по закону
q = 3·10 –7 cos800πt. Индуктивность контура 2Гн. Пренебрегая активным сопротивлением, найдите электроемкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.
Задача № 8
В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменяется заряд конденсатора в колебательном контуре с течением времени.
| t, 10 –6 (C) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q, 10 –9 (Кл) | 2 | 1,5 | –1,5 | –2 | –1,5 | 1,5 | 2 | 1,5 |
1. Напишите уравнение зависимости заряда от времени. Найдите амплитуду колебаний заряда, период, циклическую частоту, линейную частоту.
2. Какова энергия магнитного поля катушки в момент времени t = 5 мкс, если емкость конденсатора 50 пФ.
Домашнее задание. Напишите уравнение зависимости силы тока от времени. Найдите амплитуду колебаний силы тока. Постройте графическую зависимость силы тока от времени.
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур
Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.
Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.
Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.
Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.
Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.
Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.
Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.
Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).
Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.
Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.
Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.
Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.
Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.
Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).
Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.
Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.
Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.
Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .
Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).
Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.
Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).
Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.
Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).
Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.
Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).
Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.
Аналогия. Маятник вернулся в исходное положение.
Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!
Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.
В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.
Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.
Энергетические превращения в колебательном контуре
Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .
Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.
Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:
Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:
В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:
Соотношение (1) применяется при решении многих задач.
Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1) :
Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.
Гармонический закон колебаний в контуре
Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».
Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.
Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).
Рис. 10. Положительное направление обхода
Сила тока считается положительной 0)’ (I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .
Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.
При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ dot > 0′ /> .
Величины и меняются со временем, но энергия контура остаётся неизменной:
Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):
Подставляя сюда и , получим:
Но сила тока не является функцией, тождественно равной нулю; поэтому
Перепишем это в виде:
Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:
Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:
Мы снова пришли к формуле Томсона.
Гармоническая зависимость заряда от времени в общем случае имеет вид:
Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.
Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :
Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:
Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:
Амплитуда силы тока равна:
Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).
Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .
А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).
Рис. 11. Графики колебаний заряда и тока
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.
Используя формулу приведения
запишем закон изменения тока (13) в виде:
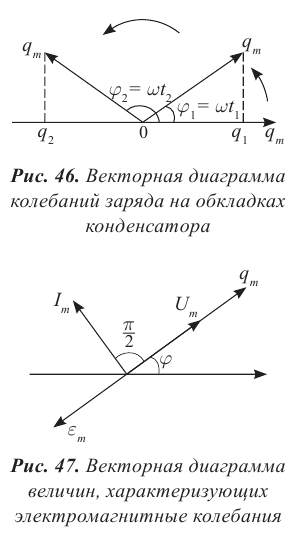
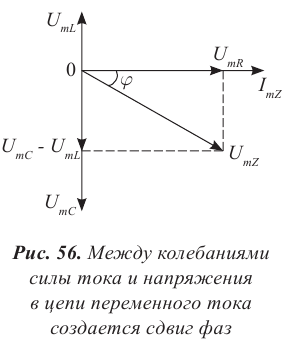
Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .
Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).
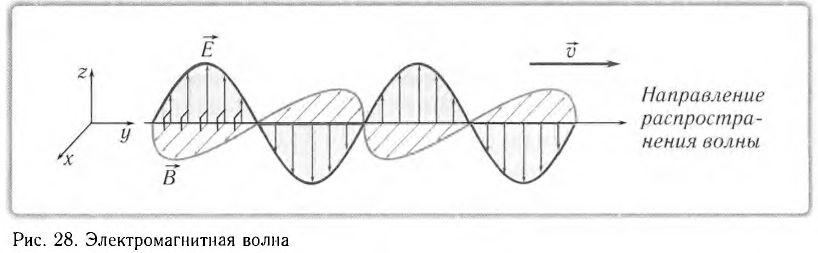
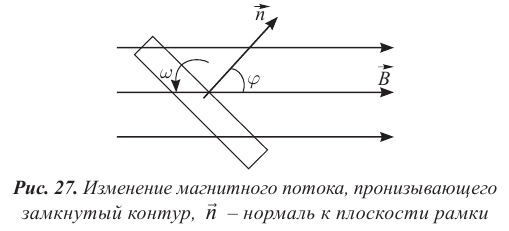
Вынужденные электромагнитные колебания
Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.
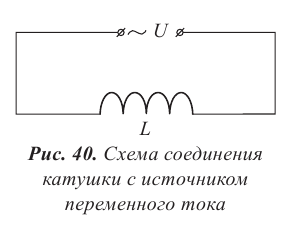
Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).
Рис. 12. Вынужденные колебания
Если напряжение источника меняется по закону:
то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .
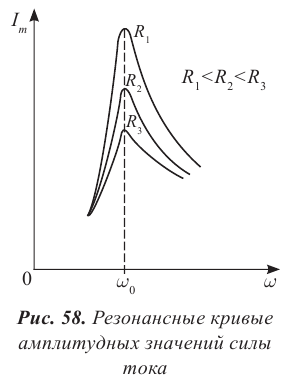
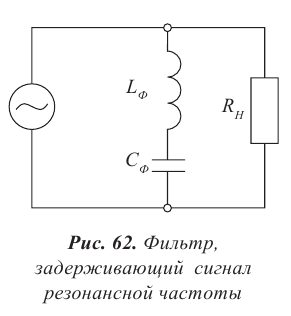
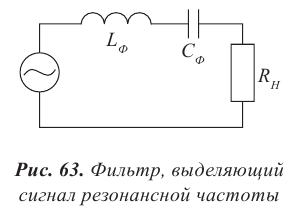
Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео
БЕСПЛАТНО
Техническая поддержка:
help@ege-study.ru (круглосуточно)
Полный онлайн-курс подготовки к ЕГЭ по математике. Структурировано. Четко. Без воды. Сдай ЕГЭ на 100 баллов!
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.
Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
Это пробная версия онлайн курса по профильной математике.
Вы получите доступ к 3 темам, которые помогут понять принцип обучения, работу платформы и оценить ведущую курса Анну Малкову.
— 3 темы курса (из 50).
— Текстовый учебник с видеопримерами.
— Мастер-класс Анны Малковой.
— Тренажер для отработки задач.
Регистрируйтесь, это бесплатно!
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных
http://online-otvet.ru/fizika/5ceab73196f4e19a2989b3b1
http://pro-smartfon.ru/uravnenie-zavisimosti-sily-toka-ot-vremeni/
Содержание:
Переменный электрический ток:
Магнитный моток Ф однородного магнитного поля индукцией
Закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, взятой с противоположным знаком,
В механической системе при действии на нее внешней периодической силы возникают вынужденные колебания. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи называются переменным электрическим током.
Ток, сила и направление которого периодически меняются, называется переменным.
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Такая функциональная зависимость силы тока от времени позволяет, по сравнению со всеми другими зависимостями, наиболее просто и экономично осуществлять передачу, распределение и использование электрической энергии.
Электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного электрического тока, называется генератором переменного тока.
Принцип действия индукционного генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S вращается с угловой скоростью со вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией 
При равномерном вращении рамки угол 
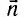
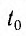
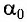
где 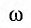
Подставляя полученное выражение в формулу Ф = BScosa, найдем зависимость магнитного потока через рамку от времени:
Поскольку магнитный поток, пронизывающий рамку, изменяется со временем (рис. 17), то в ней согласно закону Фарадея индуцируется ЭДС
Как видно, ЭДС индукции изменяется по синусоидальному закону:
где 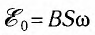
При подключении к выводам рамки устройства, потребляющего энергию (нагрузки сопротивлением R), по нему будет проходить переменный электрический ток. По закону Ома для участка цепи сила проходящего тока
где 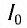
Колебания силы тока и напряжения происходят с одинаковой частотой 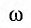
где 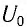
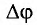
Ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Основными частями индукционного генератора переменного тока являются:
- индуктор — постоянный магнит или электромагнит, который создает магнитное поле;
- якорь — обмотка, в которой индуцируется переменная ЭДС; коллектор со
- щетками — устройство, посредством которого ток снимается с вращающихся частей.
Неподвижная часть генератора называется статором, а подвижная — ротором.
В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. Для получения переменных токов большой мощности якорь делают неподвижным, чтобы конструктивно упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1—2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1 —2 Гц. Поэтому для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока.
Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т. е. ротор должен делать 50 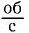
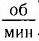
Для увеличения амплитудного значения ЭДС индукции нужно либо увеличивать индукцию магнитного поля, пронизывающего обмотки якоря, либо увеличивать число витков его обмоток. Для увеличения индукции магнитного поля 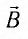
Действующие значения силы тока и напряжения
Закон Ома для однородного участка цепи: сила тока на однородном участке цепи прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению участка цепи:
До сих пор рассматривались электрические цепи, содержащие резисторы, конденсаторы и катушки индуктивности, где в качестве источника ЭДС использовался источник постоянного тока. При подключении таких цепей к источнику переменного тока возникают новые закономерности, которые мы и рассмотрим ниже.
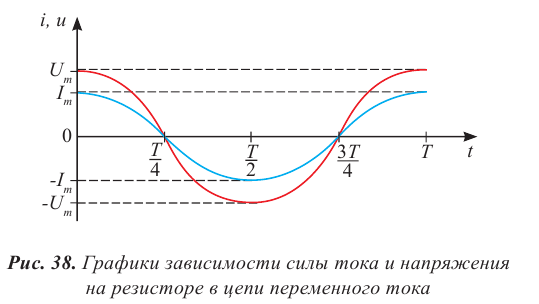
Пусть источник тока создает переменное гармоническое напряжение
Согласно закону Ома для участка цепи сила тока на участке цепи, содержащей только резистор сопротивлением R (рис. 18), подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где
Величины 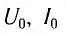
Зависящие от времени значения напряжения U(t) и силы тока I(t) называют мгновенными.
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 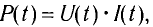
С учетом зависимости силы тока от времени перепишем выражение для мгновенной мощности на резисторе в цепи переменного тока в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину на практике в качестве характеристики длительно протекающих процессов крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла, ее среднее значение за период колебаний равно нулю (см. рис. 18).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
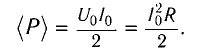
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующее (эффективное) значение силы переменного тока равно силе такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 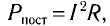
Аналогично можно ввести действующее значение и для напряжения:
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, аналогичны и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока вследствие того, что их колебания совпадают по фазе (см. рис. 18).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока вследствие того, что их колебания совпадают по фазе (см. рис. 18).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
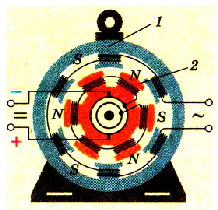
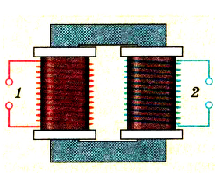
Преобразование переменного тока
Генераторы переменного тока создают в расчете на определенные, сравнительно небольшие, значения напряжения и мощности тока. Для практического использования электрической энергии в различных устройствах и приборах необходимы различные значения напряжений. Для этого используются трансформаторы (от латинского слова transformo — преобразую). Трансформатор был изобретен в 1878 г. русским ученым Павлом Николаевичем Яблочковым.
Трансформатор (рис. 19, а) — это электромагнитный аппарат, преобразующий переменный ток одного напряжения в переменный ток той же частоты, но другого напряжения. Схематическое изображение и условное обозначение трансформатора показаны на рисунке 19 6, в.
В простейшем случае трансформатор состоит из двух обмоток, надетых на общий сердечник. Обмотка трансформатора, на которую подается переменное напряжение, называется первичной, а обмотка, с которой снимается преобразованное переменное напряжение, — вторичной. Число витков в первичной обмотке трансформатора обозначим 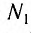
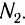
Обмотки трансформатора могут быть расположены на сердечнике различным образом (рис. 20).
Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь (без рассеяния) пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем, то согласно закону Фарадея в ней возбуждается ЭДС индукции. Подчеркнем, что трансформатор не годится для преобразования постоянного тока, поскольку магнитный поток, создаваемый в этом случае, не изменяется с течением времени.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС 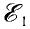
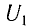
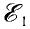
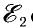
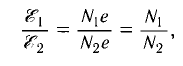
где 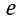
Режимом холостого хода трансформатора называется режим с разомкнутой вторичной обмоткой. В этом случае напряжение на вторичной обмотке равно индуцируемой в ней ЭДС:
Кроме того, вследствие малости активного сопротивления первичной обмотки
Следовательно, в режиме холостого хода согласно выражению (1) получаем
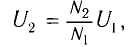
т. е. действующее значение напряжения 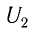
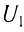
Как следует из выражения (2), в зависимости от отношения числа витков в обмотках напряжение 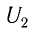
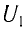
Тип трансформатора характеризуется коэффициентом трансформации, который равен отношению числа витков первичной обмотки к числу витков вторичной:
Согласно выражению (2) отношение действующих значений напряжений на концах первичной и вторичной обмоток трансформатора в режиме холостого хода равно коэффициенту трансформации:
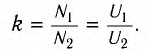
Как следует из выражения (3), 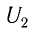
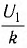
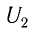
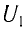
Рабочим ходом (режимом) трансформатора называется режим, при котором в цепь его вторичной обмотки включена некоторая нагрузка. Можно считать, что в этом случае действующие значения ЭДС, напряжений и токов в первичной и вторичной цепях, согласно закону Ома для полной цепи, связаны соотношениями
Включение нагрузки во вторичную цепь трансформатора приводит к появлению в ней тока. Согласно правилу Ленца, магнитный поток, создаваемый током во вторичной обмотке, стремится скомпенсировать изменение магнитного потока через витки вторичной обмотки, а значит, и через витки первичной. Это приводит к тому, что после включения нагрузки сила тока в первичной обмотке увеличивается таким образом, что суммарный магнитный поток через первичную обмотку достигает прежней величины.
Согласно закону сохранения энергии мощность тока, выделяемая во вторичной обмотке трансформатора, «черпается» из цепи его первичной обмотки. Пренебрегая потерями энергии, которые в современных трансформаторах не превышают 2 %, можем записать, что мощности тока в обеих обмотках трансформатора практически одинаковы:
Режимом короткого замыкания называется режим, при котором вторичная обмотка трансформатора замкнута без нагрузки. Данный режим опасен для трансформатора, поскольку в этом случае ток во вторичной обмотке максимален и происходят электрическая и тепловая перегрузки системы.
При работе трансформатора всегда имеются энергетические потери, связанные с такими физическими процессами, как:
- нагревание обмоток трансформатора при прохождении электрического тока;
- работа по перемагничиванию сердечника;
- рассеяние магнитного потока.
Наиболее значительные энергетические потери при работе трансформатора обусловлены тепловым действием вихревых токов (токов Фуко), возникающих в сердечнике при изменении пронизывающего его магнитного потока.
Для уменьшения тепловых потерь сердечники (магнитопроводы) трансформаторов изготовляют не из сплошного куска металла, а из тонких пластин специальной трансформаторной стали, разделенных тончайшими слоями диэлектрика (пластины покрывают лаком).
Для предотвращения перегрева мощных трансформаторов используется масляное охлаждение (рис. 21).
Современные трансформаторы имеют очень высокие КПД (до 95—99 %), что позволяет им работать практически без потерь.
Пример №1
Первичная обмотка трансформатора имеет 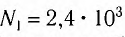
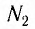
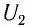
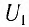
Решение
По определению коэффициент трансформации
где 
Для вторичной обмотки трансформатора по закону Ома для замкнутой цепи можно записать:
где 
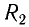
Откуда 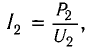
Подставляя выражения для 
Число витков во вторичной обмотке определится по формуле
Ответ: 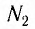
Производство, передача и потребление электрической энергии
Электроэнергия вырабатывается на электростанциях. В зависимости от вида первоначально используемого носителя энергии все современные электростанции делятся на тепловые, атомные и гидроэлектростанции. Приведем характеристики основных типов электростанций.
Тепловые электростанции (ТЭС) работают на угле, нефти, мазуте, газе и других горючих ископаемых (КПД 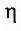
Гидроэлектростанции (ГЭС) используют энергию падающей воды (КПД 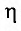
Атомные электростанции (АЭС) работают на энергии, выделяющейся при расщеплении ядер урана и плутония (КПД 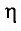
Как известно, тепловые потери в проводниках пропорциональны квадрату силы тока, поэтому для их уменьшения целесообразно передавать электроэнергию при малой силе тока. Уменьшение силы тока в п раз снижает тепловые потери в проводах в 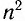
Напряжение питания отдельных потребителей должно быть низким для упрощения их конструкции и безопасности обслуживания, что легко достигается при применении трансформаторов.
Рассмотрим блок-схему производства, передачи и распределения электроэнергии (рис. 23).
Генератор переменного тока вырабатывает напряжение в десятки киловольт и подает его на повышающий трансформатор. Для передачи электроэнергии через ЛЭП напряжение повышается до сотен киловольт. Перед доставкой потребителю осуществляется каскадное (последовательное) понижение напряжения с помощью понижающих трансформаторов.
В современном обществе потребление электроэнергии распределяется примерно следующим образом: промышленность — 70 %; транспорт — 15 %; сельское хозяйство — 10 %; бытовое потребление — 5 %.
В настоящее время все большее распространение получают линии электропередач на постоянном токе. Это происходит потому, что, хотя преобразование постоянного напряжения сложнее и дороже, постоянный ток по сравнению с переменным обладает рядом преимуществ.
Во-первых, постоянный ток не создает переменных магнитных полей, которые индуцируют токи в близлежащих проводах, что приводит к потерям мощности.
Во-вторых, постоянный ток можно передавать при более высоком напряжении, так как действующее напряжение в цепи равно амплитудному, и не следует опасаться электрического пробоя изолятора или воздуха при амплитудном напряжении.
Экологические проблемы производства электрической энергии
Развитие цивилизации на нашей планете сопровождается непрерывным ростом ежегодного энергопотребления. Однако запасы природного топлива (нефти, газа, угля, дров, торфа) и иных полезных ископаемых на Земле ограничены, поскольку из-за изменения геологических условий их формирование в настоящее время практически прекратилось.
Наиболее распространенным энергоносителем на сегодняшний день является нефть, поскольку ее сравнительно легко добывать, транспортировать, очищать и использовать. Помимо этого, нефть также является сырьем для производства разнообразных синтетических материалов — красок, лекарств, синтетических волокон, пластмасс и т. д. Не зря ее называют «кровью экономики», поскольку уровень нефтедобычи определяет темпы мировой индустриализации.
По различным оценкам, в настоящее время выработка основных месторождений угля и нефти составляет около 60 %.
В нашей стране запасы нефти и угля не являются стратегическими. На территории Беларуси к основным видам добываемых топливных ресурсов следует отнести дрова и торф.
В настоящее время леса занимают около 30 % всей суши на Земле. Для сохранности леса его следует использовать лишь в тех пределах, в которых его можно восстановить. Соответственно, каждый год можно заготавливать I % нарастающих лесов, что составляет около 2 млрд 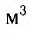
Работа электростанций вследствие их значительной мощности существенным образом влияет на состояние окружающей среды и приводит к появлению следующих экологических проблем:
- ТЭС — загрязнение атмосферы продуктами сгорания, изменение природного теплового баланса из-за рассеяния тепловой энергии;
- ГЭС — изменение климата, нарушение экологического равновесия, уменьшение пахотных площадей;
- АЭС — опасность радиоактивного загрязнения среды при авариях, проблемы захоронения радиоактивных отходов.
Одной из главных экологических проблем современности является рост выбросов в атмосферу продуктов сгорания топлива (в первую очередь углекислого газа). Углекислый газ «окутывает» Землю, подобно пленке, препятствуя ее охлаждению. Это приводит к парниковому эффекту, при котором среднегодовая температура поверхности Земли повышается. Соответственно, за последние десятилетия на планете наблюдается глобальное потепление, которое может привести к необратимым изменениям в климате Земли.
В процессе своей жизнедеятельности человек расходует химическую энергию, получаемую организмом при расщеплении пищи. Таким образом, жизнь устроена так, что в конечном итоге каждый из нас потребляет часть энергии, рожденной на Солнце. С этой точки зрения вполне объяснимо поклонение наших древних пращуров богам Солнца, «дарующим жизнь всему сущему».
Рост энергопотребления заставляет ученых и инженеров искать альтернативные источники энергии, которые были бы возобновляемыми, т. е., в отличие от нефти и газа, могли бы самостоятельно восстанавливаться с течением времени.
К возобновляемым источникам энергии относят ветер, недра Земли (геотермальная энергия), морские приливы, а также солнечное излучение, используемое напрямую.
Энергия ветра уже достаточно успешно преобразуется в электроэнергию в многочисленных небольших ветряных генераторах в зонах устойчивых ветров (рис. 24) .
Проекты будущего предлагают использовать в качестве возобновляемых источников энергии колоссальную энергию океанических и воздушных течений: волн, тропических ураганов и торнадо. Ключевая причина их формирования — неравномерное нагревание Солнцем различных участков поверхности Земли.
Геотермальная энергия в местах естественных разломов используется для нужд человека. Так, например, г. Рейкьявик (столица Исландии) полностью отапливается за счет горячих геотермальных вод. Запасы геотермальной энергии достаточно велики, о чем можно судить по разрушительной силе землетрясений, извержений вулканов, гейзеров.
В настоящее время делаются первые шаги для использования энергии океанических приливов и отливов. Инженерная идея подобных проектов проста: если наполнить резервуары при приливе, то при отливе «уходящая» вода сможет вращать турбины и производить электричество.
Развитие современных технологий позволяет активно использовать энергию, вырабатываемую солнечными батареями. Так, в южных широтах энергии подобных батарей, установленных на крыше, хватает для энергоснабжения небольшого дома.
Современные технологии позволяют, используя солнечные батареи, получать электрическую энергию непосредственно от солнечного излучения не только на Земле, но и в космосе (рис. 25). Есть даже смелые проекты, в которых предлагается разместить солнечные батареи в ближнем космосе на расстоянии 36 ООО км от поверхности Земли. Это так называемая «синхронная» орбита, на которой батареи будут казаться «неподвижными» для земного наблюдателя, поскольку период их обращения будет равен 24 ч. В этом случае батареи будут находиться в тени Земли только 2 % времени, что позволит производить в 60 раз больше электричества, чем при таких же условиях на Земле.
В настоящее время активно разрабатываются проекты использования для получения энергии реакции слияния легких ядер водорода (термоядерного синтеза). Привлекательность проектов обусловлена тем, что запасы водорода в Мировом океане практически неограниченны. Кроме того, ожидается, что энергетический выход реакторов нового поколения будет в десятки раз выше, чем у существующих АЭС.
Возобновляемые источники энергии сравнительно безопасны, поскольку их использование практически не приводит к загрязнению окружающей среды.
Электромагнитные волны и их свойства
Впервые гипотезу о существовании электромагнитных волн высказал в 1864 г. шотландский физик Джеймс Максвелл. В своих работах он показал, что источниками электрического поля могут быть как электрические заряды, так и магнитные поля, изменяющиеся со временем.
В свою очередь магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическим током), либо переменными электрическими полями.
Изменение индукции магнитного поля с течением времени вызывает появление в окружающем пространстве вихревого электрического поля. Силовые линии этого поля замкнуты, а его напряженность 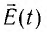
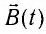
Максвелл предположил, что любое изменение напряженности вихревого электрического поля сопровождается возникновением переменного магнитного поля (рис. 26, б).
Далее этот процесс может повторяться «до бесконечности», поскольку поля смогут попеременно воспроизводить друг друга даже в вакууме.
Совокупность связанных друг с другом периодически изменяющихся электрического и магнитного полей называют электромагнитным полем. Согласно теории Максвелла переменное электромагнитное поле распространяется в пространстве с конечной скоростью.
Рассмотрим подробнее процесс образования электромагнитного поля в пространстве, окружающем проводник.
Пусть в проводнике возбуждены электромагнитные колебания, в результате чего сила электрического тока в нем меняется со временем. Поскольку сила тока связана со скоростью движения свободных зарядов в проводнике, то скорость движения последних также будет изменяться со временем.
Это говорит о том, что свободные заряды внутри проводника будут двигаться с ускорением.
Согласно теории Максвелла при ускоренном движении свободных зарядов в проводнике в пространстве вокруг него создается переменное магнитное поле, которое порождает переменное вихревое электрическое поле. Последнее, в свою очередь, вновь вызывает появление переменного магнитного поля уже на большем расстоянии от заряда и т. д. (рис. 27). Таким образом, в пространстве вокруг проводника образуются взаимосвязанные электрические и магнитные поля, которые распространяются с течением времени в виде волны.
Направление распространения волны
Электромагнитное поле, распространяющееся в вакууме или в какой-либо среде с течением времени с конечной скоростью, называется электромагнитной волной (рис. 28).
Электромагнитные волны являются поперечными, поскольку скорость 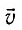
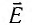
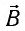
Одним из важнейших результатов теории Максвелла было теоретическое определение скорости распространения электромагнитных волн. Согласно этой теории скорость с электромагнитной волны в вакууме связана с электрической постоянной 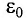
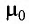
Скорость распространения электромагнитных волн в вакууме с является максимально (предельно) достижимой величиной. В любом веществе их скорость распространения меньше с и зависит от его электрических и магнитных свойств.
Перечислим основные свойства электромагнитных волн:
- Распространяются не только в различных средах, но и в вакууме.
- Отражаются и преломляются на границах раздела сред.
- Являются поперечными.
- Распространяются в вакууме со скоростью
Экспериментально электромагнитные волны были открыты в 1887 г. немецким физиком Генрихом Рудольфом Герцем. Для их генерации он использовал устройство, впоследствии названное вибратором Герца (рис. 29).
Длина волны, излучаемой при проскакивании искры между электродами устройства, была 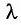
Герц считал, что такие волны невозможно использовать для передачи информации. Однако 7 мая 1905 г. русский ученый Александр Степанович Попов осуществил первую в мире передачу информации электромагнитными волнами — радиопередачу и положил начало эре радиовещания.
Свойства электромагнитных волн очень сильно зависят от их частоты. Спектр электромагнитного излучения удобно изображать в виде шкалы электромагнитных волн, приведенной на рисунке 30.
Классификация электромагнитных волн в зависимости от частот (длин волн) дается в таблице 5.
Таблица 5
Классификация электромагнитных волн
В настоящее время электромагнитные волны находят широкое применение в науке и технике:
- плавка и закалка металлов в электротехнической промышленности, изготовление постоянных магнитов (низкочастотные волны)-, телевидение, радиосвязь, радиолокация (радиоволны); мобильная связь, радиолокация (микроволны)-,
- сварка, резка, плавка металлов лазерами, приборы ночного видения (инфракрасное излучение)-,
- освещение, голография, лазеры (видимое излучение)-,
- люминесценция в газоразрядных лампах, закаливание живых организмов, лазеры (ультрафиолетовое излучение);
- рентгенотерапия, рентгеноструктурный анализ, лазеры (рентгеновское излучение)-,
- дефектоскопия, диагностика и терапия в медицине, исследование внутренней структуры атомов, лазеры, военное дело (гамма-излучение).
Электромагнитные волны и их свойства
Пример №2
Радиоприемник настроен на радиостанцию, работающую на длине волны 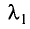
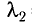
Решение
Длина волны определяется по формуле
где
Период колебаний в контуре находится по формуле
Запишем уравнения для двух длин волн:
Разделив второе уравнение на первое, получим
Из этого соотношения находим
Ответ:
Основные формулы:
В электрической цепи, состоящей из конденсатора и катушки индуктивности (идеальный колебательный контур), могут возникнуть электромагнитные колебания — периодические изменения заряда на обкладках конденсатора, тока в контуре, электрического поля между обкладками конденсатора и магнитного поля внутри катушки.
Период электромагнитных колебаний в идеальном колебательном контуре определяется формулой Томсона:
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток:
Сопротивление R резистора, на котором в цепи переменного тока происходит превращение электрической энергии во внутреннюю энергию, называется активным или омическим сопротивлением.
Трансформатор — электромагнитный аппарат, преобразующий переменный ток одного напряжения в переменный ток той же частоты, но другого напряжения. Принцип действия трансформатора основан на явлении электромагнитной индукции.
Тип трансформатора определяется коэффициентом трансформации, который равен отношению числа витков первичной обмотки к числу витков вторичной обмотки трансформатора:
Если k < 1, то трансформатор повышающий, если k > 1 — понижающий.
Совокупность связанных друг с другом периодически изменяющихся электрического и магнитного полей называют электромагнитным полем.
Электромагнитной волной называется распространяющееся в вакууме или в какой-либо среде с течением времени с конечной скоростью переменное электромагнитное поле.
Электромагнитные волны являются поперечными, так как векторы 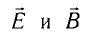
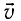
Скорость распространения электромагнитных волн в вакууме:
Преобразование переменного тока и трансформатор
Генераторы переменного тока создают в расчете на определенные значения напряжения. Для практического использования электрической энергии во всевозможных устройствах и приборах необходимы различные значения напряжений. Для этого используются трансформаторы (от лат. transforrno — преобразую). Первую модель (прототип) трансформатора создал в 1831 г. Майкл Фарадей, намотав на железное кольцо две изолированные обмотки, которую использовал в своих экспериментах. Трансформатор был впервые использован для изменения напряжения в 1878 г. русским ученым Павлом Николаевичем Яблочковым для питания изобретенных им источников света — «электрических свечей».
Трансформатор (рис. 37, а) — это электромагнитное устройство, преобразующее переменный ток одного напряжения в переменный ток другого напряжения с сохранением его частоты.
Трансформатор, увеличивающий напряжение, называют повышающим, а уменьшающий напряжение — понижающим. Схематическое изображение и условное обозначение трансформатора показаны на рисунке 37 б, в.
Самый простой трансформатор состоит из двух обмоток (катушек), надетых на общий замкнутый сердечник (см. рис. 37, а). Обмотка трансформатора, на которую подается переменное напряжение, называется первичной, а обмотка, с которой снимается преобразованное переменное напряжение, — вторичной. Число витков в первичной обмотке трансформатора обозначим 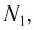
Обмотки трансформатора могут быть расположены на сердечнике различным образом (рис. 38).
Принцип действия трансформатора основан на явлении электромагнитной индукции. Магнитное поле, создаваемое переменным током в первичной обмотке (см. рис. 37, а), благодаря наличию замкнутого сердечника практически без потерь (без рассеяния) пронизывает витки вторичной обмотки. Для этого сердечник изготовляется из специального (ферромагнитного) материала, что позволяет создаваемое током в обмотках поле почти полностью локализовать внутри сердечника. В результате магнитный поток существует только внутри сердечника и одинаков во всех сечениях. Это дает возможность считать мгновенные значения магнитных потоков во всех сечениях сердечника одинаковыми.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС и на нее подается напряжение 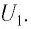
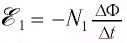
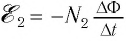
где 
Вследствие малого активного сопротивления первичной обмотки
Режимом холостого хода трансформатора называется режим с разомкнутой вторичной обмоткой. В этом случае напряжение на вторичной обмотке равно индуцируемой в ней ЭДС:
Следовательно, в режиме холостого хода из соотношения (1) получаем:
т. е. действующее значение напряжения 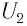
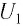
Как следует из выражения (2), в зависимости от отношения числа витков в обмотках напряжение 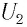
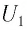
Тип трансформатора определяется коэффициентом трансформации, который равен отношению числа витков первичной катушки к числу витков вторичной:
Согласно выражению (2) отношение действующих значений напряжений на первичной и вторичной обмотках трансформатора в режиме холостого хода равно коэффициенту трансформации:
Как следует из соотношения (3), 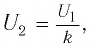
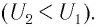
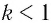
Рабочим ходом (режимом) трансформатора называется режим, при котором в цепь его вторичной обмотки включена некоторая нагрузка. Включение нагрузки во вторичную цепь трансформатора приводит к появлению в ней тока. Согласно правилу Ленца магнитный поток, создаваемый током во вторичной обмотке, стремится скомпенсировать изменение магнитного потока через витки вторичной обмотки, а значит, и через витки первичной обмотки (общий сердечник).
Это приводит к некоторому уменьшению магнитного потока в первичной обмотке, для компенсации которого действующее значение силы тока в первичной обмотке трансформатора увеличивается. Следовательно, после включения нагрузки трансформатора во вторичную обмотку сила тока в его первичной катушке увеличивается таким образом, чтобы суммарный магнитный поток через первичную обмотку достиг прежней величины.
Трансформатор не производит, а преобразовывает энергию. Согласно закону сохранения энергии мощность тока, выделяемая в цепи вторичной обмотки трансформатора в режиме нагрузки, поступает из цепи его первичной обмотки, т. е. от внешнего источника. Пренебрегая потерями энергии, связанными с нагреванием обмоток и работой по перемагничиванию сердечника, которые в современных трансформаторах не превышают 2 %, можем записать, что мощности тока в цепях обеих обмоток трансформатора практически одинаковы:
Таким образом, повышая напряжение в несколько раз, трансформатор во столько же раз уменьшает силу тока.
Режимом короткого замыкания называется режим, при котором вторичная обмотка трансформатора замкнута без нагрузки. Данный режим опасен для трансформатора, поскольку в этом случае действующее значение тока во вторичной обмотке максимально и происходят электрическая и тепловая перегрузки системы.
При работе трансформатора всегда имеются энергетические потери, связанные с такими физическими процессами, как:
- нагревание обмоток трансформатора при прохождении электрического тока;
- работа по перемагничиванию сердечника;
- рассеяние магнитного потока.
Наиболее значительные энергетические потери при работе трансформатора обусловлены тепловым действием вихревых токов (токов Фуко), возникающих в сердечнике при изменении магнитного потока.
Для уменьшения тепловых потерь сердечники (магнитопроводы) трансформаторов изготовляют не из сплошного куска металла, а из тонких пластин специальной трансформаторной стали, разделенных тончайшими слоями диэлектрика (пластины покрывают лаком). Такая конструкция сердечника позволяет значительно увеличить его электрическое сопротивление, что приводит к уменьшению потерь на его нагревание.
Для предотвращения перегрева мощных трансформаторов используется масляное охлаждение.
Современные трансформаторы имеют очень высокие КПД (до 98—99 %), что позволяет им работать практически без потерь.
Пример №3
Определите силу тока 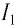
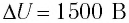
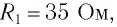
Дано:
Решение
По закону Ома сила тока в первичной обмотке:
где 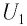
Коэффициент трансформации:
где 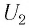
По условию задачи:
Тогда сила тока в первичной обмотке:
Ответ:
Генератор переменного тока
Под воздействием переменного электрического поля, созданного генератором, в промышленной сети возникает переменный ток, который представляет собой колебательное движение заряженных частиц.
Роль индукционного генератора переменного тока в промышленной сети
В быту и на производстве используют электрические приборы различной мощности, для питания которых создана промышленная сеть переменного тока с частотой 50 Гц. Источниками тока в этой сети являются индукционные генераторы переменного тока, расположенные на электростанциях. Переменный ток поступает по проводам линий электропередач к потребителям.
Индукционный генератор – это устройство, преобразующее механическую энергию в электрическую.
Вспомните! При изменении магнитного потока, пронизывающего замкнутый проводящий контур, в нем возникает индукционный ток.
Магнитный поток 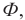
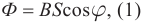
где 
Возьмите на заметку
Значение угла поворота при вращении рамки с угловой скоростью 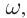
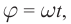
ЭДС индукции, созданная генератором переменного тока
Действие генератора переменного тока основано на законе электромагнитной индукции: переменный магнитный поток, пронизывающий замкнутую проводящую рамку, создает вихревое электрическое поле, в рамке возникает индукционный ток.
При очень малом значении промежутка времени 
где 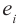
Определим производную от магнитного потока:
где 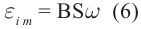
Ротор генератора состоит из большого количества рамок. Если число рамок в роторе N, то максимальное значение ЭДС генератора равно:
Устройство индукционного генератора переменного тока
Генератор состоит из: 1) индуктора – устройства, создающего магнитное поле; 2) якоря – обмотки, в которой индуцируется ЭДС; 3) колец со щетками – устройства, при помощи которого снимается или подводится ток к вращающейся части генератора (рис. 28).
Вращающуюся часть генератора называют ротором, неподвижную часть – статором. В мощных генераторах ротор используется в качестве индуктора, а статор – в качестве якоря. Это обусловлено тем, что допустимая сила тока в роторе ограничивается нагреванием скользящих контактов, а ток высоких значений, созданный на якоре, удобнее снимать с неподвижной обмотки. Для увеличения ЭДС индукции используется обмотка статора с большим количеством витков. Для увеличения магнитного потока обмотки индуктора и якоря наматывают на стальные сердечники, между которыми оставляют небольшой зазор, необходимый для вращения. При вращении ротора магнитный поток, пронизывающий якорь, меняется, возникает ЭДС индукции (рис. 29).
Вспомните! Закон электромагнитной индукции для замкнутого контура: 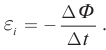
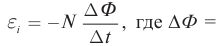
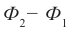
Напряжение на выходе генератора
Напряжение можно считать равным по числовому значению ЭДС индукции, если сопротивление обмотки статора значительно меньше в сравнении с сопротивлением внешней цепи: 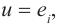
Из (8) следует, что максимальные значения ЭДС индукции и напряжения на выходе генератора равны:
где N − число витков якоря.
Генераторы электростанций создают напряжение в несколько тысяч вольт.
Частота вращения ротора генератора
Для получения переменного тока частотой 50 Гц ротор с одной парой полюсов должен вращаться с частотой 50 об/с или 3000 об/мин. Такую скорость вращения могут придать ротору паровые и газовые турбины. На гидроэлектростанциях используют тихоходные водяные турбины, поэтому для получения стандартной частоты переменного тока применяют генераторы с роторами, имеющими большое число пар полюсов. Ротор с 24 парами полюсов вращается с частотой 125 об/мин или около 2 об/с:
где n − число пар полюсов в индукторе.
Пример №4
Контур сечением S = 400 см2 , состоящий из N = 100 витков провода, равномерно вращают с угловой скоростью 
Дано:
S = 400 см2
N = 100
B = 0,01 Тл
СИ 0,04 м2
Решение:
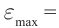
Ответ: 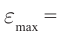
Переменный ток как пример вынужденных электромагнитных колебаний
Под воздействием переменного электрического поля, созданного генератором переменного тока с ЭДС, равным:
в цепи возникает переменный ток. Он представляет собой колебательное движение заряженных частиц.
Переменный ток – это вынужденные колебания заряженных частиц в проводнике под воздействием внешней периодически изменяющейся электродвижущей силы.
Частота промышленного тока в РК 50 Гц, циклическая частота, равная 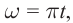
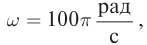
где u – мгновенное значение напряжения,
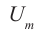
Если колебания напряжения рассматриваются с момента времени, соответствующего начальной фазе 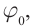
Зависимость силы тока от времени выразим на основе закона Ома, она представляет собой гармоническую функцию:
где i – мгновенное значение силы тока, 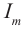
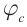
Интересно знать! В мире наиболее распространены два основных стандарта напряжения и частоты. Один из них – американский стандарт 110–127 В, 60 Гц. Другой стандарт – европейский, 220 – 240 В, 50 Гц (рис. 33).
Измерение величин, характеризующих переменный ток
Измерительные приборы, рассчитанные на постоянный ток, нельзя использовать для измерения величин, характеризующих переменный ток. Это вызвано тем, что стрелка на шкале прибора должна смещаться от нуля то в одну, то в другую сторону. Приборы для переменного тока предполагают отклонение стрелки только в одну сторону. Стрелка прибора вследствие своей инерционности не может совершать колебания с частотой 50 Гц, она «дрожит» на месте. Было решено, что показание стрелки прибора для переменного тока должно соответствовать показанию измерительного прибора для постоянного тока, если действия токов в цепи одинаковы.
Например, тепловое действие постоянного тока в 1 A должно быть идентичным тепловому действию переменного тока, если на шкале амперметра для переменного тока стрелка указывает 1 A. Такое эквивалентное значение переменного тока называют эффективным или действующим значением тока. Можно показать (это будет сделано в § 8), что действующие значения связаны с максимальными следующими соотношениями:
где U, I − действующие значения напряжения и силы тока.
Обратите внимание! На панели мультиметра размещены дисплей (у аналогового мультиметра – измерительная шкала), переключатель режимов работы, гнезда для подключения шнуров со щупами (рис. 36). Режимы работы прибора:
- OFF – прибор выключен;
- ACV – измерение переменного напряжения;
- DCV – измерение постоянного напряжения;
- ACA – измерение переменного тока;
- DCA – измерение постоянного тока;
- Ω – измерение сопротивления;
- hFE – измерение параметров транзисторов.
Переключение режимов происходит за счет поворота переключателя в нужную позицию. В нижней правой части расположены три разъема, которые используются для подключения измерительных щупов.
Напряжение и сила тока на участке цепи с активным сопротивлением.
Сдвиг фаз На рисунке 37 изображен участок цепи, содержащий резистор. Определим напряжение и силу тока на резисторе. На основании закона Ома, полагая, что напряжение в сети меняется по закону косинуса:
получим уравнение для силы тока:
где 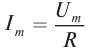
Из сравнения уравнений (1) и (2) следует, что колебание напряжения и силы тока на резисторе происходят синфазно. Графики зависимости силы тока и напряжения от времени в пределах одного периода представлены на рисунке 38.

Вспомните! Активное сопротивление резистора зависит от его длины, площади поперечного сечения и удельного сопротивления:
Напряжение и сила тока на участке цепи с катушкой индуктивности.
Сдвиг фаз На рисунке 39 изображена цепь с катушкой индуктивности.
Запомните! Катушку индуктивности изготавливают из проволоки, активное сопротивление которой 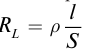
При подключении к источнику переменного тока в катушке возникает индукционный ток, препятствующий изменению тока, созданного источником. Запишем закон Ома для цепи, состоящей из источника переменного тока и катушки индуктивности, схема которой изображена на рисунке 40:
где 
При малых значениях 
С учетом выражения (5) и малого значения активного сопротивления катушки 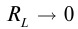
Пусть сила тока в цепи изменяется по закону:
тогда закон, по которому меняется напряжение на концах катушки, будет иметь вид:
Выразим полученную зависимость через функцию sin, используя формулу приведения:
Вспомните! Для определения сдвига фаз необходимо уравнения гармонических колебаний выразить через одну и ту же тригонометрическую функцию.
Из сравнения формул (7) и (10) следует, что колебания силы тока на катушке отстают по фазе от колебаний напряжения на 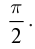
Реактивное сопротивление катушки
Запишем соотношение для амплитуды напряжения из формул (8) и (9):
выразим из (11) амплитуду силы тока:
и сравним с законом Ома для участка цепи 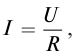
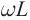
Индуктивное сопротивление измеряется в омах:
Напряжение и сила тока на участке цепи с конденсатором
На рисунке 42 изображены конденсаторы, подключенные в цепь переменного тока. В цепи с источником переменного тока течет ток перезарядки конденсатора, происходят вынужденные электромагнитные колебания. Если напряжение на обкладках конденсатора колеблется по закону: 
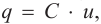
где 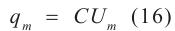
Мгновенное значение силы тока является первой производной от заряда по времени:
С использованием формул приведения и учитывая, что выражение перед функцией sin является максимальным значением величины, запишем уравнение (17) в виде:
Из уравнений (14) и (18) следует, что колебания силы тока на конденсаторе опережают колебания напряжения на 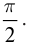
Обратите внимание! При подключении конденсатора к источнику постоянного тока, возможен только ток зарядки. В момент, когда напряжение на конденсаторе становится равным напряжению на полюсах источника, ток в цепи прекращается.
Реактивное сопротивление конденсатора
Из формул (17) и (18) приходим к выводу, что максимальное значение силы тока связано с амплитудой напряжения соотношением:
На основании закона Ома для участка цепи введем реактивное емкостное сопротивление, обозначив его 
Сопоставляя уравнения (19) и (20) получим, что реактивное емкостное сопротивление обратно пропорционально циклической частоте колебаний и емкости конденсатора:
Реактивное емкостное сопротивление измеряется в омах:
Закон Ома для последовательной электрической цепи переменного тока, содержащей активное и реактивное сопротивления
I. Сила тока и напряжение на участке цепи из последовательно соединенных катушки индуктивности, конденсатора и активной нагрузки
На рисунке 44 изображены участки цепи, состоящих из резисторов, конденсаторов и катушек индуктивности. При последовательном соединении ток, протекающий по всем участкам цепи (рис. 45), колеблется синфазно:
В любой момент времени напряжение, созданное генератором, равно сумме напряжений на каждом из последовательных участков неразветвленной цепи:
С учетом разности фаз колебаний напряжений и силы тока на катушке и конденсаторе уравнение (2) примет вид:
Для сложения напряжений используют векторную диаграмму.
Векторная диаграмма
Векторная диаграмма – это способ графического изображения гармонических колебаний.
Этот способ заключается в следующем: на плоскости выбирают произвольную точку с координатами 
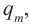
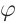
Проекция вектора на ось Ох определяет мгновенное значение величины:
Если колебания происходят по закону синуса, необходимо определить проекцию величины на вертикальную ось Оу.
Аналогично строится векторная диаграмма для любой величины: силы тока, напряжения, ЭДС (рис. 47). Преимущество данного вида графического изображения колебаний в том, что на нем наглядно показан сдвиг фаз исследуемых величин.
При вращении вектора против часовой стрелки с периодом, равным периоду колебаний Т, проекция вектора принимает все значения исследуемой величины в пределах одного периода.
Закон Ома для цепи из последовательно соединенных катушки индуктивности, конденсатора и активной нагрузки
Запишем закон Ома для максимальных значений силы тока и напряжения участка цепи, состоящего из катушки, конденсатора и резистора:
где Z − полное сопротивление цепи.
Колебания напряжения происходят с одинаковой частотой, следовательно, для нахождения суммы напряжений можно воспользоваться векторной диаграммой. Векторы силы тока и максимального значения напряжения на активной нагрузке направим вправо от произвольно выбранной на плоскости точки с координатами (0, 0) (рис. 48).
Вектор амплитуды напряжения на катушке индуктивности будет направлен вверх, а на конденсаторе вниз, так как колебания напряжения на катушке опережают колебания тока на 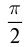
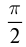
Выполнив векторное сложение амплитудных значений напряжений 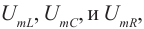
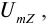
Выразим максимальные значения напряжений через амплитуду силы тока на основе закона Ома: 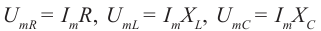
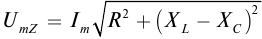
Уравнение (6) является законом Ома для последовательной цепи, состоящей из катушки индуктивности, конденсатора и активной нагрузки. Сравнив формулы (4) и (6), выразим полное сопротивление цепи:
где R − активное сопротивление цепи; 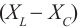
Возьмите на заметку
Вращение вектора против часовой стрелки считают положительным направлением и соответствующим опережению.
Сдвиг фаз колебаний силы тока и напряжения в цепи переменного тока
Преимущество векторных диаграмм заключается в том, что на них наглядно показан сдвиг фаз исследуемых величин. Определим сдвиг фаз между колебаниями силы тока и напряжения в неразветвленной цепи, содержащей активную нагрузку, конденсатор и катушку индуктивности по диаграмме, изображенной на рисунке 49. Направление силы тока совпадает с направлением напряжения на активном сопротивлении. Из диаграммы видно, что колебания напряжения опережают колебания силы тока, сдвиг фаз составляет 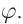
Выразим сдвиг фаз, используя треугольник напряжений (рис. 49):
Из треугольника сопротивлений (рис. 50) следует:
Пример №5
В сеть переменного тока напряжением 120 В последовательно включены проводник с активным сопротивлением 15 Ом и катушка индуктивностью 0,05 Гн. Определите частоту тока, если амплитуда силы тока в цепи равна 7 А.
Дано:
U = 120 В
R = 15 Ом
L = 0,05 Гн
Im = 7 А
Решение: Закон Ома для последовательного участка цепи:
Подставим формулы (2–4) в (1) получим:
Уравнение (5) решим относительно неизвестной величины:
Ответ:
Мощность цепи переменного тока
Среднее значение мощности переменного тока на активном сопротивлении:
Запишем зависимость мгновенного значения мощности от времени:
Выразим квадрат косинуса фазы колебаний через косинус двойного угла и подставим в формулу (1), получим:
График зависимости p(t) изображен на рисунке 53.
Не сложно доказать, что сумма значений второго слагаемого в формуле (2) имеет нулевое значение.
Тогда средняя мощность за период на активном сопротивлении равна:
Кусочки науки:
Косинус двойного угла равен: 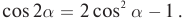
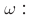
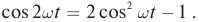
Действующие значения силы тока и напряжения
Сравнение формулы (3) с формулой расчета мощности на резисторе в цепи постоянного тока 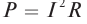
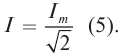
Мощность на катушке индуктивности
График зависимости мощности от времени получим, перемножая соответствующие мгновенные значения силы тока и напряжения.
Обратите внимание! Положительное значение мощности свидетельствует о потреблении резистором электрической энергии в течение всего периода колебаний.
На рисунке 54 изображены графики зависимости силы тока, напряжения и мощности тока в катушке индуктивности от времени в пределах одного периода. Из графика мощности следует, что катушка действует как накопитель энергии. В первую четверть периода она получает энергию от источника, мощность тока на катушке имеет положительное значение. В следующую четверть катушка возвращает энергию источнику, так как значение мощности отрицательное.
Обратите внимание! Идеальная катушка не превращает электрическую энергию в другие виды энергии, мощность за весь период колебаний равна нулю.
Мощность тока на конденсаторе
На рисунке 55 изображены графики зависимости силы тока и напряжения от времени на конденсаторе в пределах одного периода. График зависимости мощности от времени получен путем перемножения соответствующих мгновенных значений силы тока и напряжения.
Емкостное сопротивление используют для накопления энергии и для ограничения силы тока, протекающего через приборы небольшой мощности, в цепи переменного тока низкой частоты.
Мощность тока в цепи переменного тока, состоящего из конденсатора, катушки и активного сопротивления
Используя треугольник напряжений на векторной диаграмме (рис. 56), выразим напряжение на активном сопротивлении через амплитудное значение напряжения полной цепи:
С учетом полученного выражения запишем формулу мощности тока в цепи: 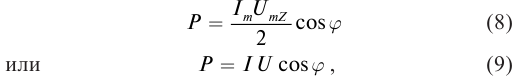
где 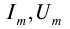
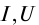
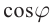
Коэффициент мощности показывает, какая часть электроэнергии в цепи переменного тока превращается в другие виды энергии.
Например, электродвигатель в цепи с коэффициентом мощности 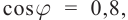
Запомните! В цепи, содержащей активное и реактивное сопротивление, только часть поступающей электроэнергии на активном сопротивлении превращается в другие виды энергии.
Пример №6
Катушка с активным сопротивлением R = 15 Ом и индуктивностью L = 52 мГн включена в сеть переменного тока с частотой 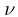
Дано:
R = 15 Ом
L = 52 мГн
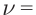
C = 120 мкФ
U = 220 В
I — ?
Im — ?
P — ?
СИ 52 · 10–3 Гн
120 · 10–6 Ф
Решение:
Из закона Ома для участка цепи:
где Im , Um − амплитудные значения силы тока и напряжения.
Полное сопротивление цепи:
Связь между действующим и амплитудным значениями напряжения выражается формулой
Подставив (2) и (3) в (1), находим амплитудное значение силы тока:
Действующее значение силы тока связано с максимальным соотношением:
Средняя мощность переменного тока:
Подставив (5) в (4), рассчитаем мощность по формуле:
Резонанс напряжений в электрической цепи
Условие резонанса:
Полное сопротивление цепи, состоящей из резистора, катушки индуктивности и конденсатора, имеет наименьшее значение при равенстве емкостного и индуктивного сопротивлений:
В этом случае полное сопротивление цепи становится равным активному сопротивлению Z = R, амплитудное значение силы тока достигает максимального значения:
Определим частоту вынуждающих колебаний, при которой сила тока достигает максимального значения.
Из равенства (1) следует, что:
Выразим циклическую частоту из полученного соотношения:
Из (3) следует, что резонанс в последовательной цепи, состоящей из резистора, конденсатора и катушки, наступает при равенстве циклической частоты внешнего напряжения с собственной циклической частотой цепи:
На рисунке 58 изображены резонансные кривые амплитудных значений силы тока. Чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
Вспомните! Резонанс в цепи переменного тока проявляется в резком увеличении амплитуды колебаний силы тока.
Резонанс:
Колебание напряжений на катушке индуктивности и конденсаторе происходит в противофазе. В режиме резонанса, когда 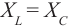
При векторном сложении общее напряжение на катушке и конденсаторе равно нулю и все напряжение подается полностью на активное сопротивление
В результате ток в цепи возрастает. Вместе с этим возрастает напряжение на катушке и на конденсаторе:
Увеличение напряжения на реактивном сопротивлении можно рассчитать по величине 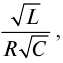
Резонанс напряжений приводит к возрастанию напряжения на реактивных элементах в Q раз. В цепях с большим активным сопротивлениям возникнуть резонанс не может.
Использование резонанса в цепи переменного тока
Радиоприемник:
Входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, изменяемая с помощью регулировки емкости конденсатора, совпадает с частотой сигнала радиостанции, которую необходимо принять (рис. 60).
Электрические фильтры (рис. 61).
Явление резонанса напряжений используют в электрических фильтрах. Если необходимо устранить из передаваемого сигнала составляющую тока определенной частоты, то параллельно приемнику ставят цепочку из конденсатора и катушки индуктивности, соединенных между собой последовательно (рис. 62). Ток резонансной частоты проходит через LC-цепочку, токи других частот – через приемник.
Если через приемник необходимо пропустить только ток определенной частоты, то LC-цепочку включают последовательно с приемником (рис. 63). В этом случае составляющие сигнала на резонансной частоте пройдут к нагрузке практически без потерь, сигналы других частот будут значительно ослаблены.
Негативные проявления резонанса:
При малом значении активного сопротивления напряжение на катушке и конденсаторе в режиме резонанса может превысить входное напряжение в несколько раз. Это необходимо учитывать, чтобы избежать пробоя диэлектрика и прогорания изоляции катушки.
В электроэнергетике возникновение резонанса напряжений возможно в случае подключения к генератору длинной кабельной линии без нагрузки – потребителя электроэнергии. Такая ситуация предотвращается применением вспомогательной нагрузки.
Производство, передача и использование электрической энергии
Устройство трансформатора, коэффициент трансформации:
Потребители рассчитаны на разные значения напряжения, поэтому возникает потребность в его преобразовании.
Прибор, с помощью которого производится преобразование напряжения переменного тока, называют трансформатором (рис. 64).
Трансформатор состоит из замкнутого стального сердечника – магнитопровода и двух или нескольких обмоток с разным количеством витков (рис. 65). Работа трансформатора основана на явлении электромагнитной индукции. При подключении первичной обмотки трансформатора к сети переменного тока напряжением 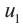
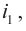
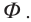
где 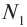
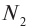
Обратите внимание! В быту и на производстве используют электрические приборы различной мощности, для питания которых создана промышленная сеть переменного тока с частотой 50 Гц. Источниками тока в этой сети являются индукционные генераторы переменного тока, расположенные на электростанциях. Переменный ток поступает по проводам к потребителям.
Полученное соотношение справедливо для действующих значений ЭДС, поскольку поток в сердечниках обмоток меняется синфазно:
На основании закона Ома мгновенное напряжение, приложенное к первичной катушке с малым активным сопротивлением, равно ЭДС индукции, взятым со знаком «минус»:
Действующие значения напряжения и ЭДС равны:
Для вторичной катушки ЭДС индукции 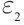
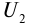
Трансформатор в этом случае находится в режиме холостого хода. С учетом (4) и (5) уравнение (3) примет вид:
Отношение числа витков в первичной обмотке трансформатора к числу витков во вторичной обмотке называют коэффициентом трансформации:
Возьмите на заметку:
Если активным сопротивлением катушки пренебречь нельзя и к вторичной обмотке подключена нагрузка, то напряжение, приложенное к первичной обмотке, равно:
ЭДС на вторичной обмотке:
где 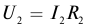
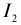
Запомните! Если коэффициент трансформации больше единицы 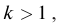
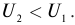
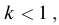
Мощность тока и сила тока в трансформаторе
При трансформации напряжения частота колебаний сохраняется. Мощность тока практически не меняется. КПД трансформатора достигает 99%. Небольшие потери энергии происходят при нагревании обмотки и перемагничивании сердечника. Считая, что 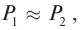
При трансформации напряжения происходит трансформация силы тока.
Передача энергии от генератора электроэнергии во вторичную цепь трансформатора
При наличии нагрузки во вторичной обмотке трансформатора амплитуда переменного тока 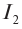
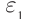
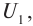
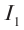
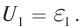
Линии электропередачи
Все электростанции расположены вблизи природных энергоресурсов, которые расположены на Земле неравномерно, поэтому полученная электроэнергия из одних регионов передается в другие по многокилометровым линиям электропередачи – ЛЭП. Не смотря на то, что провода линий электропередачи изготавливают из металла с малым удельным электрическим сопротивлением, их сопротивление остается значительным.
При передаче электроэнергии на сотни и тысячи километров тепловые потери энергии могут стать настолько значительными, что электроэнергия до потребителя не дойдет. Уменьшение потерь энергии при ее передаче имеет практическую значимость.
Из закона Джоуля – Ленца: 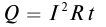
Производство и использование электрической энергии
Технологии производства электроэнергии в различных странах мира:
До конца XX столетия в большинстве стран производство электроэнергии происходило с использованием генераторов переменного тока. В генераторах энергия падающей воды, энергия органического топлива (дров, торфа, угля, нефти, газа), атомная энергия превращаются в электроэнергию. В XXI веке страны переходят на использование альтернативных возобновляемых источников энергии. Статистический обзор мировой энергетики показал, что странами-лидерами по производству электроэнергии являются Китай, США и Индия. На рисунке 70 даны результаты статистики по технологиям производства в лидирующих странах 2016 г.
Интересно знать! Производство электроэнергии человеком началось в конце 1870-х гг., когда баварский инженер З. Шуккерт построил в городе Этталь первую электростанцию. Местом ее расположения стал дворцовой сад Линдерхофа. Там находился грот, который необходимо было осветить. Свеч для этого было недостаточно, и Шуккерт решился на эксперимент. Его электростанция состояла из 24 динамоэлектрических генераторов, соединенных между собой приводом от парового двигателя.
Успешные технологии производства электроэнергии из ВИЭ (возобновляемых источников энергии) в мире:
Наиболее привлекательным ВИЭ является энергия Солнца. Если КПД первых солнечных батарей составлял 1–2 %, то к началу XXI века их КПД достигло порядка 30 %.
В Европе активнее всего развиваются ветро= и солнечная энергетика. Ветроустановки и гелиоустановки не могут стать основными источниками энергии для крупных электросетей из-за нестабильности выработки ими энергии. Если их доля начинает превышать 20 % мощности энергосистем, возникает необходимость ввода дополнительных регулирующих мощностей. На современном этапе с задачей регулирования мощности энергосети справляются крупные ГЭС. Евросоюзу удалось частично решить проблему регулирующих и накопительных мощностей в «зеленой энергетике»: «аккумуляторной батареей» Западной Европы стала Норвегия, имеющая в достаточном количестве гидроаккумулирующие станции (ГАЭС). Когда возникают излишки электроэнергии, насосы на ГАЭС качают воду из нижнего бьефа водохранилища в верхний. В моменты пика электропотребления воду вновь сбрасывают, и она приводит в движение генераторы. Норвегия соединена высоковольтными ЛЭП со Швецией, Данией и Нидерландами. С 2020 года к этой системе будет подключена Германия. Соглашение о прокладке подводной ЛЭП длиной 623 километра и мощностью в 1400 МВт было подписано в феврале 2015 года. Эта ЛЭП покроет 3 % потребления электроэнергии в Германии. В Исландии электроэнергетика по большей своей части питается от геотермальных источников. В целом по Европейскому союзу согласно Статистическому энергетическому ежегоднику (Global Energy Statistical Yearbook 2015) доля ВИЭ, включая ГЭС, в 2014 году составляла 30 %, в некоторых странах, например Норвегии, она доходила до 98 %.
Самый используемый возобновляемый ресурс из всех видов ВИЭ в США и Бразилии – это биомасса. Эти страны являются основными производителями 2/3 потребляемого в мире биотоплива – биоэтанола. США специализируется на переработке в топливо кукурузы, а Бразилия, выращивающая для этого сахарный тростник. Объем вредных выбросов в атмосферу у биоэтанола существенно меньше, чем у обычного бензина. Этанол из сахарного тростника сокращает выбросы парниковых газов примерно на 80 % по сравнению с ископаемыми видами топлива, произведенный из кукурузы на 30 %.
ИТОГИ:
Глоссарий:
- Коэффициент мощности – величина, которая показывает, какая часть электроэнергии в цепи переменного тока превращается в другие виды энергии.
- Коэффициент трансформации – величина, равная отношению числа витков в первичной обмотке трансформатора к числу витков во вторичной обмотке.
- Переменный ток – вынужденные колебания заряженных частиц в проводнике под воздействием внешней периодически изменяющейся электродвижущей силы.
- Сдвиг фаз – разность фаз колебаний одной частоты, выраженных через одну тригонометрическую функцию.
Что такое переменный ток
Жизнь современного человека невозможно представить без использования энергии электрического тока. Благодаря ему происходят многочисленные технологические процессы, работают различные машины, средства связи и коммуникаций, от него зависит весь современный комфорт.
Опыт применения энергии электрического тока показал, что самым удобным в технологическом плане является применение переменного электрического тока, в частности такого его вида, когда все изменения напряжения и силы тока происходят по законам синуса или косинуса.
Самым удобным способом получения переменного тока является вращение рамки в магнитном поле. Представим, что в начальный момент времени рамка (рис. 2.49) расположена так, что направление нормали 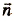
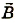
Pиc. 2.49. Вращение проволочной рамки в магнитном поле
Если рамка вращается равномерно с угловой скоростью ω, то угол поворота в любой момент равен
Проанализировав рисунок, можно заметить, что магнитный поток, пронизывающий рамку, изменяется по закону косинуса:
Поскольку магнитный поток изменяется, то в рамке возникает ЭДC индукции:
Если индукция магнитного поля и площадь рамки постоянны, а 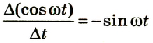
при равномерном вращении рамки в однородном магнитном поле в ней возникает электродвижущая сила индукции, ко торам изменяется по закону синуса.
Из формулы видно, что максимальное значение 
Практически переменный ток не отличается от постоянного. Это такое же направленное движение заряженных частиц. Он имеет тепловое, магнитное, химическое действия. Отличие только в том, что он периодически изменяет свое направление. Это вынужденные колебания силы тока и напряжения в электрической цепи.
Обычные измерительные приборы переменного тока показывают значения так называемых эффективных значений силы тока и напряжения. Фактически это значения характеристик постоянного тока, который производит такие же действия, как и данный переменный ток.
Между максимальным (амплитудным) значением силы тока и его эффективным значением существует определенная связь:
Аналогично определяется и эффективное значение напряжения переменного тока:
На этикетках всех современных электрических приборов указаны эффективные значения напряжения и силы тока.
Переменный ток имеет определенную частоту. В Украине стандартная частота переменного тока в сети составляет 50 Гц. Ее обязательно учитывают при разработке всех приборов переменного тока: трансформаторов, электродвигателей, генераторов и др.
В промышленных условиях переменный ток вырабатывают с помощью электромеханических генераторов (рис. 2.50).
Рис. 250. Схема устройства генератора переменного тока
Такой генератор имеет статор 7 в виде пустотелого цилиндра, на внутренней поверхности которого расположены обмотки изолированного провода. Ротор 2 укреплен на валу и вращается вместе с ним. Его соединяют с движущим механизмом, в частности с гидравлической, паровой или газовой турбиной. В пазах стального корпуса ротора расположены обмотки, создающие магнитное поле, когда по ним проходит электрический ток. Вместо с ротором вращается и вектор магнитной индукции, благодаря чему в статоре индуцируется переменная ЭДС. У большинства промышленных генераторов она составляет несколько десятков киловольт.
Трансформатор. и передача энергии переменного тока
Чрезвычайно важным свойством переменного электрического тока является то, что напряжение и силу тока можно изменять (трансформировать) без ощутимых потерь энергии. Такие превращения особо важны для передачи электроэнергии на большие расстояния с минимальными затратами.
Так, доказано, что потери в линиях электропередач существенно уменьшаются, если передача происходит при высоком напряжении — несколько десятков, сотен киловольт. В местах потребления это напряжение приходится понижать до 380-220 В.
Все такие преобразования производятся с помощью весьма простого по устройству прибора — трансформатора.
Трансформатор (рис. 2.51) в большинстве случаев состоит из двух катушек-обмоток, имеющих общий ферромагнитный сердечник. Одна из катушек (она называется первичной) соединяется с генератором, а потребители (электродвигатели, лампы-обогреватели и т. п.) присоединяются ко вторичной обмотке трансформатора.
Puc. 2.51. Трансформатор переменного тока с двумя обмотками
Принцип действия трансформатора переменного тока (рис. 2.52) основан на использовании явления электромагнитной индукции.
Рис. 2.52. Схема трансформатора переменного тока с двумя обмотками
Переменный ток, который проходит первичной обмоткой 1, например, с количеством витков N1, создает в сердечнике переменное магнитное поле, оно в свою очередь индуцирует во вторичной обмотке трансформатора 2 с количеством витков N2 электродвижущую силу. Поскольку обмотки имеют общий сердечник, то в каждом их витке возникает электродвижущая < ила, пропорциональная количеству витков:
Если вторичная обмотка разорвана, а к первичной обмотке присоединен источник переменного тока, то такой режим называют режимом холостого хода. В этом случае напряжение U2 равно электродвижущей силе 
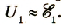
где k — коэффициент трансформации.
Если k > 1, то U2 > U1, и трансформатор называют повышающим; если k < 1, то U2 < U1 и трансформатор будет называться понижающим.
Когда трансформатор соединить с потребителями, цепь вторичной обмотки замкнется. Это будет рабочий режим трансформатора. Поскольку обмотки и сердечник образуют замкнутую систему, то в ней действует закон сохранения и преобразования энергии. В данном случае он проявляется равностью мощностей первичной и вторичной обмоток трансформатора (тепловые потери в сердечнике будут незначительными, поскольку коэффициент полезного действия современных трансформаторов равен около 99,5%).
Таким образом,
или
Только с помощью трансформатора переменного тока удалось эффективно решить проблему передачи электроэнергии па большие расстояния. Как указывалось выше, такая передача с незначительными потерями возможна при высоком напряжении. Подтверждением этого может быть решение следующей задачи.
Пример №7
Электроэнергию от электростанции мощностью 50 кВт передают с помощью линии сопротивлением 5 Ом. Определить потери напряжения и мощности в линейных про водах и коэффициент полезного действия в электросети в случаях, когда передача энергии осуществляется при напряжениях 1000 и 10 000 В.
|
Дано: |
Решение Потеря мощности в линии P = I2R. |
| U — ? P — ? η-? |
Рассчитаем значение коэффициента полезного действия для разных значений напряжений:
1)
2)
Сравнение полученных результатов позволяет сделать выводы:
1) повышение напряжения в линии в 10 раз во столько же раз уменьшает силу тока;
2) повышение напряжения в линии в 10 раз значительно уменьшает потери мощности.
Налицо преимущества передачи электроэнергии при высоком напряжении. Этого можно достичь, применяя в линиях электропередачи трансформаторы, которые повышали бы напряжение перед тем, как ток поступает в линию электропередачи, и снижали бы ее на входе к потребителю.
На рисунке 2.53 представлена схема современной линии электропередач (ЛЭП) переменного тока.
Pиc. 2.53. Система передачи электроэнергии на расстояние
На всех промышленных электростанциях Украины работают электромеханические генераторы, вырабатывающие переменный ток напряжением 20 кВ и частотой 50 Гц. Повышение напряжения генератора выше этого значения опасно из-за возможности пробоя изоляции проводов в генераторе. Поэтому повышение напряжения происходит за пределами генератора с помощью трансформаторов, которые повышают его до 500…750 кВ. Прежде чем подать электроэнергию потребителям, напряжение понижается с помощью понижающих трансформаторов согласно с потребностями предприятий, транспорта, потребителей бытовой сферы. В наши квартиры электричество подается при напряжении 220 В.
Итоги:
1. Основным признаком магнитного поля, который позволяет отличить ею от других полой, является его действие на движущийся заряд.
2. Силовое действие магнитного поля характеризуется магнитной индукцией — векторной величиной, определяющей силу, с которой магнитное поле действует на проводник с током или движущуюся заряженную частицу. Ее направление для прямого проводника определяется правилом правого винта (буравчика).
3. Сила, действующая в магнитном поле на проводник с током, называется силой Ампера. Ее модуль рассчитывается по формуле
Вектор силы Ампера лежит в плоскости, перпендикулярной к плоскости вектора скорости заряженных частиц и магнитной индукции. Ее направление определяется по правилу 126 левой руки: если левую руку расположить так, чтобы .линии магнитной индукции входили в ладонь, а четыре пальца показывали направление тока, то отставленный па 90° большой палец укажет на направление силы, действующей на проводник с током в магнитном поле.
4. На обособленную частицу, имеющую электрический за-ряд и движущуюся в магнитном поле, действует магнитная составляющая силы Лоренца:
5. Все без исключения вещества взаимодействуют с магнитным полем. Магнитные свойства вещества определяются его внутренним строением. По магнитным свойствам все вещества разделяются на диамагнетики, парамагнетики и ферромагнетики. В отличие от диа- и парамагнетиков, ферромагнетики имеют большую магнитную проницаемость как следствие их доменной структуры.
6. Магнитный поток — это физическая величина, которая характеризует магнитное поле и равна произведению магнитной индукции на площадь контура и косинус угла между вектором магнитной индукции и нормалью к плоскости контура:
Магнитный поток измеряется в веберах (Вб).
7. При изменении магнитной индукции поля в замкнутом проводнике возникает ЭДC индукции. ЭДC индукции пропорциональна скорости изменения магнитного потока:
8. ЭДС индукции в проводники, который движется в магнитном поле, возникает вследствие действия силы Лоренца на свободные электроны. Направление индукционного тока определяют по правилу правой руки и правилу Ленца: индукционный ток. возникающий в замкнутом проводнике, имеет такое направление, что его магнитное поле противодействует изменению магнитного поля, которое вызвало этот ток.
9. Вследствие взаимодействия проводника с током со своим магнитным полем возникает явление самоиндукции. Физическая величина, характеризующая электромагнитные свойства проводника, называется индуктивностью. Единицей индуктивности является генри (Гн).
Индуктивность проводника зависит от его геометрических параметров и магнитной проницаемости среды, в которой он находится.
10. ЭДС самоиндукции зависит от скорости изменения силы тока в проводнике и его индуктивности:
11. Энергия магнитного поля проводника с током пропорциональна его индуктивности и квадрату силы тока в нем:
- Катушка индуктивности в цепях переменного тока
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
Электричество. Закон сохранения электрического заряда,
закон Кулона, конденсатор, сила тока,
закон Ома для участка цепи, последовательное и параллельное соединение
проводников, работа и мощность тока,
закон Джоуля – Ленца
В. З. Шапиро
В задании 14 проверяются знания по теме «Постоянный электрический ток». Это задание базовому уровня. Задачи носят, в основном, расчетный характер. Их решение основывается на знаниях законов и закономерностей постоянного электрического тока, умении «читать» электрические схемы, работать с графическими зависимостями.
1. На графике показана зависимость силы тока I в проводнике от времени t. Определите заряд, прошедший через проводник за Δt = 60 с с момента начала отсчёта времени.
Ответ: _____________________ Кл.
Необходимая теория: Постоянный электрический ток
Используя зависимость силы тока от времени, электрический заряд можно определить как площадь геометрической фигуры под графиком. В данной задаче требуется рассчитать площадь трапеции Применяя геометрическую формулу площади трапеции и подставляя значения физических величин, получим
(Кл).
Ответ: 180 Кл.
Секрет решения. Подобный прием нахождения значения физической величины через площадь под графиком применяется во многих разделах физики: в «Механике», «МКТ и термодинамике», «Электродинамике». Здесь важно правильно выделить геометрическую фигуру, так как иногда требуется найти площадь не всей фигуры, а только ее части. Как всегда, в расчетах требует особого внимания система единиц (СИ). Пренебрежение одним из перечисленных моментов приведет к потере «легкого» балла.
2. Пять одинаковых резисторов с сопротивлением 3 Ом соединены в электрическую цепь, через которую течёт ток I (см. рисунок). Идеальный вольтметр показывает напряжение 9 В. Чему равна сила тока I?
Ответ: __________________________ А.
Необходимая теория: Соединения проводников
Резисторы, подключенные к вольтметру, соединены между собой последовательно. Отсюда следует, что сумма напряжений на каждом резисторе равна значению напряжения, которое показывает вольтметр. Запишем это в виде формулы Используя закон Ома, выразим значения напряжений
и
Здесь учтено, что в указанной точке (см. схему) ток I разделяется на две равные части из-за равенства сопротивлений в разветвленных частях цепи.
Деление силы тока на две равные части
Таким образом,
Подставляя численные значения, получим
Ответ: 2А.
Секреты решения. В задачах со схемами необходимо уметь выделять виды соединения проводников. После этого можно использовать известные закономерности для силы тока, напряжения и сопротивления. Ввиду того, что в задачах может быть большое количество проводников, решение в общем виде бывает громоздким, что может привести к математической ошибке. Поэтому лучше подставлять численные значения на ранних этапах решения.
3. На плавком предохранителе счётчика электроэнергии указано: «15 А, 380 В». Какова максимальная суммарная мощность электрических приборов, которые можно одновременно включать в сеть, чтобы предохранитель не расплавился?
Ответ: _________________________Вт.
Необходимая теория: Работа и мощность тока
Формулы для расчета мощности электрического тока имеют вид:
В зависимости от условия задачи, надо применять ту или иную формулу. Так как в задаче дается сила тока и напряжения, необходимо воспользоваться формулой
Подставляя численные значения, проведем расчет:
(Вт).
Ответ: 5700 Вт.
Секреты решения.
Формулы для расчета мощности лучше изучать как следствия формул для расчета работы тока или количества теплоты, выделяющейся в проводнике с током.
При делении этих формул на время t получим формулы для расчета мощности.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 14 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023