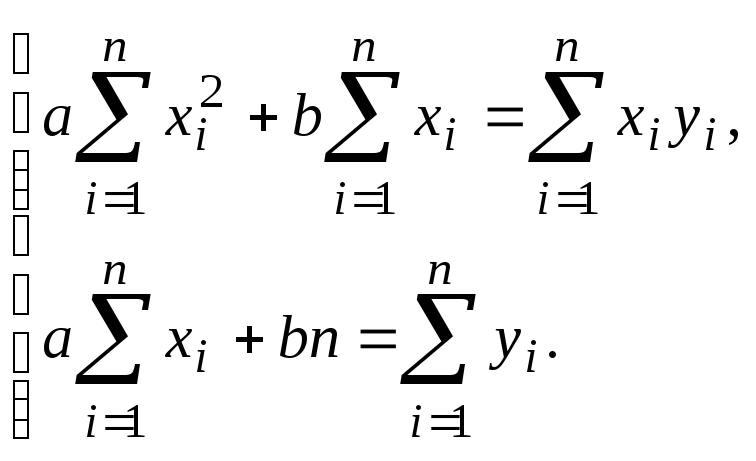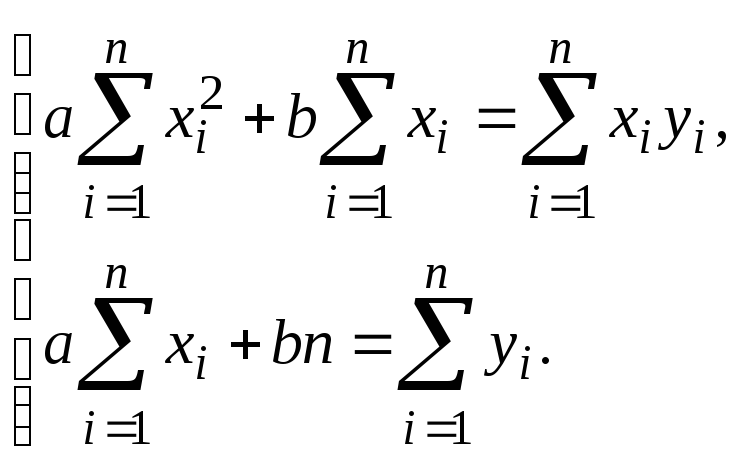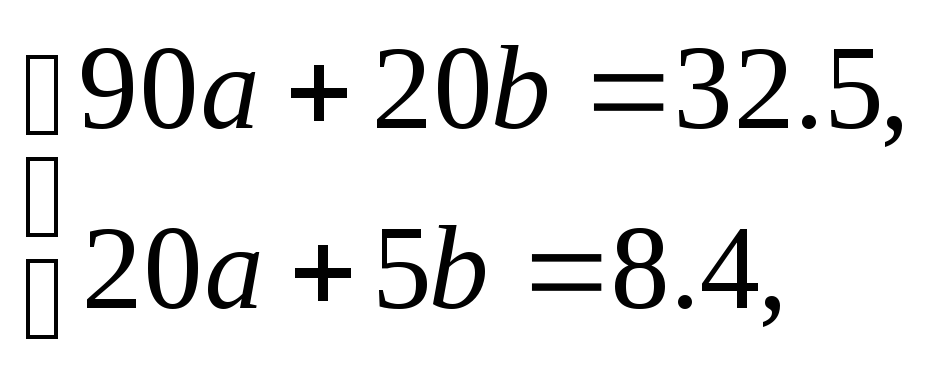Как найти зависимость между переменными - Autoru.top

Время на прочтение
8 мин

Количество просмотров 68K

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x, возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения $mu_{1y} = f(x)$ называется регрессией y по x.

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей $s = sum_{i=1}^n[y_i - f(x)_i]^2$ минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений $y_i$ вокруг регрессии $f(x)$ является дисперсия.

$D = frac{1}{n-k}sum_{i=1}^n[y_i - f(x)_i]^2$

k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x.

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

y — зависимая переменная;
x — независимая переменная;
β — коэффициенты, которые необходимо найти с помощью МНК;
ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина $y_i$ может быть интерпретирована как сумма из двух слагаемых:

Еще одно ключевое понятие — коэффициент корреляции R².

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
Экзогенность независимых переменных — $E[epsilon_i|x_{j1}, x_{j2}, ... x_{jk}] = 0$ . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ² и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

$VIF_j = frac{1}{1-R{^2}_j}$

В этой формуле $R{^2}_j$ — коэффициент взаимной детерминации между $X_j$ и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln.
Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln, или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

> hist <- read.table("~/habr_hist.txt", header=TRUE)
> hist

points  reads   comm    faves   fb  bytes
31  11937   29  19  13  10265
93  34122   71  98  74  14995
32  12153   12  147 17  22476
30  16867   35  30  22  9571
27  13851   21  52  46  18824
12  16571   44  149 35  9972
18  9651    16  86  49  11370
59  29610   82  29  333 10131
26  8605    25  65  11  13050
20  11266   14  48  8   9884
...

points — Рейтинг статьи
reads — Число просмотров.
comm — Число комментариев.
faves — Добавлено в закладки.
fb — Поделились в социальных сетях (fb + vk).
bytes — Длина в байтах.

Проверка мультиколлинеарности.

> cor(hist)
          points     reads        comm       faves         fb      bytes
points 1.0000000 0.5641858  0.61489369  0.24104452 0.61696653 0.19502379
reads  0.5641858 1.0000000  0.54785197  0.57451189 0.57092464 0.24359202
comm   0.6148937 0.5478520  1.00000000 -0.01511207 0.51551030 0.08829029
faves  0.2410445 0.5745119 -0.01511207  1.00000000 0.23659894 0.14583018
fb     0.6169665 0.5709246  0.51551030  0.23659894 1.00000000 0.06782256
bytes  0.1950238 0.2435920  0.08829029  0.14583018 0.06782256 1.00000000

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm.

regmodel <- lm(points ~., data = hist)
summary(regmodel)
    Call:
lm(formula = points ~ ., data = hist)

Residuals:
    Min      1Q  Median      3Q     Max
-26.920  -9.517  -0.559   7.276  52.851

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.029e+01  7.198e+00   1.430   0.1608
reads       8.832e-05  3.158e-04   0.280   0.7812
comm        1.356e-01  5.218e-02   2.598   0.0131 *
faves       2.740e-02  3.492e-02   0.785   0.4374
fb          1.162e-01  4.691e-02   2.476   0.0177 *
bytes       3.960e-04  4.219e-04   0.939   0.3537
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 16.65 on 39 degrees of freedom
Multiple R-squared:  0.5384,    Adjusted R-squared:  0.4792
F-statistic: 9.099 on 5 and 39 DF,  p-value: 8.476e-06

В первой строке мы задаем параметры линейной регрессии. Строка points ~. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points ~ reads, набор переменных — points ~ reads + comm.

Перейдем теперь к расшифровке полученных результатов.

Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept.
R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации.
F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
t value — Критерий, основанный на t распределении Стьюдента. Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

$F=frac{RSS*(m-1)}{ESS*(n-m)} = frac{R^2}{1-R^2}*frac{m-1}{n-m}$

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

> hist$fb = hist$fb^(4/7)
> hist$comm = hist$comm^(2/3)

Проверим значения параметров линейной регрессии.

> regmodel <- lm(points ~., data = hist)
> summary(regmodel)

Call:
lm(formula = points ~ ., data = hist)

Residuals:
    Min      1Q  Median      3Q     Max
-22.972 -11.362  -0.603   7.977  49.549

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept)  2.823e+00  7.305e+00   0.387  0.70123
reads       -6.278e-05  3.227e-04  -0.195  0.84674
comm         1.010e+00  3.436e-01   2.938  0.00552 **
faves        2.753e-02  3.421e-02   0.805  0.42585
fb           1.601e+00  5.575e-01   2.872  0.00657 **
bytes        2.688e-04  4.108e-04   0.654  0.51677
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 16.21 on 39 degrees of freedom
Multiple R-squared:  0.5624,    Adjusted R-squared:  0.5062
F-statistic: 10.02 on 5 and 39 DF,  p-value: 3.186e-06

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми, F-статистика выросла, так же как и скорректированный коэффициент детерминации.

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

> dwtest(hist$points ~., data = hist)

        Durbin-Watson test

data:  hist$points ~ .
DW = 1.585, p-value = 0.07078
alternative hypothesis: true autocorrelation is greater than 0

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

> bptest(hist$points ~., data = hist)

        studentized Breusch-Pagan test

data:  hist$points ~ .
BP = 6.5315, df = 5, p-value = 0.2579

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

Использованные материалы

Beginners Guide to Regression Analysis and Plot Interpretations
Методы корреляционного и регрессионного анализа
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
William H. Green Econometric Analysis

Источник

Учреждение
образования «Белорусская государственная

сельскохозяйственная
академия»

Кафедра
высшей математики

Методические
указания

по
изучению темы «Элементы корреляционного
и регрессионного

анализа»
студентами бухгалтерского факультета
заочной формы

получения
образования
(НИСПО)

Горки,
2013

Элементы
корреляционного и регрессионного
анализа

Основные
понятия

Одной
из важнейших задач математической
статистики является нахождение
зависимостей между переменными Х
и Y.
В естественных науках большей частью
приходится сталкиваться с зависимостями,
когда каждому значению одной величины
строго соответствует определённое
значение другой величины. Такие
зависимости называются функциональными.

В
большинстве случаев между переменными,
характеризующими экономические
показатели, существуют зависимости,
отличные от функциональных. Зависимости
между переменными, когда каждому значению
переменной Х
соответствует не одно, а множество
возможных значений переменной Y,
называются стохастическими
или корреляционными.
Эти зависимости обнаруживаются лишь
при массовом изучении переменных.

Например,
уровень производительности труда Y
на предприятиях тем выше, чем больше
его электровооружённость X.
Вместе с тем такая зависимость может
быть не обязательно однозначной. И это
потому, что зависимая переменная Y
испытывает влияние не только переменной
Х,
но и целого ряда других факторов, которые
не учитываются. Кроме этого, влияние
выделенного фактора может быть не
прямым, а проявляться через цепочку
других факторов. Поэтому в таких
зависимостях каждому значению независимой
переменной Х
может соответствовать не одно, а ряд
значений переменной Y.

При
изучении корреляционных зависимостей
( связей) возникают два основных вопроса
– о
тесноте
связи и о форме связи.
Если рассматриваются только две
переменные, то связь (корреляция) между
ними называется парной.

Если
с увеличением значений переменной Х
значения переменной Y
в среднем растут, то такая парная
корреляция называется положительной.
Если же с ростом значений переменной
Х
значения переменной Y
в среднем уменьшаются, то такая корреляция
называется отрицательной.
Если же между переменными Х
и Y
связь отсутствует, то говорят, что имеет
место нулевая
корреляция.

Каждую
пару значений
,
соответствующих значениям переменных
X
и Y
в i-м
наблюдении, можно изобразить в виде
точки на координатной плоскости.
Совокупность таких точек называется
корреляционным
полем.

Линейная
корреляционная зависимость и прямые
регрессии

Ранее
было отмечено, что корреляция по
направлению может быть положительной
и отрицательной. Положительную корреляцию
называют прямой,
а отрицательную – обратной.
По форме корреляция может быть линейной
и криволинейной.

Парная
корреляционная зависимость будет
линейной,
если она приближённо выражается линейной
функцией.

Вид
зависимости можно определить по виду
корреляционного поля, т.е. по расположению
построенных точек подбирается линия.
Если это будет прямая,
то корреляция между признаками будет
линейной.

Для
оценки тесноты связи между признаками
используется выборочный линейный
коэффициент
корреляции

где

— выборочные средние;

— выборочные средние квадратические
отклонения.

Так
как коэффициент корреляции

определяется по выборочным данным, то
он является оценкой
генерального коэффициента корреляции
.

Коэффициент
корреляции находится в пределах от -1
до 1, т.е.
.
Чем ближе

к -1 или 1, тем теснее связь между
переменными Х
и Y.
Чем ближе

к нулю, тем слабее связь между переменными.
Таким образом, по величине коэффициента
корреляции можно судить о тесноте связи
между двумя переменными.

По
знаку коэффициента корреляции можно
судить о направлении корреляционной
зависимости между переменными Х
и Y.
Если
,
то зависимость
прямая.
Если же
,
то зависимость
обратная.

Квадрат
коэффициента корреляции

называется коэффициентом
детерминации
и обозначается

в долях или

в процентах. Он показывает, на сколько
процентов в среднем изменения зависимой
переменной Y
зависят от независимой переменной Х.

Линейная
корреляционная зависимость между
переменными Х
и Y
приближённо выражается в виде линейного
уравнения

Это
уравнение называется уравнением
регрессии
Y
на Х,
а его график называется линией
регрессии.
Если уравнение регрессии описывает
зависимость между двумя переменными,
то такая регрессия называется парной.

Парная
регрессия позволяет изучить взаимосвязь
лишь двух переменных. Чаще же изменение
Y
связано с влиянием не одного, а нескольких
факторов. В этом случае в уравнение
регрессии вводят несколько переменных.
Такая регрессия называется множественной.

Уравнение
множественной регрессии позволяет
полнее объяснить поведение зависимой
переменной и даёт возможность сопоставить
эффективность влияния различных
факторов.

Уравнение
множественной регрессии с двумя
независимыми переменными имеет вид
.

Метод
наименьших квадратов

Неизвестные
параметры a
и b
уравнения регрессии находятся методом
наименьших квадратов.
Применяя этот метод, получим систему
нормальных уравнений

Решив
систему, найдём a
и b.
Параметр a
называется коэффициентом
регрессии.
Он показывает, как изменится в среднем
функция Y,
если аргумент Х
изменится на единицу своего измерения.

Уравнение
регрессии
– наиболее часто встречающийся в
практике вид
статистической модели.
Подобные модели применяются для
экономического и технико-экономического
анализа, где с помощью уравнений регрессии
измеряют влияние отдельных факторов
на зависимую переменную. Тем самым
анализ становится более конкретным, а
его познавательная ценность значительно
увеличивается. Кроме этого, уравнения
регрессии применяются при прогнозировании.

Пример.
Изучается зависимость себестоимости
одного изделия (Y,
у.е.) от величины выпуска продукции (Х,
тыс.шт.) по группе предприятий за отчётный
период. Получены следующие данные:

Х	2	3	4	5	6
Y	1,9	1,7	1,8	1,6	1,4

Провести
корреляционно-регрессионный анализ
зависимости себестоимости одного
изделия от выпуска продукции.

Решение.
Построим корреляционное поле. По
корреляционному полю определяем, что
зависимость между себестоимостью одного
изделия и выпуском продукции близка к
линейной. В этом случае уравнение
регрессии имеет вид
.

Выполним
все необходимые вычисления и запишем
в виде таблицы:

№ п/п
1	2	1.9	3.8	4
2	3	1.7	5.1	9
3	4	1.8	7.2	16
4	5	1.6	8.0	25
5	6	1.4	8.4	36
Сумма	20	8.4	32.5	90

В
данном примере
,
,
,
.
Найдём
,
,
,
,
.
Вычислим выборочный коэффициент
корреляции
.
Так как коэффициент корреляции

близок к единице, то себестоимость
одного изделия и объём выпускаемой
продукции находятся в тесной корреляционной
зависимости. Коэффициент детерминации
равен
,
т.е. себестоимость единицы продукции
на 81% зависит от объёма выпускаемой
продукции и на 19% зависит от других
факторов.

Для
вычисления параметров a
и b
уравнения регрессии результаты вычислений
из таблицы подставим в нормальную
систему

и
получим систему уравнений

из которой найдём
,
b=2.12.
Таким образом, уравнение регрессии
имеет вид
.
Из этого уравнения следует, что с
увеличением выпуска продукции на 1 тыс.
шт. себестоимость одного изделия снизится
на 0.11 у.е. Если выпуск продукции составит,
например, 5.2 тыс.шт., то можно определить
себестоимость одного изделия:
(у.е.).

Вопросы
для самоконтроля знаний

Какие
зависимости называются функциональными,
а какие – стохастическими или
корреляционными?
Когда
между двумя переменными имеет место
положительная, отрицательная или
нулевая корреляция?
Что
называется корреляционным полем?
Какой
может быть корреляция по форме?
Для
чего используется линейный коэффициент
корреляции и как он определяется?
В
каких пределах находится коэффициент
корреляции?
Что
называется коэффициентом детерминации
и для чего он используется?
Какое
уравнение называется уравнением
регрессии?
Для
чего используется метод наименьших
квадратов?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение вида зависимости между переменными

Пусть имеются данные п наблюдений, причем каждое i наблюдение характеризуется значениями переменных (y_r х_п, x_j2, . Хф . x_ik)_y где х$ — значение j-й переменной для г-го наблюдения (i = 1, 2. п), у_х — значение результативного признака для г-го наблюдения.

Наиболее часто строят множественное линейное уравнение регрессии вида

Отметим, что последнее уравнение справедливо для всех i = 1,2, . п, линейно относительно неизвестных параметров р₀, (3_t, . fy, . (3* и аргументов.

Уравнение регрессии характеризует функциональную зависимость среднего значения результативного признака у от аргументов х, где j = 1,2. k.

Как следует из (6.5), коэффициент регрессии (3у показывает, на какую величину в среднем изменится результативный признак г/, если переменную Xj увеличить на единицу его измерения при неизменных значениях остальных аргументов, т.е. является нормативным коэффициентом.

Чтобы убедиться в этом, достаточно кХ:_1> в уравнение (6.5) прибавить единицу и убедиться, что среднее значение у. изменится на величину (3_;.

В матричной форме уравнение регрессии имеет вид

Здесь Y — вектор-столбец размерности (п • 1) модельных значений результативного признака (y_v . у._у . у_п) X — матрица размерности [п • (k + 1)] наблюдаемых значений х^ аргументов, где г = 1,2. nj- 0, 1, 2. k x_i0 = 1; (3 — вектор-столбец размерности [(& + 1) • 1] неизвестных, подлежащих определению параметров (коэффициентов регрессии) модели, где

Единицы в первом столбце матрицы X призваны обеспечить наличие свободного члена в модели (6.5). Предполагается, что существует переменная х₀, которая во всех наблюдениях принимает значения, равные единице. На практике рекомендуется, чтобы п превышало к не менее чем в три раза.

Задача заключается в нахождении по данным объемом п, неизвестных коэффициентов регрессии (3₀, Р_1;. |ф_; модели (6.5) или вектора Р в (6.6).

Для оценки вектора Р наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки вектора Р принимают вектор Ь, минимизирующий сумму квадратов отклонения наблюдаемых значений //, от модельных значений т.е. квадратичную форму

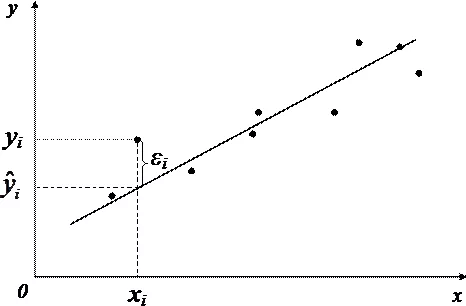
Наблюдаемые и модельные значения показаны на рис. 6.1.

Рис. 6.1. Наблюдаемые и модельные значения результативной величины у

Дифференцируя с учетом (6.6) и (6.5) квадратичную форму Q но (3₀, Pj, . Р_/; и приравнивая производные нулю, получим систему нормальных уравнений

решая которую и получаем вектор Ь, где b = (Ь₀, Ь_ь . Ь_к) т .

Согласно методу наименьших квадратов вектор оценок коэффициентов регрессии получается по формуле

— транспортированная матрица X, (ХТХ)

Х — матрица, обратная матрице Х Т Х.

Зная вектор оценок коэффициентов регрессии b, рассчитаем оценку у. уравнения регрессии:

или в матричном виде:

Одним из основных препятствий эффективного применения множественного регрессионного анализа считается мультиколлинеарность, связанная с линейной зависимостью между аргументами х_> х₂,x_k. В результате мультиколлинеарности матрица парных коэффициентов корреляции и матрица (ХТХ) становятся слабообусловленными, т.е. их определители близки к нулю.

Это вызывает неустойчивость оценок коэффициентов регрессии (6.7), так как в них входит обратная матрица (ЛТХ) -1 ; получение последней связано с делением на определитель матрицы |Х Г Х|. Мультиколлинеарность приводит к завышению значения множественного коэффициента корреляции.

На практике о наличии мультиколлинеарности, как правило, судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше 0,8, т.е. | г, | > 0,8, то считают, что имеет место мультиколлинеарность, и в уравнение регрессии следует включать только один из показателей X: или х_е.

По данным годовых отчетов десяти (п = 10) машиностроительных предприятий проведите регрессионный анализ зависимости производительности труда у (млн руб./ чел.) от объема производства х (млрд руб.). Предполагается линейная модель, т.е.

Исследование корреляционной зависимости между переменными Х1 и У

Так как переменная Х1 не подчиняется нормальному закону распределения, то для характеристики взаимосвязи будем использовать коэффициент ранговой корреляции. Построим поле корреляции.

Рисунок 2 — Поле корреляции

На поле корреляции заметна положительная корреляционная зависимость (с увеличением Х увеличивается Y). Точки на поле корреляции сгруппированы вокруг линии, направленной вверх и вправо, но имеют значительный разброс, следовательно, можно сделать предварительный вывод: между переменными Х и Y наблюдается слабая линейная зависимость.

Определим вид переменных Х и Y по типу измерения:

— численность служащих (Х) — количественная дискретная переменная;

— чистый доход (Y) — количественная дискретная переменная.

Так как обе переменные являются количественными, но одна из переменных (Х) не подчиняется нормальному распределению исходя из выводов, сделанных выше, для оценки силы корреляционной зависимости используем коэффициент ранговой корреляции Спирмена:

гдеd — разность между рангами значений переменных Х и Y;

n — объем выборки (число наблюдаемых пар значений в наборе данных).

Рангом (R) называется порядковый номер, который присваивается каждому наблюдаемому значению переменной после упорядочивания. Расчеты сведем в таблицу 2.

Таблица 2. Расчет коэффициента ранговой корреляции

По таблице 3 дадим интерпретацию полученному коэффициенту ранговой корреляции.

Таблица 3 — Интерпретация коэффициента ранговой корреляции

Коэффициент корреляции равен 0,365, что по таблице 3 можно интерпретировать следующим образом: прямая связь средней силы. Точки на поле корреляции сгруппированы вокруг прямой или кривой линии, направленной вверх и вправо, но имеют некоторый разброс, что соответствует выводу, сделанному по полу корреляции.

Для проверки гипотезы о значимости коэффициента ранговой корреляции используется критерий:

который подчинен распределению Стьюдента с числом степеней свободы = n-2.

По таблице распределения Стьюдента необходимо определим критическую точку для двустороннего уровня значимости б:

б = 0,05 = 10-2 = 23

Так как Т=1,8825< t_кр=2,06866, то критерий Т попадает область принятия гипотезы, значит, принимается нулевая гипотеза, т.е. коэффициент корреляции в генеральной совокупности незначим.

Моделирование взаимосвязи между переменными У и Х1 с помощью линейной функции

Произведем моделирование взаимосвязи между переменными У и Х1 с помощью линейной функции.

Линейный регрессионный анализ позволяет предсказывать одну переменную на основании другой с использованием прямой линии, характеризующей взаимосвязь между этими переменными: Y = b₀ + b₁ ? X

Переменную, поведение которой прогнозируют, называют результирующей переменной (Y); переменную, которая используется для прогнозирования, — фактором (Х₁). Коэффициенты b₀ и b₁ называются коэффициентами регрессии.

Угловой коэффициент b₁ показывает наклон линии регрессии, или изменение результирующего показателя Y при изменении фактора Х на единицу. Свободный член b₀ показывает сдвиг линии регрессии по вертикальной оси, т.е. определяет значение результирующего показателя Y при нулевом значении фактора Х.

С помощью метода наименьших квадратов строится уравнение регрессии, которое характеризуется наименьшей суммой квадратов отклонений реальных точек наблюдений от линии регрессии.

Метод наименьших квадратов использует следующие формулы для расчета коэффициентов регрессии:

Все необходимые промежуточные расчеты сведем в таблицу 4.

Также для расчета коэффициентов уравнения линейной линейной регрессии и показателей его качества может использоваться режим работы «Регрессия». Результаты, полученные с помощью данного режима, представлены в приложении А.

Таблица 4. Промежуточные расчеты для вычисления коэффициентов регрессии

Тогда линейное уравнение регрессии будет иметь вид:

Y = 0,6313 + 0,00804 ? X1

Приведем интерпретацию каждого из коэффициентов уравнения регрессии. Угловой коэффициент регрессии (коэффициент наклона) показывает, что если Х1 увеличивается на одну единицу, то У возрастает на 0,00804 единицы, т.е. при возрастании численности служащих на 1 тыс.чел., чистый доход У увеличивается на 0,00804 млрд.долл.

Свободный член уравнения регрессии показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов. Свободный член регрессии дает прогнозируемое значение У, если Х1 равен 0. То есть при численности служащих в 0 чел., чистый доход составит 0,6313 млрд.руб.

Проверим качество построенной модели при уровне значимости 0,05. Если существует значимая линейная взаимосвязь между фактором и результирующим показателем, построенное уравнение регрессии будет адекватно данным генеральной совокупности. Таким образом, проверка адекватности уравнения сводится к проверке значимости линейной взаимосвязи между переменными.

Проверить значимость линейной взаимосвязи можно несколькими способами:

1) проверить значимость углового коэффициента регрессии;

2) проверить значимость коэффициента детерминации.

Оба способа основаны на методе проверки статистических гипотез.

Для проверки углового коэффициента используется критерий Стьюдента:

гдеb₁ — эмпирический угловой коэффициент регрессии;

S_b1 — стандартная ошибка углового коэффициента регрессии, которая

определяется по формуле:

гдеSе 2 и Sе — остаточная дисперсия и стандартная ошибка регрессии соответственно;

Sх — среднее квадратичное отклонение переменной Х.

Критерий t_b1 имеет распределение Стьюдента с числом степеней свободы = n — 2 = 25 — 2 =23

Найдем табличный критерий Стьюдента для уровня значимости 0,05. Для этого используем функцию =СТЬЮДРАСПОБР(0,05;23)

то есть значение критерия t_b1 попадает в одну из критических областей. Вывод:

1) угловой коэффициент признается значимым;

2) существует значимая линейная связь между фактором и результирующим показателем;

3) построенное уравнение адекватно данным генеральной совокупности.

Проверим значимость свободного члена регрессии.

где b0 — эмпирический свободный член регрессии;

S_b0 — стандартная ошибка свободного члена регрессии, которая определяется по формуле:

= 3,02912 > 2,06866, то есть значение критерия t_b0 попадает в одну из критических областей, то есть значение свободного члена генеральной совокупности значимо.

Определим коэффициент детерминации по формуле:

где S_y 2 — дисперсия переменной Y. S_y 2 = 2,071667

Коэффициент детерминации показывает, какую долю вариации (разброса) результирующего показателя Y можно объяснить с помощью фактора Х. Он может принимать значения от 0 до 1. Чем ближе коэффициент детерминации к 1, тем большая доля вариации результирующего показателя объясняется действием фактора Х, т.е. тем точнее осуществляется предсказание по уравнению регрессии. Промежуточные расчеты сведем в таблицу 5.

Таблица 5. Промежуточные расчеты для вычисления коэффициента детерминации

Значение коэффициента детерминации R 2 = 0,69134 показывает, что 69% вариации результирующего показателя объясняется с помощью уравнения регрессии (действием фактора Х), а 31% — случайностью.

Проверим статистическую значимость уравнения с помощью критерия Фишера.

Табличное значение критерия рассчитаем как =FРАСПОБР(0,05;1;23).

> , значение критерия F попадает в критическую область, выводы оказываются следующими:

1) коэффициент детерминации признается значимым;

2) существует значимая линейная связь между фактором и результирующим показателем;

3) построенное уравнение адекватно данным генеральной совокупности.

Построим линию регрессии на поле корреляции (рис.4).

Рисунок 4 — Линия регрессии на поле корреляции

Проверим наличие автокорреляции остатков графическим методом и с помощью критерия Дарбина-Уотсона при уровне значимости 0,01.

Одной из предпосылок МНК является независимость между собой значений случайных отклонений. Если присутствует корреляция между ними, то говорят о наличии автокорреляции остатков. Автокорреляцией остатков называется зависимость между значениями случайных отклонений, упорядоченными по значениям фактора Х.

Наиболее наглядный способ проверки состоит в построении диагностической диаграммы: поля корреляции между случайными отклонениями (ошибками прогнозирования) е_i и прогнозируемыми значениями результирующего показателя y_i.Значения случайного отклонения откладываются по вертикальной оси, прогнозируемые значения результирующего показателя — по горизонтальной оси (рис.5).

При анализе диагностической диаграммы можно сделать следующий вывод: между точками на поле взаимосвязи не наблюдается, диаграмма представляет собой облако из точек, расположенных хаотично и неупорядоченно, следовательно, автокорреляция остатков отсутствует, значит, предпосылки МНК выполняются.

Рисунок 5 — Диагностическая диаграмма к определению автокорреляции.

Проверим наличие автокорреляции с помощью критерия Дарбина-Уотсона при уровне значимости 0,01. Упорядочим случайные отклонения по возрастанию значений фактора Х и составим вспомогательную таблицу 6.

§ 2. Функциональная зависимость между двумя переменными

Говорят, что две переменные величины х, у связаны функциональной зависимостью, если каждому значению, которое может принять одна из них, соответствует одно или несколько определенных значений другой.

Пример 1. Температура Т кипения воды и атмосферное давление р связаны функциональной зависимостью, так как каждому значению Т соответствует одно определенное значение р и обратно. Так, если Т = 100°С, то р непременно равно 760 мм рт. ст.; если Т = 70°С, то р = 234 мм рт.ст. и т.д. Напротив, атмосферное давление р и относительная влажность воздуха х (рассматриваемые как переменные величины) не связаны функциональной зависимостью: если известно, что х = 90% , то о величине р нельзя еще сказать ничего определенного.

Пример 2. Площадь равностороннего треугольника S и его периметр р связаны функциональной зависимостью. Формула S = (√3 : 36) р 2 представляет эту зависимость.

Если желательно подчеркнуть, что в данном вопросе значения переменной у должны находиться по заданным значениям переменной х, то последняя (х) называется независимой переменной или аргументом, а первая (у) — зависимой переменной или функцией.

Пример 3. Если по величине периметра р равностороннего треугольника мы хотим судить о его площади S (см. пример 2), то р есть аргумент (независимая переменная), a S — функция (зависимая переменная).

Чаще всего независимая переменная обозначается буквой х.

Если каждому значению аргумента х соответствует только одно значение функции у, то функция называется однозначной, если два или более — многозначной (двузначной, трехзначной и т.д.).

Пример 4. Тело брошено вверх; s — высота его подъема над землей; t — время, прошедшее с момента броска. Величина s есть однозначная функция t, так как в каждый данный момент высота тела — вполне определенная величина. Величина t — двузначная функция s, так как тело находится на данной высоте s дважды — один раз при полете вверх, другой раз при падении вниз.

Формула s = v₀t – 0,5gt 2 , связывающая переменные s, t (начальная скорость v₀ и ускорение свободного падения g — в данном случае постоянные величины), показывает, что при данном t имеем одно значение s, а при данном s — два значения t, определяемые из квадратного уравнения

Источник

Исследуем отношение между переменными¶

В этой главе исследуются отношения между переменными.

Мы будем визуализировать отношения с помощью диаграмм рассеяния (scatter plots), диаграмм размаха (box plots) и скрипичных диаграмм (violin plots),
И мы будем количественно определять отношения, используя корреляцию (correlation) и простую регрессию (simple regression).

Самый важный урок этой главы заключается в том, что вы всегда должны визуализировать взаимосвязь между переменными, прежде чем пытаться ее количественно оценить; в противном случае вас могут ввести в заблуждение.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve
        local, _ = urlretrieve(url, filename)
        print('Downloaded ' + local)

download('https://github.com/AllenDowney/' +
         'ElementsOfDataScience/raw/master/brfss.hdf5')

Изучение отношений¶

В качестве первого примера мы рассмотрим взаимосвязь между ростом и весом.

Мы будем использовать данные из Системы наблюдения за поведенческими факторами риска (BRFSS), которая находится в ведении Центров по контролю за заболеваниями по адресу https://www.cdc.gov/brfss.

В опросе приняли участие более 400 000 респондентов, но, чтобы произвести анализ, я выбрал случайную подвыборку из 100 000 человек.

In [2]:

import pandas as pd

brfss = pd.read_hdf('brfss.hdf5', 'brfss')
brfss.shape

Out[3]:

	SEX	HTM4	WTKG3	INCOME2	_LLCPWT	_AGEG5YR	_VEGESU1	_HTMG10	AGE
96230	2.0	160.0	60.33	8.0	1398.525290	6.0	2.14	150.0	47.0
244920	2.0	163.0	58.97	5.0	84.057503	13.0	3.14	160.0	89.5
57312	2.0	163.0	72.57	8.0	390.248599	5.0	2.64	160.0	42.0
32573	2.0	165.0	74.84	1.0	11566.705300	3.0	1.46	160.0	32.0
355929	2.0	170.0	108.86	3.0	844.485450	3.0	1.81	160.0	32.0

BRFSS включает сотни переменных. Для примеров в этой главе я выбрал всего девять.

Мы начнем с HTM4, который записывает рост каждого респондента в см, и WTKG3, который записывает вес в кг.

In [4]:

height = brfss['HTM4']
weight = brfss['WTKG3']

Чтобы визуализировать взаимосвязь между этими переменными, мы построим диаграмму рассеяния (scatter plot).

Диаграммы рассеяния широко распространены и понятны, но их на удивление сложно правильно построить.

В качестве первой попытки мы будем использовать функцию plot с аргументом o, который строит круг для каждой точки.

см. документацию по plot

In [5]:

import matplotlib.pyplot as plt
%matplotlib inline

plt.plot(height, weight, 'o')

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Похоже, что высокие люди тяжелее, но в этом графике есть несколько моментов, которые затрудняют интерпретацию.

Первый из них — перекрытие (overplotted), то есть точки данных накладываются друг на друга, поэтому вы не можете сказать, где много точек, а где только одна.

Когда это происходит, результаты могут вводить в заблуждение.

Один из способов улучшить график — использовать прозрачность (transparency), что мы можем сделать с помощью ключевого аргумента alpha. Чем ниже значение alpha, тем прозрачнее каждая точка данных.

Вот как это выглядит с alpha=0.02.

In [6]:

plt.plot(height, weight, 'o', alpha=0.02)

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Уже лучше, но на графике так много точек данных, что диаграмма рассеяния все еще перекрывается. Следующим шагом будет уменьшение размеров маркеров.

При markersize=1 и низком значении alpha диаграмма рассеяния будет менее насыщенной.

Вот как это выглядит.

In [7]:

plt.plot(height, weight, 'o', alpha=0.02, markersize=1)

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Уже лучше, но теперь мы видим, что точки строятся отдельными столбцами. Это потому, что большая часть высоты была указана в дюймах и преобразована в сантиметры.

Мы можем разбить столбцы, добавив к значениям некоторый случайный шум; по сути, мы заполняем округленные значения.

Такое добавление случайного шума называется дрожанием (jittering).

Дрожание — это добавление случайного шума к данным для предотвращения перекрытия статистических графиков. Если непрерывное измерение округлено до некоторой удобной единицы, может произойти перекрытие. Это приводит к превращению непрерывной переменной в дискретную порядковую переменную. Например, возраст измеряется в годах, а масса тела — в фунтах или килограммах. Если вы построите диаграмму разброса веса в зависимости от возраста для достаточно большой выборки людей, там может быть много людей, записанных, скажем, с 29 годами и 70 кг, и, следовательно, в этой точке будет нанесено много маркеров (29, 70).

Чтобы уменьшить перекрытие, вы можете добавить к данным небольшой случайный шум. Размер шума часто выбирается равным ширине единицы измерения. Например, к значению 70 кг вы можете добавить количество u , где u — равномерная случайная величина в интервале [-0,5, 0,5]. Вы можете обосновать дрожание, предположив, что истинный вес человека весом 70 кг с равной вероятностью находится в любом месте интервала [69,5, 70,5].

Контекст данных важен при принятии решения о дрожании. Например, возраст обычно округляется в меньшую сторону: 29-летний человек может праздновать свой 29-й день рождения сегодня или, возможно, ему исполнится 30 завтра, но ей все равно 29 лет. Следовательно, вы можете изменить возраст, добавив величину v , где v — равномерная случайная величина в интервале [0,1]. (Мы игнорируем статистически значимый случай женщин, которым остается 29 лет в течение многих лет!)

Источник: Jittering to prevent overplotting in statistical graphics

Мы можем использовать NumPy для добавления шума из нормального распределения со средним 0 и стандартным отклонением 2.

см. документацию NumPy

In [8]:

import numpy as np

noise = np.random.normal(0, 2, size=len(brfss))
height_jitter = height + noise

Вот как выглядит график с дрожащими (jittered) высотами.

In [9]:

plt.plot(height_jitter, weight, 'o',
         alpha=0.02, markersize=1)

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Столбцы исчезли, но теперь мы видим, что есть строки, в которых люди округляют свой вес. Мы также можем исправить это с помощью дрожания веса.

In [10]:

noise = np.random.normal(0, 2, size=len(brfss))
weight_jitter = weight + noise

In [11]:

plt.plot(height_jitter, weight_jitter, 'o',
         alpha=0.02, markersize=1)

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Наконец, давайте увеличим масштаб области, где находится большинство точек данных.

Функции xlim и ylim устанавливают нижнюю и верхнюю границы для осей $x$ и $y$; в данном случае мы наносим рост от 140 до 200 сантиметров и вес до 160 килограмм.

Вот как это выглядит.

In [12]:

plt.plot(height_jitter, weight_jitter, 'o',
         alpha=0.02, markersize=1)

plt.xlim([140, 200])
plt.ylim([0, 160])
plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Теперь у нас есть достоверная картина взаимосвязи между ростом и весом.

Ниже вы можете увидеть вводящий в заблуждение график, с которого мы начали, и более надежный, которым мы закончили. Они явно разные, и они предлагают разные истории о взаимосвязи между этими переменными.

In [13]:

# Set the figure size
plt.figure(figsize=(8, 3))

# Create subplots with 2 rows, 1 column, and start plot 1
plt.subplot(1, 2, 1)
plt.plot(height, weight, 'o')

plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height')

# Adjust the layout so the two plots don't overlap
plt.tight_layout()

# Start plot 2
plt.subplot(1, 2, 2)

plt.plot(height_jitter, weight_jitter, 'o',
         alpha=0.02, markersize=1)

plt.xlim([140, 200])
plt.ylim([0, 160])
plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height')
plt.tight_layout()

Смысл этого примера в том, что для создания эффективного графика разброса требуются некоторые усилия.

Упражнение: Набирают ли люди вес с возрастом? Мы можем ответить на этот вопрос, визуализировав взаимосвязь между весом и возрастом.

Но прежде чем строить диаграмму рассеяния, рекомендуется визуализировать распределения по одной переменной за раз. Итак, давайте посмотрим на возрастное распределение.

Набор данных BRFSS включает столбец AGE, который представляет возраст каждого респондента в годах. Чтобы защитить конфиденциальность респондентов, возраст округляется до пятилетних интервалов. AGE содержит середину интервалов (bins).

Извлеките переменную 'AGE' из фрейма данных brfss и присвойте ее age.
Постройте функцию вероятности (Probability mass function, PMF) для age в виде гистограммы, используя Pmf из empiricaldist.

empiricaldist — библиотека Python, представляющая эмпирические функции распределения.

In [14]:

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

In [15]:

from empiricaldist import Pmf

Упражнение: Теперь давайте посмотрим на распределение веса.

Столбец, содержащий вес в килограммах, — это WTKG3. Поскольку этот столбец содержит много уникальных значений, отображение его как функции вероятности (PMF) работает плохо.

In [17]:

Pmf.from_seq(weight).bar()

plt.xlabel('Weight in kg')
plt.ylabel('PMF')
plt.title('Distribution of weight');

Чтобы получить лучшее представление об этом распределении, попробуйте построить график функции распределения (Cumulative distribution function, CDF).

Вычислите функцию распределения (CDF) нормального распределения с тем же средним значением и стандартным отклонением и сравните его с распределением веса.

Подходит ли нормальное распределение для этих данных? А как насчет логарифмического преобразования весов?

Упражнение: Теперь давайте построим диаграмму разброса (scatter plot) для weight и age.

Отрегулируйте alpha и markersize, чтобы избежать наложения (overplotting). Используйте ylim, чтобы ограничить ось y от 0 до 200 килограммов.

Упражнение: В предыдущем упражнении возрасты указаны в столбцах, потому что они были округлены до 5-летних интервалов (bins). Если мы добавим дрожание (jitter), диаграмма рассеяния покажет взаимосвязь более четко.

Добавьте случайный шум к age со средним значением 0 и стандартным отклонением 2.5.
Создайте диаграмму рассеяния и снова отрегулируйте alpha и markersize.

Визуализация отношений¶

В предыдущем разделе мы использовали диаграммы разброса для визуализации взаимосвязей между переменными, а в упражнениях вы исследовали взаимосвязь между возрастом и весом. В этом разделе мы увидим другие способы визуализации этих отношений, в том числе диаграммы размаха и скрипичные диаграммы.

Я начну с диаграммы разброса веса в зависимости от возраста.

In [23]:

age = brfss['AGE']
noise = np.random.normal(0, 1.0, size=len(brfss))
age_jitter = age + noise

plt.plot(age_jitter, weight_jitter, 'o',
         alpha=0.01, markersize=1)

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.ylim([0, 200])
plt.title('Weight versus age');

В этой версии диаграммы разброса я скорректировал дрожание весов, чтобы между столбцами оставалось пространство.

Это позволяет увидеть форму распределения в каждой возрастной группе и различия между группами.

С этой точки зрения кажется, что вес увеличивается до 40-50 лет, а затем начинает уменьшаться.

Если мы пойдем дальше, то сможем использовать ядерную оценку плотности (Kernel Density Estimation, KDE) для оценки функции плотности в каждом столбце и построения графика. И для этого есть название — скрипичная диаграмма (violin plot).

Библиотека Seaborn предоставляет функцию, которая создает скрипичную диаграмму, но прежде чем мы сможем ее использовать, мы должны избавиться от любых строк с пропущенными данными.

Вот так:

In [24]:

data = brfss.dropna(subset=['AGE', 'WTKG3'])
data.shape

dropna() создает новый фрейм данных, который удаляет строки из brfss, где AGE или WTKG3 равны NaN.

Теперь мы можем вызвать функцию violinplot.

см. документацию по violinplot

In [25]:

import seaborn as sns

sns.violinplot(x='AGE', y='WTKG3', data=data, inner=None)

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Weight versus age');

Аргументы x и y означают, что нам нужно AGE на оси x и WTKG3 на оси y.

data — это только что созданный фрейм данных, который содержит переменные для отображения.

Аргумент inner=None немного упрощает график.

На рисунке каждая фигура представляет собой распределение веса в одной возрастной группе. Ширина этих форм пропорциональна предполагаемой плотности, так что это похоже на две вертикальные ядерные оценки плотности (KDE), построенные вплотную друг к другу (и залитые красивыми цветами).

Другой, связанный с этим способ просмотра данных, называется диаграмма размаха (ящик с усами, box plot).

Код для создания диаграммы размаха очень похож.

см. документацию по boxplot

In [26]:

sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10)

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Weight versus age');

Я включил аргумент whis=10, чтобы отключить функцию, которая нам не нужна.

Каждый прямоугольник представляет распределение веса в возрастной группе. Высота каждого прямоугольника представляет собой диапазон от 25-го до 75-го процентиля. Линия в середине каждого прямоугольника — это медиана. Шипы, торчащие сверху и снизу, показывают минимальное и максимальное значения.

На мой взгляд, этот график дает лучшее представление о взаимосвязи между весом и возрастом.

Глядя на медианы, кажется, что люди в возрасте от 40 лет являются самыми тяжелыми; люди младшего и старшего возраста легче.
Глядя на размеры ящиков, кажется, что люди в возрасте от 40 также имеют наибольший разброс в весе.
Эти графики также показывают, насколько искажено распределение веса; то есть самые тяжелые люди намного дальше от медианы, чем самые легкие.

Для данных, которые склоняются к более высоким значениям, иногда полезно рассматривать их в логарифмической шкале.

Мы можем сделать это с помощью Pyplot-функции yscale.

In [27]:

sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10)

plt.yscale('log')
plt.xlabel('Age in years')
plt.ylabel('Weight in kg (log scale)')
plt.title('Weight versus age');

Чтобы наиболее четко показать взаимосвязь между возрастом и весом, я бы использовал этот рисунок.

В следующих упражнениях у вас будет возможность создать скрипичную диаграмму и диаграмму размаха.

Упражнение: Ранее мы рассмотрели диаграмму рассеяния (scatter plot) по росту и весу и увидели, что более высокие люди, как правило, тяжелее. Теперь давайте более подробно рассмотрим диаграмму размаха (box plot).

Фрейм данных brfss содержит столбец с именем _HTMG10, который представляет высоту в сантиметрах, разбитую на группы по 10 см.

Составьте диаграмму размаха, показывающую распределение веса в каждой группе роста.
Постройте ось Y в логарифмическом масштабе.

Предложение: если метки на оси x сталкиваются, вы можете повернуть их следующим образом:

plt.xticks(rotation='45')

Упражнение: В качестве второго примера давайте посмотрим на взаимосвязь между доходом (income) и ростом.

В BRFSS доход представлен как категориальная переменная; то есть респондентов относят к одной из 8 категорий доходов. Имя столбца — INCOME2.

Прежде чем связывать доход с чем-либо еще, давайте посмотрим на распределение, вычислив функцию вероятности (PMF).

Извлеките INCOME2 из brfss и присвойте его income.
Постройте функцию вероятности (PMF) для income в виде гистограммы (bar chart).

Примечание: вы увидите, что около трети респондентов относятся к группе с самым высоким доходом; лучше, если бы было больше лидирующих групп, но мы будем работать с тем, что у нас есть.

Упражнение: Создайте скрипичную диаграмму (violin plot), которая показывает распределение роста в каждой группе дохода.

Вы видите взаимосвязь между этими переменными?

Корреляция¶

В предыдущем разделе мы визуализировали отношения между парами переменных. Теперь мы узнаем о коэффициенте корреляции, который количественно определяет силу этих взаимосвязей.

Когда люди говорят «корреляция», они имеют в виду любую связь между двумя переменными. В статистике обычно это означает коэффициент корреляции Пирсона, который представляет собой число от -1 до 1, которое количественно определяет силу линейной связи между переменными.

Для демонстрации я выберу три столбца из набора данных BRFSS:

In [31]:

columns = ['HTM4', 'WTKG3', 'AGE']
subset = brfss[columns]

Результатом является фрейм данных только с этими столбцами.

С этим подмножеством данных мы можем использовать метод corr, например:

Out[32]:

	HTM4	WTKG3	AGE
HTM4	1.000000	0.474203	-0.093684
WTKG3	0.474203	1.000000	0.021641
AGE	-0.093684	0.021641	1.000000

Результатом является корреляционная матрица. В первой строке корреляция HTM4 с самим собой равна 1. Это ожидаемо; корреляция чего-либо с самим собой равна 1.

Следующая запись более интересна; соотношение роста и веса составляет около 0.47. Коэффициент положительный, это означает, что более высокие люди тяжелее, и он умеренный по силе, что означает, что он имеет некоторую прогностическую ценность. Если вы знаете чей-то рост, вы можете лучше предположить его вес, и наоборот.

Корреляция между ростом и возрастом составляет примерно -0.09. Коэффициент отрицательный, это означает, что пожилые люди, как правило, ниже ростом, но он слабый, а это означает, что знание чьего-либо возраста не поможет, если вы попытаетесь угадать их рост.

Корреляция между возрастом и весом еще меньше. Напрашивается вывод, что нет никакой связи между возрастом и весом, но мы уже видели, что она есть. Так почему же корреляция такая низкая?

Помните, что зависимость между весом и возрастом выглядит так.

In [33]:

data = brfss.dropna(subset=['AGE', 'WTKG3'])
sns.boxplot(x='AGE', y='WTKG3', data=data, whis=10)

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Weight versus age');

Люди за сорок — самые тяжелые; люди младшего и старшего возраста легче. Итак, эта связь нелинейна.

Но корреляция измеряет только линейные отношения. Если связь нелинейная, корреляция обычно недооценивает ее силу.

Чтобы продемонстрировать, я сгенерирую несколько поддельных данных: xs содержит точки с равным интервалом между -1 и 1.

ys — это квадрат xs плюс некоторый случайный шум.

In [34]:

xs = np.linspace(-1, 1)
ys = xs**2 + np.random.normal(0, 0.05, len(xs))

Вот диаграмма рассеяния для xs и ys.

In [35]:

plt.plot(xs, ys, 'o', alpha=0.5)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Scatter plot of a fake dataset');

Понятно, что это сильная связь; если вам дано x, вы можете гораздо лучше догадаться о y.

Но вот корреляционная матрица:

Out[36]:

array([[1.        , 0.01135475],
       [0.01135475, 1.        ]])

Несмотря на то, что существует сильная нелинейная зависимость, вычисленная корреляция близка к 0.

В общем, если корреляция высока, то есть близка к 1 или -1, вы можете сделать вывод, что существует сильная линейная зависимость.
Но если корреляция близка к 0, это не означает, что связи нет; может быть связь нелинейная.

Это одна из причин, по которой я считаю, что корреляция не является хорошей статистикой.

В частности, корреляция ничего не говорит о наклоне. Если мы говорим, что две переменные коррелируют, это означает, что мы можем использовать одну для предсказания другой. Но, возможно, это не то, о чем мы заботимся.

Например, предположим, что нас беспокоит влияние увеличения веса на здоровье, поэтому мы строим график зависимости веса от возраста от 20 до 50 лет.

Я создам два поддельных набора данных, чтобы продемонстрировать суть дела. В каждом наборе данных xs представляет возраст, а ys — вес.

Я использую np.random.seed для инициализации генератора случайных чисел, поэтому мы получаем одни и те же результаты при каждом запуске.

In [37]:

np.random.seed(18)
xs1 = np.linspace(20, 50)
ys1 = 75 + 0.02 * xs1 + np.random.normal(0, 0.15, len(xs1))

plt.plot(xs1, ys1, 'o', alpha=0.5)
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake dataset #1');

А вот и второй набор данных:

In [38]:

np.random.seed(18)
xs2 = np.linspace(20, 50)
ys2 = 65 + 0.2 * xs2 + np.random.normal(0, 3, len(xs2))

plt.plot(xs2, ys2, 'o', alpha=0.5)
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake dataset #2');

Я построил эти примеры так, чтобы они выглядели одинаково, но имели существенно разные корреляции:

In [39]:

rho1 = np.corrcoef(xs1, ys1)[0][1]
rho1

In [40]:

rho2 = np.corrcoef(xs2, ys2)[0][1]
rho2

В первом примере сильная корреляция, близкая к 0.75. Во втором примере корреляция умеренная, близкая к 0.5. Поэтому мы можем подумать, что первые отношения более важны. Но посмотрите внимательнее на ось y на обоих рисунках.

В первом примере средняя прибавка в весе за 30 лет составляет менее 1 килограмма; во втором больше 5 килограммов!

Если нас беспокоит влияние увеличения веса на здоровье, второе соотношение, вероятно, более важно, даже если корреляция ниже.

Статистика, которая нас действительно волнует, — это наклон линии, а не коэффициент корреляции.

В следующем разделе мы увидим, как оценить этот наклон. Но сначала давайте попрактикуемся с корреляцией.

Упражнения: Цель BRFSS — изучить факторы риска для здоровья, поэтому в него включены вопросы о диете.

Столбец _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.

Посмотрим, как эта переменная связана с возрастом и доходом.

Во фрейме данных brfss выберите столбцы 'AGE', INCOME2 и _VEGESU1.
Вычислите корреляционную матрицу для этих переменных.

Упражнение: В предыдущем упражнении корреляция между доходом и потреблением овощей составляет около 0.12. Корреляция между возрастом и потреблением овощей составляет примерно -0.01.

Что из следующего является правильной интерпретацией этих результатов?

A: люди в этом наборе данных с более высоким доходом едят больше овощей.
B: Связь между доходом и потреблением овощей линейна.
C: Пожилые люди едят больше овощей.
D: Между возрастом и потреблением овощей может быть сильная нелинейная зависимость.

Упражнение: В общем, рекомендуется визуализировать взаимосвязь между переменными перед вычислением корреляции. В предыдущем примере мы этого не делали, но еще не поздно.

Создайте визуализацию взаимосвязи между возрастом и овощами. Как бы вы описали отношения, если они есть?

Простая регрессия¶

В предыдущем разделе мы видели, что корреляция не всегда измеряет то, что мы действительно хотим знать. В этом разделе мы рассмотрим альтернативу: простую линейную регрессию.

Давайте еще раз посмотрим на взаимосвязь между весом и возрастом. В предыдущем разделе я создал два фальшивых набора данных, чтобы доказать свою точку зрения:

In [44]:

plt.figure(figsize=(8, 3))

plt.subplot(1, 2, 1)
plt.plot(xs1, ys1, 'o', alpha=0.5)
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake dataset #1')
plt.tight_layout()

plt.subplot(1, 2, 2)
plt.plot(xs2, ys2, 'o', alpha=0.5)
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake dataset #2')
plt.tight_layout()

Тот, что слева, имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.

Но в этом контексте статистика, которая нас, вероятно, волнует, — это наклон линии, а не коэффициент корреляции.

Чтобы оценить наклон, мы можем использовать linregress из SciPy-библиотеки stats.

см. документацию по scipy.stats.linregress

In [45]:

from scipy.stats import linregress

res1 = linregress(xs1, ys1)
res1._asdict()

Out[45]:

{'slope': 0.018821034903244396,
 'intercept': 75.08049023710964,
 'rvalue': 0.7579660563439407,
 'pvalue': 1.8470158725245546e-10,
 'stderr': 0.002337849260560816,
 'intercept_stderr': 0.08439154079040351}

Результатом является объект LinregressResult, содержащий пять значений: slope — наклон линии, наиболее подходящей для данных; intercept — это пересечение линии регрессии.

Для фальшивого набора данных 1 расчетный наклон составляет около 0,019 кг в год или около 0,56 кг за 30-летний период.

Вот результаты для фальшивого набора данных 2.

In [47]:

res2 = linregress(xs2, ys2)
res2._asdict()

Out[47]:

{'slope': 0.17642069806488858,
 'intercept': 66.60980474219305,
 'rvalue': 0.47827769765763184,
 'pvalue': 0.0004430600283776228,
 'stderr': 0.046756985211216295,
 'intercept_stderr': 1.6878308158080693}

Расчетный наклон почти в 10 раз выше: около 0,18 килограмма в год или около 5,3 килограмма за 30 лет:

То, что здесь называется rvalue, — это корреляция, которая подтверждает то, что мы видели раньше; первый пример имеет более высокую корреляцию, около 0,75 по сравнению с 0,5.

Но сила эффекта, измеренная по наклону линии, во втором примере примерно в 10 раз выше.

Мы можем использовать результаты linregress для вычисления линии тренда: сначала мы получаем минимум и максимум наблюдаемых xs; затем мы умножаем на наклон и добавляем точку пересечения.

Вот как это выглядит для первого примера.

In [49]:

plt.plot(xs1, ys1, 'o', alpha=0.5)

fx = np.array([xs1.min(), xs1.max()])
fy = res1.intercept + res1.slope * fx
plt.plot(fx, fy, '-')

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake Dataset #1');

То же самое и со вторым примером.

In [50]:

plt.plot(xs2, ys2, 'o', alpha=0.5)

fx = np.array([xs2.min(), xs2.max()])
fy = res2.intercept + res2.slope * fx
plt.plot(fx, fy, '-')

plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Fake Dataset #2');

Визуализация здесь может ввести в заблуждение, если вы не посмотрите внимательно на вертикальные шкалы; наклон на втором рисунке почти в 10 раз больше.

Рост и вес¶

Теперь рассмотрим пример с реальными данными.
Вот еще раз диаграмма рассеяния для роста и веса.

In [51]:

plt.plot(height_jitter, weight_jitter, 'o',
         alpha=0.02, markersize=1)

plt.xlim([140, 200])
plt.ylim([0, 160])
plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Теперь мы можем вычислить линию регрессии. linregress не может обрабатывать значения NaN, поэтому мы должны использовать dropna для удаления строк, в которых отсутствуют нужные нам данные.

In [52]:

subset = brfss.dropna(subset=['WTKG3', 'HTM4'])
height_clean = subset['HTM4']
weight_clean = subset['WTKG3']

Теперь мы можем вычислить линейную регрессию.

In [53]:

res_hw = linregress(height_clean, weight_clean)
res_hw._asdict()

Out[53]:

{'slope': 0.9192115381848256,
 'intercept': -75.12704250330165,
 'rvalue': 0.47420308979024434,
 'pvalue': 0.0,
 'stderr': 0.005632863769802997,
 'intercept_stderr': 0.960886026543318}

Наклон составляет около 0,92 килограмма на сантиметр, а это означает, что мы ожидаем, что человек выше на один сантиметр будет почти на килограмм тяжелее. Это довольно много.

Как и раньше, мы можем вычислить линию тренда:

In [54]:

fx = np.array([height_clean.min(), height_clean.max()])
fy = res_hw.intercept + res_hw.slope * fx

In [55]:

plt.plot(height_jitter, weight_jitter, 'o', alpha=0.02, markersize=1)

plt.plot(fx, fy, '-')

plt.xlim([140, 200])
plt.ylim([0, 160])
plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.title('Scatter plot of weight versus height');

Наклон этой линии соответствует диаграмме рассеяния.

Линейная регрессия имеет ту же проблему, что и корреляция; она только измеряет силу линейной связи.

Вот диаграмма рассеяния веса по сравнению с возрастом, которую мы видели ранее.

In [56]:

plt.plot(age_jitter, weight_jitter, 'o',
         alpha=0.01, markersize=1)

plt.ylim([0, 160])
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Weight versus age');

Люди в возрасте от 40 — самые тяжелые; люди младшего и старшего возраста легче. Так что отношения нелинейные.

Если мы не посмотрим на диаграмму рассеяния и вслепую вычислим линию регрессии, мы получим вот что.

In [57]:

subset = brfss.dropna(subset=['WTKG3', 'AGE'])
age_clean = subset['AGE']
weight_clean = subset['WTKG3']

res_aw = linregress(age_clean, weight_clean)
res_aw._asdict()

Out[57]:

{'slope': 0.023981159566968686,
 'intercept': 80.07977583683224,
 'rvalue': 0.021641432889064033,
 'pvalue': 4.3743274930078674e-11,
 'stderr': 0.003638139410742186,
 'intercept_stderr': 0.18688508176870167}

Расчетный уклон составляет всего 0,02 килограмма в год или 0,6 килограмма за 30 лет.

А вот как выглядит линия тренда.

In [58]:

plt.plot(age_jitter, weight_jitter, 'o',
         alpha=0.01, markersize=1)

fx = np.array([age_clean.min(), age_clean.max()])
fy = res_aw.intercept + res_aw.slope * fx
plt.plot(fx, fy, '-')

plt.ylim([0, 160])
plt.xlabel('Age in years')
plt.ylabel('Weight in kg')
plt.title('Weight versus age');

Прямая линия плохо отражает взаимосвязь между этими переменными.

Давайте попрактикуемся в простой регрессии.

Упражнение: Как вы думаете, кто ест больше овощей, люди с низким доходом или люди с высоким доходом? Давайте выясним.

Как мы видели ранее, столбец INCOME2 представляет уровень дохода, а _VEGESU1 представляет количество порций овощей, которые респонденты ели в день.

Постройте диаграмму рассеяния порций овощей в зависимости от дохода, то есть с порциями овощей по оси y и группой доходов по оси x.

Вы можете использовать ylim для увеличения нижней половины оси y.

Упражнение: Теперь давайте оценим наклон зависимости между потреблением овощей и доходом.

Используйте dropna для выбора строк, в которых INCOME2 и _VEGESU1 не равны NaN.
Извлеките INCOME2 и _VEGESU1 и вычислите простую линейную регрессию этих переменных.

Каков наклон линии регрессии? Что означает этот наклон в контексте изучаемого нами вопроса?

Упражнение: Наконец, постройте линию регрессии поверх диаграммы рассеяния.

Источник

Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.

Одна переменная x известна как предикторная переменная .

Другая переменная, y , известна как переменная ответа .

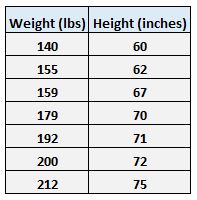
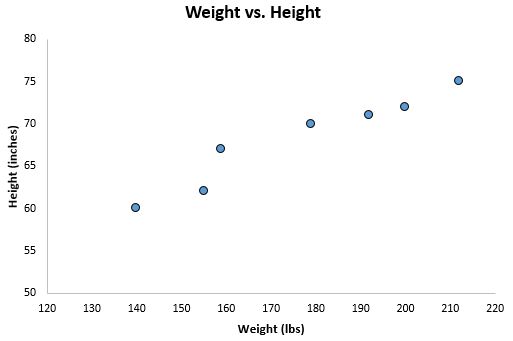
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:

Пусть вес будет предикторной переменной, а рост — переменной отклика.

Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:

Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.

Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.

Формула линии наилучшего соответствия записывается так:

ŷ = б 0 + б 1 х

где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.

Связанный: 4 примера использования линейной регрессии в реальной жизни

Поиск «Линии наилучшего соответствия»

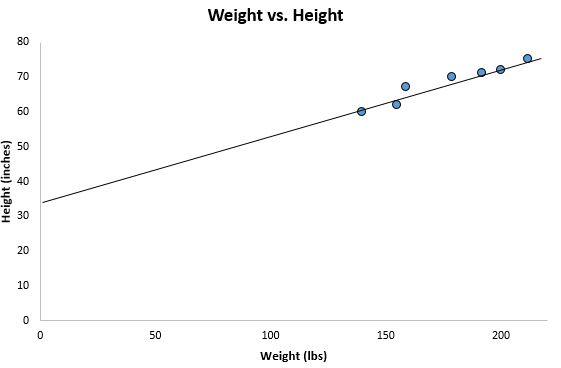
Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:

Калькулятор автоматически находит линию регрессии методом наименьших квадратов :

ŷ = 32,7830 + 0,2001x

Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:

Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.

Как интерпретировать линию регрессии методом наименьших квадратов

Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x

б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.

б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.

Как использовать линию регрессии наименьших квадратов

Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:

Какого роста мы ожидаем от человека, который весит 170 фунтов?

Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма

Какого роста мы ожидаем от человека, который весит 150 фунтов?

Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма

Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.

Коэффициент детерминации

Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .

Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.

Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.

Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:

Это говорит нам о том, что вес является очень хорошим предиктором роста.

Предположения линейной регрессии

Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:

1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.

2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.

3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.

4. Нормальность: остатки модели нормально распределены.

Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.

Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.

Источник

Введение в регрессионный анализ

Линейная регрессия

Ограничения линейной регрессии

Как преодолеть эти ограничения

Линейная регрессия плюсов на Хабре

В заключение

Использованные материалы

Определение вида зависимости между переменными

Исследование корреляционной зависимости между переменными Х1 и У

Моделирование взаимосвязи между переменными У и Х1 с помощью линейной функции

§ 2. Функциональная зависимость между двумя переменными

Исследуем отношение между переменными¶

Изучение отношений¶

Визуализация отношений¶

Корреляция¶

Простая регрессия¶

Рост и вес¶

Поиск «Линии наилучшего соответствия»

Как интерпретировать линию регрессии методом наименьших квадратов

Как использовать линию регрессии наименьших квадратов

Коэффициент детерминации

Предположения линейной регрессии

Не пропустите также: