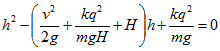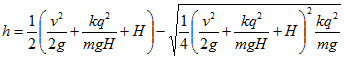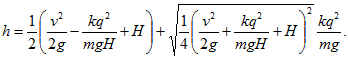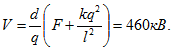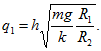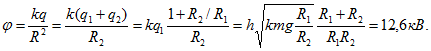Как найти заряд в центре квадрата

Решение:


15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение:

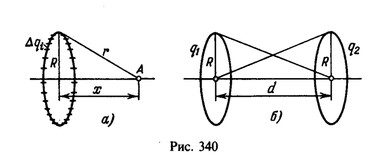
Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:


18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:

Решая его, найдем

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение:


21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

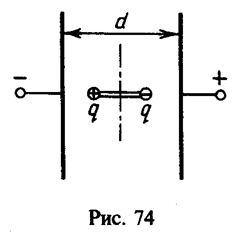
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:


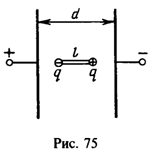
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.

Решение:


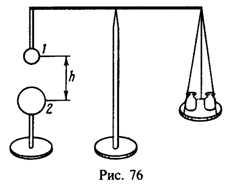
29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2

Примеры решения типовых задач

1.
В центр квадрата, в вершинах которого
находятся заряды q
= 2,33 нКл, помещен отрицательный заряд
.
Найти величину этого заряда, если
результирующая сила, действующая на
каждый заряд, равна нулю.

Решение.На рис. 1.1 приведено расположение зарядов
и силы, действующие на заряд 1 со стороны
остальных зарядов. По условию эти силы
скомпенсированы

.

Спроектируем
это равенство на прямую, совпадающую с
диагональю квадрата

.

Обозначив
сторону квадрата
и используя закон Кулона, преобразуем
это уравнение к виду

.

Отсюда
найдем искомый заряд

2,23 НКл.

2.
Два шарика одинакового радиуса и массы
=
10 г подвешены на нитях так, что их
поверхности соприкасаются, и погружены
в керосин. После сообщения шарикам
зарядаКл
они оттолкнулись друг от друга и разошлись
на угол 2
= 45°. Найти плотность материала шариков,
если расстояние от точки, подвеса до
центра шарика l
= 20 см. Плотность и относительная
диэлектрическая проницаемость керосина
= 800 кг/м³,

= 2.

Решение.
На каждый из шариков действуют силы:
тяжести,
натяжения нити,
Кулонаи Архимеда(рис. 1.2). Под действием этих сил шарик
находится в равновесии, условие которого
имеет вид

Спроектировав
эти силы на оси
и,
получим следующие уравнения:

(1)

По
закону Кулона и Архимеда имеем:

,, (2)

где
— заряд каждого шарика, который
распределился между шариками поровну,— расстояние между шариками,и—
плотность и относительная диэлектрическая
проницаемость керосина,и—
плотность, масса и объем шарика.

Плотность
шарика найдем из второго уравнения (2)

. (3)

Из
уравнений (1) и (2) найдем силу Архимеда

.

После
подстановки в (3), получим выражение для
плотности

=
4200 кг/м³.

3.
Электрон с некоторой начальной скоростью
v₀
влетает в плоский конденсатор параллельно
пластинам на равном расстоянии от них.
К пластинам конденсатора приложена
разность потенциалов U
= 300 В. Расстояние между пластинами d
= 2 см, длина конденсатора l
=10 см. Какова должна быть предельная
начальная скорость v₀
электрона, чтобы электрон не вылетел
из конденсатора?

Решение.На электрон при движении между пластинами
конденсатора действует электрическая
сила,
направленная перпендикулярно пластинам,
где— напряженность электрического поля
(рис. 1.3). Двигаясь в этом направлении с
ускорением,
электрон достигнет пластины за время.
За это время он пролетит вдоль пластин
расстояние.
Траекторией электрона будет парабола.
Если,
то электрон не вылетит из конденсатора.
Из этого неравенства находим ограничение
для скорости

4.Элемент с ЭДС= 1,1 В и внутренним сопротивлениемr= 1 Ом замкнут на внешнее сопротивлениеR= 9 Ом. Найти силу тока
в цепи, напряжениево внешней цепи и напряжениевнутри элемента. С каким КПДработает элемент?

Решение.
Из закона Ома для замкнутой цепи найдем
силу тока

0,11 А. (1)

Напряжение
на внешней цепи ивнутри элемента найдем из закона Ома
для участка цепи

=
0,99 В,0,11
В. (2)

КПД
источника тока найдем по отношению
полезной мощности
к затраченной:

=
0,9.

Здесь
иопределены из формулы (1) и (2).

5.В схеме на рис. 1.4 батарея с ЭДС ε = 120 В,R= 10 Ом, В — электрический чайник. Амперметр
показываетI= 2 А. Через
сколько времени закипитV= 0,5 л воды, находящейся в чайнике при
начальной температуреt₀= 4° С? Сопротивлением батареи и амперметра
пренебречь. КПД чайника= 76 %.

Решение.
Мощность нагревателя определим по
закону Джоуля-Ленца

. (1)

Сопротивление
нагревателя определим из закона Ома
для замкнутой цепи

50
Ом.

Время
нагревания воды
найдем из уравнения теплового баланса,
которое с учетом КПД нагревателя имеет
вид

, (2)

где
4200 Дж/кгм³
— теплоемкость воды,
— масса воды,1000
кг/м³
— плотность,
— температура кипения. Из уравнения (2)
с учетом (1) получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

2014-05-31   

Одинаковые заряды $q$ расположены в вершинах квадрата. Какой заряд $Q$ надо поместить в центр квадрата, чтобы силы, действующие на каждый заряд со стороны остальных зарядов, были в сумме равны нулю?

Решение:

Прежде всего рассмотрим силы, действующие на вносимый заряд $Q$ со стороны остальных зарядов. Эти силы направлены по диагоналям квадрата, равны друг другу по величине и попарно противоположны. Поэтому их равнодействующая, независимо от величины и знака вносимого заряда, всегда равна нулю.

Заряды $q$ совершенно равноправны. Поэтому, если один из них находится в равновесии, то в равновесии будут находиться и три остальных, и нам достаточно рассмотреть силы, действующие на любой из зарядов $q$.

Силы, действующие на заряд $q$, расположенный в правом верхнем углу квадрата, показаны на рис. Их величины, согласно закону Кулона, определяются формулами

$F_{1}=F_{2}=frac{q^{2}}{a^{2}}, F_{3}=frac{q^{2}}{2a^{2}},F_{4}=frac{2qQ}{a^{2}}$, (1)

где $a$ — длина стороны квадрата. Условие равновесия заряда $q$

$bar{F_{1}} + bar{F_{2}} + bar{F_{3}} + bar{F_{4}} = 0$.

Проецируя это векторное равенство на направление диагонали, на которой находится заряд $q$, получаем следующее равенство:

$(F_{1}+F_{2}) cos 45^{circ} + F_{3} + F_{4} = 0$.

Заменяя здесь $F_{1}, F_{2}, F_{3}$ и $ F_{4}$, правыми частями (1) и решая затем

получающееся равенство относительно $Q$, находим

$Q= -q left ( frac{1}{sqrt{2}} + frac{1}{4} right )$.

Спрятать решение

Источник: Са­вчен­ко О. Я. За­да­чи по фи­зи­ке, М.: «Наука», 1988 (№ 6.1.13)