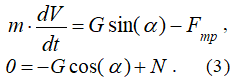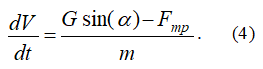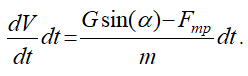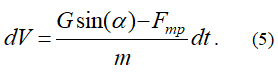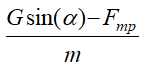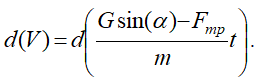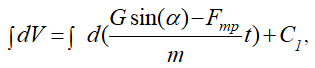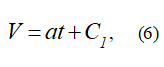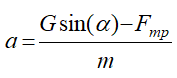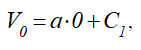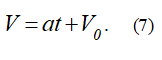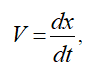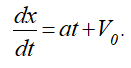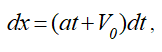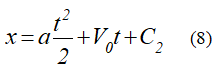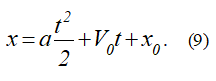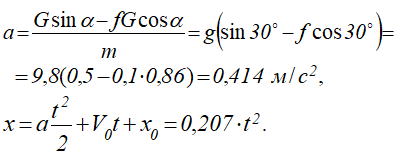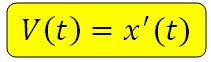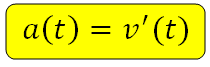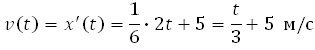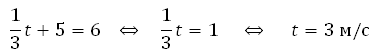Содержание:
- Динамика материальной точки
- Прямая задача динамики точки
- Основные законы динамики
- Уравнения движения материальной точки в декартовых и естественных системах отсчета
- Две основные задачи динамики материальной точки
- Порядок решения прямой задачи динамики невольной материальной точки
- Примеры решения задач на тему: Динамика материальной точки
- Решение задач на тему: Движение материальной точки по криволинейной траектории
Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика материальной точки
Динамикой называется раздел теоретической механики, в котором изучается механическое движение материальных объектов в зависимости от физических факторов, то есть от причин, вызывающих это движение.
Напомним, что в классической механике движение материальных объектов рассматривается с помощью абстрактных моделей: материальной точки, механической системы и абсолютно твердого тела.
Материальная точка — это материальное тело, размерами и разницей в движении его частей которого можно пренебречь.
Механической системой (системой материальных точек) называется совокупность материальных точек, которые между собой взаимодействуют, то есть, положение и движение которых взаимосвязаны.
Абсолютно твердым телом называется совокупность материальных точек, расстояния между которыми во время движения не меняются.
Движение механической системы определяется движением всех его точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.
В динамике точки рассматриваются две основные задачи:
— движение точки задается, а необходимо найти силы, которые это движение реализуют (первая, или прямая задача);
— силы задаются, а необходимо определить закон движения, который является результатом действия этих сил.
Для решения этих задач используются базовые сведения из статики и кинематики, а также законы динамики, то есть, общие законы движения тел и механических систем под действием приложенных к ним сил. Эти законы впервые в наиболее полном виде сформулированы Исааком Ньютоном в конце XVII века.
Прямая задача динамики точки
Первая (прямая) задача динамики содержит условие: По заданному движению, совершаемому точкой данной массы, требуется найти неизвестную действующую силу.
Основные законы динамики
В динамике изучается движение материальных систем в связи с действующими на них силами. Самым простым объектом механики является материальная точка.
Материальная точка — тело, размерами которого при решении данной задачи можно пренебречь.
Если на положение материальной точки и на ее движение не наложены никакие ограничения, точка называется свободной, в противном случае имеем дело с движением несвободной точки.
Движение механической системы определяется движением всех ее материальных точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.
В основе динамики лежат три закона И. Ньютона, которые впервые в наиболее полном и законченном виде были сформулированы в книге «Математические начала натуральной философии» (1686 г.).
1. Первый закон (закон инерции):
изолированная от внешних действий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит этого состояния.
2. Второй закон (основной закон динамики):
cила, которая действует на материальную точку, равна произведению массы точки на ее ускорение, а направление силы совпадает с направлением ускорения:
Если на точку действует несколько сил, то их можно заменить равнодействующей:
Если точка движется по какой-то поверхности, то на нее, кроме активных сил действует и реакция связи 
Таким образом в общем случае в уравнении (1.1):
3. Третий закон (закон равенства действия и противодействия):
Силы взаимодействия двух материальных точек равны между собой по модулю и направлены вдоль одной прямой, которая соединяет эти точки, в противоположные стороны.
Уравнения движения материальной точки в декартовых и естественных системах отсчета
Вместо уравнения движения (1.1) в векторной форме можно получить уравнение в скалярной форме, если спроектировать (1.1) на оси декартовой или естественной систем координат.
Уравнение движения в декартовых координатах:
Здесь 



Две основные задачи динамики материальной точки
Первая задача (прямая): зная массу точки 
определить равнодействующую приложенных к точке сил.
Сначала нужно определить проекции ускорения точки на оси координат:
Используя уравнение движения точки в декартовых координатах (1.3), определяем значения проекций равнодействующей приложенных к точке сил, а также ее модуль:
Направление вектора силы относительно осей координат определяется с помощью направляющих косинусов:
Вторая задача (обратная): зная силы, которые действуют на материальную точку, ее массу, а также первоначальные условия (положение точки и ее скорость в некоторые моменты времени, не обязательно в начальный), получить уравнение движения точки.
Порядок решения прямой задачи динамики невольной материальной точки
1. Изобразить на рисунке материальную точку в промежуточном положении.
2. Показать активные силы и реакции связей, которые на нее действуют.
3. Выбрать систему отсчета.
4. Записать векторное уравнение движения точки в форме второго закона динамики (1.1).
5. Спроектировать векторное уравнение движения точки на выделенные оси координат.
6. Из полученных уравнений определить необходимые величины.
Примеры решения задач на тему: Динамика материальной точки
Задача № 1
В шахту начинает опускаться равноускорено лифт, масса которого 
Определить натяжение 
Решение. Изобразим кабину лифта в произвольном положении (рис.1.1). На лифт действует сила тяжести 

Движение происходит по вертикали, поэтому направим ось 
Запишем уравнение движения кабины лифта в форме второго закона Ньютона:
где 
С учетом сил, действующих на кабину лифта, уравнение будет иметь вид:
Спроектируем это уравнение на ось 
С учетом того, что 
Мы получили зависимость натяжения каната от ускорения, с которым движется кабина лифта.
Проанализируем эту зависимость. Может быть три случая:
В первом случае
То есть, если кабина лифта движется без ускорения в любом направлении, натяжение троса будет равняться силе тяжести кабины лифта.
Во втором случае натяжение троса меньше силы тяжести кабины лифта, потому что 

В третьем случае натяжение троса всегда больше силы тяжести кабины лифта, потому что 
Например, когда 
В нашей задаче ускорение определится с выражения для пути при равнопеременном движении с учетом того, что начальная скорость 
Тогда:
Ответ: натяжение троса
Задача № 2
К телу весом 
Определить, с каким ускорением 
Решение: Изобразим тело с привязанной к нему нитью (рис.1.2). Покажем силы, которые действуют на тело: сила тяжести 


Запишем уравнение движения тела в векторной форме:
Спроектируем это уравнение на ось 
Откуда:
Если учесть числовые данные, то
Ответ:
Задача № 3
Пуля весом 



Определить силу сопротивления среды 
Решение. Изобразим шар в произвольном положении на траектории и покажем силы, которые на него действуют (рис.1.3):


Движение шара происходит вдоль вертикали, поэтому направим ось 

Запишем уравнение движения шара в векторной форме:
и спроектируем его на ось 
откуда
Таким образом, чтобы определить силу сопротивления 

Поскольку закон изменения координаты 
Находим первую и вторую производные от закона движения пули:
Таким образом,
Из выражения 

то есть
Ответ:
Задача № 4
Движение тела массой 
где 


Определить силу 
Решение. Проекции на оси координат силы 
где 

В данном случае
Итак
Модуль силы 
Сила 


Ответ:
Задача № 5
Прямолинейное движение ножа 



Определить силу 

Объяснение: Для привода ножа резального аппарата жатки используются плоские и пространственные механизмы. Среди плоских механизмов нашли применение кривошипно-шатунные, которые состоят из кривошипа 1, шатуна 2 и ножа жатки 3. Механизм преобразует вращательное движение кривошипа 1 в обратно поступательное движение ножа 3.
В уборочных машинах ось кривошипного пальца 

Решение. Изобразим нож резного аппарата в среднем положении на перемещении 
На нож 




Запишем уравнение движения ножа в векторной форме:
Проектируем это уравнение на направление движения ножа (ось 

Из последнего уравнения следует, что для определения силы 

Поскольку задан закон движения ножа 


Итак,
Учтем, что 
Ответ:
Задача № 6
Нагруженная вагонетка массой 


Определить натяжение каната при равномерном опускании и при торможении вагонетки, если время торможения 

Решение. Изобразим вагонетку в произвольном положении. Покажем силы, которые действуют на нее: силу тяжести 



Выбираем декартовую систему координат: ось 

Проектируем векторное уравнение движения на оси координат:
Поскольку 

Тогда общая сила сопротивления движению составляет:
Для определения натяжения 
При равномерном опусканье 

При равнозамедленном торможении
где 

Таким образом
Тогда
Ответ:
Из полученных результатов следует, что при торможении нагрузка на канат увеличивается по сравнению с нагрузкой при равномерном движении.
Задача № 7
Вагон весом 

Определить силу торможения вагона 

Решение. Изображаем вагон в виде материальной точки в произвольном положении на наклонной плоскости и показываем силы, которые на него действуют (рис.1.7): 


Выбираем декартовую систему координат, причем ось 

Запишем уравнение движения вагона в векторной форме:
и спроектируем его на оси выбранной системы координат:
По уравнению (2) определим силу торможения вагона:
По условиям задачи вагон движется с ускорением 


Если подставим в уравнение (3) 
Определим значение угла 
то
где 
Откуда получим
Из этого уравнения вытекает, что при изменении угла 


Поскольку известно, что коэффициент трения равен тангенсу угла трения 
Таким образом, при углу наклона рельсов к горизонту, что равен углу трения 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 26.2, 26.8, 26.10, 26.20, 26.24 [2].
Решение задач на тему: Движение материальной точки по криволинейной траектории
При решении задач, связанных с движением точки по криволинейной траектории, если траектория известна, удобно рассматривать движение точки в естественной системе координат 
где 

В уравнениях (1.6) и (1.8) 



Порядок решения прямой задачи динамики точки в случае использования уравнений (1.6) и (1.8) совпадает с рекомендациями пунктов 1 и 6 занятия № 1.
Если задано уравнение движения материальной точки по траектории в виде 



Далее, с уравнений (1.6), (1.7) находим значения касательной и нормальной проекции силы 
Модуль приложенной к материальной точке силы, при естественном способе обозначения движения, будет равен
Задача № 1
Материальная точка массой 

Определить модуль 
Решение. В задаче движение материальной точки задано естественным способом, поэтому для определения равнодействующей сил воспользуемся зависимостями (1.6) и (1.7):
Определим касательное и нормальное ускорение материальной точки:
Поскольку 

Находим нормальную составляющую равнодействующей сил:
Модуль равнодействующей определим из выражения (1.11):
Таким образом, заданное движение материальной точки происходит под действием силы, постоянной по модулю и направленной вдоль радиуса к центру окружности.
Ответ:
Задача № 2
Материальная точка массой 

Определить проекцию 
Решение. Для определения проекции 
Сначала найдем значение скорости материальной точки:
При
Определяем величину касательного ускорения
при
Подставив в уравнение (1) значения 

Ответ:
Задача № 3
Материальная точка массой 

Определить модуль 
Решение. Поскольку движение материальной точки задано естественным способом, то модуль равнодействующей сил, приложенных к точке, определяется по зависимостям (1.10) и (1.11):
Величины касательного и нормального ускорения материальной точки определяются по уравнениям (1.9):
Учитывая, что скорость точки
то касательное ускорение точки равно:
Поскольку в момент времени 
то нормальное ускорение точки составит:
Определяем 

Тогда модуль равнодействующей сил, действующих на материальную точку, равен:
Ответ:
Задача № 4
На криволинейных участках железнодорожного пути наружный рельс поднимают выше над внутренним (рис.1.9). При движении поезда на этом участке его скорость 
Определить величину 


Решение. На вагон действуют: сила тяжести 


Запишем уравнение движения вагона в векторной форме:
где 
Поскольку движение происходит по криволинейной траектории, то выбираем естественную систему координат: ось 


Проектируем уравнение движения (1) на ось 

Из рис. 1.8 видно, что
Итак,
Подставив числовые значения известных величин, получаем:
Ответ:
Задача № 5
Груз 




Определить величину скорости груза 

Решение. Изобразим груз 



Для решения задачи выбираем естественную систему координат: ось 


Запишем уравнение движения груза в векторной форме:
Проектируем это векторное уравнение на оси координат:
Модуль силы натяжения нити 

Из второго из уравнений (1) найдем 
Тогда
Откуда
Ответ:
Задача № 6
Материальная точка весом 




Определить модуль силы 
Решение. Изобразим точку 



С точкой 


Запишем уравнение движения точки в виде второго закона Ньютона:
Спроектируем это векторное уравнение на оси выбранной системы координат:
Поскольку закон движения известен, то:
По условиям 
Тогда:
Учитывая, что масса точки равна 
Определяем модуль искомой силы:
Ответ:
Задача № 7
Радиус закругления моста в точке 

Определить, с какой силой автомобиль давит на мост в точке 

Решение. Рассмотрим автомобиль как материальную точку, поскольку его размерами по сравнению с размерами моста можно пренебречь. Изобразим автомобиль в точке 


Поскольку автомобиль движется по криволинейной траектории, то для решения задачи воспользуемся естественной системой координат 
Запишем уравнение движения автомобиля в векторной форме:
и спроектируем его на оси выбранной системы координат:



Из уравнения (2) определяем реакцию моста 
Сила давления 
Поскольку вес автомобиля 
то, если мост выпуклый, сила давления автомобиля на него уменьшается по сравнению с тем случаем, когда автомобиль движется по горизонтальному мосту.
Зададим дополнительный вопрос: с какой скоростью 

Поскольку 

Отсюда
Ответ:
Задача № 8
Камень весом 

Определить наименьшее значение угловой скорости вращения, при которой нить разорвется, если ее сопротивление разрыву составляет
Решение. Представим камень 



На камень (точку 


С точкой 


Спроектируем это уравнение на оси выбранной системы координат:
Заметим, что 

Отсюда
Из уравнения (3) вытекает, что при 






Ответ:
Задача № 9
Трек для испытания автомобилей на кривых отрезках пути имеет виражи, профиль которых (рис.1.14) в поперечном пересечении является прямой, которая наклонена к горизонту так, что внешний край трека выше внутреннего.
Определить, с какой наименьшей и самой большой скоростью можно ехать по виражу, имеющему радиус кривизны 


Решение. На автомобиль, который движется по виражу, действуют: сила тяжести 


Рассмотрим движение центра тяжести автомобиля (точка 






Запишем уравнение движения автомобиля в векторной форме:
и спроектируем это уравнение на оси координат 

Из уравнения (1) найдем величину нормальной реакции 
Подставим найденное значение 
При максимальной скорости автомобиля 

Векторное уравнение движения автомобиля в этом случае будет иметь вид:
Проектируем уравнение (4) на оси 
Уравнение (5) перепишем в виде:
откуда
Подставим значение 

Отсюда:
Если скорость автомобиля минимальная 

Из уравнений (8) и (9) получаем:
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Пример решения задачи по определению закона движения точки твердого тела массой m, начинающего скользить из состояния покоя по наклонной плоскости с заданным углом и коэффициентом трения скольжения f.
Задача
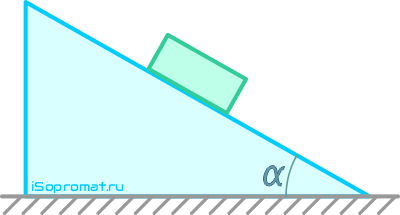
По наклонной плоскости из состояния покоя начинает скользить тело массой m = 1 кг (рисунок 5.1). Коэффициент трения скольжения f = 0,1.
Рисунок 5.1
Определить закон движения точки, если угол α = 30°.
Другие примеры решений >
Помощь с решением задач >
Решение
В данном случае тело движется поступательно, следовательно, его можно рассматривать как материальную точку. Направим ось x вдоль движения. Начало оси возьмем в начальном положении точки. Тогда x0= 0.
Поскольку движение начинается из состояния покоя, начальная скорость V0 тоже равна нулю.
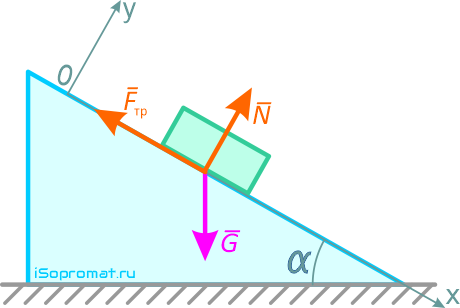
Расположим тело в произвольный момент времени и покажем все силы, действующие на него, включая реакции связей. На тело действуют сила тяжести G, сила трения Fтр и нормальная реакция наклонной плоскости N (рисунок 5.2).
Рисунок 5.2
Запишем уравнение второго закона динамики в векторном виде
и в проекциях на оси координат
Из второго уравнения системы (3) можно определить величину нормальной реакции поверхности:
Первое уравнение системы (3) разделим слева и справа на m:
С точки зрения математики полученное уравнение является простейшим дифференциальным уравнением с разделяющимися переменными. Уравнение связывает две переменные величины – скорость точки и время.
Смысл разделения переменных заключается в том, чтобы все слагаемые уравнения, куда входит скорость, были с одной стороны от знака равенства, а слагаемые, куда входит время – с другой стороны знака равенства.
Умножив уравнение (4) на dt слева и справа, получим
Сокращая слева на dt, получим:
Величина
постоянная и ее можно внести под знак дифференциала. Тогда уравнение (5) перепишется в виде равенства двух дифференциалов:
Если дифференциалы равны, то интегралы равны с точностью до постоянной величины:
или
где
это ускорение точки.
Полученный результат дает зависимость проекции скорости на ось x от времени и от постоянной интегрирования C1.
Для определения постоянной C1 воспользуемся начальным значением скорости. Зная значение скорости точки в начальный момент времени V0, и подставляя его в (6), получим
или C1 = V0.
Таким образом, зависимость скорости от времени примет вид
Учитывая, что
снова получим дифференциальное уравнение первого порядка относительно координаты x
Снова разделим переменные
и после интегрирования получим
где C2 – вторая постоянная интегрирования. Для определения C2 воспользуемся значением координаты x в начальный момент. Получим C2 = x0.
Тогда (8) запишется в виде
Подставляя начальные значения и исходные данные, получим
Ответ: Таким образом, тело движется вниз по наклонной плоскости по закону x = 0,207∙t2.
Другие примеры решения задач >
Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются они в одно действие. Итак:
Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.
Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.
Аналогично, ускорение – это производная скорости по времени:
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).
Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):
Рассмотрим задачи:
Материальная точка движется прямолинейно по закону
x (t) = t2 – 7t – 20
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)
Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с.
При t = 5 имеем:
Ответ: 3
Решить самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = 6t2 – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.
Посмотреть решение
Материальная точка движется прямолинейно по закону x (t) = 0,5t3 – 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = –t4 + 6t3 + 5t + 23
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = (1/6) t2 + 5t + 28
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Найдем закон изменения скорости:
Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с, необходимо решить уравнение:
Ответ: 3
Решите самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = t2 – 13t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = (1/3) t3 – 3t2 – 5t + 3
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Посмотреть решение
Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.
Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной со скоростью и ускорением тела
Если (x=x(t)) – уравнение, задающее движение точки, зависящее от времени, то:
(blacktriangleright) производная (x'(t)) задает скорость в момент времени (t);
(blacktriangleright) вторая производная (производная от производной) (x»(t)) задает ускорение в момент времени (t).
Задание
1
#740
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = 7t^2 — 12t), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени (t = 1) с. Ответ дайте в метрах в секунду.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 14t — 12), тогда в момент (t = 1) с:
(x'(1) = 14cdot 1 — 12 = 2) м/с.
Ответ: 2
Задание
2
#741
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = 2t^2 — 8t), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени (t = 2) с. Ответ дайте в метрах в секунду.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 4t — 
(x'(2) = 4cdot 2 — 8 = 0) м/с.
Ответ: 0
Задание
3
#742
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = t^2 + 2t + 3), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени (t = 1) с. Ответ дайте в метрах в секунду.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 2t + 2), тогда в момент (t = 1) с:
(x'(1) = 2cdot 1 + 2 = 4) м/с.
Ответ: 4
Задание
4
#743
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = 2t^3 — t^2 + 2t + 3), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени (t = 2) с. Ответ дайте в метрах в секунду.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 6t^2 — 2t + 2), тогда в момент (t = 2) с:
(x'(2) = 6cdot 2^2 — 2cdot 2 + 2 = 22) м/с.
Ответ: 22
Задание
5
#744
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = 7t^4 + 6t^3 + 5t^2 + 4t + 2016), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени (t = 0,5) с. Ответ дайте в метрах в секунду.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 28t^3 + 18t^2 + 10t + 4), тогда в момент (t = 0,5) с:
(x'(0,5) = 28cdot dfrac{1}{8} + 18cdot dfrac{1}{4} + 10cdot dfrac{1}{2} + 4 = 3,5 + 4,5 + 5 + 4 = 17) м/с.
Ответ: 17
Задание
6
#745
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = 3t^2 + 6t + 2), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. В какой момент времени её скорость составляла (15) м/с? Ответ дайте в секундах.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 6t + 6), тогда для момента (t), когда скорость материальной точки была равна (15) м/с, выполнено (6t + 6 = 15), откуда (t = 1,5) с.
Ответ: 1,5
Задание
7
#746
Уровень задания: Равен ЕГЭ
Материальная точка движется прямолинейно по закону (x(t) = t^2 + 3t — 1), где (x) – расстояние от точки (x = 0) в метрах, (t) – время в секундах, измеренное с начала движения. В какой момент времени её скорость составляла (11) м/с? Ответ дайте в секундах.
Скорость материальной точки, прямолинейно движущейся по закону (x(t)), в момент времени (t_0) равна (x'(t_0)).
(x'(t) = 2t + 3), тогда для момента (t), когда скорость материальной точки была равна (11) м/с, выполнено (2t + 3 = 11), откуда (t = 4) с.
Ответ: 4

УСТАЛ? Просто отдохни
План урока:
Закон сложения скоростей
Мгновенная скорость, направление мгновенной скорости
Ускорение. Касательное ускорение. Центростремительное ускорение
Равноускоренное движение
Свободное падение
Равномерное движение точки по окружности
Закон сложения скоростей
Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью 

Рисунок 1 – Первоначальная скорость пчелы и ветра
Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):
Рисунок 2 – Изменившаяся скорость пчелы
Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v2 системе отсчета.
Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре
Мгновенная скорость, направление мгновенной скорости
Средняя скорость. Средняя путевая скорость
Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.
Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.
Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:
Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.
То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.
Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt1, Δt2,…Δtn, и найти средние скорости за эти отрезки времени:
А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δtb направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.
Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:
Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:
Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)
Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).
Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2
Равноускоренное движение
Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении
Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:
Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.
При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:
v = v0 + a * t
Если же ускорение противонаправлено начальной скорости, это выражение станет таким:
v = v0 — a * t
Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (vox) , ускорение (ax) – взяты в проекции на эту ось.
Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении
Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.
Свободное падение
Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение
Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.
- Свободное падение
Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).
Рисунок 9 – Свободное падение тела
Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:
- Движение тела, брошенного вертикально вверх
Представим, что тело подкинули вертикально наверх с начальной скоростью v0 (см. рисунок 10).
Рисунок 10 – Тело бросили вертикально вверх
Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v0 (вообще нужно было бы писать voy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).
Отсюда можно найти полное время полета:
- Движение тела, брошенного под углом к горизонту
Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.
Рисунок 11 – Тело брошено под углом к горизонту
Уравнения движения в общем виде по двум осям выглядят так:
Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:
Равномерное движение точки по окружности
Центростремительное ускорение
Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).
Рисунок 12 – Изменение направления скорости при равномерном движении по окружности
За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:
где R – радиус окружности, по которой циклически движется тело.