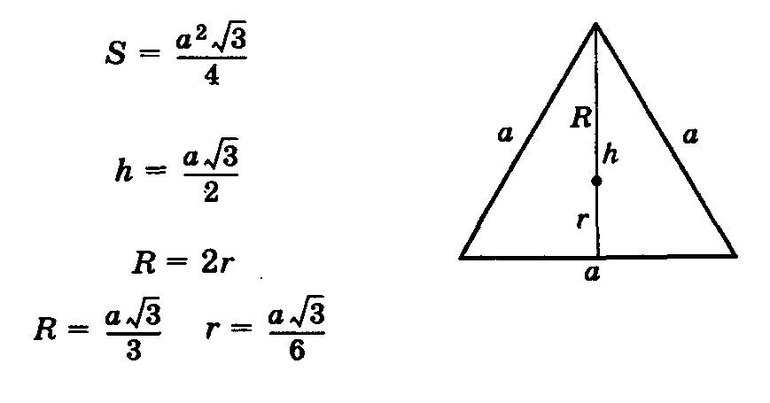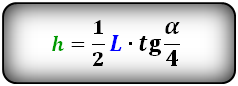Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
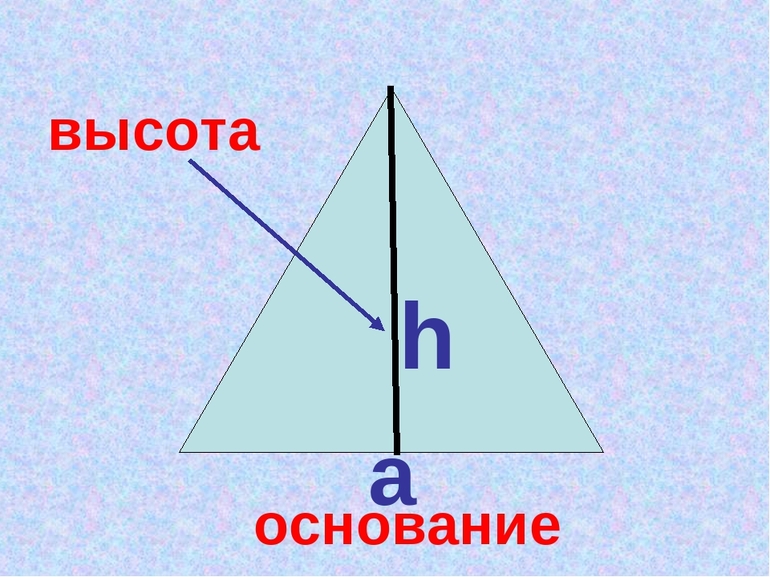
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Высота равностороннего треугольника — свойства, формулы и примеры нахождения
Формулы, используемые для этого, несложны. Вывод выражений основан на свойствах треугольника, при этом точка пересечения высот считается замечательной и даже имеет своё название — ортоцентр.
Общие сведения
Три отрезка, не принадлежащие одной прямой, каждый из которых соединяется с другими в двух точках, образуют геометрическую фигуру — треугольник. Прямые линии — это стороны, а точки их соприкосновения вершины. Один из отрезков, обычно который проходит параллельно горизонтальной плоскости, называют основанием.
В зависимости от размера внутренних углов замкнутой фигуры, треугольники разделяют на следующие виды:
- остроугольные — все углы тела не превышают 90 градусов;
- тупоугольные — один из разворотов имеет тупую форму;
- прямоугольные — размер одного из трёх углов составляет 90 градусов.
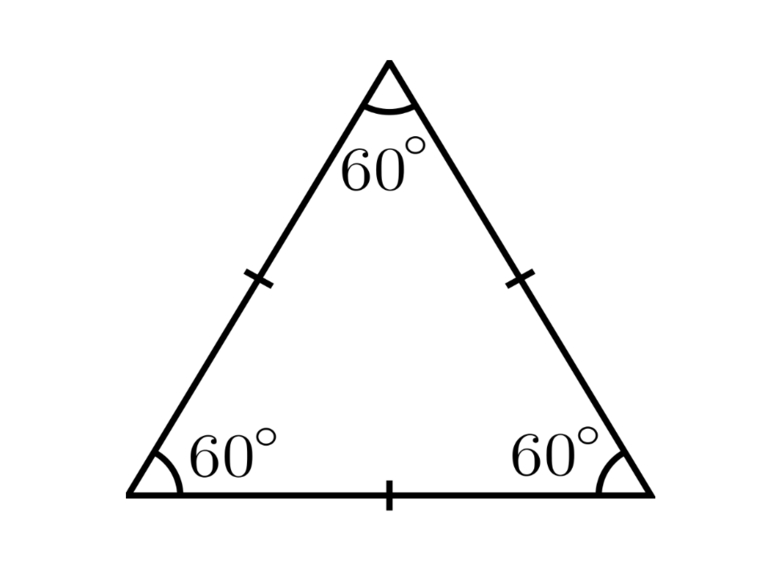
По числу равных сторон треугольные фигуры разделяют на разносторонние, равнобедренные, равносторонние. Последние часто называют правильными, так как все стороны у такого объекта равны друг другу. Кроме этого, из особенностей равносторонней фигуры можно отметить, что центры вписанной и описанной окружности совпадают, а каждый из углов равен 60 градусам. Сумма всех углов треугольника равняется 180 градусам.
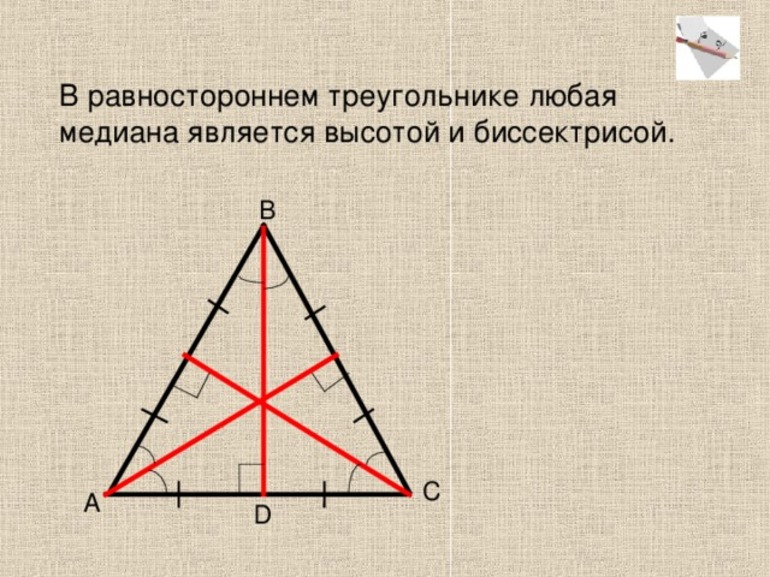
В любой трёхугольной фигуре можно построить так называемые 3 замечательные линии: медиана, биссектриса и высота.
В правильном треугольнике эти 3 отрезка совпадают, то есть линия, опущенная из вершины к противолежащей стороне, одновременно являясь медианой, биссектрисой и высотой, образует прямой угол с основанием. При этом она делит его пополам. Фактически высота играет роль катета.
Получается, что в середине фигуры можно построить 3 отрезка, которые и будут высотами. Две из них будут опущены на боковые грани, а одна на основание. Точка пересечения перпендикулярных линий называется ортоцентром. Она располагается внутри геометрического тела и совпадает с центром вписанной окружности.
Для трёхугольного тела существует 2 теоремы. Одна из них утверждает, что противолежащие боковые стороны имеют одинаковую длину, а вторая, что если 2 угла невырожденного треугольника равны, то грани, противоположные им, также равны.
Интересно то, что эти правила справедливы как для абсолютной, так и сферической геометрии.
Свойства равносторонней фигуры
При решении задач, связанных с нахождением высоты в равностороннем треугольнике, часто приходится использовать его свойства. Зная их, найти нужные параметры будет несложно. Тем более что все они связаны с главной особенностью фигуры — равенством его всех сторон.
Равностороннее тело с тремя углами обладает следующими особенностями:
- в нём все углы одинаковые и равны 60 градусов;
- середина пересечения отрезков, совпадающих с высотой, биссектрисой и медианой, является центром геометрического тела;
- радиус описанной окружности превышает радиус вписанной в 2 раза;
- в равностороннем треугольнике длины всех элементов выражаются через длину стороны.
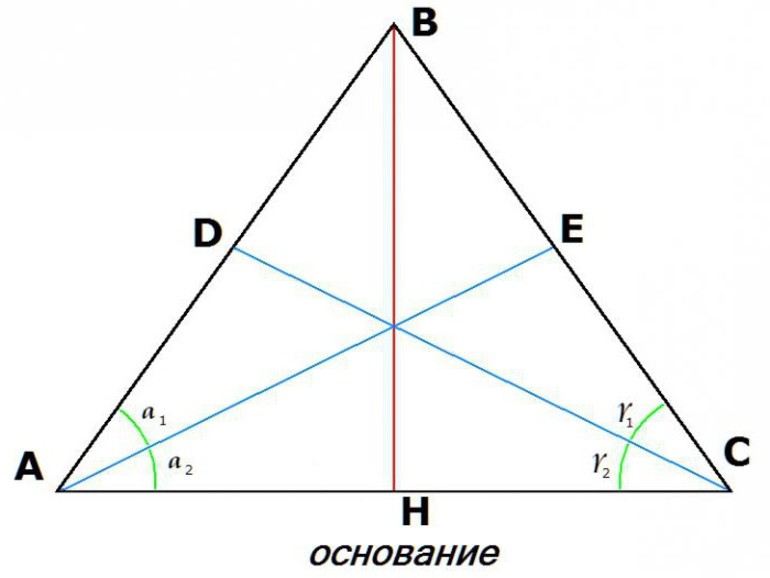
Эти свойства очевидны. Если начертить треугольник с равными сторонами и вписать его в окружность, за центр можно принять точку O, при этом радиус описанного круга будет OK. Тогда линия, проведённая из неё к вершине, будет радиусом. Пусть конечная точка будет B. Но так как место пересечения является общим и для высот и медиан, из свойства последних можно сделать вывод, что в точке линия делится в отношении 2 к 1. Отсчёт следует вести с вершины треугольника. Значит: OB = 2 * OK.
Из основных формул, которые используются при вычислениях, в первую очередь нужно запомнить:
- радиус описанной окружности: R = (a * √3) / 3;
- диаметр вписанного круга: r = (a * √3) / 6;
- медиана: h = (a * √3) / 2;
- площадь: s = (a2 * √3) / 4;
- периметр: p = 3 * a.
Если рассмотреть треугольник ABC с проведённой высотой BN, можно утверждать, что грань АВ = ВС = АС = AN /2 = NC /2. Так как фигура ABN является копией BNC в зеркальном отражении, разделённые углы у вершины будут одинаковыми, а и их разворот составлять 30 градусов. Из этого следует, что угол A равен 60 градусам, значит, отрезок BN = AB * sin 60 0 = (AB * √3) / 2.
Зная длину медианы (высоты), вычислить другие параметры треугольника не составит труда. Например, периметр, P = 2 √3 * h; площадь — S = (h * 2) / √3.
При этом замечательным свойством является ещё и то, что ортоцентр одновременно будет в фигуре и центром тяжести (центроидом), поэтому точка пересечения высот и делит отрезок в отношении 2 к 1.
Формула высоты
В равностороннем треугольнике длина стороны равна произведению удвоенной высоты и квадратного корня из трёх. Эту формулу легко доказать, используя теорему Пифагора. Так как высота одновременно является и биссектрисой, она, проведённая на противоположное основание, разделяет треугольник на 2 симметричные фигуры. Исходя из того, что отрезок — это перпендикуляр, полученные геометрические тела будут прямоугольными.
Гипотенуза будет являться гранью основного тела, одним из катетов — проведённая линия, а вторым — половина основания. Последнее утверждение правдиво, так как в равносторонней фигуре все стороны равны. Соответственно, используя теорему Пифагора: c 2 = b 2 + a 2 , для рассматриваемого случая можно записать следующую формулу: a 2 = h 2 + a 2 / 2 2 , где: a — грань. После математических преобразований выражение примет вид: a = (2 * h) / √3. Отсюда уже можно вывести формулу для нахождения длины: h = (a * √3) / 2.
Аналогичное определение можно получить, используя для доказательства формулу Герона. Отрезок, являющийся высотой, можно найти из выражения: h = (2 * √p * (p — a) * (p — b) * (p — a)) / b. В равенстве p является периметром и находится как сумма всех сторон: p = (a + b + a). Так как одна из граней делится пополам, формулу можно привести к виду: p = (a + b + a) / 2 = a + b / 2.
После подстановки полученного выражения в формулу Герона, оно примет вид: h = 2 * √((a + b/2) * (b/2) * (a -b/2) * (b/2)) / b. Используя формулу сокращённого умножения: разность квадратов, равенство можно привести к виду: (a + b / 2) * (a — b / 2) = a 2 — (b / 2) 2 .
Для упрощения выражения под корень можно внести двойку и знаменатель b. Таким образом, формула примет вид: h = √(2 2 * (a 2 — (b/2) 2 * (b/2) 2 ) * b 2 ). Выполнив ряд сокращений, равенство можно будет представить: h = √(a 2 — (b 2 /4)). Из-за того, что стороны в трёхугольной фигуре совпадают, окончательный вариант можно записать: h = (a√3) / 2. Что и следовало доказать.
Высоту можно определить, и зная радиус вписанной окружности. Её можно найти по формуле: r = (a √ 3) / 6. Если выражение переписать как r = (1 / 3) * ((a √3) / 2), возможно увидеть, что второй множитель как раз и есть высота. Соответственно, r = (1/3) * h. Отсюда: h = 3 * r. Это довольно простая формула, которая часто используется при геометрических вычислениях, поэтому её тоже нужно запомнить.
Решение примеров
Самостоятельное решение задач позволяет закрепить теоретические знания и запомнить формулы. Существуют определённые типы примеров, с помощью которых можно довольно быстро проработать весь изученный материал. Вот некоторые из них, рассчитанные на учеников восьмых классов средней школы:
- Определить высоту равносторонней фигуры, если её грань равняется 6 см. Решение задачи нужно строить следующим образом. У такого треугольника все стороны равны. Так как высота является медианой, она делит противоположную сторону вершины, из которой опущена, на 2 равные части. Треугольник можно обозначить ABC, а искомый перпендикуляр BH. Образованное геометрическое тело является прямоугольным. Причём, согласно условию, у него известна гипотенуза и катет. Оставшийся катет, который и является высотой, легко найти по теореме Пифагора: BH 2 + 3 2 = 6 2 . Отсюда: BH 2 = 25. Высота рассматриваемой фигуры будет равна 5 см.
- Сторона правильного треугольного тела равна √3. Узнать, чему будет равен радиус описанной окружности. Эту задачу можно решить, воспользовавшись свойством высоты в равностороннем треугольнике: точка пересечения медиан делит их в отношении 2 :1. Для наглядности можно нарисовать треугольник c вершинами ABC и высоту AK, а точку пересечения обозначить буквой O. Линия AO будет искомым радиусом окружности и составлять 2/3 от всей высоты AK. Длина отрезка равна: AK = √ (AB2 — AK2). Отсюда: R = (2 * √ (AB2 — AK2)) / 3 = (2 * √ (√ 32 — (3/2)2)) / 3 = 1. Задача решена.
Проверить правильность решения можно, используя онлайн-калькуляторы. Это интернет-сервисы, которые позволяют своим пользователям в автоматическом режиме вычислять различные математические примеры. Свои услуги они предоставляют бесплатно, от пользователя требуется только установленный веб-обозреватель и подключение к сети.
Важно ещё, что калькуляторы не только выдают быстро правильный ответ, но и показывают пошаговое решение. Это очень удобно, когда необходимо определить, на каком этапе была допущена ошибка.
Кроме этого, на своих страницах такого рода сервисы содержат краткий теоретический материал и даже примеры заданий. Так что калькуляторы будут полезны и на стадии обучения.
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
http://nauka.club/matematika/geometriya/vysot%D0%B0-ravnostoronnego-treugolnika.html
Формула высоты сегмента круга
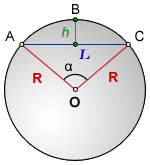
Сегмент — часть круга ABC, отсеченная хордой AC
h — высота сегмента ABC
L — хорда AC
R — радиус кружности
O — центр окружности
α — центральный угол AOC
Формула высоты через радиус и центральный угол, (h):
Формула высоты через хорду и центральный угол, (h):
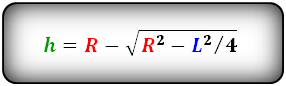
Формула высоты через радиус и хорду, (h):
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021
Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу.
cos〖α/2〗=1-h/r
Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141).
P=αr
c=2r sin〖α/2〗
Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса.
S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
Геометрия круга
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L


высота сегмента 

2. Даны диаметр D и длина хорды X


высота сегмента 

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол 
3. Даны диаметр D и центральный угол φ


длина хорды 

4. Даны диаметр D и высота сегмента H


длина хорды 

6. Даны длина дуги L и центральный угол φ


длина хорды 

8. Даны длина хорды X и центральный угол φ


диаметр 

9. Даны длина хорды X и высота сегмента H


диаметр 

10. Даны центральный угол φ и высота сегмента H


длина дуги 

Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:


и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности 
площадь круга 
площадь сектора 
площадь сегмента 
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Программа Segment

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент — все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.