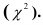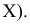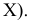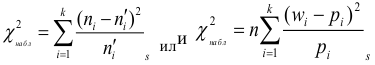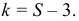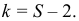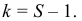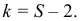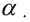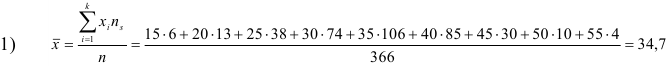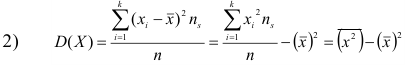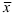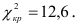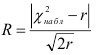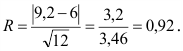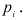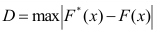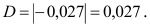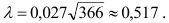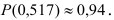А.
Дискретное распределение.
Рассмотрим дискретную
случайную величину X,
закон
распределения которой
неизвестен. Пусть произведено п
испытаний,
в которых
величина X
приняла n1
раз
значение х1,
n2
раз значение
x2,
….
nk
раз
значение xk,
причем
.
Эмпирическими частотами
называют фактически
наблюдаемые
частоты ni.
Пусть
имеются основания предположить, что
изучаемая
величина X
распределена
по некоторому определенному
закону. Чтобы проверить, согласуется
ли это предположение
с данными наблюдений, вычисляют частоты
наблюдаемых
значений, т. е. находят теоретически
частоту
ni‘
каждого
из наблюдаемых значений в предположении,
что величина X
распределена
по предполагаемому закону.
Выравнивающими
(теоретическими)
в отличие от фактически
наблюдаемых эмпирических частот называют
частоты
ni‘
найденные
теоретически (вычислением). Выравнивающие
частоты находят с помощью равенства
ni‘
=
nPi,
где n
— число испытаний; Рi
—
вероятность наблюдаемого значения
хi,
вычисленная
при допущении, что X
имеет
предполагаемое
распределение.
Итак, выравнивающая
частота наблюдаемого значения xi
дискретного распределения равна
произведению числа испытаний
на вероятность этого наблюдаемого
значения.
Пример.
В
результате эксперимента, состоящего
из n
= 520 испытаний,
в каждом из которых регистрировалось
число хi
появлений
некоторого
события, получено следующее эмпирическое
распределение:
набл.
значения . . xi
0 1 2 34567
эмп.
частота . ni
120
167 130 69 27 5 1 1
Найти
выравнивающие частоты ni‘
в
предположении, что случайная величина
X
(генеральная
совокупность) распределена по
закону Пуассона.
Решение.
Известно, что параметр λ,
которым
определяется распределение
Пуассона, равен математическому ожиданию
этого распределения.
Поскольку в качестве оценки математического
ожидания
принимают выборочную среднюю (см. гл.
XVI,
§ 5), то и в качестве
оценки λ
можно
принять выборочную среднюю
.
Легко
найти
по условию, что выборочная средняя равна
1,5, следовательно, можно
принять λ
=1,5.
Таким образом,
формула Пуассона
принимает вид
Пользуясь
этой формулой, найдем вероятности
Р520(К)
при
k
= 0,
1,
2,
3, 4, 5, 6, 7 (для простоты записи индекс 520
далее опущен): Р(0)
= 0,22313, Р
(1)
= 0,33469, Р
(2)
= 0,251 021, Р
(3)
= 0,125511, Р
(4)
= 0,047066, Р (5) = 0,014120, Р
(6)
= 0,003530, P
(7) =0,000755. Найдем выравнивающие частоты
(результаты умножения округлены до
единицы):
n1‘
= nР(0)
= 520-0,22313 =116,
n2‘
= nP(1)
= 520-0,33469= 174.
Аналогично
находят и остальные выравнивающие
частоты. В итоге
получим:
эмп. частота .
. 123 167 130 69 27 5 1 1
выр.
частота . . 116 174 131 65 25 7 2 0
Сравнительно
небольшое расхождение эмпирических и
выравнивающих
частот подтверждает предположение, что
рассматриваемое распределение
подчинено закону Пуассона.
Заметим,
что если подсчитать выборочную дисперсию
по данному распределению,
то окажется, что она равна выборочной
средней, т.е.
1,5. Это служит еще одним подтверждением
сделанного предположения,
поскольку для распределения Пуассона
λ
= М (X)
= D
(X)
Сравнения
эмпирических и теоретических частот
сна глаз», конечно,
недостаточно. Чтобы сделать это более
обоснованно, надо использовать,
например, критерий Пирсона (см. гл. XIX,
§ 23). Проверка
гипотезы о распределении случайной
величины по закону Пуассона
изложена в книге: Гмурман В. Е. Руководство
к решению
задач по теории вероятностей и
математической статистике. М.,
«Высшая школа», 1972 (см. гл. XIII,
§ 17).
Б.
Непрерывное распределение.
В случае непрерывного распределения,
вероятности отдельных возможных значений
равны нулю (см. гл, X,
§ 2, следствие 2). Поэтому весь
интервал возможных значений делят на
k
непересекающихся
интервалов и вычисляют вероятности Pi
попадания
X
в
i-й
частичный интервал, а затем, как и для
дискретного
распределения, умножают число испытаний
на
эти вероятности.
Итак,
выравнивающие частоты непрерывного
распределения находят по равенству
ni‘=nPi,
где п —
число испытаний; Рi
— вероятность попадания
X
в i-й
частичный интервал, вычисленная при
допущении, что
X
имеет
предполагаемое распределение.
В
частности, если имеются основания
предположить, что случайная величина
X
(генеральная
совокупность) распределена
нормально, то выравнивающие частоты
могут
быть найдены по формуле
,
(*)
где п
—
число испытаний (объем выборки), h
—
длина частичного
интервала, σв
— выборочное среднее квадрати-ческое
отклонение,
(xi
—
середина i-гo
частичного
интервала),
.
Пример на применение формулы (*) приведен
в § 7.
Пояснение.
Поясним происхождение формулы (*).
Напишем
плотность общего нормального распределения:
.
(**)
При а
= 0
и σ = 1 получим плотность нормированного
распределения:
или, изменив обозначение аргумента,
Положив
и
= (х
—
а)/σ,
имеем
(***)
Сравнивая (**) и (***), заключаем, что
.
Если математическое ожидание
а и
среднее квадратическое
отклонение σ неизвестны, то в качестве
оценок этих
параметров принимают соответственно
выборочную среднюю
и выборочное среднее
квадратическое отклонение
σв
(см. гл. XVI,
§ 5,9). Тогда
,
где
.
Пусть
xi—
середина i-гo
интервала
(на которые разбита
совокупность всех наблюдаемых значений
нормально распределенной
случайной величины X)
длиной h.
Тогда вероятность
попадания X
в
этот интервал приближенно равна
произведению длины интервала на значение
плотности распределения
f
(x)
в любой точке интервала
и, в частности,
при х=xi
(см.
гл. XI,
§ 5):
.
Следовательно, выравнивающая частота
,
где
.Мы
получили формулу (*).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эмпирические и выравнивающие частоты
Дискретное распределение.
Рассмотрим дискретную случайную величину , закон распределения которой неизвестен. Пусть произведено
испытаний, в которых величина
приняла
раз значение
,
раза — значение
раз — значение
, причем
Определение 5. Эмпирическими частотами называют фактически наблюдаемые частоты .
Предположим, что у нас имеются основания предположить, что изучаемая величина распределена по некоторому определенному закону. Для того, чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, то есть находят теоретически сколько раз величина
должна была принять каждое из наблюдаемых значений, если она распределена по наблюдаемому закону.
Определение 6. Выравнивающими (теоретическими), в отличии от фактически наблюдаемых эмпирических частот, называют частоты , найденные теоретически (вычислениями). Их находят по соотношению
где: число испытаний;
вероятность наблюдаемого значения
, вычисленная при допущении, что
имеет предполагаемое распределение.
Непрерывное распределение.
В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на непересекающихся интервалов и вычисляют вероятности
попадания
в
й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности.
Итак, выравнивающие частоты непрерывного распределения находят по соотношению:
где: число испытаний;
вероятность наблюдаемого значения
, вычисленная при допущении, что
имеет предполагаемое распределение.
В частности, если имеются основания предположить, что случайная величина (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле

где: число испытаний (объем выборки);
длина частичного интервала;
выборочное среднее квадратическое отклонение;

го частичного интервала
Замечание: Как известно, дифференциальная функция (функция плотности распределения вероятностей) общего нормального распределения имеет следующий вид

При и
получим дифференциальную функцию нормированного распределения
или, заменив обозначение аргумента
Далее, положив, 

Сравнивая (IV.7) и (IV.8), можно сделать заключение, что
Если математическое ожидание и среднее квадратическое отклонение
неизвестны, то в качестве оценок этих параметров принимают соответственно выборочную среднюю
и выборочное среднее квадратическое отклонение
Тогда
где
Пусть середина
го частичного интервала (на которые разбита совокупность всех наблюдаемых значений нормально распределенной случайной величины
) длиною
Тогда вероятность попадания
в этот интервал приближенно равна произведению длины интервала на значение дифференциальной функции
в любой точке интервала и, в частности, при
Следовательно, выравнивающая частота

Таким образом, формула (IV.5) получена.
Проверка гипотезы о нормальном распределении генеральной совокупности
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Проверка дискретного распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности равноотстоящих
вариант и соответствующих им частот:
|
|
|
|
… |
|
|
|
|
|
… |
|
Требуется, используя критерий Пирсона, проверить
гипотезу о том, что генеральная совокупность
распределена нормально.
Для того,
чтобы при заданном уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1. Вычислить
выборочную среднюю
и выборочное среднее квадратическое отклонение
.
2.
Вычислить теоретические частоты
где
– объем выборки,
— шаг (разность между двумя соседними
вариантами)
3. Сравнить эмпирические и теоретические частоты
с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
— гипотезу отвергают.
Проверка интервального распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности интервалов
и соответствующих им частот
.
Требуется,
используя критерий Пирсона, проверить гипотезу о том, что генеральная
совокупность
распределена нормально.
Для того,
чтобы при уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1.
Вычислить выборочную среднюю
и выборочное среднее квадратическое отклонение
, причем в качестве вариант
принимают среднее арифметическое концов
интервала:
2.
Пронормировать
, то есть перейти к
случайной величине
и
вычислить концы интервалов:
причем
наименьшее значение
, то есть
полагают равным
, а наибольшее, то есть
полагают равным
.
3. Вычислить теоретические
частоты:
где
– объем выборки
– вероятности попадания
в интервалы
– функция Лапласа.
4. Сравнить эмпирические и
теоретические частоты с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
— гипотезу отвергают.
Замечание.
Малочисленные частоты
следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле
следует в качестве
принять число групп выборки, оставшихся после
объединения частот.
Примеры решения задач
Пример 1
Используя
критерий Пирсона при уровне значимости 0,05, проверить, согласуется ли гипотеза
с нормальным распределением генеральной совокупности X с заданным эмпирическим
распределением:
| xi | -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 |
| ni | 1 | 4 | 21 | 30 | 63 | 59 | 34 | 18 | 5 | 2 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим
характеристики распределения. Для этого составим расчетную таблицу.
Выборочная средняя:
Средняя
квадратов:
Выборочная
дисперсия:
Среднее квадратическое
отклонение:
Вычислим
теоретические частоты.
Вероятность
попадания в соответствующий интервал:
Теоретические
частоты:
где
-объем выборки
Составим
расчетную таблицу:
Проверим
степень согласия эмпирического и теоретического распределения по критерию
Пирсона. Объединяем малочисленные частоты (
).
Из
расчетной таблицы
Уровень
значимости
Число
степеней свободы
По
таблице критических точек распределения:
Нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности.
Пример 2
Из большой партии по схеме случайной
повторной выборки было проверено 150 изделий с целью определения процента
влажности древесины, из которой изготовлены эти изделия. Получены следующие
результаты:
|
Процент влажности, xi |
11-13 |
13-15 |
15-17 |
17-19 |
19-21 |
|
Число изделий, ni |
8 |
42 |
51 |
37 |
12 |
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) X, используя критерий χ2 — Пирсона.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную таблицу
Средняя:
Средняя квадратов:
Дисперсия:
Исправленная дисперсия:
Исправленное среднее квадратическое
отклонение:
Вычислим теоретические частоты.
Составим расчетную таблицу:
Вероятность попадания в
соответствующий интервал:
, где
— функция Лапласа
Теоретические частоты:
, где
-объем выборки
Составим расчетную таблицу:
Проверим степень согласия
эмпирического и теоретического распределения по критерию Пирсона:
Из расчетной таблицы
Уровень значимости
Число степеней свободы
По таблице критических точек
распределения:
Нет оснований отвергать гипотезу о
распределении случайной величины по нормальному закону.
Задачи контрольных и самостоятельных работ
Задача 1
Выборка X
объемом n=100 задана таблицей:
|
|
0.8 | 1.1 | 1.4 | 1.7 | 2 | 2.3 | 2.6 |
|
|
5 | 13 | 25 | 25 | 19 | 10 | 3 |
1) Построить
полигон относительных частот
.
2) Вычислить
среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
.
3) Вычислить
теоретические частоты
. Построить график
на одном рисунке с полигоном.
4) С помощью
критерия χ2 проверить гипотезу о нормальном распределении
генеральной совокупности при уровне значимости α=0.05.
Задача 2
Построить
нормальную кривую по опытным данным. Рассчитать теоретические (выравнивающие) частоты
и сравнить с опытным распределением.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Выборка X
объемом N=100 измерений задана таблицей:
|
|
0.6 | 1.5 | 2.4 | 3.3 | 4.2 | 5.1 | 6 |
|
|
5 | 13 | 26 | 24 | 19 | 10 | 3 |
а)
Построить полигон относительных частот
б)
вычислить среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
;
в) по
критерию χ2 проверить гипотезу о
нормальном распределении генеральной совокупности при уровне значимости α=0.05.
Задача 4
Для
изучения количественного признака
из генеральной совокупности извлечена выборка
объема n, имеющая данное
статистическое распределение.
а)
Построить полигон частот по данному распределению выборки.
б) Найти
выборочное среднее
, выборочное среднее
квадратическое отклонение
и исправленное среднее квадратическое
отклонение
.
в) При
данном уровне значимости
проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.
г) В
случае принятия гипотезы о нормальном распределении генеральной совокупности
найти доверительные интервалы для математического ожидания
и среднего квадратического отклонения σ при
данном уровне надежности γ=1-α; α=0.05
|
|
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
|
|
5 | 9 | 15 | 19 | 20 | 16 | 10 | 6 |
Задача 5
Для выборки
объема N=100, представленной вариационным рядом
|
|
-1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
3 | 8 | 11 | 19 | 37 | 17 | 5 |
построить
полигон относительных частот и гистограмму накопленных частот. Найти выборочное
среднее
и выборочное среднее квадратичное отклонение
. Определить доверительный интервал с
доверительной вероятностью β=0,95 для оценки математического ожидания
генеральной совокупности в предположении, что среднее квадратическое отклонение
генеральной совокупности σ равно исправленному выборочному среднему s. Проверить
гипотезу о нормальности закона распределения генеральной совокупности,
используя критерий Пирсона с уровнем значимости α=0,05.
Задача 6
Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.
| 7 | 4 | 4 | 15 | 1 | 1 | 7 | 15 | 19 | 4 |
| 0 | 4 | 8 | 14 | 10 | 0 | 1 | 11 | 8 | 2 |
| 6 | 2 | 5 | 3 | 12 | 2 | 9 | 6 | 2 | 5 |
| 13 | 5 | 7 | 3 | 3 | 10 | 0 | 11 | 17 | 11 |
| 9 | 6 | 11 | 7 | 20 | 1 | 14 | 6 | 7 | 4 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Данные о
продолжительности телефонных разговоров, отобранные по схеме
собственно-случайной бесповторной выборки, приведены в таблице:
| Время, мин | 1.5-2.5 | 2.5-3.5 | 3.5-4.5 | 4.5-5.5 | 5.5-6.5 | 6.5-7.5 | 7.5-8.5 | 8.5-9.5 | 9.5-10.5 | Итого |
| Число разговоров | 3 | 4 | 9 | 14 | 37 | 12 | 8 | 8 | 5 | 100 |
Используя χ2-критерий Пирсона при уровне
значимости α=0.05 проверить гипотезу о том, что случайная величина X —
продолжительность телефонных разговоров — распределена по нормальному закону.
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.
Задача 8
Распределение
случайной величины X – заработной платы сотрудников на фирме (в у.е.) –
задано в виде интервального ряда:
Найти:
. Построить теоретическое
нормальное распределение и сравнить его с эмпирическим с помощью критерия
согласия Пирсона χ2 при α=0,05.
Задача 9
Записать для выборки интервальное
распределение, построить гистограмму относительных частот. По критерию Пирсона
проверить гипотезу нормальном распределении.
| 7.81 | 3.15 | 2.27 | 32.64 | 4.72 | 5.33 | 8.51 | 7.72 | 30.23 | 20.12 |
| 9.83 | 8.33 | 9.61 | 31.83 | 8.52 | 27.22 | 27.22 | 8.43 | 15.91 | 25.46 |
| 24.82 | 26.54 | 46.73 | 17.31 | 13.05 | 53.24 | 5.23 | 18.28 | 40.93 | 17.44 |
| 32.34 | 28.26 | 9.75 | 3.72 | 8.16 | 22.91 | 0.74 | 12.97 | 12.05 | 1.53 |
| 43.15 | 45.57 | 2.02 | 32.23 | 8.67 | 4.83 | 9.12 | 6.77 | 6.48 | 19.22 |
| 36.42 | 47.81 | 40.64 | 5.45 | 0.21 | 26.51 | 17.36 | 3.62 | 15.57 | 23.21 |
| 58.73 | 62.52 | 10.15 | 38.36 | 35.55 | 6.10 | 3.04 | 4.54 | 1.95 | 5.24 |
| 64.71 | 67.63 | 1.21 | 0.81 | 2.03 | 10.17 | 5.51 | 8.35 | 43.76 | 8.74 |
| 4.72 | 17.54 | 17.32 | 29.43 | 5.91 | 6.92 | 4.72 | 16.04 | 57.54 | 15.46 |
| 13.31 | 36.45 | 3.45 | 16.15 | 15.77 | 2.43 | 14.24 | 2.25 | 15.63 | 23.72 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 10
Результаты наблюдений над случайной
величиной
оказались
лежащими на отрезке
и были
сгруппированы в 10 равновеликих интервалов. Значения
и частоты
попадания в интервалы приведены в таблице. Построить: гистограмму частот,
эмпирическую функцию распределения, найти медиану. Найти выборочное среднее
и исправленное
среднеквадратическое отклонение
. Указать 95-процентные доверительные интервалы для
. С помощью критерия Пирсона проверить гипотезу о
нормальном (с параметрами
) законе распределения (уровень значимости α=0.02
.
Задача 11
В таблице приведены результаты
измерения роста (см.) случайно отобранных 100 студентов:
|
Интервалы роста |
154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
|
Число студентов, |
10 | 14 | 26 | 28 | 12 | 8 | 2 |
С помощью критерия Пирсона при
уровне значимости α=0.05 проверить правдоподобие гипотезы о нормальном
распределении роста студентов.
Задача 12
При массовых стрельбах из пушек для
одинаковых общих условий были зафиксированы продольные ошибки (м) попадания
снарядов в цель:
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) L, используя критерий χ2— Пирсона.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Содержание:
Предмет математической статистики (МС) — любой объект, изучаемый с количественной стороны в целях более точной оценки его качественного состояния.
При этом имеются в виду групповые объекты, т.е. явления массовые, в сфере которых проявляют свое действие статистические законы.
Единица наблюдения — составной элемент или член группового объекта.
Статистическая совокупность — множество относительно однородных, но индивидуально различимых единиц, объединенных для совместного (группового) изучения. Например, недопустимо изучать показатели изменчивости человеческого организма, объединяя в одну совокупность людей разного возраста и пола.
Статистический комплекс слагается из разнородных групп, каждая из которых состоит из однородных элементов, для совместного (комплексного) изучения. Вопрос о форме объединения экспериментатор решает сам в зависимости от объекта и цели исследования.
Признак — свойство, проявлением которого один предмет отличается от другого.
Пример:
Исследуется признак
Характерное свойство признаков — варьирование величины признака в определенных пределах. Эти колебания величины одного и того же признака, наблюдаемые в массе однородных элементов статистической совокупности, называются вариациями, а отдельные числовые значения варьирующего признака называются вариантами.
Признаки делятся на качественные (атрибутивные) и количественные.
Качественные признаки не поддаются непосредственному измерению и учитываются по наличию их свойств у отдельных членов изучаемой группы.
Пример:
Признак
Количественные признаки поддаются непосредственному измерению или счету. Их делят на мерные и счетные.
Мерные признаки варьируют непрерывно, их величина может принимать в определенных пределах (от — до) любые числовые значения. Аналог мерного признака в теории вероятностей есть непрерывная случайная величина.
Счетные признаки варьируют прерывисто (дискретно), их числовые значения часто выражаются целыми числами (число зерен в колосьях и т.п.).
Аналогом счетного признака в теории вероятности является дискретная случайная величина.
Признаки обозначаем так же, как случайные величины: 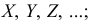
Признаки варьируют под влиянием различных, в том числе и случайных причин. Наряду с естественным варьированием на величине признака сказываются и ошибки, неизбежно возникающие при измерении изучаемых объектов.
Погрешность или ошибка — разница между результатами измерений и действительно существующими значениями измеряемого признака.
Технические ошибки — связаны с неточностью измерительных приборов и инструментов.
Личные ошибки возникают из-за личных качеств исследователя, его навыков и мастерства.
Случайные ошибки возникают из-за целого ряда других, не поддающихся регулированию и неустранимых причин.
Технические + личные ошибки = систематические ошибки. Их можно преодолеть соответствующими методами.
Случайные ошибки, как независимые от воли человека, остаются и сказываются на результатах наблюдений. Следовательно, варьирование признака складывается из естественной изменчивости признака и ошибок измерений.
При измерении количественного признака и при вычислении его характеристик применяются два вида округления:
- — округление с недостатком: если за последней сохраняемой цифрой следуют цифры 0, 1,2, 4, то они отбрасываются. Например, точность измерения
т.е. последняя сохраняемая цифра — вторая после запятой. Тогда
- — округление с избытком: если за последней сохраняемой цифрой следуют цифры 5, 6, 7, 8, 9, то последняя сохраняемая цифра увеличивается на единицу. Например,
Наблюдения над объектами могут охватывать все члены изучаемой совокупности без единого исключения или ограничиваться обследованием лишь некоторой части данной совокупности.
В первом случае наблюдения полные или сплошные, во втором — частичные или выборочные.
Полное обследование совокупности позволяет получить исчерпывающую информацию об объекте, но требует больших затрат времени, труда, ресурсов и в некоторых случаях невозможно или нецелесообразно. Например, чтобы определить всхожесть партии семян, нецелесообразно высеивать всю партию. Невозможно учесть всех обитателей фитопланктона для небольшого водоема и т.п.
Определение. Генеральной совокупностью называется вся совокупность объектов для изучения.
Выборкой или выборочной совокупностью называется отобранная тем или иным способом часть генеральной совокупности.
Количество членов генеральной совокупности обозначается 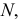
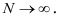
Чтобы выборка наиболее полно отображала структуру генеральной совокупности, необходимо, чтобы она была представительной (репрезентативной), т.е. для каждого элемента генеральной совокупности должна быть одинаковая возможность (вероятность) попасть в выборку, т.е. выборка должна быть случайной.
Отбор в выборку может быть повторный, если учтенная единица возвращается в генеральную совокупность и может попасть в выборку повторно.
Бесповторный отбор — учтенная единица не возвращается в генеральную совокупность, т.е. каждая отобранная единица регистрируется только один раз.
Таким образом, повторный отбор не влияет на состав генеральной совокупности и вероятность каждой единицы попасть в выборку не меняется. При бесповторном отборе вероятность единиц генеральной совокупности попасть в выборку изменяется, т.к. предшествующий отбор влияет на результаты последующего и на состав генеральной совокупности.
Идеальный случайный выбор производится по методу жеребьевки или лотереи, а также с помощью «случайных чисел». Существуют типический, серийный, механический и другие разновидности отборов.
Типический отбор используют тогда, когда генеральная совокупность расчленяется на отдельные типические группы. В таких случаях из каждой группы случайным образом отбирают одинаковое или пропорциональное число единиц. Затем вычисляют групповые характеристики, объединяемые далее в общую характеристику генеральной совокупности.
Серийный отбор используют, когда генеральная совокупность делится на серии обычно по территориальному принципу. Например, из 30 групп подростков намечено исследовать выборочно 6 групп, т.е. работают не с отдельными единицами, а с целыми сериями относительно однородных единиц.
Механический отбор используется, когда генеральную совокупность разбивают на несколько равных частей или групп. Затем из каждой группы отбирают по одной единице. Например, при исследовании посева ржи на урожайность намечено отобрать 100 растений, следовательно, поле должно быть разделено на 100 равных частей, из каждой части отбирается одна единица.
Отбор будет также механическим если из генеральной совокупности в выборку попадет каждая десятая, сотая и т.д. единица.
Систематизация наблюдений
Процесс систематизации результатов массовых наблюдений, объединения их в относительно однородные группы по некоторому признаку 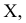
Наиболее распространенная форма группировки — статистические таблицы.
Особая форма группировки — статистические ряды, видное место среди них занимают вариационные ряды.
Определение. Вариационным рядом или рядом распределения называется двойной ряд чисел, показывающий как числовые значения признака (варианты) связаны с их повторяемостью в данной статистической совокупности.
Пример:
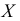
Число 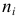
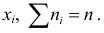
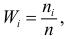
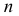
Ранжированный вариационный ряд выстроен по возрастанию или убыванию членов ряда.
В примере имеем ранжированный вариационный ряд вида:
Вариационные ряды есть безынтервальные, если признак дискретный, и интервальные, если признак непрерывный. Если признак варьирует дискретно, но в широких границах, то по данным наблюдений можно построить интервальный вариационный ряд. Будем рассматривать равноинтервальные ряды. Если признак варьирует непрерывно, то из интервального ряда можно построить безынтервальный ряд, т.е. разделение на ряды (безынтервальные и интервальные) по типу признака (дискретный или непрерывный) не однозначное.
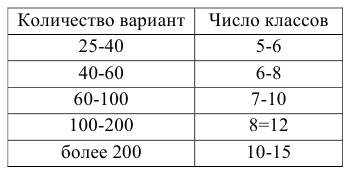
Для получения хорошо обозримого вариационного ряда и обеспечения достаточной точности вычисляемых по нему числовых характеристик следует разбить вариацию признака (в пределах от 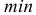
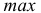
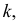
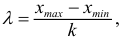
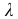
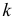
Существует формула Стерджеса 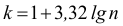
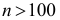
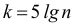
Техника построения вариационного ряда:
- Найдем
- Вычислим
- Значение
должно попасть примерно в середину первого классового интервала, поэтому нижняя граница
первого классового интервала будет
Прибавив к
число
получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет
- Верхние границы интервалов уменьшаем на величину
равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.
- Подсчитаем количество вариант
попавших в каждый интервал.
Пример:
Наблюдается признак 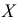
Выборка имеет вид: 8, 10, 6, 10, 8, 5, 11, 7, 10, 6, 9, 7, 8, 7, 9, 11, 8, 9, 10, 8, 7, 8, 11, 8, 7, 10, 8, 8, 5, 11, 8, 10, 12, 7, 5, 7, 9, 7, 10, 5, 8, 9, 7, 12, 8, 9, 6, 7, 8, 7, 11, 8, 6, 7,9, 10,6, 6,6,7,8, 10, И, 12.
Если 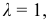
Полученный вариационный ряд выражает зависимость между отдельными вариантами и частотой (повторяемостью) вариант.
Пример:
Наблюдается признак 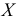
Выборка имеет вид:
1) Лимиты выборки:
Классовые интервалы:
4) Уменьшаем верхние границы интервалов на величину точности, принятой при измерении, т.е. на величину 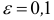
Итак, интервальный вариационный ряд имеет вид:
Соответствующий безынтервальный ряд, построенный по интервальным данным, будет иметь вид:
где 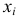
Графики вариационных рядов
Более наглядное изображение закономерности варьирования количественного признака — график вариационного ряда.
Полигон распределения
Полигон распределения (или многоугольник распределения) строится для безынтервального ряда: по оси 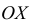
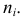
Гистограмма распределения частот
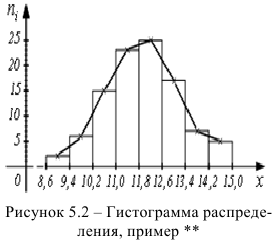
Гистограмма распределения частот 
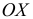
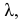
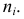
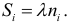
Пример:
Гистограмма данного распределения изображена на рис. 5.2. Если на приведенной гистограмме верхнее основание клетки поделить пополам точкой, соединить полученные точки ломаной, то получим вариационную кривую.
Аналогично можно построить гистограмму относительных частот 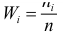
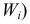
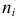
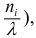
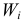
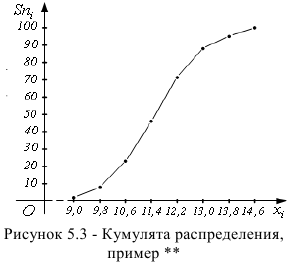
Кумулята
Кумулята (или график накопленных частот 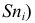
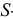
По оси 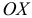
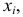
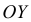
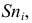
Пример:
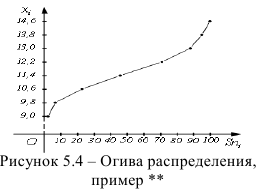
Огива
По оси 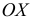
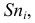
Пример:
Огива данного распределения приведена на рис. 5.4. Огива служит для сравнения вариационных рядов с разным количеством наблюдений.
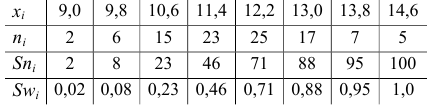
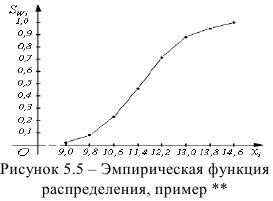
Эмпирическая функция распределения
Эмпирическая функция распределения 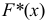
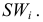
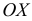
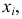
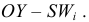
Пример:
Эмпирическая функция данного распределения приведена на рис. 5.5.
Аналогом 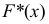
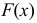
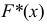
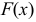
Основные характеристики варьирующих признаков
Средние величины:
Средние величины обладают способностью характеризовать целую группу однородных единиц одним (средним) числом. Например, средний рост, средняя продуктивность, средняя успеваемость и т.п.
Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один групповой объект от другого.
Средние величины могут характеризовать только однородную совокупность вариант, в противном случае средняя величина фиктивная. Средняя величина -это абстрактная величина, т.к. в действительности не существует, а иногда и не может существовать, но очень подходит для сравнения признаков.
При вычислении средних величин не обязательно группировать исходные данные в вариационный ряд.
Средняя арифметическая
Средняя арифметическая 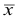
В случае, если выборка не сгруппированная, то 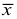
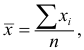
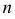
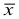
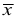
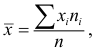
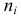
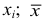
Свойства
1) если каждую варианту 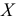
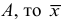
2) Если каждую варианту 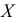
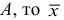
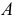
Средняя квадратическая
Средняя квадратическая 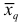
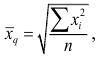
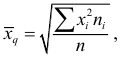
Пример:
Измерение диаметров нефтяных пятен при загрязнении водоема дало следующие результаты: 15, 20, 10, 25, 30 м.
Требуется определить средний диаметр нефтяного пятна. Применим формулу
Средняя арифметическая диаметров 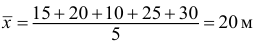
площадь всех пяти пятен равна 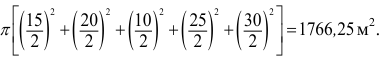
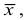
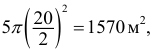
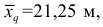
Средняя кубическая
Средняя кубическая 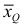
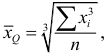
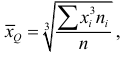
Средняя кубическая 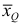
Средняя гармоническая
Средняя гармоническая 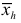
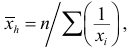
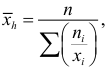
Пример:
Пять рабочих в течение одного часа (60 мин.) изготовили: первый — 10 деталей, второй — 20, третий — 25, четвертый — 30, пятый — 20. Всего за один час изготовлено 105 деталей. Средние количества деталей за один час 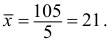
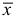
С помощью 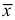
Найдем количество минут, затраченное на одну деталь каждым рабочим:
Найдем среднее время, затраченное на одну деталь одним рабочим:
Количество деталей в среднем изготовленных за час будет:
Аналогичный результат получим, если используем формулу среднего гармонического:
Следовательно, в случае усреднения меняющихся производительностей ил скоростей надо применять
Показатели вариации
Лимиты и размах выборки:
Простейшими показателями вариации (показателями разнообразия) являются лимиты: 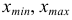
Пример:
Признаки 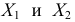
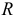
Среднее линейное отклонение
Среднее линейное отклонение 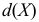
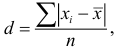
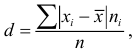
В условиях предыдущего примера линейные отклонения признаков:
Отсюда
Следовательно, признак 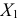
Дисперсия
Дисперсия 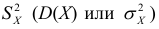
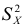
Расчетная формула дисперсии:
Таким образом, 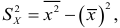
квадрата величины минус квадрат среднего арифметического.
Аналог в теории вероятностей — дисперсия 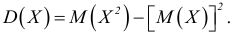
Свойства дисперсии:
1) если каждую варианту 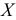
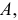
Следовательно, можно вычислять не только по 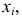
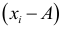
2) Если каждую варианту 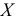
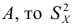
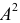
Следовательно, при наличии в совокупности многозначных вариант их можно сократить на некоторое постоянное число 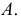
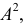
Свойства 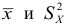
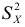
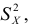
При 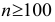
Пример:
Пусть признак 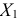
Обозначим сумму квадратов отклонений значений признака от центра 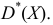
Дисперсия выборочная
Дисперсия исправленная
Пусть признак 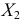
Дисперсия выборочная
Дисперсия исправленная
Среднее квадратическое отклонение
Среднее квадратическое отклонение (СКО) более удобная характеристика, чем дисперсия, т.к. выражается в тех же единицах, что 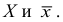
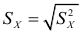
В условиях предыдущего примера
При одинаковых лимитах и размахе дисперсия и СКО не одинаковы. На их величине сказался различный характер варьирования признака.
Поправка Шеппарда.
При создании безынтервального вариационного ряда из интервального ряда частоты 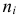
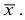
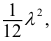
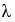
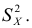
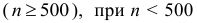
Пример:
Введем поправку Шеппарда:
Анализируя результат, приходим к выводу, что в этом примере данную поправку можно не использовать.
Коэффициент вариации
Дисперсия 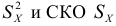
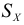
2) средние сравниваемых групп незначительно отличаются друг от друга. Если указанные условия не выполняются и необходимо сравнить разнообразие разных признаков или одинаковых при значительном различии средних, то СКО непосредственно не может быть использовано. В этих случаях используют не абсолютные, а относительные показатели вариации.
Коэффициент вариации 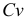
Примеры:
1) Сравнить два варьирующих признака. Для первого признака среднее 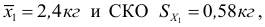
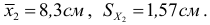
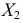
Следовательно, сильнее варьирует признак
2) Средняя длина зеркального карпа в одном садке 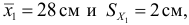
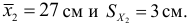
втором садке разнообразия больше и рыбы менее стандартны.
Отметим, варьирование признака 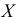
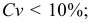
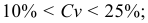
Структурные средние
На величину средней арифметической 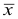
Медиана
Медиана 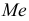
Если число вариант небольшое, то данные ранжируют и при нечетном 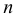
В данном случае медиана
Если число вариант четное, то медиана равна полусумме его центральных членов. Например,
В этом случае медиана
Если имеем вариационный интервальный ряд, то медиану находим по формуле
Вначале находим класс или интервал, к которому принадлежит медиана 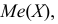
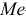
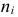
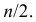
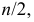
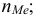
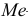
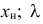
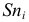
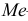
Пример:
Если из интервального вариационного ряда сформирован безынтервальный вариационный ряд, то медиану находим по формуле
где 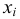
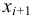
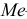
Пример:
Пример:
По предыдущей формуле:
Мода
Мода 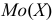
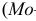
Если ряд безынтервальный, то 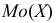
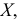
Если ряд интервальный, то моду находим по формуле
где 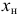
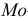
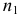
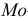
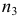
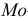
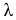
Пример:
Квантили
Квантили — значения признака 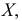
Квартили — три значения признака 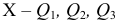
Децили — девять значений делят ряд на десять равных частей.
Перцентили — 99 значений делят ряд на 100 равных частей. Обозначают перцентили
Точечные и интервальные оценки генеральных параметров
Числовые показатели, характеризующие генеральную совокупность, называются генеральными показателями. Например, математическое ожидание генеральной совокупности 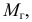
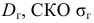
Числовые показатели, характеризующие выборку, называются выборочными характеристиками или статистиками. Например, 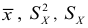
Выборочные характеристики — это величины случайные, варьирующие около своих генеральных параметров и являющиеся их приближенными оценками.
Пусть исследуется количественный признак 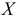
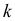
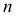
По каждой выборке подсчитаем некоторую статистику 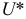
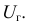
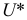
В большинстве случаев средние характеристики имеют нормальный закон распределения.
Определение. Характеристики, вычисленные одним числом, называются точечными оценками генеральных параметров.
Такие оценки должны удовлетворять условиям:
- состоятельность, т.е. оценка
стремится по вероятности к оцениваемому параметру
- эффективность, т.е. оценка
должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака
— наиболее эффективной будет оценка
наименее эффективной —
Для дисперсий этих оценок характерно неравенство
- несмещенность оценки, т.е. математическое ожидание ее выборочного распределения совпадает со значением генерального параметра:
При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.
Доказано, что наилучшими оценками для генеральных параметров 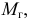
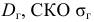
При выборке малого объема точечная оценка параметра может значительно отличаться от генерального значения. В таких случаях используют интервальные оценки. Интервальная оценка определяется двумя числами — границами интервала; такая оценка позволяет установить точность и надежность оценки.
Пусть по данным выборки подсчитана статистика 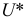
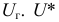
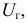
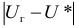
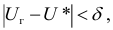
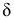
Так как работаем со статистическим материалом (массовыми однородными объектами), то категорически утверждать, что оценка 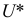
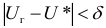
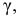
Определение. Доверительной вероятностью или надежностью называется вероятность
На практике наиболее часто задают надежность 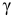
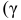
Противоположная вероятность 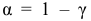
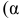
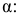
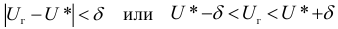
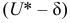
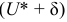
Говорим, что доверительный интервал заключает в себе 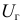
Для любой выборочной характеристики по соответствующей методике можно найти доверительный интервал с надежностью
Например, пусть количественный признак 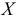
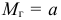
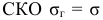
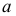
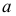
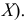
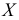
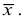
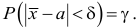
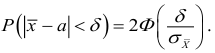
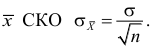
Обозначим 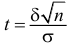
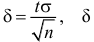
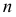
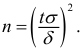
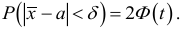
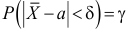
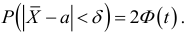
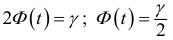
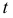
Таким образом, интервал 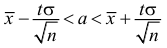
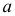
Пример:
Количественный признак 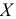
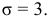
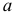
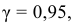
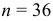
Точность оценки
Доверительный интервал:
Надежность 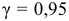
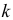
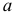
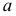
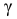
Рассмотрим случай, когда СКО 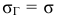
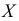
Случайная величина 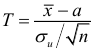
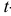
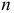
Дифференциальная функция этого распределения (плотность вероятности) обозначается 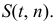
Доверительный интервал:
Величина 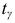
Пример:
Количественный признак 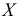
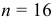
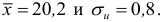
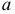
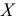
При 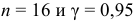
Замечание. Можно доказать, что при 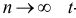
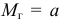
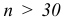
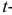
Построение нормальной кривой по опытным данным
Пусть признак 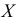
Если 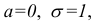
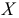
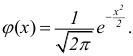
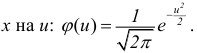
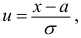
Сравниваем (5.1) и (5.2), получим:
Если параметры 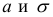
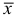
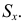
Пусть имеем безынтервальный вариационный ряд, где 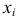
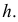
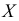
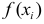
Величина 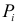
наблюдений выборки объемом 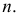
Один из способов построения нормальной кривой по данным наблюдений следующий:
1) поданным наблюдений вычислим параметры
2) найдем выравнивающие (теоретические) частоты по формуле
где 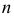
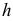
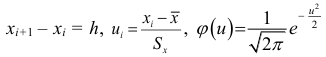
3) строим точки 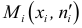
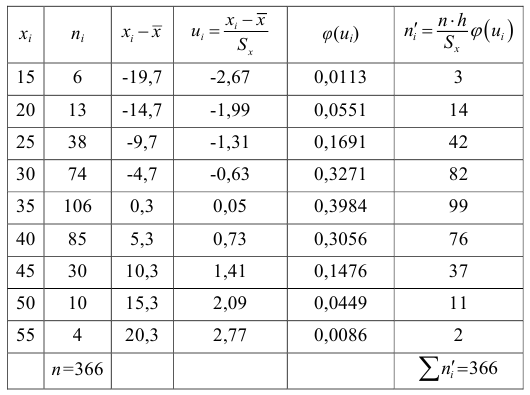
Пример:
Пусть статистическое распределение признака 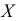
Найдем выравнивающие (теоретические) частоты 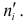
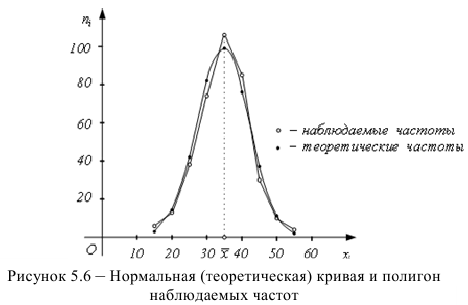
На рис.5.6 построены нормальная (теоретическая) кривая и полигон наблюдаемых частот. Сравнение графиков показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.
Статистическая гипотеза
Статистическая проверка гипотез является вторым после статистического оценивания параметров распределения и в то же время важнейшим разделом математической статистики.
Методы математической статистики позволяют проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например 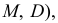
Пусть по некоторым данным имеются основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача заключается в том, чтобы подтвердить или опровергнуть это предположение, используя выборочные (экспериментальные) данные.
Проверить статистическую гипотезу — это значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. Проверка осуществляется с помощью статистического критерия.
Определение 1. Статистический критерий — правило, устанавливающее условия, по которым статистическая гипотеза принимается или отвергается.
Этот критерий называют еще критерием согласия (имеется в виду согласие принятой гипотезы с результатами, полученными из выборки).
Определение 2. Статистический критерий — это случайная величина 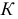
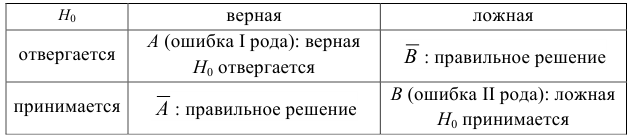
Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезой и обозначают 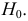
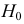
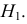
При проверке статистических гипотез можно допустить ошибку двух видов. Относительно гипотезы 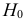
Определение. Уровнем значимости 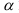
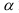
Чем меньше уровень значимости 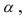
Тогда вероятность события 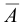
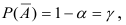
Определение. Критической областью 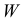
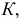
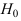
Критическая область 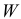
- вероятность попадания
при условии справедливости
была равна
при минимальном
- вероятность попадания
если справедлива
должна быть такой, что вероятность ошибки II рода, т.е.
должна быть минимальной. Вероятность не допуска ошибки II рода
называется мощностью критерия
эта величина должна быть максимальной.
- единственный способ одновременного уменьшения вероятностей ошибок I и II рода состоит в увеличении объема выборки.
Критерии согласия
Обычно эмпирические 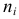
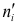
Возникает необходимость установить критерий (правило), который позволит судить, является ли расхождение между 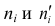
Если расхождение случайно, то говорим, что данные выборки согласуются с гипотезой о распределении генеральной совокупности и, следовательно, гипотезу можно принять. Если же расхождение значимо, то гипотезу следует отвергнуть.
Критерий согласия (критерий соответствия) — критерий, который позволяет судить о том, что расхождение эмпирического и теоретического распределений случайно или значимо (принимать гипотезу или отвергать).
Критерий «хи-квадрат» Пирсона
Критерий «хи-квадрат» Пирсона
Пусть количественный признак 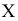
Выдвигается нулевая гипотеза 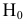
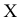
Вычисляется статистическая характеристика:
Критерий 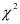
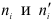
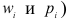
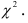
Величина 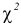
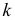
Число степеней свободы 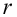
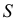
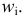
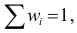
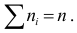
Если подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статистическое средние, то 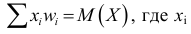
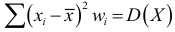
В случае, если признак 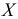
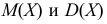
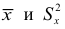
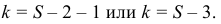
Если проверяем равномерный закон распределения, то его параметры 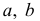
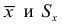
В случае закона Пуассона параметр 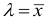
Если проверяем биномиальный закон распределения, то 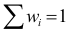
Если закон показательный, то его параметр 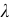
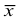
Вычисляем число степеней свободы 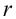
Итак, при проверке гипотезы о нормальном распределении 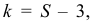
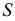
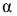
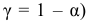
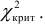
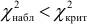
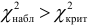
При использовании критерия «хи-квадрат» необходимо интервалы с числом 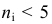
Пример:
Пусть количественный признак 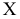
Такое задание признака 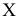
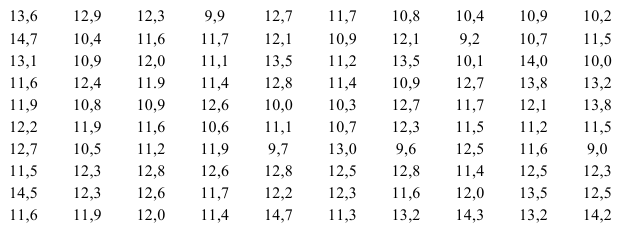
вариационному ряду вычислим основные числовые характеристики:
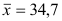
У нас 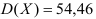
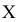
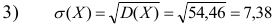
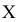
Выдвигаем нулевую гипотезу 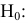
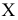
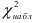
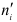
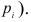
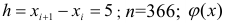
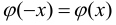
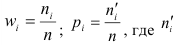
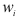
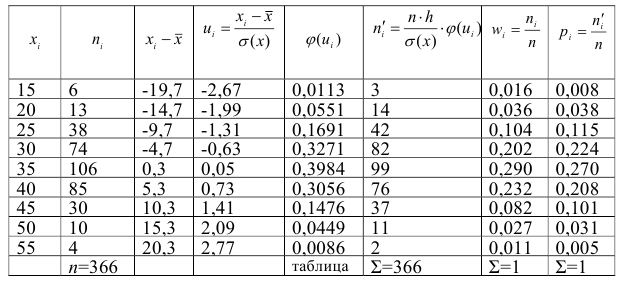
Приведем расчетную таблицу.
Сравниваем графы 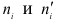
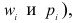
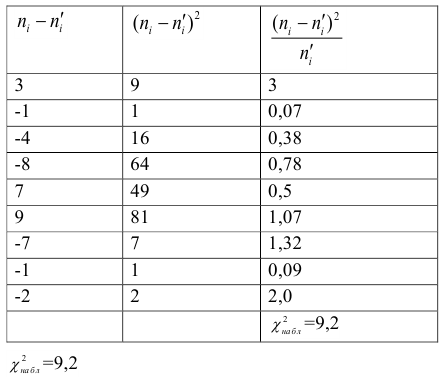
Вычисляем 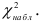
Вычисляем число степеней свободы 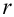
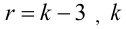
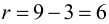
Задаем уровень значимости 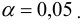
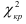
Вывод: 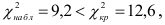
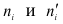
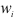
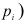
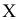
Критерий Романовского
Найдем величину (число)
В примере
Если 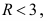
У нас: 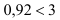
Если 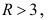
Критерий Колмогорова.
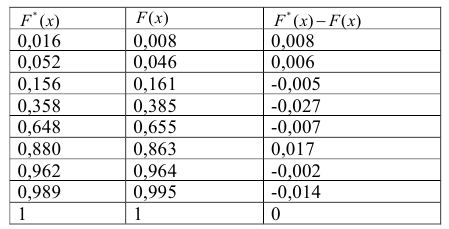
Этот критерий в расчетную таблицу требует еще три графы.
Графа 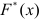
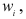
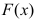
Найдем величину
В примере
Вычислим 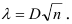
По таблице 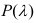
Вывод. Если 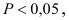
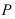
В примере: 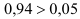
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
Критерий согласия Пирсона
Опр Критерий проверки гипотезы о предполагаемом законе неизвестного распределения называется критерием согласия.
Имеется несколько критериев согласия: $chi ^2$ { хи-квадрат } К. Пирсона, Колмогорова, Смирнова и др.
Обычно теоретические и эмпирические частоты различаются. Случай расхождения может быть не случайным, значит и объясняется тем, что не верно выбрана гипотеза. Критерий Пирсона отвечает на поставленный вопрос, но как любой критерий он ничего не доказывает, а лишь устанавливает на принятом уровне значимости её согласие или несогласие с данными наблюдений.
Опр Достаточно малую вероятность, при которой событие можно считать практически невозможным называют уровнем значимости.
На практике обычно принимают уровни значимости, заключённые между 0,01 и 0,05, $alpha =0,05$ — это $5 { % } $ уровень значимости.
В качестве критерия проверки гипотезы примем величину begin{equation} label { eq1 } chi ^2=sum { frac { ( { n_i -n_i’ } )^2 } { n_i’ } } qquad (1) end{equation}
здесь $n_i -$ эмпирические частоты, полученные из выборки, $n_i’ -$ теоретические частоты, найденные теоретическим путём.
Доказано, что при $nto infty $ закон распределения случайной величины { 1 } независимо от того, по какому закону распределена генеральная совокупность, стремится к закону $chi ^2$ { хи-квадрат } с $k$ степенями свободы.
Опр Число степеней свободы находят по равенству $k=S-1-r$ где $S-$ число групп интервалов, $r-$ число параметров.
1) равномерное распределение: $r=2, k=S-3 $
2) нормальное распределение: $r=2, k=S-3 $
3) показательное распределение: $r=1, k=S-2$.
Правило. Проверка гипотезы по критерию Пирсона.
- Для проверки гипотезы вычисляют теоретические частоты и находят $chi _ { набл } ^2 =sum { frac { ( { n_i -n_i’ } )^2 } { n_i’ } } $
- По таблице критических точек распределения $chi ^2$ по заданному уровню значимости $alpha $ и числу степеней свободы $k$ находят $chi _ { кр } ^2 ( { alpha ,k } )$.
- Если $chi _ { набл } ^2 <chi _ { кр } ^2 $ то нет оснований отвергать гипотезу, если не выполняется данное условие — то отвергают.
Замечание Для контроля вычислений применяют формулу для $chi ^2$ в виде $chi _ { набл } ^2 =sum { frac { n_i^2 } { n_i’ } -n } $
Проверка гипотезы о равномерном распределении
Функция плотности равномерного распределения величины $X$ имеет вид $f( x )=frac { 1 } { b-a } xin left[ { a,b }right]$.
Для того, чтобы при уровне значимости $alpha $ проверить гипотезу о том, что непрерывная случайная величина распределена по равномерному закону, требуется:
1) Найти по заданному эмпирическому распределению выборочное среднее $overline { x_b } $ и $sigma _b =sqrt { D_b } $. Принять в качестве оценки параметров $a$ и $b$ величины
$a = overline x _b -sqrt 3 sigma _b $, $b = overline x _b +sqrt 3 sigma _b $
2) Найти вероятность попадания случайной величины $X$ в частичные интервалы $( { x_i ,x_ { i+1 } } )$ по формуле $ P_i =P( { x_i <X<x_ { i+1 } } )=intlimits_ { x_i } ^ { x_ { i+1 } } { f( x )dx=left. { frac { 1 } { b-a } x }right| { begin{array} { c } { x_ { i+1 } } \ { x_i } \ end{array} } } =frac { x_ { i+1 } } { b-a } -frac { x_i } { b-a } . $
3) Найти теоретические { выравнивающие } частоты по формуле $n_i’ =np_i $.
4) Приняв число степеней свободы $k=S-3$ и уровень значимости $alpha =0,05$ по таблицам $chi ^2$ найдём $chi _ { кр } ^2 $ по заданным $alpha $ и $k$, $chi _ { кр } ^2 ( { alpha ,k } )$.
5) По формуле $chi _ { набл } ^2 =sum { frac { ( { n_i -n_i’ } )^2 } { n_i’ } } $ где $n_i -$ эмпирические частоты, находим наблюдаемое значение $chi _ { набл } ^2 $.
6) Если $chi _ { набл } ^2 <chi _ { кр } ^2 -$ нет оснований, отвергать гипотезу.
Проверим гипотезу на нашем примере.
1) $overline x _b =13,00,,,sigma _b =sqrt { D_b } = 6,51$
2) $a=13,00-sqrt 3 cdot 6,51=13,00-1,732cdot 6,51=1,72468$
$b=13,00+1,732cdot 6,51=24,27532$
$b-a=24,27532-1,72468=22,55064$
3) $P_i =P( { x_i <X<x_ { i+1 } } )=frac { x_ { i+1 } } { b-a } -frac { x_i } { b-a } $ $ P_1 =( { -1<X<3 } )=frac { 3 } { 22,55064 } -frac { -1 } { 22,55064 } =0,13303+0,04434=0,177375 $
$ P_2 =( { 3<X<7 } )=frac { 7 } { 22,55064 } -frac { 3 } { 22,55064 } =0,177375 $
$ P_3 =( { 7<X<11 } )=frac { 11 } { 22,55064 } -frac { 7 } { 22,55064 } =0,177375 $
$ P_4 =( { 11<X<15 } )=frac { 15 } { 22,55064 } -frac { 11 } { 22,55064 } =0,177375 $
$ P_5 =( { 15<X<19 } )=frac { 19 } { 22,55064 } -frac { 15 } { 22,55064 } =0,177375 $
$ P_6 =( { 19<X<23 } )=frac { 23 } { 22,55064 } -frac { 19 } { 22,55064 } =0,177375 $
В равномерном распределении если одинакова длина интервала, то $P_i -$ одинаковы.
4) Найдём $n_i’ =np_i $.
5) Найдём $sum { frac { ( { n_i -n_i’ } )^2 } { n_i’ } } $ и найдём $chi _ { набл } ^2 $.
Занесём все полученные значения в таблицу
begin{array} { |l|l|l|l|l|l|l| } hline i& n_i & n_i’ =np_i & n_i -n_i’ & ( { n_i -n_i’ } )^2& frac { ( { n_i -n_i’ } )^2 } { n_i’ } & Контроль~ frac { n_i^2 } { n_i’ } \ hline 1& 1& 4,43438& -3.43438& 11,7950& 2,659898& 0,22551 \ hline 2& 6& 4,43438& 1,56562& 2,45117& 0,552765& 8,11838 \ hline 3& 3& 4,43438& -1,43438& 2,05744& 0,471463& 2,0296 \ hline 4& 3& 4,43438& -1,43438& 2,05744& 0,471463& 2,0296 \ hline 5& 6& 4,43438& 1,56562& 2,45117& 0,552765& 8,11838 \ hline 6& 6& 4,43438& 1,56562& 2,45117& 0,552765& 8,11838 \ hline & & & & & sum = chi _ { набл } ^2 =3,261119& chi _ { набл } ^2 =sum { frac { n_i^2 } { n_i’ } -n } =3,63985 \ hline end{array}
$chi _ { кр } ^2 ( { 0,05,3 } )=7,8$
$chi _ { набл } ^2 <chi _ { кр } ^2 =3,26<7,8$
Вывод отвергать гипотезу нет оснований.







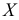
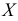
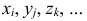
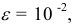 т.е. последняя сохраняемая цифра — вторая после запятой. Тогда
т.е. последняя сохраняемая цифра — вторая после запятой. Тогда 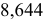
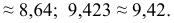
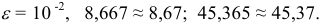
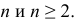
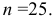

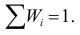

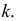
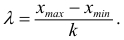
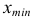 должно попасть примерно в середину первого классового интервала, поэтому нижняя граница
должно попасть примерно в середину первого классового интервала, поэтому нижняя граница 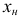 первого классового интервала будет
первого классового интервала будет 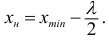 Прибавив к
Прибавив к 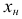 число
число 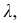 получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет
получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет 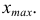
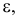 равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.
равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.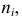 попавших в каждый интервал.
попавших в каждый интервал.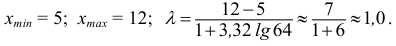

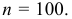
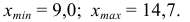
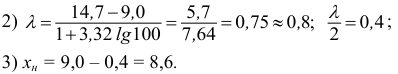

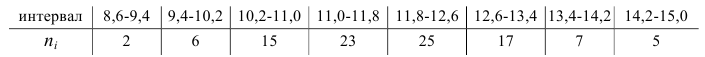


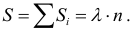
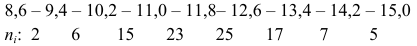


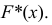
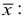
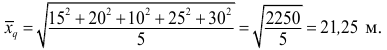
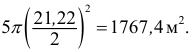
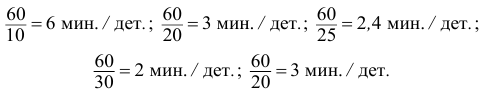
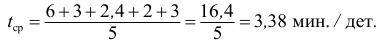
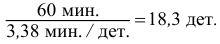
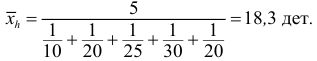
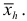
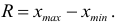
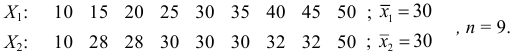
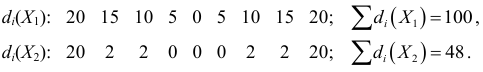
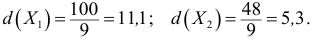
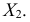
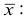
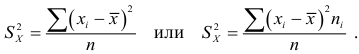
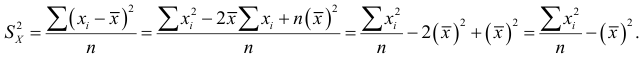
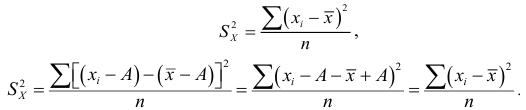
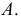
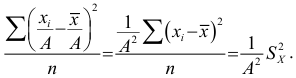
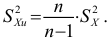
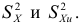
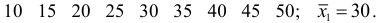
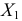
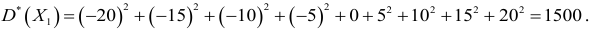
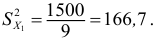
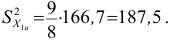
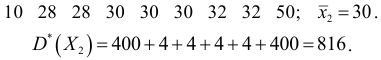
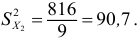
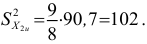
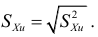
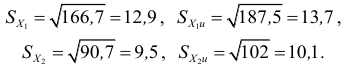
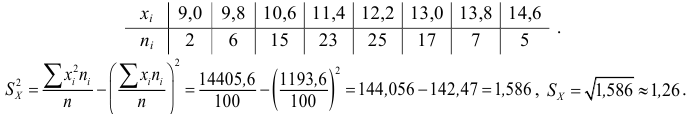
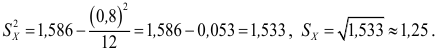
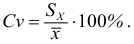
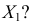
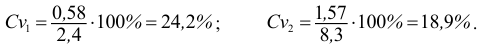
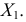
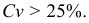
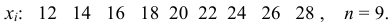
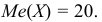
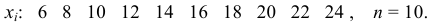
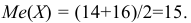
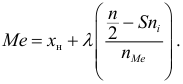
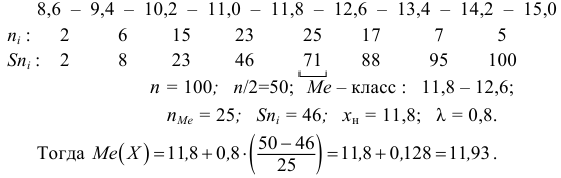
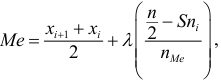
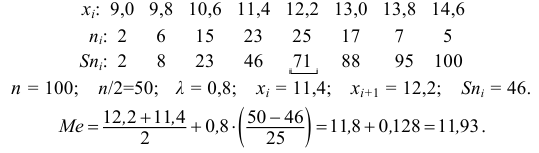
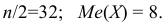
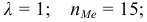
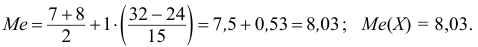
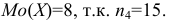
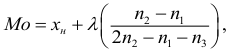
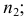
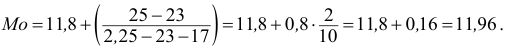
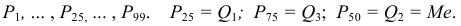
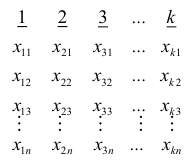
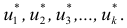
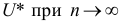 стремится по вероятности к оцениваемому параметру
стремится по вероятности к оцениваемому параметру 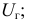
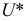 должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака
должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака 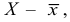
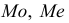 — наиболее эффективной будет оценка
— наиболее эффективной будет оценка 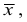 наименее эффективной —
наименее эффективной — 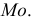 Для дисперсий этих оценок характерно неравенство
Для дисперсий этих оценок характерно неравенство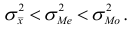
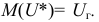 При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.
При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.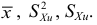
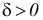
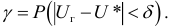
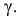
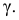
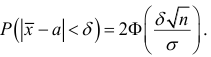
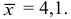
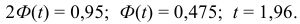
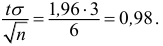
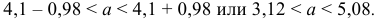
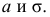
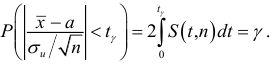
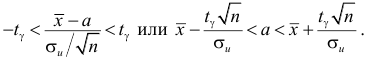
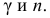
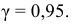
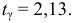
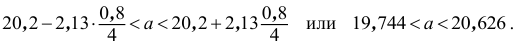
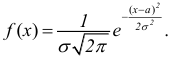
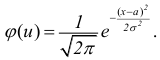
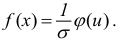
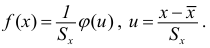
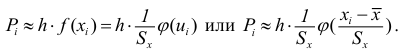
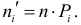
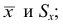
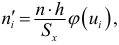
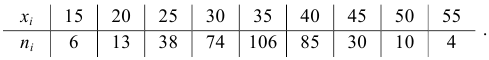
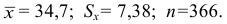
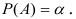
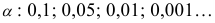
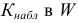 при условии справедливости
при условии справедливости 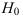 была равна
была равна 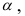 при минимальном
при минимальном 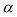
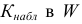 если справедлива
если справедлива 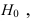 должна быть такой, что вероятность ошибки II рода, т.е.
должна быть такой, что вероятность ошибки II рода, т.е. 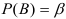 должна быть минимальной. Вероятность не допуска ошибки II рода
должна быть минимальной. Вероятность не допуска ошибки II рода 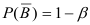 называется мощностью критерия
называется мощностью критерия 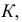 эта величина должна быть максимальной.
эта величина должна быть максимальной.