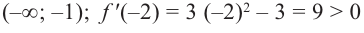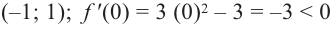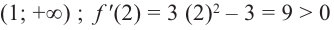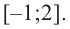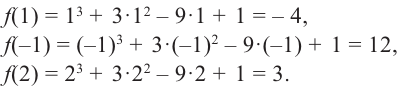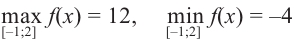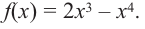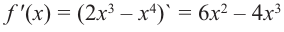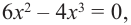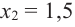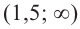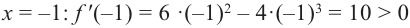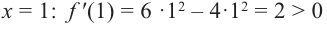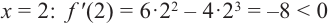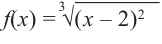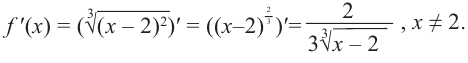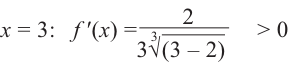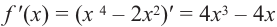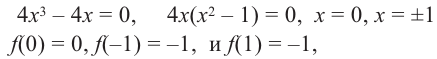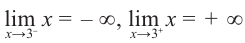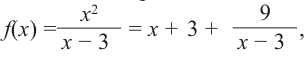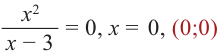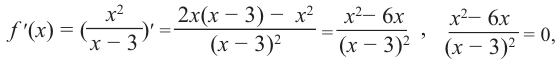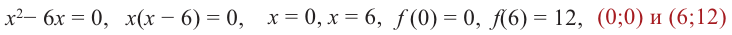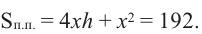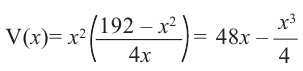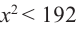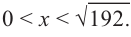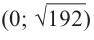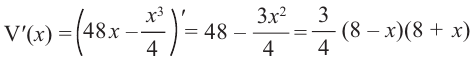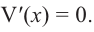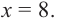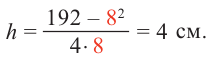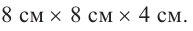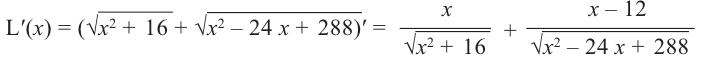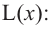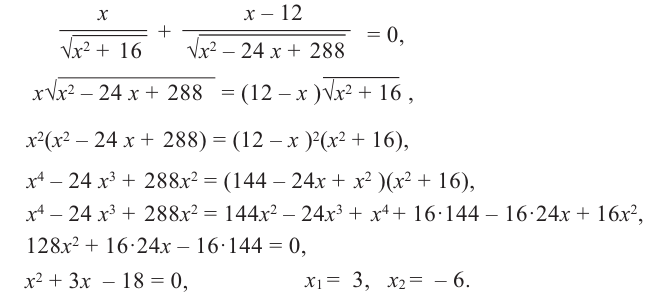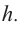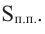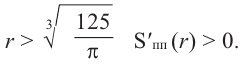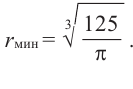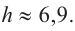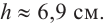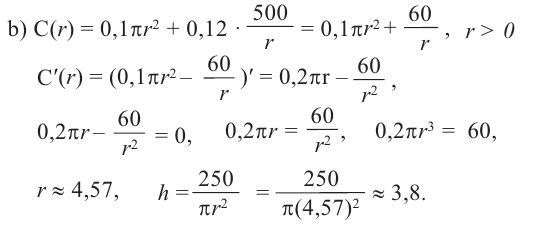Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Функция «y = kx» — это первый тип функции, который изучается в математике.
Важно!
Буквенный множитель «k» в функции «y = kx» называют
числовым коэффициентом.
На месте «k» может стоять любое число (положительное, отрицательное или дробь).
Другими словами, можно сказать, что «y = kx» — это семейство всевозможных функций, где вместо
«k» стоит число.
Примеры функций вида «y = kx».
- y = 4x
- y = −1,5x
- y = x
Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент
«k».
| Функция | Коэффициент «k» | ||||
|---|---|---|---|---|---|
| y = 4x | k = 4 | ||||
| y = −1,5x | k = −1,5 | ||||
y =
x |
k =
|
Как построить график функции «y = kx»
Запомните!
Графиком функции «y = kx» является прямая.
Из геометрии вспомним аксиому (утверждение, которое не требует доказательства),
что через любые две точки можно провести прямую и притом только одну.
Исходя из этой аксиомы, что
чтобы построить график функции вида «у = kx» нам будет достаточно найти всего
две точки.
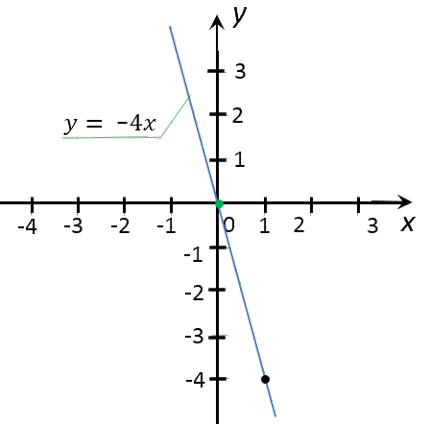
Для примера построим график функции «y = −4x».
Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».
Важно!
Выбирая произвольные числовые значения вместо «x», лучше брать числа
«0» и «1».
С этими числами легко выполнять расчеты.
| x | Расчет «y» |
|---|---|
| 0 | y(0) = −4 · 0 = 0 |
| 1 | y(1) = −4 · 1 = −4 |
Полученные значения «x» и «y» — это координаты точек графика
функции «y = −4x».
Запишем полученные координаты точек «y = −4x» в таблицу.
| Точка |
Координата по оси «Оx» (абсцисса) |
Координата по оси «Оy» (ордината) |
|---|---|---|
| (·)A | 0 | 0 |
| (·)B | 1 | −4 |
Отметим полученные точки на системе координат.
Теперь проведем прямую через отмеченные точки. Эта прямая и будет
являться графиком функции «y = −4x».
После построения не забудьте подписать график функции.
Как решать задачи на функцию «y = kx»
Рассмотрим задачу.
Построить график функции «y = −1,5x». Найти по графику:
- значение «y» соответствующее значению «x» равному 1; 0; 2; 3;
- значение «x», если значение «y» равно
−3; 4,5; 6; - несколько целых значений «x», при которых значения
«y» положительны (отрицательны).
Вначале построим график функции «y = −1,5x».
Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = −1,5x» достаточно найти всего две точки.
Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».
Выполним расчеты и запишем их результаты в таблицу.
| Точка | Координата по оси «Оx» | Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = −1,5 · 0 = 0 |
| (·)B | 1 | y(1) = −1,5 · 1 = −1,5 |
Отметим полученные точки на прямоугольной системе координат.
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = −1,5x».
Теперь работаем с построенным графиком функции «y = −1,5x».
Требуется найти значение «y»,
соответствующее значению «x» равному 1; 0; 2; 3.
Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Запомните!
Чтобы найти значение «y» по известному значению «x» на графике
функции необходимо:
- провести перпендикуляр от оси «Ox»
(ось абсцисс)
из заданного числового значения «x»
до пересечения
с графиком функции; - из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«Oy»
(ось ординат); - полученное числовое значение на оси «Oy» и будет искомым значением.
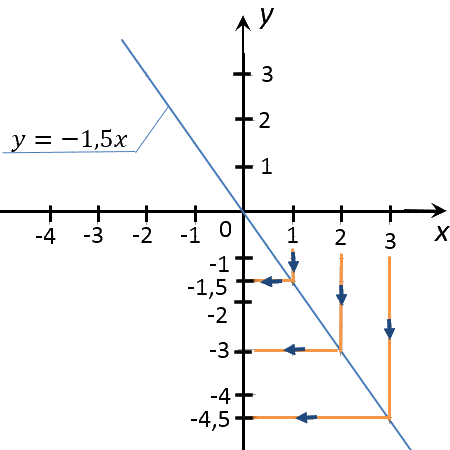
По правилам выше найдем на построенном ранее графике функции «y = −1,5x»
необходимые значения функции «y» для
«x» равным 1; 0; 2; 3.
Запишем полученные результаты в таблицу.
| Заданное значение «x» | Полученное с графика значение «y» |
|---|---|
| 0 | 0 |
| 1 | −1,5 |
| 2 | −3 |
| 3 | −4,5 |
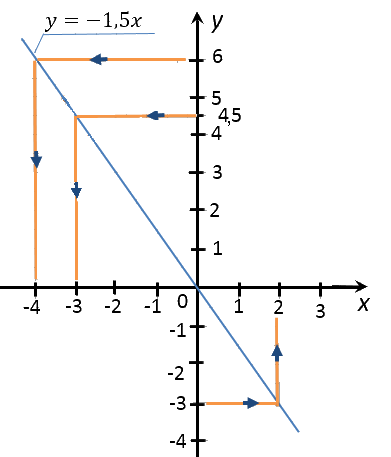
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно −3; 4,5; 6.
Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси «Oy».
Запишем полученные результаты в таблицу.
| Заданное значение «y» | Полученное с графика значение «x» |
|---|---|
| −3 | 2 |
| 4,5 | −3 |
| 6 | −4 |
Перейдем к последнему заданию. Нас просят найти несколько целых значений «x»,
при которых значения «y» положительны (отрицательны).
Для решения этой задачи необходимо внимательно изучить
график функции
«y = −1,5x».
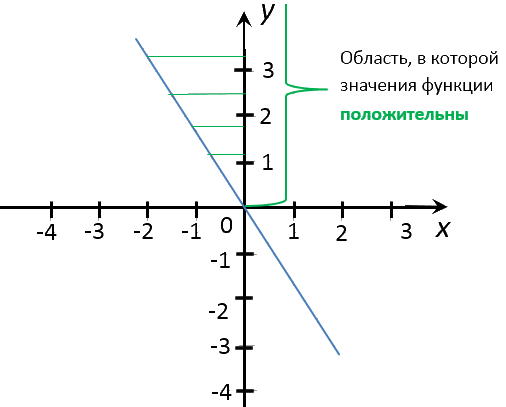
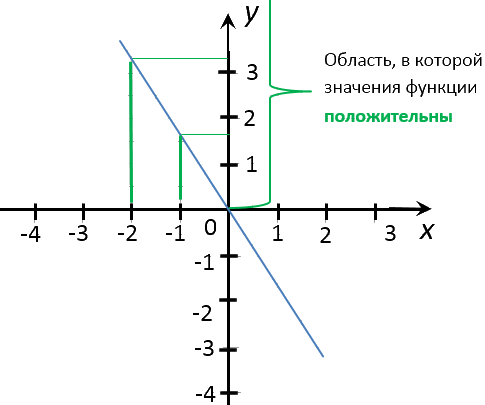
Отметим область на оси
«Oy», где значения «y» для графика функции «y = −1,5x»
положительны.
Из этой области проведем от графика функции несколько перпендикуляров
к оси «Ox».
Помните, что по заданию, нас просят найти несколько «целых» значений «x».
Поэтому перпендикуляры мы будем проводить к оси «Ox» в целые числовые значения.
Запишем ответ. При x = −2; x = −1 значения
y > 0.
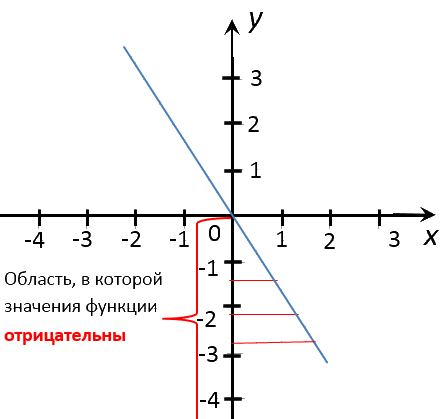
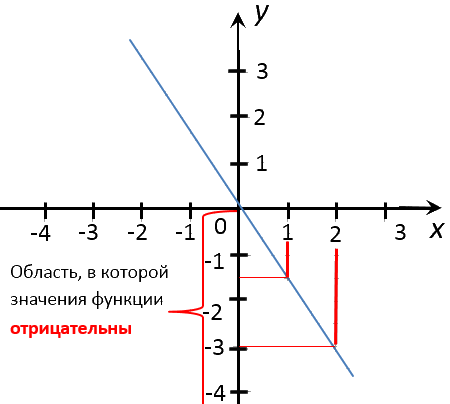
Теперь найдем при каких «x», значения
«y» отрицательны.
Отметим область на оси «Oy», где значения
«y» на графике функции отрицательны.
Проведем перпендикуляры из отмеченной области к оси «Ox» в
целые числовые значения «x».
Запишем ответ. При x = 1; x = 2 значения
y < 0.
Рассмотрим другую задачу.
Какие из точек A(5; −3), D(2; 1)
принадлежат графику функции, заданной
формулой
«y = x»?
Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке
«Как решать задачи на функцию».
В этом уроке мы вспомним только основные моменты решения подобных задач.
Запомните!
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит точка принадлежит графику функции.
- Если получится не верное равенство, значит точка
не принадлежит графику функции.
Подставим в функцию
«y = x»
координаты точки (·)A(5; −3).
−3 = · 5
−3 = (неверно)
Это означает, что точка (·)А(5; −3)
не принадлежит графику функции «y = x»
Проверим точку (·)D(2; 1).
Также подставим её координаты в функцию «y = x».
1 = ·2
1 =
1 = 1(верно)
Это означает, что точка (·)D(2; 1)
принадлежит графику функции «y = x».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
21 мая 2020 в 17:01
Айдос Мурзагалиев
Профиль
Благодарили: 0
Сообщений: 1
Айдос Мурзагалиев
Профиль
Благодарили: 0
Сообщений: 1
Как называется точка x0, если существует такая окрестность точки x0, что для всех x, не равных x0, из этой окрестности выполняется неравенство f(x)<f(x0)?
0
Спасибо
Ответить
18 августа 2020 в 1:11
Ответ для Айдос Мурзагалиев
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
xо − точка максимума.
0
Спасибо
Ответить
6 октября 2016 в 19:18
Алёна Липская
Профиль
Благодарили: 0
Сообщений: 1
Алёна Липская
Профиль
Благодарили: 0
Сообщений: 1
Постройте графики функции y=6 и y=-1
0
Спасибо
Ответить
7 октября 2016 в 8:58
Ответ для Алёна Липская
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Графиком функции является прямая линия параллельная оси X, проходящие через точки (0;6) и (0;-1) соотвественно.
0
Спасибо
Ответить
5 июня 2015 в 14:28
Диана Кривунец
Профиль
Благодарили: 0
Сообщений: 1
Диана Кривунец
Профиль
Благодарили: 0
Сообщений: 1
построить график функции y=x^2-2x-3
по графику найти значение y, если x=-1,5
найти значение x, если y=5
найти нули функции
0
Спасибо
Ответить
30 мая 2016 в 12:04
Ответ для Диана Кривунец
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
На сайте нет возможности построить график, но это будет параболла с центром в точке (0; -3). При значении x=-1,5 y=2,5. При значении y=5, x= -2. Нули функции 3 и -1.
0
Спасибо
Ответить
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
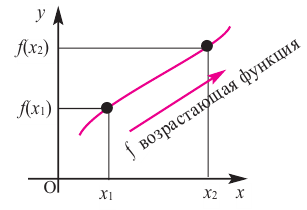
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
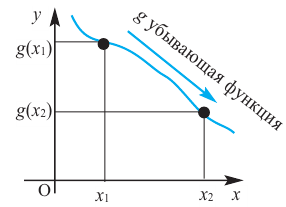
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
Загрузить PDF
Загрузить PDF
График функции – это наглядное представление поведения некоторой функции на координатной плоскости. Графики помогают понять различные аспекты функции, которые невозможно определить по самой функции. Можно построить графики множества функций, причем каждая из них будет задана определенной формулой. График любой функции строится по определенному алгоритму (если вы забыли точный процесс построения графика конкретной функции).
-
1
-
2
Воспользуйтесь константой, чтобы отметить точку на оси Y. Константа (b) является координатой «у» точки пересечения графика с осью Y. То есть это точка, координата «х» которой равна 0. Таким образом, если в формулу подставить х = 0, то у = b (константе). В нашем примере
константа равна 5, то есть точка пересечения с осью Y имеет координаты (0,5). Нанесите эту точку на координатную плоскость.
-
3
Найдите угловой коэффициент прямой. Он равен множителю при переменной. В нашем примере
при переменной «х» находится множитель 2; таким образом, угловой коэффициент равен 2. Угловой коэффициент определяет угол наклона прямой к оси X, то есть чем больше угловой коэффициент, тем быстрее возрастает или убывает функция.
-
4
Запишите угловой коэффициент в виде дроби. Угловой коэффициент равен тангенсу угла наклона, то есть отношению вертикального расстояния (между двумя точками на прямой) к горизонтальному расстоянию (между этими же точками). В нашем примере угловой коэффициент равен 2, поэтому можно заявить, что вертикальное расстояние равно 2, а горизонтальное расстояние равно 1. Запишите это в виде дроби:
.
- Если угловой коэффициент отрицательный, функция убывает.
-
5
От точки пересечения прямой с осью Y нанесите вторую точку, используя вертикальное и горизонтальное расстояния. График линейной функции можно построить по двум точкам. В нашем примере точка пересечения с осью Y имеет координаты (0,5); от этой точки передвиньтесь на 2 деления вверх, а затем на 1 деление вправо. Отметьте точку; она будет иметь координаты (1,7). Теперь можно провести прямую.
-
6
При помощи линейки проведите прямую через две точки. Во избежание ошибок найдите третью точку, но в большинстве случаев график можно построить по двум точкам. Таким образом, вы построили график линейной функции.
Реклама
-
1
Определите функцию. Функция обозначается как f(x). Все возможные значения переменной «у» называются областью значений функции, а все возможные значения переменной «х» называются областью определения функции. Например, рассмотрим функцию y = x+2, а именно f(x) = x+2.
-
2
Нарисуйте две пересекающиеся перпендикулярные прямые. Горизонтальная прямая – это ось Х. Вертикальная прямая – это ось Y.
-
3
Обозначьте оси координат. Разбейте каждую ось на равные отрезки и пронумеруйте их. Точка пересечения осей – это 0. Для оси Х: справа (от 0) наносятся положительные числа, а слева отрицательные. Для оси Y: сверху (от 0) наносятся положительные числа, а снизу отрицательные.
-
4
Найдите значения «у» по значениям «х». В нашем примере f(x) = х+2. Подставьте в эту формулу определенные значения «х», чтобы вычислить соответствующие значения «у». Если дана сложная функция, упростите ее, обособив «у» на одной стороне уравнения.
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-
5
Нанесите точки на координатную плоскость. Для каждой пары координат сделайте следующее: найдите соответствующее значение на оси Х и проведите вертикальную линию (пунктиром); найдите соответствующее значение на оси Y и проведите горизонтальную линию (пунктиром). Обозначьте точку пересечения двух пунктирных линий; таким образом, вы нанесли точку графика.
-
6
Сотрите пунктирные линии. Сделайте это после нанесения на координатную плоскость всех точек графика. Примечание: график функции f(х) = х представляет собой прямую, проходящую через центр координат [точку с координатами (0,0)]; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).[2]
Реклама
-
1
-
2
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
-
3
Найдите и отметьте горизонтальные асимптоты. Асимптота – это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0). Асимптоту отметьте пунктирной линией. Если переменная «х» находится в знаменателе дроби (например,
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
-
4
Найдите координаты нескольких точек и нанесите их на координатную плоскость. Просто выберите несколько значений «х» и подставьте их в функцию, чтобы найти соответствующие значения «у». Затем нанесите точки на координатную плоскость. Чем сложнее функция, тем больше точек нужно найти и нанести. В большинстве случаев подставьте х = -1; х = 0; х = 1, но если функция сложная, найдите по три точки с каждой стороны от начала координат.[5]
- В случае функции
подставьте следующие значения «х»: -1, 0, 1, -2, 2, -10, 10. Вы получите достаточное количество точек.
- Выбирайте значения «х» с умом. В нашем примере несложно понять, что отрицательный знак не играет роли: значение «у» при х = 10 и при х = -10 будет одним и тем же.
- В случае функции
-
5
Определите поведение функции при больших значения переменной «х». Так можно найти общее направление графика функции, который иногда до бесконечности приближается к асимптоте. Например, нетрудно догадаться, что график функции
возрастает до бесконечности: при увеличении огромного значения «х» всего-навсего на 1 (с 1000000 на 1000001), значение «у» увеличится на гораздо большую величину. Определить поведение функции при больших значения «х» можно несколькими способами:
- В функцию подставьте 2-4 больших значения «х» (половину отрицательных и половину положительных), а затем полученные точки нанесите на координатную плоскость.
- Подумайте, что будет, если вместо «х» подставить «бесконечность»? Значение «у» будет бесконечно большим или бесконечно малым?
- Если в функции показатели степени одинаковые (например,
), разделите множители при «х» (
), чтобы найти асимптоту (-0,5).[6]
- Если в функции показатели степени разные, разделите выражение, стоящее в числителе, на выражение, стоящее в знаменателе.
-
6
Соедините точки (5-6 точек), чтобы построить график функции. При этом график не должен пересекать (и касаться) асимптоты. График продолжите в соответствии с найденным поведением функции при больших значениях переменной «х».
-
7
Постройте совершенный график при помощи графического калькулятора. Графические калькуляторы представляют собой мощные карманные компьютеры, при помощи которых можно построить точный график любой функции. Такие калькуляторы способны находить точные координаты точек и угловые коэффициенты прямых, а также быстро строить графики самых сложных функций. Просто введите точную формулу функции (обычно это делается при помощи клавиши «F(х)=») и нажмите соответствующую клавишу, чтобы построить график.
Реклама
Советы
- Практикуйте ваши навыки с использованием графических калькуляторов. Сначала попробуйте построить график вручную, а затем воспользуйтесь калькулятором, чтобы получить точный график и сравнить оба результата.
- Если вы не знаете, что делать, начните с подстановки в функцию различных значений «х», чтобы найти значения «у» (и, следовательно, координаты точек). Теоретически график функции можно построить при помощи только этого метода (если, конечно, подставить бесконечное разнообразие значений «х»).
Реклама
Об этой статье
Эту страницу просматривали 120 687 раз.
Была ли эта статья полезной?
Как найти дополнительную точку на графике?
Есть вот решение задания. Подскажите пожалуйста, откуда взялась еще одна точка на пересечении оси X? Как ее вычислить?
-
Вопрос заданболее трёх лет назад
-
298 просмотров
Пригласить эксперта
Точки пересечения с осями. Это же из школы еще: если игрек равен нулю, то икс равен какомуто уравнению, которое надо решить. Если функция известна то в нее и подставляем вместо игрек ноль.
-
Показать ещё
Загружается…
24 мая 2023, в 19:11
15000 руб./за проект
24 мая 2023, в 18:50
3000 руб./за проект
24 мая 2023, в 18:20
50000 руб./за проект
Минуточку внимания
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
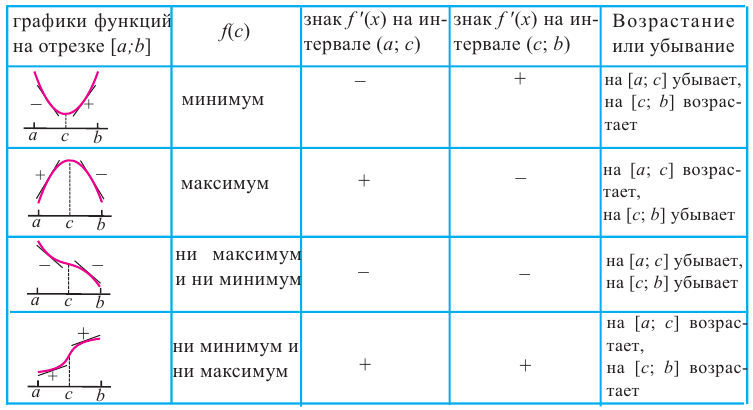
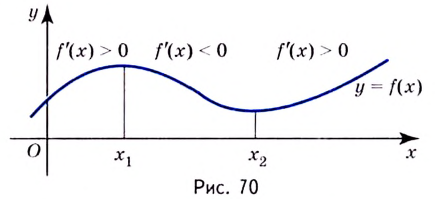
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 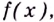
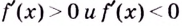
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 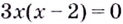
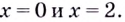
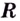
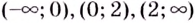
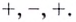
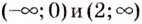
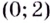
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 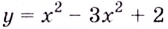
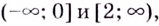
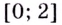
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 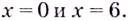
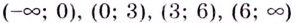
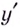
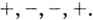
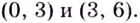
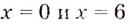
Пример:
Найдите критические точки функции 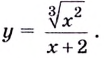
Решение:
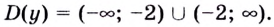
Найдём точки, в которых производная равна нулю или не существует: 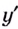
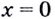
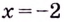

Ответ. 0 и 4.
Пример:
Докажите, что функция 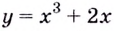
Решение:
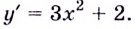
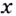
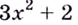
Пример:
Установите, на каком промежутке функция 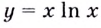
Решение:
Способ 1. 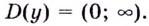
Найдём критические точки функции:
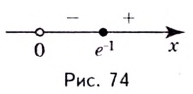
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 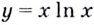
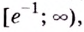
Способ 2. Решим неравенство 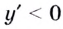
Ответ. Возрастает, если 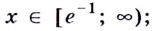
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 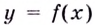
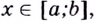
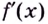
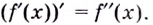
Например, найти производную 2-го порядка функции 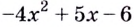
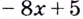
Кривая 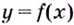
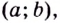
Кривая 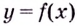
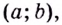
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 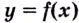
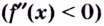
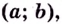
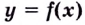
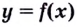
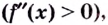
Из теоремы следует, что точками перегиба кривой 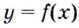
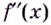
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 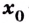
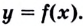
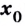
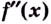
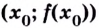
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 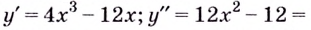
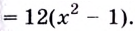
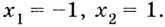
3) Разбиваем область определения на интервалы 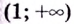
Если 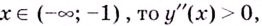
Если 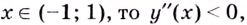
Если 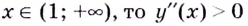
Следовательно, точки 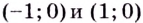
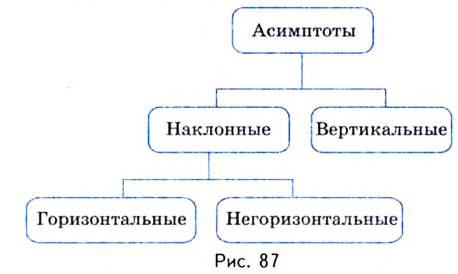
Напомним, что прямая 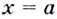
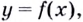
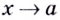
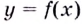
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 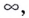
Если 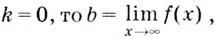
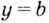
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 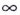
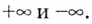
Пример №2
Найдите асимптоты кривых:
Решение:
а) 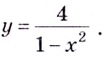
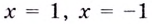
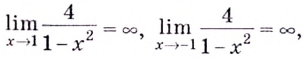
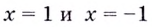
Найдём наклонную асимптоту: 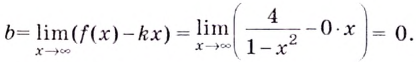
Следовательно, заданная кривая имеет три асимптоты:
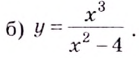
Поскольку функция не определена в точках 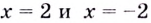
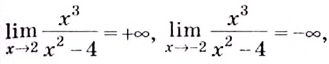
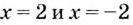
Для наклонной асимптоты
Значит прямая 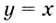
Итак, асимптоты кривой:
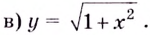
Следовательно, 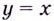
2) если 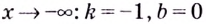

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
Если для любых 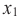
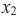
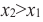
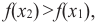
убывающая
Если для любых 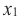
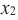
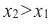
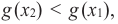
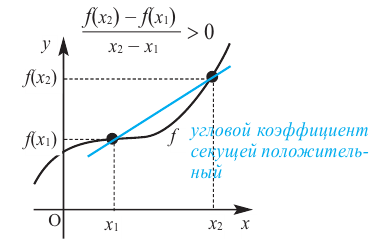
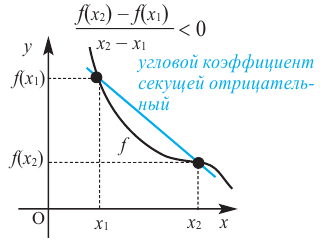
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 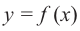
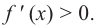
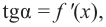
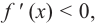
Теорема. Если функция 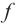
Примечание: если функция 
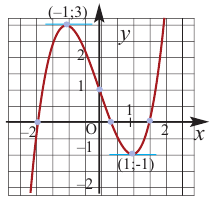
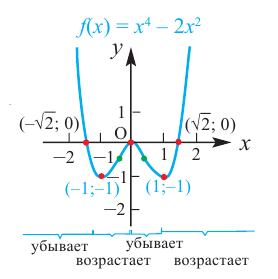
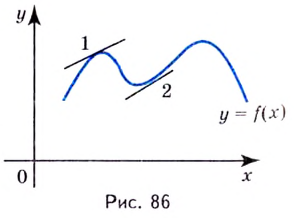
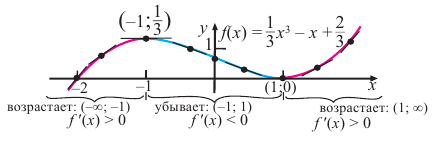
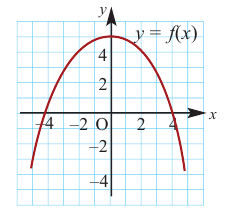
По графику функции 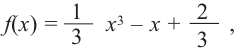
На интервалах 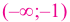
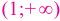
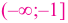
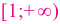
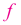
На интервале 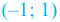
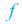
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 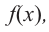
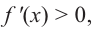
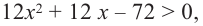
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 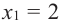
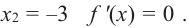
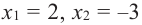
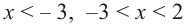
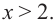
Из таблицы и непрерывности функции 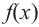
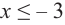
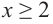
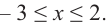
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 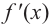
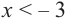
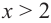
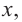
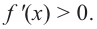
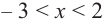
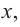
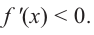
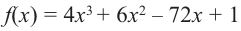
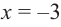
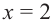
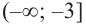
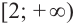
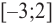
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 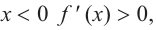
b) при 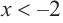
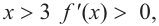
Решение:
а) при 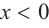
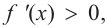
функция возрастает. При 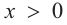
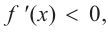
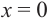
b) При 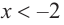
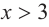
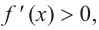
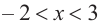
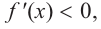
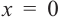
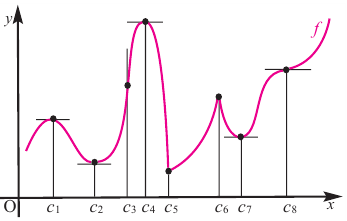
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 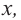
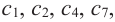
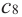
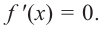
2. В точках 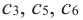
3. Для рассматриваемой нами функции критические точки 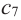
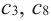
По графику видно, что в точках внутреннего экстремума(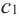
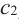
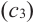
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 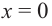
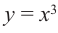
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 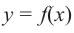
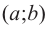
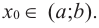
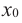
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 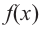
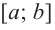
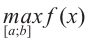
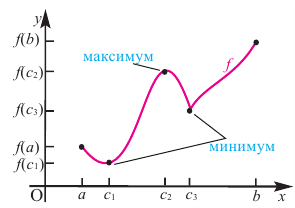
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции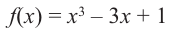
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 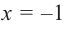
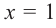
Проверим знак 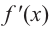
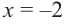
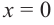
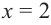

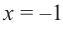
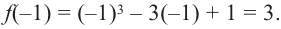
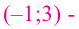
При 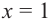
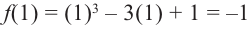
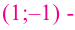
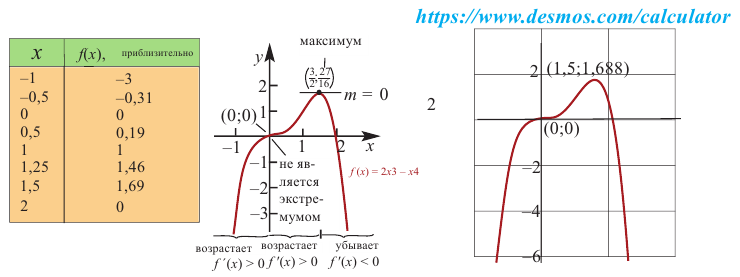
4. Используя полученные для функции 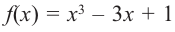
Пример №6
Найдите наибольшее и наименьшее значение функции 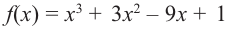
Решение: Сначала найдем критические точки.
Так как 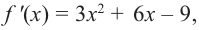
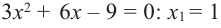
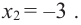
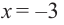
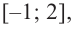
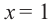
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
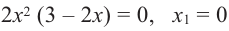
3. Интервалы, на которые критические точки делят область определения функции:
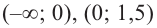
Проверим знак 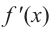
Для промежутка 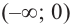
Для промежутка 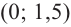
Для промежутка 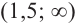
Используя полученную для функции 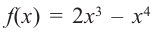
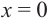
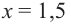
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 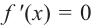
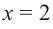
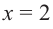
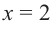
3. Промежутки, на которые критическая точка делит область определения функции: 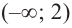
Определим знак 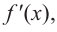
Для 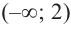
Для 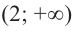
Пример №9
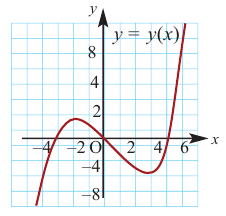
По графику функции производной 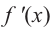
Решение:
Производная 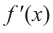
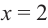
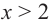
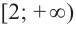
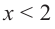
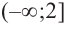
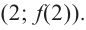
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
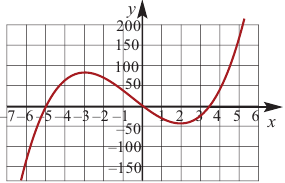
Пример:
Постройте график функции
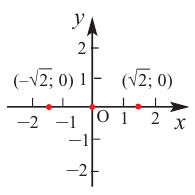
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 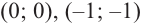
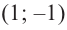
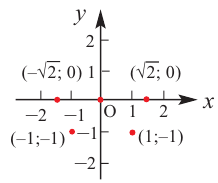
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 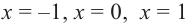
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
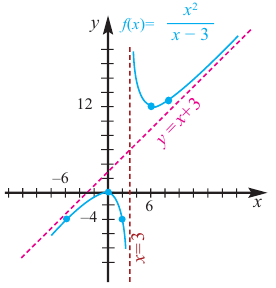
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 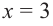
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
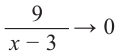
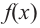
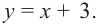
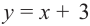
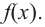
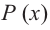
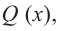
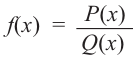
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 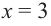
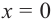
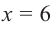
6) Построим график. Отметим на координатной плоскости точки 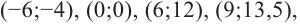
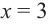
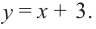
Обратите внимание! В области, близкой к точке 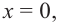
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 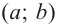
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
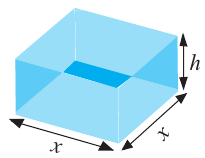
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 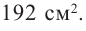
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 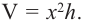
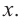
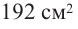
Тогда выразим 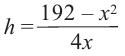
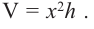
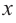
Теперь найдем область определения функции 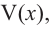
Понятно, что длина не может быть отрицательной, т. е. 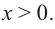
или 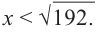
Найдем максимальное значение функции 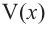
Для этого используем производную первого порядка:
При 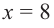
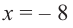
Однако. 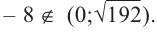
При 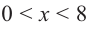
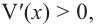
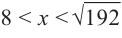
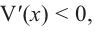
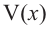
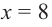
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
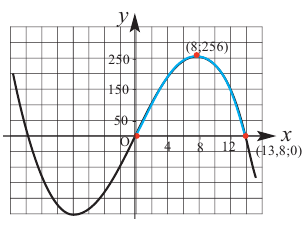
Построив при помощи графкалькулятора график функции 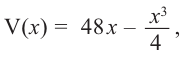
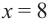
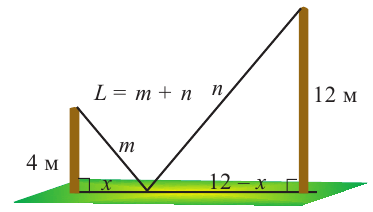
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 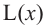
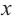
Производная функции
Найдем критические точки функции
Сравнивая значения функции 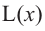
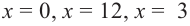
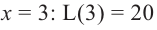
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 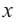
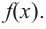
4. Полученные значения объясните экспериментально.
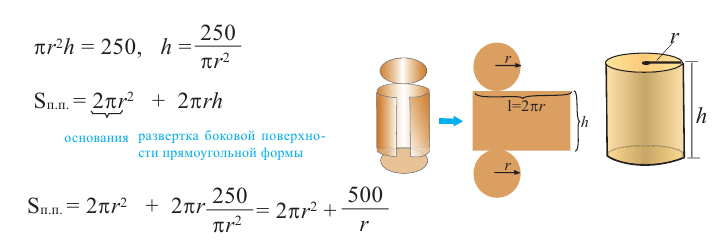
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 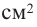
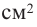
Решение: а) По условию задачи объем равен 250 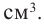
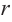
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 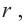
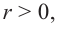
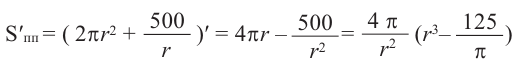
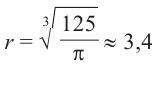
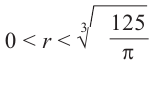
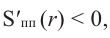
Значит,
Подставим значение 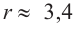
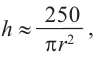
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 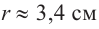
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности


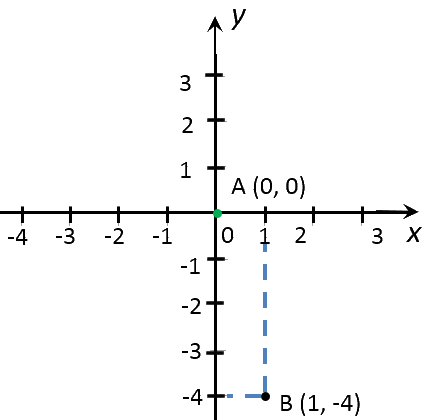
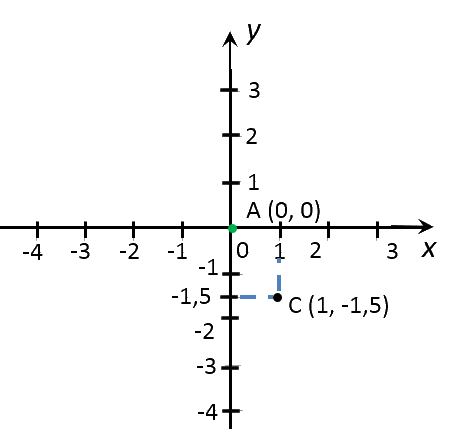
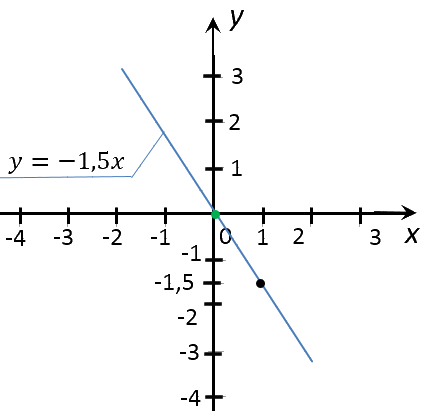

















































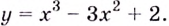
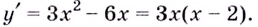
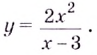
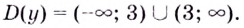
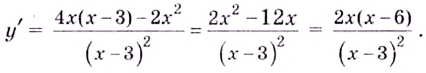
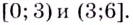
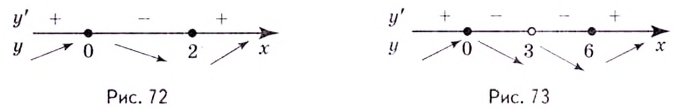
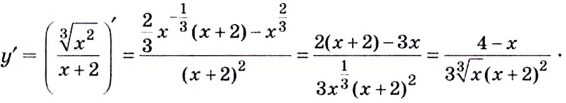
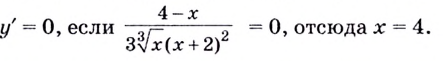
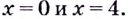
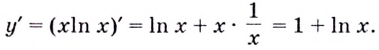
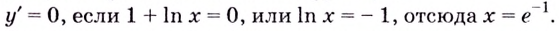
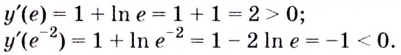
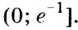
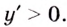
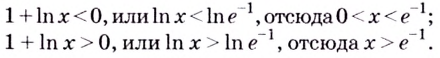
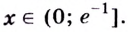
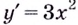
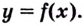
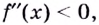 то кривая выпуклая; если
то кривая выпуклая; если 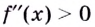 — кривая вогнутая;
— кривая вогнутая;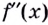 меняет знак при переходе через точку
меняет знак при переходе через точку 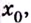 то точка
то точка 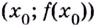 является точкой перегиба кривой
является точкой перегиба кривой 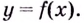
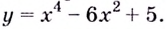
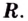
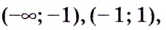
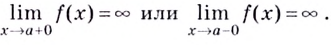
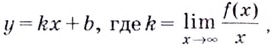
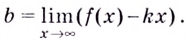
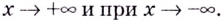
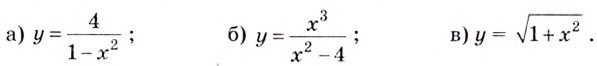
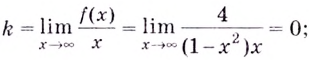
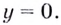
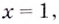
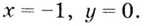
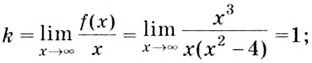
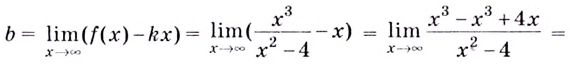
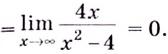
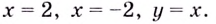
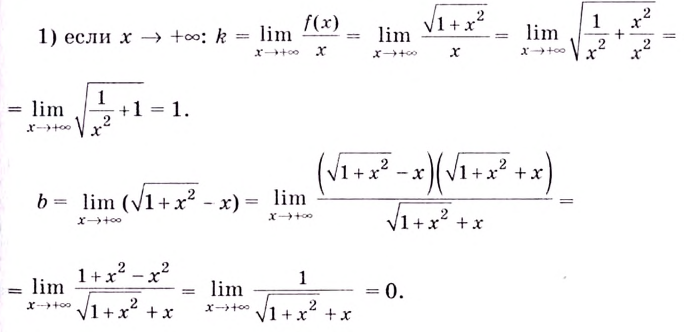
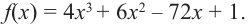

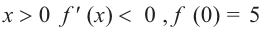
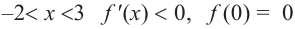
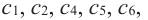
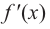 слева от точки
слева от точки 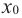 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 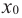 является точкой максимума.
является точкой максимума.