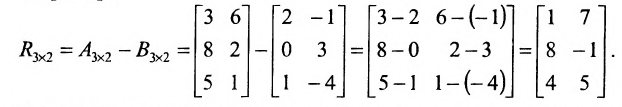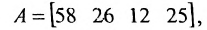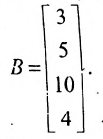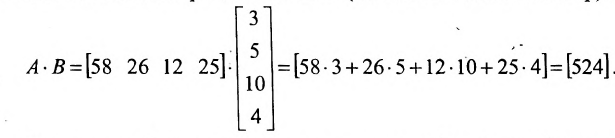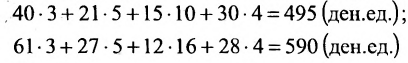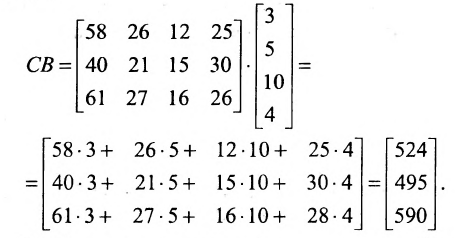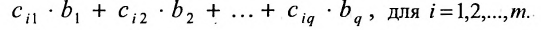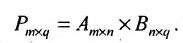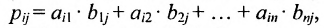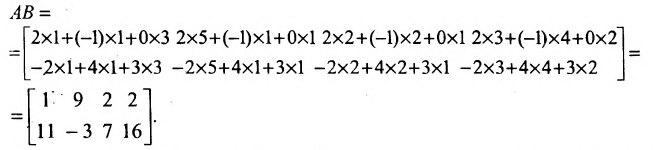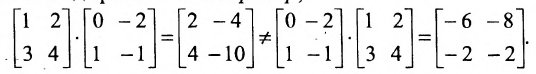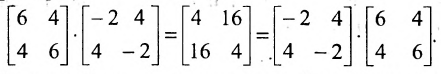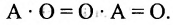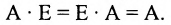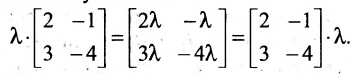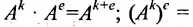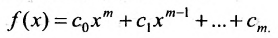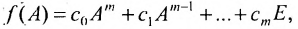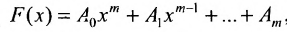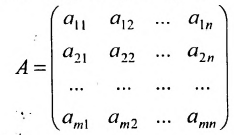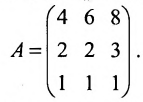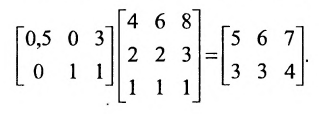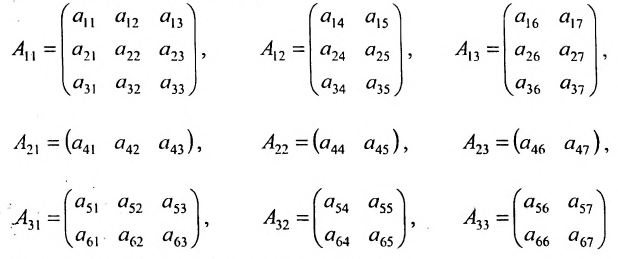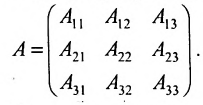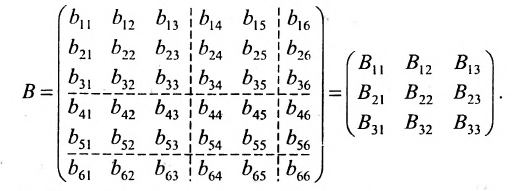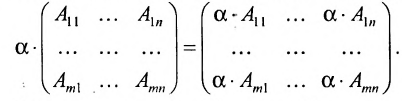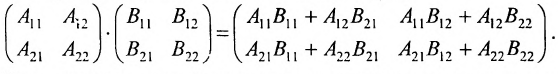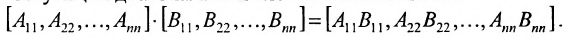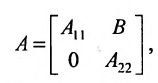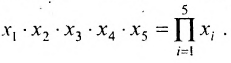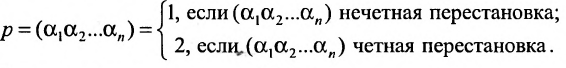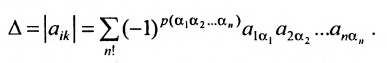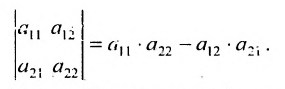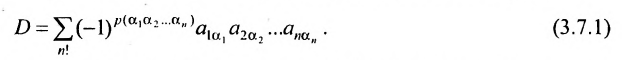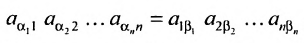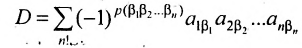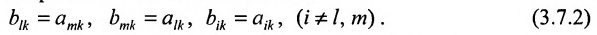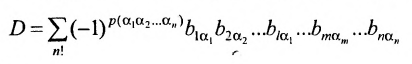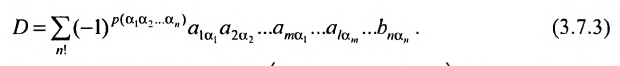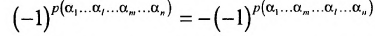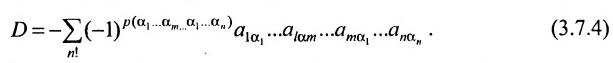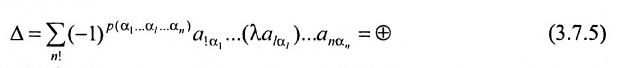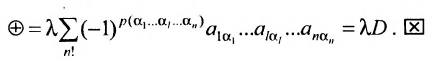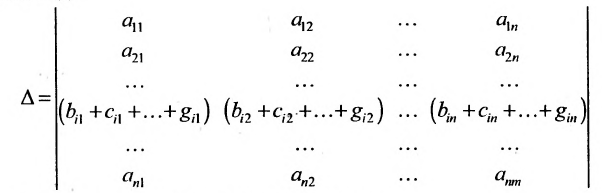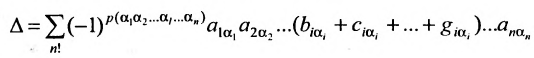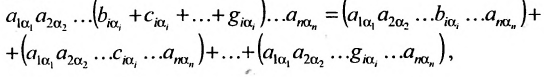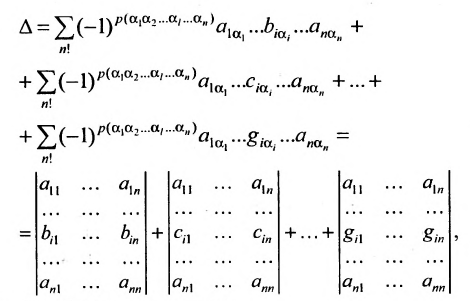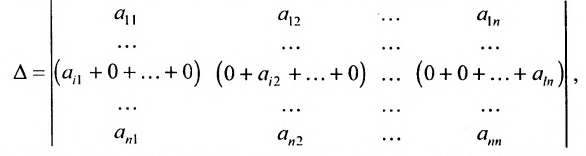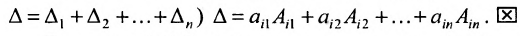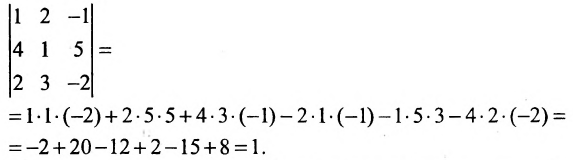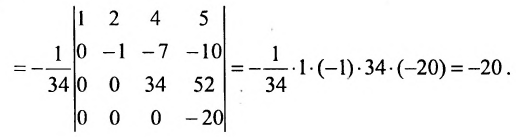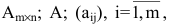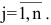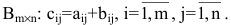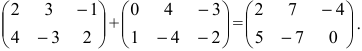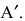Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(15271810)K=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу L=(3516)L=begin{pmatrix}35\16end{pmatrix}.
Матрица KK состоит из 2 строк и 2 столбцов, а матрица LL — из 2 строк и 1 столбца. Число столбцов матрицы KK равно числу строк матрицы LL, значит, матрицу KK можно умножить на матрицу LL.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516)F=begin{pmatrix}35\16end{pmatrix} на матрицу C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix}.
Матрица FF состоит из 2 строк и 1 столбца, а матрица CC — из 2 строк и 2 столбцов. Число столбцов матрицы FF не равно числу строк матрицы CC, значит, матрицу FF нельзя умножить на матрицу CC.
Произведение матрицы AA размера m×nmtimes n и матрицы BB размера n×kntimes k — это матрица CC размера m×kmtimes k, в которой элемент cijc_{ij} равен сумме произведений элементов ii строки матрицы AA на соответствующие элементы jj столбца матрицы B:cij=ai1b1j+ai2b2j+…+ainbnjB: c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}.
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
Рассмотрим пример умножения матрицы
A=(a11a12a21a22a31a32a41a42)A=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}
на матрицу
B=(b11b12b13b21b22b23)B=begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}.
Матрица AA состоит из 4 строк и 2 столбцов, а матрица BB — из 2 строк и 3 столбцов. Число столбцов матрицы AA равно числу строк матрицы BB, значит, можно найти произведение C=A⋅BC=Acdot B. Причем матрица CC будет иметь размер 4×34times 3. Найдем элементы c12c_{12} (выделен красными стрелками) и c33c_{33} (выделен синими стрелками):
Для того чтобы найти элемент c12c_{12} нужно перемножать соответствующие элементы 1 строки матрицы AA и 2 столбца матрицы B:c12=a11⋅b12+a12⋅b22B: c_{12}=a_{11}cdot b_{12}+a_{12}cdot b_{22}. Для того чтобы найти элемент c33c_{33} нужно перемножать соответствующие элементы 3 строки матрицы AA и 3 столбца матрицы BB: c33=a31⋅b13+a32⋅b23c_{33}=a_{31}cdot b_{13}+a_{32}cdot b_{23}. Так находят все элементы.
Таким образом, матрица CC может быть найдена следующим образом:
A⋅B=(a11a12a21a22a31a32a41a42)⋅(b11b12b13b21b22b23)=Acdot B=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}cdot begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}=
=(a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a11⋅b13+a12⋅b23a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22a21⋅b13+a22⋅b23a31⋅b11+a32⋅b21a31⋅b12+a32⋅b22a31⋅b13+a32⋅b23a41⋅b11+a42⋅b21a41⋅b12+a42⋅b22a41⋅b13+a42⋅b23)=begin{pmatrix}a_{11}cdot b_{11}+a_{12}cdot b_{21}&a_{11}cdot b_{12}+a_{12}cdot b_{22}&a_{11}cdot b_{13}+a_{12}cdot b_{23}\a_{21}cdot b_{11}+a_{22}cdot b_{21}&a_{21}cdot b_{12}+a_{22}cdot b_{22}&a_{21}cdot b_{13}+a_{22}cdot b_{23}\a_{31}cdot b_{11}+a_{32}cdot b_{21}&a_{31}cdot b_{12}+a_{32}cdot b_{22}&a_{31}cdot b_{13}+a_{32}cdot b_{23}\a_{41}cdot b_{11}+a_{42}cdot b_{21}&a_{41}cdot b_{12}+a_{42}cdot b_{22}&a_{41}cdot b_{13}+a_{42}cdot b_{23}end{pmatrix}
Произведение B⋅ABcdot A нельзя найти, поскольку число столбцов матрицы BB неравно числу строк матрицы AA.
Найти произведение матрицы C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу F=(3516)F=begin{pmatrix}35\16end{pmatrix}.
Матрица CC имеет размер 2×22times 2, матрица FF имеет размер 2×12times 1, значит, размер матрицы произведения будет 2×12times 1.
C⋅F=(15271810)⋅(3516)=(15⋅35+27⋅1618⋅35+10⋅16)=(957790)Ccdot F=begin{pmatrix}15&27\18&10end{pmatrix}cdot begin{pmatrix}35\16end{pmatrix}=begin{pmatrix}15cdot 35+27cdot 16\18cdot 35+10cdot 16end{pmatrix}=begin{pmatrix}957\790end{pmatrix}.
Как отмечалось выше, произведение матриц F⋅CFcdot C невозможно.
Найти произведение матриц K⋅LKcdot L и L⋅KLcdot K, если K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} на матрицу L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix}.
Матрица KK имеет размер 2×22times 2, матрица LL имеет размер 2×22times 2, значит, размер матрицы произведения будет 2×22times 2.
K⋅L=(12171314)⋅(18111210)=(12⋅18+17⋅1212⋅11+17⋅1013⋅18+14⋅1213⋅11+14⋅10)=(420302402283)Kcdot L=begin{pmatrix}12&17\13&14end{pmatrix}cdot begin{pmatrix}18&11\12&10end{pmatrix}=begin{pmatrix}12cdot 18+17cdot 12&12cdot 11+17cdot 10\13cdot 18+14cdot 12&13cdot 11+14cdot 10end{pmatrix}=begin{pmatrix}420&302\402&283end{pmatrix}
Произведение L⋅KLcdot K существует и его размер — 2×22times 2.
L⋅K=(18111210)⋅(12171314)=(18⋅12+11⋅1318⋅17+11⋅1412⋅12+10⋅1312⋅17+10⋅14)=(359460274344)Lcdot K=begin{pmatrix}18&11\12&10end{pmatrix}cdot begin{pmatrix}12&17\13&14end{pmatrix}=begin{pmatrix}18cdot 12+11cdot 13&18cdot 17+11cdot 14\12cdot 12+10cdot 13&12cdot 17+10cdot 14end{pmatrix}=begin{pmatrix}359&460\274&344end{pmatrix}
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B≠B⋅AAcdot Bneq Bcdot A.
Так, для матриц K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} и L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix} из рассмотренного примера K⋅L≠L⋅KKcdot L neq Lcdot K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅AAcdot B=Bcdot A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы CC и DD, если C=(2342)C=begin{pmatrix}2&3\4&2end{pmatrix}, D=(3343)D=begin{pmatrix}3&3\4&3end{pmatrix}.
Найдем произведения этих матриц C⋅DCcdot D и D⋅CDcdot C.
C⋅D=(2342)⋅(3343)=(2⋅3+3⋅42⋅3+3⋅34⋅3+2⋅44⋅3+2⋅3)=(18152018)Ccdot D=begin{pmatrix}2&3\4&2end{pmatrix}cdot begin{pmatrix}3&3\4&3end{pmatrix}=begin{pmatrix}2cdot 3+3cdot 4&2cdot 3+3cdot 3\4cdot 3+2cdot 4&4cdot 3+2cdot 3end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix},
D⋅C=(3343)⋅(2342)=(3⋅2+3⋅43⋅3+3⋅24⋅2+3⋅44⋅3+3⋅2)=(18152018)Dcdot C=begin{pmatrix}3&3\4&3end{pmatrix}cdot begin{pmatrix}2&3\4&2end{pmatrix}=begin{pmatrix}3cdot 2+3cdot 4&3cdot 3+3cdot 2\4cdot 2+3cdot 4&4cdot 3+3cdot 2end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix}.
Таким образом, для заданных матриц выполняется равенство C⋅DCcdot D и D⋅CDcdot C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы FF и HH, если F=(3421)F=begin{pmatrix}3&4\2&1end{pmatrix}, H=(0593)H=begin{pmatrix}0&5\9&3end{pmatrix}.
Найдем произведения этих матриц F⋅HFcdot H и H⋅FHcdot F.
F⋅H=(3421)⋅(0593)=(3⋅0+4⋅93⋅5+4⋅32⋅0+1⋅92⋅5+1⋅3)=(3627913)Fcdot H=begin{pmatrix}3&4\2&1end{pmatrix}cdot begin{pmatrix}0&5\9&3end{pmatrix}=begin{pmatrix}3cdot 0+4cdot 9&3cdot 5+4cdot 3\2cdot 0+1cdot 9&2cdot 5+1cdot 3end{pmatrix}=begin{pmatrix}36&27\9&13end{pmatrix},
H⋅F=(0593)⋅(3421)=(0⋅3+5⋅20⋅4+5⋅19⋅3+3⋅29⋅4+3⋅1)=(1053339)Hcdot F=begin{pmatrix}0&5\9&3end{pmatrix}cdot begin{pmatrix}3&4\2&1end{pmatrix}=begin{pmatrix}0cdot 3+5cdot 2&0cdot 4+5cdot 1\9cdot 3+3cdot 2&9cdot 4+3cdot 1end{pmatrix}=begin{pmatrix}10&5\33&39end{pmatrix}.
Таким образом, для заданных матриц не выполняется равенство F⋅HFcdot H и H⋅FHcdot F, поэтому они не являются перестановочными.
Контрольные работы на заказ онлайн от практикующих исполнителей!
Умножение матриц
21 мая 2018
- Домашняя работа
- Ответы
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=left[ mtimes n right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Определение. Матрицы вида $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются согласованными.
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
- Нам важен порядок матриц. Например, матрицы $A=left[ 3times 2 right]$ и $B=left[ 2times 5 right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=left[ 2times 5 right]$ и $A=left[ 3times 2 right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
- Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $left[ ntimes n right]$ согласованы всегда.
В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $left( 1;0 right)$ и $left( 0;1 right)$ задают разные точки на плоскости.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $left( A;B right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».
Ну и что с того?
Определение умножения
Рассмотрим две согласованные матрицы: $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$. И определим для них операцию умножения.
Определение. Произведение двух согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой считаются по формуле:
[begin{align} & {{c}_{i;j}}={{a}_{i;1}}cdot {{b}_{1;j}}+{{a}_{i;2}}cdot {{b}_{2;j}}+ldots +{{a}_{i;n}}cdot {{b}_{n;j}}= \ & =sumlimits_{t=1}^{n}{{{a}_{i;t}}cdot {{b}_{t;j}}} end{align}]
Обозначается такое произведение стандартно: $C=Acdot B$.
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
- Что это за лютая дичь?
- А почему так сложно?
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
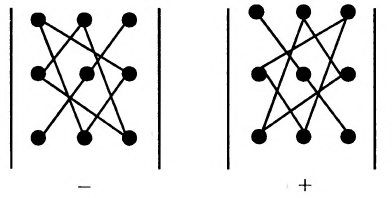
Прежде всего заметим, что длинная строчка для расчёта ${{c}_{i;j}}$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:
- Берём $i$-ю строку в первой матрице;
- Берём $j$-й столбец во второй матрице;
- Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.
Данный процесс легко понять по картинке:
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем ${{c}_{ij}}$. И так для всех $1le ile m$ и $1le jle k$. Т.е. всего будет $mtimes k$ таких «извращений».
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
[begin{align} & vec{a}=left( {{x}_{a}};{{y}_{a}};{{z}_{a}} right); \ & overrightarrow{b}=left( {{x}_{b}};{{y}_{b}};{{z}_{b}} right). \ end{align}]
Тогда их скалярным произведением будет именно сумма попарных произведений:
[overrightarrow{a}times overrightarrow{b}={{x}_{a}}cdot {{x}_{b}}+{{y}_{a}}cdot {{y}_{b}}+{{z}_{a}}cdot {{z}_{b}}]
По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $overrightarrow{a}$ на вектор-столбец $overrightarrow{b}$.
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
Задача 1. Выполните умножение:
[left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]]
Решение. Итак, у нас две матрицы: $A=left[ 2times 2 right]$ и $B=left[ 2times 2 right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:
[begin{align} & left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]=left[ begin{array}{*{35}{r}} 1cdot left( -2 right)+2cdot 3 & 1cdot 4+2cdot 1 \ -3cdot left( -2 right)+4cdot 3 & -3cdot 4+4cdot 1 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 4 & 6 \ 18 & -8 \end{array} right]. end{align}]
Вот и всё!
Ответ: $left[ begin{array}{*{35}{r}}4 & 6 \ 18 & -8 \end{array} right]$.
Задача 2. Выполните умножение:
[left[ begin{matrix} 1 & 3 \ 2 & 6 \end{matrix} right]cdot left[ begin{array}{*{35}{r}}9 & 6 \ -3 & -2 \end{array} right]]
Решение. Опять согласованные матрицы, поэтому выполняем действия:[]
[begin{align} & left[ begin{matrix} 1 & 3 \ 2 & 6 \end{matrix} right]cdot left[ begin{array}{*{35}{r}} 9 & 6 \ -3 & -2 \end{array} right]=left[ begin{array}{*{35}{r}} 1cdot 9+3cdot left( -3 right) & 1cdot 6+3cdot left( -2 right) \ 2cdot 9+6cdot left( -3 right) & 2cdot 6+6cdot left( -2 right) \end{array} right]= \ & =left[ begin{matrix} 0 & 0 \ 0 & 0 \end{matrix} right]. end{align}]
Как видим, получилась матрица, заполненная нулями
Ответ: $left[ begin{matrix} 0 & 0 \ 0 & 0 \end{matrix} right]$.
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
- Некоммутативно: $Acdot Bne Bcdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $Acdot B=Bcdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
- Ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
- Дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$ и $left( A+B right)cdot C=Acdot C+Bcdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
[left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]cdot left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]=left[ begin{array}{*{35}{r}}4 & 6 \ 18 & -8 \end{array} right]]
Но если поменять матрицы местами, то получим совсем другой результат:
[left[ begin{array}{*{35}{r}} -2 & 4 \ 3 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 & 2 \ -3 & 4 \end{array} right]=left[ begin{matrix} -14 & 4 \ 0 & 10 \end{matrix} right]]
Получается, что $Acdot Bne Bcdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $left[ 2times 3 right]$ и $left[ 3times 5 right]$ вполне себе согласованы в указанном порядке, но те же матрицы $left[ 3times 5 right]$ и $left[ 2times 3 right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)
Тем не менее, умножение матриц ассоциативно:
[left( Acdot B right)cdot C=Acdot left( Bcdot C right)]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $left[ ntimes n right]$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=left[ ntimes n right]$ и [Ain {{M}^{n}}] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.
Определение. Единичная матрица размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=left[ ntimes n right]$ выполняется равенство:
[Acdot E=Ecdot A=A]
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
[begin{align} & Acdot left( B+C right)=Acdot B+Acdot C; \ & left( A+B right)cdot C=Acdot C+Bcdot C. \ end{align}]
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
Задача 3. Выполните умножение:
[left[ begin{matrix} begin{matrix} 5 \ 2 \ 3 \end{matrix} & begin{matrix} 4 \ 5 \ 1 \end{matrix} \end{matrix} right]cdot left[ begin{array}{*{35}{r}} -2 & 5 \ 3 & 4 \end{array} right]]
Решение. Имеем две матрицы: $A=left[ 3times 2 right]$ и $B=left[ 2times 2 right]$. Выпишем числа, обозначающие размеры, в ряд:
[3; 2; 2; 2]
Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=left[ 3times 2 right]$:
[begin{align} & left[ begin{matrix} begin{matrix} 5 \ 2 \ 3 \end{matrix} & begin{matrix} 4 \ 5 \ 1 \end{matrix} \end{matrix} right]cdot left[ begin{array}{*{35}{r}} -2 & 5 \ 3 & 4 \end{array} right]=left[ begin{array}{*{35}{r}} 5cdot left( -2 right)+4cdot 3 & 5cdot 5+4cdot 4 \ 2cdot left( -2 right)+5cdot 3 & 2cdot 5+5cdot 4 \ 3cdot left( -2 right)+1cdot 3 & 3cdot 5+1cdot 4 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 41 \ 11 & 30 \ -3 & 19 \end{array} right]. end{align}]
Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=left[ 3times 2 right]$.
Ответ: $left[ begin{array}{*{35}{r}} begin{array}{*{35}{r}} 2 \ 11 \ -3 \end{array} & begin{matrix} 41 \ 30 \ 19 \end{matrix} \end{array} right]$.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
[A=left[ begin{array}{*{35}{r}} begin{matrix} 1 \ 1 \end{matrix} & begin{array}{*{35}{r}} -1 \ 1 \end{array} & begin{matrix} 2 \ 2 \end{matrix} & begin{array}{*{35}{r}} -2 \ 2 \end{array} \end{array} right]]; $B=left[ begin{matrix} begin{matrix} 0 \ 2 \ 0 \ 4 \end{matrix} & begin{matrix} 1 \ 0 \ 3 \ 0 \end{matrix} \end{matrix} right]$; $C=left[ begin{matrix}0 & 1 \ 1 & 0 \end{matrix} right]$.
Решение. Для начала запишем размеры матриц:
[A=left[ 2times 4 right]; B=left[ 4times 2 right]; C=left[ 2times 2 right]]
Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:
[Acdot B=left[ begin{array}{*{35}{r}} 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end{array} right]cdot left[ begin{array}{*{35}{r}} 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end{array} right]=left[ begin{array}{*{35}{r}}-10 & 7 \ 10 & 7 \end{array} right]]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
[A cdot B=left[ 2times 4 right]cdot left[ 4times 2 right]=left[ 2times 2 right]]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
Какие ещё возможны варианты? Безусловно, можно найти $Bcdot A$, поскольку $B=left[ 4times 2 right]$, $A=left[ 2times 4 right]$, поэтому упорядоченная пара $left( B;A right)$ является согласованной, а размерность произведения будет:
[B cdot A=left[ 4times 2 right]cdot left[ 2times 4 right]=left[ 4times 4 right]]
Короче говоря, на выходе будет матрица $left[ 4times 4 right]$, коэффициенты которой легко считаются:
[Bcdot A=left[ begin{array}{*{35}{r}} 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end{array} right]=left[ begin{array}{*{35}{r}}1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end{array} right]]
Очевидно, можно согласовать ещё $Ccdot A$ и $Bcdot C$ — и всё. Поэтому просто запишем полученные произведения:
[Ccdot A=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end{array} right]]
[Bcdot C=left[ begin{array}{*{35}{r}}1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end{array} right]]
Это было легко.:)
Ответ: $AB=left[ begin{array}{*{35}{r}} -10 & 7 \ 10 & 7 \end{array} right]$; $BA=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end{array} right]$; $CA=left[ begin{array}{*{35}{r}} 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end{array} right]$; $BC=left[ begin{array}{*{35}{r}}1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end{array} right]$.
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Определение. Вектор-столбец — это матрица размера $left[ mtimes 1 right]$, т.е. состоящая из нескольких строк и только одного столбца.
Вектор-строка — это матрица размера $left[ 1times n right]$, т.е. состоящая из одной строки и нескольких столбцов.
На самом деле мы уже встречались с этими объектами. Например, обычный трёхмерный вектор из стереометрии $overrightarrow{a}=left( x;y;z right)$ — это не что иное как вектор-строка. С точки зрения теории разницы между строками и столбцами почти нет. Внимательными надо быть разве что при согласовании с окружающими матрицами-множителями.
Задача 5. Выполните умножение:
[left[ begin{array}{*{35}{r}} 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 \ 2 \ -1 \end{array} right]]
Решение. Перед нами произведение согласованных матриц: $left[ 3times 3 right]cdot left[ 3times 1 right]=left[ 3times 1 right]$. Найдём это произведение:
[left[ begin{array}{*{35}{r}} 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end{array} right]cdot left[ begin{array}{*{35}{r}} 1 \ 2 \ -1 \end{array} right]=left[ begin{array}{*{35}{r}} 2cdot 1+left( -1 right)cdot 2+3cdot left( -1 right) \ 4cdot 1+2cdot 2+0cdot 2 \ -1cdot 1+1cdot 2+1cdot left( -1 right) \end{array} right]=left[ begin{array}{*{35}{r}} -3 \ 8 \ 0 \end{array} right]]
Ответ: $left[ begin{array}{*{35}{r}}-3 \ 8 \ 0 \end{array} right]$.
Задача 6. Выполните умножение:
[left[ begin{array}{*{35}{r}} 1 & 2 & -3 \end{array} right]cdot left[ begin{array}{*{35}{r}} 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end{array} right]]
Решение. Опять всё согласовано: $left[ 1times 3 right]cdot left[ 3times 3 right]=left[ 1times 3 right]$. Считаем произведение:
[left[ begin{array}{*{35}{r}} 1 & 2 & -3 \end{array} right]cdot left[ begin{array}{*{35}{r}} 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end{array} right]=left[ begin{array}{*{35}{r}}5 & -19 & 5 \end{array} right]]
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Ответ: $left[ begin{matrix} 5 & -19 & 5 \end{matrix} right]$.
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
[Acdot A=left[ ntimes n right]cdot left[ ntimes n right]=left[ ntimes n right]]
И обозначаются точно так же, как и обычные степени:
[begin{align} & Acdot A={{A}^{2}}; \ & Acdot Acdot A={{A}^{3}}; \ & underbrace{Acdot Acdot ldots cdot A}_{n}={{A}^{n}}. \ end{align}]
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
${{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}$
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{2}}=left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1cdot 1+1cdot 0 & 1cdot 1+1cdot 1 \ 0cdot 1+1cdot 0 & 0cdot 1+1cdot 1 \end{array} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 2 \ 0 & 1 \end{array} right] end{align}]
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}={{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 2 \ 0 & 1 \end{array} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 1 & 3 \ 0 & 1 \end{array} right] end{align}]
Вот и всё.:)
Ответ: $left[ begin{matrix}1 & 3 \ 0 & 1 \end{matrix} right]$.
Задача 8. Возведите матрицу в указанную степень:
[{{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{10}}]
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
[begin{align} & {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{10}}={{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot {{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{3}}cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]= \ & =left( left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right] right)cdot left( left[ begin{matrix} 1 & 3 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right] right)= \ & =left[ begin{matrix} 1 & 6 \ 0 & 1 \end{matrix} right]cdot left[ begin{matrix} 1 & 4 \ 0 & 1 \end{matrix} right]= \ & =left[ begin{matrix} 1 & 10 \ 0 & 1 \end{matrix} right] end{align}]
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Ответ: $left[ begin{matrix} 1 & 10 \ 0 & 1 \end{matrix} right]$.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
[{{left[ begin{matrix} 1 & 1 \ 0 & 1 \end{matrix} right]}^{n}}=left[ begin{array}{*{35}{r}} 1 & n \ 0 & 1 \end{array} right]]
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $left[ 3times 3 right]$.
Задача 9. Возведите матрицу в указанную степень:
[{{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}]
Решение. Не будем искать закономерности. Работаем «напролом»:
[{{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}={{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{2}}cdot left[ begin{matrix}0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]]
Для начала возведём эту матрицу в квадрат:
[begin{align} & {{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{2}}=left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]cdot left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end{array} right] end{align}]
Теперь возведём в куб:
[begin{align} & {{left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]}^{3}}=left[ begin{array}{*{35}{r}} 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end{array} right]cdot left[ begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right]= \ & =left[ begin{array}{*{35}{r}} 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end{array} right] end{align}]
Вот и всё. Задача решена.
Ответ: $left[ begin{matrix} 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end{matrix} right]$.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Смотрите также:
- Определитель
- Обратная матрица
- Тест к уроку «Что такое логарифм» (средний)
- Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
- Координаты вершин правильного тетраэдра
- Нестандартная задача B5 на площадь круга
Содержание:
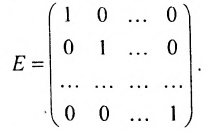
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде
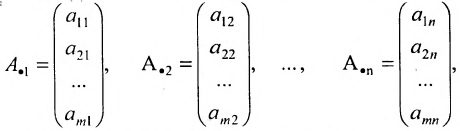
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 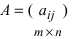
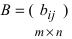
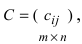
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 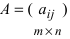
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 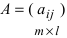
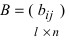
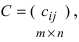
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 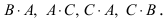
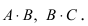
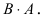
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
Определение: Обратной матрицей к исходной квадратной матрице 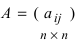
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 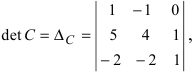
Вычислим алгебраические дополнения всех элементов определителя: 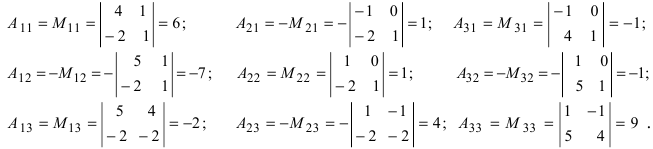
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 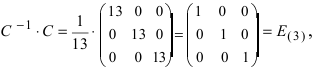
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 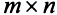
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 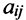
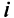
Например, матрица
или, в сокращенной записи,
Например, 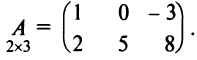
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 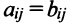
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 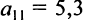
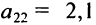
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 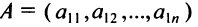
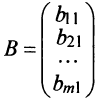
Матрица называется квадратной 
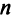
Например, 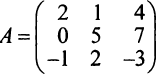
Элементы матрицы 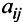
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
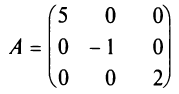
Если у диагональной матрицы 

Например,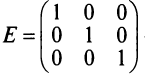
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 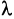
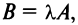
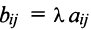
Например, если 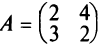
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
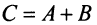
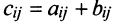
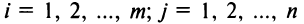
Например,
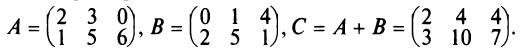
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
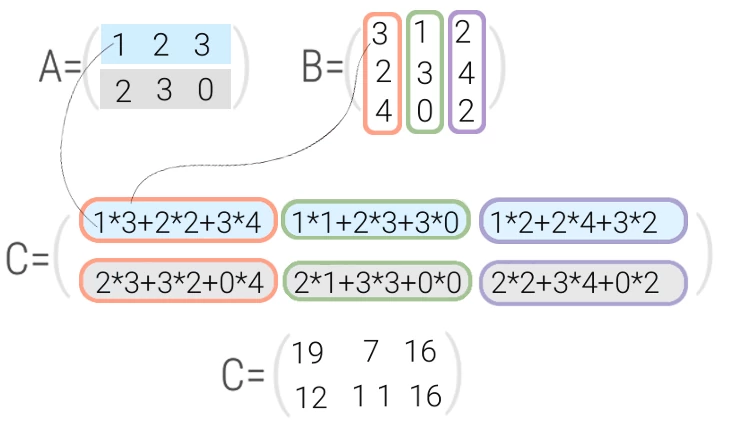
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй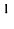
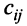

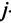
Пример №1
Вычислить произведение матриц 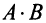
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 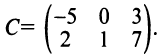
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
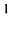
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 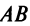
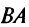
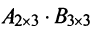
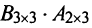
б)Если даже произведения 

Пример №2
Найти произведения матриц 

Решение:
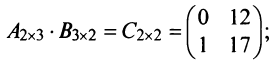
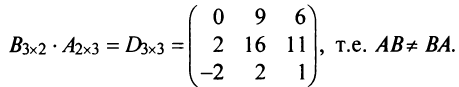


Пример №3
Найти произведения матриц 

Решение:
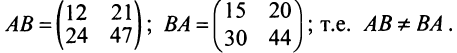
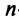
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 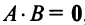
Возведение в степень
Целой положительной степенью 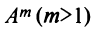
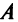
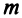

Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 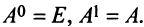
Пример №4
Найти 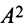
Решение:
Обращаем внимание на то, что из равенства 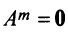
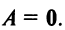
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 



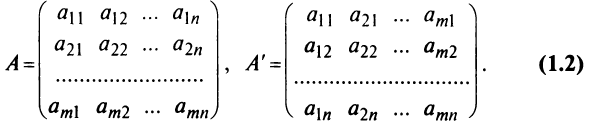

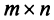

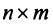
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 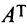
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 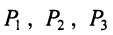
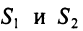
где каждый элемент 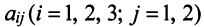
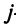
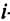
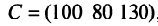
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 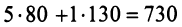
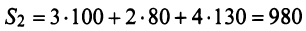
Тогда общая стоимость сырья 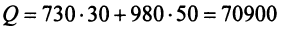
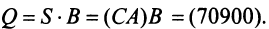
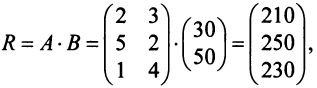
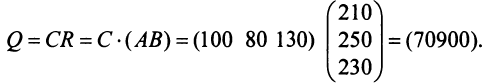
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 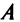
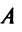
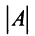
Определителем матрицы первого порядка 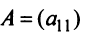
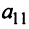
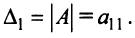
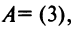
Определителем матрицы второго порядка 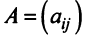
Произведения а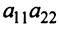
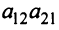
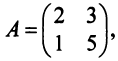
Пусть дана квадратная матрица третьего порядка: 
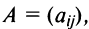
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
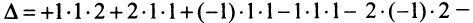
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 
Из общего числа 
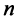
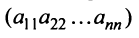
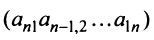
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 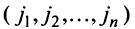
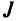
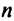

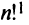
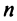
Введем понятие беспорядка, или инверсии, в перестановке 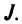
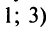
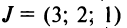
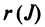
Возвращаясь к наборам (1.5) из элементов матрицы 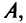
и число 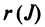
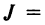
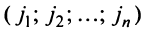
Определение. Определителем квадратной матрицы 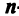
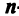
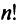
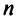
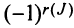
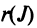
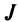
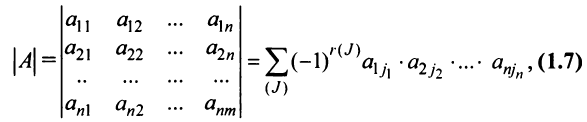
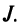
то же число, что и по формуле (1.4).
Заметим, что с ростом 
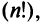
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
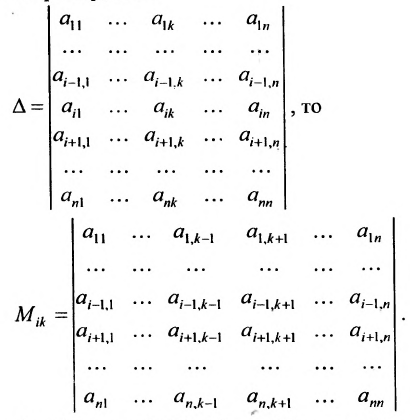
Пусть дана квадратная матрица 

Минором 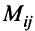
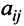

определитель матрицы 

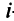
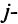
Например, минором элемента 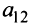

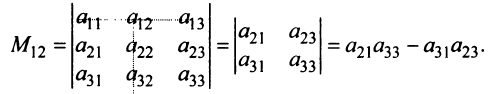

Алгебраическим дополнением 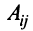
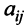

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца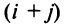
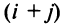
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
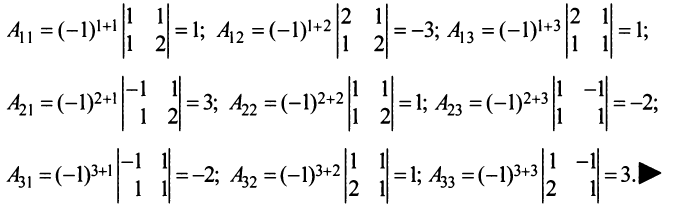
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
(разложение по элементам 

После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы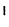
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 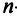
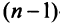
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 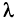

Пусть определитель исходной матрицы равен 

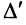
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 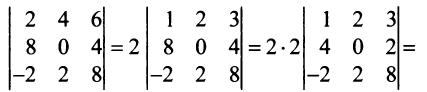
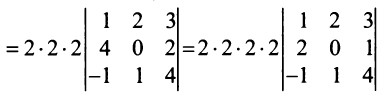
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: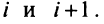


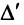
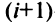
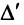
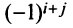
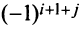
Если переставить не соседние строки, а, скажем, 
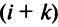

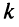
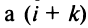
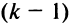
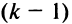
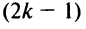
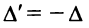
Доказательство для столбцов аналогично.
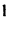
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.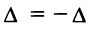
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 
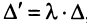

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 
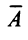



т.е. матрица 

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
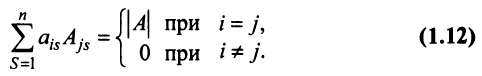
Пусть для определенности к элементам 


где 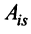

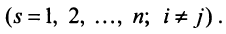
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 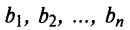
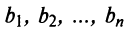
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 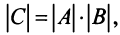
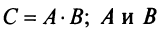
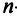
Замечание. Из свойства 10 следует, что даже если 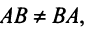
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
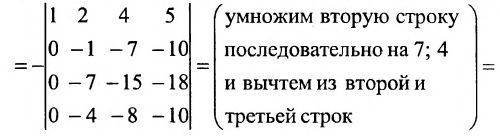
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа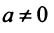
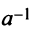
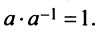
Определение. Матрица 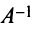

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 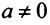
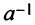

Если определитель матрицы отличен от нуля 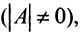
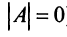
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 

Достаточность. Пусть 


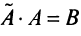
Аналогично доказывается, что произведение 
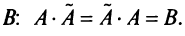
то произведения 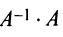
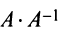
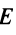
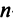
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 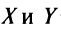
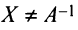
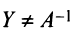

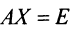
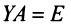

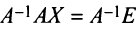
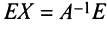
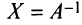

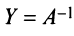
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы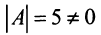


2°. Находим матрицу 

3°. Находим алгебраические дополнения элементов матрицы 
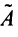
4° . Вычисляем обратную матрицу
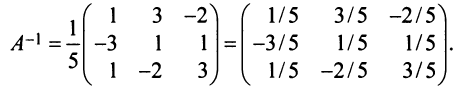
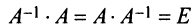
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
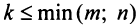
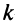

Например, из матрицы 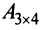
Определение. Рангом матрицы 
Ранг матрицы 
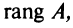
Из определения следует: а) ранг матрицы 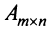
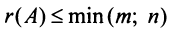
б) 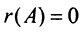
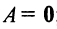
в) для квадратной матрицы 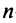
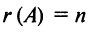

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
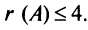
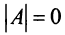

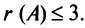
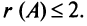
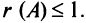

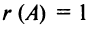
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 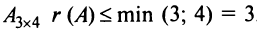
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,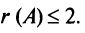
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
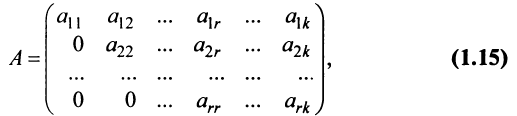
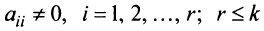
Замечание. Условие 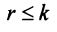
Очевидно, что ранг ступенчатой матрицы равен 
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 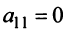
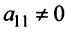
2°. Если 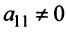
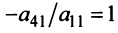
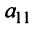
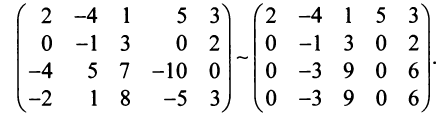
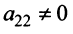
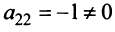
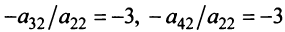
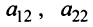
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
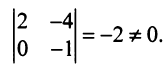
Для рангов матриц справедливы следующие соотношения:
5)

6) 
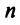


Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.


Две строки матрицы называются равными, если равны их соответствующие элементы: 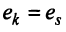
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 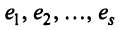
где 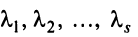
Строки матрицы 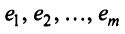
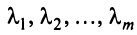
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

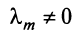
где
Таким образом, строка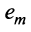
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 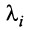
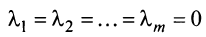
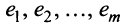
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


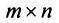
Это означает, что существует отличный от нуля минор 

Тогда строки матрицы 
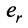
Вычтем из элементов 
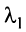
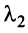
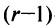
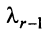


Строки 
Покажем, что любые 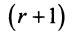
Рассмотрим минор 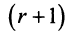
при дополнении рассматриваемого минора элементами еще одной строки 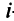
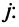
Этот минор равен нулю, так как ранг матрицы равен 
Раскладывая его по элементам последнего (добавленного) столбца, получаем 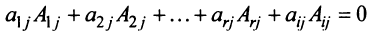
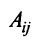

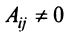
Разделив последнее равенство на 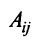
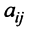
где
Фиксируем значение 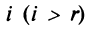
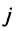
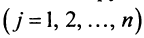
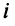
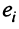

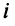
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
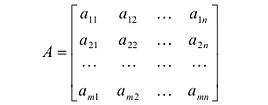
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 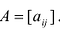
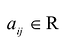
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 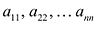
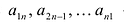
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 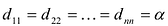
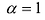
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 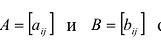
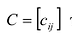
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 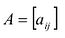
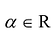
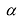
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 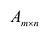
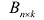
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 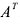
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 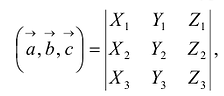
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 
Минором 

Пример №14
Найти минор 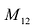
По определению, минор 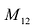
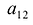
Алгебраическим дополнением элемента 
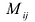
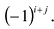

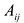
Пример №15
Найти алгебраическое дополнение элемента 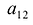
Определителем квадратной матрицы А n-го порядка 
где аи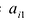
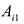
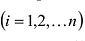
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 
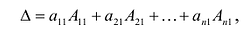
где 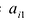
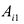
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
Умножим элементы i-той строки на 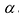
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 
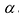
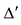


Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 


Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 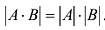
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 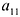
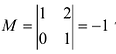
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 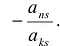
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 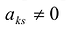
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 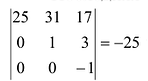
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 
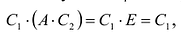
Откуда 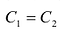

Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 
Пусть А имеет обратную матрицу. Тогда 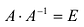
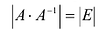
Следовательно, 
Пусть 

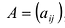
здесь 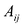
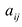
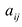
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 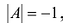

Матрицу 
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 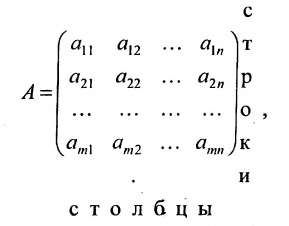
Числа 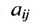
Матрицы удобно обозначать в виде 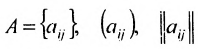
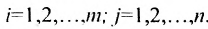
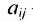
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
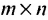
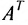
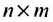
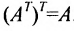
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 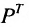
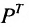
Если, элементы 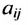
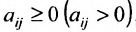
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом
Если в диагональной матрице
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 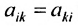
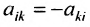
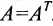
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 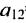
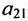
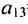
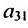
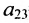
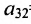
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 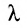
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 
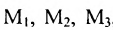
где 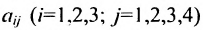
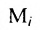
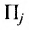
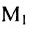
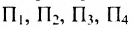
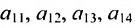
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 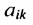
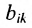
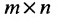
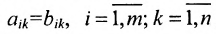
Определение 3.2.1. Суммой матриц А а В размерности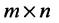
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 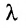
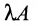
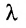
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 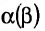
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 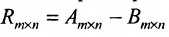
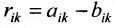
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
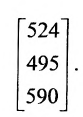
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 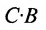
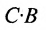
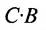
Аналогичным образом определяется произведение матрицы-строки 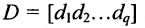
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 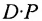
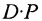
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =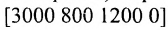
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 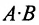
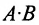
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 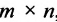
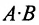
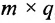
Определение 3.2.4. Произведением матрицы А размерности 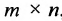
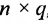
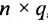
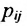
, при 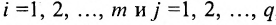
- Заказать решение задач по высшей математике
Пример №22
Пусть 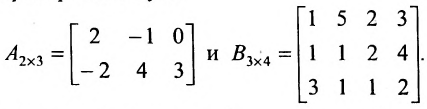
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 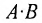
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 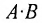
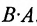
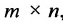
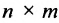
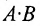
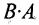
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 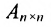
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 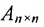
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 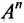
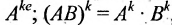
Значением многочлена
с числовыми коэффициентами 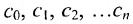
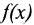
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 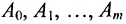
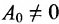
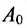
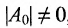
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 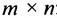
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
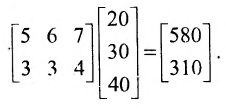
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
Пример №24
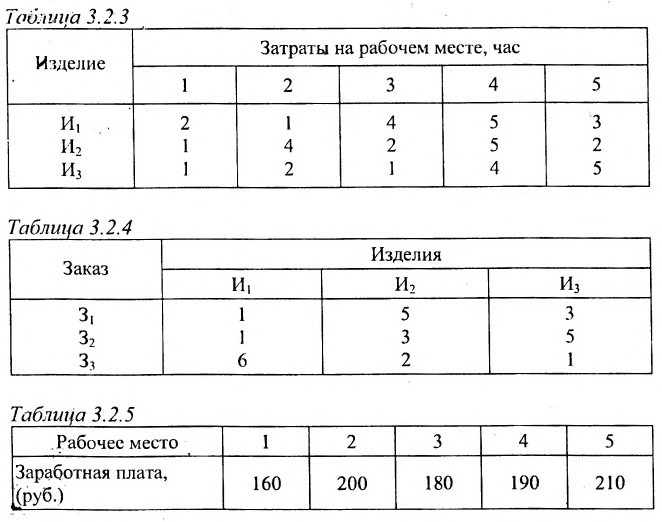
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
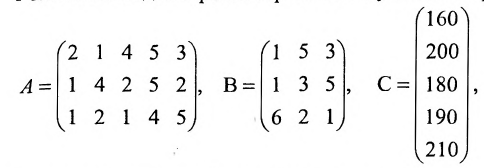
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

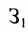
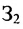
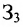
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 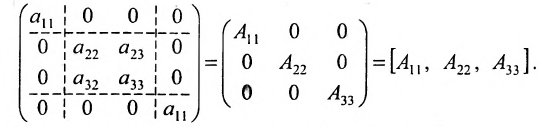
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 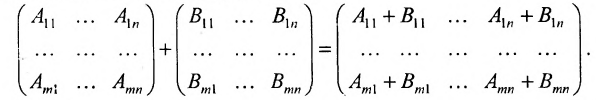
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 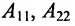
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или
суммирования служит заглавная греческая буква 
например, сумму 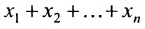
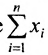
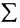
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 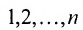
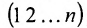
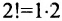
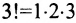
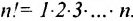
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 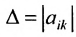
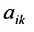
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 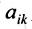
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 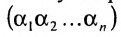
В частности, определителем второго порядка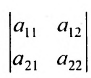
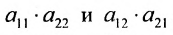
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
Доказательство. Рассмотрим определитель 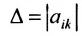
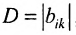
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 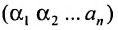
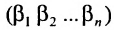
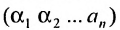
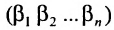
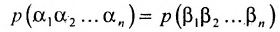
Так как 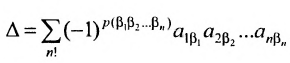
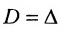
Из свойства 
Доказательство. Рассмотрим определитель 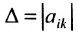
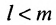
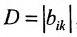

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 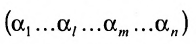
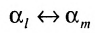
Затем поменяем местами сомножители 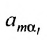
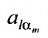
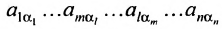
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 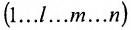
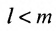
вторых индексов такая же, как и в выражении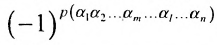
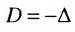
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 
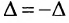
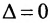
Доказательство. Пусть в определителе 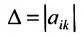
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 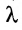
Из свойства 
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 
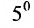
Доказательство. Пусть все элементы 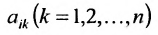

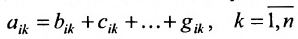
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
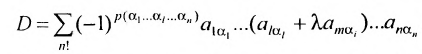
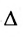
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 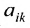

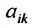
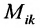
Определение 3.8.1. Минор 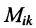
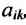
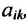

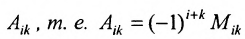
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 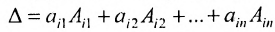
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 
Определитель 
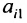
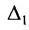

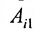
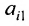
Следовательно,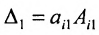
Аналогично 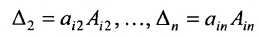
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
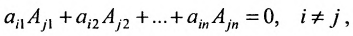
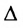
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 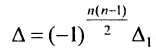
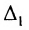
3) Если определитель 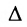
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
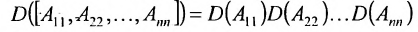
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
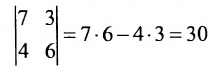
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 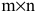
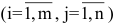
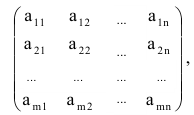
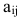
Например, элемент 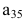
Суммой двух матриц одинакового размера 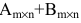
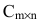
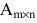
Например,
Произведением матрицы 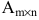
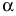
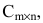
Например,
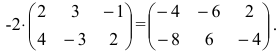
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 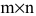
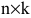
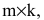
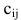
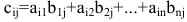
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Произведение матриц
Для того, чтобы найти произведение матриц нужно строки левой матрицы умножить на столбцы правой матрицы. $$begin{pmatrix} a_{11}&a_{12}&a_{13} \ *&*&* \ *&*&* end{pmatrix} times begin{pmatrix} b_{11}&*&* \ b_{21}&*&* \ b_{31}&*&* end{pmatrix} = begin{pmatrix} c_{11}&*&* \ *&*&* \ *&*&* end{pmatrix}$$
Умножение строки на столбец производим по правилу скалярного произведения. То есть находим сумму произведений соответствующих элементов. Например, при умножении первой строки на первый столбец получаем $$c_{11}=a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}.$$
Обязательно перед умножением матриц необходимо убедиться, чтобы число столбцов левой матрицы совпадало с числом строк правой матрицы. Только в этом случае матрицы можно перемножать. В результате получается матрица, у которой число строк равняется количеству строк левой матрицы, а количество столбцов равно числу столбцов правой матрицы. $$ underbrace{A}_{n times p} times underbrace{B}_{p times m} = underbrace{C}_{ntimes m}$$
Важное замечание!
Умножение матриц не коммутативно, т.е. $AB neq BA$.
| Пример 1 |
| Найти произведение матриц $Atimes B$ $$A=begin{pmatrix} 2&1 \ -3&4 end{pmatrix}, B = begin{pmatrix} 1&-3 \ 2&0 end{pmatrix}.$$ |
| Решение |
|
Проверяем, что число столбцов матрицы $A$ равно числу строк матрицы $B$. Далее берем первую строчку левой матрицы и умножаем её на первый столбец второй матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} 2cdot1+1cdot2 &* \*&* end{pmatrix} = begin{pmatrix} 4&* \*&* end{pmatrix}$$ Теперь умножаем первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&2cdot(-3)+1cdot0 \*&* end{pmatrix}=begin{pmatrix} *&-6 \*&* end{pmatrix}$$ Далее вторую строчку левой матрицы и умножаем на первый столбец второй матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} *&* \(-3)cdot1+4cdot2&* end{pmatrix}=begin{pmatrix} *&* \5&* end{pmatrix}$$ И осталось умножить первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&* \ *&(-3)cdot(-3)+4cdot0 end{pmatrix}=begin{pmatrix} *&* \*&9 end{pmatrix}$$ Вот теперь можно составить полный ответ. $$Atimes B=begin{pmatrix} 2&1 \ -3&4 end{pmatrix} times begin{pmatrix} 1&-3 \ 2&0 end{pmatrix} = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A times B = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ |
| Пример 2 |
| Умножить матрицы $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix}.$$ |
| Решение |
|
Убеждаемся, что число столбцов матрицы $A$ равно количеству строк матрицы $B$ для того, чтобы можно было выполнить умножение. Так как количество строк в $A$ равно двум, а количество столбцов в $B$ равно 2, то в результате должна получиться матрица с размерностью два на два. $$A times B = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} *&* \ *&* end{pmatrix}$$ Умножаем первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1&* \ *&* end{pmatrix} = begin{pmatrix} 8&* \*&* end{pmatrix}$$ Умножим первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2) \ *&* end{pmatrix} = begin{pmatrix} 8&-3 \*&* end{pmatrix}$$ Аналогично поступаем теперь со второй строкой левой матрицы. Умножаем её на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1cdot1+(-1)cdot2+2cdot1&* end{pmatrix} = begin{pmatrix} 8&-3 \1&* end{pmatrix}$$ Умножим вторую строку левой матрицы на второй столбец правой матрицы.$$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2) end{pmatrix} = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ Вот таким образом можно перемножить матрицы разной размерности. |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ |
| Пример 3 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
|
Умножаем первую строку левой матрицы на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1 &*&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&*&* \ *&*&* \ *&*&* end{pmatrix}$$ Перемножим первую строку матрицы $A$ со вторым столбцом матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2)&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&* \ *&*&* \ *&*&* end{pmatrix}$$ Найдем произведение первой строки матрицы $A$ на третий столбец матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&2cdot2+3cdot(-2)+0cdot4 \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ *&*&* \ *&*&* end{pmatrix}$$ Возьмем вторую строку левой матрицы и умножим на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \(-1)cdot1+2cdot2+3cdot1&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&*&* \ *&*&* end{pmatrix}$$ Аналогично умножим вторую строчку на второй столбец. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&(-1)cdot0+2cdot(-1)+3cdot(-2)&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&* \ *&*&* end{pmatrix}$$ Таким же образом перемножим вторую строчку с третьим столбцом. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&(-1)cdot2+2cdot(-2)+3cdot4 \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ *&*&* end{pmatrix}$$ Аналогично поступаем с третьей строкой левой матрицы, умножая её на три столбца правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1cdot1+(-1)cdot2+2cdot1&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&*&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2)&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&1cdot2+(-1)cdot(-2)+2cdot4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Пример 4 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
| Количество столбцов в матрице $A$ равно трём и не совпадает с числом строк в матрице $B$, поэтому нельзя выполнить произведение $A times B$, но вот наоборот произведение $B times A$ можно сделать, так как количество столбцов в матрице $B$ равно количеству строк в $A$. Но так как в условии требуется вариант $Atimes B$, то ответ прост: нельзя выполнить умножение. |
| Ответ |
| Матрицы нельзя перемножить |
Математические операции с матрицами
Матрица представляет собой двумерный массив чисел и является базовой единицей для формирования тензоров. А так как тензоры можно смело назвать пищей для нейронных сетей, то для приготовления этих самых тензоров, специалисту по работе с большими данными нужно уметь совершать простейшие манипуляции с матрицами. Поэтому предлагаю «прокачать скилы» и подробно рассмотреть возможные математические операции с матрицами.
Однако, прежде взглянем на матрицу и договоримся называть строками горизонтальные группы чисел, а столбцами — вертикальные:
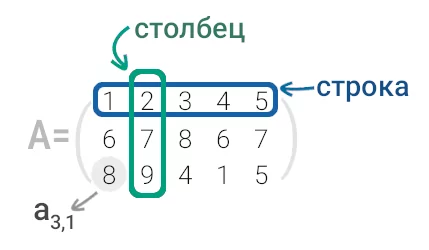
Размером матрицы будем называть упорядоченную пару чисел, таких как: (число рядов матрицы, число столбцов матрицы). Таким образом, размер приведенной выше матрицы равен (3, 5).
Числа, из которых состоит матрица, будем именовать элементами матрицы. Элемент матрицы A, расположенный в i-м ряду и j-м столбце будем называть aij — элементом матрицы А. Например, в приведенной выше матрице, элемент, расположенный в 3-м ряду и 1-м столбце равен 8, то есть а3,1 = 8.
Для более удобной навигации, на все разделы статьи приведены ссылки ниже. После описания каждой математической операции в статье приведен простой вариант аналогичного вычисления в Python
- Умножение матрицы на число
- Транспонирование матрицы
- Cложение матриц
- Вычитание матриц
- Умножение матриц
1. Умножение матрицы на число
Здесь все просто: при умножении матрицы на число, каждый элемент этой матрицы умножается на заданное число. Например:
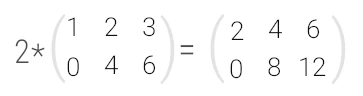
Как умножить матрицу на число в Python?
Для этого нам необходимо импортировать библиотеку numpy и воспользоваться функцией dot():
import numpy as np a = np.array([[1,2,3],[0,4,6]]) b = 2 result = np.dot(b, a) print(result)
Результат работы кода: [[ 3 6 9] [ 0 12 18]]
2. Транспонирование матрицы
Транспонировать матрицу — это значит превратить столбцы этой матрицы в строки. Для наглядности рассмотрим пример: транспонируем матрицу A:
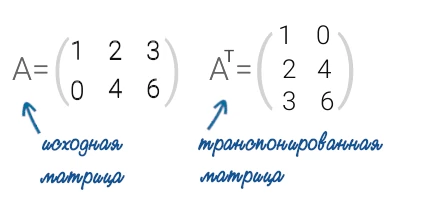
Обратите внимание, что при транспонировании меняется размер матрицы. На приведенном выше изображении, размер исходной матрицы (2, 3), а размер транспонированной — (3, 2).
Как транспонировать матрицу в Python?
import numpy as np a = np.array([[1,2,3],[0,4,6]]) print(a.T)
Результат работы кода: [[1 0] [2 4] [3 6]]
3. Cложение матриц
Какие матрицы можно складывать?
Складывать можно только матрицы с одинаковыми размерами!
Как посчитать сумму матриц с одинаковым размером?
При суммировании матриц А и Б, получим матрицу С, элементы которой равны сумме элементов матриц А и Б, расположенных в соответствующих позициях. То есть c1,1 = a1,1+b1,1, c1,2 = a1,2+b1,2, c2,1 = a2,1+b2,1, и так далее. Рассмотрим на примере:
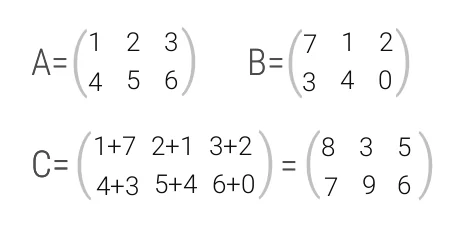
Как сложить матрицы в Python?
import numpy as np a = np.array([[1,2,3],[4,5,6]]) b = np.array([[7,1,2],[3,4,0]]) result = a + b print(result)
Полученный результат: [[8 3 5] [7 9 6]]
4. Вычитание матриц
Какие матрицы можно вычитать?
Вычитать можно только матрицы с одинаковыми размерами!
Как посчитать разность матриц с одинаковым размером?
При вычислении разности двух матриц A и B, получим матрицу C, элементы которой равны разностям элементов матриц А и Б, расположенных в соответствующих позициях. То есть c1,1 = a1,1 — b1,1, c1,2 = a1,2 — b1,2, c2,1 = a2,1 — b2,1 и так далее. Рассмотрим на примере:

Как вычитать матрицы в Python?
import numpy as np a = np.array([[1,2,3],[4,5,6]]) b = np.array([[7,1,2],[3,4,0]]) result = a - b print(result)
Результат работы кода: [[-6 1 1] [ 1 1 6]]
5. Умножение матриц
Какие матрицы можно умножать?
Чтобы умножить две матрицы, необходимо, чтобы число столбцов первой матрицы было равно числу строк второй матрицы.
Например, на приведенном ниже изображении представлены 4 матрицы: D, E, F, G:
Перечислим все возможные произведения этих матриц:
D * G — произведение существует, так как число столбцов матрицы D равно числу строк матрицы G
E * G — число столбцов матрицы E = 3, число строк матрицы G=3
F * D — число столбцов матрицы F = 2, число строк матрицы D=2
F * E — число столбцов матрицы F = 2, число строк матрицы E=2
Нельзя умножать: D * E, D * F, E * D, E * F, F * G, G * D, G * E
Правило умножения матриц:
Рассмотрим на примере умножения матриц A и B, представленных на изображении:
Произведение матриц A*B обозначим, как матрицу С. Тогда сij элементы полученной матрицы С, вычисляются как:
с11 = a11*b11 + a12*b21 + a13*b31
c12 = a11*b12 + a12*b22 + a13*b32
То есть для вычисления cij нужно взять i-ю строку первой матрицы А, поэлементно умножить ее на j-й столбец матрицы B, и полученные произведения сложить.
Как перемножить матрицы в Python?
Для вычисления скалярного произведения матриц можно воспользоваться функцией dot():
import numpy as np a = np.array([[1,2,3],[2,3,0]]) b = np.array([[3,1,2],[2,3,4],[4,0,2]]) result = np.dot(a,b) print(result)
Полученный результат: [[19 7 16] [12 11 16]]

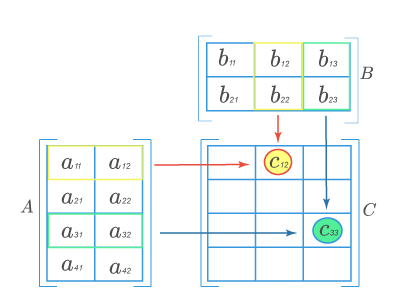
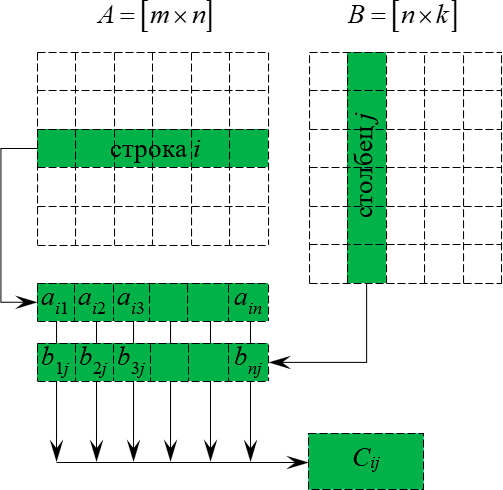

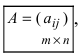
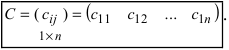
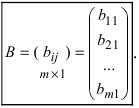
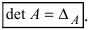


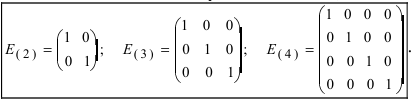
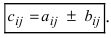
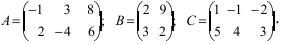
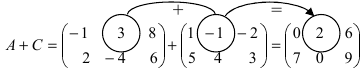
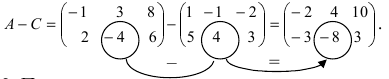

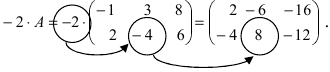
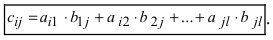
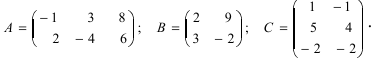
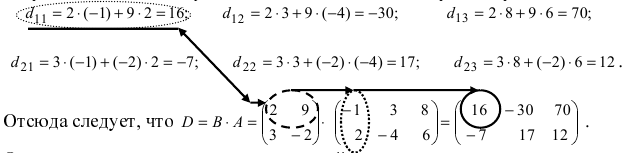
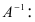
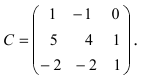
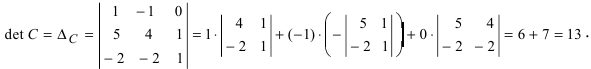
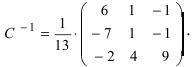
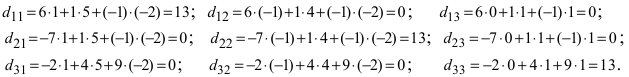
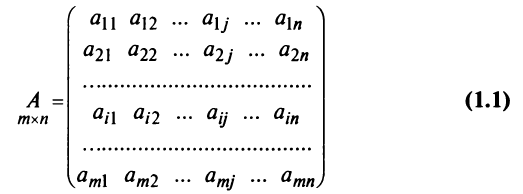
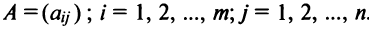
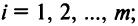
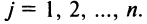

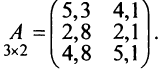
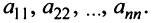

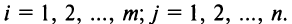
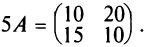
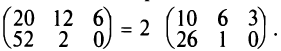
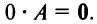
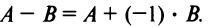
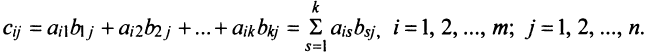
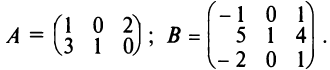
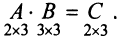
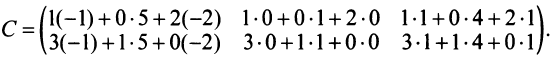
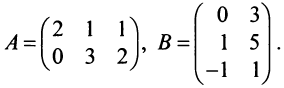
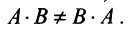
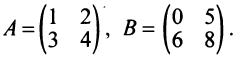
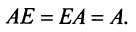
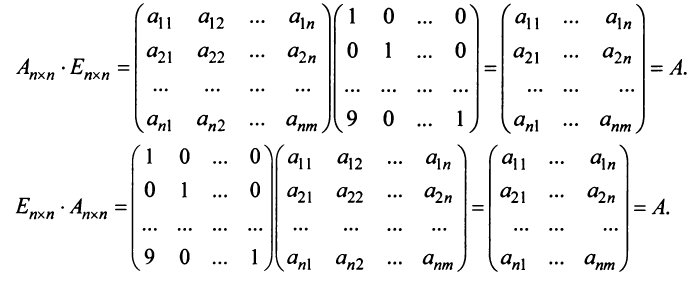
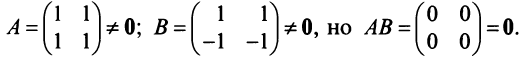
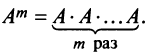
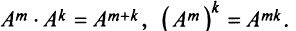
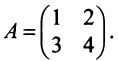
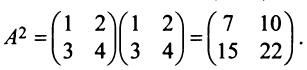
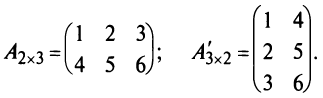

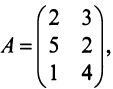
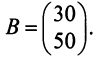
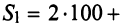
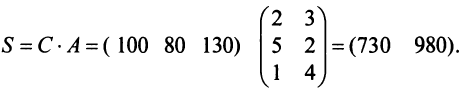

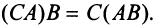

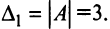
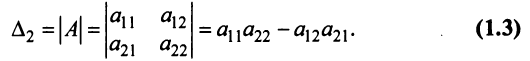
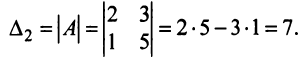
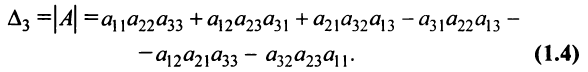

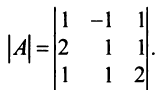



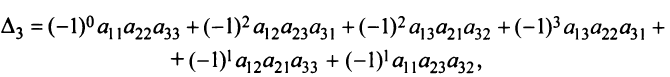

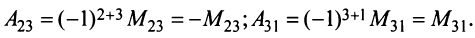
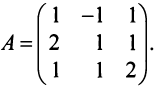
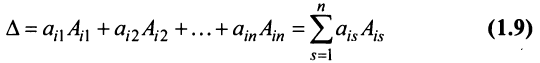
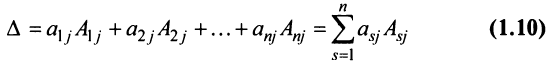
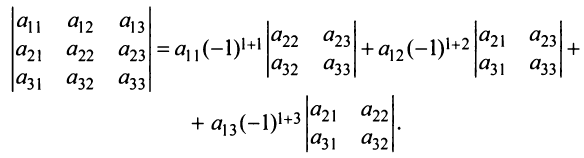

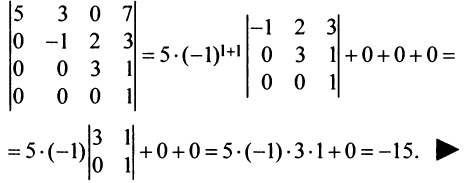
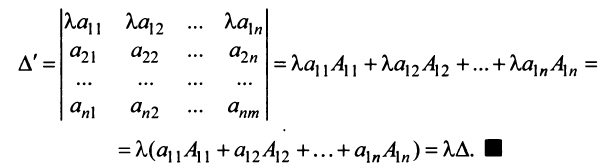
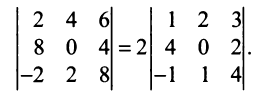
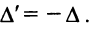

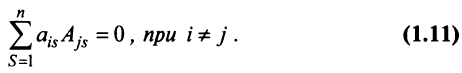
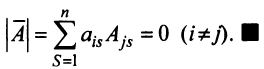
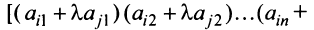
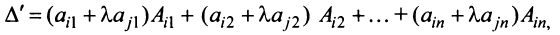
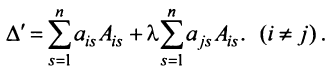
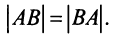
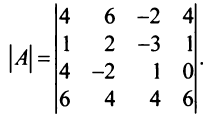
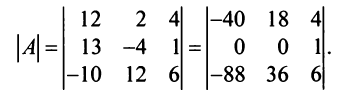
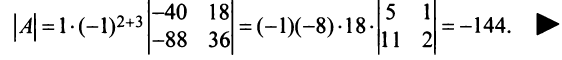

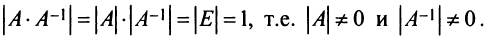
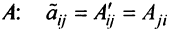
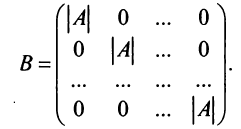
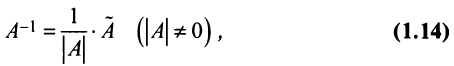
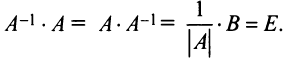

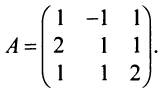
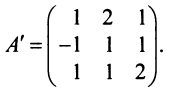
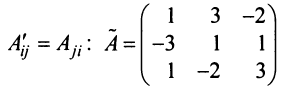
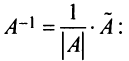
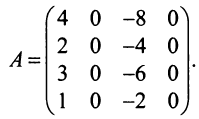

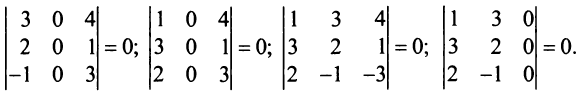

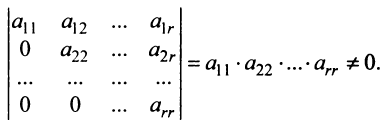
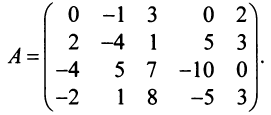
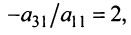
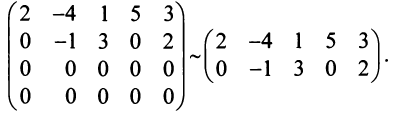

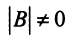
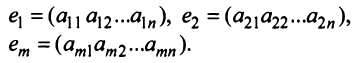
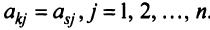
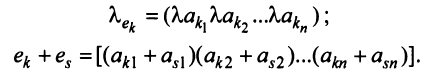
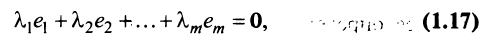
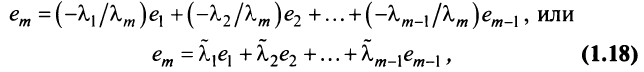
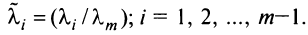

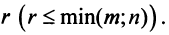

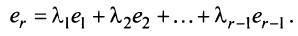


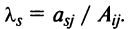
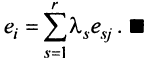
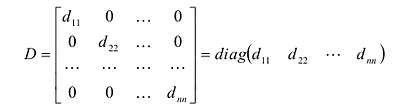
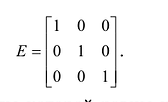
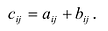
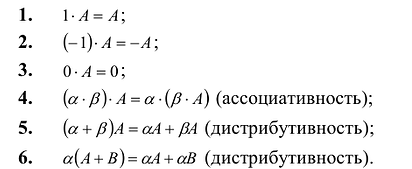
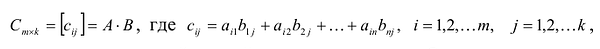
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;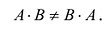
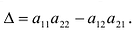
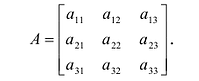
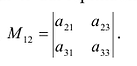
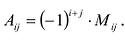
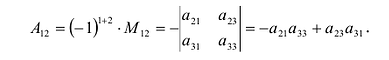
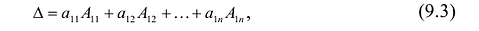
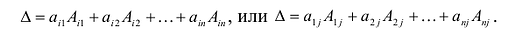
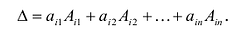
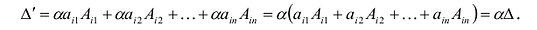
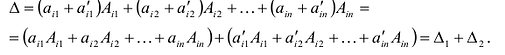

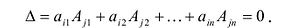
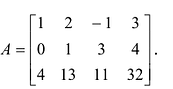
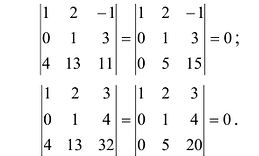

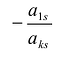 и т.д.;
и т.д.;

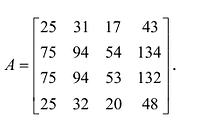


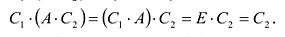
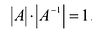
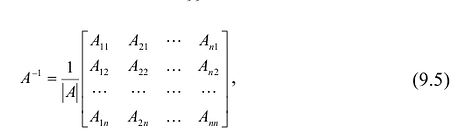
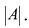

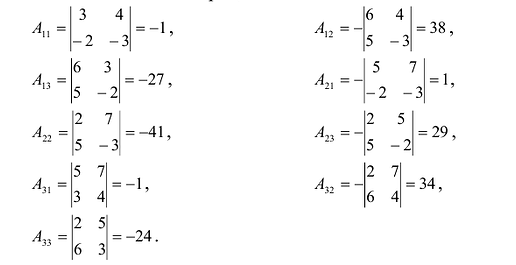
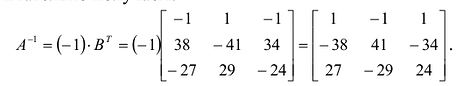
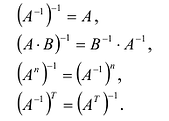


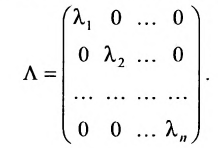
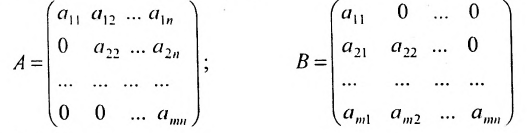





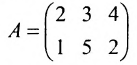

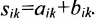
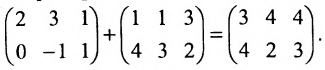
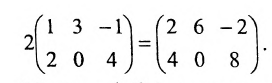
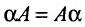 .
.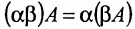 .
.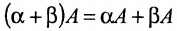 .
.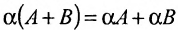 .
.