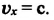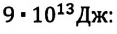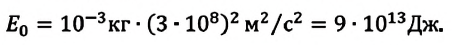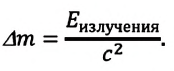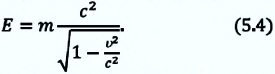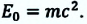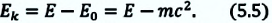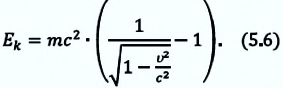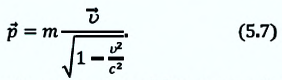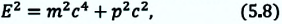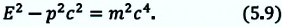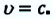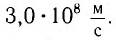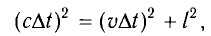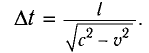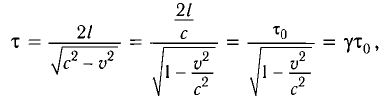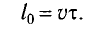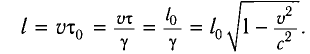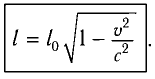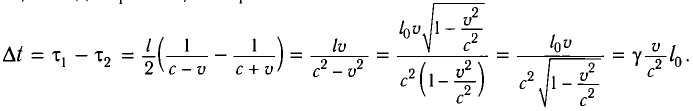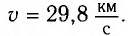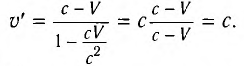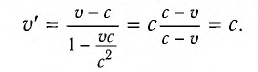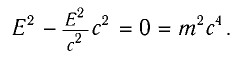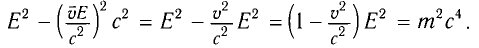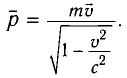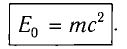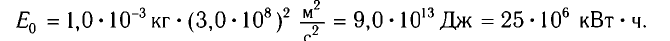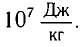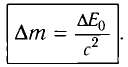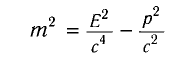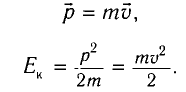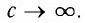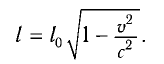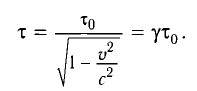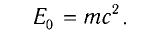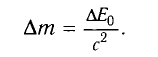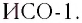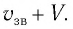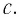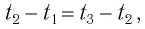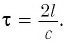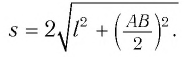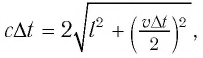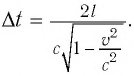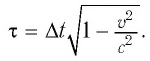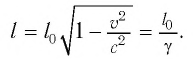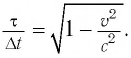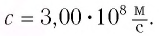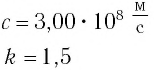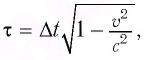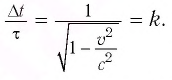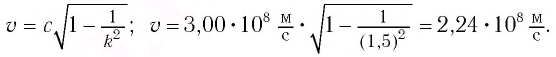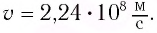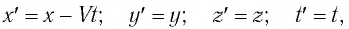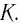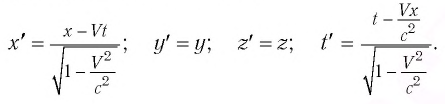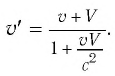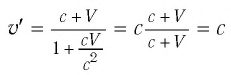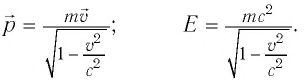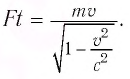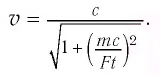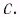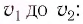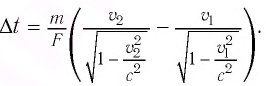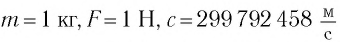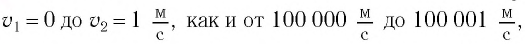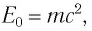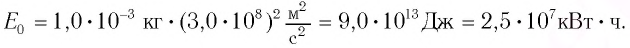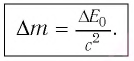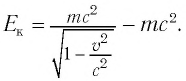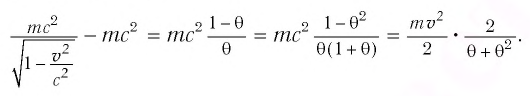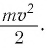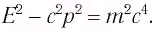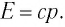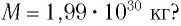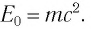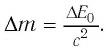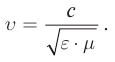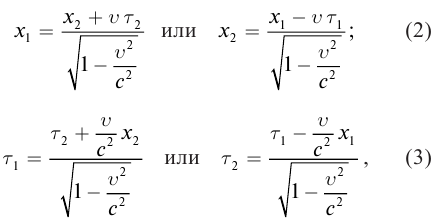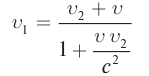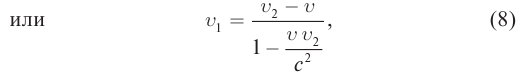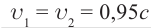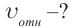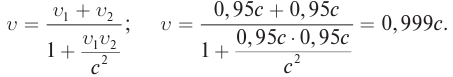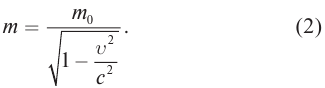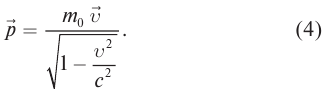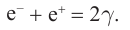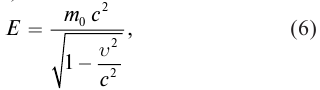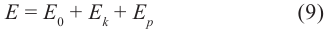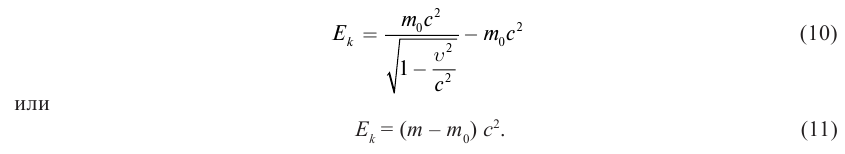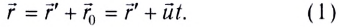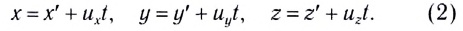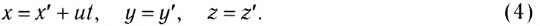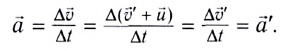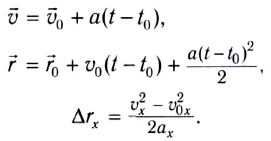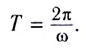Министерство
образования и науки Российской Федерации
Государственное
образовательное учреждение
высшего
профессионального образования
«Санкт-Петербургский
государственный университет
технологии и
дизайна»
Ю. И. Соколов
Курс физики
Учебное пособие
Санкт-Петербург
2010
Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
М
— это раздел
физики, в котором изучают механическое
движение — изменение положения тела в
пространстве с течением времени.
Положение тела в пространстве определяют
по отношению к другому телу, с которым
связывают систему координат, например,
декартову, представляющую собой три
взаимно перпендикулярные оси x,
y,
z
(рис. 1.1).
Система координат плюс часы для отсчета
времени образуют систему
отсчета.
Рассмотрим
кинематику
движения
тела, т. е.
движение без учета его причины. Размерами
движущегося тела будем пренебрегать и
называть его просто частицей.
Положение
тела (частицы) в любой момент времени
можно задать с помощью радиуса-вектора
,
проведенного
из начала координат 0 в точку пространства,
в котором находится тело в момент времени
(рис. 1.1).
Из рис. 1.1
видно, что радиус-вектор
можно записать в виде
(1.1)
где
— координаты точки пространства,
,
— орты системы координат — единичные
по модулю безразмерные векторы,
направленные по осям
соответственно.
Длина
радиуса-вектора (его модуль)
(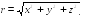
Очевидно,
при движении частицы ее радиус-вектор
меняется в общем случае как
по
модулю, так и по направлению, т. е.
радиус-вектор зависит от времени
:
(1.3)
Если
известна зависимость
,
говорят, что задан закон
движения частицы.
Линию,
описываемую частицей при ее движении,
называют траекторией
частицы
(рис. 1.2).
Пусть за промежуток времени
частица переместилась вдоль траектории
из точки 1 в точку 2 (рис.
1.2) Проведем
из точки 1 в точку 2 вектор
и назовем его перемещением
частицы за
промежуток времени
Из рис. 1.2
видно, что
(1.4)
приращению
радиуса-вектора
частицы за промежуток времени
.
С
учетом выражения (1.1) можем написать
Рис. 1.2
(1.5)
Элементарное
перемещение частицы из точки 1 за
элементарный (очень малый) промежуток
времени
(1.6)
причем
нетрудно видеть, что вектор
направлен по касательной к траектории
в точке 1.
Назовем
длину отрезка траектории между точками
1 и 2 путем
S,
пройденным частицей за промежуток
времени
Из рис. 1.2
видно, что обычно путь больше длины
(модуля) перемещения. Однако по мере
уменьшения пути это различие уменьшается.
Для элементарного (очень малого) пути
оно становиться ничтожным, что дает
право написать
(1.7)
где
— модуль элементарного перемещения
частицы.
§ 2. Скорость и ускорение
Мы
уже говорили, что при движении частицы
ее радиус-вектор меняется в общем случае
как по модулю, так и по направлению. В
кинематике вводят величину, характеризующую
быстроту изменения радиуса-вектора со
временем. Ее называют скоростью
частицы.
Пусть
в момент времени
частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.1). За
элементарный (очень малый) промежуток
времени
радиус-вектор частицы получит элементарное
приращение
.
Векторную величину
(2.1)
называют
скоростью частицы в точке 1 траектории.
Вектор
направлен, так же как и вектор
,
по касательной к траектории в точке 1.
Рис. 2.1
Аналогично
определяют скорость частицы в любой
точке траектории или, что то же самое,
в любой момент времени
движения частицы. В математике правую
часть равенства (2.1) называют производной
радиуса-вектора по времени. Следовательно,
скорость v
частицы в момент времени
равна производной по времени от
радиуса-вектора этой частицы. Очевидно,
для определения скорости частицы в
любой момент времени надо знать закон
движения частицы (1.3).
Можем написать
(2.2)
где
— проекции вектора
на координатные
оси.
Модуль скорости
(2.3)
Принимая
во внимание соотношения (1.7) и (2.1), можем
записать выражение для элементарного
пути, проходимого частицей за элементарный
(очень малый) промежуток времени
:
(2.4)
где
v
— модуль скорости.
Чтобы
определить путь S,
проходимый частицей за промежуток
времени
,
надо просуммировать элементарные пути
по длине отрезка траектории, проходимой
частицей за этот промежуток времени. В
математике такую операцию называют
интегрированием. Можем написать
(2.5)
Путь,
проходимый частицей за промежуток
времени
равен
определенному интегралу от функции
v(t),
взятому в пределах от
,
до
.
Очевидно,
чтобы произвести интегрирование (2.5),
надо знать зависимость модуля скорости
частицы от времени
При
движении частицы ее скорость может
меняться как по модулю, так и по
направлению. В кинематике вводят
величину, характеризующую быстроту
изменения скорости со временем. Ее
называют ускорением
частицы.
Пусть
в момент времени
частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.2).
Рис. 2.2
За
элементарный (очень малый) промежуток
времени
скорость частицы получит элементарное
приращение
.
Векторную величину
(2.6)
называют
ускорением частицы в точке 1 траектории.
Вектор
направлен так же, как и вектор.
Аналогично
определяют ускорение частицы в любой
точке траектории или, что то же самое,
в любой момент времени
движения частицы. Ускорение
частицы в момент времени
равно производной по времени от скорости
этой частицы.
Очевидно,
зная закон движения частицы (1.3), можно
найти зависимость скорости
от времени
а
затем ускорение
в любой момент времени.
Можем написать
,
(2.7)
где
— проекции вектора
на координатные оси.
Модуль ускорения
(2.8)
Проведем
через некоторую точку траектории частицы
две оси: ось τ, направленную по касательной
к траектории в сторону вектора
,
и ось
,
направленную по нормали к траектории
к центру кривизны траектории в одной
точке (центру окружности, дугой которой
является элементарный (очень малый)
отрезок траектории частицы в районе
данной точки) (рис.
2.3). Тогда
вектор
можно представить в виде суммы двух
составляющих
и
:
,
(2.9)
где
и
— орты осей
и
;
и
— проекции векторов
и
на эти оси.
Вектор
называют
касательной
или
тангенциальным
ускорением,
вектор
— нормальным
ускорением.
Рис. 2.3
Можно показать,
что проекция
(2.10)
производной
по времени от модуля скорости частицы.
Тангенциальное ускорение частицы
характеризует быстроту изменения модуля
ее скорости. При ускоренном движении
вектора
совпадает с направлением скорости
частицы. При замедленном движении вектор
противоположен направлению скорости
.
Можно показать,
что проекция
(2.11)
где
R
— радиус кривизны траектории в данной
точке. Нормальное ускорение характеризует
быстроту изменения направления скорости
частицы. Вектор
всегда направлен к центру кривизны
траектории.
Модуль ускорения
.
(2.12)
Пример
2.1. Радиус-вектор
при движении частицы по траектории
изменяется по закону
,
м. Найти модуль
скорости частицы в момент t1
= 2с.
|
Дано:
|
Решение |
|
|
Ответ:
Пример
2.2. Закон
движения частицы
м. Найти проекцию
ускорения частицы в момент времени t1
= 5c.
|
Дано:
|
Решение
|
|
|
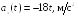
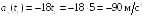
Ответ:
ax(t1)
= – 90 м/с2.
Пример
2.3. В момент
времени
скорость частицы
ускорение
Найти радиус кривизны R
траектории в той точке, в которой частица
находится в момент времени
.
|
Дано:
|
Решение
|
Ответ:
Пример
2.4. Закон
движения частицы
Найти путь
частицы
за одиннадцатую секунду ее движения.
|
Дано:
|
Решение
|
|
|
Ответ:
S12
= 63 м.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Конев В.В. Определенные интегралы
Движение частицы с переменной скоростью
| Рассмотрим задачу о вычислении перемещения s частицы за промежуток времени от 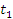 до до 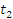 при движении частицы вдоль некоторой прямой с переменной скоростью при движении частицы вдоль некоторой прямой с переменной скоростью 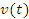 . .
|
Траектория движения
Определение и основные понятия траектории движения
Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.
Линию, которую описывает частица при своем движении, называется траекторией движения.
В зависимости от формы траектории механическое движение можно разделить на:
- прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
- и криволинейное перемещение (траектория — кривая линия).
Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.
При движении точки с постоянным ускорением, которое описывает уравнение:
Уравнение траектории движения
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:
Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.
Вершина этой параболы находится в точке с координатами:
Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.
Обратимость движения
Из представления о траектории можно конкретизировать смысл обратимости механического движения.
Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.
Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.
Параметры траектории движения
Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:
- Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
- При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
- Третьим способом описания движения является описание с помощью параметров траектории.
Путь — это скалярная величина, равная длине траектории.
Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:
Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:
где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.
Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.
Примеры задач с решением
Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit<>
Решение: Рассмотрим уравнение изменения скорости частицы:
Из этого уравнения следует, что:
Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):
Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:
Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.
Решение: Рассмотрим систему уравнений, которая задана в условии задачи:
Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:
Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:
Уравнение траектории тела — определение и формулы
Общие сведения
Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.
В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.
Существует несколько видов механического перемещения (во времени) физической точки:
- равномерное и равноускоренно прямолинейное;
- по дуге;
- гармоническое колебание.
При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.
Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.
Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.
Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.
Горизонтальное перемещение
Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).
Таким образом, система начальных условий будет выглядеть так: x (t = 0) = 0; y (t = 0) = 0; v0x = v0; voy = 0. Вектор ускорения постоянный, поэтому a = g. Если тело представить как совокупность материальных точек, движущихся по одинаковому пути, то путь можно определить как сумму перемещений по прямым. Уравнение скорости примет вид: v (t) = v0 + gt. Об изменении положения можно сказать, что оно выполняется с постоянной скоростью и ускорением в горизонтальной плоскости, являясь равномерным. Значит, проекцию на оси ординаты и абсциссы можно записать как vx = v0; vy = -gt.
Скорость перемещения рассчитывают по формуле: V = √(V 2 x + V 2 y). После подстановки полученных ранее выражений равенство примет вид: V = √(V 2 0 + g 2 t 2 ). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2 ) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.
Так как s0 = y (t = 0) = h0, то скалярные выражения для координат изменяющей положение частицы можно представить в виде системы: x = V0t; y = h0 — (gt 2 / 2). Перемещение происходит по прямой как отдельное движение в двух плоскостях, при этом из формулы следует, что изменение положения будет соответствовать правой половине направленной вниз параболы. Учитывая то, что время можно определить из отношения икса к начальной скорости (t = x /V0), можно записать окончательную формулу для вычисления траектории движения тела: y = h0 — (gx 2 ) / (2 2 V0) .
Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.
Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.
Движение тела под углом
Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.
Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.
Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:
- ускорения: ax = 0, ay = — g, az = 0;
- радиус-вектора: rx (t) = V0 * cosat, ry (t) = v * sin (at — (g * t2)/2)), rz (t) = 0;
- скорости: vx (t) = V0 * cosa, vy (t) = V0 * sin (a — gt), vz (t) = 0.
Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).
Если полученную формулу для времени подставить в уравнение для игрек координаты, то вместо временного параметра появится икс. То есть можно будет вывести зависимость абсциссы от ординаты: y = V 0 * sinat — (g * t 2 ) / 2 = (tga) * x — (g / 2 * V0 * cos 2 a) * x 2 . Значение t нужно подставить в каждое слагаемое, но при этом учесть, что отношение синуса к косинусу называют тангенсом. Альфа в формуле — это угол между направлением начальной скорости и горизонтальным направлением (угол броска). После исключения времени из этих уравнений получим уравнение траектории.
В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.
Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.
Решение задач
Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.
Вот два таких задания:
- Пусть имеется тело, движение которого описывается равенствами: x = Vx * t; y = y0 + Vy * t. Нужно определить траекторию его перемещения, учитывая, что Vx = 20 см/с, Vy = 2 м/с, Yo = 0,2 м. Для решения задачи нужно записать систему, определяемую исходными данными. Затем из первого равенства выразить время: t = x / Vx. Полученную формулу можно подставить в выражение нахождения координат абсциссы: y = y0 + (Vy * x) / Vx. Если теперь использовать исходные данные, то уравнение, описывающее траекторию, примет вид: y = 0.2 + 4x. Равенство напоминает собой формулу прямой: y = k * x + b. Исходя из этого можно утверждать, что траектория пути также будет представлять собой прямую линию. Действительно, в этом можно убедиться, если построить график движения. Для этого нужно взять несколько произвольных значений для икса, подставить их в формулу и найти вторую координату.
- Следующая задача довольно интересная. Нужно составить траекторию движения для тела, движущегося равномерно со скоростью два метра в секунду, при отклонении пути от оси икс на 60 градусов. За начало координат нужно принять точку (0, 0). Тогда начальный радиус-вектор тоже будет равен нулю: R = 0. Для успешного решения примера понадобится вспомнить скалярные уравнения для проекции при равномерном движении. Так как по условию вектор задан, то можно найти его проекцию на ось игрек: Vx = v * cos60 = 1; Vy = v * cos30 = √3. Отсюда: x = Vx * t = t; y = Vy * t = √3t.
Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.
Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.
Как определить уравнение траектории частицы
2017-05-07
Частица движется в плоскости $xy$ с постоянным ускорением $vec$, направление которого противоположно положительному направлению оси $y$. Уравнение траектории частицы имеет вид $y = ax — bx^<2>$, где $a$ и $b$ — положительные постоянные. Найти скорость частицы в начале координат.
В соответствии с проблемой $vec = w (- vec)$
Дифференцируя уравнение траектории, $y = ax — bx^<2>$, по времени
Получаем, $left . frac
Опять дифференцируя по времени
или, $- w = a(0) — 2b left ( frac
Используя (3) в (2) $left . frac
Следовательно, скорость частицы в начале координат
http://nauka.club/fizika/formula-uravneniya-traektorii-tela-dvizhushchegosya-pod-uglom.html
http://earthz.ru/solves/Zadacha-po-fizike-3295
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Содержание:
Основы специальной теории относительности:
Специальная теория относительности создана в 1905 году А. Эйнштейном. Она является новым представлением, пришедшим на место классических понятий о пространстве и времени.
Механика Ньютона изучает движение тел при малых скоростях, т.е. в случаях
Вспомним теорию преобразований Галилея. Она позволяет вычислять координаты и скорость двух тел относительно друг друга, которые движутся относительно инерциальных систем отсчета К и К’.
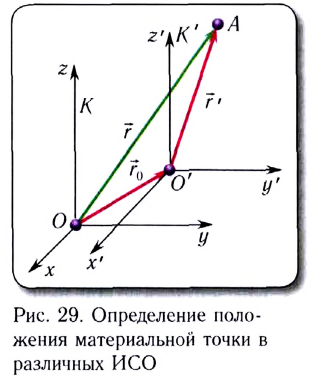
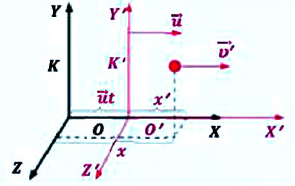
В частном случае система отсчета К’ движется по оси X системы отсчета К (рис. 5.1). В этом случае преобразования Галилея относительно неподвижной системы отсчета будут записаны в следующем виде:
В начальном случае 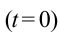
Согласно преобразованиям Галилея при переходе из одной системы отсчета в другую систему отсчета скорости будут
Ускорение тела во всех системах отсчета будет одинаковым:
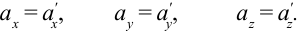
Значит, второй закон Ньютона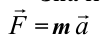
На основе теории Максвелла скорость распространения электромагнитных волн во всех инерциальных системах отсчета одинакова и равна скорости распространения света в вакууме.
Независимость скорости света от системы отсчета или скорости движения тел отсчета (отражающие света зеркалом) экспериментально доказана А. Майкельсоном и Э. Морли.
Из этого вытекает, что скорость распространения электромагнитных волн (в данном случае свет) инвариантна относительно преобразованиям Галилея. Если электромагнитная волна в вышеупомянутой системе отсчета К’ распространяется со скоростью v, ее скорость в системе отсчета К должна быть v + c, но не с!
Такое противоречие решено А. Эйнштейном. Он отказался от классических представлений о пространстве и времени. Эйнштейн предложил свою теорию относительности, где в отличие от классической физики физические величины, которые считались абсолютными, в том числе время, в релятивистской физике (от англ. relativity -относительность) приняли относительные величины.
Теория относительности заключается в комплексе законов механики, включающем в себя законы движения тел, движущихся с меньшей скоростью, чем скорость света, но ближе к ней, и дали название «релятивистская механика». Основу специальной теории относительности Эйнштейна составляет два постулата — принцип относительности и принцип постоянства скорости света:
- Принцип постоянства скорости света: скорость света в вакууме во всех инерциальных системах отсчета одинакова и постоянна и не зависит от движения источника и регистрирующих приборов.
- Принцип относительности Эйнштейна: в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково. Значит, все законы физики во всех инерциальных системах отсчета имеют одинаковую форму.
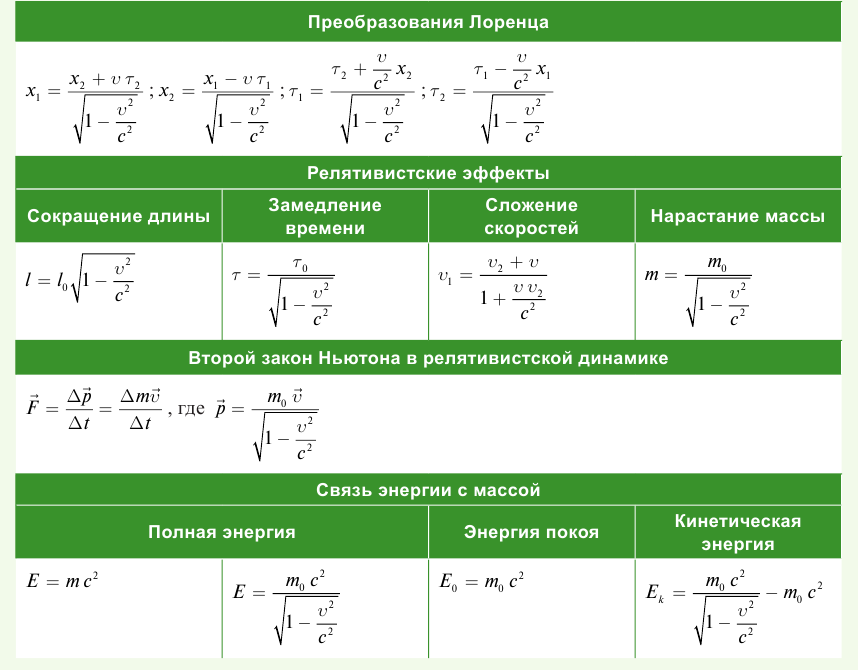
Постулаты Эйнштейна и математические анализы, проведенные на их основе, показали, что преобразования Галилея не подходят для релятивистских случаев. В этом случае имеют место преобразования Лоренца. Эти преобразования объясняют все релятивистские эффекты при переходе из одной инерциальной системы отсчета в другую систему отсчета, при близких к скорости света скоростях. При малых скоростях они 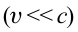
Кинематические формулы преобразования координаты и времени в специальной теории относительности называются преобразованиями Лоренца, которые были предложены в 1904 году.
Преобразования Лоренца для системы отсчета, рассмотренные на рис. 5.1, записываются в следующей форме:
Релятивистский закон сложения скоростей
Из преобразований Лоренца следует ряд важных результатов и выводов по свойствам пространства и времени. Первый из них — это эффект релятивистского сокращения времени.
Представим себе, что в точке X системы К’ в промежутке времени 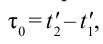
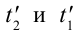
Период происхождения этого процесса в системе отсчета К будет: 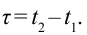
Значит, если 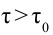
Точно по этому принципу можно доказать, что в релятивистских системах уменьшается длина.
Здесь: 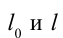
Таким образом, линейный размер тела, движущегося относительно неподвижного наблюдателя, укорачивается. Этот релятивистский эффект называется сокращением длины по Лоренцу. Один из важных результатов, вытекающих из преобразования Лоренца, эта релятивистский закон сложения скоростей.
Представим себе, что тело движется со скоростью 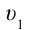
Если скорость тела относительно системы отсчета К’ будет 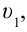
относительно системы отсчета К будет 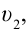
Если скорость намного меньше, чем скорость света, 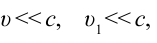
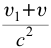
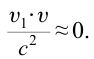
Если 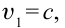
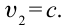
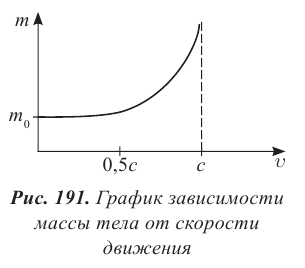
Зависимость массы от скорости
Принцип относительности Эйнштейна объясняет инвариантность всех законов природы при переходе из одной системы отсчета в другую систему отсчета. Это означает, что формулы, выражающие все законы природы, относительно преобразований Лоренца, должны быть инвариантными. Однако уравнения механики Ньютона оказались неинвариантными в отношении преобразований Лоренца. При малых скоростях второй закон Ньютона пишется в виде: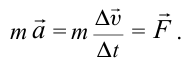
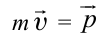
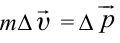
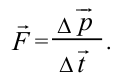
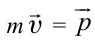
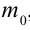
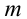
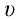
На рисунке 5.3 приводится график зависимости массы от скорости. При скорости тела 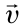
скорость света, член 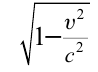
Таким образом, как описал Ньютон, масса тела не зависит от скорости и импульс тела зависят от его скорости.
В релятивистской механике закон сохранения энергии выполняется, как и в классической механике. Кинетическая энергия тела 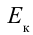
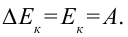
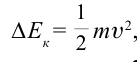
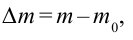
Выражение общей энергии тела на основе теории относительности Эйнштейн вывел в следующем виде:
Значит, полная энергия тела или системы тел в релятивистской механике равна произведению массы т при движении и квадрата скорости света. Это является формулой Эйнштейна и называется законом взаимосвязи массы и энергии.
Полная энергия тела равна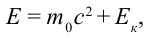
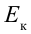
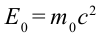
При превращении частицы, имеющей массу покоя, частица с массой покоя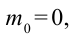
В теории относительности кинетическая энергия тела определяется из следующего:
Из формулы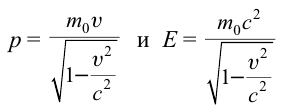
Из этих уравнений можно вывести формулу: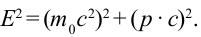
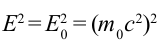
Из этой формулы следует, что если частица не имеет массы покоя 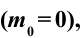
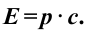
Примером таких частиц можно привести фотон. Масса покоя фотона равна нулю, но имеет и импульс, и энергию. Частицы, лишенные массы покоя в состоянии покоя не существуют, и они во всех инерциальных системах отсчета движутся с ограниченными скоростями с.
Пример решения задачи №1
В противоположном направлении от Земли движутся два космических корабля. Их скорость движения относительно Земли равна 0,5 с. Найдите скорость первого корабля относительно второго корабля?
Дано: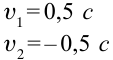
Формула:
Решение:
Правила и законы
- Теория относительности: Специальная теория относительности Эйнштейна является новым представлением, пришедшим на место классических понятий о пространстве и времени.
- Постоянство скорости света в вакууме : Скорость света в вакууме во всех системах отсчета одинакова, равна с и не зависит от природы источника и приемника. Это доказано Майкельсоном экспериментально.
- Постулаты Эйнштейна 1. Скорость света в вакууме во всех системах отсчета одинакова и не зависит от движения источника и регистрирующих приборов. В любых инерциальных системах отсчета все законы природы и явления происходят одинаково.
- Преобразования Лоренца :Математическую основу теории относительности составляют преобразования Лоренца.
- Релятивистское
— собственное время.
- Релятивистское сокращение длины
собственная длина.
- Формула релятивистского импульса
- Основной закон релятивистской динамики
- Релятивистский закон сложения скорости
- Релятивистское увеличение массы
масса покоя.
- Полная энергия тела : Энергия тела или частицы равна произведению массы на квадрат скорости света:
- Зависимость изменения массы тела от изменения энергии
- Энергия покоя тела
- Кинетическая энергия тела
Карта теории относительности:
Основы теории относительности
Принцип относительности Галилея. В 1636 году Г. Галилей, обобщая исследования по изучению движения тел, сформулировал принцип относительности:
Законы механики во всех инерциальных системах отсчета одинаковы.
Этот принцип поставил определенные ограничения при составлении уравнений механического движения: уравнения, выражающие механическое движение во всех инерциальных системах отсчета, имеют одинаковый вид.
По этим представлениям, называемым классическими, пространство и время, характеризующие механическое движение, считаются абсолютными — линейные размеры тела не зависят от того, покоится тело или движется, скорость же света считается бесконечно большой величиной. Ньютоновская механика целиком была построена на этом принципе. Таким образом, в классической механике координата, время, длина и скорость тел относительно любой инерциальной системы отсчета были представлены в связанной компактной форме с помощью преобразований, называемых «Преобразованиями Галилея» (см.: таблица 5.1). Однако явлениям, возникающим при скоростях, близких к скорости света, например, в электромагнитных, гравитационных и внутриатомных процессах, классические представления не могут дать объяснения.
Специальная теория относительности Эйнштейна
Астрономические исследования, проведенные Олафом Рёмером в конце XVII века, лабораторные исследования Луи Физо в середине XIX века по определению скорости света и тогда же проведенные теоретические работы Дж.Максвелла по исследованию электромагнитного поля доказали конечность скорости распространения света. В начале XX века классический принцип относительности и результаты получаемые из него, были исследованы заново. Были определены формулы, связывающие физические величины, характеризующие пространство и время в инерциальных системах отсчета, движущихся со скоростями, близкими к скорости света.
Обобщив все проведенные в этой области исследования, А.Эйнштейн в 1905 году сформулировал новую теорию — «Специальную теорию относительности» (СТО), тем самым заложив теоретическую основу релятивистской механики.
Релятивистская механика — раздел физики, изучающий законы механики при движении тел со скоростями, сравнимыми со скоростью света.
Математическими расчетами Эйнштейн доказал, что при переходе от подвижной системы отсчета к неподвижной пространственно-временные координаты подвергаются соответствующим преобразованиям при помощи универсального множителя 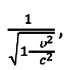
Основу СТО составляют два постулата:
- I постулат: Все законы физики одинаковы во всех инерциальных системах отсчета и ни одним физическим опытом невозможно отличить инерциальные системы друг от друга.
- II постулат: Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника и приемника света. Скорость света —максимальная скорость, существующая в природе.
В специальной теории относительности Эйнштейну удалось установить связь между пространством и временем и объединить их в единый пространственно-временной континуум — «пространство-время». Это означает, что произвольное явление характеризуется свойствами не только пространства, где оно происходит, но и времени, характеризующим последовательность происходящих явлений.
Таблица 5.1
Здесь: а) величины без штриха характеризуют данное явление, произошедшее в неподвижной системе отсчета 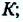 b) величины же со штрихом характеризуют это же явление, произошедшие в системе отсчета b) величины же со штрихом характеризуют это же явление, произошедшие в системе отсчета 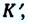 движущемся со скоростью движущемся со скоростью 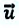 и относительно системы отсчета и относительно системы отсчета 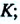 с) с) 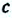 — скорость света по классическим представлениям бесконечна, а в релятивистской механике имеет конечное значение. — скорость света по классическим представлениям бесконечна, а в релятивистской механике имеет конечное значение. |
 |
||
| Преобразование Галилея | Преобразование Лоренца | ||
| Прямое преобразование | Обратное преобразование | Прямое преобразование | Обратное преобразование |
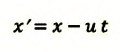 |
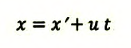 |
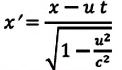 |
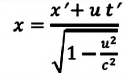 |
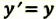 |
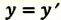 |
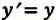 |
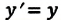 |
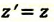 |
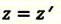 |
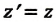 |
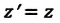 |
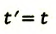 |
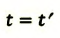 |
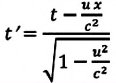 |
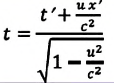 |
| Результаты, получаемые из преобразования Галилея | Результаты, получаемые из преобразований Лоренца согласно постулатам Эйнштейна | ||
|
Промежутки времени абсолютны: |
Промежутки времени относительны: время в подвижной системе координат замедляется относительно неподвижной системы координат: где |
||
|
Пространственные размеры абсолютны: |
Пространственные размеры относительны: линейный размер тела в подвижной системе координат короче, чем в покоящейся системе координат: где |
||
|
Масса инвариантна: выполняется во всех системах отсчета: |
Масса инвариантна: во всех системах отсчета выполняется равенства 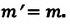 |
||
|
Правило сложения скоростей по Галилею другую значение скорости может увеличиваться до бесконечности: |
Скорость света в вакууме одинакова в любом направлении во всех инерциальных системах отсчета:
|
Общая теория относительности (ОТО)
С целью устранения недостатков специальной теории относительности и объяснения «теории гравитации» с релятивистской точки зрения, А.Эйнштейн в 1911—1916 годах сформулировал общую теорию относительности. Недостатки СТО следующие:
- a) эта теория выполняется только для инерциальных систем отсчета. СТО не выполняется в системах, движущихся с ускорением относительно друг друга;
- b) эта теория может использоваться только в плоскости прямолинейных координат, в других системах координат ее использование невозможно.
ОТО состоит го двух основных принципов:
I принцип — принцип эквивалентности или слабый принцип эквивалентности: на основании этого принципа инерциальная масса эквивалентна гравитационной массе, то есть они равны друг другу. В классической механике используются два понятия «массы»: инертная масса, находящаяся в соотношении с ускорением, на основе II закона Ньютона и являющаяся источником гравитационного поля — гравитационная масса. Эйнштейн физическими экспериментами доказал, что обе эти массы одинаковы.
II принцип — сильный принцип эквивалентности: по этому принципу в системе, падающей с ускорением, равным ускорению свободного падения, все законы физики выполняются как бы в отсутствии гравитации, то есть в этой системе невозможно различить эффект притяжения и ускоренное движение.
Главные результаты, получаемые из этих принципов:
1. Нарушение закона прямолинейного распространения света и искривление луча света под действием гравитационного поля Солнца: пространственно-временные координаты подвергаются искривлению. Этот эффект нашел свое подтверждение в результате проведенных наблюдений во время затмения Солнца в 1919 году.
2. Замедление времени в гравитационном поле — возникновение гравитационного «красного» смещения. Этот эффект был опытно подтвержден в 1960 году в лаборатории Гарвардского университета физиками США Р. Паундом и Г. Ребки.
3. Излучение гравитационных волн в результате столкновения бинарных (двойных) звездных систем, расширения Вселенной и другие. Существование гравитационных волн было обнаружено через 100 лет, учеными США, в 2016 году, при наблюдении столкновения «Черных дыр» (потухшие звезды).
Закон взаимосвязи между энергией и массой
Взаимосвязь между массой и энергией. В классической механике имеются два вида материи: вещество и физическое поле. Главное свойство вещества — его масса, а главное свойство физического поля — наличие у него энергии.
Согласно теории относительности между массой и энергией существует взаимосвязь, то есть если вещество обладает массой, то оно обладает и энергией. В 1905 году А. Эйнштейн сформулировал закон взаимосвязи массы и энергии:
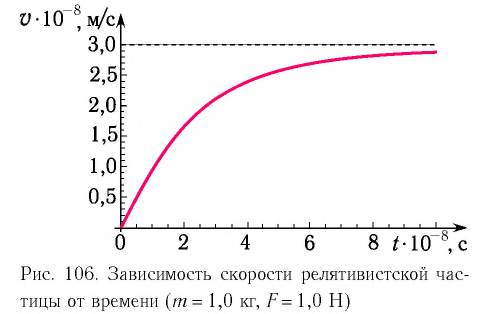
Любое тело обладает энергией покоя, эта энергия равна произведению массы тела на квадрат скорости света в вакууме:
Энергия покоя 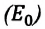
Такая энергия возникает в процессе взрыва атомной бомбы и этой энергии достаточно, чтобы превратить 30 000 тонн воды в пар.
Электромагнитное излучение системы, например, световое излучение, это процесс превращения внутренней энергии системы в энергию излучения. В этом процессе масса системы также уменьшается эквивалентно уменьшению внутренней энергии:
Изменение массы эквивалентно изменению энергии:
Непрерывное излучение Солнца и других звезд означает, что они подвергаются непрерывной потере энергии и массы. Из проведенных вычислений было определено, что за каждую секунду в результате излучения масса Солнца уменьшается на 4 000 000 тонн.
Энергия в релятивистской механике (или полная энергия)
Согласно теории относительности полная энергия системы равна сумме его энергии покоя и кинетической энергии:
Эйнштейн определил, что полная энергия частицы, движущейся со скоростью 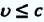
Если тело находится в состоянии покоя: 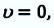
Кинетическая энергия в релятивистской механике
Кинетическая энергия тела равна разности его полной энергии и энергии покоя:
Если в этом выражении вместо полной энергии запишем выражение (5.4), то получим:
Импульс в релятивисткой механике
Согласно теории относительности импульс системы при переходе из одной инерциальной системы отсчета в другую подвергается релятивистскому преобразованию:
Связь между полной энергией и импульсом
Между полной энергией и импульсом в релятивисткой механике существует нижеприведенная связь:
или
Это соотношение выполняется во всех инерциальных системах отсчета. При переходе из одной инерциальной системы отсчета в другую полная энергия и импульс изменяются, однако их разность не меняется. Если масса будет равна нулю 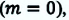
Приняв во внимание формулы (5.4) и (5.7) в последнем выражении, получим соотношение между полной энергией и импульсом частицы:
Из этого выражения видно, что если 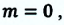
Теория относительности
Согласно современным данным, точное значение скорости света в вакууме с = 299792458 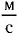
Развитие науки и техники на рубеже XIX—XX вв. позволило физикам провести достаточно точные измерения скорости света в вакууме, которая оказалась «рекордно большой» по сравнению со скоростями иных объектов, доступных для наблюдения.
Как показали дальнейшие исследования, при движении со скоростями, сравнимыми со скоростью света с в вакууме, проявляются новые свойства пространства и времени. Эти новые свойства подробно изучаются в рамках специальной теории относительности (СТО).
Таким образом, специальная теория относительности — раздел физики, в котором изучаются свойства пространства и времени при движении со скоростями, близкими к скорости света в вакууме (v~с).
Теория относительности называется также релятивистской теорией (от латинского слова relativus — относительный).
В повседневной жизни мы практически не сталкиваемся с движениями, происходящими со скоростями, близкими к скорости света в вакууме. Зачем же тогда изучать специальную теорию относительности? Для этого существует целый ряд причин.
- Во-первых, около 90 % информации об окружающем мире мы получаем посредством зрения, т. е. напрямую воспринимая световое излучение. Таким образом, свет играет ключевую, особую роль в жизни человека.
- Во-вторых, ни один сигнал или частица не может иметь скорость, превышающую скорость света с в вакууме.
- В-третьих, при изучении ряда физических явлений в квантовой физике (фотоэлектрический эффект), ядерной физике (свойства элементарных частиц) необходимо знание соотношений между энергией, импульсом и массой при скоростях движения, равных или близких к скорости света в вакууме.
- В-четвертых, многие галактики во Вселенной движутся со скоростями, близкими к скорости света, а свойства таких астрономических объектов, как черные дыры, пульсары, нейтронные звезды, могут быть корректно описаны только в рамках релятивистской теории.
Кроме того, каждый современный культурный человек должен иметь представление о связи энергии с массой, о таких интересных релятивистских эффектах, как относительность одновременности, замедление времени, сокращение длины.
Экспериментальные предпосылки создания специальной теории относительности
Система отсчета называется инерциальной (ИСО), если при отсутствии воздействий на данное тело (или их компенсации) скорость тела относительно этой системы отсчета остается постоянной с течением времени.
Создание специальной теории относительности исторически связано с развитием электродинамики. За два столетия, которые отделяли физику эпохи Галилея и Ньютона от физики эпохи Максвелла и Герца, в ней накопилось огромное количество новых научных фактов. Особенно бурно в это время развивались электромагнетизм и оптика. В то же время представление о мироздании базировалось на механистической картине мира, трактовавшей все явления с позиций классической механики XVII в., носившей универсальный характер.
Соответственно, при построении электродинамики движущихся сред был использован принцип относительности Галилея, согласно которому электромагнитные процессы (взаимодействие зарядов и токов, распространение света и т. д.) должны протекать одинаково во всех ИСО.
Однако электромагнитные процессы происходят со скоростями, близкими к скорости света в вакууме, которые значительно больше скоростей различных механических тел. В связи с этим возникает вопрос: не скажется ли это на справедливости принципа относительности Галилея при описании электромагнитных явлений?
Напомним, что звуковые волны могут распространяться только в какой-либо упругой среде — газообразной, жидкой или твердой. Именно упругие свойства среды делают возможной передачу колебаний от одной точки среды к другой. Так, в вакууме звуковые волны распространяться не могут.
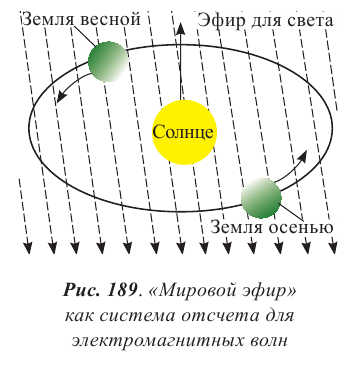
Проводя аналогию между звуковыми и электромагнитными волнами, ученые пришли к выводу, что для распространения света также необходима некоторая упругая среда, которую назвали эфиром. Эфир должен был обладать такими уникальными свойствами, как:
Впервые гипотезу о существовании эфира, который заполняет все пространство, выдвинул в 1678 г. Гюйгенс.
По мере развития электродинамики во второй половине XIX в. основным стал вопрос о влиянии эфира на движение света. Ответы на возникшие вопросы мог дать только эксперимент.
Измерения скорости света в произвольной ИСО позволили бы обнаружить движение этой системы относительно эфира и определить скорость этого движения, т. е. обнаружить «эфирный ветер».
Для разрешения «проблемы эфира» американский физик Альберт Майкельсон предложил схему эксперимента, позволявшего с помощью интерференции обнаружить движение Земли относительно эфира. Действительно, если бы свет распространялся в эфире, а эфир был неподвижен относительно Солнца (в гелиоцентрической системе), то при своем движении по орбите Земля должна была бы испытывать «эфирный ветер», подобно тому, как при езде на мотоцикле или велосипеде мы ощущаем встречный поток воздуха даже в безветренную погоду.
В 1887 г. Майкельсон и Морли провели эксперимент, точность измерений в котором была достаточной для обнаружения «эфирного ветра».
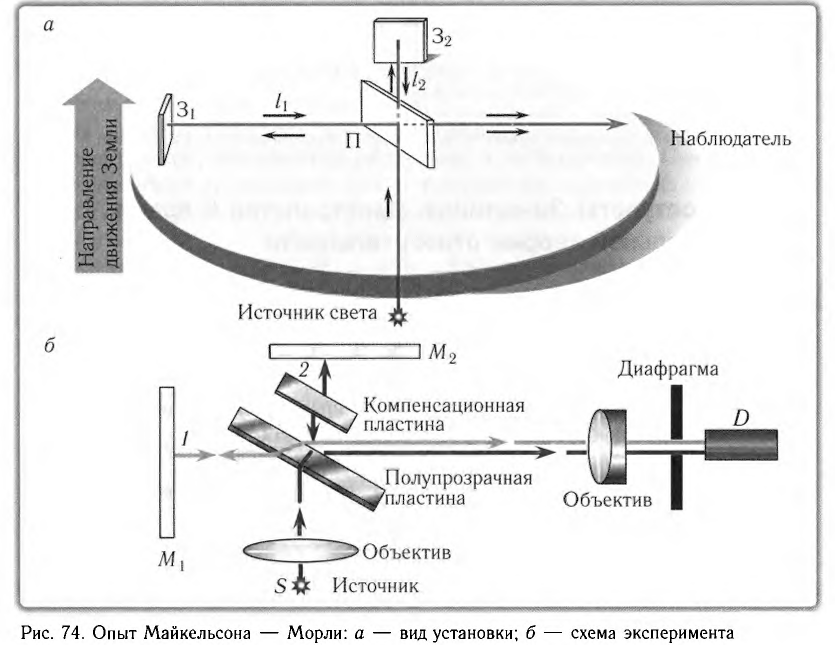
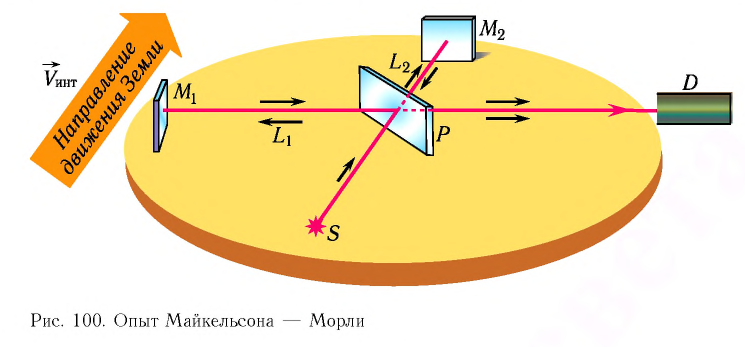
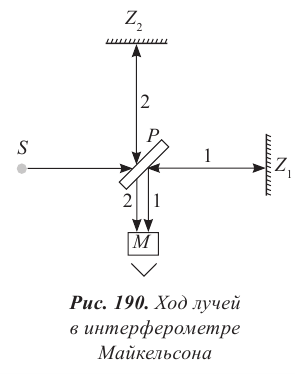
Разберем принципиальную схему их экспериментальной установки (рис. 74, а). На массивной каменной платформе площадью (1,5Х 1,5) м2 и толщиной более 30 см, плававшей в бассейне со ртутью, была собрана оптическая схема, получившая впоследствии название интерферометра Майкельсона. Такая конструкция обеспечивала независимость наблюдаемой интерференционной картины от механических колебаний платформы.
Свет от источника S (рис. 74, б) делился на два пучка I и 2, распространявшихся в дальнейшем во взаимно перпендикулярных направлениях. Пучки отражались от зеркал 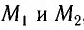
Если заставить один из лучей двигаться вдоль направления движения Земли по орбите относительно Солнца (см. рис. 74, а), а второй — перпендикулярно, то «эфирный ветер» будет «разным» для этих лучей, что должно привести к изменению (сдвигу) интерференционной картины.
Согласно расчетам при развороте платформы на 90° относительно направления движения Земли интерференционная картина должна была сдвинуться на расстояние, приблизительно равное 0,4 интерференционной полосы. Однако ожидаемое смещение не было обнаружено, хотя интерферометр позволял наблюдать сдвиг интерференционной картины даже на 0,01 полосы.
Эти эксперименты повторялись в разное время суток и в различные времена года, но движение Земли относительно эфира не было обнаружено.
Отрицательный результат опыта Майкельсона — Морли был одной из величайших загадок физики конца XIX — начала XX в.
Постулаты Эйнштейна. Пространство и время в специальной теории относительности
Фундаментальное утверждение, лежащее в основе теории и принимаемое без f доказательства, называется постулатом (аксиомой). В физике постулат, как правило, является обобщением экспериментальных фактов.
Для объяснения отрицательного результата опыта Майкельсона — Морли немецкий физик Альберт Эйнштейн в 1905 г. предложил новую теорию, получившую название специальная теория относительности (СТО).
Согласно принципу относительности Галилея все ИСО равноправны по отношению к механическим явлениям. Отрицательный результат опыта Майкельсона — Морли показал, что все ИСО равноправны и но отношению к электромагнитным явлениям (распространению света).
Кроме того, посредством многочисленных экспериментов был установлен факт постоянства скорости света в вакууме в любых ИСО, который не согласуется с классическим законом сложения скоростей. Для преодоления противоречий между механическими и электромагнитными явлениями Эйнштейну пришлось изменить классические представления о пространстве и времени.
В 1915 г. Эйнштейн разработал общую теорию относительности, которая ; представляет собой релятивистскую теорию тяготения.
В основе специальной теории относительности, или в дальнейшем просто теории относительности, лежат два постулата.
В первом постулате Эйнштейн зафиксировал важнейший факт равноправия всех ИСО. Этот постулат представляет собой обобщение принципа относительности Галилея на все физические явления.
Первый постулат (постулат относительности)
- все законы физики, описывающие любые физические явления, должны иметь одинаковый вид во всех ИСО.
Этот же постулат может быть переформулирован и таким образом:
- в любых ИСО все физические явления при одинаковых начальных условиях протекают одинаково.
Другими словами, в любых ИСО все одинаковые эксперименты дают одинаковые результаты. Это означает, что никакими экспериментами невозможно установить, например, движемся мы равномерно и прямолинейно или покоимся относительно некоторой системы отсчета.
Для примера представим, что мы находимся в полностью закрытом вагоне (без окон) поезда, движущегося равномерно и прямолинейно. Понятно, что в этом случае будут отсутствовать толчки, покачивания, торможения и другие свидетельства движения в обычных поездах. Сможем ли мы установить факт движения поезда?
Согласно постулату относительности никакими физическими экспериментами, проводимыми в этом вагоне, невозможно установить факт движения поезда относительно Земли. Иными словами, любые эксперименты, даже с использованием самой современной аппаратуры, приведут к тем же результатам, что и в неподвижном относительно Земли вагоне.
Первый постулат стимулировал появление второго постулата. Как известно, самая большая скорость, измеренная физиками, — это скорость света в вакууме. Для равноправия всех ИСО необходимо потребовать, чтобы эта предельная скорость была в них одинаковой. В противном случае, измеряя эту скорость, можно установить факт движения или, по крайней мере, факт отличия данной системы отсчета от других, что запрещено первым постулатом. Оказалось, что построение строгой теории, объясняющей все известные физические явления в ИСО, невозможно без использования еще одного постулата.
Второй постулат (постулат постоянства скорости света)
- во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Таким образом, скорость света в вакууме в теории Эйнштейна занимает особое положение. Кроме того, эта скорость является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Этим механика теории относительности принципиально отличается от классической механики.
Известный немецкий физик Герман Минковский считал, что время следует рассматривать как четвертое измерение. В 1908 г. он начал свою лекцию на 80-м съезде немецкого общества естествоиспытателей и врачей следующими словами: «Взгляды на пространство и время, которые я хочу изложить перед вами, развивались на основе экспериментальной физики, и в этом их сила. Они радикальны. Отныне пространство само по себе и время само по себе обратились в простые тени, и только какое-то единство их обоих сохранит независимую реальность».
Сложившуюся ситуацию в 1926 г. в стихах описал Федор Сологуб:
Постулаты Эйнштейна. Пространство и время в СТО
Другими словами, в любых ИСО все одинаковые эксперименты дают одинаковые результаты. Это означает, что никакими экспериментами невозможно установить, например, движемся мы равномерно и прямолинейно или покоимся относительно некоторой системы отсчета.
Для примера представим, что мы находимся в полностью закрытом вагоне (без окон) поезда, движущегося равномерно и прямолинейно. Понятно, что в этом случае будут отсутствовать толчки, покачивания, торможения и другие свидетельства движения в обычных поездах. Сможем ли мы установить факт движения поезда?
Согласно постулату относительности никакими физическими экспериментами, проводимыми в этом вагоне, невозможно установить факт движения поезда относительно Земли. Иными словами, любые эксперименты, даже с использованием самой современной аппаратуры, приведут к тем же результатам, что и в неподвижном относительно Земли вагоне.
Первый постулат стимулировал появление второго постулата. Как известно, самая большая скорость, измеренная физиками, — это скорость света в вакууме. Для равноправия всех ИСО необходимо потребовать, чтобы эта предельная скорость была в них одинаковой. В противном случае, измеряя эту скорость, можно установить факт движения или, по крайней мере, факт отличия данной системы отсчета от других, что запрещено первым постулатом. Оказалось, что построение строгой теории, объясняющей все известные физические явления в ИСО, невозможно без использования еще одного постулата.
Второй постулат (постулат постоянства скорости света):
во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Таким образом, скорость света в вакууме в теории Эйнштейна занимает особое положение. Кроме того, эта скорость является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Этим механика теории относительности принципиально отличается от классической механики.
Известный немецкий физик Герман Минковский считал, что время следует рассматривать как четвертое измерение. В 1908 г. он начал свою лекцию на 80-м съезде немецкого общества естествоиспытателей и врачей следующими словами: «Взгляды на пространство и время, которые я хочу изложить перед вами, развивались на основе экспериментальной физики, и в этом их сила. Они радикальны. Отныне пространство само по себе и время само по себе обратились в простые тени, и только какое-то единство их обоих сохранит независимую реальность».
Относительность одновременности событий, длин и промежутков времени
Для описания движения тел необходимо не только выбрать систему отсчета, но и установить способ определения моментов времени, в которые та или иная точка движущегося тела занимает известное положение.
Когда движущееся тело и часы находятся в одном месте, то можно непосредственным наблюдением констатировать одновременность двух событий. Если же часы и движущееся тело находятся в разных местах, то речь идет об установлении одновременности двух событий, из которых одно происходит «здесь», а другое — «там». В этом случае ситуация совершенно иная, так как нужен сигнал, который дал бы возможность знать, что «там» это событие произошло. В этом случае необходимо знать закономерности распространения реальных сигналов, так как сигнал не сможет «добраться» до часов мгновенно — для этого ему потребуется некоторый промежуток времени.
Для определения момента времени можно использовать любые сигналы, однако наиболее практичны световые импульсы. Действительно, из второго постулата СТО следует, что скорость света в вакууме одинакова во всех ИСО, т. е. она не зависит ни от частоты, ни от интенсивности световой волны. На этот процесс не влияет также движение источников или приемников света. В этой связи можно утверждать, что световые импульсы, испущенные из одной точки пространства в одном направлении, распространяются в вакууме с одной и той же скоростью, ни один из импульсов не сможет обогнать другого.
Если бы мы располагали сигналами, которые распространяются мгновенно, то могли бы отсчитывать момент времени, когда «там» произошло событие, непосредственно по часам, находящимся «здесь». Однако такими сигналами мы не располагаем. Даже наиболее быстрые световые сигналы распространяются, хоть и с очень большой, но конечной скоростью. Вследствие этого, в показания часов необходимо вносить поправку на время распространения светового сигнала «отсюда» — «туда» и «оттуда» — «сюда». При использовании различных часов 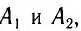
Для синхронизации часов, находящихся в точках 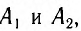
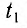
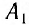
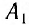
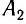
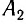
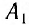
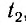
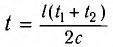
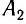
Часы синхронизированы между собой, т. е. идут с одинаковой скоростью. Приращению показаний часов 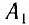
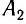
Таким образом, скорость световых сигналов играет существенную роль, если для отсчета времени в разных местах мы пользуемся одинаковыми синхронизированными часами. Именно поэтому в набор «инструментов», при помощи которых производятся измерения промежутков времени и расстояний, должны входить источники световых сигналов, поскольку скорость света в соответствии с постулатом Эйнштейна является величиной постоянной.
Замедление времени
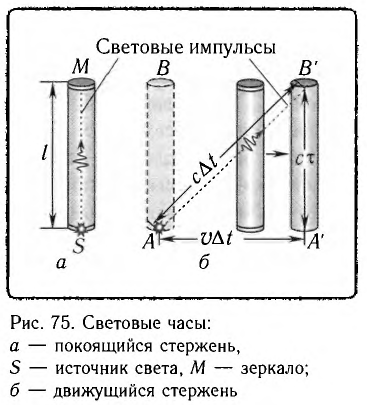
Рассмотрим воображаемые световые часы (рис. 75). Лампа S и зеркало М закреплены на противоположных концах стержня длиной l (рис. 75, а). Свет от вспышки лампы S отражается зеркалом М и попадет на фотоэлемент, находящийся рядом с лампой. Он снова включает лампу. Для наблюдателя, покоящегося относительно стержня, промежуток времени между вспышками 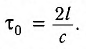
Найдем теперь промежуток времени, который понадобится световому сигналу для возвращения к фотоэлементу, если стержень движется со скоростью 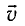
Если сигнал достигает зеркала за промежуток времени 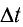
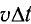
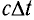
откуда находим
С учетом того, что такой же промежуток времени займет возвращение сигнала к лампе 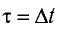
где 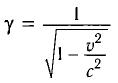
Окончательно имеем:
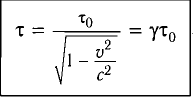
Промежуток времени 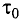
Замедление времени — это объективное свойство самого времени, поэтому при движении замедляются физические, биологические процессы, химические реакции и т. д. Соответственно, при движении будет замедляться биологический процесс старения.
Однако следует заметить, что люди, находящиеся на космическом корабле, движущемся со скоростью, близкой к скорости света, не заметят и не почувствуют замедления жизненного ритма. К сожалению, человечество пока не имеет возможности использовать эффект замедления времени для совершения путешествий к звездам.
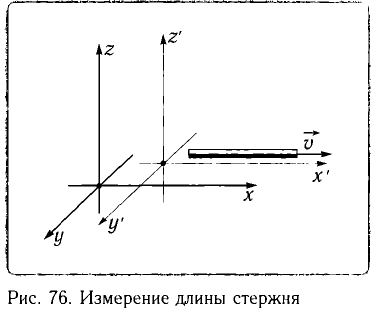
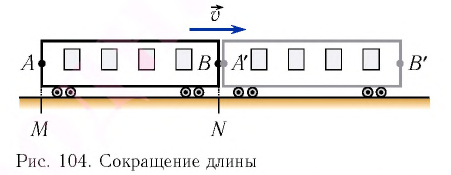
Сокращение длины (масштаба)
Измерить длину стержня означает указать одновременно координаты его начала и конца. Рассмотрим стержень, который движется вдоль своей оси со скоростью 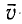
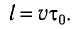
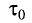
В системе отсчета, связанной со стержнем, также можно определить его длину, измеряя время 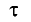
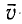
С учетом того, что 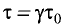
Длина 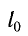
Таким образом, движущееся тело сокращается в направлении своего движения, например вдоль оси Ох. Это сокращение называется лоренцовским сокращением. Поперечные размеры тела, измеренные вдоль осей Оу и Oz, при таком движении не изменяются.
Относительность одновременности
Свет от вспышки, произведенной посередине неподвижного стержня длиной 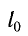
Пусть стержень движется со скоростью 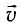
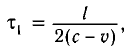
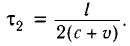
Причина неодновременного прихода света к концам движущегося стержня очевидна: один конец движется навстречу свету, другой — в противоположном направлении.
Таким образом, два события, происходящие в различных точках, одновременные в покоящейся ИСО 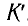
События, которые были одновременными в одной инерциальной системе отсчета, перестают быть таковыми в другой системе отсчета, движущейся относительно первой с некоторой постоянной скоростью.
Это означает, что в рамках СТО время теряет свою абсолютность. Оно, как и пространственная координата, зависит от системы отсчета и преобразуется определенным образом при переходе от одной инерциальной системы отсчета к другой.
Для оценки сокращения длины и замедления времени можно воспользоваться таблицей 7.
Таблица 7
Сокращение длины и замедление времени при релятивистском движении
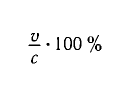 |
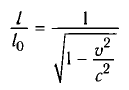 |
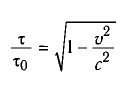 |
| 10,00 | 1,005 | 0,9950 |
| 50,00 | 1,155 | 0,8660 |
| 80,00 | 1,667 | 0,6000 |
| 90,00 | 2,294 | 0,4360 |
| 99,00 | 7,090 | 0,1410 |
| 99,90 | 22,36 | 0,04470 |
| 99,99 | 70,71 | 0,01410 |
| 99,999 | 223,6 | 0,004470 |
Из таблицы видно, что, например, даже при скорости движения 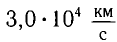
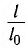
Ракеты и спутники для их движения вокруг Земли необходимо запускать с
первой космической скоростью, модуль которой 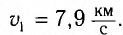
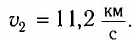
Результаты СТО привели к изменению закона сложения скоростей. Пусть тело движется вдоль осей Ох и Ох’ инерциальных систем отсчета К и 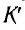
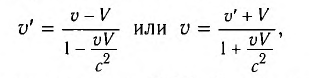
где V — модуль скорости движения ИСО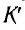
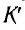
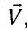
Из соотношений (2) видно, что предельной скоростью распространения материальных объектов или сигналов является скорость света с в вакууме.
Если, например, тело в одной ИСО движется со скоростью, модуль которой равен скорости света v = с, то и в другой ИСО модуль его скорости также будет равен скорости света в вакууме:
Аналогично, если одна ИСО движется относительно другой ИСО со скоростью, модуль которой равен скорости света в вакууме V=c, то модуль скорости движения тела также будет равен скорости света:
При 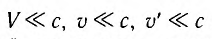
Закон взаимосвязи массы и энергии
В классической механике импульс тела определяется как произведение его массы и скорости:
Сформулированные Эйнштейном постулаты, положенные в основу СТО, заставили физиков пересмотреть взгляды на классическую (ньютоновскую) механику. Классические выражения для импульса и энергии нужно было изменить для новой, уточненной формы записи законов сохранения импульса и энергии.
Таким образом, теория относительности потребовала пересмотра и уточнения законов механики.
Уравнения динамики следует изменить так, чтобы они оставались неизменными при переходе из одной ИСО в другую согласно принципу относительности. В случае малых скоростей (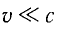
В СТО эффективно применяется соотношение, связывающее полную энергию E и импульс 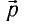
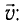
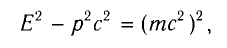
причем масса m здесь та же величина, что и в классической механике.
Выражение для импульса 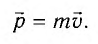
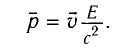
Особенно важно отметить, что формулы (1) и (2) описывают движение частиц во всем интервале возможных скоростей: 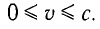
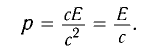
Подставив выражение (3) в формулу (1), получим
Откуда следует, что масса частицы, движущейся со скоростью света, равна нулю (m = 0).
Для частиц с ненулевой массой выразим энергию и импульс через массу и скорость. Подставим выражение (2) в формулу (1):
Откуда получим
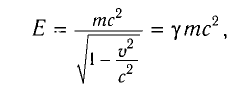
где 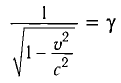
Подставляя выражение (4) в формулу (2), имеем
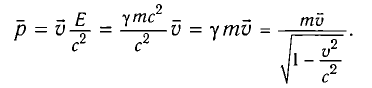
Таким образом, для тел, движущихся со скоростями, близкими к скорости света, их энергия и импульс определяются соотношениями (4) и (5).
Основное уравнение релятивистской динамики записывается в виде
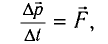
Важнейшим отличием СТО от классической механики является то, что энергия тела не обращается в нуль, даже когда оно покоится (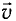
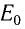
Таким образом, в покоящемся теле таится огромный запас энергии. Трудно переоценить практическое значение этой несложной формулы, поскольку именно она указала на взаимосвязь энергии и массы вещества. На этой формуле основана вся энергетика, в которой энергия покоя топлива переходит в другие виды энергии.
Например, при сгорании 1 м3 метана в газовой горелке (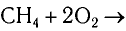
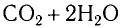
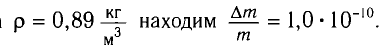
Энергия покоя имеет огромные значения. Например, тело массой m= 1,0 г обладает энергией покоя
Она эквивалентна энергии, выделяющейся при сгорании нефти массой т=2,0 • 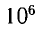
Таким образом, увеличение энергии тела на 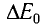
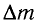
Это соотношение выражает закон взаимосвязи массы тела и энергии покоя.
Подчеркнем, что масса тела меняется всегда, когда меняется его внутренняя энергия. Например, при полном превращении льда массой т в воду относительное изменение массы 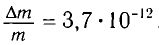
Согласно СТО масса частицы является мерой энергии, содержащейся в покоящейся частице, т. е. мерой энергии покоя. Это свойство массы было неизвестно в классической механике.
Масса элементарной частицы является одной из ее важнейших характеристик, которую стараются измерить с наибольшей точностью. Ее определяют из формулы (I):
посредством измерения энергии и импульса частицы.
В СТО, так же как и в классической механике, масса изолированной системы тел сохраняется и не изменяется со временем.
Кинетическую энергию 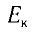
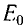
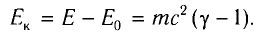
В случае, когда скорость частицы стремится к скорости света, кинетическая энергия частицы стремится к бесконечности. Это означает, что частицу, обладающую некоторой массой, невозможно разогнать до скорости света.
Полученные формулы применимы к любому сложному телу, состоящему из многих частиц, причем под массой m необходимо понимать полную массу тела, а под скоростью 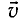
При малых скоростях 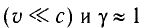
Как видим, теория Эйнштейна не противоречит теории Ньютона. Более того, она содержит ее в себе как частный случай при малых скоростях.
Согласно принципу соответствия любая новая теория, претендующая на более глубокое описание физических явлений (соответственно и на более широкую область применимости), должна включать в себя предшествующие теории как предельные случаи.
Принцип соответствия определяет условия согласования между собой различных моделей данного явления. Этот принцип выражает требование преемственности знаний. Таким образом, новая теория должна включать в себя предшествующую ей теорию и указывает пределы применимости ее идей и методов расчета. На практике все формулы СТО переходят в формулы классической механики, в предположении, что
Итоги:
Первый закон Ньютона постулирует существование инерциальных систем отсчета (ИСО), в которых свободное тело (не подверженное внешним воздействиям) находится в состоянии покоя или движется равномерно и прямолинейно.
Специальная теория относительности (СТО) основывается на двух постулатах (принципах).
Первый постулат (постулат относительности):
- все законы физики, описывающие любые физические явления, должны иметь одинаковый вид во всех ИСО.
Второй постулат (постулат постоянства скорости света):
- во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Скорость света в вакууме является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Релятивистские эффекты:
- замедление времени;
- сокращение длины;
- относительность одновременности.
Сокращение испытывает только размер предмета вдоль направления своего движения:
Поперечные размеры остаются неизменными.
Промежуток времени 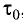
Часы, движущиеся равномерно относительно данной ИСО, идут медленнее неподвижных часов и показывают тем больший промежуток времени, чем больше их скорость движения:
Энергия покоя 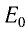
Закон взаимосвязи массы и энергии покоя:
Основы специальной теории относительности
Роль скорости распространения света в вакууме настолько важна в физике и технике, а современные методы ее измерения настолько надежны, что в 1983 г. было принято решение считать значение этой скорости точным. Оно равно 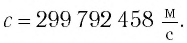
распространяется в вакууме не только видимый свет, но и любое электромагнитное излучение — от радиоволн до гамма-излучения.
Развитие науки и техники позволило физикам уже на рубеже XIX—XX вв. провести достаточно точные измерения скорости света. Как оказалось, скорость света в вакууме не зависит ни от скорости движения приемника света, ни от скорости источника, излучающего свет.
Эти удивительные экспериментальные результаты привели физиков к пересмотру представлений о свойствах пространства и времени. Была создана специальная теория относительности (СТО) — раздел физики, в котором изучаются свойства пространства и времени, а также законы движения тел при скоростях, сравнимых со скоростью света.
Специальная теория относительности называется также релятивистской теорией (от лат. relativus — относительный). Явления, происходящие при скоростях, сравнимых со скоростью света, характеризующие их величины (скорость, энергия, импульс и т. д.) и законы этих явлений тоже называются релятивистскими.
Заметим, что помимо специальной теории относительности (СТО) имеется и общая теория относительности (ОТО), которая обобщает СТО на случай, когда существенны гравитационные явления.
В повседневной жизни и в современных технологиях (даже космических) мы не встречаемся с релятивистскими скоростями. Зачем же изучать теорию относительности? Для этого имеется целый ряд причин.
- Во-первых, основную информацию об окружающем мире мы получаем с помощью зрения, непосредственно воспринимая световое излучение. Таким образом, «самый релятивистский» объект природы — свет играет важнейшую роль в жизни каждого человека.
- Во-вторых, как показывает весь накопленный опыт, скорость света в вакууме имеет фундаментальное, выделенное значение: ни один сигнал не может распространяться, ни одна частица не может двигаться быстрее света.
- В-третьих, релятивистская теория необходима для объяснения явлений в атомной и ядерной физике, в физике элементарных частиц. Без использования законов СТО невозможно и создание ускорителей элементарных частиц.
- В-четвертых, релятивистская теория играет важную роль в изучении Вселенной. Обнаружены галактики, движущиеся с огромными скоростями. Без релятивистской теории нельзя объяснить свойства таких астрономических объектов, как «черные дыры», нейтронные звезды, пульсары.
Наконец, каждый человек должен иметь современные представления о пространстве и времени, об относительных и абсолютных явлениях, о таких удивительных релятивистских эффектах, как относительность одновременности, замедление времени и сокращение длины при движении объектов.
Принцип относительности Галилея и электромагнитные явления
Система отсчета, относительно которой все тела покоятся или движутся с постоянной скоростью при отсутствии воздействия на них, называется инерциальной (ИСО).
Принцип относительности Галилея: во всех ИСО все механические явления при одинаковых начальных условиях происходят одинаковым образом. Классический закон сложения скоростей: 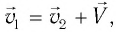
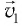
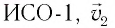
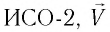
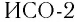
Создание специальной теории относительности исторически связано с развитием электродинамики — науки об электрических и магнитных явлениях. За два столетия, которые отделяли физику Галилея и Ньютона от физики Максвелла и Герца, в ней накопилось огромное количество новых научных фактов. В то же время представление о мироздании базировалось на механической картине мира, основанной на механике Галилея — Ньютона (классической механике).
Как известно, в классической механике такие понятия, как координата, скорость, траектория тела, являются относительными — они изменяются при переходе от одной ИСО к другой. В то же время, некоторые понятия и величины в классической физике считались абсолютными. Например, как само собой разумеющееся принималось положение об абсолютности времени (ход времени везде одинаков). Очевидным следствием этих представлений является классический закон сложения скоростей. Согласно этому закону при переходе к ИСО, которая движется со скоростью 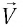
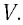
Такие представления согласовывались как с повседневным опытом, так и с экспериментами в механике, акустике, гидродинамике и т. д.
Однако электромагнитные процессы происходят со скоростями, сравнимыми со скоростью света, т. е. гораздо большими, чем скорости движения тел, с которыми имеет дело механика. В связи с этим возникают вопросы: будет ли справедлив принцип относительности Галилея (важнейший принцип классической механики) для электромагнитных явлений? Зависит ли скорость света в вакууме от движения источника и/или приемника излучения, как это должно быть по классической теории? Существует ли в природе предельная скорость? Для ответа на эти вопросы были необходимы новые эксперименты.
Рассматривая проблему распространения электромагнитных волн (света), полезно обратиться к хорошо изученным закономерностям поведения звуковых волн. Они могут распространяться только в упругой среде — газообразной, жидкой или твердой. Естественно принять предположение, что и для распространения света необходима некоторая среда. Ее назвали мировым эфиром. При таком подходе решающим становится вопрос о скорости света, измеренной наблюдателем, который движется относительно эфира.
Вернемся к аналогии со звуком. Пусть скорость звука в покоящейся среде равна 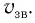
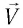
А что получится для распространения света? Зависит ли скорость света от движения лаборатории, в которой проводятся измерения этой скорости? В качестве такой быстро движущейся лаборатории 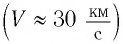
Как повлияет «эфирный ветер» на скорость света в системе отсчета «Земля»?
В 1887 г. американские физики А. Майкельсон и R Морли провели эксперимент, точность измерений в котором была достаточной для обнаружения влияния «эфирного ветра».
Разберем принципиальную схему их экспериментальной установки, получившей название интерферометр Майкельсона (рис. 100). Он состоял из оптического устройства, расположенного на массивной каменной платформе, плавающей в бассейне с ртутью. Такая конструкция практически исключала влияние механических колебаний платформы на оптические процессы. Свет от источника 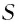
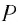
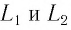
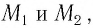
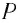
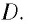
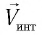
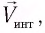
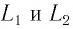
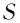
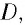
При повороте платформы на 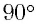
Эксперимента повторялись в разное время суток и в разные времена года (т. е. при различных направлениях скорости интерферометра относительно эфира). Во всех случаях смещение отсутствовало. Это было настолько же невероятно, как если при езде на мотоцикле вы не почувствовали бы встречного воздушного потока.
Результаты опыта Майкельсона — Морли и многих других экспериментов по измерению скорости света привели к выводу о независимости скорости света в вакууме как от движения приемника, так и от движения источника излучения. Представления о существовании мирового эфира оказались несостоятельными.
Данный факт был одной из величайших загадок физики конца XIX — начала XX в. Обнаружилось явное противоречие между экспериментом и классическими представлениями. Так, при переходе от одной ИСО к другой, согласно классическому закону сложения скоростей, к скорости света должна векторно прибавляться скорость движения этих ИСО друг относительно друга. Однако эксперимент упрямо утверждал, что скорость света в вакууме постоянна и во всех ИСО одинакова.
Это был вызов механической картине мира, которая складывалась веками.
Выдающиеся ученые того времени (А. Пуанкаре, Г. А. Лоренц и др.) выдвинули целый ряд полезных идей для объяснения этого противоречия. Однако решающий шаг был сделан в 1905 г. 25-летним физиком .Альбертом Эйнштейном, работавшим тогда техническим экспертом Федерального патентного бюро в Берне (Швейцария). Им была создана новая теория пространства и времени, получившая название специальная теория относительности. Эта революционная теория позволила не только объяснить результат опыта Майкельсона — Морли, но и положила начало новому этапу развития физики.
Постулаты специальной теории относительности. Относительность одновременности
Фундаментальное утверждение, лежащее в основе теории и принимаемое без доказательства, называется постулатом (аксиомой). В физике постулат, как правило, является обобщением экспериментальных фактов.
Как отмечалось в предыдущем параграфе, физика столкнулась с противоречием между постоянством скорости света в вакууме и классическим законом сложения скоростей. Проиллюстрируем эту проблему на простом примере: автомобиль движется со скоростью 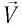
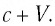
Для преодоления указанного противоречия пришлось глубоко проанализировать и пересмотреть классические представления о пространстве и времени, в результате чего была создана специальная теория относительности.
В основу данной теории Эйнштейн положил два постулата, являющихся обобщением экспериментальных фактов.
Первый постулат СТО (постулат относительности): во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.
Данный постулат представляет собой обобщение механического принципа относительности на все физические явления. Он говорит о том, что никакими экспериментами, проведенными внутри ИСО, невозможно установить, покоится она или движется.
Представим себе вагон, движущийся равномерно и прямолинейно без толчков и покачиваний. Можно ли установить факт движения вагона с помощью экспериментов (механических, электромагнитных и любых других), проводимых внутри него? Весь накопленный в физике опыт показывает, что это невозможно в полном соответствии с первым постулатом СТО.
Второй постулат СТО (постулат постоянства скорости света): во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.
Как уже говорилось, этот постулат полностью соответствует результатам многократно проводившихся экспериментов, но противоречит классическому закону сложения скоростей.
Эйнштейн разрешил это противоречие, проведя глубокий анализ представлений о времени и пространстве.
В основе этого анализа лежит понятие событие. Под событием понимают некоторое явление, происходящее в определенной точке пространства в определенный момент времени. Понятие «событие» является идеализацией реального явления, происходящего очень быстро в очень малой области пространства. Примером события может служить вспышка света, выстрел орудия, соударение двух частиц, пересечение спортсменом линии финиша и т. д. Для характеристики времени и места события в определенной ИСО достаточно указать три его координаты и момент времени.
События, произошедшие в один и тот же момент времени, называются одновременными. В классической физике принималось положение об абсолютности одновременности: если два события произошли одновременно в некоторой ИСО, то они одновременны и в любой другой ИСО.
Эйнштейн обратил внимание на то, что абсолютность одновременности вовсе не очевидна. Для решения вопроса об одновременности (или неодновременности) двух событий, происходящих в разных местах некоторой ИСО, необходимо в каждом месте иметь часы, покоящиеся относительно этой ИСО и синхронизованные между собой. Только тогда можно решать вопрос об одновременности событий относительно данной ИСО.
Процедура синхронизации должна опираться на надежно проверенные физические законы. Эйнштейн предложил следующий способ. Пусть в точке 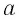
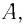
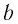
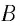
Световой сигнал идет из точки 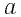
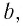
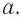
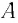
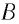
где 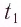
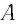
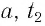
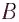
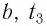
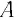
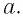
Теперь можно приступить к проверке абсолютности (или относительности) одновременности. Рассмотрим мысленный эксперимент с вагоном и двумя наблюдателями, один из которых 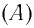
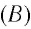
Пусть в центре вагона, в точке 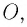
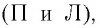
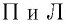
Пусть теперь вагон движется относительно платформы вправо равномерно и прямолинейно (см. рис. 102) со скоростью 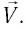
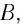
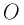
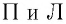
Иную картину видит наблюдатель 
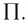
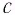
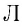
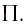
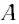
Кто же из наблюдателей прав? Правы оба. События, одновременные в одной ИСО, могут оказаться не одновременными в другой ИСО, движущейся относительно первой.
Таким образом, одновременность событий — понятие относительное. Отметим однако, что одновременные события, произошедшие в одном и том же месте, одновременны в любой ИСО. Их одновременность абсолютна.
Пространство и время в специальной теории относительности
Установление того факта, что одновременность относительна, заставило по-новому взглянуть на свойства пространства и времени. Как изменяются свойства пространства и времени при скоростях, близких к скорости света? Где и как это необходимо учитывать?
Рассмотрим два эффекта СТО: эффект замедления времени и эффект сокращения длины.
Эффект замедления времени
Кажется очевидным, что промежуток времени между двумя событиями не зависит от того, измерен он движущимися или покоящимися часами. Пусть, например, участник автогонки измерил по часам, находящимся в его автомобиле, промежуток времени от старта до финиша. Он не сомневается, что результат будет таким же и у судейской бригады. А отличаются ли эти результаты на самом деле?
Рассмотрим простой мысленный эксперимент. Закрепим лампу 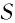
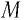
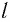
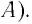
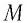
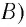
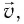
В системе отсчета 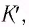
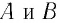
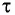
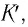
Найдем теперь промежуток времени 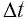
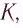
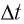
С точки зрения лабораторной системы 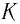
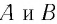
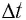
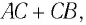
Относительно системы 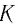
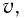
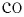
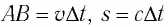
Откуда:
Сравнивая 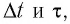
Соотношение (2) показывает, что промежуток собственного времени 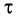
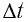
Связь (2) между собственным и лабораторным временем записывают также в виде 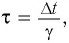
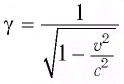
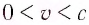
Релятивистское замедление времени состоит в том, что собственное время в 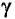
Как определяются понятия собственного и лабораторного времени в общем случае?
Собственным временем 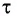
Промежуток времени, измеренный часами ИСО, относительно которой события произошли в разных местах, мы называем лабораторным временем. Для его измерения необходимо как минимум двое часов, синхронизованных между собой.
Вернемся к примеру с автогонками. Промежуток времени от старта до финиша, измеренный по часам в автомобиле, является собственным временем, а промежуток времени между этими событиями, измеренный по часам судейской бригады, — лабораторным. Значит, судьи зафиксируют время, в 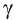
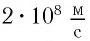
Эффект замедления времени — это его объективное свойство. При релятивистских скоростях эффект может быть очень существенным. Отметим однако, что на воображаемом космическом корабле, движущемся с релятивистской скоростью, находящиеся в нем люди не почувствуют замедления жизненного ритма. Дело в том, что все происходящие в движущейся ИСО процессы (физические, химические, биологические) будут замедляться в одной и той же мере — все они будут идти в соответствии с ходом собственного времени этой ИСО.
Из-за эффекта релятивистского замедления времени, ход часов на орбитальных спутниках отличается от земного на несколько десятков микросекунд за сутки. Это отличие учитывается в спутниковых системах навигации. Без такого учета они не обеспечивали бы необходимой точности позиционирования объектов.
Эффект сокращения длины
Пусть вагон 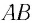
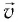
Не останавливая вагон, нанесем на платформу метки 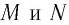
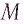
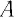
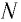
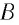
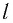
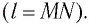
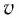
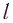
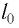
Релятивистская теория утверждает, что это не так. Согласно СТО величины 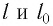
С точки зрения неподвижного наблюдателя движущееся тело сокращается в направлении своего движения в 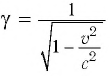
Это явление называется лоренцевым (или релятивистским) сокращением длины. Заметим, что при этом поперечные размеры тела (т. е. измеренные вдоль осей, перпендикулярных направлению движения) не изменяются. Постоянство поперечных размеров мы использовали при выводе формулы (2).
Для оценки эффекта лоренцева сокращения можно воспользоваться таблицей 7. Из нее видно, что при расчетах с точностью 0,5 % для скоростей 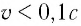
Выведем соотношение (3). Представим, что при прохождении точки вагона 
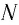
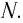
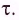
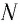
С точки зрения ИСО «вагон» события 1 и 2 произошли в разных местах: красная вспышка — в точке 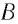
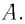
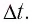
Относительно ИСО «платформа» точка 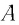
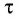
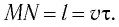
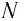
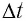
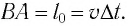
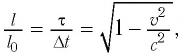
Пример решения задачи №2
Определите модуль скорости 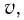
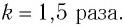
Дано:
Решение Из формулы замедления времени:
где 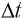
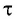
Из этого выражения находим модуль скорости движения корабля:
Ответ:
Преобразования Галилея. Преобразования Лоренца
Пусть в начальный момент времени оси координат двух инерциальных систем отсчета 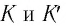
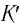
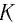
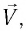
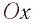
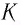
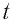
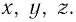
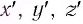
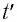
В рамках классических представлений о пространстве и времени ответ очевиден:
где 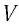
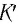
Соотношения (1) называются преобразованиями Галилея. Они отражают абсолютность времени в классической механике 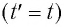
Ясно, что преобразования Галилея противоречат СТО, в которой и время, и длина могут измениться при переходе от одной ИСО к другой. При учете эффектов релятивистского замедления времени и сокращения длины вместо преобразований Галилея (1) получатся соотношения:
Они были найдены нидерландским физиком Хендриком Лоренцом и называются преобразованиями Лоренца. Отметим, что при малых скоростях 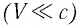
С помощью преобразований Лоренца можно получить релятивистский закон сложения скоростей. Приведем без вывода формулу, выражающую этот закон для простого частного случая. Пусть некоторый объект (тело, частица, световой импульс и т. д.) движется относительно системы 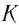
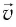
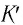
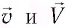
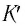
По формуле (3) легко найти, что световой импульс, для которого 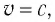
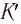
при любом возможном значении 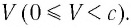
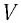
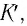
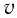
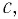
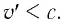
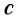
Заметим, что при 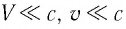
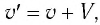
Элементы релятивистской динамики. Взаимосвязь массы и энергии
Изменение представлений о свойствах пространства и времени привело к обнаружению тесной взаимосвязи между массой и энергией и к изменению законов динамики. Чем законы релятивистской динамики отличаются от законов динамики Ньютона?
Необходимость изменения динамики очевидна хотя бы из того, что, согласно законам Ньютона, любое тело можно в принципе разогнать до любой скорости. Приложим к покоящемуся телу массой 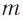
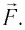
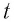
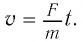
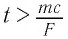
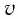
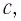
Какие же соотношения динамики изменились при переходе к СТО, а какие — остались неизменными?
Сохранили свой вид законы изменения импульса и энергии тела:
где 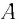
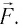
Решим задачу о движении тела под действием постоянной силы по законам динамики СТО. Если при 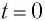
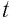
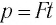
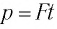
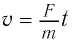
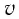
Выразив 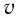
График зависимости 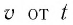
С помощью формулы (3) легко найти промежуток времени 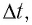
Численные расчеты поданной формуле при
показывают: разгон тела от
произойдет практически за одну секунду, как и по законам Ньютона. Разгон от 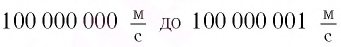
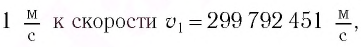
О чем говорит этот пример? О том, что инертность тела неограниченно возрастает по мере приближения скорости тела к скорости света
При этом масса 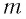
Согласно соотношениям (2) при скорости 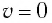
называемой энергией покоя. Таким образом, согласно СТО, масса тела является мерой его энергии в состоянии покоя. Это свойство массы было неизвестно в классической механике. В каждом теле таится огромный запас энергии. Например, тело массой 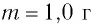
Она эквивалентна энергии, выделяющейся при сгорании 2000 т нефти. Так, благодаря прогрессу физики в 1905 г. человечество узнало о практически неисчерпаемых запасах энергии, содержащихся в любом веществе.
Из равенства (4) следует, что изменение энергии покоя тела на 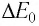
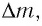
Утверждение о том, что энергия покоя пропорциональна массе, а изменение энергии покоя вызывает изменение массы, называют законом взаимосвязи массы и энергии. Математическим выражением этого закона служат формулы (4) и (5).
Формула (5) применима ко всем явлениям, в которых изменяется внутренняя энергия вещества. При процессах, происходящих на атомно-молекулярном уровне, изменения массы крайне малы. Так, при полном превращении льда в воду относительное изменение массы 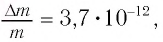
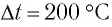
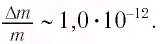
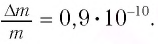
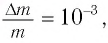
В формуле (2) энергия 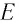
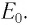
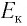
Если соответствие между релятивистским импульсом и классическим импульсом при 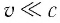
и проделаем простые преобразования
Множитель 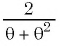
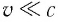
Исключая скорость 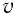
Формула (7) позволяет с большой точностью определить массу частицы по результатам измерений ее энергии и импульса. Такой метод широко используется в физике элементарных частиц.
В начале параграфа было показано, что согласно СТО частица не может достичь скорости света. Данный запрет не распространяется на частицы, масса которых 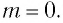
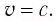
Согласно принципу соответствия любая новая физическая теория, претендующая на более глубокое описание физических явлений, должна включать в себя классическую (ньютоновскую) теорию как предельный случай.
Специальная теория относительности полностью удовлетворяет принципу соответствия. При скоростях 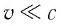
Пример решения задачи №3
Солнце ежесекундно излучает в пространство 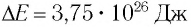
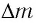
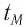
Дано:
Решение
Из закона взаимосвязи массы и энергии находим:
Ответ:
Итоги:
Постулаты специальной теории относительности
Постулат относительности: во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.
Постулат постоянства скорости света: во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.
Предельная скорость
Скорость света в вакууме является предельной скоростью движения материальных объектов и распространения сигналов.
Релятивистское замедление времени
Промежуток собственного времени 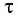
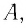
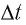
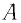
Релятивистское сокращение длины
Линейный размер движущегося тела сокращается в направлении его движения: 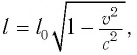
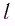
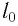
Энергия и импульс тела
Энергия, импульс тела и его инертность неограниченно растут при приближении скорости тела к предельной скорости
Взаимосвязь энергии и массы
Энергия покоя 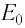
Изменения массы и энергии покоя взаимосвязаны:
Элементы теории относительности
Специальная теория относительности А. Эйнштейна, созданная в начале XX в., в корне изменила мировоззрение ученых. Согласно его теории скорость света абсолютна и не зависит от выбора системы отсчета, время и пространство в различных системах отсчета отличаются. К пересмотру представлений о пространстве и времени привело развитие электродинамики.
Изучив подраздел, вы сможете:
- сопоставлять теорию относительности Эйнштейна с принципом относительности Галилея;
- объяснять релятивистские эффекты, используя постулаты Эйнштейна и преобразования Лоренца, при решении задач;
- объяснять принцип действия ускорителей заряженных частиц с учетом имеющих место в них релятивистских эффектов.
Принцип относительности в механике
Принцип относительности в классической механике позволяет использовать три основных закона динамики в любых инерциальных системах отсчета. Для определения скорости, перемещения и координаты тела при переходе из одной системы отсчета в другую используют формулы сложения скоростей и перемещений и формулы преобразования Галилея. Изменение скорости движения тела не зависит от выбора системы отсчета, все механические явления протекают в них одинаково.
Конечность и предельность скорости света
Во второй половине XIX в. Максвелл сформулировал законы электродинамики.
Изучая вопрос о том, как влияет выбор системы отсчета на протекание электромагнитных явлений, ученые выявили противоречия электродинамики и принцип относительности Галилея. В соответствии с формулой сложения скоростей скорость света может быть равной 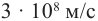
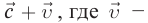
Вспомните! Один из выводов теории Максвелла – это конечность и предельность скорости света. Для вакуума: 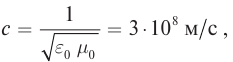
«Мировой эфир» как преимущественная система отсчета в электродинамике.
Опыт Майкельсона и Морли
Ученые XIX века были уверены, что электромагнитные колебания и связанные с ними процессы происходят в упругой среде – эфире, который заполняет все пространство и проникает во все тела. Голландский физик Х. Лоренц предположил, что всепроникающий «мировой эфир» − это преимущественная система отсчета, относительно которой выполняются законы электродинамики Максвелла. Скорость света в вакууме относительно «мирового эфира» имеет одинаковое значение по всем направлениям.
Если в системе отсчета, связанной с «мировым эфиром», скорость света равна 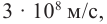
Интерферометр Майкельсона, с помощью которого ученые должны были определить скорость Земли относительно эфира, представляет собой массивную плиту, плавающую на поверхности ртути. Такие меры были необходимы для сохранения длины плеча интерферометра при его повороте на 90° к направлению движения Земли.
Если скорость света зависит от скорости движения системы отсчета, то время распространения лучей от пластины до зеркал и обратно должно отличаться. По расчетам ученых, различие в скоростях распространения света к зеркалам должно было привести к появлению разности хода лучей 1 и 2; поскольку время распространения первого луча больше времени распространения второго. Расчеты показывают, что время распространения лучей отличается в 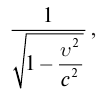
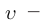
В момент достижения точки наблюдения M, колебания векторов 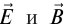
- Заказать решение задач по физике
Принцип действия интерферометра:
На плите установлен источник света S. Луч от источника проходит через полупрозрачную пластину 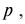
Пластина разделяет луч на два: первый, дважды преломившись, распространяется по направлению движения Земли, отражается зеркалом 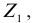
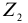
Преобразования Лоренца
Изучив результаты опыта Майкельсона и Морли, Лоренц предположил, что плечо интерферометра, расположенного по направлению движения Земли и распространения луча, сокращается в результате взаимодействия с эфиром. Оно становится равным:
где 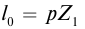
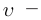
При этом условии время распространения двух лучей, при равных скоростях станет одинаковым. На основе такого предположения и уравнений кинематики Лоренц вывел обобщенные формулы расчета координаты и времени движения тела, при переходе из одной инерциальной системы отсчета в другую:
где 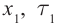
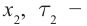
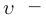
Постулаты теории относительности А. Эйнштейна
Результаты опытов Майкельсона и Морли совершенно иначе были интерпретированы А.Эйнштейном. Он отказался от классических представлений о пространстве и времени и ввел два постулата на основе двух принципов: принципа относительности и принципа постоянства скорости света:
- Все физические процессы протекают одинаково в различных инерциальных системах отсчета.
- Скорость света в вакууме одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости движения источника, ни от скорости движения приемника.
В соответствии с постулатами Эйнштейна пространство и время не абсолютны. При переходе из одной системы отсчета в другую они меняются. Этот эффект наблюдается при движении тел со скоростью, сравнимой со скоростью света.
Альберт Эйнштейн (1879–1955) – физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 г., общественный деятель-гуманист. Эйнштейн – автор более 300 научных работ по физике. Он разработал несколько значительных физических теорий.
Нет пространства и времени, а есть их единство. А. Эйнштейн
Релятивистские эффекты
Явления, описываемые теорией относительности Эйнштейна, называют релятивистскими (от лат. relatives – относительный). Такими эффектами являются:
1. Замедление времени:
где 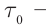
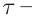
2. Сокращение длины:
где 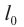
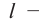
3. Сложение скоростей:
где 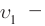
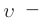
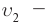
Пример решения задачи №5
Два ускорителя выбрасывают частицы навстречу друг другу со скоростями 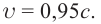
Дано:
Решение:
Ответ: 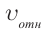
Зависимость массы тела и импульса от скорости
Тело под действием силы движется с ускорением. Согласно второму закону Ньютона импульс и скорость тела со временем возрастает:
Скорость конечна и не может превышать скорость света, следовательно, при достижении значения 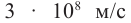
Второй закон Ньютона в импульсном виде для релятивистской динамики имеет вид:
На рисунке 191 дан график зависимости массы тела от скорости его движения. При увеличении скорости до скорости света 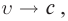
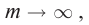
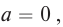
Зависимость импульса тела от скорости в релятивистской механике имеет вид:
Связь между массой и энергией
Согласно специальной теории относительности Эйнштейна масса тела зависит от скорости его движения, следовательно, между массой и энергией существует связь.
В механических и тепловых явлениях скорость движения тел и молекул значительно меньше скорости света, поэтому релятивистский эффект не наблюдается.
Вспомните! Внутренняя энергия тела зависит от скорости молекул, механическая энергия от скорости движения тела. Чем больше скорость движения частицы и тела, тем больше полная энергия тела.
Расчеты показывают, что изменение массы при увеличении температуры 1 кг воздуха на 100 K составляет 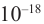
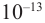
При увеличении скорости движения до скорости, близкой к скорости света, масса и энергия тел резко возрастают.
Формула Эйнштейна
На основе специальной теории относительности Эйнштейн установил связь между массой и энергией тела:

Формула (5) носит глубокий физический смысл: возможно превращение одного вида материи в другой, вещества в поле и, наоборот, поля в вещество. Доказательством такого превращения является взаимодействие элементарных частиц, масса которых полностью превращается в энергию электромагнитного поля в соответствии с формулой Эйнштейна. Примером таких реакций являются аннигиляция пары частица-античастица с образованием двух фотонов. Например, при аннигиляции электрона и позитрона образуется два гамма-кванта, и энергия покоя пары полностью переходит в энергию фотонов:
Существуют также обратные процессы, увеличивающие энергию покоя, а следовательно, и массу, например, − столкновение элементарных частиц. В подобных реакциях могут рождаться новые частицы, массы которых существенно больше, чем у исходных. «Источником» массы таких частиц является кинетическая энергия столкновения.
Учитывая зависимость массы тела от скорости, запишем формулу (5) в виде:
из которой следует, что неподвижное тело обладает энергией покоя:
Справедливость формулы Эйнштейна и существование массы покоя тел подтвердились
Интересно знать! Для получения энергии, равной годовому производству электрической энергии в Республике Казахстан (89,7 млрд кВт · ч), достаточно энергии покоя вещества массой:
экспериментально при взаимодействии элементарных частиц и превращениях атомных ядер. Ядерные реакции сопровождаются выделением колоссальной энергии. При малом значении коэффициента перевода энергии в массу: 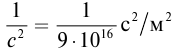
Ускорители заряженных частиц
Ускорители заряженных частиц – это установки для получения заряженных частиц высоких энергий с использованием электрического поля. Управление частицами осуществляется магнитным полем. В зависимости от траектории движения частиц различают циклические и линейные ускорители, в зависимости от вида частиц – ускорители электронов, мезонов, протонов.
В линейных ускорителях, циклотроне, фазотроне, синхротроне, синхрофазотроне заряженные частицы разгоняют до больших скоростей и приводят в столкновение с мишенями. В результате столкновения рождаются новые частицы, массы которых в соответствии с релятивистскими эффектами могут значительно превышать массу покоя ускоренных частиц. В коллайдерах сталкиваются заряженные частицы высоких энергий во встречных пучках. Результат взаимодействия подвергается компьютерной обработке (рис. 192). Основная цель создания ускорителей – исследовать частицы микромира, хранящие тайны строения материи, пространства и времени.
Запомните! Кинетическую энергию тела, движущегося со скоростью, близкой к скорости света, определяют как разность полной энергии и энергии покоя.
Кинетическая энергия в классической и релятивистской механике
В релятивистской механике расчет кинетической энергии с использованием формулы 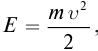
Очевидно, что энергия взаимодействия частицы с другими телами ничтожно мала в сравнении с кинетической энергией, ввиду малой массы и высокой скорости движения, следовательно, потенциальной энергией можно пренебречь. Подставим формулы расчета полной энергии (6) и энергии покоя (7) в формулу (9), получим:
Релятивистская и классическая механика
Согласно принципу относительности Галилея мы считаем, что время и пространство абсолютны, они не зависят ни от тел, находящихся в пространстве, ни от событий, происходящих во времени. Все явления на Земле происходят практически одновременно, их длительность для всех систем отсчета одинакова. Пространство трехмерно и не искажается. Cкорость − величина относительная, она меняется при переходе из одной системы отсчета в другую.
Специальная теория относительности Эйнштейна в корне изменила представление о пространстве и времени. Его теория основана на постоянстве скорости света. Скорость света – величина абсолютная, не зависящая от выбора системы координат. Тогда величины, характеризующие пространство и время, должны быть относительными. Для тел, движущихся со скоростью, близкой к скорости света, пространство искажается: сокращается по направлению движения частицы; время замедляется. Одно и то же событие в различных системах отсчета происходят в разное время, за разный промежуток времени.
Теория Эйнштейна не исключает принцип Галилея. При малых значениях скоростей формулы релятивистской механики превращается в формулы классической механики. Выполняется принцип соответствия, теория относительности Эйнштейна является обобщающей теорией.
Обратите внимание! Ускорители получили практическое применение не только в исследованиях микромира, но и в различных сферах жизни человека. В Институте ядерной физики (ИЯФ) Казахстана производят на циклотронах У-150М, С-30 (рис. 193) радиоизотопы для промышленности и медицины. На ускорителе тяжелых ионов УКП-2-1 проводят ядерно-физический анализ состава образцов твердых тел. Разработан метод измерения содержания плутония-239 в биологических образцах, что позволяет исследовать влияние Семипалатинского ядерного полигона на организм человека.
Итоги:
Постулаты теории относительности А. Эйнштейна:
- 1. Все физические процессы протекают одинаково в различных инерциальных системах отсчета.
- 2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости движения источника, ни от скорости движения приемника.
Принцип относительности
Инерциальными системами отсчета (ИСО) в классической механике принято считать такие системы отсчета, в которых выполняется первый закон Ньютона — закон инерции. Любая система отсчета, движущаяся равномерно относительно ИСО, также является инерциальной.
При ускоренном движении, например при разгоне электропоезда, мы без труда (даже с закрытыми глазами) сможем указать направление ускорения. Однако при равномерном движении электропоезда на перегоне между станциями, не выглядывая в окно, практически невозможно определить, движется он или нет.
Галилео Галилей первым установил, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя определить, покоится данная система отсчета или движется равномерно. Он пришел к выводу, что все механические явления протекают и описываются одинаковым образом в различных ИСО. Это утверждение называется принципом относительности (принципом Галилея).
Согласно этому принципу законы динамики должны иметь одинаковый вид в различных ИСО. С этой точки зрения все инерциальные системы отсчета тождественны (одинаковы).
Для доказательства принципа относительности рассмотрим две системы отсчета: неподвижную инерциальную систему К (с координатами х, у, z) и систему К’ (с координатами х’, у’, z’) (рис. 29), движущуюся с постоянной скоростью 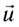
В начальный момент времени начала координат обеих систем и их координатные оси совпадают. На рисунке 29 видно, что в любой момент времени t от начала движения радиус-векторы некоторой точки А в различных системах отсчета связаны соотношением
Это уравнение в проекциях на оси координат можно записать следующим образом:
К преобразованиям координат при переходе от одной ИСО к другой необходимо добавить еще одно уравнение, связывающее время в системах отсчета. В классической механике оно имеет вид
t = t’. (3)
Уравнения (2) и (3), описывающие преобразования координат и времени, носят название преобразований Галилея.
Если рассмотреть случай, когда система К’ движется со скоростью 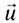
Подчеркнем, что преобразования Галилея справедливы лишь в классической механике (при скоростях движения, малых по сравнению со скоростью света).
При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются преобразованиями Лоренца.
Рассмотрим изменения радиус-векторов в различных ИСО за промежуток времени 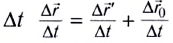
Соответственно, ускорение материальной точки в системе отсчета К определяется выражением
Таким образом, ускорения точки А в системах отсчета, движущихся друг относительно друга равномерно и прямолинейно, одинаковы:
Следовательно, если на точку А в инерциальной системе отсчета К другие тела не действуют 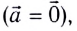
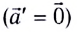
Таким образом, из последнего соотношения следует подтверждение механического принципа относительности: уравнения динамики не изменяются при переходе от одной ИСО к другой. В таком случае говорят, что они инвариантны по отношению к преобразованиям Галилея.
Основные формулы
Кинематические уравнения равноускоренного движения:
Угловая скорость:
Частота вращения:
Период вращения:
Линейная скорость:
Центростремительное (нормальное) ускорение:
- Термодинамика — основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Релятивистская механика в физике

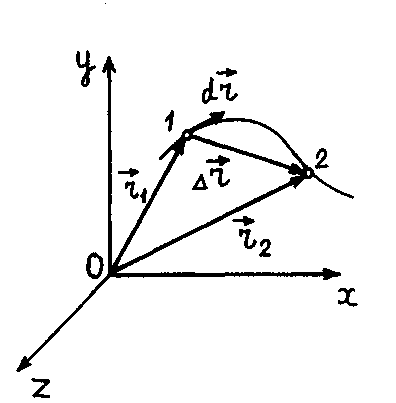
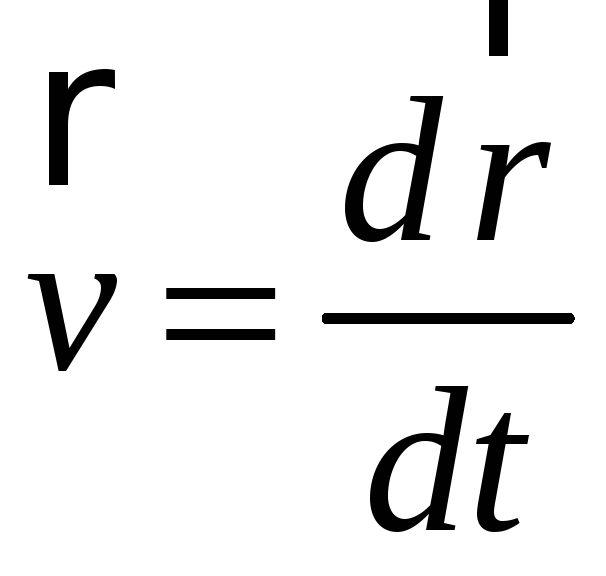
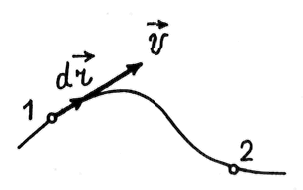
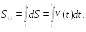
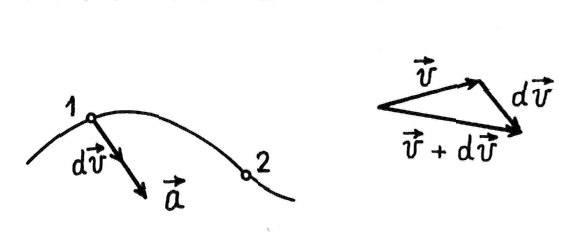
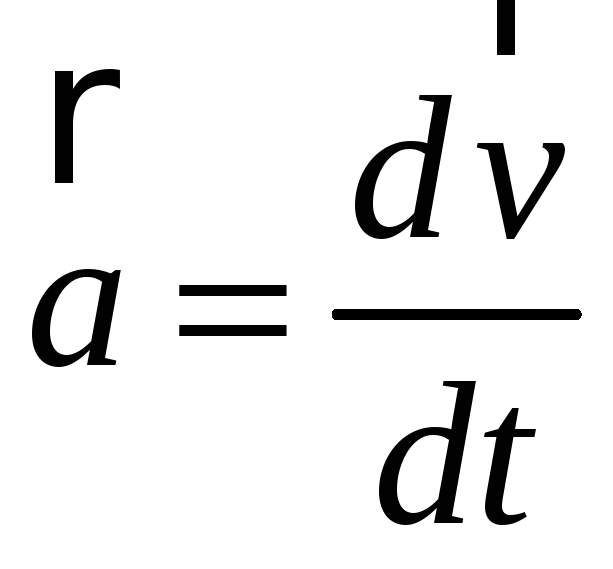
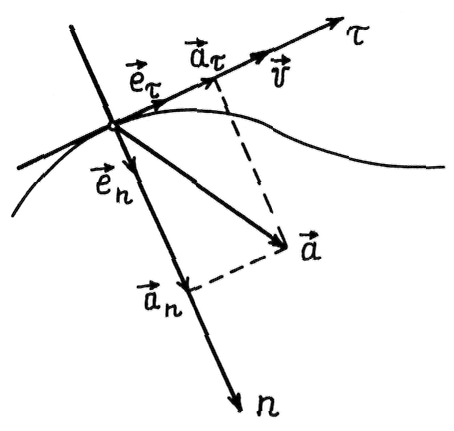
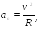
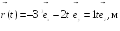
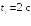
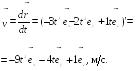
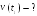
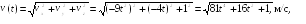
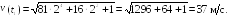
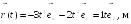
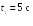
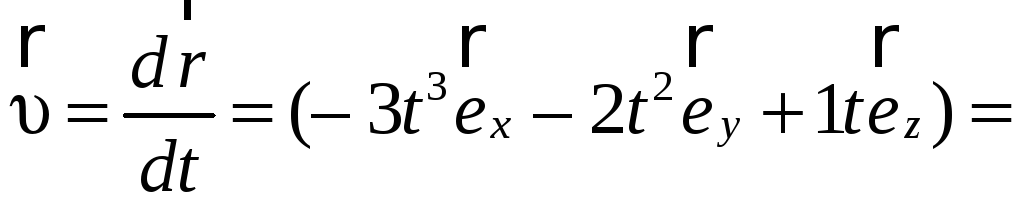
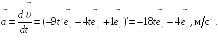
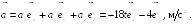

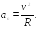
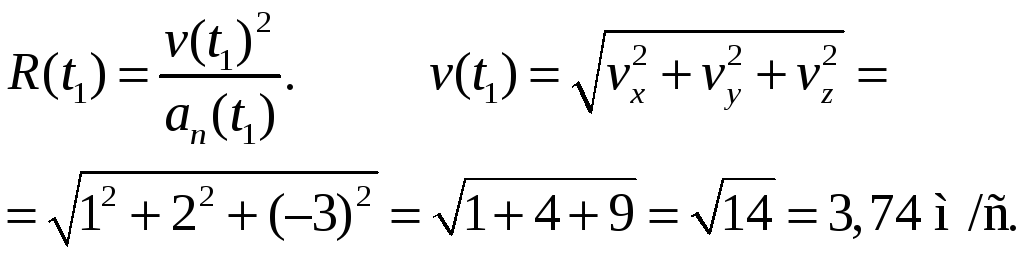
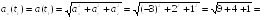

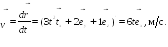
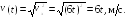
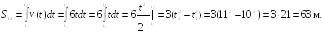
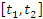 на столь малые интервалы
на столь малые интервалы 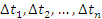 , чтобы изменением скорости частицы в пределах каждого интервала можно было пренебречь.
, чтобы изменением скорости частицы в пределах каждого интервала можно было пренебречь.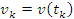 – скорость частицы на промежутке времени
– скорость частицы на промежутке времени 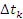 . Тогда перемещение
. Тогда перемещение 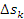 частицы за время
частицы за время 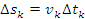 .
.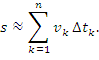
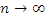 и все
и все 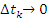 , получаем точную формулу для перемещения частицы за промежуток времени от
, получаем точную формулу для перемещения частицы за промежуток времени от 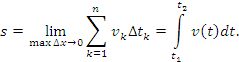
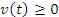 на промежутке
на промежутке 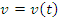 на этом промежутке.
на этом промежутке.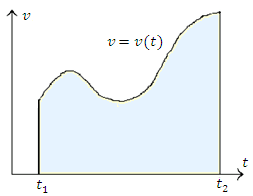
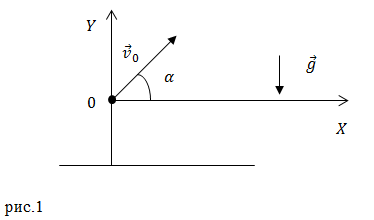
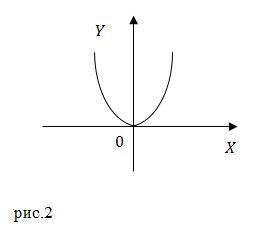
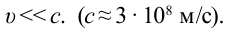
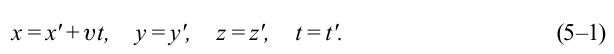
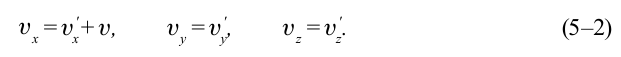
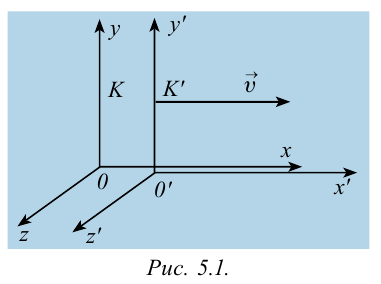
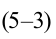

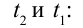
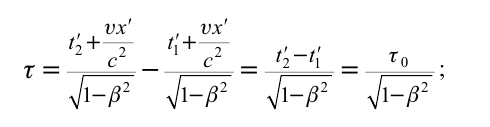

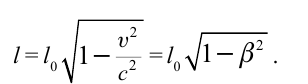
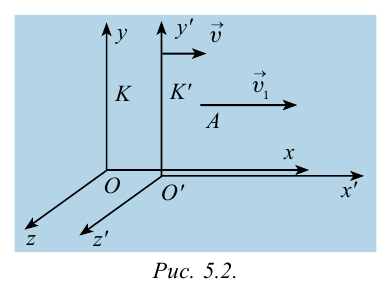

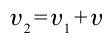
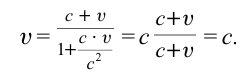

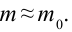
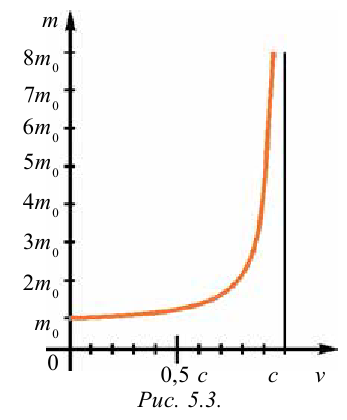
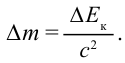

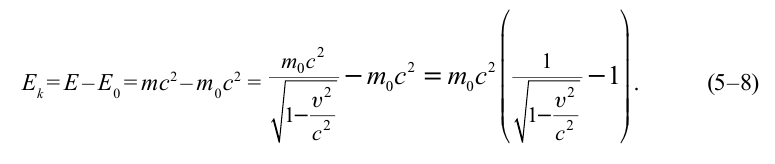
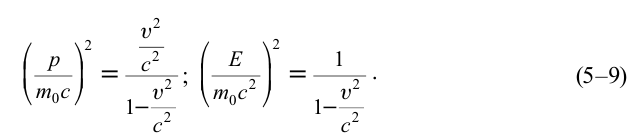
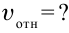
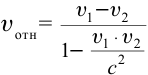
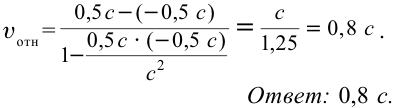
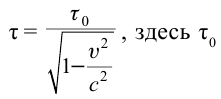 — собственное время.
— собственное время.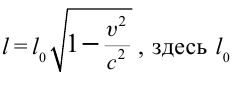 собственная длина.
собственная длина.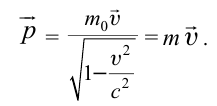
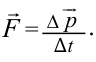
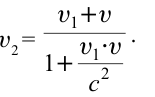
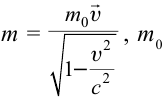 масса покоя.
масса покоя.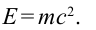
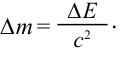
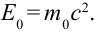
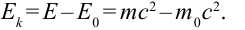
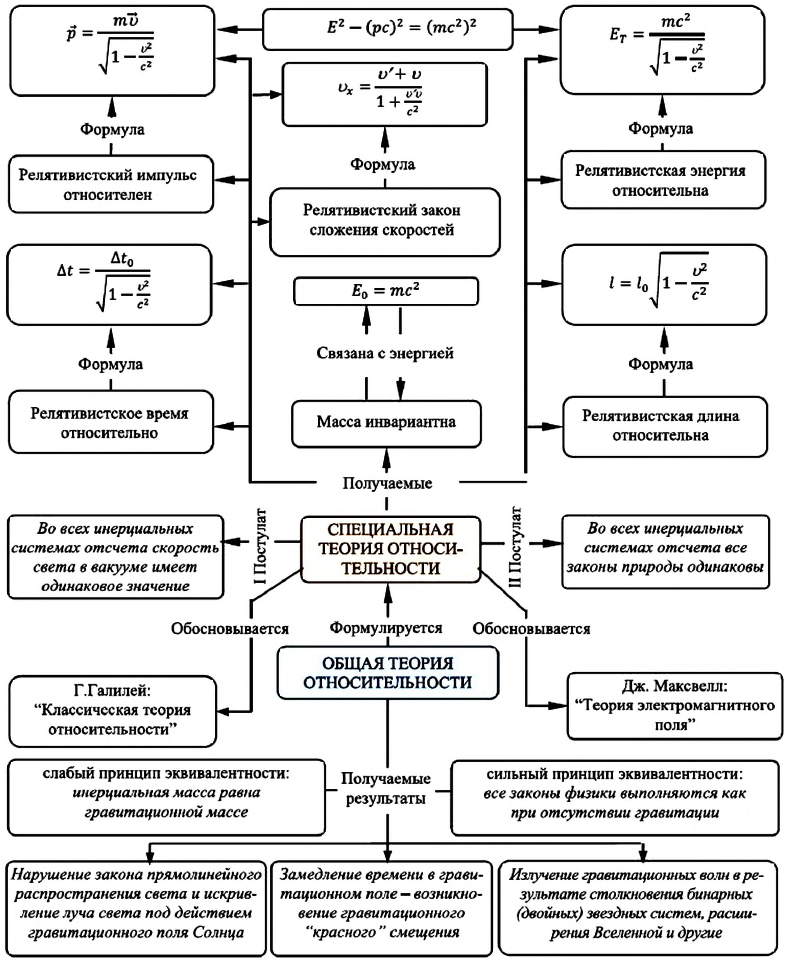
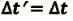
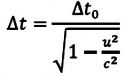
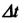 — промежуток времени в неподвижной системе координат,
— промежуток времени в неподвижной системе координат, 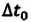 — собственный промежуток времени, связанный с подвижной системой координат.
— собственный промежуток времени, связанный с подвижной системой координат.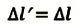
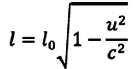
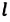 — длина тела в неподвижной системе координат,
— длина тела в неподвижной системе координат, 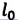 — длина тела в подвижной системе координат.
— длина тела в подвижной системе координат.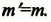
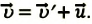 Взаимодействие передается не с конечной скорости с, а мгновенно. При переходе из одной системы координат в
Взаимодействие передается не с конечной скорости с, а мгновенно. При переходе из одной системы координат в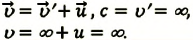
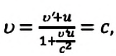 или
или 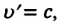 то
то