Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Типы зависимостей
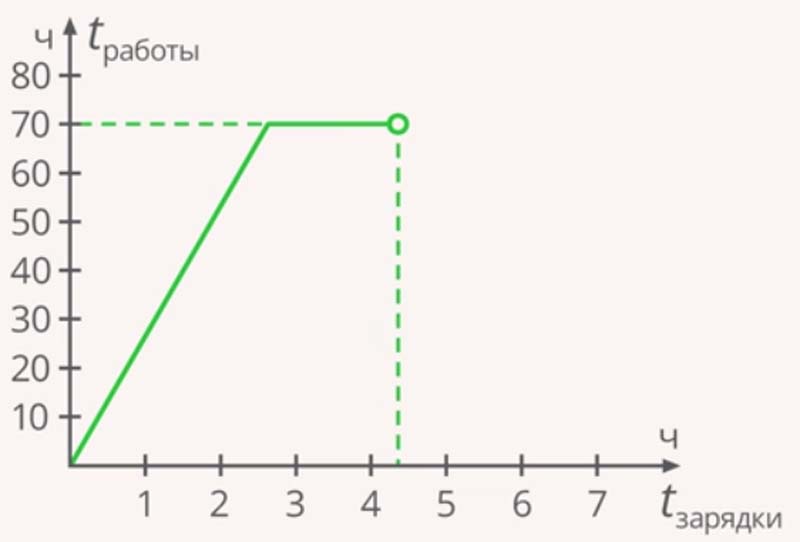
Рассмотрим зарядку батареи. В качестве первой величины возьмем время, которое она заряжается. Вторая величина – время, которое она будет работать после зарядки. Чем дольше будет заряжаться батарея, тем дольше она будет работать. Процесс будет длиться до тех пор, пока батарея не полностью зарядится.
Зависимость времени работы батареи от времени, которое она заряжается
Замечание 1
Такая зависимость называется прямой:
С увеличением одной величины увеличивается и вторая. С уменьшением одной величины уменьшается и вторая величина.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим другой пример.
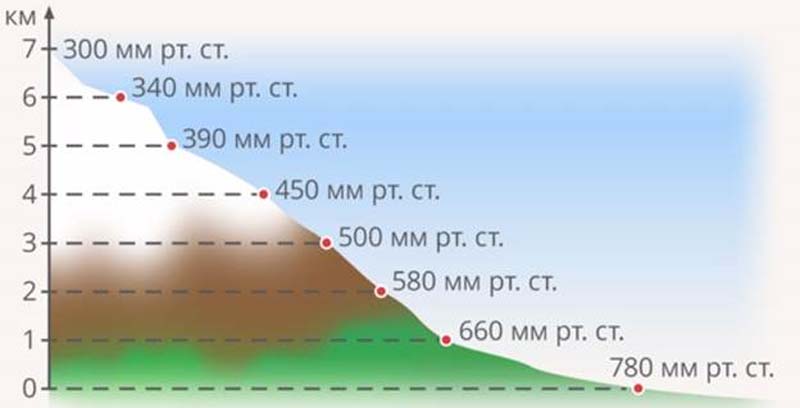
Чем больше книг прочитает ученик, тем меньше ошибок сделает в диктанте. Или чем выше подняться в горы, тем ниже будет атмосферное давление.
Замечание 2
Такая зависимость называется обратной:
С увеличением одной величины уменьшается вторая. С уменьшением одной величины увеличивается вторая величина.
Таким образом, в случае прямой зависимости обе величины изменяются одинаково (обе либо увеличиваются, либо уменьшаются), а в случае обратной зависимости – противоположно (одна увеличивается, а другая уменьшается либо наоборот).
Определение зависимостей между величинами
«Прямая и обратная пропорциональности» 👇
Пример 1
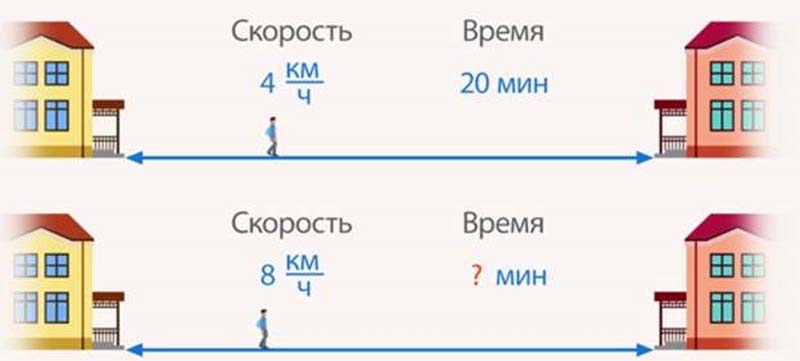
Время, затраченное для похода в гости к другу, составляет $20$ минут. При увеличении скорости (первой величины) в $2$ раза найдем, как изменится время (вторая величина), которое будет затрачено на путь к другу.
Очевидно, что время уменьшится в $2$ раза.
Замечание 3
Такую зависимость называют пропорциональной:
Во сколько раз изменится одна величина, во столько раз изменится и вторая.
Пример 2
За $2$ булки хлеба в магазине нужно заплатить 80 рублей. Если нужно купить $4$ булки хлеба (количество хлеба увеличивается в $2$ раза), во сколько раз придется больше заплатить?
Очевидно, что стоимость также увеличится в $2$ раза. Имеем пример пропорциональной зависимости.
В обоих примерах были рассмотрены пропорциональные зависимости. Но в примере с булками хлеба величины изменяются в одну сторону, следовательно, зависимость является прямой. А в примере с походом к другу зависимость между скоростью и временем – обратная.
Таким образом, существует прямо пропорциональная зависимость и обратно пропорциональная зависимость.
Прямая пропорциональность
Рассмотрим $2$ пропорциональные величины: количество булок хлеба и их стоимость. Пусть $2$ булки хлеба стоят $80$ рублей. При увеличении количества булок в $4$ раза ($8$ булок) их общая стоимость будет составлять $320$ рублей.
Отношение количества булок: $frac{8}{2}=4$.
Отношение стоимости булок: $frac{320}{80}=4$.
Как видно, эти отношения равны между собой:
$frac{8}{2}=frac{320}{80}$.
Определение 1
Равенство двух отношений называется пропорцией.
При прямо пропорциональной зависимости получается отношение, когда изменение первой и второй величины совпадает:
$frac{A_2}{A_1}=frac{B_2}{B_1}$.
Определение 2
Две величины называются прямо пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменяется (увеличивается или уменьшается соответственно) и другая величина.
Пример 3
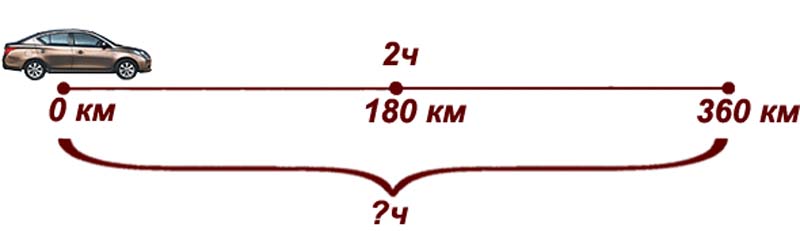
Автомобиль проехал $180$ км за $2$ часа. Найти время, за которое он с той же скоростью проедет в $2$ раза большее расстояние.
Решение.
Время прямо пропорционально расстоянию:
$t=frac{S}{v}$.
Во сколько раз увеличится расстояние, при постоянной скорости, во столько же раз увеличится время:
$frac{2S}{v}=2t$;
$frac{3S}{v}=3t$.
Запишем условие задачи в виде таблицы:
Автомобиль проехал $180$ км – за время $2$ часа
Автомобиль проедет $180 cdot 2=360$ км – за время $x$ часов
Чем больше расстояние проедет автомобиль, тем большее время ему понадобится. Следовательно, зависимость между величинами прямо пропорциональная.
Составим пропорцию:
$frac{180}{360}=frac{2}{x}$;
$x=frac{360 cdot 2}{180}$;
$x=4$.
Ответ: автомобилю потребуется $4$ часа.
Обратная пропорциональность
Определение 3
При обратно пропорциональной зависимости получается отношение, первая часть которого показывает, во сколько раз увеличилась первая величина, а вторая часть – во сколько раз уменьшилась вторая:
$frac{N_2}{N_1}=frac{S_1}{S_2}$.
Определение 4
Две величины называются обратно пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменится (уменьшится или увеличится соответственно) другая величина.
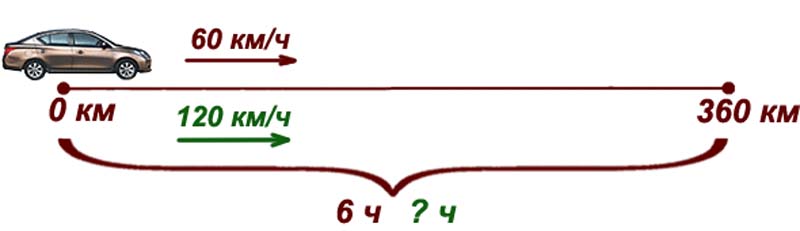
Пример 4
Автомобиль, который двигается со скоростью $60$ км/ч, проехал путь за $6$ часов. Найти время, за которое автомобиль проедет этот же путь, но со скоростью в $2$ раза больше прежней.
Решение.
Время обратно пропорционально скорости:
$t=frac{S}{v}$.
Во сколько раз увеличивается скорость, при том же пути, во столько же раз уменьшается время:
$frac{S}{2v}=frac{t}{2}$;
$frac{S}{3v}=frac{t}{3}$.
Запишем условие задачи в виде таблицы:
Автомобиль проехал $60$ км — за время $6$ часов
Автомобиль проедет $120$ км – за время $x$ часов
Чем больше скорость автомобиля, тем меньше времени ему понадобится. Следовательно, зависимость между величинами обратно пропорциональная.
Составим пропорцию.
Т.к. пропорциональность обратная, второе отношение в пропорции переворачиваем:
$frac{60}{120}=frac{x}{6}$;
$x=frac{60 cdot 6}{120}$;
$x=3$.
Ответ: автомобилю потребуется $3$ часа.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Цели:
- Образовательная: обобщить и систематизировать знания учащихся по
теме “Пропорция”, выявить и устранить пробелы, подготовить к предстоящей
контрольной работе. - Воспитательная: способствовать воспитанию настойчивости и
упорства в достижении цели, умению работать в группе и в паре, умению
адекватно оценивать свои знания. - Развивающая: способствовать развитию интереса к предмету,
логического мышления, математически грамотной речи.
План урока.
- Организационный момент. Сообщение цели и задач урока.
- Повторение и систематизация теоретических знаний.
- Повторение и систематизация практических ЗУНов.
- Проверка знаний и умений при помощи самостоятельной работы.
- Подведение итогов, постановка домашнего задания, рефлексия.
Оборудование: мел, доска, презентация, диагностическая карта, карточки
для самостоятельной работы.
Ход урока
I. Урок начался с постановки перед детьми целей урока: (Cлайд
2).
На уроке мы:
- Повторим все необходимые теоретические факты;
- Повторим способы решения различных заданий на тему “Пропорция”;
- Напишем небольшую самостоятельную работу;
- Сделаем выводы о том как мы усвоили тему.
II. Устный опрос:
(Cлайд 3).
- Что такое пропорция?
- Как проверить, верна ли пропорция?
- Как найти неизвестный член пропорции?
- Как вы думаете, кто первым ввел в обиход слово пропорция? Ответ мы
узнаем выполнив сведущее задание:
(Слайд 4).
Н 1,5 : 1/3 =
Е (1/3)^3 =
О 1:5:2 =
Р 2,8*2/7 =
И 1/3 + 1/4
=
Ц 0,25*4/5 =
| 1/5 | 7/12 | 0,2 | 1/27 | 0,8 | 0,1 | 4,5 |
Цицерон был римским оратором, юристом, политическим деятелем и
мыслителем I века до нашей эры. Многие из его философских работ известны и
актуальны спустя 20 веков после их написания! И даже нам с вами известны
высказывания, принадлежащие этому римскому оратору, а какие именно вы узнаете
найдя на свитках верные пропорции.
(Рисунки свитков.)
(Слайды
5, 6).
Оставшееся же третье высказывание принадлежит не менее известному
древнегреческому ученому Пифагору. Перед вами три портрета, чтобы узнать на
котором из них изображен Пифагор необходимо решить уравнения и выбрать
наибольший корень. (Решение по рядам, по одному представителю).
(Портреты ученых.)
(Слайд
7)
Каждый ряд проверяет правильность решения своего представителя и вместе
находим наибольший корень, а с ним и портрет Пифагора.
III. Устный опрос: (Слайд
9).
- На какие два вида делятся все пропорциональные зависимости?
- Какая зависимость называется прямой?
- Формула?
- Какая зависимость называется обратной?
- Формула?
Определите вид зависимости заданной формулой:
(На экране формулы, ответы оформляем в виде таблицы.)
Слайд
10).
| прямая | обратная | Не является пропорциональной зависимостью |
Определите вид пропорциональной зависимости и задайте ее формулой:
(На экране графики функций, каждый работает в паре,
определяет вид зависимости и записывает формулу, затем учитель дает правильные
ответы, ученики проверяют.)
(Слайды
11, 12).
Дополни предложения словами “БОЛЬШЕ” или “МЕНЬШЕ”. Отметь знаками вид
зависимости: (Слайды
13–18)
- Чем больше путь, проделанный Дедом Морозом, с постоянной скоростью, тем
время его прибытия на ёлку __________________________. - Чем больше новогодних подарков будет куплено по одной цене, тем их общая
стоимость будет _______________________. - Чем больше новогодних подарков изготавливают в день, тем
___________________________ их сделают за определенное число дней. - Чем больше новогодних подарков делают в день, тем за
______________________ число дней сделают определенное количество подарков. - Чем больше ёлок машина может увезти за один рейс, тем
_________________________ рейсов ей надо сделать для перевозки одного и того
же количества деревьев. - Чем больше людей упаковывают новогодние подарки, тем
_______________________ времени они затратят для упаковки определенного
количества подарков.
IV. Устный опрос:
(Слайд 19).
- Какой метод решения задач на пропорции вы знаете?
- В чем он заключается?
Внимательно прочитайте условие задачи, выполните краткую запись,
определите вид пропорциональной зависимости и запишите соответствующую пропорцию:
(Слайды
20–23).
- Пешеход, скорость которого 3 км/ч, прошел некоторое расстояние за 2 часа
40 минут. За какое время пройдет это расстояние повозка, если ее скорость 6
км/ч? - На конвейерной линии расфасовывается 5,4 кг сухого картофеля за 2,5
минуты. Сколько кг сухого картофеля будет расфасовано на этой линии за один
час? - Картошка стоила 4,5 рубля за килограмм, ее цена увеличилась на 20%.
Какова новая цена картошки?
V. Самостоятельная работа.
(Слайды
24).
Вам предлагается один вариант самостоятельной работы.
(Один ученик выполнят у доски, остальные у себя в
тетрадях, затем проводится проверка.)
- Автобус проезжает расстояние от города до деревни со скоростью 60 км/ч
за 3,6 ч. Сколько времени затратит на этот путь автомобилист, если будет
ехать со скоростью 90 км/ч? - Машинистка печатает 4 страницы за 26 мин. За какое время она сможет
напечатать 100 страниц. - Вкладчик положил деньги в банк под 7 % годовых и через год получил
прибыль 315 рублей. Сколько денег он положил в банк.
VI. Рефлексия.
Перед вами лежат диагностические карты, в них вы должны честно оценить
свои знания по основным разделам темы.
| Фамилия: _____________________________________ |
|||||
| Знание теории | Определение верности пропорции | Нахождение неизвестного члена пропорции | Умение определять вид пропорциональной зависимости | Самостоятельная работа | Активность на уроке |
В конце урока после звонка вы сдадите диагностические карты, а я сделаю
выводы о том насколько готов к контрольной работе класс, для себя, я думаю, вы
выводы уже сделали. (Слайд
25).
VII. Домашнее задание.
- Исправить ошибки, допущенные в самостоятельной работе.
- № 293, 294, 295.
На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.
Эта информация доступна зарегистрированным пользователям
Давайте сначала разберемся, что такое пропорциональность.
Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: (mathbf{y = kx})
Обратная пропорциональность выражается так: (mathbf{y = frac{k}{x}})
где k — это число, которое называют коэффициентом пропорциональности.
x и y величины, зависящие друг от друга.
Пример
Площадь прямоугольника равна (mathbf{S = a cdot b}), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.
Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
(mathbf{S = a cdot b})
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
(mathbf{a = frac {S}{b}}) или (mathbf{b = frac {S}{a}})
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Эта информация доступна зарегистрированным пользователям
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
Увеличим ширину прямоугольника — сторону a1 на 1 см, получим
a2 = 7 см
Эта информация доступна зарегистрированным пользователям
Найдем площади прямоугольников S1 и S2
(mathbf{S_{1} = a_{1} cdot b = 6 cdot 4 = 24}) см2
(mathbf{S_{2} = a_{2} cdot b = 7 cdot 4 = 28}) см2
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Эта информация доступна зарегистрированным пользователям
Площадь прямоугольника S постоянная величина
S = 24 см2
b1 = 4 см
(mathbf{a_{1} = frac{S}{b_{1}} = 6}) (см)
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
(mathbf{a_{2} = frac{S}{b_{2}} = 4}) (см)
Эта информация доступна зарегистрированным пользователям
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
Эта информация доступна зарегистрированным пользователям
Итак:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
Эта информация доступна зарегистрированным пользователям
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Эта информация доступна зарегистрированным пользователям
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается
Эта информация доступна зарегистрированным пользователям
Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:
- Обозначить буквой значение неизвестной величины (чаще всего для этого выбирают латинскую букву Х)
- Проанализировать задачу и кратко записать ее условия (краткую запись можно делать в виде таблицы или изображать в виде логической схемы)
- Установить зависимость между величинами
- В краткой записи задачи обозначить стрелками пропорциональную зависимость
— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин
— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.
5. Записать пропорцию, учитывая характер пропорциональности величин
6. Составить уравнение
7. Найти неизвестный член уравнения (искомую величину)
8. Записать ответ задачи
Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.
Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.
Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.
Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
Эта информация доступна зарегистрированным пользователям
Рассмотрим некоторые варианты задач на пропорциональную зависимость, в которых величины зависят прямо пропорционально одна от другой.
Задача 1
Для приготовления из 3 кг черной смородины по рецепту требуется 3,3 кг сахара.
Сколько сахара потребуется для приготовления варенья из 5 кг черной смородины?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х (кг) сахара потребуется для приготовления варенья из 5 кг ягод.
Составим краткую запись задачи в виде таблицы:
Эта информация доступна зарегистрированным пользователям
Определим, как зависят масса сахара и масса ягод.
Чем больше ягод, тем больше нужно сахара, следовательно, между величинами прямо пропорциональная зависимость.
В таблице вертикальными стрелками изображаем прямо пропорциональную зависимость величин.
Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.
Отношение значений одной величины равно отношению соответствующих значений другой величины.
Получим (mathbf{frac{3,3}{x} = frac{3}{5}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{{3}cdot{x} = {5}cdot{3,3}})
(mathbf{ {x} = {(5}cdot{3,3)}div{3}})
(mathbf{ {x} = {5,5}}) (кг) сахара потребуется для приготовления варенья из 5 кг ягод.
Ответ: (mathbf{ {x} = {5,5}}) (кг)
Задача 2
Автомобиль, двигаясь с постоянной скоростью, проехал 400 км за 5 часов.
За какое время автомобиль проедет 600 км?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х (ч) – время, за которое автомобиль проедет 600 км.
Составим краткую запись задачи в виде таблицы:
Эта информация доступна зарегистрированным пользователям
Определим, как зависят величины S от t, где S — это путь, а t — это время.
Так как движение происходит с постоянной скоростью, то (mathbf{ {S} = {V}cdot{t}}).
Чем больше расстояние, тем больше требуется времени для преодоления этого расстояния, значит, зависимость между величинами S и t прямо пропорциональная.
Изображаем в таблице краткой записи задачи вертикальными стрелками прямо пропорциональную зависимость величин.
Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.
Отношение значений одной величины равно отношению соответствующих значений другой величины.
Получим (mathbf{frac{5}{x} = frac{400}{600}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{ {400}cdot{x} = {5}cdot{600}})
(mathbf{ {x} = {(5}cdot{600)}div{400}})
(mathbf{ {x} = {7,5}}) (ч) время, за которое автомобиль проедет 600 км
Ответ: (mathbf{ {x} = {7,5}}) (ч)
Примеры решения задач, в которых величины зависят обратно пропорционально одна от другой.
Задача 1
Для перевозки гравия потребовалось 42 машины грузоподъемностью 5 т.
Сколько нужно машин грузоподъемностью 7 т, чтобы перевезти тот же объем гравия?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х (шт) — это количество машин грузоподъемностью 7 т, необходимых для перевозки груза.
Краткую запись задачи оформим в виде таблицы:
Эта информация доступна зарегистрированным пользователям
Определим, как зависят величины друг от друга.
Чем больше грузоподъемность машины, тем меньше машин потребуется для перевозки груза.
Получаем обратно пропорциональную зависимость.
Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
А это значит, что при составлении пропорции одно из отношений получится перевернутым.
Получим (mathbf{frac{42}{x} = frac{7}{5}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{ {7}cdot{x} = {42}cdot{5}})
(mathbf{ {x} = {(42}cdot{5)}div{7}})
(mathbf{ {x} = {30}}) (шт.) машин грузоподъёмностью 7 т понадобится для перевозки гравия.
Ответ: (mathbf{ {x} = {30}}) (шт.)
Задача 2
Велосипедист проехал путь от дачи до дома за час со скоростью 10 км/ч. Сколько понадобится времени велосипедисту на преодоление этого пути со скоростью 20 км/ч?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч. Составим краткую запись задачи в виде таблицы:
Эта информация доступна зарегистрированным пользователям
Определим, как зависят V и t, где V— скорость движения велосипедиста, t— время движения.
Чем больше скорость велосипедиста, тем меньше времени ему потребуется для преодоления пути.
Получаем обратно пропорциональную зависимость величин друг от друга.
Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
А это значит, при составлении пропорции одно из отношений получаем перевернутым.
Получим (mathbf{frac{x}{1} = frac{10}{20}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{ {20}cdot{x} = {10}cdot{1}})
(mathbf{ {x} = {(10}cdot{1)}div{20}})
(mathbf{ {x} = {0,5}}) (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч.
Ответ: (mathbf{ {x} = {0,5}}) (ч)
Эта информация доступна зарегистрированным пользователям