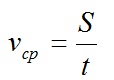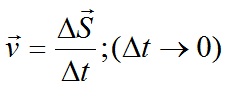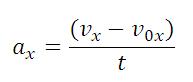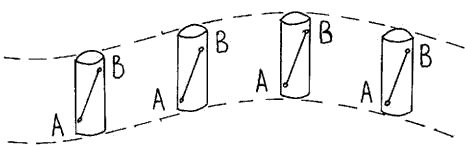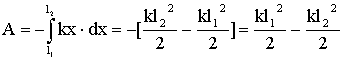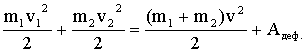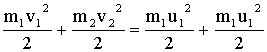Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
- Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
- Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
- Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.
По типу линии, вдоль которой движется тело, выделяют два вида движения:
- Прямолинейное — тело движется по прямой линии.
- Криволинейное — тело движется по кривой линии, в том числе замкнутой.
По скорости выделяют два вида движения:
- Равномерное — скорость движущегося тела остается неизменной.
- Неравномерное — скорость движущегося тела с течением времени меняется.
По ускорению выделяют три вида движения:
- Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
- Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
- Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
- Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
- Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
- Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.
Способы описания механического движения
Описать механическое движение можно двумя способами:
- координатным
- векторным
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
- перемещение
- скорость
- ускорение
Перемещение
Определение
Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.
Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).
Внимание!
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
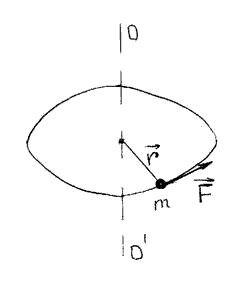
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Определение
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
В физике скорость обозначается V. Математически скорость определяется формулой:
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Определение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
В физике ускорение обозначается a. Математически оно определяется формулой:
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с2).
Математическое определение модуля скорости:
v — скорость тела в данный момент времени, v0— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.
Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Определение
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
- Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
- Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.
Внимание!
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Задание EF17612
Тело начинает двигаться из состояния покоя с ускорением 4 м/с2. Через 2 с его скорость будет равна…
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 39k
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
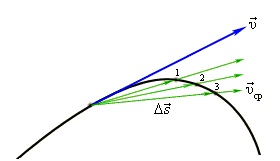
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
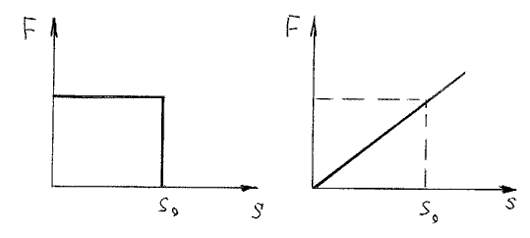
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
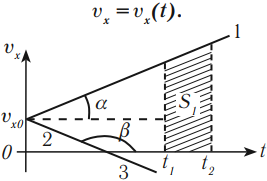
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
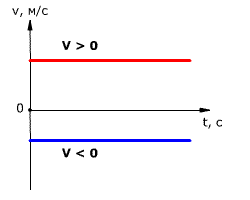
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
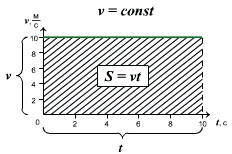
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
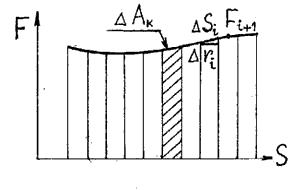
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
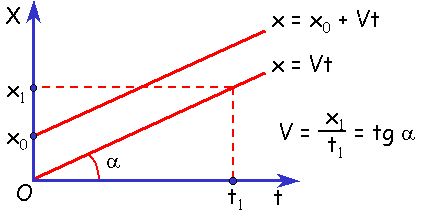
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
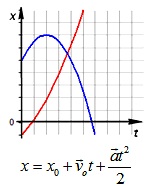
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
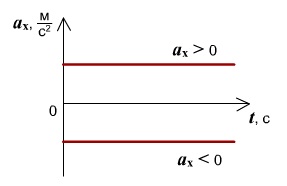
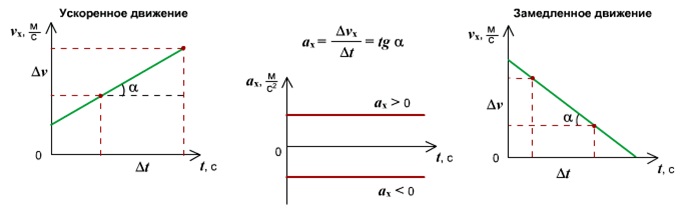
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
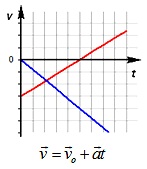
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
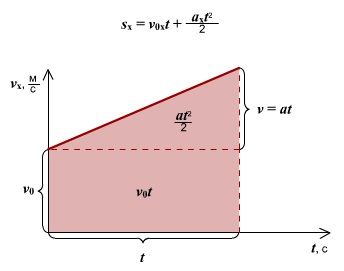
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
3 (60.28%) 142 votes
Механическое движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.
Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
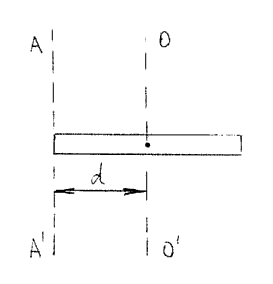
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат
. Начало координат
является телом отсчёта.
 |
| Рисунок 1. |
Вектор называется радиус-вектором точки
. Координаты
точки
являются в то же время координатами её радиус-вектора
.
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени:
.
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.
К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.
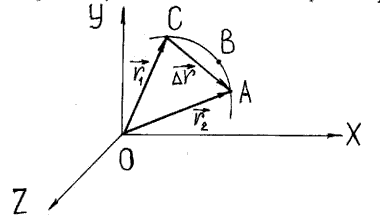
Траектория, путь, перемещение.
В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.
Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора
.
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке
(рис. 2). Тогда путь, пройденный телом, это длина траектории
. Перемещение тела — это вектор
.
 |
| Рисунок 2. |
Скорость и ускорение.
Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).
 |
| Рисунок 3. |
Пусть в момент времени тело находилось в точке
с радиус-вектором
Спустя малый промежуток времени тело оказалось в точке
с
радиус-вектором
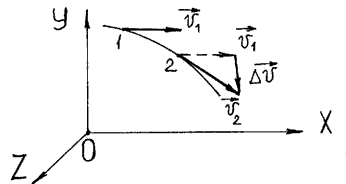
Перемещение тела:
(1)
Мгновенная скорость в момент времени
— это предел отношения перемещения
к интервалу времени
, когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:
(2)
Из (2) и (1) получаем:
Коэффициенты при базисных векторах в пределе дают производные:
(Производная по времени традиционно обозначается точкой над буквой.) Итак,
Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:
Когда стремится к нулю, точка
приближается к точке
и вектор перемещения
разворачивается в направлении касательной. Оказывается, что в пределе вектор
направлен точно по касательной к траектории в точке
. Это и показано на рис. 3.
Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна
, а спустя малый интервал
скорость стала равна
.
Ускорение — это предел отношения изменения скорости
к интервалу
, когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:
Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:
Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):
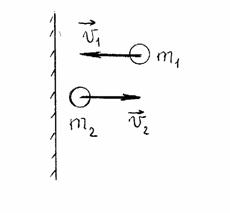
Закон сложения скоростей.
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим
и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта
, которое движется относительно тела
со скоростью
. Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы
перемещаются параллельно самим себе (нет вращения системы координат), так что вектор
можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью
, это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта
.
Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью
. Муха переносится вагоном, и потому скорость
движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается
и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе
) обозначается
и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
— радиус-вектор точки
в неподвижной системе
;
— радиус-вектор точки
в движущейся системе
;
— радиус-вектор тела отсчёта
в неподвижной системе
.
 |
| Рисунок 4. |
Как видно из рисунка,
Дифференцируя это равенство, получим:
(3)
(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки
в системе
, то есть абсолютная скорость:
.
Аналогично, производная есть скорость точки
в системе
, то есть относительная скорость:
А что такое ? Это скорость точки
в неподвижной системе, то есть — переносная скорость
движущейся системы относительно неподвижной:
В результате из (3) получаем:
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!
Виды механического движения.
Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).
Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.
А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.
В терминах вектора скорости можно дать более короткие определения данным типам движения:
Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:
- равноускоренное движение
Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.
Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).
 |
| Рисунок 5. |
Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.
На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.
 |
| Рисунок 6. |
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Механическое движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Виды движения (равномерное, равноускоренное) и их графическое описание
По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).
При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути
Равномерное прямолинейное движение.
Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Скорость равномерного прямолинейного движения.
— это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:
vх=S/t
Скорость — это физическая величина, показывающая быстроту изменения координаты.
Единицы измерения скорости — метры в секунду [1 м/с]
Уравнение равномерного движения (перемещение тела при равномерном движении):
S=vх·t
Уравнение координаты тела:
х=х0+vх·t
Обозначения:
х— координата движущегося тела
х0 — начальная координата движущегося тела
vср-Средняя скорость равномерного прямолинейного движения
vх — Скорость равномерного прямолинейного движения
S — Перемещение тела (расстояние, на которое передвинулось тело)
t — Промежуток времени перемещения (время)
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
v(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
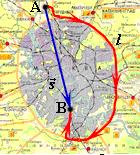
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно (v=const), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) — наклонная линия:
Зависимость координаты от времени. График х(t) — наклонная линия:
Из графика видно, что проекция скорости равна:
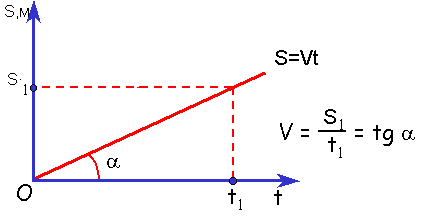
vх=S/t=tga
Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Обозначения:
vх — конечная скорость тела при равноускоренном движении по прямой
v0х — начальная скорость тела
a — ускорение тела
t — время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с2].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения:
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Обозначения:
— Перемещение тела при равноускоренном движении по прямой
— Начальная скорость тела
— Скорость тела при равноускоренном движении по прямой
— Ускорение тела
— Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
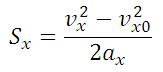
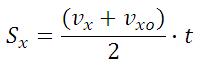
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
v(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости .
Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
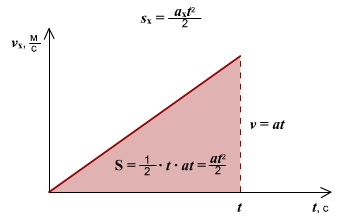
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
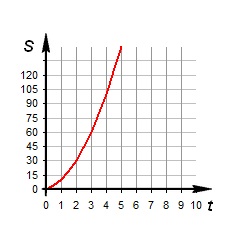
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости
В координатах зависимость имеет вид .
Графиком является ветка параболы.
Расширения для Joomla
2.1. Кинематика
2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений
2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения
2.1.3. Кинематические характеристики. Скорость
2.1.4. Кинематические характеристики. Ускорение
2.1.5. Поступательное и вращательное движение твердого тела
2.1.6. Связь между кинематическими характеристиками при различных видах движений
2.2. Динамика. Законы Ньютона
2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс
2.2.2. Виды сил
2.2.3. Первый закон Ньютона
2.2.4. Второй закон Ньютона
2.2.5. Третий закон Ньютона
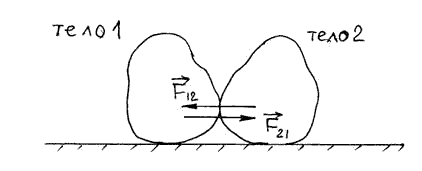
2.2.6. Закон сохранения импульса
2.2.7. Динамические характеристики вращательного движения
2.2.8. Основное уравнение динамики вращательного движения
2.2.9. Закон сохранения момента импульса
2.3. Работа и механическая энергия
2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы
2.3.2. Энергия
2.3.3. Кинетическая энергия
2.3.4. Потенциальная энергия
2.3.5. Закон сохранения механической энергии
2.3.6. Сравнение кинематических и динамических характеристик поступательного и вращательного движений
2.3.7. Применение законов сохранения в теории ударов тел
Вопросы для самоконтроля. Задачи. Ответы к задачам
Приложение. Международная система единиц — CИ — (System International — SI)
Механика. Введение
Объектом человеческого познания является окружающий нас реальный мир. Но этот мир бесконечно разнообразен и находится в непрерывном движении и изменении. Изучение огромного разнообразия мира не может быть охвачено одной наукой: разнообразны формы существования материи, различны явления, в которых проявляется реальный мир, отличительны способы их изучения. Человечество в своем развитии создало множество наук, изучающих реальный мир, все они могут быть разбиты на три группы:
— естествознание — совокупность наук о природе (физика, химия, астрономия, геология, биология и т.д.);
— группа прикладных и технических наук, изучающая применение результатов, полученных в области естествознания (теплофизика, радиотехника, электроника, вычислительная техника и т.д.);
— социально-экономические науки, изучающие человеческое общество и законы его развития (экономика, социология, соционика, психология).
Среди всех естественных наук физике принадлежит роль фундаментальной науки. Главная цель физики — выявить и объяснить законы природы, которые определяют все физические явления, изучить наиболее общие свойства материального мира. Вследствие этой общности физические законы лежат в основе естествознания. Они пригодны для всех видов материи: живой и неживой, простой и сложной, материи в виде частиц, космических тел, Земли в целом, Вселенной, и материи в виде полей (полей сил тяготения, электромагнитных, биологических и т.д.). Объекты, изучаемые физикой, универсальны, в то время как в других естественных науках объекты исследования ограничены. Так, биология изучает живую материю, геология — земную кору и Землю, астрономия — космические тела, космические системы, Вселенную.
Исторически изучение окружающего мира привело к разделению физики на отдельные разделы.
Механика изучает наиболее простую форму существования материи — механическое движение. В механике несущественно нагрето, заряжено, намагничено тело или нет. В процессе изучения механических явлений были введены многие понятия (масса, скорость, ускорение, сила, работа, энергия и т.д.). Оказалось, что законы механики верны не только для механических движений.
Из литературных источников, список которых приведен в конце данного курса лекций, [1,2] являются основными учебниками, рекомендованными для ВУЗов, [3-6,15] — дополнительная учебная литература, [10-12] — справочная литература, [7-9,13,14] — наши методические разработки. По ходу изложения учебного материала в случае необходимости мы будем ссылаться на литературные источники.
Принятые обозначения
Векторы обозначаются жирным прямым шрифтом ( r, F, a) или стрелкой над величиной ().
Модуль вектора обозначается прямым светлым обычным шрифтом (r, F ,a) или | r|, | F|, | a|.
Средние величины обозначаются скобками < >, например < r>, < P>.
Символы перед величинами:
Δ — приращение величины, т.е. разность ее конечного и начального значений, например Δ Wкин = Wкин2 – Wкин1.
d-дифференциал (бесконечно малое приращение величины), дифференциал можно находить и от вектора, например, dr, и от переменной величины ( dх) и от функции (dF) и т.д.
2.1. Кинематика
2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений
1. Механическое движение — изменение положения тела или отдельных его частей в пространстве с течением времени.
Внутреннее строение движущихся тел, их химический состав не влияет на механическое движение. Для описания движения реальных тел в зависимости от условий задачи пользуются различными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.
Материальной точкой называется тело, размерами и формой которого можно пренебречь в условиях данной задачи. В дальнейшем вместо термина «материальная точка» будем употреблять термин «точка». Одно и то же тело можно свести к материальной точке в одной задаче, и необходимо учитывать его размеры в условиях другой задачи. Например, расчет движения самолета, летящего над Землей, можно производить, считая его материальной точкой. А при расчете обтекания воздухом крыла того же самолета надо учитывать форму и размеры крыла.
Любое протяженное тело можно рассматривать как систему материальных точек.
Абсолютно твердое тело (а.т.т.) — тело, деформацией которого можно пренебречь в условиях данной задачи. А.т.т. можно рассматривать как систему жестко связанных между собой материальных точек, т.к. расстояние между ними не изменяются при любых взаимодействиях.
Абсолютно упругое тело — тело, деформация которого подчиняется закону Гука (см. § 2.2.2.), и после прекращения силового воздействия оно полностью восстанавливает первоначальные размеры и форму.
Абсолютно неупругое тело — тело, которое после прекращения силового воздействия на него не восстанавливается, а полностью сохраняет деформированное состояние.
2. Для определения положения тела в пространстве и во времени надо ввести понятие системы отсчета. Выбор системы отсчета произволен.
Системой отсчета называется тело или группа тел, считающиеся условно неподвижными и снабженные устройством отсчета времени (часами, секундомером и т.д.), относительно которых рассматривается движение данного тела.
Неподвижное тело (или группу тел) называют телом отсчета и для удобства описания движения с ним связывают систему координат (декартову, полярную, цилиндрическую и т.д.).
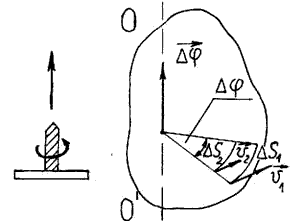
Выберем в качестве системы координат декартову прямоугольную систему XYZ (подробно см.[8]). Положение точки С в пространстве можно определить координатами х, y, z (Рисунок 1).
Рисунок 1 — Определение положения точки в декартовой системе координат
Однако положение той же точки в пространстве можно задать с помощью одной векторной величины r = r(x, y, z), называемой радиус-вектором точки С (Рисунок 1).
3. Линия, которую тело описывает при своем движении, называется траекторией. По виду траектории движения можно разделить на прямолинейные и криволинейные. Траектория зависит от выбора системы отсчета. Так, траектория движения точек винта самолета относительно летчика — окружность, а относительно Земли — винтовая линия. Другой пример: какова траектория движения кончика иглы проигрывателя относительно пластинки? корпуса проигрывателя? корпуса звукоснимателя? Ответы таковы: спираль, дуга окружности, состояние покоя (игла неподвижна).
2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения
1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:
x = x(t), y = y(t), z = z(t).
Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.
2. Путь — часть траектории, пройденной телом за определенный промежуток времени. Момент времени t0, от которого начинается его отсчет, называется начальным моментом времени, обычно t0=0 в силу произвольного выбора начала отсчета времени.
Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин дуги СА и дуги АВ.
2.1.3. Кинематические характеристики. Скорость
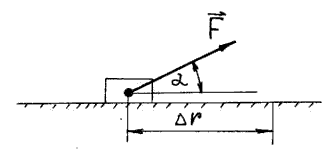
1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость — вектор, а значит, характеризуется величиной, направлением, точкой приложения.
Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.
Если за время ∆ произошло перемещение точки на ∆r, то величина является средней скоростью движения:
.
Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.
Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.
2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда
Используя понятие производной, можно записать для скорости
Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).
Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.
2.1.4. Кинематические характеристики. Ускорение
1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.
Пусть в момент времени t скорость тела равна v1, а через промежуток времени ∆t в момент времени t + ∆t равна v2, приращение вектора скорости за ∆t равно ∆v.
Средним ускорением тела в интервале времени от t до t + ∆t называется вектор аср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:
Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.
2. Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:
Используя понятие производной, можно дать для ускорения следующее определение: Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.
3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)
Рисунок 2 — Изменение скорости точки при вращении по окружности
На рисунке 2 в положении 1 скорость точки v1, в положении 2 скорость точки v2. Модуль скорости v2 больше модуля скорости v1 , ∆v— вектор изменения скорости ∆v = v2 —v1
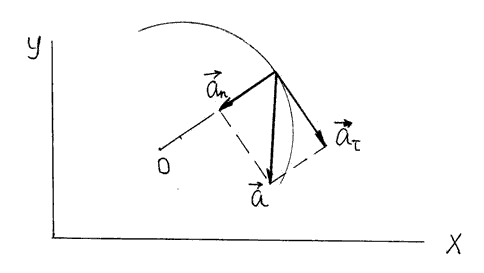
Вращающаяся точка имеет тангенциальное ускорение, равное аτ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное аn= v2/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)
Рисунок 3 — Полное, тангенциальное и нормальное ускорения вращающейся точки
Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального aτ и нормального an ускорений. Модуль полного ускорения равен:
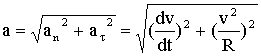
2.1.5. Поступательное и вращательное движение абсолютно твердого тела
1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к движению каких частей тела относятся понятия пути, скорости, ускорения, введенные ранее?
Прежде, чем ответить на этот вопрос, надо выделить формы механического движения. Каким бы сложным не было движение тела, его можно свести к двум основным: поступательному движению и вращению вокруг неподвижной оси. Колебательное движение будет рассмотрено отдельно. В примере с автомобилем поступательно движется кузов автомобиля. Сам автомобиль является телом, которое может быть рассмотрено с помощью модели абсолютно твердого тела (а.т.т.). Для краткости мы будем называть абсолютно твердое тело просто твердое тело.
Поступательным движением твердого тела называется движение, при котором любая прямая, проведенная между его двумя точками, остается при движении параллельна самой себе.
Поступательное движение может быть и не прямолинейным движением.
Примеры. 1) В аттракционе «Колесо обозрения» кабинки — люльки, в которых сидят люди, двигаются поступательно. 2) Если стакан с водой перемещать по траектории, представленной на рисунке 5 так, чтобы поверхность воды и направляющая стакана составляли бы прямой угол, то движение стакана является не прямолинейным, но поступательным. Прямая АВ остается при движении стакана параллельна самой себе.
Рисунок 4 — Пример поступательного движения твердого тела.
Особенностью поступательного движения твердого тела является то, что все точки тела описывают одинаковую траекторию, проходят за определенные промежутки времени ∆t одинаковые пути и в любой момент времени имеют одинаковые скорости. Поэтому кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек. Поступательное движение тела может быть сведено к движению материальной точки. В динамике обычно за такую точку принимают центр масс тела. Кинематические характеристики и кинематические уравнения, вводимые для материальной точки, описывают и поступательное движение твердого тела.
2. Движение колес автомобиля отличается от движения кузова. Точки колеса, находящиеся на разных расстояниях от его оси, описывают разные траектории, проходят различные пути и имеют разные скорости. Чем дальше точка находится от оси колеса, тем больше ее скорость, тем больший путь она проходит за определенный промежуток времени. Движение, в котором участвуют колеса автомобиля, называется вращательным. Ясно, что модель материальной точки для описания вращения реального тело не подходит. Но и здесь вместо реального тела (например, колеса автомобиля с деформируемыми шинами и т.д.) используют физическую модель — абсолютно твердое тело.
Вращательным движением твердого тела называется движение, когда все точки тела описывают окружности, центры которых лежат на прямой, называемой осью вращения и перпендикулярной к плоскостям, в которых вращаются точки тела (Рисунок 5).
Так как для разных точек вращающегося тела траектории, пути, скорости различны, то встает вопрос: можно ли найти физические величины, которые имели бы одинаковые значения для всех точек вращающегося тела, Да, оказывается, есть такие величины, они называются угловыми.
Рисунок 5 — Вращение твердого тела
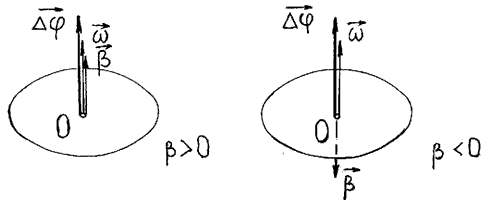
Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, его положение в пространстве полностью определяется значением угла поворота ∆φ из некоторого начального положения (Рисунок 5). Все точки твердого тела повернутся за промежуток времени ∆ на угол ∆φ.
При малых промежутках времени, когда углы поворота невелики, их можно рассматривать как векторы, хотя и не совсем обычные. Вектор элементарного (бесконечно малого) угла поворота ∆φ направлен вдоль оси вращения по правилу правого буравчика, его модуль равен углу поворота (Рисунок 5). Вектор ∆φ называется угловым перемещением.
Правило правого буравчика заключается в следующем:
Если рукоятка правого буравчика вращается вместе с телом (точкой), то поступательное движение буравчика совпадает с направлением ∆φ.
Другая формулировка правила: Из конца вектора ∆φ видно, что движение точки (тела) происходит против часовой стрелки.
Положение тела в любой момент времени t определяется кинематическим уравнением вращательного движения ∆φ = ∆φ(t).
3. Для характеристики быстроты вращения служит угловая скорость.
Средней угловой скоростью называется физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло
Предел, к которому стремится средняя угловая скорость при ∆→0, называется мгновенной угловой скоростью тела в данный момент времени или просто угловой скоростью вращения твердого тела (точки).
Угловая скорость равна первой производной от углового перемещения по времени. Направление мгновенной угловой скорости определяется по правилу правого буравчика и совпадает с направлением ∆φ (Рисунок 6). Кинематическое уравнение движения для угловой скорости имеет вид ω = ω (t).
Рисунок 6 — Направление векторов угловых характеристик при вращательном движении.
4. Для характеристики быстроты изменения угловой скорости тела при неравномерном вращении вводится вектор углового ускорения β, равный первой производной от его угловой скорости ω по времени t.
Среднее угловое ускорение есть величина отношения изменения угловой скорости ∆ω к промежутку времени ∆t, за которое это изменение произошло β ср = ∆ω/∆t
Вектор углового ускорения направлен вдоль оси вращения и совпадает с направлением угловой скорости, если движение ускоренное, и противоположен ему, если вращение замедленное (Рисунок 6).
5. При вращательном движении твердого тела все его точки двигаются так, что вращательные характеристики (угловое перемещение, угловая скорость, угловое ускорение) для них одинаковы. А линейные характеристики движения зависят от расстояния точки до оси вращения.
Связь между этими величинами v, ω, r задается следующим соотношением:
v = [ω∙r],
т.е. линейная скорость v любой точки С твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна векторному произведению ω на радиус-вектор r точки С относительно произвольной точки О на оси вращения.
Подобное соотношение существует между линейным и угловым ускорениями вращающейся точки твердого тела:
а = [β∙r].
2.1.6. Связь между кинематическими характеристиками при различных видах движений
По зависимости скорости и ускорения от времени все механические движения делятся на равномерное, равнопеременное (равноускоренное и равнозамедленное) и неравномерное.
Рассмотрим кинематические характеристики и кинематические уравнения, введенные в предыдущих параграфах, для разных видов движений.
1. Прямолинейное движение
Прямолинейное равномерное движение.
Направление движения задается осью ОХ.
Ускорение а = 0 (аn = 0, аτ = 0), скорость v = const, путь s = v∙t, координата x = x0 v∙t, где x0 — начальная координата тела на оси ОХ.
Путь — величина всегда положительная. Координата может быть и положительной и отрицательной, поэтому в уравнении, задающем зависимость координаты от времени, перед величиной v∙t в уравнении стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.
Прямолинейное равнопеременное движение.
Ускорение а = аτ = const, аn = 0, скорость , путь
, координата
.
Перед величиной (at) в кинематическом уравнении для скорости знак плюс соответствует равноускоренному движению, а знак минус — равнозамедленному движению. Это замечание верно и для кинематического уравнения пути, разные знаки перед величинами (at2/2) соответствуют разным видам равнопеременного движения.
В уравнении для координаты знак перед (v0t) может быть и плюс, если направления v0 и оси ОХ совпадают, и минус, если они направлены в разные стороны.
Разные знаки перед величинами соответствуют равноускоренному или равнозамедленному движениям.
Прямолинейное неравномерное движение.
Ускорение а = аτ>≠ const, аn = 0,
скорость 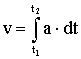
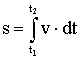
2. Поступательное движение
Для описания поступательного движения можно использовать законы, приведенные в §2.1.6. (пункт 2) или §2.1.4. (пункт3). Использование тех или иных законов для описания поступательного движения зависит от его траектории. Для прямолинейной траектории используются формулы из §2.1.6. (пункт 2), для криволинейной — §2.1.4. (пункт3).
3. Вращательное движение
Отметим, что решение всех задач на вращательное движение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины s, vх, aх на соответствующие угловые величины φ, ω, β, и мы получим все закономерности и соотношения для вращающегося тела.
Равномерное вращение по окружности
(R — радиус окружности).
Ускорение: полное а = аn, нормальное , тангенциальное аτ = 0, угловое β = 0.
Скорость: угловая ω = const, линейная v = ωR = const.
Угол поворота ∆φ = ∆ φ0 + ωt, ∆φ0 — начальное значение угла. Угол поворота величина положительная (аналог пути).
Периодом вращения называется промежуток времени T, в течении которого тело, равномерно вращаясь с угловой скоростью ω, совершает один оборот вокруг оси вращения. При этом тело поворачивается на угол 2π.
.
Частота вращения показывает число оборотов, совершаемых телом за единицу времени при равномерном вращении с угловой скоростью ω:
.
Равнопеременное вращение по окружности
Ускорение: угловое β = const, тангенциальное аτ = βR=const, нормальное аn = ω 2R ≠ const, полное
Скорость: угловая ω = ω0 ( βt), линейная
Угловое перемещение .
Все сказанное ранее относительно знаков в кинематических уравнениях для прямолинейного равнопеременного движения остается верным и для кинематических уравнений вращательного движения: плюс в формулах относится к равноускоренному вращению, минус — к равнозамедленному.
Неравномерное вращение
Ускорение: аτ = аτ (t), аn = а n(t), β ≠ const,
Скорость:
Угловая ω = dφ/dt, линейная .
2.2. Динамика. Законы Ньютона
2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс
До сих пор мы рассматривали перемещение тел в зависимости от времени без выяснения причин, вызывающих эти перемещения. Законы динамики устанавливают связь между движением тел и причинами, которые вызвали или изменили то или иное движение.
Рассмотрим поступательное движение материальной точки, для этого введем динамические характеристики, с помощью которых будем описывать такое движение. К таким характеристикам относятся понятие силы, массы, импульса. Начнем рассмотрение с движений тел в системах отсчета, которые называются инерциальными, и определение которых будет дано позднее.
1. Движение любого тела в инерциальной системе отсчета вызывается или изменяется только при взаимодействии с другими телами. Для описания взаимодействия между телами вводится понятие силы, которая дает количественную меру этого взаимодействия.
Физическая природа взаимодействия может быть различной, существуют гравитационные, электрические, магнитные и другие взаимодействия (см. Таблицу 1). В механике физическая природа сил несущественна, вопрос об их происхождении не выясняется. Но для всех видов взаимодействий их количественная мера должна быть выбрана единым образом. Измерять силы различной природы надо с помощью одних и тех же эталонов и единиц измерений. Законы механики универсальны, т.е. они описывают движение тел под действием силы любой природы. Для взаимодействий, которые рассматриваются в механике, сила может быть определена следующим образом.
Силой называется векторная величина F, являющаяся мерой механического воздействия одного тела на другое.
Механическое взаимодействие может осуществляться как между непосредственно контактирующими телами (сила трения, сила реакции опоры и т.д.), так и между удаленными телами.
Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем, или просто полем.
Взаимодействия между удаленными телами осуществляется посредством гравитационных (сила тяжести) или электромагнитных полей.
Механическое действие силы может вызвать ускорение тела или его деформацию. Сила — результат взаимодействия двух тел. Для правильного определения сил, действующих на тело, можно воспользоваться литературой [7,9], где приведены многочисленные примеры.
Сила F — вектор — полностью определена, если заданы ее модуль (величина), направление в пространстве и точка приложения. Прямая, вдоль которой направлен вектор F, называется линией действия силы.
Если говорить о силе, приложенной не к материальной точке, а к твердому телу и вызывающей его поступательное движение, то воздействие на тело не изменится при переносе точки действия силы вдоль линии ее действия.
Одновременное действие на материальную точку С нескольких сил F1 ,F2….. Fn эквивалентно действию одной силы, равной их геометрической (векторной) сумме и называемой результирующей или равнодействующей силой (см. Рисунок 7):
Fрез. = F1 +F2 + ….. +Fn.
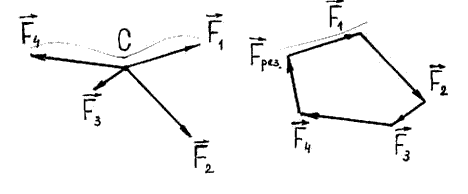
Силы, действующие на тело или систему тел, можно разделить на внешние и внутренние. Тела, не входящие в состав исследуемой механической системы, называются внешними и силы, действующие с их стороны, — внешние. Внутренние силы — силы, действующие на точку или тело со стороны точек или тел, входящих в рассматриваемую систему.
Система, на которую не действуют внешние силы, называется изолированной или замкнутой.
2. Основополагающим понятием в динамике является понятие массы m, о котором в кинематике даже не упоминалось, не было необходимости. Любой материальный объект (тела, элементарные частицы, поля) обладает массой. Масса выступает как многосторонняя характеристика тела.
Она определяет его гравитационные свойства, т.е. силы, с которыми тело притягивается к другим телам, в частности, к Земле.
Масса характеризует инерционные свойства тела, т.е. способность тела сохранить состояние покоя или равномерного прямолинейного движения, или изменить скорость.
Масса тела m определяет количество вещества в данном теле и равна произведению плотности вещества ρ на объем V тела:
m = ρ∙V.
Масса тела вместе с его скоростью определяет импульс и кинетическую энергию тела.
В классической механике для понятия массы характерно следующее:
- m = const, она не зависит от состояния движения тела,
- масса — величина аддитивная, т.е. масса системы равна арифметической сумме масс тел, входящих в систему,
- масса замкнутой системы остается неизменной при любых процессах, происходящих внутри системы (закон сохранения массы).
Итак, для массы можно дать следующее определение.
Масса — мера инертности тела или мера гравитационного взаимодействия.
3. Импульсом материальной точки называется векторная величина, равная произведению ее массы на ее скорость P = mv.
Импульсом системы материальных точек называется вектор, равный геометрической (векторной) сумме импульсов всех материальных точек системы:
P = P1 + P2 +…..+ Pn = Pi
Используя понятие массы, импульс системы равен произведению массы всей системы на скорость ее центра масс P = mvц.
Импульс P — вектор, по направлению совпадающий с направлением скорости.
Импульс — одна из фундаментальных характеристик физической системы. И масса, и скорость были определены ранее, но только импульс обладает уникальным свойством. Для него сформулирован закон сохранения импульса, который является универсальным законом. Он выполняется и в микромире (на уровне элементарных частиц, атомов и молекул), и в макромире (мир вокруг нас), и в мегамире (на уровне планет, Вселенной, Галактики). До сих пор не открыто явлений, в которых бы нарушался закон сохранения импульса.
2.2.2. Виды сил
1. В настоящее время понятия основных взаимодействий, известных в природе, связано с понятием основных полей. Понятие физического поля мы определили ранее. Вообще понятие поля более широкое. Всякую физическую величину, плавно изменяющуюся в пространстве и однозначно определенную во всех его точках, можно рассматривать как поле. Поля бывают векторные и скалярные. Примерами скалярных полей является поле температур вблизи нагретой пластины или поле давлений около поверхности Земли. Примерами векторных полей является электрические и магнитные поля, гравитационное поле Земли и т.д. В Таблице 1 приведены характеристики различных взаимодействий, известных к настоящему времени в природе. Соответственно название физических полей совпадает с названием взаимодействий.
Таблица 1 (данные взяты из [1], том 3, стр263).
| Взаимодействие/ Поле | Радиус взаимодействия | Const взаимодействия | Время взаимодействия |
| Гравитационное | ¥ | 10 –39 | – |
| Электромагнитное | ¥ | ≈10 -2 | 10-16 -10-20 с |
| Ядерное (сильное) | 10 –15 м | 10 | 10-23 с |
| Слабое (распадное) | 10 –15 м | 10 –14 | 10 -9 с |
Интенсивность взаимодействия принято характеризовать с помощью безразмерной величины, пропорциональной вероятности процессов, обусловленных данным видом взаимодействия. Гравитационное взаимодействие является универсальным, ему подвержены все без исключения элементарные частицы, но оно обладает предельно малой интенсивностью. Понятие времени взаимодействия является весьма условным. Эмпирически его можно ввести как минимальное время жизни частиц, подверженных распадам за счет данного взаимодействия. Прочерк в соответствующей графе для гравитационного взаимодействия стоит потому, что предполагаемый переносчик гравитационного взаимодействия – гравитон — экспериментально пока не обнаружен.
2. Силы в механике. Наиболее фундаментальные силы, лежащие в основе всех механических явлений, это силы гравитационные и электрические. Сила тяжести относится к гравитационному взаимодействию, сила трения и силы упругости — к электромагнитному взаимодействию.
Сила тяжести F = mg , где m — масса тела, g — ускорение силы тяжести. Заметим, что вес тела P — это сила, с которой тело действует на опору или подвес P = m (g – a), где a — ускорение тела (и опоры) относительно Земли. Если а = g, то вес тела равен нулю Р = 0 (состояние невесомости).
Упругая сила – сила, пропорциональная смещению точки из положения равновесия и направленная к положению равновесия. Примером такой силы может быть сила упругой деформации при растяжении (сжатии) пружины или стержня. В соответствии с законом Гука эта сила определяется так:
Fупр. = — k∙∆l, где k — коэффициент жесткости пружины (стержня), ∆l — величина упругой деформации. Знак минус означает, что противоположны направления смещения точки и силы упругости, возникающей при этом смещении и действующей на смещенную точку.
Величина силы трения скольжения, возникающая при скольжении одного тела по поверхности другого, равна Fтр. = μN, где μ — коэффициент трения, зависящий от соприкасающихся поверхностей, N — сила реакции опоры.
Сила трения направлена в сторону противоположную направлению движения данного тела относительно другого. Есть другие виды сил трения — силы трения покоя и сила трения качения.
Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости определяется зависимостью Fсопр. = αv, где v — скорость тела относительно среды, α — положительный коэффициент, характерный для данного тела и данной среды, при малых скоростях практически постоянен. Сила сопротивления всегда направлена противоположно вектору скорости тела.
Выталкивающая сила Архимеда равна весу вытесненной жидкости или газа: FАрх. = gρсрV, где ρср. — плотность среды, V — объем тела, g — ускорение свободного падения.
2.2.3. Первый закон Ньютона
Законы Ньютона представляют собой обобщение опытных данных (фактов). Эти законы устанавливались на основании наблюдений медленных по сравнению со скоростью света в вакууме движений.
1-й закон Ньютона
Всякая материальная точка или тело сохраняет состояние покоя или равномерного прямолинейного движения, пока на них не действуют силы или действие сил скомпенсировано.
Этот закон называется законом инерции, а движение точки или тела, свободных от внешних воздействий, называется движением по инерции.
Покой — частный случай равномерного прямолинейного движения, когда а = 0 и v = const, или v = 0.
Любое механическое движение — относительное движение, его характер зависит от системы отсчета. Закон инерции справедлив не во всех системах отсчета.
Системы, в которых выполняется первый закон Ньютона, называются инерциальными.
Системы, в которых не выполняется первый закон Ньютона, называются неинерциальными.
Инерциальных систем бесконечно много. Любая система, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, является также инерциальной системой.
2.2.4. Второй закон Ньютона
Первый закон Ньютона говорит о состоянии тел, если на них не действуют силы. Каким будет движение, если на точку или тело действуют силы? Ответ на этот вопрос дает второй закон Ньютона, он связывает три величины — силу, массу и ускорение.
Второй закон Ньютона
Произведение массы материальной точки (тела) на ее ускорение равно действующей на нее силе F = ma.
Если на тело действует несколько сил, то в формулировке 2-ого закона используется равнодействующая сила (см. Рисунок 7)
Fрез = ma.
Это является следствием независимости действия сил на тело (точку) или говорят, что силы подчиняются принципу суперпозиции. Такое утверждение надо рассматривать как обобщение опытных фактов.
Так как в классической механике а = dv/dt и m = const, то второй закон можно переписать в виде:
И еще один вид уравнения 2-ого закона:
F∙dt = dP
Величина F∙dt называется вектором импульса силы, а величина dP — вектор изменение импульса тела под действием данной силы.
Основное уравнение динамики (второй закон Ньютона в векторном виде) можно записать в проекциях на касательное направление и нормаль к траектории в данной точке, используя полученные ранее выражения для нормального и тангенциального ускорений (§2.1.4):
,
.
Если тело (или точка) вращается по окружности, то можно записать уравнение для силы, действующей по касательной к траектории , и для силы, действующей по радиусу окружности (Рисунок

.
Рисунок 8 – Разложение вектора F на составляющие Fτ и Fn, R – радиус окружности, по которой вращается тело (или точка).
2.2.5. Третий закон Ньютона
В первом и во втором законах Ньютона речь идет о силах, действующих на данное тело, и его движении под действием этих сил, но нет упоминания о других телах, со стороны которых эти силы действуют. Роль второго тела во взаимодействии отражена в третьем законе Ньютона.
3-й закон Ньютона
Силы, с которыми два тела действуют друг на друга, равны по величине, направлены в противоположные стороны F12 = — F21.
F12 — сила, действующая со стороны второго тела на первое, приложена к первому телу, F21 — сила, действующая на второе тело со стороны первого, приложена ко второму телу (Рисунок 9).
Рисунок 9 — Взаимодействие двух тел.
2.2.6. Закон сохранения импульса
1. Совокупность тел, частиц (например, в газе) или отдельное твердое можно рассматривать как систему материальных точек. Если система с течением времени изменяется, то это означает, что изменяется ее состояние. Зная законы действующих на частицы системы сил и состояние системы в начальный момент времени, можно с помощью уравнений движения рассчитать состояние системы в любой момент времени. Но в некоторых случаях это может быть задачей достаточно сложной (сложна сама система или неизвестны законы действующих сил, или детальное рассмотрение поведения отдельных частиц системы не имеет смысла, например, в газе).
Возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задач и обойти возникшие трудности? Оказалось, такие принципы есть. Это законы сохранения энергии, импульса и момента импульса (см. [7], стр. 52-57).
Эти законы справедливы не только в рамках классической механики. Все они являются универсальными законами природы, выполняются и в макромире, и в микромире, и во всей Вселенной. В настоящее время неизвестно ни одного эксперимента и ни одного физического явления, в котором упомянутые универсальные законы сохранения нарушались бы.
Закон сохранения импульса выполняется для замкнутых систем (см. 2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс, п.1).
2. Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из двух тел, применяя второй и третий законы Ньютона. Пусть первое тело, имеющее массу m1, движется со скоростью , второе тело, масса которого m2, движется со скоростью
2.
При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила 12 = —
21. По второму закону Ньютона сила F12, действующая на первое тело, изменит импульс первого тела, можно записать
12=
, Точно так же можно записать, что сила F21 изменит импульс второго тела:
21=
. Подставим значения F12 и F21 в третий закон Ньютона:
= —
, Т.к. время взаимодействия
— одно и то же, то:
= —
или
+
=
.
Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы =
+
,
+
=
— это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса
= 0, следовательно, полный вектор импульса системы при взаимодействии не изменился: если
= 0, то P = const.
Если система состоит из N тел, то P = m1∙ v1 + m2∙ v2 + ……..+ mN∙ v N есть полный вектор импульса замкнутой системы, и P = const.
Закон сохранения импульса (ЗСИ).
Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы. Только внешние силы изменяют импульс системы.
3. Если векторная сумма внешних сил не равна нулю, то надо посмотреть, нет ли такого направления, вдоль которого внешние силы не действуют или сумма их проекций на это направление равна нулю. Если такое направление в движении тел, входящих в систему, есть, то можно применять закон сохранения для проекции полного вектора импульса системы на выделенное направление.
2.2.7. Динамические характеристики вращательного движения. Момент силы. Момент импульса
При поступательном движении системы все ее точки проходят одинаковые пути, имеют в данный момент времени одинаковые скорости и ускорения. При вращательном движения твердого тела все эти характеристики различны для разных точек вращающегося тела, поэтому и математическая форма 2-го закона Ньютона будет иной. При вращательном движении существенно изменяются сами понятия причины, вызывающей вращение, и величины, определяющей инертность тела.
При поступательном движении динамическими характеристиками являются сила, масса, импульс. При вращательном движении динамическими характеристиками являются момент силы, момент инерции, момент импульса. Эти характеристики можно рассматривать относительно точки вращения (полюса) и относительно оси вращения. В дальнейшем будем рассматривать эти характеристики относительно оси вращения. Определим эти характеристики.
1. Момент силы, действующей на материальную точку, относительно оси вращения
а) Пусть материальная точка массы m вращается относительно оси ОО ΄. Обозначим r — радиус-вектор, проведенный от оси вращения до точки приложения силы F (Рисунок 10).
Рисунок 10. Вращение материальной точки
Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [ r∙ F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика Модуль вектора момента силы равен M = F∙r∙sinα, где α — угол между векторами rи F.
2. Момент импульса
Моментом импульса материальной точки относительно оси вращения называется вектор L, равный векторному произведению радиуса-вектора r на вектор импульса P: L = [ r∙P] = [ r∙ mv], где m, v — соответственно масса и вектор скорости точки. Направление Lопределяется по правилу правого буравчика. Модуль вектора L = mv∙ r∙ sinα, где α — угол между векторами r и v.
3. Момент инерции материальной точки относительно оси вращения
Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения (Рисунок 10).
I = mr2
Момент инерции — величина скалярная.
Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения.
I = mi∙ ri2
Для твердого тела, разбитого на элементарные массы ∆ mi, момент инерции относительно оси равен I = ∆ mi∙ ri2.
Моменты инерции тел правильной геометрической формы могут быть легко вычислены. В Таблице 2 приведены результаты расчетов моментов инерции для тел правильной формы относительно оси вращения ОО’, проходящей через их центр масс.
Для расчета моментов инерции вращающихся тел вокруг оси, не проходящей через центр масс тела, можно использовать теорему Штейнера.
4. Теорема Штейнера
Момент инерции тела относительно произвольной оси АА’ равен сумме момента инерции тела относительно оси ОО’, проходящей через центр масс тела и параллельной данной оси АА’, и произведения массы тела как целого на квадрат расстояния d между осями АА’ и ОО’ (Рисунок 11).
IАА’ = IОО’ + md2
Рисунок 11.
Пример. Применение теоремы Штейнера для расчета момента инерции стержня длины l и массы m (см. Таблицу 2), если ось вращения проходит не через центр масс, а через конец стержня, приводит к следующему:
IАА’ = IОО’ + md2 = 
Рисунок 12. Вращение стержня вокруг оси
2.2.8. Основное уравнение динамики вращательного движения
1. В разделе «Кинематика» при рассмотрении поступательного и вращательного движений мы показали, что кинематические уравнения обоих движений имеют одинаковый вид, но при поступательном движении мы используем линейные характеристики (путь, скорость, ускорение), а при вращательном — угловые характеристики (угловое перемещение, угловую скорость, угловое ускорение). Используем эту аналогию и в динамике. При поступательном движении уравнение второго закона Ньютона имеет вид dP/dt = F.
Для вращательного движения: dL/dt = M.
Это уравнение называется уравнением моментов или основным законом вращательного движения. Вид уравнения не изменится и для системы материальных точек и для вращения твердого тела, только L определяется как момент импульса для системы точек.
2. Еще один вид уравнения второго закона Ньютона для вращательного движения имеет вид:
M∙ dt = dL,
где величина M∙ dt называется импульс момента сил, а dL — изменение момента импульса системы.
2.2.9. Закон сохранения момента импульса
Обратимся к уравнению моментов dL/ dt = M, где M — главный вектор момента внешних сил.
Если M = 0, то и L = const.
Если относительно некоторой точки О выбранной системы отсчета момент всех сил, действующих на систему материальных точек, равен нулю, то относительно этой точки вектор момента импульса системы не изменяется с течением времени (закон сохранения момента импульса относительно полюса).
Примеры.
а) Человек стоит на скамье Жуковского, представляющей массивный, диск, который может вращаться вокруг оси, проходящей через его центр, с пренебрежимо малым трением. Момент импульса системы «человек — диск» равен нулю. Человек начинает идти вдоль обода диска. Диск начинает вращаться в обратную ходу человека сторону.
б) Фигурист выполняет «волчок», его руки раскинуты в стороны, его момент инерции относительно вертикальной оси вращения I1, угловая скорость ω1. Затем он резко прижимает руки к груди, его момент инерции уменьшается и становится I2, а угловая скорость ω2 увеличивается. При этом выполняется закон сохранения момента импульса относительно вертикальной неподвижной оси, проходящей через линию симметрии тела фигуриста I1∙ ω1 = I2∙ω2.
2.3. Работа и механическая энергия
2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы
В физике работа неразрывно связана с изменением состояния тела или системы. Это изменение может выражаться самым различным образом: а) тело приобретает другую скорость, б) тело поднимается на другой уровень, в) тело деформируется, г) тело заряжается, д) тела намагничивается и т.д. Состояние механической системы (или тела) характеризуется одновременным заданием координат и скоростей всех точек системы (или тела) и может изменяться в процессе движения.
Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса вводят понятия силы и работы, совершаемой силой.
1. Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r:
∆А = (F∙∆r) = ½ F½½∆ r½ cos a ,
где a — угол между направлениями векторов силы F и перемещения ∆r, ( F∙ ∆r) – скалярное произведение двух векторов (см.[8]).
Рисунок 13 — Перемещение тела под действием постоянной силы.
Работа ∆А — скаляр. Если угол a — острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a — тупой, то ∆А — отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 900, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.
2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 900), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.
На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F i и ∆ r i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F i на своем малом участке (Рисунок 14):
А = ∆А1 + ∆А2 +….+ ∆А N = ( F1∙∆ r1) + (F 2∙∆ r2) + …+( F N∙∆ rN) = ( Fi∙∆ ri),
где i = 1,2…… N — номер элементарного участка траектории.
Рисунок 14 — График зависимости силы от пути.
На участке ∆r i силу Fi можно считать постоянной, тогда элементарная работа ∆Аi на участке ∆r i равна ∆Аi= Fi∙∆ r i и равна площади заштрихованной фигуры на рисунке 14.
А=∆Аi — это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.
3. Примеры вычисления работы.
а) Тело, поднятое над землей на высоту h, падает на землю (без трения) из точки В в точку С и возвращается обратно (Рисунок 15). Определить работу силы по замкнутому пути.
Сила, действующая на тело, постоянна и равна силе притяжения тела к Земле (сила тяжести). Работа этой силы на участке ВС равна .
Чтобы поднять тело без ускорения из точки С в точку В, надо приложить к телу силу, равную силе тяжести, но противоположно направленную, и работа на участке пути СВ равна (работа совершается против силы тяжести).
Полная работа на участке (ВС+СВ) равна нулю.
Рисунок 15. Падение тела с высоты h (a) и поднятие тела на высоту h (б)
б) Пружину длиной l1 растягиваем до длины l2. Какая работа при этом совершается?
Пусть х — длина, на которую растянута пружина, отсчет х от положения равновесия (Рисунок 16). При этом на пружину будет действовать упругая сила, старающаяся вернуть пружину в состояние равновесия, что соответствует минусу в формуле F = — kх (закон Гука). Если растянуть пружину еще на малую длину ∆х, надо совершить элементарную работу ∆А = — kх∙ ∆х.
Возникающая упругая сила будет переменной, т.к. она зависит от длины, на которую растягивают пружину. Для определения работы, которую надо затратить для растяжения пружины от длины l1 до l2, надо воспользоваться операцией интегрирования:
Работа силы упругости определяется только начальным и конечным положением пружины.
Рисунок 16. Сжатие пружины
4. Полная работа внешних сил при вращательном движении тела равна произведению момента этих сил относительно оси вращения на угол поворота тела за время действия сил. ∆ A= М∆.
И момент сил, и угловое перемещение (равное по модулю углу поворота) — векторы, направленные вдоль оси вращения. Если направление этих векторов совпадает, то ∆ A>0. Если направление этих векторов противоположное, то ∆ A<0.
5. Силы, работа которых определяется только начальной и конечной точками их приложений, и не зависят ни от вида траектории, ни от характера движения тела, называются консервативными или потенциальными силами.
Другое определение для этих сил таково. Силы, работа которых по замкнутой траектории равна нулю, называются потенциальными.
Соответственно, если работа силы по замкнутой траектории не равна нулю, то такая сила неконсервативная ( непотенциальная).
К непотенциальным силам относятся силы трения и силы, величина которых зависит от скорости движения точки (тела).
Сила тяжести и сила упругости являются потенциальнымисилами (см. приведенные выше примеры).
2.3.2. Энергия
1. Наиболее общим определением понятия энергии можно считать то, которое связано с понятием состояния системы (или тела). Энергия всегда является функцией состояния системы (тела). В любом состоянии система имеет определенное значение энергии и может сохранять это состояние, а значит и энергию этого состояния, сколь угодно долго. Для перехода системы (тела) в другое состояние должна быть совершена работа.
Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией.
Состояние системы (тела) может меняться в процессе движений. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии. Поэтому можно дать другое определение для энергии.
Энергией называется физическая величина, являющаяся общей мерой различных форм движения материи.
Различают виды энергии механическую, внутреннюю, электромагнитную, химическую, ядерную и т.д.
Механическая энергия может быть обусловлена или движением тела с некоторой скоростью (кинетическая энергия), или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия) Wмех. = Wкин. + Wпот..
2.3.3. Кинетическая энергия
1. Кинетической энергией тела называется энергия его механического движения.
Изменение кинетической энергии тела под действием силы равно работе этой силы.
Физическая величина называется кинетической энергией, а величина
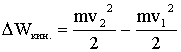
Если на тело действуют несколько сил, и каждая из них совершает работу, и в результате этого меняется кинетическая энергия тела, то полная работа равна алгебраической сумме работ всех сил, действующих на тело. Энергия тела меняется за счет совершения работы.
Итак, связь работы и кинетической энергии задается соотношением:
Авсех сил = ∆ Wкин = ( Wкин)кон. — ( Wкин.) нач.,
т.е. работа всех сил равна изменению кинетической энергии тела (или системы).
Работа — мера изменения энергии (физический смысл работы).
2. Кинетическая энергия вращающегося тела.
Твердое тело вращается вокруг неподвижной оси. Полная кинетическая энергия вращающегося тела равна:
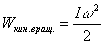
где I — момент инерции тела относительно оси вращения.
2.3.4. Потенциальная энергия
1. Потенциальная энергия — энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга.
Когда меняется конфигурация системы тел или частиц одного тела относительно друг друга, должна совершаться работа.
Пространство, в каждой точке которого на тело действует определенная сила, называется физическим или силовым полем.
Поэтому когда тело перемещается вблизи Земли, то говорят, что тело двигается в силовом поле тяготения Земли или в потенциальном поле Земли. Потенциальная энергия тяготения равна (Wпот)тяг. = mgh,
h — расстояние между телом и Землей.
В растянутой (или сжатой) пружине на каждую ее точку действует сила упругости, в этом случае можно говорить о потенциальном поле упругости. Потенциальная энергия упругости равна ( Wпот) упр. = ( kl2)/2, l — длина растянутой пружины, отсчет х от положения равновесия.
При делении сил, действующих на тело, на внешние и внутренние рассмотренные в примерах сила тяготения (в системе «тело — Земля») и сила упругости растянутой (сжатой) пружины можно отнести к внутренним силам. Поэтому верно утверждение, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия, и работа всех внутренних потенциальных сил, приводящая к изменению этой конфигурации, равна взятому со знаком минус приращению ( убыли) потенциальной энергии системы.
2.3.5. Закон сохранения механической энергии системы
Обобщая материал, рассмотренный в данной главе, можно основные выводы сформулировать так:
1) Приращение кинетической энергии системы равно произведенной работе всех сил, приложенных к системе.
Авсех сил = ∆ Wкин = ( Wкин)кон. — ( Wкин.) нач.
2) Все силы, действующие на систему можно разделить на внешние и внутренние. Внутренние силы можно разделить на потенциальные и непотенциальные (к последним относятся силы трения и сопротивления). Тогда Авсех сил = Авнеш. + .Апот. + Атр.
3) Работа потенциальных внутренних сил равна приращению потенциальной энергии системы, взятому со знаком минус.
Апот. = — ∆ Wпот = ( Wпот) нач. — ( Wпот.)кон..
4) Полная механическая энергия система равна сумме кинетической и потенциальной энергии системы.
Wмех. = Wкин. + Wпот..
Суммируя все эти положения и сделав соответствующие преобразования, получим
∆ Wмех. =( Wмех) кон. — (Wмех.) нач = Авнеш. + Атр.
Если внешние силы на систему не действуют, то система называется замкнутой или изолированной и Авнеш. = 0. С замкнутой системой мы работали при рассмотрении законов сохранения импульса (ЗСИ) и момента импульса (ЗСМИ).
Если внутри системы действуют только потенциальные силы, а сил трения и сопротивления нет, то Атр. = 0.
И тогда ∆ Wмех. = ( Wмех) кон. — (Wмех.) нач. = 0 и выполняется закон сохранения механической энергии ( ЗСЭмех):
Полная механическая энергия замкнутой системы, в которой не действуют силы трения, остается постоянной, независимо от взаимодействий внутри системы.
Wмех. = ( Wмех) кон. = (Wмех.) нач = const.
Если система замкнутая, но в ней действуют силы трения, то
∆ Wмех. = ( Wмех) кон. — ( Wмех.) нач. = Атр.
Так как работа силы трения всегда отрицательна, то ее действие приводит к уменьшению полной механической энергии системы:
( Wмех) кон. < ( Wмех.) нач..
2.3.6. Сравнение кинематических и динамических характеристик поступательного и вращательного движений
Воспользуемся аналогией записи кинематических и динамических характеристик, законов поступательного и вращательного движений(см. таблицу 3).
Таблица 3. Сравнение кинематических и динамических характеристик поступательного и вращательного движений.
2.3.7. Применение законов сохранения в теории ударов тел
Ударом называется явление конечного изменения скоростей твердых тел за весьма малый промежуток времени при их столкновении.
Поведение соударяющихся тел можно рассчитать с помощью законов сохранения. Потенциальная энергия взаимодействующих тел не учитывается.
Абсолютно неупругий удар — удар, в результате которого тела после столкновения двигаются с одинаковыми скоростями. Поведение тел при таких ударах может быть описано моделью, называемой абсолютно неупругое тело.
Рассмотрим центральный неупругий удар двух шаров массой m1 и m2. Скорости шаров лежат на одной линии, соединяющей их центры: v1 и v2 — скорости шаров до удара, v — общая скорость шаров после удара. ЗСИ в векторной форме имеет вид:
m1∙ v1 + m2∙ v2 = ( m1 + m2)∙ v
Если v1 и v2 имеют одинаковые направления, то ЗСИ примет вид:
m1∙ v1 + m2∙ v2 = ( m1 + m2)∙v.
Если шары двигаются навстречу друг другу, тогда
m1∙ v1 — m2∙ v2 = ( m1 + m2)∙v
Закон сохранения механической энергии при таком ударе не выполняется, но с учетом энергии, затраченной на деформацию тел, общий закон сохранения энергии имеет вид:
Абсолютно упругий удар — такое кратковременное взаимодействие тел, при котором в обоих взаимодействующих телах не остается никаких деформаций. Поэтому кинетическая энергия, которой тела обладали до взаимодействия, превращается в кинетическую энергию тех же тел после взаимодействия.
Поведение тел при таких ударах может быть описано моделью, называемой абсолютно упругое тело.
Рассмотрим центральный упругий удар двух шаров массой m1 и m2. Скорости шаров лежат на одной линии, соединяющей их центры: v1 и v2 — скорости шаров до удара, u1 и u2 — скорости шаров после удара.
(ЗСИ) m1∙ v1 + m2∙ v2 = m1∙ u1 + m2∙ u2
( ЗСЭмех)
В ЗСИ надо учитывать направления скоростей до удара. Значения и направления скоростей после удара получаются при решении приведенной выше системы двух уравнений.
Механика. Вопросы и задачи для самоконтроля
1. Запишите формулы для определения кинематических величин: скорости и ускорения для
а) поступательного движения
б) для вращательного движения (см. 2.1.3. Кинематические характеристики. Скорость; 2.1.4. Кинематические характеристики. Ускорение; 2.1.5. Поступательное и вращательное движение твердого тела).
2. На рисунке 16 даны графики зависимости различных кинематических характеристик от времени. Какие виды движения представлены на рисунках 16(а), 16(б), 16(в) (см. 2.1.6. Связь между кинематическими характеристиками при различных видах движений)
Рисунок 16 – Виды движения
3. Задача. Одно тело двигается с постоянной скоростью =
в течение промежутка времени
. Другое тело разгоняется от
и за тот же промежуток времени
достигает скорости
. Найти отношение пройденных телами путей
.
4. Материальная точка вращается по окружности. Сделайте рисунок и покажите, как направлены ускорения: — аτ – тангенсальное, а n — нормальное и а – полное (см. 2.1.6. Связь между кинематическими характеристиками при различных видах движений, п.3).
5. Проведите аналогию динамических характеристик поступательного и вращательного движений (см. Таблица 3 — Сравнение кинематических и динамических характеристик поступательного и вращательного движений).
6. Задача. Мяч, летящий перпендикулярно стене, со скоростью =
, отскакивает от нее со скоростью
=
. Масса мяча m=0,2кг. На сколько изменился импульс мяча?
7. Задача. Человек выпрыгнул на берег из лодки. Почему лодка стала двигаться от берега? (см. 2.2.6. Закон сохранения импульса)
8. Задача. Тело массой m=10 кг за
при торможении изменило свою скорость от
=
до
=0. Какая сила действовала на тело?
9. Как определяется работа, совершаемая постоянной силой?, переменной силой? (см. 2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы)
10. Задача. Тело под действием силы перемещается на расстояние. Сила действует вдоль линии движения. В каком случае сила совершит большую работу? Графики F= F(S) представлены на рисунке 17,
Рисунок 17 – Зависимость силы от перемещения.
11. Какие виды механической энергии вы знаете? (см. 2.3.3. Кинетическая энергия)
12. Задача. Тело массой m соскальзывает с наклонной плоскости, высота которого h. Какую скорость приобретет тело у подножия наклонной плоскости? Силой трения пренебрегать.
13. От каких величин зависит кинетическая энергия вращающегося тела?
14. Задача. В каком случае шар, масса которого “m”, радиус “R”, будет иметь большую кинетическую энергию, вращаясь около оси или
(см. рисунок 18)?
Рисунок 18 – Вращение шара.
Решения и ответы к задачам
Задача 3. Первое тело двигалось равномерно, поэтому ; второе тело двигалось равноускоренно, его путь
, по условию задачи
,
— по определению ускорения, тогда
,
,
Задача 6. Мяч, летящий перпендикулярно стене, имел импульс , после отскакивания от стены импульс его стал
(рисунок 20)
Рисунок 19. Удар мяча о стену.
, векторы
и
имеют противоположное направление.
Перейдем от векторной разности к скалярной:
, т.е.
Задача 7. Лодка с человеком была неподвижна и общий импульс такой системы . Когда человек выпрыгивал из лодки, у него был импульс
, но, согласно закону сохранения импульса
, поэтому
и
, т.е. лодка со скоростью V
отойдет от берега.
Задача 8. Согласно второму закону Ньютона , по определению
, тогда
, F=
, (перед вычислением F надо выразить скорость в СИ:
).
Задача 10. Работу можно определить по площади фигуры, ограниченной кривой зависимости F(S) и осью S, поэтому площадь фигуры на рисунке 17а) равна , а на рисунке 17б)
. Следовательно, в случае а) работа будет совершена в два раза больше, чем в случае б).
Задача 12. На высоте h тело имело потенциальную энергию W, у подножия плоскости тело стало иметь кинетическую энергию
. Так как энергия не тратилась на работу против сил трения, на основании закона сохранения энергии можно записать:
, отсюда
.
Задача 14. Кинетическая энергия вращающегося тела равна , где I — момент энергии, относительно оси вращения
(см. таблицу 2),
(см. 2.2.7. Динамические характеристики вращательного движения, п.5).
.
Считая, что угловая скорость остается постоянной, получим отношение
Следовательно, при вращении вокруг оси шар будет обладать большей энергией.
Приложение. Международная система единиц — СИ — (System International – SI)
Основные принципы построения систем единиц физических величин
Физические законы имеют количественную форму. Они устанавливают точные количественные отношения, выражающие объективные законы природы. Физические законы выражаются через соотношения или уравнения, которые дают связь между величинами. Для каждой из величин, входящих в уравнение, определяются единицы измерения.
В физике огромное значение придается измерениям физических величин. Нередко результат измерений, полученный в том или ином научном эксперименте, давал решающий ответ на принципиальный вопрос, поставленный наукой. Иногда результаты опытов позволяли сделать выбор между двумя теориями, а нередко приводили и к появлению новой теории или даже новой отрасли науки. Например, измерение скорости света в различных средах способствовало утверждению волновой теории света. А измерение распределения энергии в спектре абсолютно черного тела послужило зарождению теории квантов и развитию квантовой оптики. Немаловажную роль играет точность измерений. Например, уточнения в измерениях некоторых постоянных позволили разрешить противоречия, существовавшие в квантовой электродинамике.
Измерить какую-либо величину — это, значит, сравнить ее с эталоном, т.е. опытным путем определить отношение измеряемой величины к соответствующей единице измерения.
Вопрос о том, как определить единицу измеряемой величины может быть решен произвольно. И действительно, существует громадное количество разнообразных единиц измерения длины (метр, фут, дюйм, миля), площади (квадратный метр, акр, гектар), массы (килограмм, тонна), давления (паскаль, бар, атмосфера, миллиметр ртутного столба) и т.д.
Требование единообразия при измерениях физических величин приводит к созданию согласованной системы измерений. Однако таких систем довольно много (СГС, абсолютная, техническая и т.д.). Наличие большого числа разнообразных единиц измерений, которые использовались в разных странах, создавало затруднения в обмене результатами научных исследований, международных торговых отношениях и т.п. Вследствие этого ученые разных стран попытались установить общие единицы измерений, которые действовали бы во всех странах. Положение было окончательно урегулировано после введения международной системы единиц, обозначаемой символом СИ.
Международная система единиц распадается на несколько различных систем, предназначенных для измерений в различных областях (в механике, электродинамике, акустике и т.д.). В данной части конспекта мы приводим систему механических и тепловых единиц.
В СИ выбраны основные единицы (эталоны), установленные произвольно и независимо друг от друга. Производные единицы измерений получаются через основные единицы из физических законов и определений.
Основными единицами СИ являются:
единица длины — метр — [м],
единица времени — секунда — [с],
единица массы — килограмм — [кг],
единица силы электрического тока — ампер — [А],
единица термодинамической температуры — кельвин — [К],
единица количества вещества — моль — [моль],
единица силы света — кандела — [кд].
Дополнительные единицы СИ:
для плоского угла — радиан — [рад],
для телесного угла — стерадиан — [стер].
Остальные единицы являются производными.
Основные единицы
За единицу длины 1 метр принято расстояние, проходимое в вакууме плоской электромагнитной волной за 1/299792458 долю секунды.
За единицу времени 1 секунда принята продолжительность 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия с массовым числом 133.
За единицу массы 1 килограмм принята масса платино-иридиевой гири, хранящейся в Международном бюро мер и весов.
Единица количества вещества 1 моль определяется как количество вещества, содержащее столько структурных элементов (атомов, молекул, ионов и т.д.), сколько атомов содержится в 0,012 кг изотопа углерода 12С.
Единица температуры 1 кельвин определяется как (1/273,16) часть термодинамической температуры тройной точки воды.
За единицу плоского угла 1 радиан принимается угол, длина дуги которого равна единице длины при радиусе, равном также единице длины.
Определения остальных основных единиц СИ (ампер, кандела, стерадиан) будут приведены в других частях конспекта лекций в соответствующих разделах курса.
Таблица 3. Производные единицы механических величин
Таблица 4. Некоторые внесистемные единицы измерения механических величин и их связь с единицами СИ.
| Величина | Единица измерения и ее связь с единицами СИ ( в квадратных скобках приведены сокращенные обозначения величин) |
| Длина | 1 ангстрем [Ǻ] = 10–10 м 1 дюйм [дюйм] = 0,0254 м 1 ярд = 0,9144 м 1 верста = 1,0668 км |
| Масса | 1 тонна [т] = 103 кг 1 центнер [ц] 102 кг 1 атомная единица массы (1а.е.м.) = = 1,66∙10—27 кг |
| Плоский угол | 1 градус [°] = π/180 рад 1 минута [‘] = (π/108)∙ 10–2 рад = = 1/60 градуса 1 секунда [»] = (π/648)∙10–3 рад = = 1/60 угловой минуты |
| Площадь | 1 ар [ар] = 100 м2 1 гектар [га] = 104 м2 |
| Объем | 1 литр [л] = 10–3 м3 |
| Сила | 1 дина [дин] = 10–5 Н |
| Давление | 1 бар = 105 Па 1 миллиметр ртутного столба (мм рт.ст.) = 133 Па 1 физическая атмосфера [атм] = = 1,013∙105 Па 1 техническая атмосфера [ат] = = 0,981∙105 Па |
| Работа | 1 эрг = 10–7 Дж 1 ватт-час = 3,6∙103 Дж 1 электрон-вольт [эВ] = 1,6∙10–19 Дж 1 калория [кал] = 4,19 Дж |
| Мощность | 1 лошадиная сила [л.с.] = 736 Вт |
Таблица 5. Единицы измерения электрических и магнитных величин
| Физическая величина и ее обозначение | Единица измерения | Сокращенное обозначение единицы измерения | Определение | |
| Русское | Международн. | |||
| Электрический заряд (количес-тво электричества), Q, q. | кулон | Кл | C | Кулон – количество электричества, проходящее через попе-речное сечение проводника при токе силой 1 А за 1 с. |
| Плотность электрического тока, j | ампер на квадратный метр | А/м2 | A/m2 | Ампер на квадратный метр – плотность равномерно распреде-ленного по поперечному сечению площадью 1 м2 электрического тока 1 А. |
| Объемная плотность электрического заряда, |
кулон на кубический метр | Кл/м3 | C/m3 | Кулон на кубический метр – объемная плотность электрического заряда, при которой в объеме 1 м3 равно-мерно распределен заряд 1 Кл. |
| Поверхностная плотность электрического заряда, |
кулон на квадратный метр | Кл/м2 | C/m2 | Кулон на квадратный метр – поверхностная плотность электрического заряда, при которой на поверхности 1 м2 равномерно распределен заряд 1 Кл. |
| Линейная плотность электрического заряда, |
кулон на метр | Кл/м | C/m | Кулон на метр – линейная плотность электрического заряда, при которой на длине 1 м равномерно распределен заряд 1 Кл. |
| Момент электрического диполя, р | кулон-метр | Кл·м | C·m | Кулон-метр – момент электрического диполя, заряды которого, рав-ные 1 Кл каждый, расположены на расстоянии 1 м друг от друга. |
| Напряженность электрического поля, Е | вольт на метр | В/м | V/m | Вольт на метр – напряженность однородного электрического поля, при кото-рой между точками, находящимися на расстоянии 1 м вдоль линии напряженности поля, создается разность потенциалов 1 В. |
| Электрическое смещение, Д | кулон на квадратный метр | Кл/м2 | C/m2 | Кулон на квадратный метр – электричес-кое смещение, при котором поток электрического смещения через поперечное сечение площадью 1 м2 равен 1 Кл. |
| Поток электрического смещения, |
кулон | Кл | C | Кулон – поток электрического смещения сквозь замкнутую поверхность, внутри которой содержится свободный заряд 1 Кл. |
| Напряжение электрическое | вольт | В | V | Вольт – электрическое напряжение, вызывающее в электрической цепи постоян-ный ток силой 1 А при мощности 1 Вт. |
| Потенциал электрический | вольт | В | V | То же |
| Разность потенциалов электрических | вольт | В | V | То же |
| Электродви-жущая сила | вольт | В | V | То же |
| Электрическая емкость | Фарада | Ф | F | Фарада – емкость конденсатора, между обкладками которого при заряде 1 Кл возникает напряжение 1 В. |
| Электрическое сопротивление, r,R | ом | Ом | Ώ | Ом – сопротивление проводника, между концами которого при силе тока 1 А возникает напряжение 1 В. |
| Удельное электрическое сопротивление, |
ом-м | Ом·м | Ω·m | Ом-метр – удельное электрическое сопротивление, при котором цилиндрический прямолинейный проводник площадью поперечного сечения 1 м2 и длиной 1 м имеет сопротивление 1 Ом. |
| Электрическая проводимость, G | сименс | См | S | Сименс – электрическая проводимость проводника сопротивлением 1 Ом. |
| Удельная электрическая проводимость, |
сименс на метр | См/м | S/m | Сименс на метр – удельная электрическая проводимость, при которой цилиндрический прямолинейный проводник площадью поперечного сечения 1 м2 и длиной 1 м имеет электрическую проводимость 1 С. |
| Магнитная индукция, В | тесла | Тл | Т | Тесла – магнитная индукция, при которой магнитный поток через попереч-ное сечение площадью 1 м2 равен 1 Вб. |
| Магнитный поток, Ф | вебер | Вб | Wb | Вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивле-нием 1 Ом проходит количество электричества 1 Кл. |
| Напряженность магнитного поля, Н | Ампер на метр | А/м | A/m | Ампер на метр – напряженность магнитного поля в центре длинного соленоида с n витками на каждый метр длины, по которым проходит ток силой 1/n А. |
| Индуктивность, L | генри | Гн | Н | Генри – индуктивность контура, с которым при силе постоянного тока в нем 1 А сцепляется магнитный поток 1 Вб. |
| Магнитный момент электрического тока, р | ампер-квадратный метр | А·м2 | A·m2 | Ампер-квадратный метр — магнитный момент электрического тока силой 1 А, проходящего по плоскому конту-ру площадью 1 м2. |
| Намагничен-ность, J | ампер на метр | А/м | A/m | Ампер на метр – намагничен-ность, при которой вещество объемом 1 м3 имеет магнитный момент 1 А·м2. |
| Электромаг-нитная энергия, W | джоуль | Дж | J | Джоуль – электромагнит-ная энергия, эквивалентная механической работе 1 Дж. |
Таблица 6. Соотношение между электромагнитными единицами измерения СИ и некоторыми другими единицами
| Физическая величина | Перевод из единиц СИ | Перевод в единицы СИ |
| Заряд | 1 Кл = 2,78·10-4 а·ч | 1 А·ч =3600 Кл |
| Электрическая емкость | 1 Ф = 9·1011 см | 1 см = 1/9·10-11 Ф |
| Магнитная индукция | 1 Тл = 1·104 гс | 1 гс = 1·10-4 Тл |
| Магнитный поток | 1 Вб = 1·108 мкс | 1 мкс = 1·10-8 Вб |
| Напряженность магнитного поля | 1 А/м = 1,26·10-2 э | 1 э = 79,6 А/м |
| Индуктивность | 1 Гн = 1·109 см | 1 см = 1·10-9 Гн |
Акустические единицы
Хотя Международная система единиц рекомендуется для всех областей науки и техники, в акустике широкое применение сохранила система СГС. Ниже, в таблице 4 приведены важнейшие акустические величины в СИ и в таблице 5 дана их связь с единицами системы СГС.
Таблица 7. Объективные характеристики механических волновых процессов
Таблица 8. Связь акустических единиц системы СГС с единицами СИ
Для характеристики величин, определяющих восприятие звука, существенными являются не столько абсолютные значения интенсивности звука и звукового давления, сколько их отношение к некоторым пороговым значениям. Поэтому вводятся понятие относительных уровней интенсивности и звукового давления.
Для того, чтобы звуковая волна воспринималась на слух, необходимо, чтобы ее интенсивность превышала минимальную величину, называемую порогом слышимости. Величина
различная для разных частот. Для частоты
порог слышимости составляет величину порядка
. Опытом установлено, что на каждой частоте есть верхняя граница силы звука
, при превышении которого у человека возникают болевые ощущения. Величина
называется порогом болевого ощущения.
Уровень интенсивности (уровень силы звука) равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при той же частоте на пороге слышимости:

Уровень громкости равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при частоте 1000 Гц на пороге слышимости:

Единицей измерения уровня интенсивности является бел (Б): . Одна десятая часть бела называется децибел (дБ): 0,1 Б = 1 дБ. Формула для определения уровня интенсивности в децибелах примет вид:

Если записать формулу для уровня громкости в виде 
Уровень звукового давления равен произведению 20 на логарифм отношения звукового давления при данной частоте к звуковому давлению на пороге слышимости. Единицей измерения в данном случае является децибел.

Единицы излучения
Величины, характеризующие энергетическую сторону излучения электромагнитных волн, измеряются общими энергетическими единицами, которыми измеряются энергия, объемная плотность энергии, поток энергии и т.д. Световые измерения тех же физических величин имеют ту особенность, что в них большую роль играют непосредственные ощущения, связанные с приемниками излучения (и в первую очередь человеческим глазом). Переход от энергетических единиц измерения излучения к световым, производится неоднозначно при разных длинах волн излучения. Ниже в таблице приведены и энергетические, и световые единицы различных характеристик излучения. Дополнительно к рассмотренным ранее основным величинам СИ (метр, килограмм, секунда, ампер) добавляется единицы силы света – кандела (кд), измеряемая по световому эталону.
Таблица 9
Приставки для образования кратных и дольных единиц
В Таблице 10 приведены приставки, служащие для образования кратных и дольных единиц. Приведенные приставки можно присоединять только к простым наименованиям единиц измерений (метр, грамм и т.д.).
Таблица 10
| Приставка | Числовое значение | Обозначение | Приставка | Числовое значение | Обозначе-ние |
|
Атто |
10—18 |
А |
Деци |
10—1 |
Д |
|
Фемто |
10—15 |
Ф |
Дека |
101 |
Да |
|
Пико |
10—12 |
п |
Гекто |
102 |
Г |
|
Нано |
10—9 |
н |
Кило |
103 |
К |
|
Микро |
10—6 |
Мк |
Мега |
106 |
М |
|
Милли |
10—3 |
м |
Гига |
109 |
Г |
|
Санти |
10—2 |
с |
Тера |
1012 |
Т |
Некоторые постоянные величины
Таблица 11. Универсальные физические величины
| № п.п. | Величина |
Обозначение. |
Значение |
| 1. | Магнитная постоянная |
m 0 |
4p · 10 |
| 2. | Электрическая постоянная |
e 0 |
8,85418782·10-12 Ф/м |
| 3. | Скорость света в вакууме |
с |
299792458 м/с |
| 4. | Элементарный заряд |
е |
1,6021892·10-19 Кл |
| 5. | Постоянная Планка |
h |
6,626176·10-34 Дж·с |
| Постоянная Планка |
|
1,0545887· 10-34Дж· с | |
| 6. | Число Авогадро |
NА |
6,0220943· 1023 моль-1 |
| 7. | Атомная единица массы |
а.е.м. |
1,6605655· 10-27 кг |
| 8. | Энергетический эквивалент одной а.е.м. | 931,5016 МэВ | |
| 9 | Масса покоя: электрона |
mе |
9,109534· 10-31 кг |
| 5,4858026· 10-4 а.е.м. | |||
| 10 | мюона |
mm |
1,883566· 10-28 кг |
| 0,11342920 а.е.м. | |||
| 11 | протона |
mp |
1,6726485· 10-27 кг |
| 1,007276470 а.е.м. | |||
| 12 | нейтрона |
mn |
1,6749543· 10-27 кг |
| 1,008665012 а.е.м. | |||
| 13. | Удельный заряд электрона |
е/me |
1,7588047·1011 Кл× кг |
| 14. | Число Фарадея |
F |
9,648456· 104 ККл/моль |
| 15. | Постоянная Ридберга |
R |
1,097373142· 107 м-1 |
| 16. | Боровский радиус |
a0 |
5,2917706· 10-11 м |
| 17 | Комптоновская длина волны: электрона |
l се |
2,4263089· 10-12 м |
| 18 | протона |
l ср |
1,3214099· 10-15 м |
| 19. | Магнетон Бора |
m Б |
9,274078· 10-24 Дж/Т |
| 20. | Ядерный магнетон |
m яд |
5,050824· 10-27 Дж/Т |
| 21 | Магнитный момент: электрона |
m е |
9,284832· 10-24 Дж/Т |
| 22 | протона |
m p |
1,4106171· 10-26 Дж/Т |
| 23. | Газовая постоянная |
R |
8,31441 Дж/(моль· К) |
| 24. | Объем 1 моля идеального газа |
V 0 |
2,241383· 10-2 м3/моль |
| 25. | Постоянная Больцмана |
k |
1,380662· 10-23 Дж/К |
| 26. | Постоянная Стефана |
s |
5,67032· 10-8 Вт/(м2· К4) |
| 27. | Гравитационная постоянная |
G |
6,6720· 10-11 Н· м2/кг2 |
| 28. | Квант магнитного потока |
Ф0 |
2,0678506· 10-15 Вб |
| 29. | Квант циркуляции | 3,6369455· 10-4 Дж/(Гц· кг) |
Таблица 12. Некоторые астрономические величины
| период (год) | ср. радиус орбиты (млн. км) | диаметр (км) | масса (кг) | |
| Солнце | 1.39 × 106 | 1,99 1030 | ||
| Меркурий | 0,24 | 57.9 | 4.840× 103 | 3,28 1023 |
| Венера | 0,61 | 108.0 | 1.240× 104 | 4,82 1024 |
| Земля | 1.00 | 149.6 | 1.274 × 104 | 5,977 1024 |
| Марс | 1,88 | 227.8 | 6.780× 103 | 6,4 1023 |
| Юпитер | 11,86 | 777.8 | 1.397 × 105 | 1,9 1027 |
| Сатурн | 29,48 | 1426 | 1.151 × 105 | 5,7 1026 |
| Луна | 0.075 | 384.4 | 3.476 × 103 | 7,35 1022 |
Таблица 13
|
Величина |
Значение |
| Продолжительность времени 1 год, с |
3,1536·107 |
| Ускорение свободного падения вблизи поверхности Земли, м/с |
9,81 |
Таблица 14. Диэлектрическая проницаемость диэлектриков
|
Воск |
7,8 |
Парафин |
2 |
Эбонит |
2,8 |
|
Вода |
81 |
Слюда |
6 |
Парафинированная бумага |
2 |
|
Керосин |
2 |
Стекло |
6 |
Янтарь |
2,8 |
|
Масло |
5 |
Фарфор |
6 |
Список литературы
- Савельев И.В. Курс общей физики. – М.: Наука, 1982, т 1, с. 432.
- Яворский Б.М. Курс физики. – М.: Наука, 1975-1988, т 1.
- Яворский Б.М., Детлаф. Физика. – М.: Дрофа, 1998, с.795.
- Берклиевский курс физики. Ч. Киттель, В. Найт, М. Рудерман. Механика – М.: Наука, 1983, с. 447.
- Иродов И.Е. Основные законы механики. — М.: Высшая школа, 1978, с. 240.
- Александров Н.В., Яшкин А.Я. Курс общей физики. Механика. – М.: Просвещение,1978, с. 415.
- Иванова А.Г., Пинегина Т.Ю. Проблемы современного естествознания (методическое пособие). – Новосибирск: Издательство СибГУТИ, 1998.
- Математическое введение в курс физики (часть 1). Под редакцией Пинегиной Т.Ю. – Новосибирск: Издательство СибГУТИ, 1998, с. 72.
- Лисейкина Т.А., Пинегина Т.Ю., Серебрякова Т.К., Хайновская В.В. Методические указания по курсу физики для студентов заочников. — Новосибирск: Издательство НЭИС, 1992, с.57.
- Советский энциклопедический словарь. – М.: Советская энциклопедия, 1985, с. 1600.
- Физический энциклопедический словарь. — М.: Советская энциклопедия, 1984, с. 944.
- Сена Л.А. Единицы физических величин и их размерности. — М.: Наука, 1977, с. 335.
- Лисейкина Т.А., Пинегина Т.Ю.. Методические указания к решению задач по курсу физики средней школы (часть 1). — Новосибирск: Изд-во СибГУТИ, 1998.
- Сборник индивидуальных заданий по физике (часть 1). Под редакцией Пинегиной Т.Ю. — Новосибирск: Изд-во СибГУТИ, 1998, с.85.
- Тарасов Л.В., Тарасова А.Н. Вопросы и задачи по физике. – М.: Высшая школа, 1984, с. 255.