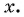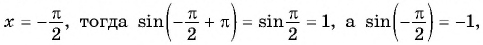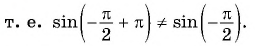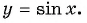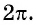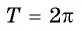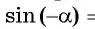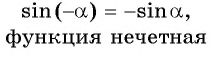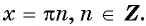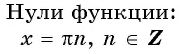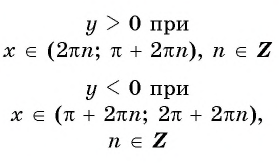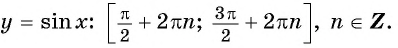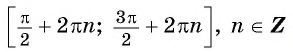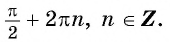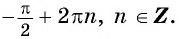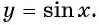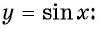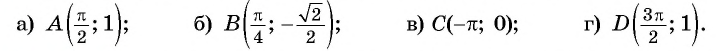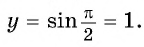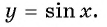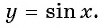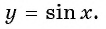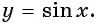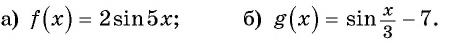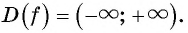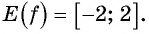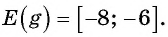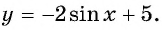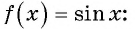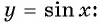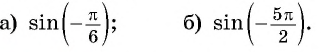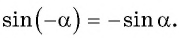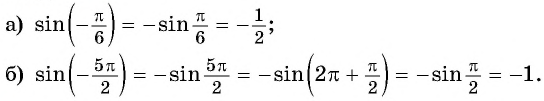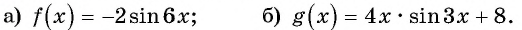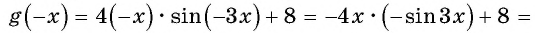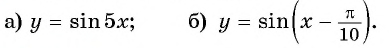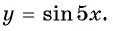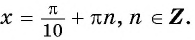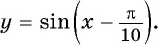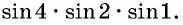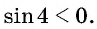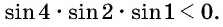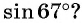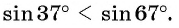Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
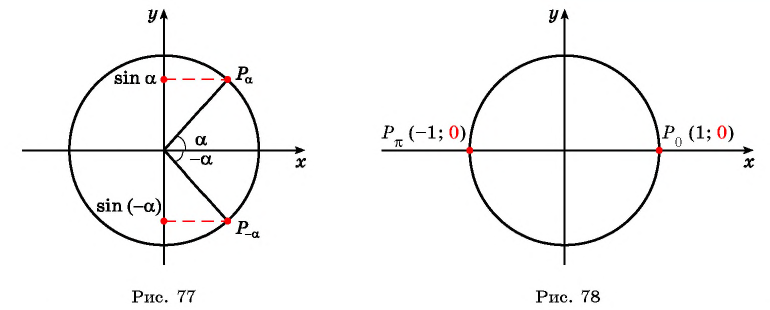
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


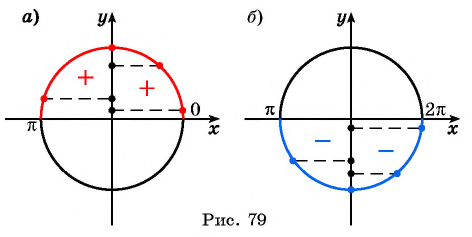
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Тригонометрические функции
В школьной программе изучаются четыре тригонометрических функции — синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.
1. Начнем с построения графика функции y = sin x.
Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда
— одна клеточка,
— две клетки.
По оси Y: две клетки примем за единицу.
Область определения функции y = sin x — все действительные числа, поскольку значение sin α можно посчитать для любого угла α.
Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
| x | 0 | ||||
| sin x | 0 |
Можем добавить, для большей плавности графика, точки и
В них значение синуса равно
Соединим полученные точки плавной кривой.
Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть
Это значит, что функция y = sin x является периодической. Мы уже построили участок графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Синусоида построена.
Перечислим основные свойства функции y = sin x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее — минус единице.
3) Функция y = sin x — нечетная. Ее график симметричен относительно нуля.
4) Функция y = sin x — периодическая. Ее наименьший положительный период равен 2π.
2. Следующий график: y = cos x. Масштаб — тот же. Отметим на графике точки, в которых косинус является рациональным числом:
| x | 0 | ||||
| cos x | 1 | 0 |
Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.
Функция y = cos x — тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. «Копируем» участок графика, который уже построили, и повторяем периодически.

Перечислим основные свойства функции y = cos x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее — минус единице.
3) Функция y = cos x — четная. Ее график симметричен относительно оси Y.
4) Функция y = cos x — периодическая. Ее наименьший положительный период равен 2π.
Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть — по одной из формул приведения,
.
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!
Функции синус и косинус идеально подходят для описания колебаний и волн — то есть процессов, повторяющихся во времени.
По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.
3. Перейдем к графику функции y = tg x.
Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.
Непонятно только, как быть с точкой Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к
то есть к 90 градусам?
Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть
.
Синус угла — это почти 1. Точнее, sin
= 0,9998. Косинус этого угла близок к нулю. Точнее, cos
= 0,0175.
Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к
), значение функции y = tg x стремится к бесконечности.
Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности.
Осталось только «скопировать» этот участок графика и повторить его с периодом π.
Перечислим свойства функции y = tg x.
1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = tg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = tg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = tg x возрастает при , то есть на каждом участке, на котором она непрерывна.
4. График функции y = ctg x строится аналогично. Вот он:
1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = сtg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = сtg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = сtg x убывает при , то есть на каждом участке, на котором она непрерывна.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 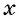
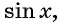
Рассмотрим свойства функции 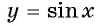
Область определения функции y=sin x
Областью определения функции 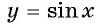
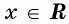
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 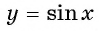
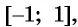
Графически это означает, что график функции 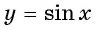
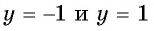
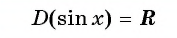
Периодичность функции y=sin x
Периодичность функции 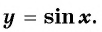
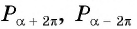
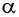
Говорят, что число 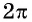
Определение:
Функция 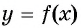
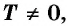
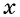
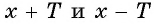
Чтобы определить, является ли функция периодической с периодом 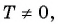
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 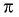
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 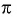
Периодом функции 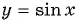
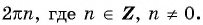
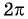
Функция 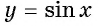
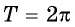
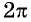
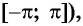
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 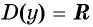
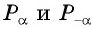
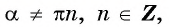
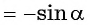
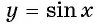
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 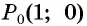
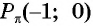
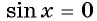
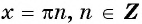
Промежутки знакопостоянства функции y=sin x
На промежутках 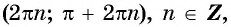
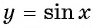
На промежутках 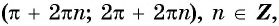
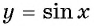
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 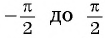
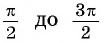
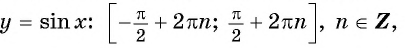
Функции 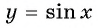
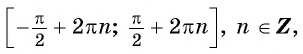
Наибольшее значение функции 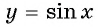
Наименьшее значение функции 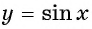
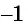
На основании проведенного исследования построим график функции 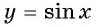
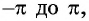
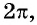
На этом периоде функция
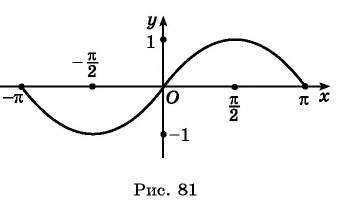
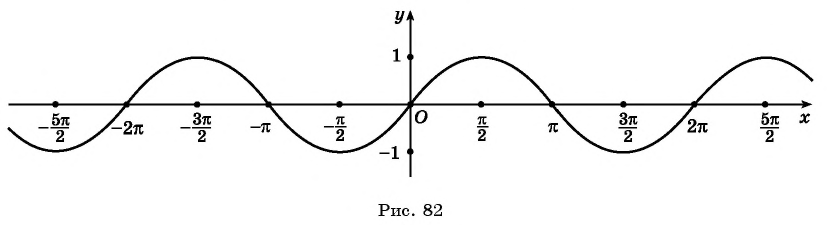
На рисунке 81 изображена часть графика функции 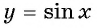
Перенесем эту часть на другие периоды и получим график функции 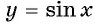
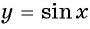
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 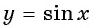
Решение:
а) Подставим в формулу 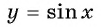
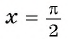
Полученное значение функции равно ординате точки 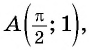
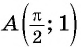
б) При 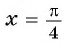
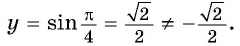
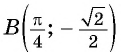
в) При 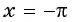
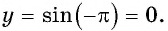
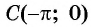
г) При 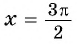
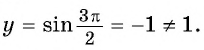
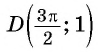
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 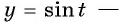
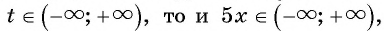
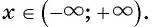
Множеством значений функции 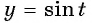
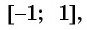
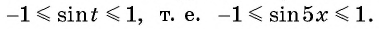
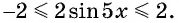
б) 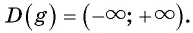
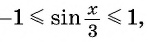
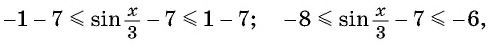
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 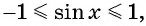
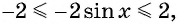
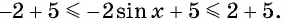
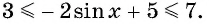
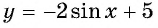
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 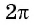
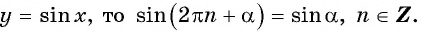
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 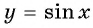
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
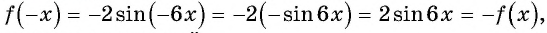
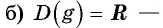
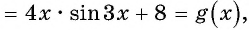
Пример №7
Найдите нули функции:
Решение:
а) Пусть 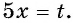
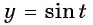
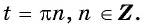
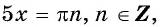
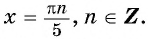
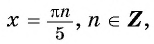
б) Пусть 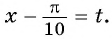
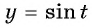
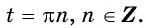
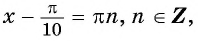
Таким образом, числа 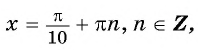
Пример №8
Определите знак произведения
Решение:
Так как 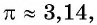
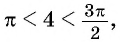
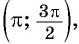
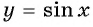
Углы 2 радиана и 1 радиан принадлежат промежутку 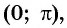
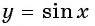
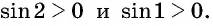
Пример №9
Что больше: 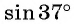
Решение. Так как функция 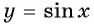
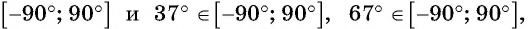
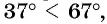
Пример №10
Постройте график функции:
Решение:
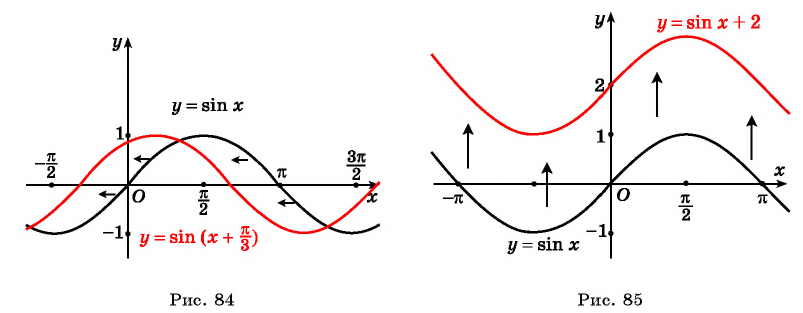
а) График функции 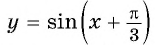
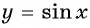
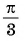
б) График функции 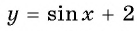
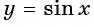
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Развертка ординаты движения точки по числовой окружности в функцию от угла
- Свойства функции y=sinx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
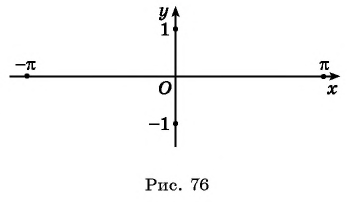
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=sinx для любого (xinmathbb{R}).
График y=sinx называют синусоидой.
Часть синусоиды для 0≤x≤2π называют волной синусоиды.
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды.
п.2. Свойства функции y=sinx
1. Область определения (xinmathbb{R}) — множество действительных чисел.
2. Функция ограничена сверху и снизу
$$ -1leq sinxleq 1 $$
Область значений (yin[-1;1])
3. Функция нечётная
$$ sin(-x)=-sinx $$
4. Функция периодическая с периодом 2π
$$ sin(x+2pi k)=sinx $$
5. Максимальные значения (y_{max}=1) достигаются в точках
$$ x=fracpi2+2pi k $$
Минимальные значения (y_{min}=-1) достигаются в точках
$$ x=-fracpi2+2pi k $$
Нули функции (y_{0}=sinx_0=0) достигаются в точках (x_0=pi k)
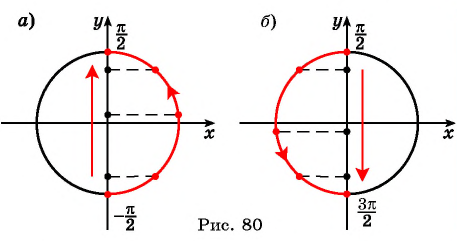
6. Функция возрастает на отрезках
$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$
Функция убывает на отрезках
$$ fracpi2+2pi kleq xleqfrac{3pi}{2}+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=sinleft(fracpi6right)=frac12, y_{max}=sinleft(fracpi2right)=1 $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=sinleft(frac{3pi}{2}right)=-1, y_{max}=sinleft(frac{5pi}{6}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (sinx=3x)
Один корень: x = 0
б) (sinx=2x-2pi)
Один корень: x = π
в) (sinx-sqrt{x-pi}=0)
(sinx=sqrt{x-pi}) 
Один корень: x = π
г*) (sinx=left(x-fracpi2right)^2-frac{pi^2}{4})
(y=left(x-fracpi2right)^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_1=0, x_2=pi)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$ 
(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) — исходная функция поднимается вверх на 2. Область значений (yin[1;3]).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) — период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac{x}{2}) — период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).

![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)




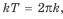














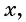
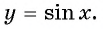
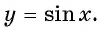
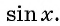
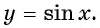
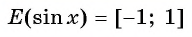
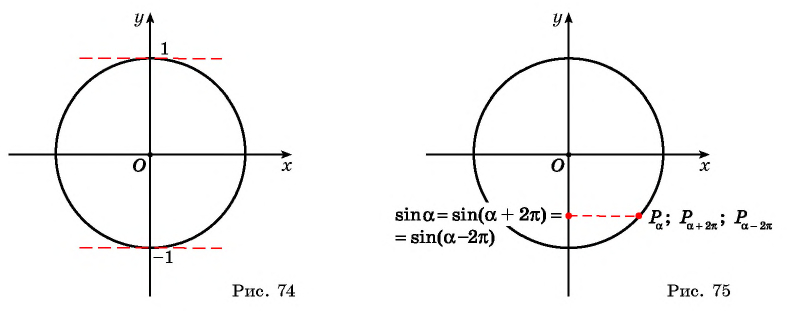
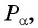
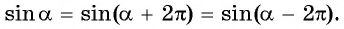
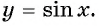
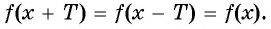
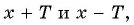 если
если 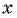 принадлежит области определения функции;
принадлежит области определения функции;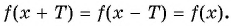
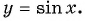
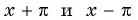 принадлежат области определения функции, так как
принадлежат области определения функции, так как 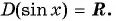
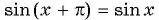 для всех
для всех