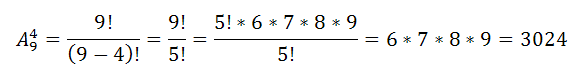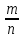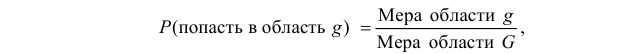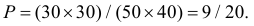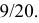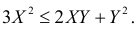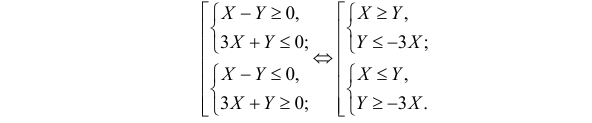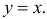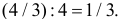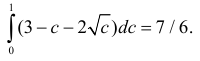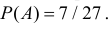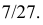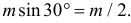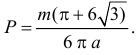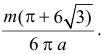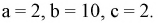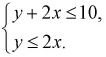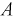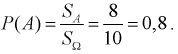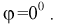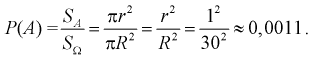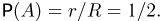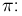-
Основные формулы комбинаторики: размещения, перестановки, сочетания.
Комбинации
из n элементов по m элементам, которые
отличаются или самими элементами, или
порядком их следования, называются размещениями.
Формула размещения:

Пусть
имеются три буквы А,
В и С.
Составим всевозможные комбинации только
из двух букв: АВ,
ВА, АС, СА, ВС, СВ. Эти комбинации отличаются
друг от друга только расположением букв
или самими буквами.
Пример
1
На
третьем курсе изучается 9 предметов.
Сколькими способами можно составить
расписание занятий на один день, если
в учебный день разрешается проводить
занятия только по четырем разным
предметам?
Решение
Различных
способов составления расписания столько,
сколько существует четырехэлементных
комбинаций из девяти элементов, которые
отличаются друг от друга или самими
элементами, или их порядком, т.е.
Ответ: 3024
Комбинации
из n элементов, которые отличаются друг
от друга только порядком элементов,
называются перестановками.
Перестановки обозначаются Рn, где n —
число элементов, входящих в перестановку.
Формула
перестановки:
Рn=n!
Пусть
имеются три буквы А, В и С.
Составим всевозможные комбинации из
этих букв: ABC, АСВ, ВСА, ВАС, CAB, CBA. Эти
комбинации отличаются друг от друга
только расположением букв.
Пример
1
В
турнире участвуют семь команд. Сколько
вариантов распределения мест между
ними возможно?
Решение:
В
итоговой таблице турнира команды будут
отличаться занятыми местами, поэтому
для подсчета вариантов распределения
мест между ними воспользуемся формулой
перестановки:
Р7=7!=1*2*3*4*5*6*7=5040
Ответ: 5040
Комбинации из n элементов
по m элементам, которые отличаются
друг от друга хотя бы одним элементом,
называются сочетаниями.
Формула сочетания:

Пусть
имеются три буквы А, В и С.
Составим всевозможные комбинации только
из двух букв, которые отличаются друг
от друга хотя бы одним элементом: АВ,
АС, ВС. Нетрудно увидеть, что их в два
раза меньше, чем размещений из этих
элементов.
Пример
1
Сколькими
способами можно распределить три путевки
в один санаторий между пятью желающими?
Решение:
Так
как путевки предоставлены в один
санаторий, то варианты распределения
отличаются друг от друга хотя бы одним
желающим. Поэтому число способов
распределения
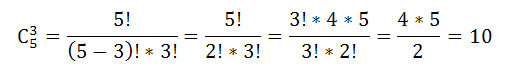
Ответ: 10.
-
Виды случайных событий.
Случайным
событием
называется результат (исход) наблюдения
какого-нибудь явления при выполнении
некоторого комплекса условий (опыта).
Виды событий:
-
Элементарные
события
— возможно исключающие друг друга
события опыта. -
Невозможное
событие
— не может произойти в результате опыта. -
Достоверное
событие –
в результате опыта обязательно
произойдет. -
Случайное
событие
– при осуществлении некоторых условий
может произойти или не произойти. -
Несовместные
события
– появление одного из них исключает
появление других событий в одном и том
же испытании. -
Совместные
события
– в результате опыта могут появиться
одновременно. -
Равновозможные
события
– одинакова возможность появления в
результате опыта. -
Равносильные
события
– событие А влечет за собой событие В,
а событие В влечет за собой событие А.
-
Алгебра
событий.
-
Суммой
(объединением)
событий А и В называется событие С,
состоящее в появлении события А или
событие В или одновременно событий А
и В. С=А+В -
Произведением
(пересечением)
событий А и В называется событие С,
состоящее в совместном появлении
событий А и В. С=А*В -
Разностью
событий А и В называется событие С,
состоящее в появлении событии А и не
появлении события В. С=А-В
-
Классическое
определение вероятности события.
Свойства вероятности.
Вероятностью
р
события А
называется
отношение числа m-благоприятствующих
случаев к числу всех возможных случаев
n,
образующих полную группу равновозможных
несовместимых событий:
P
(A)=
Свойства
вероятности:
-
Число
появления m-любого
события входит в интервал 0<P<1. -
Вероятность
достоверного события равна 1. -
Вероятность
невозможного события равна 0.
-
Теоремы
сложения вероятностей несовместных
событий.
Теорема
1. Вероятность
появления одного из двух несовместных
событий, безразлично какого, равна сумме
вероятностей этих событий:
Р
(А + В) = Р (А) + Р (В).
Доказательство:
Введем обозначения: n — общее число
возможных элементарных исходов испытания;
m1 —
число исходов, благоприятствующих
событию A; m2—
число исходов, благоприятствующих
событию В.
Число
элементарных исходов, благоприятствующих
наступлению либо события А, либо события
В, равно m1 +
m2.
Следовательно,
Р
(A + В)
= (m1 +
m2)
/ n = m1 /
n + m2 /
n.
Приняв
во внимание, что m1 /
n = Р (А) и m2 /
n = Р (В), окончательно получим
Р
(А + В) = Р (А) + Р (В).
Теорема
2. Сумма
вероятностей событий А1 ,
А2 ,
…, Аn , образующих
полную группу, равна единице:
Р
(A1)
+ Р (А2)
+ … + Р (Аn)
= 1.
Доказательство:
Так
как появление одного из событий полной
группы достоверно, а вероятность
достоверного события равна единице, то
Р
(A1 +
A2 +
… + An)
= 1. (*)
Любые
два события полной группы несовместны,
поэтому можно применить теорему сложения:
Р
(А1 +
А2 +
… + Аn)
= Р (A1)
+ Р (A2)
+ … + Р (Аn).
(**)
Сравнивая
(*) и (**), получим
Р
(А1)
+ Р (А2)
+ … + Р (Аn)
= 1.
Пример:
Консультационный
пункт института получает пакеты с
контрольными работами из городов А, В
и С. Вероятность получения пакета из
города А равна 0,7, из города В — 0,2. Найти
вероятность того, что очередной пакет
будет получен из города С.
Р
е ш е н и е.
События «пакет получен из города А»,
«пакет получен из города В», «пакет
получен из города С» образуют полную
группу, поэтому сумма вероятностей этих
событий равна единице:
0,7
+ 0,2 + p =1.
Отсюда
искомая вероятность
р
= 1 — 0,9 = 0,1.
Теорема
3. Сумма
вероятностей противоположных событий
равна единице:

Доказательство:
Пусть дано А и
.
Тогда А+
будет достоверным. Сумма достоверного
события равно 1. Тогда

З
а м е ч а н и е 1.
Если вероятность одного из двух
противоположных событий обозначена
через р, то вероятность другого события
обозначают через q. Таким образом, в силу
предыдущей теоремы
p
+ q = l
З
а м е ч а н и е 2.
При решении задач на отыскание вероятности
события А часто выгодно сначала вычислить
вероятность противоположного события,
а затем найти искомую вероятность по
формуле
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Геометрические вероятности:
Область применения классического определения вероятности – испытания с конечным числом равновозможных исходов. Существенным является условие равновозможности. От конечности числа исходов опыта можно отказаться и определять вероятности не с помощью числа исходов, 27 а с помощью отношения длин, площадей и т.д., но при сохранении условия равновозможности.
Геометрическое определение вероятности
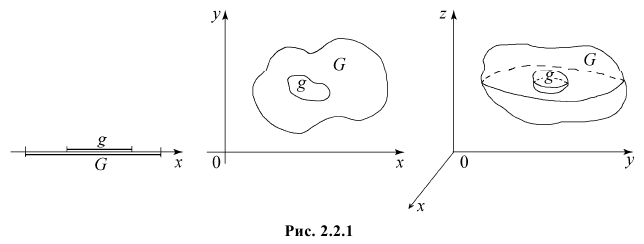
Пусть область
Если равновозможно попадание точки в любую точку области G, то вероятность попасть в область 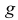
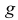
где «мера» – означает: 1) длину, если область G часть прямой или кривой линии; 2) площадь, если G часть плоскости; 3) объем, если G часть пространства, и т.д. в зависимости от характера области G.
Пример:
Две радиостанции течение часа независимо друг от друга должны передать сообщения длительностью 10 мин. и 20 мин. соответственно. Какова вероятность того, что сообщения не перекроются по времени.
Решение. Пусть 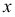
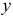
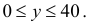
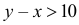
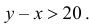
Так как все положения точки 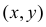
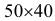
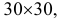
Ответ.
Пример:
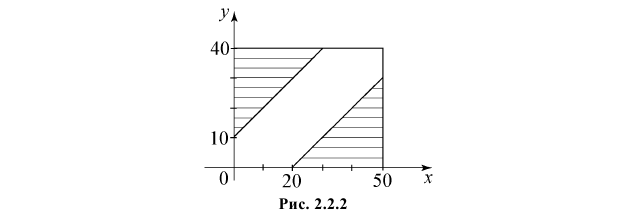
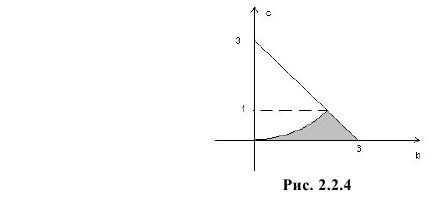
В треугольник с вершинами A(0;0), B(4;0) и C(0;2) наугад брошена точка, причем все положения точки в этом треугольнике равновозможны. Найдите вероятность того, что координаты точки X и Y будут удовлетворять неравенству
Решение. Полагая в квадратном трехчлене 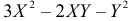
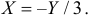
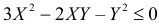
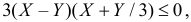
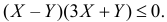
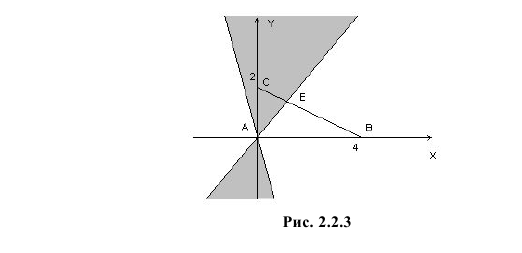
Точки плоскости, координаты которых удовлетворяют этой совокупности систем неравенств, на рис. 2.2.3 выделены штриховкой. Часть из них содержится в треугольнике ABC.
Так как по условию все положения точки 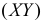
Площадь треугольника ABC равна половине произведения AB на AC, т.е. равна 4. Линия BC имеет уравнение 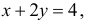
Их точка пересечения имеет координаты E(4/3;4/3). Абсцисса точки E равна высоте треугольника AEC, опущенной на сторону AC. Поэтому площадь треугольника AEC равна 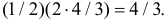
Ответ. 1/3.
Пример:
Координаты случайной точки 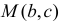
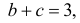
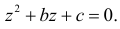
Решение. Пусть А – интересующее нас событие. Уравнение имеет действительные корни, если его дискриминант 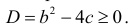
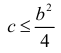
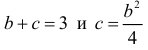
Так как площадь всего треугольника равна 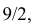
Ответ.
Пример:
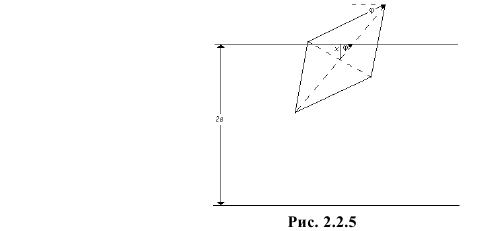
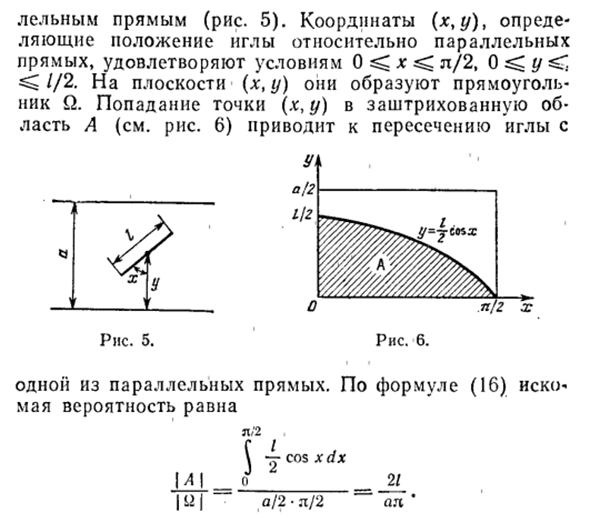
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 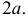
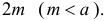
Решение. Бросание ромба «наугад» подразумевает, что центр ромба с равными шансами может оказаться на любом расстоянии 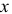
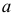
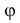
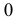
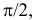
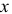
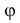
Если 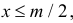
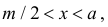
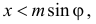
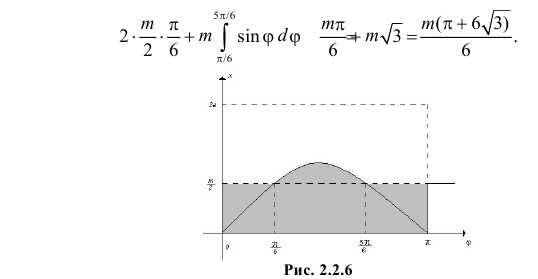
Названные условия выполняются в заштрихованной области на рис. 2.2.6. Графики функций 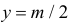
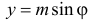
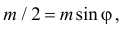
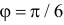
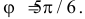
Любое положение ромба относительно ближайшей прямой можно охарактеризовать точкой в прямоугольнике со сторонами 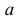
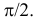
Ответ.
Пример:
Наудачу взяты два положительных числах 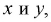
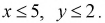
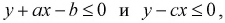
Подставляя значения коэффициентов в неравенства, получаем
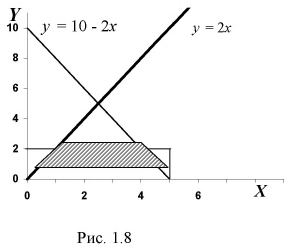
Строим на рис. 1.8 оси координат и область, которая определяет пространство элементарных событий 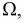
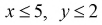
Площадь прямоугольника 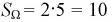
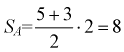
Пример:
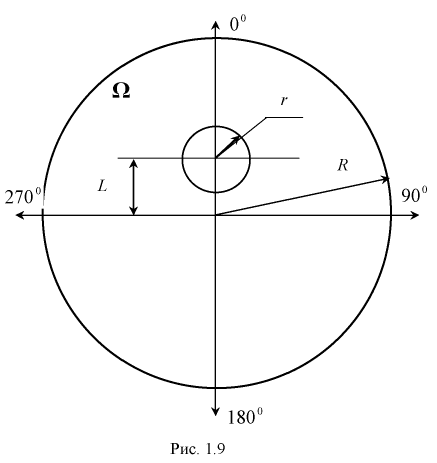
Найти вероятность того, что на экране радиолокатора отметка от цели появится в кружке радиусом 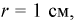
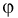
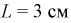
Экран радиолокатора, рис. 1.9, представляет собой электронно-лучевую трубку с радиальной разверткой, в которой от центра до края экрана движется электронный луч и после достижения края движение луча опять начинается от центра к краю, но с некоторым смещением по азимуту. Это перемещение луча от центра экрана соответствует началу излучения радиоимпульса антенного радиолокатора, который укреплен на боковой стенке кабины с передающим устройством, а кабина, в свою очередь, вращается вокруг вертикальной оси, что соответствует смещению луча на экране по азимуту. И когда радиоимпульс отражается от цели, на экране радиолокатора вспыхивает яркая точка. По положению этой точки на экране легко определить расстояние до цели и ее азимут.
Зная геометрическое определение вероятности, можно сразу сказать, что вероятность появления отметки от цели в кружке радиусом 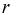
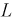
Определяем область благоприятствующих исходов, которой является кружок радиусом 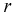
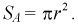
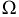
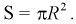
- Теоремы сложения и умножения вероятностей
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Элементы теории ошибок
- Методы математической статистики
Пусть рассматривается непрерывная вероятностная схема, т.е. пространство элементарных исходов представляет собой некоторую ограниченную область (отрезок, многоугольник, круг, параллелепипед, шар и т. п.) k-мерного пространства (прямой, плоскости, трехмерного пространства и т.д.). Естественно желание обобщить принцип равновероятности элементарных исходов классической вероятности и на эту схему. Однако в непрерывном случае число элементарных исходов бесконечно и, воспользовавшись принципом равновероятности, мы не смогли бы приписать каждому элементарному исходу иной вероятности, кроме нуля. Поэтому подойдем к определению геометрической вероятности по-другому. Рассмотрим сначала отрезок [0, 1] и предположим, что идеальная частица равномерно бросается на этот отрезок. Понятию равномерности придадим следующий смысл. Каждому отрезку 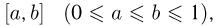
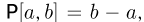
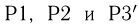
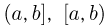
Однако, как уже говорилось, имеется препятствие к такому продолжению, связанное с существованием подмножеств, которым разумным образом с сохранением трех аксиом вероятность мы никак не сможем приписать. Поэтому приходится ограничиваться только элементами борелевской 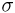
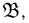
В общем случае геометрическая вероятность определяется совершенно аналогично. Пусть 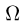
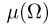
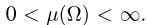
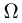
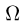
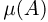
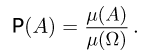
Пример:
В круг радиусом 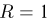
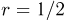
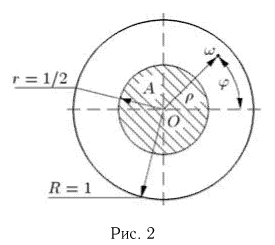
Рассмотрим два способа решения этой задачи:
1)вероятность Р(А) определяется как отношение площади внутреннего круга к площади внешнего:
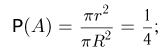
2) заметим, что в силу принципа геометрической вероятности как угол 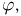
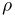
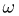
Итак, мы получили в одной и той же задаче два разных ответа. Причина кроется в том, что понятие геометрической вероятности не инвариантно относительно преобразований рассматриваемой области 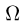
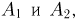
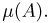
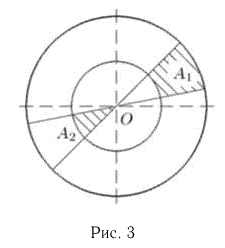
Возвращаясь к рассматриваемому примеру, отметим, что в приведенной постановке задачи предпочтительным нужно считать первый способ. Однако не следует думать, что второе решение относится к числу математических фокусов. Представляемая этим решением модель сигнала с равномерно распределенными фазой (углом) и амплитудой (радиусом) находит широкое применение в статистической радиофизике.
Пример:
На Землю параллельно плоскости экватора падает поток метеоритов. Найдем вероятность того, что упавший метеорит попадет между 15° и 45° северной широты (событие А). Естественно предполагать, что поток метеоритов равномерно распределен на плоскости, перпендикулярной плоскости экватора. Если мы теперь спроецируем земной шар на эту плоскость (рис. 4), то получим, что вероятность наступления события А пропорциональна площади 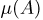
На Землю параллельно плоскости экватора падает поток метеоритов. Найдем вероятность того, что упавший метеорит попадет между 15° и 45° северной широты (событие А). Естественно предполагать, что поток метеоритов равномерно распределен на плоскости, перпендикулярной плоскости экватора. Если мы теперь спроецируем земной шар на эту плоскость (рис. 4), то получим, что вероятность наступления события А пропорциональна площади 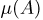
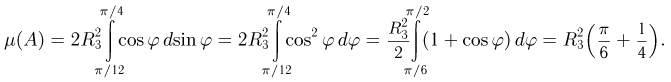
Окончательно получаем
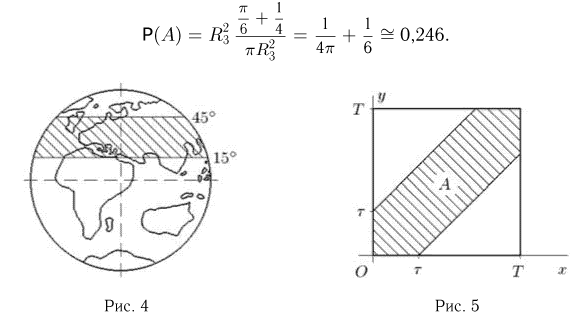
Пример:
Поступление каждого из двух сигналов в приемник равновозможно в любой момент промежутка времени Т. Найдем вероятность того, что приемник будет «забит» (событие А), что происходит в том случае, когда промежуток времени между моментами поступления обоих сигналов меньше 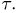
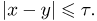
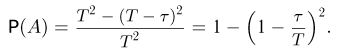
Пример:
Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 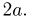
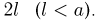
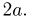
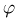
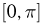
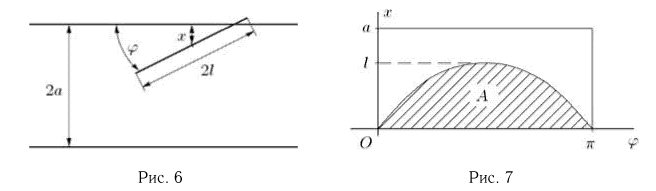
не влияет расстояние от центра до прямой. Поэтому изобразим результат бросания точкой с координатами 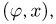
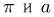
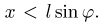
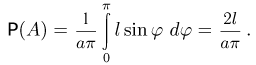
Задача Бюффона может быть использована для экспериментального определения числа 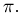
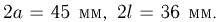
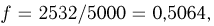
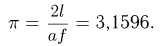
Более точное определение числа 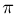
Геометрические вероятности
Смотрите также:
Предмет теория вероятностей и математическая статистика
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
Геометрическая вероятность
- Геометрическая вероятность на прямой
- Геометрическая вероятность на плоскости
- Геометрическая вероятность в пространстве
- Примеры
Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.
п.1. Геометрическая вероятность на прямой
В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ lA – попадание в отрезок lA ≤ L.
Тогда вероятность события A $$ mathrm{ P(A)=frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.
Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см?
Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания (mathrm{P_{text{справа}}=frac{l_A}{L}, P_{text{слева}}=frac{l_A}{L}}). По правилу суммы, искомая вероятность при L=100 см, lA=20 см $$ mathrm{ P_{text{справа}}+P_{text{слева}}=frac{2l_A}{L}, P=frac{2cdot 20}{100}=0,4 } $$ Ответ: 0,4.
п.2. Геометрическая вероятность на плоскости
В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ SΩ.
Событие A ↔ sA – попадание в замкнутую подобласть с площадью sA ≤ SΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{s_A}{S_{Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.
Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи?
Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: (left{ begin{array}{ l} mathrm{yleq x+15} &\ mathrm{ygeq x-15} & end{array}right. ). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: begin{gather*} mathrm{ S_{Omega}=60cdot 60=3600, s_A=3600-2S_{Delta}=3600-2cdot frac{1}{2}cdot 45^2=1575 }\ mathrm{ P(A)=frac{s_A}{S_{Omega}}=frac{1575}{3600}=frac{7}{16}=0,4375 } end{gather*} Ответ: 0,4375.
п.3. Геометрическая вероятность в пространстве
В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ VΩ.
Событие A ↔ vA – попадание в замкнутую подобласть с объёмом vA ≤ VΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{v_A}{V_{Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.
Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации?
Пространству всех событий соответствует сфера объемом: $$ mathrm{ V_{Omega}=frac{4}{3}pi R^3, R=10000 text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ mathrm{ v_{A}=frac{4}{3}pi R^3, R=100 text{км} } $$ Вероятность того, что астероид будет замечен: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}=frac{frac{4}{3}pi R^3}{frac{4}{3}pi R^3}=left(frac{r}{R}right)^3, P(A)=left(frac{100}{10000}right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.
п.4. Примеры
Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?
Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь (mathrm{ S_{Omega;}=pi R^2}).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь (mathrm{ s_{A}=pi r^2}).
Вероятность попадания: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{pi r^2}{pi R^2}=left(frac{r}{R}right)^2, P(A)=left(frac{4}{40}right)^2=0,01 } $$ Ответ: 0,01.
Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?
Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью (mathrm{ S_{Omega}=frac{sqrt{3}}{4}a^2}).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ mathrm{ frac{CO}{OE}=frac{CB}{OB}Rightarrowfrac{acdot sin60^{circ}}{r}=frac{a}{a/2}Rightarrow r=frac{a}{2}cdot sin60^{circ}=frac{sqrt{3}}{4}a } $$ Площадь вписанного полукруга: (mathrm{ s_{A}=frac{pi r^2}{2}=frac{pi}{2}left(frac{sqrt{3}}{4}aright)^2=frac{3pi}{32}a^2}).
Вероятность попасть в полукруг: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{frac{3pi}{32}a^2}{frac{sqrt{3}}{4}a^2}=frac{sqrt{3}}{8}pi approx 0,68 } $$ Ответ: (mathrm{ frac{sqrt{3}}{8}pi approx 0,68. })
Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x2 > 0,64
2) (left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. )
1) (mathrm{x^2geq 0,64Rightarrow (x^2-0,64)geq 0Rightarrow (x-0,8)(x+0,8)geq 0Rightarrow} left{ begin{array}{ l} mathrm{xleq -0,8} &\ mathrm{xgeq 0,8} & end{array}right. )
Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{xleq -0,8Rightarrow 0,8leq xleq 1} &\ mathrm{xgeq 0,8} & end{array}right.& end{array}right. $$ Мерой в данной задаче является длина: LΩ = 1, lA = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: ( mathrm{P(A)=frac{0,2}{1}=0,2} )
begin{gather*} 2) left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2leq 0,009} &\ mathrm{x^2geq 0,004} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2-0,009leq 0} &\ mathrm{x^2-0,004geq 0} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{(x-0,3)(x+0,3)leq 0} &\ mathrm{(x-0,2)(x+0,2)geq 0} & end{array}right. Rightarrow \ Rightarrow left{ begin{array}{ l} mathrm{-0,3leq xleq 0,3} &\ left[ begin{array}{ l} mathrm{xleq -0,2} &\ mathrm{xgeq 0,2} & end{array}right.& end{array}right. Rightarrow left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right. end{gather*} Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right.& end{array}right. Rightarrow 0,2 leq x leq 0,3 $$ Мерой в данной задаче является длина: LΩ = 1, lA = 0,3 — 0,2 = 0,1
Вероятность выбора точки при данных условиях: (mathrm{P(A)=frac{0,1}{1}=0,1})
Ответ: 1) 0,2; 2) 0,1.
Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом
VΩ = πR2h, R = 20 см = 2 дм, h = 12 см = 1,2 дм
VΩ = π · 22 · 1,2 = 4,8 π дм3 = 4,8 π л
Событие A – зачерпнуть жемчужину в горсти объемом vA = 0,1 л
Вероятность: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}, P(A)=frac{0,1}{4,8pi} approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, VΩ = 4,8π л. Вероятность не изменится.
3) Если высыпать зерно в сторону, пространство всех событий уменьшится:
V‘Ω = VΩ – vA = (4,8π – 0,1) л
Вероятность увеличится: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}^{‘}}, P(A)=frac{0,1}{4,8pi -0,1} approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ mathrm{ V_{Omega}^{»} = V_{Omega}-Nv_{A}=(4,8pi-0,1N) text{л} } $$ По условию: $$ mathrm{ P(A)frac{0,1}{4,8pi -0,1N}geq frac13 } $$ Получаем: (mathrm{4,8pi -0,1Nlt 0,3Rightarrow Ngt frac{4,8pi-0,3}{0,1}=147,8})
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.
Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?
По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, SΩ = 42 = 16.
Ответ: (mathrm{ 1) frac{23}{32}; 2) frac{7}{16}. })
Полезная страница? Сохрани или расскажи друзьям
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.
Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
$$
P(A)=frac{m(A)}{m(G)},
$$
где $m(G)$, $m(A)$ – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов $G$ и события $А$ соответственно.
Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном — о площадях фигур, в трехмерном — об объемах тел.
При этом, некоторые задачи сразу имеют геометрическую интерпретацию (первый пример), а другие выглядят как задачи «про жизнь», самая распространенная из них — задача о встрече (второй пример).
Основная сложность при решении задач такого типа — построить математическую модель эксперимента, нужным образом выбрать пространство элементарных исходов, обозначить событие, выразить его математически как некоторую область. К сожалению, единого рецепта решения подобых заданий нет, нужно «набить» руку на разных задачах (см. примеры тут, например).
Примеры решений на геометрическую вероятность
Пример. На плоскость, разграфленную параллельными полосами шириной $2d$, расстояние между осевыми линиями которых равно $2D$, наудачу брошен круг радиуса $r$ ($r+dlt D$). Найти вероятность того, что круг пересечет некоторую полосу.
Решение. В качестве элементарного исхода этого испытания будем считать расстояние $x$ от центра круга до осевой линии ближайшей к кругу полосы (ее обозначим за 0). Тогда все пространство элементарных исходов – это отрезок, равный половине расстояния между осями полос $G={x: 0le x le D}$. Его мера — это длина отрезка, то есть $m(G)=D$.
Рассмотрим теперь случаи, благоприятствующие событию $A$ = (Круг пересечет полосу), и найдем меру соответствующей области точек. На чертеже выше покажем различные варианты выпадения круга.
Пересечение круга с полосой очевидно произойдет в том случае, если его центр попадет в полосу (точнее, ее половину), т.е. координата центра круга удовлетворяет неравенству $0 le x le d$, длина этого отрезка $d$.
Также круг пересечет полосу, если его центр будет находится от края полосы на расстоянии меньшем чем радиус (если равен радиусу — круг коснется полосы, если больше — то отстоит от полосы), т.е. когда $d le x le d+r$ (длина этого отрезка $r$).
Тогда вероятность события $A$ по геометрическому определению вероятности:
$$
P(A)=frac{d+r}{D}.
$$
Пример. Два человека договорились встретиться в определенном месте от 17 до 18 часов. При этом каждый обязался после прихода на место встречи ожидать другого 30 минут. Какова вероятность встречи этих людей, если каждый из них равновозможно придет в течение указанного интервала времени?
Решение. Обозначим моменты прихода первого и второго человека за $x$ и $y$. Так как они приходят в промежуток длительности 60 минут (от 17 до 18 часов), то справедливы следующие условия: $0 le x le 60$ и $0 le y le 60$.
Рассмотрим прямоугольную систему координат $xOy$. В этой системе координат всем возможным значениям времени прихода людей соответствуют точки квадрата со стороной 60.
Лица встретятся, если один человек придет раньше, чем уйдет другой, то есть если $y lt x+30$, когда $y gt x$ (второй пришел позже первого, но не позже чем через 30 минут от него) и $x lt y+30$, когда $y lt x$ (первый пришел позже второго, не но позже чем через 30 минут).
Более компактно запишем условия
$$
x lt y lt x+30 quad text{ или } quad x-30 lt y lt x. quad (*)
$$
Построим прямые $y=x$, $y=x-30$, $y=x+30$ и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (серый шестиугольник в центре) являются благоприятствующими событию $A$ =(люди встретятся).
Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади квадрата:
$$
P=frac{60^2-1/2cdot 30^2-1/2cdot 30^2}{60^2}=frac{3600-900}{3600}=frac{3}{4}=0,75.
$$
Больше примеров на геометрическую вероятность