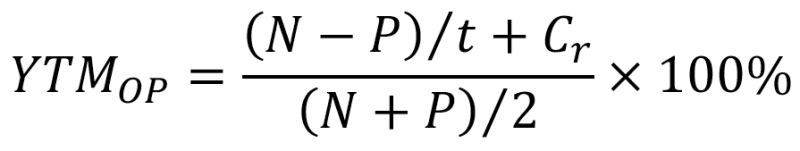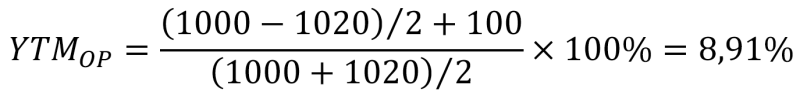Найдите величину дохода кредитора, если за предоставление в долг на полгода некоторой суммы денег он получил 46,55 тыс. руб. При этом применялась простая процентная ставка в 22%.
Решение:
F=46,55
r=0,22
P=46,55/(1+6/12*0,22)=41,94 тыс. руб.
I=F-P=46,55-41,94=4,61 тыс. руб.
Автор:
Алиса Пономарева
Облигации считаются самым простым финансовым инструментом на бирже. Однако при этом у данных ценных бумаг есть свои нюансы, о которых должен знать каждый инвестор прежде, чем их купить. В этой статье расскажем о том, что такое доходность облигации, от чего она зависит и как её посчитать.
Что такое доходность облигации простыми словами
Облигация — долговое обязательство эмитента бумаги (того, кто её выпустил) перед держателем (тем, кто ей владеет). Эта бумага подтверждает, что тот, кто выпустил облигацию (компания или государство), одолжил капитал у инвестора с обещанием вернуть деньги с процентами в определённый срок.
Чтобы понимать, насколько прибыльна долговая бумага, инвестор должен уметь рассчитать её доходность. Если говорить простыми словами, доходом по облигации называется величина прибыли, полученная инвестором от вложений в ценную бумагу.
От чего зависит доход
Факторов, влияющих на доход облигации, много. Рассмотрим основные.
Рост котировок. Заработать инвестор может путём продажи бумаги по цене выше её покупки, так как облигациям, как и другим ценным бумагам на рынке, характерна волатильность.
Волатильность — показатель изменчивости цены актива за определённый промежуток времени.
Размер купона. Процент по облигации называется купоном. Эмитент облигации платит инвестору определённую сумму раз в месяц / квартал / год за то, что он одолжил у инвестора деньги.
По способу получения купонного дохода долговые бумаги бывают трёх видов:
- Купонная облигация. Инвестору в равные промежутки времени начисляется купонный платёж, а в конце срока обращения выплачивается обратно номинал бумаги.
- Облигация с плавающим купоном. Доходность по бумаге не фиксирована и изменяется вместе с внешними показателями: инфляцией, ключевой ставкой ЦБ и т. д.
- Дисконтная облигация. По ним не выплачиваются проценты за владение. Доходность бескупонной облигации фиксирована и формируется за счёт разницы между ценой покупки ниже номинала и первоначальной стоимостью облигации.
Погашение облигации. Это дата, в которую долговая бумага перестаёт торговаться на рынке. Как правило, в этот день эмитент выплачивает последний купон и возвращает инвестору номинал в полном размере.
Если инвестор приобрёл облигацию изначально ниже цены номинала, то при погашении, помимо купонов, он получит доход в виде курсовой разницы бумаги. Если же облигация покупалась по цене выше её первоначальной стоимости, то после выплаты номинала инвестор зафиксирует убыток.
Какие бывают виды
Чтобы выбрать облигацию, нужно сперва оценить её доходность. С одной стороны, инвестору не обязательно самостоятельно рассчитывать все показатели. Доходность бумаг можно узнать на сайтах Московской и Санкт-Петербургской бирж, а также в онлайн-приложении своего брокера.
С другой стороны, долговые бумаги не всегда продаются по номинальной стоимости. Соответственно, облигация может принести как больше прибыли, так и меньше ранее заявленным значениям. И чтобы правильно определить эту величину, необходимо различать виды доходности по облигациям.
Купонный доход
Данный показатель необходим, чтобы понимать, какой процент от номинала облигации (купон) начисляется каждый месяц / квартал / полгода / год.
Несмотря на то, что купонный доход выплачивается в определённые сроки, сумма купона начисляется инвестору ежедневно. Поэтому, если решите продать облигацию раньше следующего платежа, то уже начисленные неполные купоны вы не потеряете — следующий держатель облигации выплатит вам накопленный купонный доход (НКД) автоматически.
В этом примере есть и обратный эффект. Если вы только покупаете облигацию, то при выплате очередного купонного дохода часть полученной прибыли с вас спишут в пользу предыдущего владельца. Сумма списаний зависит от того, сколько дней прошло с момента выплаты прошлого купона.
Текущая доходность облигации
Если купонная доходность облигации определяется на основе номинала бумаги, то текущая учитывает только реальную цену приобретения бумаги на рынке.
Доходность к погашению облигации (простая)
Доходность к погашению облигации — экономический показатель, который отражает прибыльность бумаги на протяжении всего срока её обращения.
Простая доходность к погашению учитывает не только реальную цену покупки, но и ожидаемую стоимость погашения.
Если инвестор намерен владеть облигацией до конца её срока, то планируемая цена погашения бумаги будет равна её номиналу.
Эффективная к погашению
Эффективная доходность облигации — полный доход инвестора от вложений в долговую бумагу с учётом реинвестирования купонов по аналогичной купонной ставке.
Как рассчитать доходность облигации
Определить доходность долговой ценной бумаги можно 4 способами. Перед тем как считать доходность облигации, важно узнать некоторые данные:
- номинал облигации;
- размер купона / купонную ставку;
- срок погашения бумаги;
- рыночную стоимость облигации;
- частоту купонных выплат.
1 способ. Если покупать облигацию по номиналу и определять только купонный доход, потребуется следующая формула:
Купонный доход, за год = (Размер годовых купонов / Номинал) × 100%
Пример расчёта доходности облигации.
Эмитент выпустил облигацию номиналом 1000 руб. с ежеквартальной выплатой 25 руб. Определим купонный доход.
Купонный доход, за год = (25 руб. х 4 / 1000 руб.) х 100% = 10%
Таким образом, годовой купонный доход составляет 10%. Для простоты восприятия в данном случае учитывается тот факт, что инвестор приобрёл корпоративную облигацию по номиналу и держал её в своём инвестиционном портфеле весь срок обращения.
2 способ. При приобретении бумаги по цене, отличной от номинала, необходимо будет рассчитать текущую доходность облигации:
Доходность, годовых = (Купонный доход за год / Цена покупки облигации) × 100%
Пример расчёта справедливой доходности облигации.
Номинал долговой бумаги компании А равен 1000 р. Доходность по облигации составляет 8%. Купонный доход за год — 80 р. Инвестор покупает эту бумагу на вторичном рынке по цене 970 р. Определим её текущую доходность.
Доходность, годовых = (80 р. / 970 р.) х 100% = 8,24%
В данном случае показатель выше первоначальной купонной ставки, так как текущая стоимость облигации ниже номинала. По доходности бумага выглядит привлекательной, её необходимо покупать.
3 способ. Если же инвестор купил облигацию не по номиналу и знает, по какой цене он готов будет её продать, то его расчёт должен сводиться к формуле простой доходности облигации:
((Номинал − Полная цена покупки + Все купоны за период владения) / Полная цена покупки) × (365 / Количество дней до погашения) × 100%
Определим простую доходность к погашению долговой бумаги на основе следующего примера.
Номинал облигации — 1000 руб. Купон в размере 20 руб. выплачивается 4 раза в год (каждый квартал). Срок обращения — 2 года. Облигация начала торговаться на рынке 1 марта. При этом инвестор приобретает бумагу по цене 950 руб. 1 июня, сразу же после первой выплаты купона. Соответственно, предыдущему владельцу инвестор не перечисляет ничего из накопленного купонного дохода (НКД).
Купонов для выплат осталось 7 (4 раза х 2 года − 1 купон). Общая сумма оставшихся купонов — 140 руб. (7 х 20 р). Количество дней до погашения — 638 (365 х 2 года − 92 дня).
Примечание. Суммарно весенних дней в календаре — 92.
Считаем:
((1000 руб. − 950 руб. + 140 руб.) / 950 руб.) × (365 / 638) × 100% = 11,44%
Получается, что годовая доходность облигации составит 11,44% с учетом неполученного купона, но с ценовым дисконтом при покупке.
4 способ. Наиболее объективным и полным вариантом определения доходности облигации с учётом возможности реинвестирования купонных платежей можно считать формулу расчёта эффективной доходности:
- YTMOP — доходность к погашению;
- Cr — сумма купонных выплат за год;
- P — текущая рыночная цена облигации;
- N — номинал облигации;
- t — лет до погашения.
Простой пример для расчёта эффективной доходности.
Номинал облигации — 1000 руб. Инвестор приобрел бумагу за 1020 руб. Ставка купона — 10%. Соответственно, сумма купонных выплат составит 100 руб. Срок обращения — 2 года.
Рассчитаем:
Итоговая доходность по бумаге составляет для инвестора не 10% годовых, а лишь 8,91%.
Налог на доход и комиссия брокера
По состоянию на 2022 год ставка НДФЛ по операциям с ценными бумагами равна 13%. Налоговым агентом на фондовом рынке является сам брокер. Это значит, что при продаже ценной бумаги из полученного инвестором дохода брокерская фирма автоматически вычтет сумму налога.
Если совокупный доход за год более 5 млн руб., то сумма превышения данного порога облагается НДФЛ по ставке 15%.
Помимо налогов, с инвестора также взимаются различные комиссии — сборы со стороны брокера. Их размер зависит от выбранного вами тарифа.
За что брокер может взимать комиссию:
- За ведение счёта. Как правило, российские брокеры взимают подобную комиссию, если клиент совершал хоть одну торговую операцию за месяц.
- За сделки. Это основной вид брокерской комиссии. Плата в пользу брокера взимается за каждую покупку и продажу ценной бумаги. У всех посредников величина сбора разная и может варьироваться в диапазоне от 0,05 до 0,1% от суммы сделки.
- За вывод средств. Согласно тарифу, брокер имеет право взимать с клиента фиксированный процент от величины вывода средств. Однако данная форма комиссии всё реже практикуется на рынке.
- За доступ к торговым платформам. Зачастую брокер не берёт комиссию за установку торгового терминала, разработанного брокерской компанией. Однако посредник может взять с инвестора фиксированную комиссию, если сумма депозита меньше заявленной для бесплатной установки ПО.
- Депозитарная комиссия. Когда инвестор откроет у посредника брокерский счёт, ему автоматически открывается и депозитарный счёт для учёта ценных бумаг. Сейчас почти все российские брокеры отказались от данной комиссии. Однако нередко этот вид комиссии может быть прописан в общих условиях тарифа.
Важно! Прежде чем выбрать брокера, тщательно ознакомьтесь с тарифными планами каждого. Зачастую в правилах пользования тарифом могут прописываться дополнительные комиссии за те или иные действия, совершаемые инвестором.
Почему меняется доходность к погашению?
Доходность к погашению облигации нередко в течение всего срока обращения изменяется. Причиной этому может быть изменчивость процентных ставок ЦБ, кризис в экономике, обострение политической обстановки в стране и в мире и многое другое.
Что происходит с доходностью облигации, когда цена облигации растёт?
Когда облигация начинает дорожать, то уровень её доходности падает.
Где посмотреть доходность к погашению облигации?
Наиболее эффективный и быстрый способ узнать доходность к погашению облигации — воспользоваться облигационным калькулятором на сайте биржи. Также можно посмотреть доходность в личном кабинете у брокера или рассчитать её значение самостоятельно.
Как рассчитать НКД по облигации?
Накопленный купонный доход по облигациям рассчитывается по следующей формуле:
НКД = Н × (С / 100) × Д / 365, где
- Н — величина номинала,
- С — годовая ставка купона,
- Д — число дней с момента прошедшей выплаты по купону.
Содержание материала
- Почему важно считать кредит самому?
- Видео
- Как рассчитать годовые проценты по кредиту?
- Как самостоятельно рассчитать аннуитетный платеж
- Какие данные нужны для расчета платежа по кредиту
- Воспользуемся банковскими калькуляторами
- Виды ежемесячных выплат по кредитам
- Самостоятельный подсчет при аннуитетных платежах
- Из чего состоит ежемесячный платеж
- Формула расчета процентов по кредиту
- Какие данные нужны для расчета
- Пример расчета процентов по кредиту
- Погашать долг можно по-разному
- Как составить график платежей
- График выплаты кредита с аннуитетными платежами
- График выплаты кредита с дифференцированными платежами
Почему важно считать кредит самому?
Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.
Видео
Как рассчитать годовые проценты по кредиту?
Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:
10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.
При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.
То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.
При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.
Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.
Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.
Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.
Как самостоятельно рассчитать аннуитетный платеж
Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.
Стандартная формула расчета аннуитетного платежа выглядит так:
Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.
А вот как рассчитывается коэффициент аннуитета:
Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.
Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.
Количество платежей равно количеству месяцев — 18.
Подставляем данные в формулу и считаем коэффициент аннуитета:
0,0125 × (1 + 0,0125)18 / ((1 + 0,0125)18 − 1) = 0,062385
Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.
Какие данные нужны для расчета платежа по кредиту
Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.
Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:
- ставка,
- размер желаемого займа,
- срок, на который вы хотите занять деньги.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Самостоятельный подсчет при аннуитетных платежах
Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:
- Процентная ставка — 18%.
- Период кредитования — 24 месяца.
- Сумма кредита — 500000 рублей.
Классическая формула для расчета аннуитетного платежа выглядит так:
Разовый аннуитетный платеж = Сумма кредита * Ка
где Ка — это коэффициент аннуитета.
Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)
где ЕПС — ежемесячная процентная ставка.
Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.
Итоговый расчет примет вид:
500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.
Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.
Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:
24 962,05 * 24 = 599 089,24 рублей.
Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.
Из чего состоит ежемесячный платеж
Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.
Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.
Формула расчета процентов по кредиту
S = (s3 x i x Kk / Kr) / 100
- S = вычисляемые проценты;
- S3 = общая сумма кредита;
- i = процентная ставка по кредиту;
- Kk = кол-во дней по платежам;
- Kr = кол-во дней на календарный год.
Какие данные нужны для расчета
- Сумма, выданная в кредит;
- Процентная ставка за год;
- Кол-во календарных дней в текущем году.
Пример расчета процентов по кредиту
65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как составить график платежей
Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.
Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.
Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.
При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.
В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.
Сначала считаем проценты:
Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году
Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.
Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.
Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.
На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).
Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.
График выплаты кредита с аннуитетными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 18 715,44 | 15 016,81 | 3698,63 | 284 983,19 |
| 2 | 18 715,44 | 15 084,83 | 3630,61 | 269 898,37 |
| 3 | 18 715,44 | 15 387,92 | 3327,51 | 254 510,44 |
| 4 | 18 715,44 | 15 473,04 | 3242,39 | 239 037,40 |
| 5 | 18 715,44 | 15 670,17 | 3045,27 | 223 367,24 |
| 6 | 18 715,44 | 16 053,39 | 2662,05 | 207 313,85 |
| 7 | 18 715,44 | 16 074,31 | 2641,12 | 191 239,53 |
| 8 | 18 715,44 | 16 357,69 | 2357,75 | 174 881,84 |
| 9 | 18 715,44 | 16 487,49 | 2227,95 | 158 394,35 |
| 10 | 18 715,44 | 16 762,63 | 1952,81 | 141 631,73 |
| 11 | 18 715,44 | 16 911,09 | 1804,35 | 124 720,64 |
| 12 | 18 715,44 | 17 126,53 | 1588,91 | 107 594,11 |
| 13 | 18 715,44 | 17 388,93 | 1326,50 | 90 205,18 |
| 14 | 18 715,44 | 17 566,25 | 1149,19 | 72 638,93 |
| 15 | 18 715,44 | 17 819,89 | 895,55 | 54 819,04 |
| 16 | 18 715,44 | 18 017,06 | 698,38 | 36 801,98 |
| 17 | 18 715,44 | 18 246,59 | 468,85 | 18 555,40 |
| 18 | 18 768,91 | 18 555,39 | 213,51 |
Первый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 016,81
Сумма платежа в погашение процентов
3698,63
Остаток долга 284 983,19
Второй платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 084,83
Сумма платежа в погашение процентов
3630,61
Остаток долга 269 898,37
Третий платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 387,92
Сумма платежа в погашение процентов
3327,51
Остаток долга 254 510,44
Четвертый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 473,04
Сумма платежа в погашение процентов
3242,39
Остаток долга 239 037,40
Пятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 670,17
Сумма платежа в погашение процентов
3045,27
Остаток долга 223 367,24
Шестой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 053,39
Сумма платежа в погашение процентов
2662,05
Остаток долга 207 313,85
Седьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 074,31
Сумма платежа в погашение процентов
2641,12
Остаток долга 191 239,53
Восьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 357,69
Сумма платежа в погашение процентов
2357,75
Остаток долга 174 881,84
Девятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 487,49
Сумма платежа в погашение процентов
2227,95
Остаток долга 158 394,35
Десятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 762,63
Сумма платежа в погашение процентов
1952,81
Остаток долга 141 631,73
Одиннадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 911,09
Сумма платежа в погашение процентов
1804,35
Остаток долга 124 720,64
Двенадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 126,53
Сумма платежа в погашение процентов
1588,91
Остаток долга 107 594,11
Тринадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 388,93
Сумма платежа в погашение процентов
1326,50
Остаток долга 90 205,18
Четырнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 566,25
Сумма платежа в погашение процентов
1149,19
Остаток долга 72 638,93
Пятнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 819,89
Сумма платежа в погашение процентов
895,55
Остаток долга 54 819,04
Шестнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 017,06
Сумма платежа в погашение процентов
698,38
Остаток долга 36 801,98
Семнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 246,59
Сумма платежа в погашение процентов
468,85
Остаток долга 18 555,40
Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга
При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.
В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.
График выплаты кредита с дифференцированными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 20 365,30 | 16 666,67 | 3698,63 | 283 333,33 |
| 2 | 20 276,26 | 16 666,67 | 3609,59 | 266 666,67 |
| 3 | 19 954,34 | 16 666,67 | 3287,67 | 250 000,00 |
| 4 | 19 851,60 | 16 666,67 | 3184,93 | 233 333,33 |
| 5 | 19 639,27 | 16 666,67 | 2972,60 | 216 666,67 |
| 6 | 19 248,86 | 16 666,67 | 2582,19 | 200 000,00 |
| 7 | 19 214,61 | 16 666,67 | 2547,95 | 183 333,33 |
| 8 | 18 926,94 | 16 666,67 | 2260,27 | 166 666,67 |
| 9 | 18 789,95 | 16 666,67 | 2123,29 | 150 000,00 |
| 10 | 18 515,98 | 16 666,67 | 1849,32 | 133 333,33 |
| 11 | 18 365,30 | 16 666,67 | 1698,63 | 116 666,67 |
| 12 | 18 152,97 | 16 666,67 | 1486,30 | 100 000,00 |
| 13 | 17 899,54 | 16 666,67 | 1232,88 | 83 333,33 |
| 14 | 17 728,31 | 16 666,67 | 1061,64 | 66 666,67 |
| 15 | 17 488,58 | 16 666,67 | 821,92 | 50 000,00 |
| 16 | 17 303,65 | 16 666,67 | 636,99 | 33 333,33 |
| 17 | 17 091,32 | 16 666,67 | 424,66 | 16 666,67 |
| 18 | 16 858,45 | 16 666,67 | 191,78 |
Первый платеж
Сумма платежа
20 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3698,63
Остаток долга 283 333,33
Второй платеж
Сумма платежа
20 276,26
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3609,59
Остаток долга 266 666,67
Третий платеж
Сумма платежа
19 954,34
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3287,67
Остаток долга 250 000,00
Четвертый платеж
Сумма платежа
19 851,60
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3184,93
Остаток долга 233 333,33
Пятый платеж
Сумма платежа
19 639,27
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2972,60
Остаток долга 216 666,67
Шестой платеж
Сумма платежа
19 248,86
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2582,19
Остаток долга 200 000,00
Седьмой платеж
Сумма платежа
19 214,61
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2547,95
Остаток долга 183 333,33
Восьмой платеж
Сумма платежа
18 926,94
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2260,27
Остаток долга 166 666,67
Девятый платеж
Сумма платежа
18 789,95
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2123,29
Остаток долга 150 000,00
Десятый платеж
Сумма платежа
18 515,98
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1849,32
Остаток долга 133 333,33
Одиннадцатый платеж
Сумма платежа
18 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1698,63
Остаток долга 116 666,67
Двенадцатый платеж
Сумма платежа
18 152,97
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1486,30
Остаток долга 100 000,00
Тринадцатый платеж
Сумма платежа
17 899,54
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1232,88
Остаток долга 83 333,33
Четырнадцатый платеж
Сумма платежа
17 728,31
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1061,64
Остаток долга 66 666,67
Пятнадцатый платеж
Сумма платежа
17 488,58
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
821,92
Остаток долга 50 000,00
Шестнадцатый платеж
Сумма платежа
17 303,65
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
636,99
Остаток долга 33 333,33
Семнадцатый платеж
Сумма платежа
17 091,32
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
424,66
Остаток долга 16 666,67
Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга
Теги
Типовые примеры и методы их решения
Пример 1.2.1. Вы поместили в банк вклад
10 тыс. руб. под простую процентную ставку
26% годовых. Какая сумма будет на вашем
счете через 3 года? Какова будет величина
начисленных процентов? Если банк
осуществляет регулярные выплаты
начисленных процентов, то какую сумму
Вы будете получать: а) каждый год; б)
каждый квартал?
Решение. Полагая в формуле (9) Р =
10 тыс. руб., n = 3 года, r=
0,26, получим наращенную сумму через 3
года, если не происходят выплаты простых
процентов:
F=10 .
(1+3 .
0,26) = 17,8 тыс. руб.
Следовательно, величина начисленных
процентов / составит:
I = F – P =17,8
– 10 = 7,8 тыс. руб.
Величину начисленных простых процентов,
выплачиваемых ежегодно, определяем из
формулы (12) при / = 1:
I1 = 10 .
1. 0,26 =2,6 тыс.
руб.
При ежеквартальных выплатах / = 0,3.5
года, и поэтому величина каждой выплаты
составит:
I2 =10 . 0,25 .
0,26 = 0,65 тыс. руб.
Заметим, что проценты на уже начисленные
проценты не начисляются независимо от
срока хранения вклада. Поэтому имеет
смысл начисленные простые проценты
регулярно получать и использовать,
например, для иных инвестиций. Поскольку
приращение вклада при наращении простыми
процентами растет линейно вместе со
сроком его хранения, то величины I1
и I2 можно найти,
поделив I соответственно
на 3 и на 12.
Пример 1.2.2. На какой срок необходимо
поместить денежную сумму под простую
процентную ставку 28% годовых, чтобы она
увеличилась в 1,5 раза?
Решение. Искомый срок определяем
из равенства множителя наращения
величине 1,5:
1 + n . 0,28=1,5.
Решая это уравнение относительно n,
получим n =
=
1,786 года. Таким образом, если в году 365
дней, то необходимый срок составит 1 год
и 287 дней.
Пример 1.2.3. Предпринимателю 14 февраля
была предоставлена ссуда в размере 20
тыс. руб. с погашением 14 июля того же
года под процентную ставку 30% годовых.
Рассчитайте различными способами сумму
к погашению, если начисляются простые
проценты и год невисокосный.
Решение. Величина уплачиваемых
процентов за пользование ссудой зависит
от числа дней, которое берется в расчет.
Для упрощения процедуры расчета точного
числа дней пользуются специальными
таблицами (одна — для обычного года,
вторая -для високосного), в которых все
дни в году последовательно пронумерованы.
Продолжительность финансовой операции
определяется вычитанием номера первого
дня из номера последнего дня. Поэтому
точное число дней находим по таблице 1
в приложении 2: 195 — 45 ^ 150 дней. Естественно,
это число можно найти и непосредственно,
исходя из количества дней в соответствующих
месяцах. Приближенное число дней ссуды
состоит из 16 дней февраля (30 — 14); 120 дней
(по 30 дней четырех месяцев: март, апрель,
май, июнь) и 14 дней июля. Т.е. приближенное
число дней составляет: 16 + 120 + 14 = 150. Теперь
с помощью формулы (10) можно рассчитать
возможные значения суммы к погашению.
Во всех случаях Р = 20 тыс. руб., г = 03
.
1. В расчет принимаются точные проценты
и точное число дней ссуды (т.е. T=365,
t =150):
F = 20 (1 +
0,3) = 22,466 тыс. руб.
2. В расчет принимаются обыкновенные
проценты и точное число дней ссуды (т.е.
T = 360, t =
150):
F = 20 (1 +
О,З) — 22,5 тыс. руб.
3. В расчет принимаются обыкновенные
проценты и приближенное число дней
ссуды (т.е. Т = 360, t =
150):
F = 20 (1 +
О,З)
= 22,5 тыс. руб.
Очевидно, что обыкновенные проценты и
точное число дней ссуды доставляют
большее значение суммы к погашению, чем
точные проценты и точное число дней
ссуды. В условиях этого примера второй
и третий варианты расчета обеспечивают
одинаковые суммы при возврате долга.
Вообще, как правило, число точных и число
приближенных дней краткосрочной (до
одного года) ссуды либо очень близки,
либо совпадают, что позволяет в банковских
расчетах обычно пользоваться приближенным
числом дней ссуды. Так, если бы ссуда
была выдана с 15 января по 14 июля, то
точное число дней ссуды — 180, а приближенное
-179. Следовательно, по второму и третьему
вариантам расчета соответственно
получим:
F = 20(1 +
0,3)
= 23 тыс. руб.;
F = 20(1 +
0,3)
= 22,983 тыс. руб.;
Вообще видно, что во всех случаях суммы
к погашению различаются незначительно,
но при больших величинах ссуд даже
небольшие расхождения могут иметь
значение.
Отметим, что число точных и число
приближенных дней ссуды могут достаточно
сильно отличаться друг от друга, если
срок ссуды более 360 дней. Если, например,
ссуда предоставлена с 14 февраля одного
года до 13 февраля следующего, то точное
число дней равно 364, а приближенное —
359. Отсюда следуют и более существенные
различия в суммах к погашению.
Пример 1.2.4. Предприниматель 18 апреля
обратился в банк за ссудой до 19 ноября
того же года под простую процентную
ставку 25% годовых. Банк, удержав в момент
предоставления ссуды проценты за весь
ее срок, выдал предпринимателю 12 тыс.
руб. Какую сумму необходимо будет вернуть
банку, если при расчете начисленных
процентов использовались обыкновенные
проценты с точным числом дней?
Решение. Обозначим через F сумму,
которую необходимо будет вернуть банку,
и вначале для определения процентов /,
удержанных банком, воспользуемся
формулой (14), где P=F
. Число дней находим либо прямым
подсчетом, либо по таблице:
T = 215 дней (323 — 108). Так как
T=360, r=0,25,
дивизор D’=
=1440,
P – I = F – I =
12 тыс. руб.,
то
I=
=2,106
тыс. руб.
Следовательно, предприниматель обязан
возвратить долг в размере:
F = 12 +
I = 12
+ 2,106 = 14,
106 тыс. руб.
Для проверки найдем простые проценты,
начисленные за 215 дней на сумму 14,106 тыс.
руб.:
14,106
0,25
=2,106 тыс. руб.,
что подтверждает правильность вычислений.
Заметим, что проценты / представляют
собой проценты «во 100″ с 12 тыс.
руб. Действительно, поскольку процентная
ставка за 215 дней (215/360 года) составляет
0,25
= 0,1493, то
I=
=
2,106 тыс. руб.
При решении примера можно было рассуждать
и таким образом. Поскольку проценты,
удержанные банком, составили величину
0,25,
то предпринимателю выдана сумма F
– F
0,25=12
тыс. руб. Отсюда:
F =
= 14,106 тыс. руб.
Забегая немного вперед, можно сказать,
что на 12 тыс. руб. в течение 215 дней
происходит наращение по простой учетной
ставке 25% годовых.
Пример 1.2.5. Сберегательный счет был
открыт 10 марта и на него была положена
сумма 8 тыс. руб. В следующем месяце (14
апреля) на счет поступило 4 тыс. руб.
Затем 25 июня со счета было снято 3 тыс.
руб. и 4 сентября — 2 тыс. руб. Счет был
закрыт 20 декабря. Все операции
осуществлялись в течение високосного
года. Определите сумму, полученную
владельцем счета, если процентная ставка
равнялась 30% годовых и при расчете
использовались обыкновенные проценты
с точным числом дней.
Решение. Этот пример можно решить
обычным способом, определяя величину
начисленных процентов последовательно
за промежутки времени, когда сумма на
счете не менялась. Мы же воспользуемся
(как это и делают в банках при обслуживании
текущего счета) величинами
,
которые, так же как и Pt
называются процентными числами (через
Р обозначена величина вклада, через
t — время его
хранения). В этом случае в формуле для
вычисления дивизора D
=
ставка
r выражена не десятичной
дробью, а в процентах.
Для того чтобы найти общую величину
начисленных процентов за весь срок,
определим процентные числа за каждый
промежуток времени, когда сумма на счете
не менялась. Затем сложим все процентные
числа и полученное значение поделим на
дивизор.
Вначале определяем суммы, которые
последовательно фиксировались на счете:
8 тыс. руб., 12 (8 + 4) тыс. руб., 9 (12 — 3) тыс.
руб., 7 (9 — 2) тыс. руб. Затем находим сроки
хранения этих сумм. Они соответственно
равны 35 (105 — 70) дням, 72 (177 -105) дням, 71 (248 —
177) дню, 107 (355 — 248) дням. Сумма процентных
чисел составит:
=25,32
Дивизор в данном случае равен: D =
=
12. Следовательно,
общая величина начисленных процентов
составит:
= 2,11 тыс.руб., а владелец счета получит:
7 + 2,11 = 9,11 тыс. руб.
Отметим, что процентные числа можно
было вычислять и с несколько иным образом
найденными сроками, а именно: для каждого
поступления срок хранения определяется
исходя из даты поступления и даты
закрытия счета. Если происходило изъятие
денег, то соответствующее процентное
число берется со знаком минус. Тогда:
для 8 тыс. руб. — 285 (355 — 70) дней, для 4 тыс.
руб. — 250 (355 — 105) дней, для 3 тыс. руб. — 178
(355 — 177) дней и для 2 тыс. руб. — 107 (355 — 248)
дней. Находим (учитывая знаки) сумму
процентных чисел:
=25,32
т.е. получили такую же величину, как и
способом, изложенным ранее.
Поскольку февраль не входит в период
работы со сберегательным счетом, то при
осуществлении операций и в течение
невисокосного года получим окончательно
также 9,11 тыс. руб.
Пример 1.2.6. Господин N поместил в
банк 16 тыс. руб. на следующих условиях:
в первые полгода процентная ставка
равна 24% годовых, каждый последующий
квартал ставка повышается на 3%. Найдите
наращенную сумму за полтора года, если
проценты начисляются только на
первоначальную сумму вклада. При какой
постоянной процентной ставке можно
получить такую же наращенную сумму?
Найдите наращенную сумму за полтора
года, если с изменением ставки происходит
одновременно и капитализация процентного
дохода.
Решение. Пусть вначале проценты
начисляются только на первоначальную
сумму вклада. Рассмотрим отдельно
периоды, в течение которых ставка была
постоянной. Поскольку на первый период
длительностью n1=
0,5 года установлена процентная ставка
i1= 0,24, то приращение
капитала (в тыс. руб.) за этот период
равно величине 16 . 0,5 .
0,24. На второй период длительностью
n2 = 0,25 года (квартал)
установлена процентная ставка
i2=0,24+0,03=0,27, и,
следовательно, приращение капитала за
этот период равно величине 16 . 0,25
. 0,27. Аналогичным образом на периоды
n3, n4,
n5, каждый из которых
равен 0,25 года, установлены соответственно
ставки i3=03,
i4=0,33, i5=0,36,
доставляющие приращения капитала
16.0,25.0,3; 16.0,25. 0,33;
16.0,25. 0,36.
Суммируя первоначальный капитал и все
его приращения, получим наращенную
сумму за полтора года (общий множитель
всех слагаемых 16 вынесем за скобки):
F =16. (1+0,5.0,24
+0,25.0,27+0,25.0,3+0,25.0,33
+ 0,25.0,36) = 22,96 тыс.
руб.
Такую же наращенную сумму можно получить,
если простые проценты начисляются за
полтора года по ставке
Действительно, F=16.(1+1,5.0,29)=22,96
тыс. руб.
Отметим, что в указанных обозначениях
величины F и
,
конечно, можно найти по формулам (15)
и (16). Записывая (16) в виде
,
замечаем, что ставка i равна взвешенной
сумме процентных ставок, где весом для
каждой ставки | служит доля длительности
периода п^, которую он составляет
от общей суммы длительностей периодов
, причем очевидно, что сумма всех весов
равна единице. Таким образом, для ставки
24% весом является дробь /э (так как полгода
составляют третью часть от полутора
лет), для каждой исследующей ставки
весом будет дробь /» (так как квартал
составляет шестую часть от полутора
лет).
Если же с изменением ставки происходит
одновременно и капитализация процентного
дохода (т.е наращенная сумма вкладывается
вновь под измененную простую процентную
ставку), то за полтора года наращенная
сумма составит:
F= 16. (1+0,5.
0,24)(1+0,25. 0,27)(l+0,25.0,3)(1
+ 0.25 . 0,33)(1 + 0,25* *0,36) = 24,264 тыс. руб.
Естественно, получили сумму, превышающую
22,96 тыс. руб., поскольку в этом случае за
каждый период проценты начисляются не
только на первоначальную сумму вклада,
но и на проценты, начисленные за предыдущий
период.
Пример 1.2.7. В финансовом договоре
клиента с банком предусмотрено погашение
долга в размере 8,9 тыс. руб. через 120 дней
при взятом кредите в размере 8 тыс. руб.
Определите доходность такой сделки для
банка в виде годовой процентной ставки.
При начислении банк использует простые
обыкновенные проценты.
Решение. Подставляя в формулу (23)
значения F = 8,9 тыс. оуб., Р = 8 тыс.
руб., t = 120 дней, Т=
360 дней, получим:
r=
.
Таким образом, инвестируя 8 тыс. руб. под
простую процентную ставку 33,75% годовых,
через 120 дней при использовании
обыкновенных процентов можно получить
8,9 тыс. руб. Действительно,
8 . (1 +
0,3375)
= 8,9 тыс. руб.
Пример 1.2.8. Банк в начале года выдал
кредит на сумму 30 тыс. руб. сроком на два
месяца по ставке 28% годовых и через два
месяца — кредит на сумму 45 тыс. руб. сроком
на четыре месяца по ставке 34% годовых.
Определите общую доходность этих
кредитных операций за полгода в виде
годовой процентной ставки в двух случаях:
когда при выдаче второго кредита не
используются и когда используются
деньги, возвращенные банку после
погашения первого кредита. За предоставление
кредита банк начислял простые обыкновенные
проценты.
Решение. Найдем начисленные проценты
за первый кредит по формуле С 12) пои Р=30
тыс. руб., l=60/360
года., r=0,28:
тыс.
Аналогичным образом при Р=45 тыс.
руб., l=120/360 года, r
= 0,34 находим для второго кредита:
Следовательно, общий доход, полученный
банком, равен:
/ = /I + /2 = 1,4 + 5,1 = 6,5 тыс. руб.
Если при выдаче второго кредита не
использовались деньги, возвращенные
банку после погашения первого кредита,
то общая величина вложенных средств
равна 75 (30 + 45) тыс. руб Поэтому общая
доходность этих кредитных операций за
полгода в виде простой годовой процентной
ставки по формуле (23) сосоставляет:
r =
,
или 17,33%
Если же второй кредит в размере 45 тыс.
руб. включает 3( тыс. руб. (первый кредит),
то
r =
или 28,89%
Очевидно, повторное использование
финансовых ресурсов повышает доходность.
Пример 1.2.9. Предприниматель получил
в банке кредит на 90 дней по процентной
ставке 36% годовых, при этом банком были
удержаны комиссионные в размере 2,5% от
величины кредита. Найдите доходность
такой финансовой операции для банка в
виде годовой простой процентной ставки,
если банк начисляет простые проценты
на исходную сумму кредита, полагая что
в году 360 дней. Как изменится доходность
при выдаче кредита на 60 дней и на 120 дней?
Решение. Обозначим через Р
величину кредита (в каких либо денежных
единицах), тогда величина удержанных
комиссионных составит 0.025Р и, следовательно,
предприниматели будет выдана сумма Р
— 0,025Р = 0.975Р. Через 90 дней предприниматель
должен будет вернуть сумму
Таким образом, общий доход банка составит:
1,09.Р – 0,975Р = 0,115Р. Теперь, используя
формулу (23), можно определить доходность
финансовой операции для банка в виде
годовой процентной ставки:
,
т.е. г = 47,18%, что больше объявленных банком
36% годовых. Таким образом, удержание
комиссионных увеличивает доходность
финансовой операции для кредитора
(банка).
При выдаче кредита на 60 дней его величина
вместе с начисленными процентами
составит:
= 1,06 Р, и, следовательно, доходность
для банка будет равна:
,
или 52,31%
т.е. больше, чем при выдаче кредита на
90 дней.
Если же срок кредита составляет 120 дней,
то предприниматель должен будет вернуть
1,12/» и доходность для банка в виде
простой годовой процентной ставки
составит:
,
или 44,62%
т.е. меньше, чем при сроке кредита 90 дней.
Рассмотренный пример показывает, что
при удержании комиссионных увеличение
срока кредита уменьшает доходность
финансовой сделки для кредитора. Конечно,
если комиссионные не взимаются, то при
любом сроке кредита доходность такой
финансовой сделки в виде простой годовой
процентной ставки будет постоянна и
равна 36%.
Пример 1.2.10. Банк за использование
в течение двух месяцев 800 тыс. руб. должен
выплатить 60 тыс. руб. Определите стоимость
привлеченных средств в виде простой
годовой процентной ставки в условиях
начисления обыкновенных процентов.
Решение. Стоимость привлеченных
средств можно найти по формуле (23), где
через Р обозначена использованная
сумма средств; через F
– P — проценты,
выплаченные за использование суммы Р
в течение времени n. Полагая
P=800 тыс. руб., F
– P=60 тыс. руб.,
n=2/12=1/6 года, получим:
,
или, что эквивалентно, 45% годовых.
Пример 1.2.11. Из какого капитала можно
получить 24 тыс руб. через два года
наращением по простым процентам по
процентной ставке 25%? Чему равен дисконт?
Решение. Пользуясь формулой (18), где
F = 24 тыс. руб., n
= 2 года, r = 0,25, получим:
P=
тыс.
руб.
Отсюда можно найти дисконт: Dr=F
– P=24 – 16=8 тыс. руб. Этот
дисконт представляет собой 50% (процентная
ставка за два года) «на 100» с 24
тыс. руб. Действительно, по формуле (7):
тыс.
руб.
С целью проверки можно по формуле (9)
определить нара щениуто сумму с капитала
Р = 16 тыс. руб. за 2 года по просто
процентной ставке 25% годовых:
тыс.
руб.
Дисконтный множитель
представляет величину, обратную множителю
наращения 1 + 2 • 0,25, и показывает долю
капитала Р=16 тыс. руб. в капитале F
= 24 тыс. руб.
Пример 1.2.12. Вам 27 декабря будет нужна
сумма 15 ты( руб. Какую сумму 10 июня этого
же года Вы должны положит в банк под
простую процентную ставку 36% годовых,
если расчете применяется обыкновенный
процент с точным числом дней?
Решение. Полагая в формуле (18) F
=15 тыс. руб., n = 200/360 года
(200 дней), r = 0,36, получим:
тыс. руб.
Если
бы в расчете применялся точный процент
с точным числом дней, то величина вклада
должна быть несколько большей. Так, для
невисокосного года:
тыс.
руб.
что превышает полученную ранее сумму
на 29 руб.
Пример 1.2.13. На какой срок клиент
банка может взять кредит в размере 20
тыс. руб. под простые проценты с условием,
чтобы величина возврата долга не
превышала 22 тыс. руб., если процентная
ставка равна 34%, в расчет принимаются
точные проценты с точным числом дней и
год високосный?
Решение. Полагая в формуле (21) для
расчета срока в днях F=22
тыс. руб., Р=20 тыс. руб., T=
366 дней, r=0,34, получим:
дня
Так что клиент банка может взять кредит
не более чем на 107 дней. Для проверки по
формуле (9) найдем наращенную сумму за
107 дней:
тыс.
руб.
Кстати, если взять 108 дней, то получим
22,007 тыс. руб., т.е. превышение всего на 7
руб., что, конечно, не является существенным.
Пример 1.2.14. Депозитный сертификат
номиналом 20 тыс. руб. с начислением
процентов по простой процентной ставке
40% годовых выпущен на один год. По какой
цене его можно приобрести за 60 дней до
срока погашения, чтобы обеспечить
доходность такой финансовой сделки в
виде простой процентной ставки 45%
годовых? Расчетное количество дней в
году равно 365.
Решение. Депозитный сертификат —
документ, подтверждающий, что его
владелец является держателем срочного
депозита в банке. Для определения
допустимой цены покупки сертификата
необходимо его номинал вместе с
начисленными за год процентами
дисконтировать по простой процентной
ставке 45% годовых, исходя из периода в
60 дней:
тыс. руб.
Если бы в расчете применялся точный
процент с точным числом дней, то величина
вклада должна быть несколько бол шей.
Так, для невисокосного года:
Если цена покупки депозитного сертификата
будет больше! полученной величины 26,071
тыс. руб., то при его приобретении
доставляется доходность, меньшая 45%.
Задачи
1.2.1. Клиент поместил в банк вклад в сумме
4,5 тыс. руб. под 18% годовых с ежеквартальной
выплатой простых процентов, Какую сумму
клиент будет получать каждый квартал?
Как изменится сумма при выплате простых
процентов каждый месяц?
1.2.2.Клиент поместил в банк вклад 6 тыс.
руб. под простую процентную ставку 20%
годовых. Какая сумма будет на счет»
клиента через: а) 7 месяцев; б) 3 года; в)
3 года 9 месяцев?
1.2.3. Банк принимает депозиты на 3 месяца
по процентной ставке 28% годовых, на 6
месяцев — по 32% годовых и на год — по 34%
годовых. Определите сумму, которую
получит владелец депозита в размере 20
тыс. руб. при начислении простых процентов
во всех трех случаях.
1.2.4. В финансовом договоре клиента с
банком предусмотрено погашение долга
в размере 24 тыс. руб. через 150 дней при
взятом кредите в 20 тыс. руб. Определите
доходность такой сделки для банка в
виде годовой процентной ставки. При
начислении банк использует простые
обыкновенные проценты.
1.2.5. Банк в начале года выдал кредит на
сумму 20 тыс. руб сроком на три месяца по
ставке 30% годовых и через три месяца
кредит на сумму 40 тыс. руб. сроком на
полгода по ставке 35% годовых. Определите
общую доходность этих кредитных операций
за девять месяцев в виде простой годовой
процентной ставки в двух случаях: когда
при выдаче второго кредита не используются
и когда используются деньги, возвращенные
банку после погашения первого кредита.
За предоставление кредита банк начислял
простые обыкновенные проценты.
1.2.6. Предприниматель взял в банке ссуду
на два года под процентную ставку 32%
годовых. Определите, во сколько раз
сумма долга к концу срока ссуды будет
больше выданной банком суммы, если банк
начисляет простые проценты.
1.2.7. Банк выдал ссуду на 45 дней в размере
10 тыс. руб. под простую процентную ставку
30% годовых. Рассчитайте доход банка,
если при начислении простых процентов
считается, что в году: а) 360 дней; б) 365
дней.
1.2.8. Имеются две денежные суммы, одна из
которых больше другой на 2 тыс. руб. Обе
суммы помещаются в банк под простые
проценты, причем большая сумма — на 9
месяцев под 30% годовых, а меньшая — на 4
месяца под 25% годовых. Начисленные
проценты за большую сумму в 3 раза больше
начисленных процентов за меньшую сумму.
Найдите размеры первоначальных денежных
сумм.
1.2.9. Найдите величину дохода кредитора,
если за предоставление в долг на полгода
некоторой суммы денег он получил 46,55
тыс. руб. При этом применялась простая
процентная ставка в 22%.
1.2.10. Сертификат, выданный на 120 дней,
обеспечивает держателю доход в виде
дисконта, равного 15% от суммы погашения.
Определите размер простой годовой
процентной ставки, доставляющей такой
же доход при начислении: а) обыкновенных
процентов; б) точных процентов (год
невисокосный); в) точных процентов (год
високосный).
1.2.11. Вклад до востребования был размещен
с 10 января по 14 апреля того же года.
Рассчитайте двумя способами (приближенно
и точно) количество дней, которое может
быть использовано для начисления
процентов, если год: а) високосный; б)
невисокосный. Выполните аналогичные
расчеты, если вклад до востребования
был размещен с 18 марта по 26 июля.
1.2.12. Определите количество дней для
начисления процентов при точном и
приближенном способе подсчета, если
вклад до востребования был размещен:
а) с 12 февраля по 15 мая того же года; б) с
5 июня по 3 ноября того же года. Как
изменились бы результаты, если бы
рассматриваемый год был високосный?
1.2.13. Предоставлена ссуда в размере 180
тыс. руб. 16 января с погашением через 9
месяцев под 25% годовых (год невисокосный).
Рассчитайте сумму к погашению при
различных способах начисления простых
процентов: а) обыкновенный процент с
точным числом дней; б) обыкновенный
процент с приближенным числом дней; в)
точный процент с точным числом дней.
1.2.14. Предоставлена ссуда в размере 60
тыс. руб. 12 марта с погашением 15 августа
того же года под процентную ставку 32%
годовых. Рассчитайте различными
возможными способами сумму к погашению,
если начисляются простые проценты и
го, високосный.
1.2.15. Предприниматель 7 февраля обратился
в банк за ссудой до 14 мая того же года
под простую процентную ставку 18% годовых.
Банк, удержав в момент предоставления
ссуды про центы за весь ее срок, выдал
предпринимателю 50 тыс. руб. Какую сумму
необходимо будет вернуть банку, если
при расчете начисленных процентов
использовались обыкновенные проценты
с точным числом дней и год високосный?
1.2.16. Предприятие обратилось 1 марта в
банк за кредитом в 150 тыс. руб., обязуясь
вернуть сумму с процентами в конце го
да. Какой способ начисления простых
процентов выгоден для предприятия и
какой — для банка, если используется
процентная ставка 26% годовых и год
невисокосный?
1.2.17. Вы получили ссуду 12 февраля на
условиях начисления простых процентов.
Взятую сумму с процентами необходимо
вернуть 27 декабря того же года. Во сколько
раз вырастет долг при различных способах
начисления простых процентов, если
применяется процентная ставка 32% годовых
и год невисокосный?
1.2.18. Вклад в размере 40 тыс. руб. был
размещен в банке 12 марта под простую
процентную ставку 30% годовых. При
востребовании вклада 15 октября того же
года вкладчику были начислены проценты
в размере 47,134 тыс. руб. Какой способ
начисления процентов использовал банк?
1.2.19. За срок ссуды величина обыкновенных
процентов (с точным числом дней) составила
6,4 тыс. руб. Определите величину точных
процентов при условии, что год невисокосный.
Как изменится ответ, если год високосный?
1.2.20. За срок ссуды сумма к погашению
составила 86 тыс. руб., причем начислялись
обыкновенные проценты с точным числом
дней. Определите величину суммы к
погашению при начислении точных процентов
при условии, что размер ссуды 71 тыс. руб.
и год: а) невисокосный; б) високосный.
1.2.21. Какое необходимо время, чтобы 28
тыс. руб., помещенные в банк под простую
процентную ставку 20% годовых увеличились
на такую же величину, как и 30 тыс. руб.,
помещенные в банк с 16 февраля по 28 июля
того же года под простую процентную
ставку 25% годовых? На первый капитал
начисляются обыкновенные проценты с
точным числом дней, на второй обыкновенные
проценты с приближенным числом дней.
1.2.22. По депозитному 30-дневному сертификату
номиналом в 10 тыс. руб. начисляются
обыкновенные проценты по ставке 25%
годовых. Рассчитайте, какой должна быть
годовая процентная ставка при начислении
точных процентов с условием, чтобы они
были равны обыкновенным. Какова величина
начисленных процентов? Год високосный.
1.2.23. За какой срок вклад 5 тыс. руб.
возрастет до 6 тыс. руб. при начислении
процентов по простой процентной ставке
32% годовых?
1.2.24. На какой срок необходимо поместить
имеющуюся денежную сумму под простую
процентную ставку 20% годовых, чтобы она
увеличилась в 2,5 раза?
1.2.25. На какой срок необходимо поместить
имеющуюся денежную сумму под простую
процентную ставку 30% годовых, чтобы
начисленные проценты были в 1,8 раза
больше первоначальной суммы?
1.2.26. Предпринимателю через некоторое
время понадобится сумма в 25 тыс. руб.,
между тем он располагает лишь 22 тыс.
руб. С целью накопления требуемой суммы
предприниматель собирается положить
в банк 22 тыс. руб. Предлагаемая банком
процентная ставка равна 30% годовых.
Какое количество дней необходимо для
накопления требуемой суммы, если банк
начисляет простые проценты, используя
в расчетах точные проценты, и год
невисокосный?
1.2.27. Заемщик собирается взять в банке
кредит в размере 20 тыс. руб. с погашением
его суммой, не превышающей 22 тыс. руб.
Простая процентная ставка банка по
кредитам равна 27% годовых. На какое
максимальное количество дней заемщик
может взять кредит, если банк начисляет
точные проценты, полагая в году 365 дней?
1.2.28. Вкладчик, владея суммой в 20,5 тыс.
руб., хочет получить, положив деньги на
депозит, через год не менее 27 тыс. руб.
Имеет ли смысл ему обратиться в банк,
применяющий простую процентную ставку
26% годовых? Какая ставка необходима для
осуществления намерения вкладчика?
1.2.29. Вкладчик хочет положить на депозит
15 тыс. руб. и за 5 месяцев накопить не
менее 18 тыс. руб. Определите требуемую
простую годовую процентную ставку, на
основании которой вкладчик должен
выбрать банк для размещения свои;
средств, если в расчете применяются
обыкновенные проценты 1 приближенное
число дней.
1.2.30. Банк за использование в течение
четырех месяцев 961 тыс. руб. должен
выплатить 70 тыс. руб. Определите стоимость
привлеченных средств в виде простой
годовой процентной ставки в условиях
начисления обыкновенных процентов.
1.2.31. Вкладчик намеревается положить в
банк 8 тыс. руб. чтобы через 200 дней
накопить 9,2 тыс. руб. Какова должна быть
простая процентная ставка, обеспечивающая
такое накопление? Зависит ли величина
ставки от способа начисления простых
процентов?
1.2.32. Банк выдал кредит на 9 месяцев по
простой процентной ставке 28% годовых,
при этом удержав комиссионные размере
3% от суммы кредита. Определите
действительную доходность для банка
такой кредитной операции в виде годобо!
простой процентной ставки, если
простые проценты начислялись на исходную
сумму кредита.
1.2.33. Предприниматель получил в банке
кредит на 151 дней по процентной ставке
30% годовых, при этом банком был! удержаны
комиссионные в размере 1,5% от величины
кредита. Найдите доходность такой
финансовой операции для банка в виде
годовой простой процентной ставки, если
банк начисляет простые проценты на
исходную сумму кредита, полагая в году
360 дней. Изменится ли величина доходности
при выдаче кредита на 90 дней?
1.2.34. Выдается ссуда по процентной ставке
40% годовых, при этом взимаются комиссионные
в размере 2% от величины ссуды. Простые
точные проценты начисляются на исходную
величину ссуды, год високосный. На какой
срок должна быть выдана ссуда, чтобы
доходность такой сделки для кредитора
в виде годовой простой процентной ставки
составляла 100%?
1.2.35. При выдаче ссуды по процентной
ставке 42% годовых были удержаны
комиссионные в размере 2,5% от величины
ссуды. Простые точные проценты начислялись
на исходную величину ссуды, год високосный.
На какой срок была выдана ссуда, если
доходность такой сделки для кредитора
в виде годовой простой процентной ставки
составила 64%?
1.2.36. При выдаче банком ссуды на 80 дней
по процентной ставке 38% годовых сразу
удерживаются комиссионные. Простые
обыкновенные проценты начисляются на
исходную величину ссуды, год невисокосный.
Определите, какой процент от величины
ссуды составили комиссионные, если
доходность такой финансовой операции
для банка в виде простой годовой
процентной ставки оказалась равной
40%.
1.2.37. Банк выдал одному предпринимателю
30 тыс. руб. на 80 дней, затем полученные
от него деньги выдал второму предпринимателю
на 60 дней и, наконец, полученную от
второго предпринимателя сумму выдал
третьему предпринимателю на 160 дней.
Все ссуды были выданы под простую
процентную ставку 30% годовых, и начислялись
обыкновенные проценты. Какую сумму
должен вернуть банку третий предприниматель?
Определите доходность для банка всей
финансовой операции в виде годовой
простой процентной ставки.
1.2.38. Банк выдавая кредиты своим четырем
клиентам А, В, С и D —
следующим образом: клиенту А — на 45 дней
под 28% годовых; все деньги, полученные
от клиента А, сразу выдал клиенту В на
120 дней под 33% годовых; всю сумму, полученную
от клиента В, выдал клиенту С на 100 дней
под 32% годовых и, получив деньги от
клиента С, выдал их клиенту D на 40 дней
под 30% годовых. Клиент D в конце срока
вернул банку 37 632 руб. Какую сумму получил
клиент А, если во всех случаях начислялись
простые обыкновенные проценты?
1.2.39. Банк выдал клиенту ссуду в размере
20 тыс. руб. 5 января с условием возврата
долга 4 мая. Всю полученную сумму банк
в этот же день выдал другому клиенту,
который 3 июля вернул в банк 23,1 тыс. руб.
В обоих случаях применялась одинаковая
простая процентная ставка и расчет
велся способом 365/360 (обыкновенный процент
с точным числом дней). Определите эту
ставку, если все действия совершались
в течение одного года, являющегося
високосным.
1.2.40. Банк продает депозитные сертификаты
на следующих условиях:
сертификат сроком на 3 месяца под
40% годовых или на год — под 45% годовых.
Какие сертификаты выгоднее приобретать
с целью получения в конце года наибольшего
дохода, если банк начисляет по вкладам
простые обыкновенные проценты?
1.2.41. Банк продает депозитные сертификаты
на следующих условиях: сертификат сроком
на 3 месяца под 40% годовых; i
6 месяцев — под 42% годовых; на год — под
45% годовых. Какие сертификаты выгоднее
приобретать с целью получения в конце
года наибольшего дохода, если банк
начисляет по вкладам простые обыкновенные
проценты?
1.2.42. Какую сумму необходимо положить в
банк под процентную ставку: а) 25% годовых;
б) 50% годовых; в) 80% годовых, чтобы получать
ежегодную ренту в 400 руб., а сумма i счете
в банке оставалась бы неизменной?
1.2.43. Какую сумму необходимо положить в
банк под простую процентную ставку 30%
годовых, чтобы получать: а) еж1 квартально
ренту в 300 руб.; б) ежемесячно ренту в 100
руб., сумма на счете в банке оставалась
бы неизменной?
1.2.44. Банк предоставляет клиенту кредит
в размере 8 тыс. руб. под простую процентную
ставку 20% годовых. Используя дивизор
найдите доход банка, если срок кредита
составляет: а) 40 дна б) 4 месяца; в) 200 дней.
Расчет ведется способом 360/360.
1.2.45. Используя дивизор, вычислите простой
процент с к. питала 4,8 тыс. руб., отданного
в долг по ставке 20% годовых на срок с 8
июля по 25 ноября (год невисокосный), если
расчет ведется способом 365/365 (точный
процент с точным число дней).
1.2.46. Банк за предоставление кредита с
18 апреля по 10 сeноября
того же года под 24% годовых получил от
заемщика в совокупности 12 тыс. руб.
Используя дивизор, определите доход
банка и сумму, полученную заемщиком,
если начисленные простые проценты были
удержаны банком в момент предоставления
кредита и использовался способ 365/360.
Чему равны был1 бы искомые величины,
если бы применялся способ 360/3 60?
1.2.47. При открытии сберегательного счета
на него 16 января была положена сумма 14
тыс. руб., однако 20 февраля со счета было
снято 8 тыс. руб. Позже, 14 апреля, на счет
была добавлена сумма 3 тыс. руб., 16 июня
— 2 тыс. руб., а 10 сентября счет бы закрыт.
Рассчитайте с помощью процентных чисел
сумму, полученную владельцем счета,
если процентная ставка составляла 20°/
годовых, начислялись простые проценты
способом 365/360 и в операции осуществлялись
в течение одного високосного года.
1.2.48. Предприниматель открыл счет в
банке, положив на него 20 тыс. руб. Затем
4 июля он добавил 5 тыс. руб. и 20 ноября
этого же года счет закрыл, получив 28,2
тыс. руб. Найдите дату открытия счета,
если простая процентная ставка составляла
24% годовых и использовался способ
365/360.
1.2.49. Какую сумму необходимо поместить
в банк под простую процентную ставку
40% годовых, чтобы накопить 26 тыс. руб.:
а) за 9 месяцев; б) за 2,5 года; в) за 4 года?
1.2.50. Какую сумму необходимо поместить
в банк под простую процентную ставку
36% годовых, чтобы накопить 12 тыс. руб.:
а) за 20 дней; б) за 70 дней; в) за 300 дней?
Рассмотрите отдельно случай начисления
обыкновенных процентов и случай
начисления точных процентов в високосном
году.
1.2.51. Предпринимателю 18 ноября будет
нужна сумма в 25 тыс. руб. Какую сумму 10
февраля этого же года он должен положить
в банк под простую процентную ставку
34% годовых, если в расчете применяется
обыкновенный процент с приближенным
числом дней?
1.2.52. Предприниматель взял 14 апреля
банковский кредит и погасил его 10 августа
того же года суммой в 180 тыс. руб. Какой
величины был кредит, если процентная
ставка по кредитам равна 25% годовых и
банк начислял простые проценты способом:
а) 365/360; б) 365/365?
1.2.53. Господин N поместил свой капитал в
банк под про-цевтную ставку 30% годовых.
Через год он взял из своего капитала
половину, а затем через 8 месяцев закрыл
счет. Величина начисленных процентов
за весь период нахождения денег в банке
составила 2340 руб. Определите величину
капитала, помещенного в банк, если банк
начисляет простые проценты способом
360/360.
1.2.54. Клиент поместил в банк свободные
денежные средства под процентную ставку
30% годовых. Через 1 год и 8 месяцев клиент
закрыл счет, получив 9 тыс. руб. Определите
величину наращенной суммы, которая была
в конце первого года, если банк начисляет
простые проценты способом 360/360. Если бы
клиент не закрыл счет, то через какое
время он смог бы получить 9,6 тыс. руб.?
1.2.55. Сумма в 30 тыс. руб. помещена в банк
под 20% годовых на два счета таким образом,
чтобы брат и сестра по мере достижения
ими возраста 18 лет получили по одинаковой
сумме.
Определите, сколько получит каждый из
них, если в данный момент брату 15 лет 4
месяца и 3 дня, а сестре 14 лет 1 месяц 20
дней. Каким образом 30 тыс. руб. будут
распределены на да счета? Банк начисляет
простые проценты, используя в расчет;
обыкновенный процент с приближенным
числом дней.
1.2.56. Сумма в 50 тыс. руб. помещена в банк
под 30% годовых на три счета таким образом,
чтобы три брата по мере достижения ими
возраста 18 лет получили по одинаковой
сумме. О делите, сколько получит каждый
из братьев, если в данный момент старшему
брату 16 лет 5 месяцев и 10 дней, среднему
брату 12 лет 6 месяцев и 2 дня, а младшему
брату 10 лет и 3 месяца. Каким образом 50
тыс. руб. будут распределены на три
счета? б! начисляет
простые проценты, используя в расчетах
обыкновенный процент с приближенным
числом дней.
1.2.57. На сумму 200 тыс. руб. начисляются
простые проценты по процентной ставке
35% годовых. Определите наращенную сумму
на конец первого квартала, если ежемесячно
проводится операция реинвестирования
и начисляются обыкновенные про центы.
Какова была бы наращенная сумма в случае
непроведения операции реинвестирования?
1.2.58. Контрактом предусматриваются
следующие процентные ставки на год: за
первый квартал — 30% годовых; за второй
квартал — 32% годовых; за третий и четвертый
кварталы — 1УА годовых. Определите
множитель наращения за год, если в
течение года начисляются простые
проценты. Какой одной простой годовой
процентной ставкой можно заменить
данные ставки?
1.2.59. За предоставленный на год кредит
предусмотрены следующие процентные
ставки: за первый квартал — 3% ежемесячно;
за второй квартал — 3,5% ежемесячно; за
третий и четвертый кварталы — 2,5%
ежемесячно. Определите множитель
наращения за год, если в течение года
начисляются простые проценты. Какой
одной простой годовой процентной ставкой
можно заменить данные ставки?
1.2.60. Контрактом было предусмотрено, что
после первого квартала годовая процентная
ставка повысится на 3%; после второго —
еще на 5% и после третьего квартала — еще
на 7%. Множитель наращения за год оказался
равным 1,365. Определите величину
первоначальной годовой процентной
ставки, если в течение года начислялись
простые проценты.
1.2.61. Заключается финансовое соглашение
на 3 года, в котором предусматривается
схема начисления простых процентов по
следующим годовым процентным ставкам:
за первый год -20%; в каждые следующие два
полугодия процентная ставка повышается
на 5%; в каждом последующем квартале
годовая процентная ставка повышается
на 1%. Определите множитель наращения
за 3 года.
1.2.62. На некоторую сумму в течение полугода
начисляются простые проценты по следующим
процентным ставкам: за первые два месяца
— 30% годовых; за третий месяц — 32% годовых
и за оставшиеся месяцы — 35% годовых.
Определите множитель наращения за
полгода, если: а) первоначальная сумма,
на которую начисляются проценты, не
изменяется; б) при каждом изменении
процентной ставки происходит
реинвестирование (капитализация
процентов).
1.2.63. Простая процентная ставка по вкладам
до востребования, составляющая в начале
года 26% годовых, через квартал была
увеличена до 30%, а еще через полгода — до
35% годовых. Определите величину процентов,
начисленных за год на вклад 10 тыс. руб.
При какой постоянной годовой процентной
ставке можно обеспечить такую же величину
начисленных простых процентов?
1.2.64. Вклад 15 тыс. руб. был положен в банк
9 апреля при простой процентной ставке
40% годовых. С 1 июня банк снизил процентную
ставку по вкладам до 35% годовых. Вклад
был закрыт 10 августа того же года.
Рассчитайте различными возможными
способами величину начисленных процентов.
1.2.65. Господин N поместил в банк свободные
денежные средства, на которые согласно
договору начисляются простые проценты
по изменяющейся процентной ставке: за
первые четыре месяца — 27% годовых, каждый
следующий месяц ставка увеличивается
на 0,5%. Через год, закрыв счет, господин
N получил 64,25 тыс. руб. Определите, какую
сумму получил бы господин N,
закрыв счет через 9 месяцев.
1.2.66. Вкладчик поместил в банк 35 тыс. руб.
на следующих условиях: в первый год
процентная ставка равна 28% годовых,
каждые следующие полгода ставка
повышается на 2%. Найдите наращенную
сумму за три года, если начисляются
простые проценты. При какой постоянной
процентной ставке можно получить такую
же наращенную сумму? Найдите наращенную
сумму за три года, если с изменением
ставки происходит одновременно и
капитализация процентного дохода.
1.2.67. Клиент 4 января положил в банк 5 тыс.
руб. и закрыл счет 10 сентября этого же
года, являющегося високосным. Какую
сумму банк выдал клиенту, если в течение
всего срока начислялись простые проценты
способом 365/365 (точные проценты с точным
числом дней), но процентная ставка
менялась: в начале года — 24%, с 1 апреля —
28% и с 1 июня — 32% годовых?
1.2.68. Депозитный сертификат номиналом
60 тыс. руб. с начислением процентов по
простой процентной ставке 35% годовых
выпущен на один год. По какой цене его
можно приобрести за 150 дней до срока
погашения, чтобы обеспечить доходность
такой финансовой сделки в виде простой
процентной ставки 42% годовых? Расчетное
количество дней в году равно 365.

Если нравится — подписывайтесь на телеграм-канал Бробанк.ру и не пропускайте новости
Эксперт в области финансовой грамотности и инвестиций. Образование высшее экономическое. Опыт работы в банке – более 15 лет. Регулярно повышает квалификацию и проходит курсы по финансам и инвестициям, что подтверждено сертификатами Банка России, Ассоциации Развития Финансовой Грамотности, Нетологии и других образовательных платформ. Сотрудничает со Сравни.ру, Тинькофф Инвестиции, ГПБ Инвестиции и другими финансовыми изданиями. treskova@brobank.ru
Открыть профиль
Всем им нужно узнать, от чего зависит ежемесячный платеж по кредиту и можно ли его вычислить самостоятельно.Бробанк расскажет, как рассчитывается кредит, какие методики использовать для подсчета ежемесячных процентов и итоговой суммы переплаты. В статье собраны формулы, которые расписаны на конкретном примере, чтобы стало понятно, как был получен тот или иной результат.
-
Что входит в ежемесячный платеж
-
Виды ежемесячных выплат по кредитам
-
Что берут за основу при расчете ежемесячного платежа
-
Как рассчитать ежемесячную сумму платежа
-
Самостоятельный подсчет при аннуитетных платежах
-
График расчетов для аннуитетной схемы
-
Самостоятельный подсчет при дифференцированных платежах
-
График расчетов при дифференцированных выплатах
-
Какой из вариантов выгоднее заемщику
-
Какую схему начисления процентов выбрать
Проц. ставка
7.9% годовых
Платеж в месяц
9 964.29 ₽
Сумма выплат
358 714 ₽
Переплата
58 714 ₽
График платежей
| №, Месяц |
Сумма платежа Платеж |
Проценты + долг | Остаток долга |
|---|---|---|---|
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
График платежей
Что входит в ежемесячный платеж
Банки выдают на руки график погашения при оформлении кредита. Сумма ежемесячной выплаты может быть указана одним числом или несколькими. Вид графика погашения зависит от того, какая форма предоставления данных принята в банке. Некоторые кредиторы расписывают данные в двух колонках:
- основной долг, иногда его называют тело;
- начисленные проценты.
Другие банки указывают только общую сумму к выплате в указанную дату.
Если заемщик отклоняется от графика и допускает просрочки, то к основной сумме добавляют штрафы, пени, комиссии или неустойки. Каждый банк самостоятельно устанавливает очередность удержания накопленных штрафных санкций из последующих поступлений. Какой порядок предусмотрен у компании, прописано в кредитном договоре. Например, из суммы очередного поступления списывания происходят в такой очередности:
- Проценты на просроченные проценты.
- Проценты за заемные средства, которые были просрочены по выплате.
- Погашение просроченной задолженности.
- Проценты по текущей задолженности.
- Погашение текущей задолженности.
Банки применяют и другие схемы, но такой вариант считается наиболее распространенным в банковской практике.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Что берут за основу при расчете ежемесячного платежа
Для самостоятельного подсчета суммы ежемесячного платежа по кредиту нужны такие данные:
- общая сумма кредита;
- процентная ставка;
- период кредитования.
Но часто в итоговую сумму выплат включают и другие суммы. Например, страховка по кредиту, услуги смс-информирования или другие платные сервисы от банка. Кроме того сумма будет немного отличаться в зависимости от способа поступления средств. Так, некоторые банки берут комиссию за зачисление наличными.
Дополнительные расходы возникают и при пересылке суммы из другого банка: процент от суммы могут брать как в банке-отправителе, так и банке-получателе. Такие моменты желательно выяснять заранее, чтобы отправленной сумму хватило на ежемесячный платеж, и какая-то его часть не вышла на просрочку.
Как рассчитать ежемесячную сумму платежа
Для расчета ежемесячной суммы платежа по кредиту используют:
- кредитный калькулятор;
- помощь сотрудника банка;
- самостоятельный расчет по формулам
- таблицы в Excel/
Кредитный калькулятор. Такие сервисы размещают в интернете или на сайте банка, который предлагает выдать кредит.
Кредитные калькуляторы позволяют не только рассчитать сумму ежемесячного платежа, но и показывают график выплат. Понадобится внести: сумму, срок и ставку, а также указать, какой тип выплат аннуитетный или дифференцированный. Но данные не всегда будут полностью совпадать с реальными. Потому что платеж может быть внесен не через 30 дней, а через 25, либо равными долями дважды в месяц. Кроме того калькуляторы не учитывают дополнительные платные услуги банка.
Помощь специалиста в отделении банка. Каждый потенциальный заемщик вправе обратиться к менеджеру или позвонить по горячей линии до того, как оформит кредит. Сотрудники банка подскажут диапазон процентной ставки. Затем на основе суммы и срока могут дать информацию по ежемесячному платежу. Но эти сведения предварительные.

После рассмотрения заявки, изучения кредитной истории и платежеспособности, банк установит индивидуальные условия кредитования. В договоре будет указана точная сумма и график платежей.
Самостоятельный расчет по готовым формулам. Ежемесячные платежи можно вычислить самому, если знать все входные данные. Для этого разработаны специальные формулы, куда понадобится подставить свои значения.
Таблицы в Excel. Для вычисления ежемесячного платежа по кредиту понадобятся встроенные функции программы. Подсчитать аннуитетные платежи поможет функция ПЛТ, она же PMT, если искать в латинской версии.
В строке подсчета ежемесячного платежа понадобится вписать такую формулу: =ПЛТ(18%/12;24;-500000). Где 18%/12 — это процентная ставка по кредиту, 24 — количество выплат, а 500 000 — сумма долга. Аннуитетный платеж при таких цифрах будет равен 24 962,05 рублей в месяц.
Какой из вариантов выбрать, зависит от вас. Некоторые предпочитают делать расчеты в онлайн-калькуляторах, другим удобнее один раз внести свои данные в таблицу в Excel и потом только менять параметры.
Самостоятельный подсчет при аннуитетных платежах
Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:
- Процентная ставка — 18%.
- Период кредитования — 24 месяца.
- Сумма кредита — 500000 рублей.
Классическая формула для расчета аннуитетного платежа выглядит так:
Разовый аннуитетный платеж = Сумма кредита * Ка
где Ка — это коэффициент аннуитета.
Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)
где ЕПС — ежемесячная процентная ставка.
Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.
Итоговый расчет примет вид:
500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.
Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.
Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:
24 962,05 * 24 = 599 089,24 рублей.
Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.
График расчетов для аннуитетной схемы
| Дата | Сумма платежа | Проценты | Тело | Остаток платежа |
| 02.04.2020 | 0 | 0 | 0 | 500 000.00 |
| 02.05.2020 | 24 962.05 | 7 500.00 | 17 462.05 | 482 537.95 |
| 02.06.2020 | 24 962.05 | 7 238.07 | 17 723.98 | 464 813.97 |
| 02.07.2020 | 24 962.05 | 6 972.21 | 17 989.84 | 446 824.13 |
| 02.08.2020 | 24 962.05 | 6 702.36 | 18 259.69 | 428 564.44 |
| 02.09.2020 | 24 962.05 | 6 428.47 | 18 533.58 | 410 030.86 |
| 02.10.2020 | 24 962.05 | 6 150.46 | 18 811.59 | 391 219.27 |
| 02.11.2020 | 24 962.05 | 5 868.29 | 19 093.76 | 372 125.51 |
| 02.12.2020 | 24 962.05 | 5 581.88 | 19 380.17 | 352 745.34 |
| 02.01.2021 | 24 962.05 | 5 291.18 | 19 670.87 | 333 074.47 |
| 02.02.2021 | 24 962.05 | 4 996.12 | 19 965.93 | 313 108.54 |
| 02.03.2021 | 24 962.05 | 4 696.63 | 20 265.42 | 292 843.12 |
| 02.04.2021 | 24 962.05 | 4 392.65 | 20 569.40 | 272 273.72 |
| 02.05.2021 | 24 962.05 | 4 084.11 | 20 877.94 | 251 395.78 |
| 02.06.2021 | 24 962.05 | 3 770.94 | 21 191.11 | 230 204.67 |
| 02.07.2021 | 24 962.05 | 3 453.07 | 21 508.98 | 208 695.69 |
| 02.08.2021 | 24 962.05 | 3 130.44 | 21 831.61 | 186 864.08 |
| 02.09.2021 | 24 962.05 | 2 802.96 | 22 159.09 | 164 704.99 |
| 02.10.2021 | 24 962.05 | 2 470.57 | 22 491.48 | 142 213.51 |
| 02.11.2021 | 24 962.05 | 2 133.20 | 22 828.85 | 119 384.66 |
| 02.12.2021 | 24 962.05 | 1 790.77 | 23 171.28 | 96 213.38 |
| 02.01.2022 | 24 962.05 | 1 443.20 | 23 518.85 | 72 694.53 |
| 02.02.2022 | 24 962.05 | 1 090.42 | 23 871.63 | 48 822.90 |
| 02.03.2022 | 24 962.05 | 732.34 | 24 229.71 | 24 593.19 |
| 02.04.2022 | 24 962.09 | 368.90 | 24 593.19 | 0 |
| Всего выплат | 599 089.24 | 99 089.24 | 500 000.00 | 0 |
Самостоятельный подсчет при дифференцированных платежах

Дифференцированный платеж изменяется каждый месяц. Сумма уменьшается, и клиент меньше переплачивает. Формула подсчета выглядит так:
Ежемесячный дифференцированный платеж = ЧОД + Сумма процентов
ЧОД — это часть основного долга, фиксированная величина при дифференцированных выплатах кредита, если будет соблюден график выплат с точностью до дня. Для ее вычисления потребуется сумму кредита поделить на его срок. С данными из примера это выглядит так:
ЧОД = 500000/24 = 20 833,33 рубля
Сумма процентов постоянно уменьшается, так как уменьшается общая итоговая задолженность по кредиту. Банки используют разные формулы для подсчета этой величины, но наиболее распространена такая:
Сумма процентов = ОстЗ * ПСГ * КД/365 или 366 дней в году
ОстЗ — остаток задолженности,
ПСГ — процентная ставка за год,
КД — количество календарных дней, за которые были начислены проценты.
Расширим входящие данные в примере. Предположим, что кредит взят в 2020 году, он високосный, но будет выплачиваться два года, поэтому в 2021 году в формуле будет 365, а не 366 дней. Дополнительные вводные данные: деньги получены 02.04.2020 года, а первый платеж предстоит 02.05.2020 года. Между этими платежами 30 календарных дней. Подставленные в формулу данные будут выглядеть так:
Сумма процентов = 500 000 * 18% * 30/366 = 7377,05 рублей.
Дифференцированный платеж за первый месяц = 20 833,33 + 7 377,05 = 28 210,38 рублей.
Остаток долга к следующему месяцу уменьшится, поэтому:
500 000 — 20 833,33 = 479 166,67 рублей
Следовательно, и сумма начисленных процентов будет меньше. Кроме того в мае 31 день, поэтому формула примет вид:
Сумма процентов во втором месяце = 479 166,67 * 18% * 31/366 = 7 305,33 рублей.
Дифференцированный платеж за второй месяц = 20 833,33 + 7 305,33 = 28 138,66 рублей.
По этой методике подсчитаем все выплаты за 24 месяца пользования кредитом. Итоговая сумма переплаты составит 93 712,98 рублей. При условии, что платежи буду внесены день в день по графику.
График расчетов при дифференцированных выплатах
| Дата | Сумма платежа | Проценты | Тело | Остаток платежа |
| 02.04.2020 | 0 | 0 | 0 | 500 000.00 |
| 02.05.2020 | 28 210.38 | 7 377.05 | 20 833.33 | 479 166.67 |
| 02.06.2020 | 28 138.66 | 7 305.33 | 20 833.33 | 458 333.34 |
| 02.07.2020 | 27 595.63 | 6 762.30 | 20 833.33 | 437 500.01 |
| 02.08.2020 | 27 503.41 | 6 670.08 | 20 833.33 | 416 666.68 |
| 02.09.2020 | 27 185.79 | 6 352.46 | 20 833.33 | 395 833.35 |
| 02.10.2020 | 26 673.49 | 5 840.16 | 20 833.33 | 375 000.02 |
| 02.11.2020 | 26 558.23 | 5 724.90 | 20 833.33 | 354 166.69 |
| 02.12.2020 | 26 058.74 | 5 225.41 | 20 833.33 | 333 333.36 |
| 02.01.2021 | 25 915.30 | 5 081.97 | 20 833.33 | 312 500.03 |
| 02.02.2021 | 25 610.73 | 4 777.40 | 20 833.33 | 291 666.70 |
| 02.03.2021 | 24 860.73 | 4 027.40 | 20 833.33 | 270 833.37 |
| 02.04.2021 | 24 968.18 | 4 134.85 | 20 833.33 | 250 000.04 |
| 02.05.2021 | 24 531.96 | 3 698.63 | 20 833.33 | 229 166.71 |
| 02.06.2021 | 24 336.76 | 3 503.43 | 20 833.33 | 208 333.38 |
| 02.07.2021 | 23 915.52 | 3 082.19 | 20 833.33 | 187 500.05 |
| 02.08.2021 | 23 699.77 | 2 866.44 | 20 833.33 | 166 666.72 |
| 02.09.2021 | 23 381.28 | 2 547.95 | 20 833.33 | 145 833.39 |
| 02.10.2021 | 22 990.87 | 2 157.54 | 20 833.33 | 125 000.06 |
| 02.11.2021 | 22 746.86 | 1 913.53 | 20 833.33 | 104 166.73 |
| 02.12.2021 | 22 374.43 | 1 541.10 | 20 833.33 | 83 333.40 |
| 02.01.2022 | 22 107.30 | 1 273.97 | 20 833.33 | 62 500.07 |
| 02.02.2022 | 21 788.81 | 955.48 | 20 833.33 | 41 666.74 |
| 02.03.2022 | 21 408.67 | 575.34 | 20 833.33 | 20 833.41 |
| 02.04.2022 | 21 151.48 | 318.07 | 20 833.41 | 0 |
| Всего выплат | 593 712.98 | 93 712.98 | 500 000.00 | 0 |
Какой из вариантов выгоднее заемщику
Если ориентироваться исключительно на сумму переплаты, то однозначно дифференцированный способ начисления и выплаты процентов выгоднее для заемщика. Логично, что при аннуитетных платежах, больше выгод у банка. Но не у всех заемщиков получится соблюдать повышенную нагрузку по дифференциальной схеме, когда первоначальные ежемесячные платежи значительно выше. В приведенном примере выплаты в первый месяц при разных способах отличались на 3,2 тысячи рублей. Но при длительном периоде кредитования и большой сумме этот разрыв значительно выше.
Например, если заемная сумма по ипотеке 5 млн рублей, ставка 10% и срок кредитования 15 лет, данные приобретут такой вид:
| Суммы | Аннуитетный платеж | Дифференцированный платеж |
| Первый ежемесячный платеж | 53 730,26 | 70 070,59 |
| Итоговая сумма переплаты | 4 761 445,18 | 3 771 213,11 |
Не каждый заемщик осилит первоначальную разницу в 17 тысяч рублей, хотя итоговая сумма переплаты представлена наглядно.
Какую схему начисления процентов выбрать
Таблица поможет определить, какая из схем начисления процентов подойдет больше в разных ситуациях:
| Условие | Аннуитетная схема | Дифференцированная схема |
| Равные суммы платежей на протяжении всего срока | Да, но можно вносить больше, главное оповестить банк, чтобы досрочное погашение было оформлено своевременно. | Нет, суммы постепенно уменьшаются. Но если есть возможность и желание можно платить еще больше, чем предложено по графику. В этом случае следует оповестить банк-кредитор о своем желании. |
| Сумма итоговой переплаты по кредиту | Больше | Меньше |
| Методика самостоятельного подсчета | Проще | Сложнее, но можно использовать онлайн-калькуляторы |
| Кому подходит больше | Тем, у кого фиксированная и стабильная заработная плата с понятными ожиданиями на длительную перспективу. | Тем, у кого высокие доходы в ближайшем будущем, но более отдаленные перспективы менее поняты. Например, проектным работникам. |

Чтобы уменьшить переплату при аннуитетной схеме, погашайте кредит досрочно. Если удастся досрочно вносить такие же суммы, как предусмотрены в графике дифференцированных платежей, то итоговая переплата почти такая же, как в дифференцированной схеме.
В этом случае самое главное условие предупреждать сотрудников банка, зачем вы вносите на счет сумму большие, чем предусмотрены в вашем графике выплат. О том, как и когда надо уведомлять банк, пишут в кредитном договоре. В некоторых компаниях допускают уведомление на горячую линию, в других через сообщения в интернет-банке, в третьих — через личное заявление у офисе.
Оценивайте свои финансовые возможности до подписания договора. Не берите взаймы больше, чем способны погасить, и тогда вы сохраните свою кредитную историю и сможете своевременно выплатить долги.