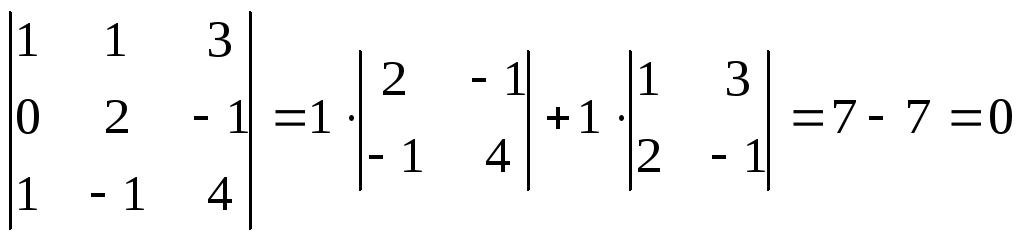Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах
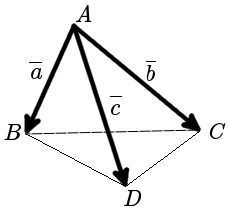
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти вектора на пирамиде
Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.
Что представляет собой пирамида?
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
Как рассчитывается объем пирамиды?
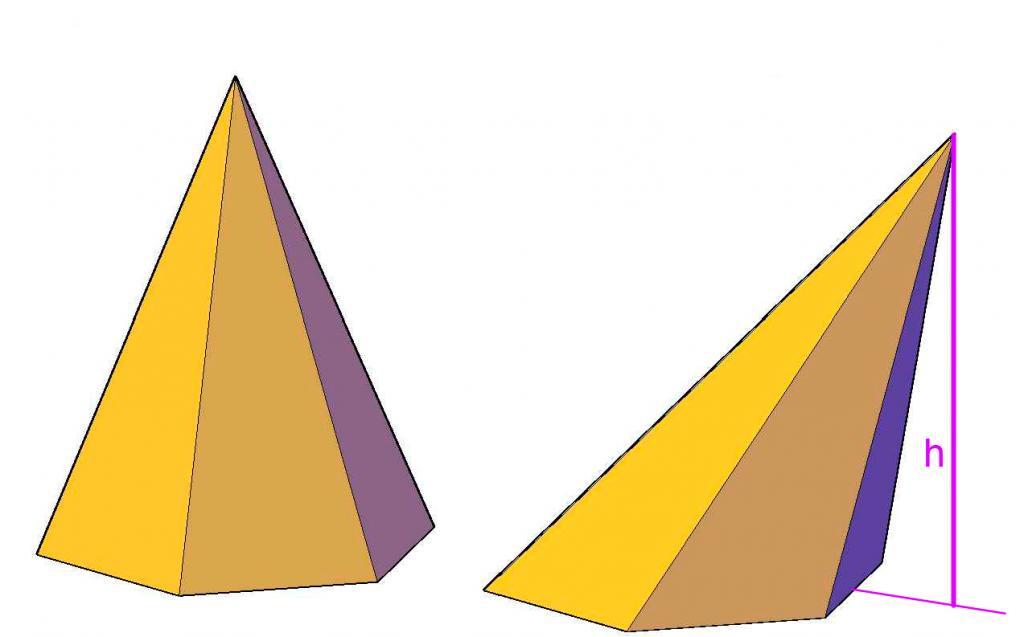
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
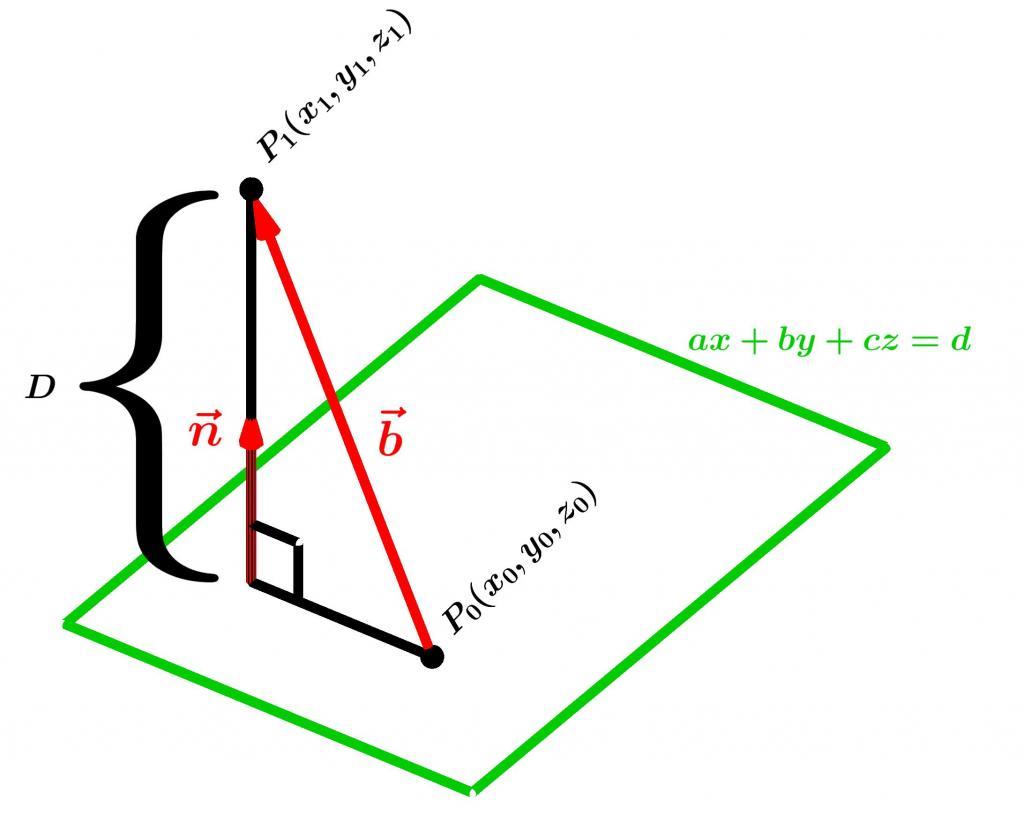
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) — координаты точки.
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой
Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x — 10 * y — 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.
Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Уставление
компланарности векторов в пространстве
Пример
12: Доказать
компланарность векторов
=
1
1; 3 ,
= 0
2 -
1 ,
= 1
— 1
4 .
Решение.
Найдем смешанное произведение векторов
:
=
(определитель
вычислен путем его разложения по
элементам первого столбца).
Так
как смешанное произведение векторов
,
и
равно нулю, то эти векторы компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Пример
13:Найти объём
треугольной пирамиды с вершинами в
точках
Решение.
Найдем
координаты векторов
,
,
,
на которых построена пирамида:
Вычислим
смешанное произведение этих векторов
Объём
треугольной пирамиды, построенной на
векторах
,
,
,
равен
Определение взаимной ориентации векторов
Определение
взаимной ориентации векторов
,
,
основано
на следующих соображениях. Если
>0,
то тройка векторов правая, если
<
0, то тройка векторов левая.
2. Задачи для самостоятельной работы
1.
По данным векторам а
и b
построить следующие их линейные
комбинации: а) 2а
+ b;
б) а
— Зb;
в) — а
+ 4-b;
2.
Векторы
служат сторонами треугольника ABC.
Выразить через а,
b,
с
векторы
совпадающие с медианами треугольника.
3.
В треугольной пирамиде SABC известны
векторы Найти вектор
,
если точка О является центром масс
треугольника
ABC.
4.
Дана прямоугольная трапеция ABCD, длины
оснований AD н ВС которой соответственно
равны 4 и 2, а угол D равен 45°. Найти проекции
векторов
на
ось
определяемую вектором
.
5.
Вектор а
составляет с координатными осямн Ох и
Оу углы
.
Вычислить его координаты, если |а|
=2.
6.
Найти длины диагоналей параллелограмма,
построенного на векторах
7.
Векторы
определяют
стороны треугольника ABC. Найти длину
вектора
,
совпадающего с медианой, проведенной
из вершины С.
8.В
параллелограмме ABCD
даны стороны
Выразить
через
и
векторы
9.
В ТреугольникеABCпроведины меридианыaAK,BLиCM.
Выразить
и
через векторы
и
.
10.
Даны векторыи
.
Найти векторы:
;
.
11.
Найти направляющие
косинусы вектора
12.Дано
=5,
=6.
Найти скалярное произведение векторови
,
если уголмежду ними равен 120°
13.
Найти угол А в треугольнике с вершинами
A(1;2;-1),B(5;5;11),C(13;18;20)
14.
Даны векторы
,
,
.
Найти проекцию векторана вектор
.
15.
Даны векторы
,
и
.
Найти проекцию векторана вектор
.
16.
Найти
,
если
17.
Даны векторы
и
.
При каком значенииm
эти векторы перпендикулярны?
18.Даны
три последовательные вершины
параллелограмма А (-3;-2;0), В(3;-3;1) и С(5;0;2).
Найти четвёртую вершину D
и угол между векторами
и
.
19.
Даны векторы
и
.
При каком значенииm
векторы перпендикулярны?
20.
Найти площадь треугольника с вершинами
А (2;2;2), В(1;3;3), С(3;4;2).
21.
Упростить:
22.
Известно, что
а
угол между
и
равен
Найти
.
23.
Найти площадь треугольника с вершинами
в точках
24.
Вычислить площадь треугольника с
вершинами А (1;1;1), В (2;3;4), С (4;3;2).
25.
Вычислить площадь и высоту параллелограмма,
построенного на векторах
26.
Найти площадь параллелограмма,
построенного на векторах
и
,
где.
27.
Вычислить диагонали и площадь
параллелограмма, построенного на
векторах
и
.
28.
Найти значения α и β, при которых векторы
=
и
=
являются коллинеарными.
29.
На оси аппликат найти точку, равноудаленную
от точек А(3;9;-1) и В(7;-3;9)
30.
Определите координаты концов P
и Q
отрезка, который точками М(3;1;3) и N(6;-1;1)
разделён на три части.
31.
Проверить, является ли векторы
компланарными?
32.
Найти объём тетраэдра с вершинами в
точках А (-1;1;0), В(2;-2;1), С(3;1;-1), D(1;0;-2).
33.
Вычислить объём параллелепипеда,
построенного на векторах
и
.
34.
Установить, лежат ли в одной плоскости
точки А (4;3;10), В (5;1;5), С (2;2;5), D
(3;4;12).
35.
В тетраэдре с вершинами D
(-3;-3;-3), A
(2;-1;-3), B
(-1;2;3) и
C(-2;-2;1).
Найти площадь грани АВС и длину высоты,
проведённой к этой грани.
36.Выяснить,
компланарны ли векторы
?
34.
Определить
,
при котором компланарны векторы
и
37.
Найти объем тетраэдра с вершинами в
точках А (-1; 1; 0 ), В ( 2; -2; 1 ), С (3; 1; -1 ),
D
=(1; 0; -2 ).
38.
На прямой проходящей через точки А
(-3;8;2) и B
(1;-2;0) найти точку С, абсцисса которой
39.
Найти объём треугольной пирамиды с
вершинами в точках
40.
Найти точку пересечения медиан
треугольника, если вершинами его служат
точки А(7;-4;5), В(-1;8;-2), С(-12;-1;6).
41.
Найти все значения m, при
которых вектора (1;m;
3) линейно выражается через векторыb(2;3;7),c(3;-2;4),d(-1;1;-1).
42.
Предприятие выпускает 4 вида продукции
Р1, Р2;
Р3,
Р4
в количествах 50, 80, 20,120 единиц. При этом
нормы расхода сырья составляют
соответственно 7; 3,5; 10; 4 кг. Определите
суммарный расход сырья и его изменение
при изменениях выпуска продукции Р1,
Р2; Р3,
Р4 соответственно
+5, -4, -2, +10 единиц.
43.
Предприятие выпускает три вида продукции
Р1, Р2;
Р3
в количестве 15, 25, 40 штук, реализуемых
по ценам 30, 40, 50 усл. Ед. соответственно.
Найти выручку предприятия от реализации
продукции и ее изменение при изменении
Р1, Р2;
Р3цен
продукции соответственно на +5, -3, +2 усл.
ед.
44.
Выяснить, являются ли векторы а1=(4;-5;2;6),
а2=(2;-2;1;3),
а3=(6;-3;3;9),
а4=(4;
-1;5;6) линейно зависимыми?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 


вектору 
обозначен 
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора 
длина отрезка и обозначается 

не имеет. Вектор 
направление которого совпадает с направлением вектора 

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора 
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора 

свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства 
представлен в виде разности двух векторов, исходящих из начала координат: 


координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
При λ>0
– вектор





4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 


знаком «+», если вектор 
знаком «–», если 
Если
в качестве оси l взять некоторый другой вектор 


Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора 
вектора 
между вектором и осью, то есть 
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 


число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Теорема 2.3. Скалярное произведение двух векторов 
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами 

Отсюда
следует условие перпендикулярности ненулевых векторов



Нахождение проекции вектора 
заданное вектором 

С помощью скалярного произведения векторов находят
работу постоянной силы 
прямолинейном участке пути.
Предположим, что под действием постоянной силы 
положения А в положение B. Вектор силы 



равна 
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
соответствующего ресурса 
Тогда 
ресурсов 
векторов 
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала


Угол φ между 

формуле (2.29), то есть
6. Три некомпланарных вектора 
тройку, если при наблюдении из конца третьего вектора 
поворот от первого вектора 
вектору 
если по часовой стрелке.
Векторным
произведением 


вектор 
– 


– имеет длину, равную 


– векторы 
тройку (рис. 2.15).

условием коллинеарности двух векторов является равенство нулю их векторного
произведения 
Теорема 2.5. Векторное произведение векторов 
третьего порядка вида

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
построенного на векторах 


. Следовательно,

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы 
точки O называется вектор 
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
— 


Следовательно,
момент силы 
точки O представляет собой векторное произведение


Линейная скорость 
угловой скоростью 
неподвижной оси, определяется формулой Эйлера 
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 

. Следовательно, искомая площадь равна 
площади)
7. Рассмотрим произведение трех векторов 

результирующий вектор – скалярно на третий. Такое произведение 
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

Нетрудно показать, что объем параллелепипеда,
построенного на векторах 
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
Объем треугольной пирамиды, построенной на этих же
векторах, равен

Пример 2.13. Вершинами пирамиды служат точки 
Решение. Найдем
координаты векторов

По формуле (2.36) объем пирамиды, построенной на
векторах 


Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
линейно зависимой, если существуют такие числа 
место равенство

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
получим выражение вектора 
остальные векторы
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все


независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа

вектора 
векторов 
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт 
линейно независимых векторов, то есть каждый вектор 
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт 

по ортам 

пространстве.
Вопросы для самопроверки