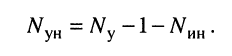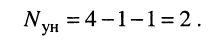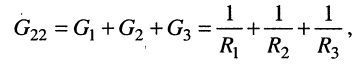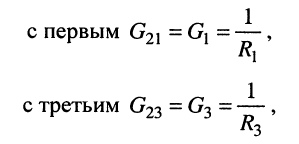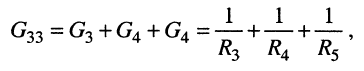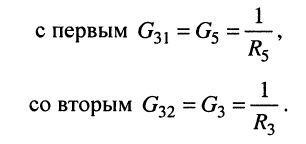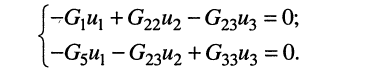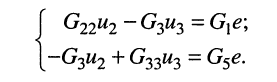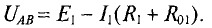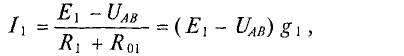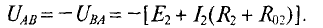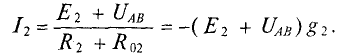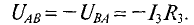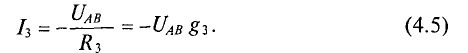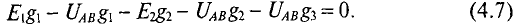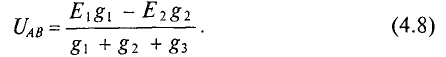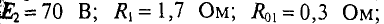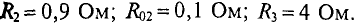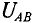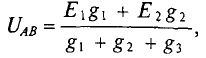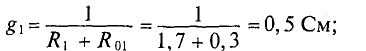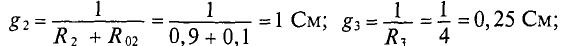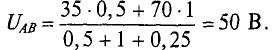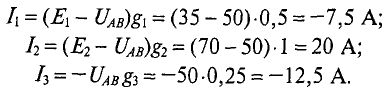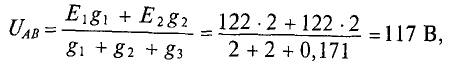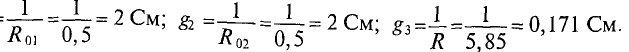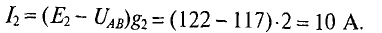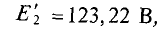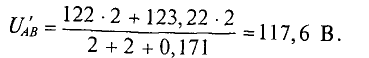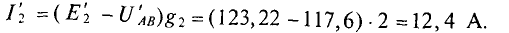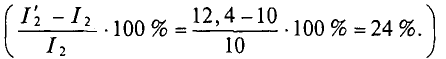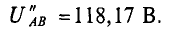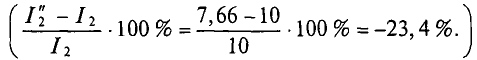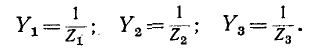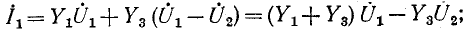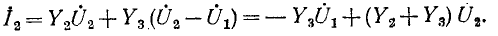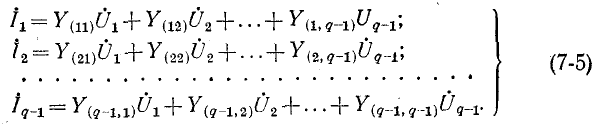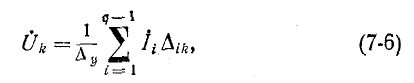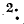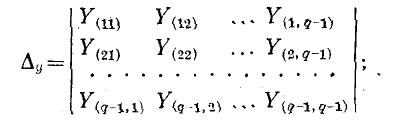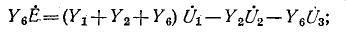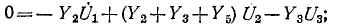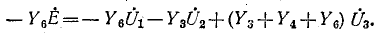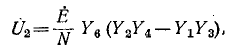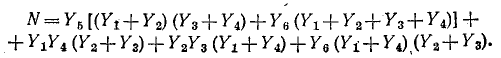Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
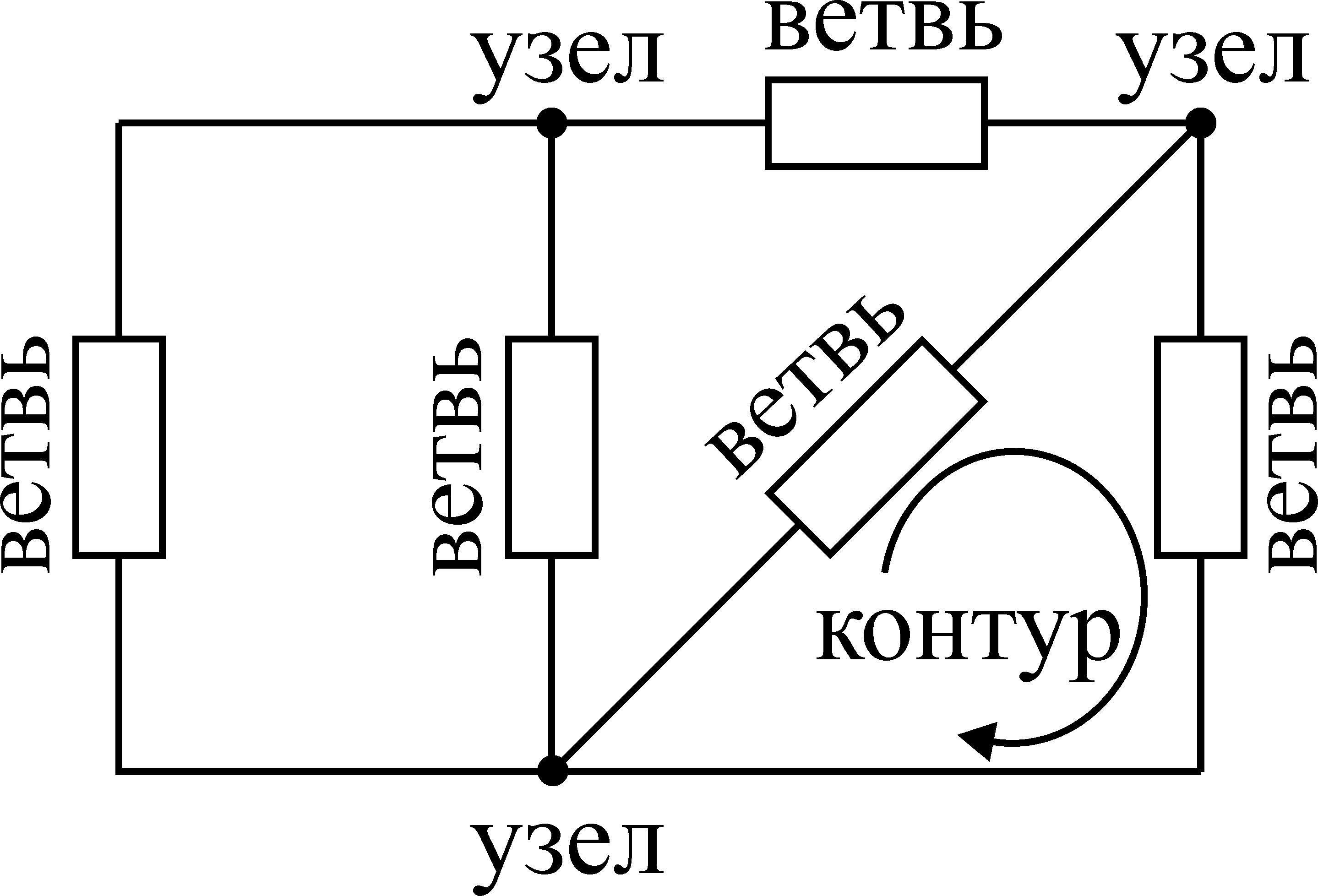
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
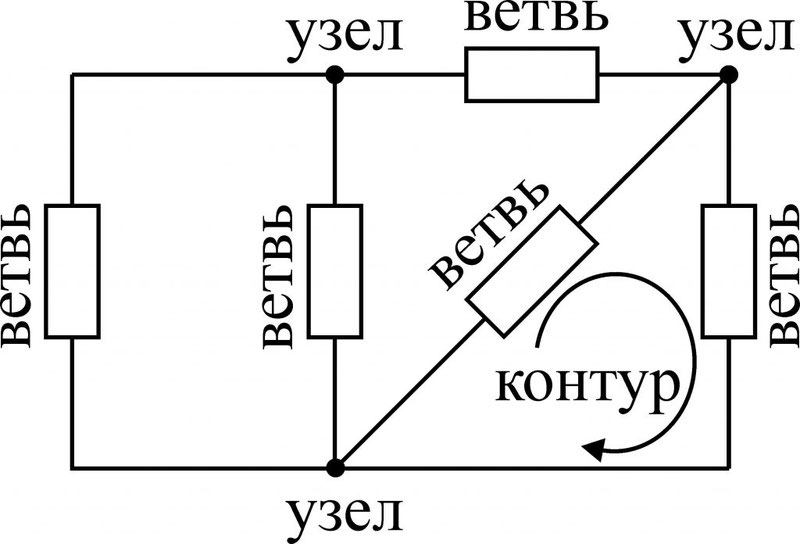
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и 
- Узел A
- Узел B
- Узел C
- Узел D
Точки К и Е не являются узлами.
Содержание
- Электрическая цепь
- Определение
- Графическое изображение электрической цепи и ее элементов
- Законы электрических цепей
- Законы электрических цепей
- Параметры электрических цепей
- Параметры электрических цепей
- Понятие о линейных и нелинейных электрических цепях
- Идеальные элементы электрической цепи
- Идеальные элементы электрической цепи
- Соотношение между током и напряжением в идеальных элементах цепи
- Основная задача анализа электрической цепи
Электрическая цепь
Определение
Электрической цепью называется совокупность электротехнических устройств, создающих замкнутый путь электрическому току. Она состоит из источников (генераторов) энергии, приемников энергии (нагрузки) и соединительных проводов. В цепи могут быть также различные преобразователи (играют роль как роль источников, так и приемников), защитная и коммутационная аппаратура.
В источниках неэлектрические виды энергии преобразуются (в соответствии с законом сохранения энергии) в энергию электромагнитного поля. Так, например, на гидроэлектростанциях энергия падающей воды (энергия гравитационного поля) преобразуется в энергию электромагнитного поля. В приемниках энергия электромагнитного поля преобразуется в тепловую и другие виды энергии. Кроме того, некоторая часть энергии запасается в электрических и магнитных полях цепи.
Электромагнитные процессы в электрической цепи описываются с помощью понятий о токе, напряжении, электродвижущей силе (ЭДС), сопротивлении, индуктивности и емкости. Буквенные обозначения этих, а также других величин, используемых в этом учебном пособии представлены в табл.1.1. Там же дана их русская транскрипция и единицы измерений. Заметим здесь, что ЭДС, токи и напряжения, изменяющиеся во времени, обозначаются строчными латинскими буквами е, i, u, а ЭДС, токи и напряжения, неизменные во времени, обозначаются заглавными латинскими буквами E, I, U.
Графическое изображение электрической цепи и ее элементов
Графическое изображение электрической цепи называется ее схемой. В схеме различают ветви, узлы и контуры. Ветвь – это часть схемы, состоящая только из последовательно соединенных источников и приемников. Узел – точка схемы, в которой сходятся не менее трех ветвей (ветви начинаются и заканчиваются на узлах цепи). Контур – часть схемы, образованная ветвями; число контуров определяется числом вариантов обходов по ветвям цепи. На рис.1.1 даны структурные схемы трех электрических цепей и указано количество ветвей узлов и контуров в каждой из них.
Принятые в настоящем учебном пособии графические обозначения основных элементов цепи, показаны на рис.1.2.
На этом рисунке : 1 — источник ЭДС; 2 — источник тока; 3 — соединительный провод; 4 — сопротивление R цепи; 5 — индуктивность L цепи; 6 — емкость С цепи; 7 — двухполюсник (цепь с неизвестной структурой, имеющая два входных зажима).
В цепях постоянного тока (рис.1.3,а) направление действия ЭДС источника принято указывать в сторону того зажима, на котором образуются положительные заряды. Направление тока во внешней цепи принято указывать от положительно заряженного полюса (зажима) источника к отрицательно заряженному. Направление действия напряжения в приемнике всегда указывают в ту же сторону, что и направление действия тока.
В цепях синусоидального тока (рис.1.3,б) принято обозначать направления ЭДС тока и напряжения, используя положительный полупериод тока, при котором ток не изменяет своего направления. При этом картина этих направлений получается аналогичной с цепью постоянного тока.
Законы электрических цепей
Законы электрических цепей
Ими являются первый и второй законы Кирхгофа.
Первый закон Кирхгофа относится к узлам цепи: в любой момент времени алгебраическая сумма токов в узле равна нулю
где К – число ветвей, подходящих к узлу (три и более).
Токи, подходящие к узлу, и токи, отходящие от узла, имеют противоположные знаки. Будем считать подходящие к узлу токи положительными и брать их в уравнениях первого закона Кирхгофа со знаком (+), а отходящие от узла, – отрицательными и брать их со знаком (−) . Первый закон Кирхгофа фактически является следствием известного из курса физики принципа непрерывности электрического тока, согласно которому линии тока всегда замкнуты и не имеют ни начала, ни конца.
Пример 1.1. На рис.1.4,а показан узел цепи с пятью подходящими к нему ветвями. Требуется составить для этого узла уравнение по первому закону Кирхгофа.
Решение. На основании формулы (1.1) имеем
Таким образом, всегда сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла.
Второй закон Кирхгофа относится к контурам цепи: в любой момент времени алгебраическая сумма ЭДС всех источников энергии контура равна алгебраической сумме напряжений на всех приемниках этого контура.
где Q – число источников ЭДС в контуре; N – число приемников контура.
Для составления уравнения по второму закону Кирхгофа необходимо предварительно (произвольно) выбрать направление обхода этого контура. Те ЭДС и напряжения, направления которых совпадают с выбранным 9
направлением обхода, считаются положительными и берутся в уравнении со знаком (+), а остальные − со знаком (−).
Пример 1.2. На рис.1.4,б показан один из контуров сложной электрической цепи. Направления действия ЭДС источников и напряжений на приемниках известны. Требуется составить для этого контура уравнение по второму закону Кирхгофа.
Решение. Для этого предварительно выбираем (произвольно) направление обхода контура и в соответствии с формулой (1.2) составляем следующее уравнение:
Здесь е2 и е3 , u1 и u2 взяты со знаком (−), так как их направление действия не совпадает с направлением обхода контура; е1, u4 и u3 взяты со знаком (+), так как их направление действия совпадает с направлением обхода контура.
Параметры электрических цепей
Параметры электрических цепей
Любая электрическая цепь и каждый ее элемент в отдельности обладают тремя параметрами: сопротивлением R, индуктивностью L и емкостью С.
Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую. Количество тепловой энергии WТ , выделяющееся в сопротивлении R при протекании тока i в течение времени t, определяется соотношением (1.3) и измеряется в джоулях (Дж):
Величина сопротивления любого элемента цепи определяется как отношение постоянного напряжения на этом элементе к постоянному току в нем и измеряется в омах (Ом):
Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладает любой проводник с током или система проводов. Количество этой энергии WM , накопленной в цепи, зависит от величины тока i и измеряется в джоулях (Дж):
Эта энергия не преобразуется в тепло, а существует в цепи в виде некоторого запаса. Когда ток в цепи равен нулю, запаса энергии магнитного поля в ней нет.
Величина индуктивности определяется как отношение потокосцепления цепи ψ к току i и измеряется в генри (Гн)
Потокосцеплением называется сумма магнитных потоков всех витков катушки. В простейшем случае для катушки на замкнутом стальном сердечнике можно считать, что ее потокосцепление есть магнитный поток Ф, умноженный на число витков w: Ψ = Ф w.
Емкость С характеризует способность цепи накапливать энергию электрического поля. Такой способностью обладают любые два провода, разделенные диэлектриком, например провод, висящий над землей, любые два провода линии передачи.
Количество энергии электрического поля W Э , накопленной в цепи с емкостью С , зависит от величины напряжения между проводами и измеряется в джоулях (Дж):
Эта энергия не может преобразовываться в тепловую, а существует в цепи в виде некоторого запаса. Если напряжение между проводами отсутствует, то и запаса энергии электрического поля в цепи нет.
Величина емкости С определяется как отношение электрического заряда q одного из проводов к напряжению u между ними и измеряется в фарадах (Ф):
В табл.1.2 представлены конструкции некоторых простейших электротехнических устройств и формулы для расчета их параметров. В этой табл.: γ − удельная электрическая проводимость провода (1/Ом⋅м); μ a − абсолютная магнитная проницаемость стали (Гн/м); ε a абсолютная диэлектрическая проницаемость диэлектрика (Ф/м); l −длина провода, средняя длина стального сердечника, расстояние между пластинами конденсатора (м); S – площадь поперечного сечения провода, площадь поперечного сечения стального сердечника, площадь пластины конденсатора (м 2 ); w – число витков обмотки; Ф – магнитный поток в сердечнике, измеряемый в веберах (Вб).
Понятие о линейных и нелинейных электрических цепях
Если γ, μa и εa (и следовательно R, L и С ) являются постоянными величинами и не зависят от тока (или напряжения), то такие устройства, называются линейными, а цепи, их содержащие, называются линейными цепями. Именно такие цепи рассматриваются в данном учебном пособии.
Существует, однако, целый ряд устройств, у которых γ, μa и εa зависят от величин токов (или напряжений). Таковыми, в частности, являются все полупроводниковые приборы, катушки на насыщенных стальных сердечниках, нагревательные устройства с большим диапазоном изменения температур (электрическая дуга, лампы накаливания), конденсаторы с сегнетодиэлектриками. Цепи, содержащие такие устройства, называются нелинейными.
Свойства нелинейного элемента электрической цепи не могут быть выражены одним постоянным числом и поэтому описываются его характеристикой. Для сопротивлений это зависимости напряжения от тока (вольтамперные характеристики); для индуктивностей это зависимости потокосцепления от тока (веберамперные характеристики); для емкостей это зависимости электрического заряда от напряжения (кулонвольтные характеристики). На рис.1.5 показаны примеры характеристик некоторых линейных (ЛЭ) и нелинейных (НЭ) элементов цепи. Заметим, что характеристики всех линейных элементов цепи являются прямыми линиями, а нелинейных элементов – кривыми.
Идеальные элементы электрической цепи
Идеальные элементы электрической цепи
Любое электротехническое устройство содержит все три параметра: сопротивление R , индуктивность L и емкость С. Рассмотрим (рис.1.6), катушку, выполненную из провода с конечной проводимостью (это может быть и нить лампы накаливания, и обмотка трансформатора или электродвигателя).
При подаче на ее зажимы напряжения u на концах катушки появляются разноименные заряды (+)q и (−)q и в обмотке начинает протекать ток i. При этом вокруг витков обмотки возникает магнитное поле, характеризуемое потокосцеплением ψ. Таким образом, в соответствии с формулами (1.4), (1.6) и (1.8) рассматриваемая катушка обладает всеми тремя вышеуказанными параметрами.
Для удобства анализа и расчета электрических цепей вводят в рассмотрение такие элементы, которые при всех условиях обладают только одним параметром: только сопротивлением, только индуктивностью, только емкостью. Они называются идеальными.
Графическое изображение идеальных элементов электрической цепи показано на рис.1.2 позициями 4, 5 и 6. В природе таких элементов не существует, но есть устройства, по своим свойствам близкие к идеальным. Реостат (резистор) при низких частотах обладает практически только сопротивлением R, а индуктивностью L и емкостью С этого устройства можно пренебречь. Катушка индуктивности на замкнутом ферромагнитном сердечнике с малыми тепловыми потерями в нем обладает на низких частотах практически только индуктивностью L, а сопротивлением R и емкостью С такой катушки можно пренебречь. Конденсатор с малыми внутренними тепловыми потерями обладает практически только емкостью С, а его активной проводимостью G и индуктивностью L можно пренебречь.
Заметим, что реостат, катушку индуктивности и конденсатор широко используют для имитации (моделирования) идеальных элементов при проведении лабораторного практикума по теории цепей.
Любое реальное электротехническое устройство можно изобразить в виде электрической схемы, состоящей из комбинации идеальных элементов и, следовательно, произвести его электрический расчет. В табл.1.3 приведено несколько примеров изображения реальных устройств в виде электрических схем.
Соотношение между током и напряжением в идеальных элементах цепи
Прежде чем приступать к расчету сколько-нибудь сложных электрических цепей, следует выяснить, каким образом связаны между собой ток и напряжение в каждом из идеальных элементов цепи. Эти соотношения, известные из курса физики, приведены в табл.1.4. Они имеют всеобщий характер и справедливы для цепей, у которых ток и напряжение изменяются во времени по любому закону. Это важнейшие формулы теории цепей, которые встретятся нам много раз в этом учебном пособии ∗. Заметим здесь, что формулы позиции 1 соответствуют закону Ома, формулы позиции 2 вытекают из закона электромагнитной индукции, а формулы позиции 3 следуют из определения электрической емкости.
Из табл.1.4 видно, что только в сопротивлении R ток и напряжение связаны между собой алгебраическим соотношением. Между током и напряжением в индуктивности и емкости имеют место интегро-дифференциальные соотношения.
Пример 1.3. В цепи с идеальной индуктивностью (рис.1.7,а) действует пилообразный периодический ток (рис.1.7,б). Требуется определить форму приложенного напряжения.
Решение. Для нахождения графика напряжения используем соотношение u = di/dt (поз.2 табл.1.4), из которого следует, что форма кривой напряжения соответствует производной от тока по времени. Из курса математики известно, что графически производная di/dt определяется в каждой точке кривой тока, как тангенс угла наклона касательной к этой кривой относительно оси t.
В нашем примере на участке от 0 до T/2 кривая тока представляет собой прямую, проходящую через начало координат под острым углом α 1 90°, и поэтому производная di/dt на этом участке есть постоянная и отрицательная величина. tgα 2 = tg(180 — α 1) = -tgα 1
Таким образом, график искомого напряжения представляет собой отрезки прямых, меняющих каждую половину периода свой знак, как это показано на рис.1.7,б.
Основная задача анализа электрической цепи
Анализ электрических цепей осуществляется с помощью законов Кирхгофа. При этом можно преследовать различные цели. Например, определять напряжения во всех ветвях цепи по их известным параметрам. Можно также определять необходимые ЭДС всех источников энергии по известным токам и параметрам приемников и источников. Для придания нашему курсу логической стройности основной задачей анализа (расчета) будем считать определение токов во всех ветвях цепи по известным параметрам всех источников и известным параметрам всех приемников. Научившись решать эту задачу, мы сможем решать и другие задачи, связанные с анализом и расчетом электрических цепей.
Источник
8. Топологические элементы схемы: ветви, узлы, контуры.
Электрическая
схемапредставляет собой графическое
изображение электрической цепи. Она
показывает как осуществляется соединение
элементов рассматриваемой электрической
цепи.
«Электрическими»
элементами схемы служат активные и
пассивные элементы цепи.
«Геометрическими»
элементами схемы являются ветви и узлы.
Ветвь
– участок схемы, расположенный между
двумя узлами и образованный одним или
несколькими последовательно соединенными
электрическими элементами цепи (рис.
11).
Рис. 11. Изображение
ветвей электрической схемы.
Под последовательным
соединением
элементов цепи понимается такое их
соединение, при котором через все эти
элементы проходит один и тот же ток.
Узел
– место соединения трех или большего
числа ветвей. Место соединения двух
ветвей рассматривается как устранимый
узел.
Рис. 12. Изображение
узла электрической схемы.
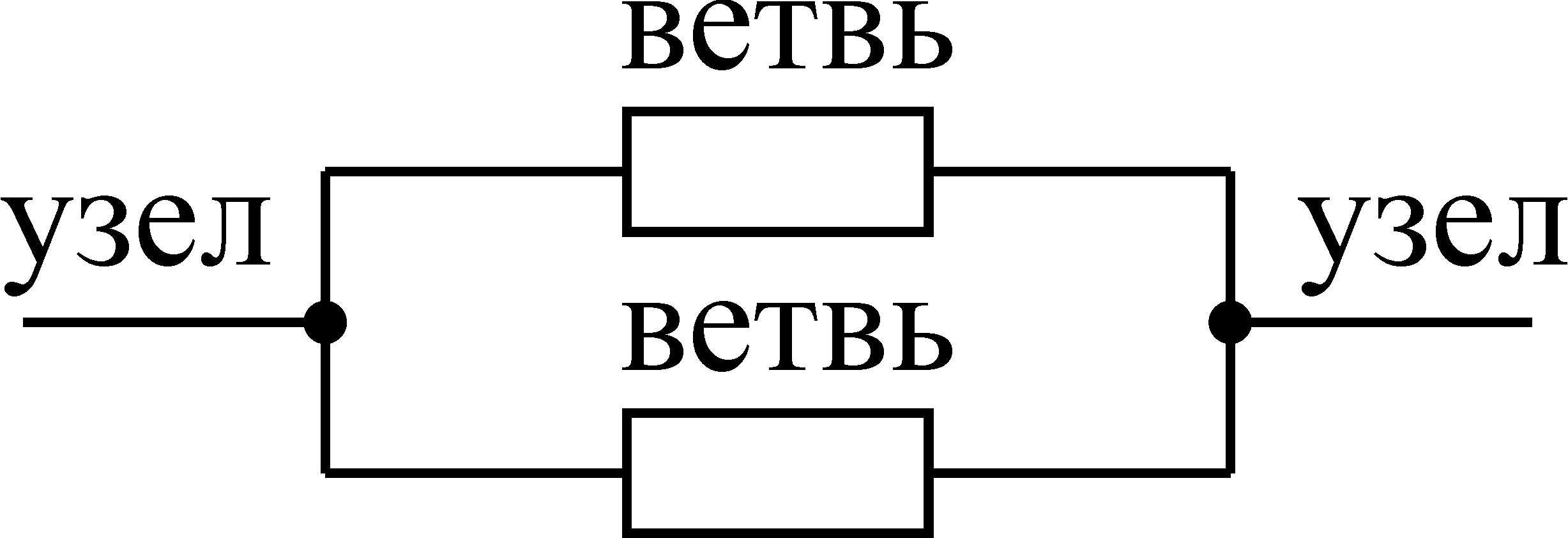
Ветви присоединенные
к одной паре узлов называются параллельными
(рис. 13).
Рис. 13. Параллельное
соединение двух ветвей.
На рис. 14 изображена
электрическая схема пять ветвей и три
узла.
Стрелкой на рис.
указано направление обхода одного из
контуров.
Рис. 14. Схема
электрической цепи.
Под контуром
понимается любой замкнутый путь,
проходящий по нескольким ветвям.
В зависимости от
числа контуров, имеющихся в схеме,
различают многоконтурные и одноконтурные
схемы.
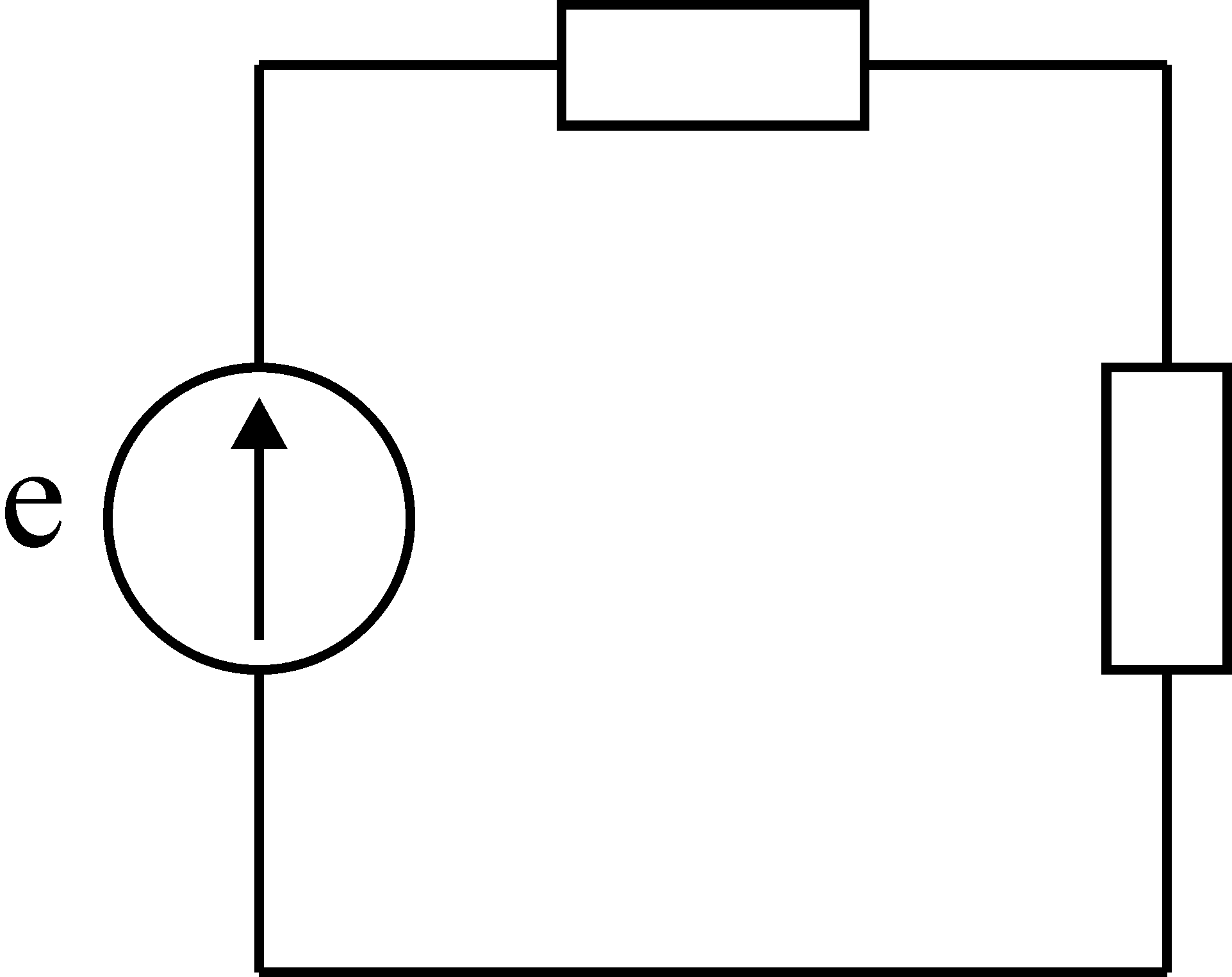
Одноконтурная
замкнутая схема показана на рис. 15.
Одноконтурная
схема является простейшей.
Рис. 15. Одноконтурная
схема.
9. Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.
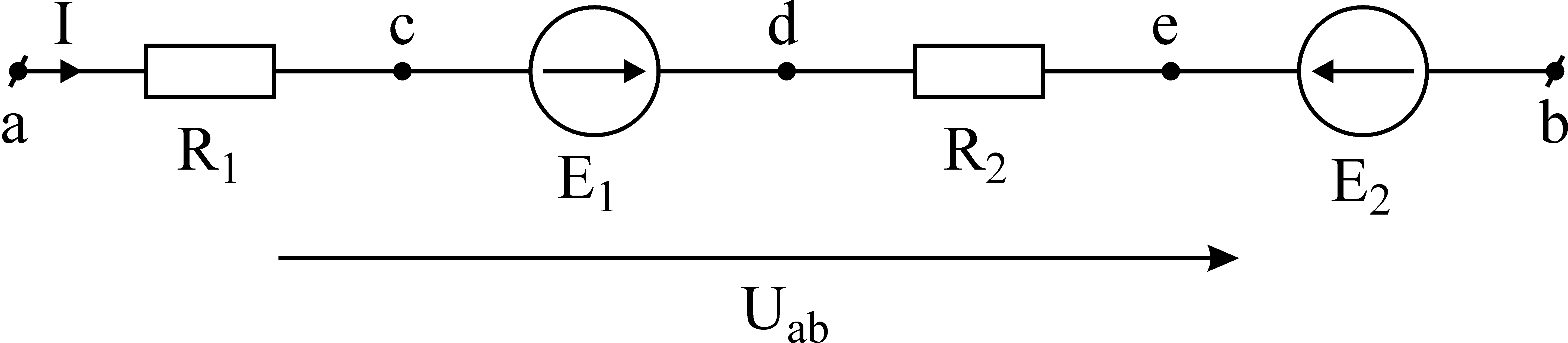
Рассмотрим участок
электрической цепи (рис. 16)
Рис. 16.
Участок ветви,
содержащий один или несколько источников
энергии, является активным.
Положительные
направления тока и напряжения указаны
стрелкой.
Определим потенциалы
точек c,
d,
e,
b,
предположив, что известен потенциал
точки a-a.
Для правильного
выбора знаков следует
помнить,
что:
-
ток в сопротивлении
всегда направлен от более высокого
потенциала к более низкому, т.е. потенциал
падает по направлению тока. -
э.д.с., направленная
от точки «с» к точке «d»,
повышает потенциал последней на величину
E. -
напряжение U=Uac
положительно, когда потенциал точки а
выше, чем потенциал точки с.
При обозначении
напряжения (разности потенциалов) на
схемах посредством стрелки она ставится
в направлении от точки высшего потенциала
к точке низшего потенциала.
На рис. 16 ток
протекает от точки «а» к точке «с»,
значит потенциал с
будет меньше a
на величину
падения напряжения на сопротивлении
R1,
которое по закону Ома равно IR1:
с = a
— IR1
На участке cd
э.д.с. E1
действует в сторону повышения потенциала,
следовательно:
d =
с
+ E1
= a
—
IR1+
E1
Потенциал точки
«e»
меньше потенциала точки «d»
на величину падения напряжения на
сопротивлении R2:
e
=
d
–
IR2
= a
—
IR1+
E1–
IR2
На участке e
в э.д.с. E2
действует
таким образом, что потенциал точки «b»
меньше потенциала точки «e»
на величину E2:
b =
e
–
E2
= a
—
IR1+
E1–
IR2
–
E2
= a
– I(R1+R2)
+ E1-E2
(15)
Чтобы наглядно
оценить распределение потенциала вдоль
участка цепи, полезно построить
потенциальную диаграмму, которая
представляет график изменения потенциала
вдоль участка цепи или замкнутого
контура.
По оси абсцисс
графика откладываются потенциалы точек,
а по оси ординат – сопротивления
отдельных участков цепи. Для участка
цепи рис. 16 распределение потенциала
построено на рис. 17.
Рис. 16. Потенциальная
диаграмма участка цепи.
Потенциальная
диаграмма рис. 16 построена, начиная с
точки a,
которая условно принята за начало
отсчета. Потенциал a
принят
равным нулю.
Точка цепи, потенциал
которой условно принимается равным
нулю, называется базисной.
Если в условии
задачи не оговорено, какая точка является
базисной, то можно потенциал любой точки
условно приравнивать к нулю. Тогда
потенциалы всех остальных точек будут
определяться относительно выбранного
базиса.
Соседние файлы в папке Конспект 2
- #
- #
- #
- #
- #
- #
- #
Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Электрические цепи
Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
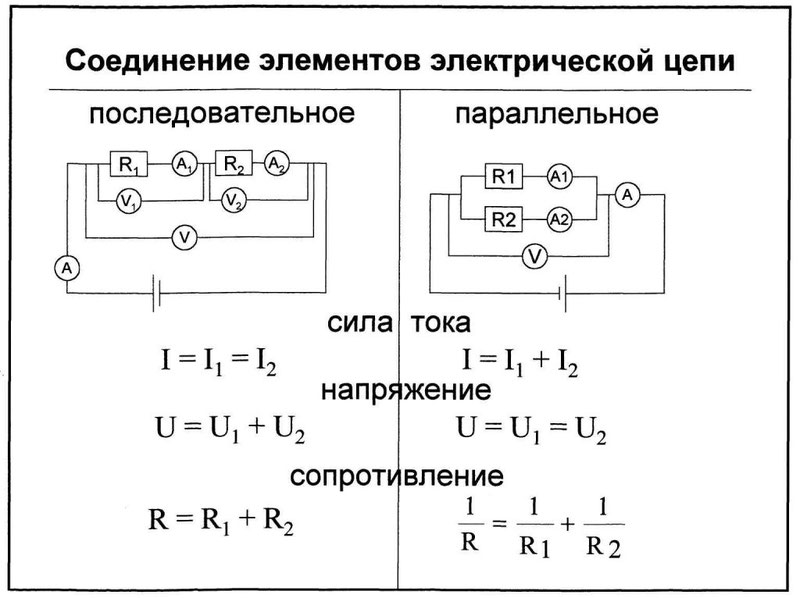
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Классификация электрических цепей
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
Расчет электрических цепей
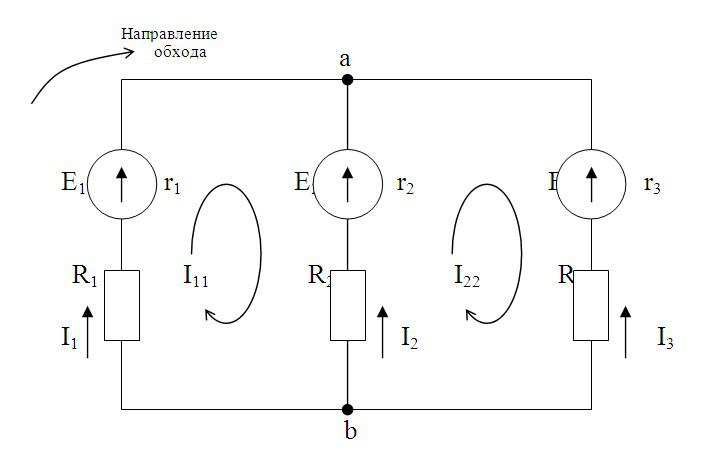
Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов
Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!
Содержание:
Метод узловых напряжений:
Метод узловых напряжений (узловых потенциалов) является наиболее общим. Он базируется на первом законе Кирхгофа (ЗТК) и законе Ома. В отличие от методов, рассмотренных в лекции 4, метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной количеству рёбер (ветвей) дерева (2.1)
Идея метода состоит в следующем:
- Выбирается базисный узел — один из узлов цепи, относительно которого рассчитываются напряжения во всех узлах; базисный узел помечается цифрой 0.
- Потенциал базисного узла принимается равным нулю.
- Рассчитываются напряжения во всех узлах относительно базисного.
- По закону Ома находятся токи и напряжения в соответствующих ветвях.
Напряжения в узлах цепи, отсчитанные относительно базисного, называют узловыми напряжениями.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений.
В дальнейшем будем полагать, что цепь имеет
Предварительно покажем, что при известных узловых напряжениях можно найти напряжения на всех элементах цепи, а потому и все токи. Действительно, напряжение на любой ветви определяется по второму закону Кирхгофа (ЗНК) как разность соответствующих узловых напряжений, а токи в элементах найдутся по закону Ома. Для контура, включающего элементы 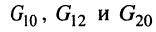
откуда
Аналогично можно записать
что и требовалось показать.
Составление узловых уравнений
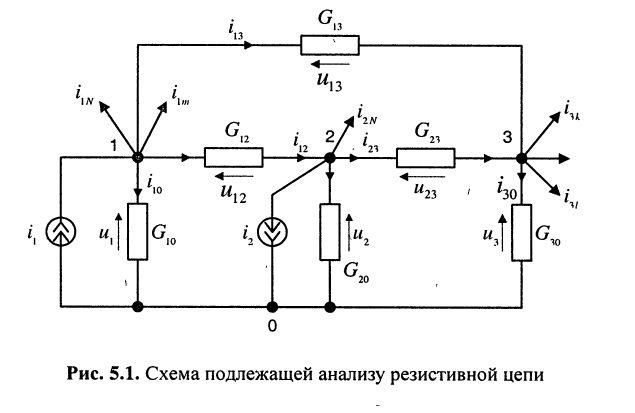
При составлении уравнений для, схемы рис. 5.1 будем полагать, что задающие токи 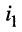
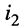
Тогда согласно первому закону Кирхгофа для узлов 1 и 2 в предположении, что в общем случае они связаны со всеми другими узлами, получим:
Выразим токи в уравнениях через узловые напряжения, как показано в разд. 5.1:
Раскрыв скобки и приведя подобные члены, получаем узловые уравнения:
Полученный результат позволяет сделать следующие выводы:

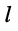
Аналогично записываются узловые уравнения для всех других узлов цепи, в результате чего образуется система узловых уравнений вида:
где:
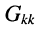


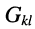

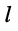

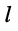
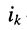



Систему узловых уравнений принято записывать в канонической форме, а именно:
- токи, как свободные члены, записываются в правых частях уравнений;
- неизвестные напряжения записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами узлов. Такая запись применена в (5.2).
Система (5.2) является линейной неоднородной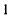
Метод узловых напряжений даёт существенное сокращение необходимого числа уравнений по сравнению с методом токов элементов. Выигрыш оказывается тем значительнее, чем больше независимых контуров имеет цепь.
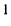
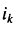
Особенности составления узловых уравнений
Метод узловых напряжений можно применять и в тех случаях, когда в анализируемой цепи имеются источники напряжения. При этом:
- напряжение между любой парой узлов, к которым подключён источник напряжения, известно;
- в качестве базисного желательно выбирать узел, к которому одним из своих зажимов подключён источник напряжения — тогда узловое напряжение, отсчитываемое между базисным узлом и вторым зажимом источника, равно ЭДС источника или отличается от него знаком; кроме того, базисным может быть выбран узел, к которому подключено наибольшее число элементов, если этот выбор не противоречит первой рекомендаций;
- уменьшается число независимых узловых напряжений, а потому понижается и порядок системы, т. е. число входящих в систему независимых уравнений;
- если цепь содержит
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
Пример 5.1.
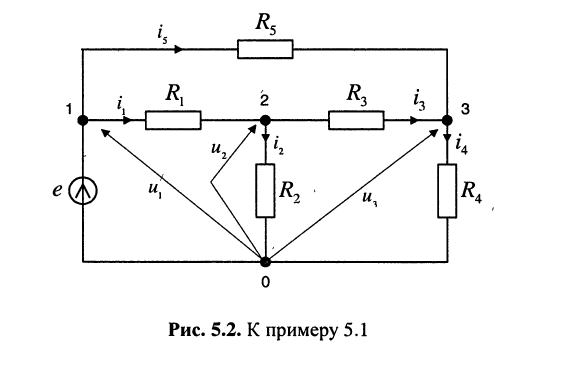
Записать систему узловых уравнений для удлинителя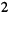
Решение. Удлинитель содержит четыре узла и один источник тока, поэтому согласно (5.3) достаточно составить всего два узловых уравнения
Положим узел 0 базисным, поскольку к нему одним из своих зажимов подключён источник напряжения. Узловое напряжение узла 1 известно и равно. ЭДС источника напряжения 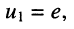
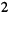
Собственная проводимость второго узла
взаимные проводимости второго узла
собственная проводимость третьего узла
взаимные проводимости третьего узла
Теперь получим систему узловых уравнений, записав узловые уравнения для второго и третьего узлов:
Поскольку 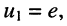
Эта система уравнений и является окончательным результатом решения задачи, поставленной в примере.
Если содержащиеся в цепи источники напряжения не имеют общего зажима, то задачу анализа следует решать или методом узловых напряжений в сочетании с принципом наложения или путём эквивалентных преобразований перейти к другой модели цепи.
При составлении узловых уравнений для цепей, содержащих многополюсники (например, транзисторы, операционные усилители
и т. д), следует прежде всего заменить эти многополюсники их схемами замещения.
Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение межи узлами и называется узловым. UAB R3 узловое напряжение цепи (рис. 4.9) Для различных ветвей (рис. 4.9) узловое напряжение UAB можно опредо лить следующим образом.
1. Поскольку для первой ветви источник работает в режиме генератор:
Величина тока определяется как
где 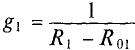
2.Для второй ветви источник работает в режиме потребителя следовательно
Тогда ток
3.Для третьей ветви
(Потенциал точки В для третьей ветви больше, чем потенций точки А, так как ток направлен из точки с большим потенциалом в точку с меньшим потенциалом)
Величину тока 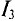
По первому закону Кирхгофа для узловой точки А (или В):
Подставив в уравнение (4.6) значения токов из уравнений (4.3), .4) и (4.5) для рассматриваемой цепи, можно записать
Решив это уравнение относительно узлового напряжения UAB, можно определить его значение
Следовательно, величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:
Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т.е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус». Таким образом, для определения токов в сложной цепи с двумя узлами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5). Узловое напряжение UAB может получиться положительным или отрицательным, как и ток в любой ветви.
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно словно выбранному.
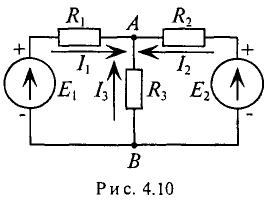
Пример 4.7
В ветвях схемы (рис. 4.10) требуется определить токи, если: 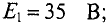
Решение
Узловое напряжение
где
тогда
Токи в ветвях будут соответственно равны
Как видно из полученных результатов, направление токов 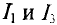
Пример 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 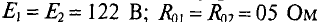
Как изменится ток второго генератора: 1) при увеличении его ЭДС (£2) на 1 %; » 2) при увеличении узлового напряжения (UAB) на 1 %.
Решение
Определяется узловое напряжение UAB цепи (рис. 4.11)
где
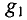
Тогда ток второго генератора
При увеличении Е2 на 1 %, его величина станет равной
тогда
При этом
Следовательно, увеличение ЭДС генератора Е2 на 1 % приводит увеличению тока этого генератора на 24 %.
2. При увеличении узлового напряжения на 1% его величины станет равной
При этом 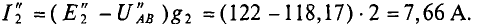
Знак «минус» означает уменьшение, а не увеличение тока 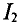
Определение метода узловых напряжений
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах электрической цепи относительно некоторого базисного узла. Эти разности потенциалов называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 7-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла: 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
обозначим узловые напряжения точек 1 и 2 через 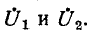
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно: для узла 1
для узла 2
Величина 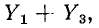
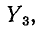
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае если электрическая схема содержит q узлов, то на основании первого закона Кирхгофа получается система из q — 1 уравнений (узел q принят за базисный):
Здесь ток источника тока, подходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус;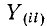
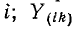
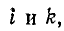
Решив систему уравнений (7-5) при помощи определителей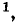
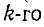
где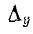
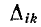
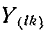
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс 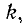
Уравнения (7-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников э. д. с. последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д, с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
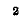
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если заданная электрическая схема имеет q узлов и р ветвей, то в соответствии со сказанным выше, метод узловых напряжений представляет преимущество при q — 1 < р — q + 1. или, что то же, при 2 (q — 1) < р.
Здесь имеется в виду общий случай, когда число уравнений не сокращается за счет известных контурных токов
или узловых напряжении.
Пример 7-3.
Пользуясь методом узловых напряжений определить ток в диагонали мостовой схемы (см. рис. 7-6).
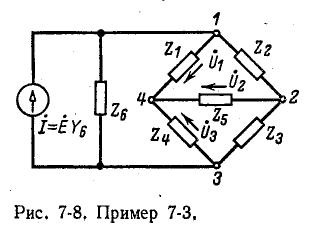
В результате замены заданного источника э. д. с. .эквивалентным источником тока получается схема (рис. 7-8), содержащая четыре узла. Для этой схемы по первому закону Кирхгофа записывают 4—1 = 3 уравнения (по числу независимых узлов). Если выбрать в данной схеме в качестве базиса узел 4 и направить узловые напряжения к базису, то уравнения примут вид:
для узла 1
для узла 2
для узла 3
Решение полученной системы уравнений относительно 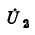
где
Умножив найденное узловое напряжение 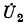
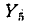
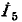
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
- Методы анализа сложных электрических цепей

























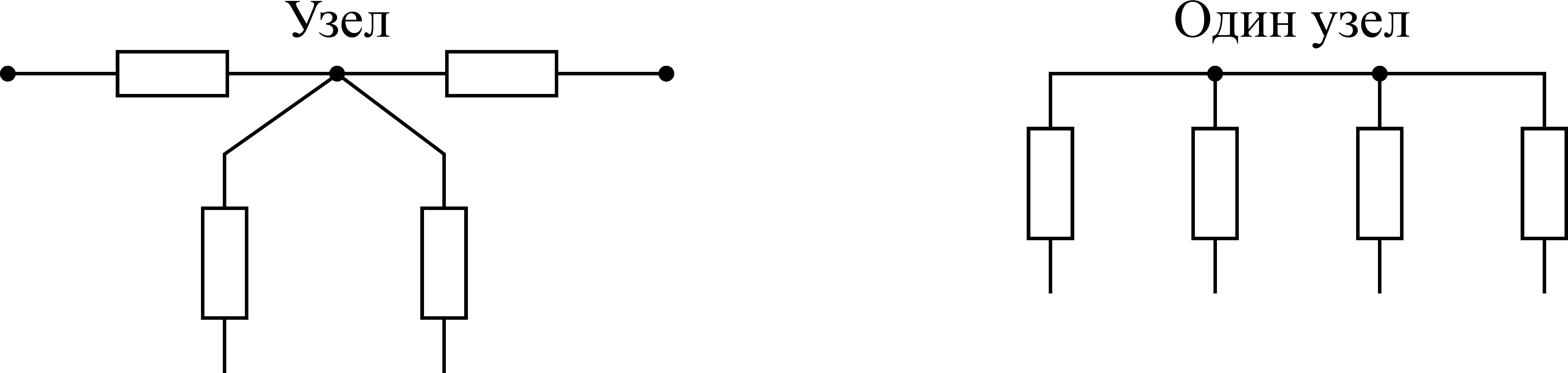


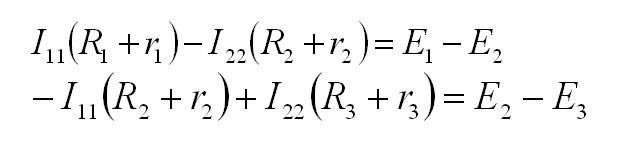
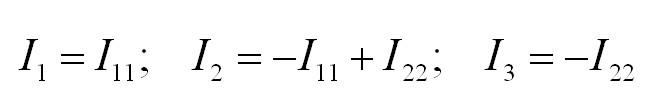
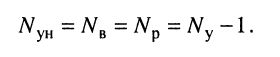
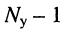
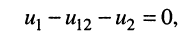
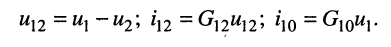
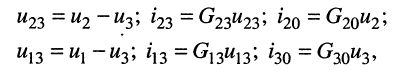
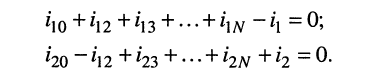
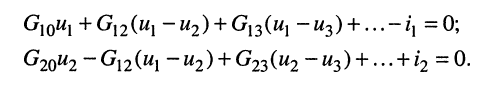
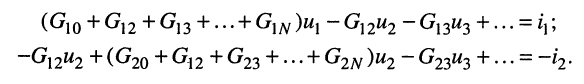
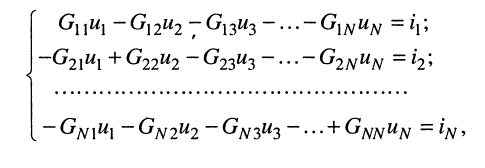
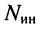 источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно