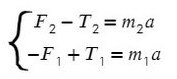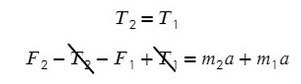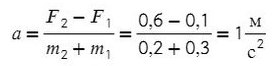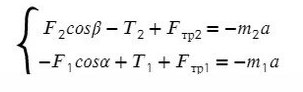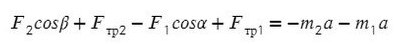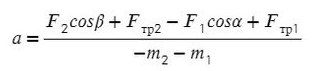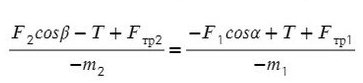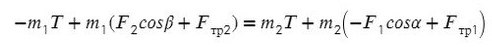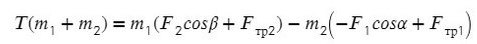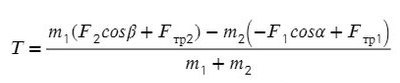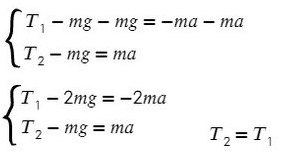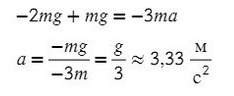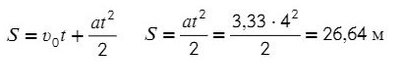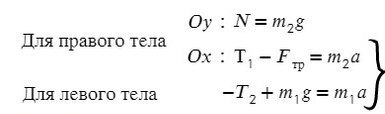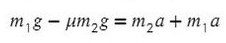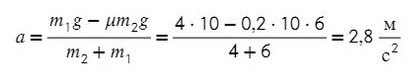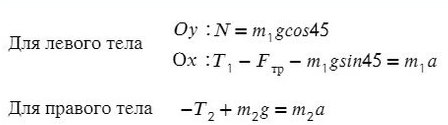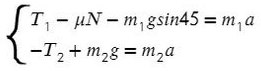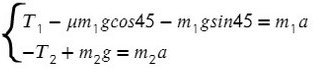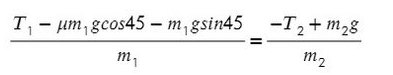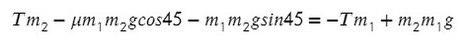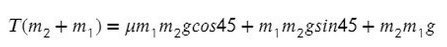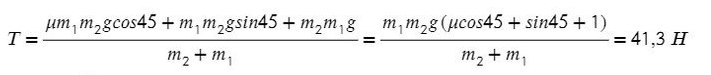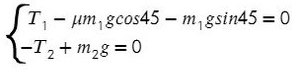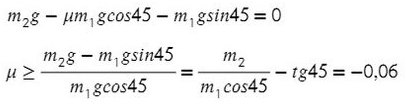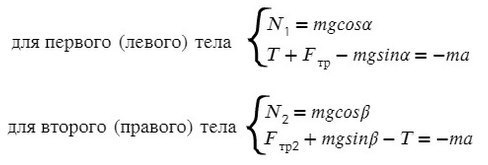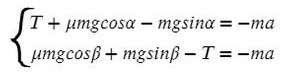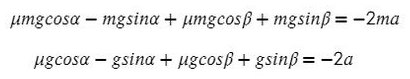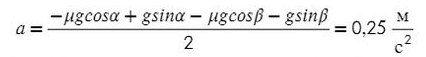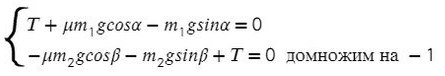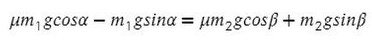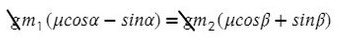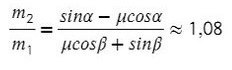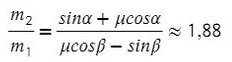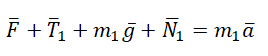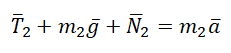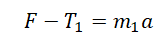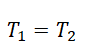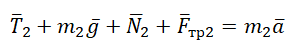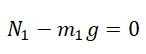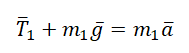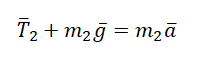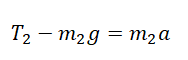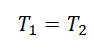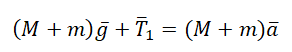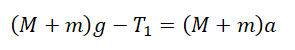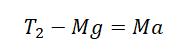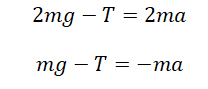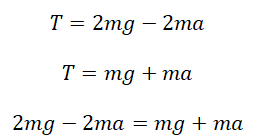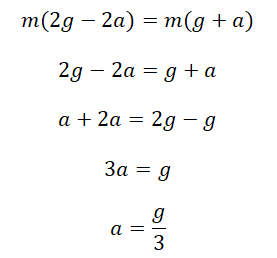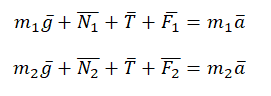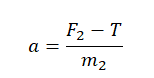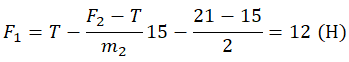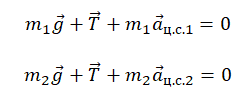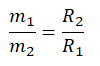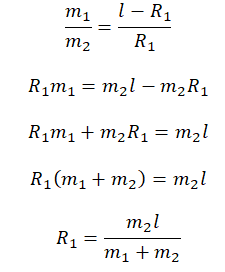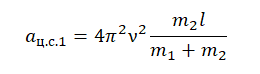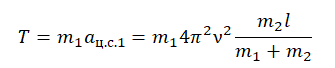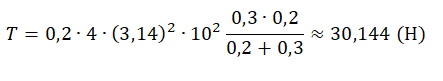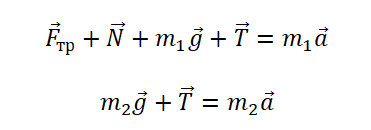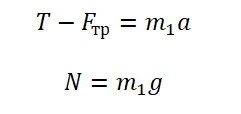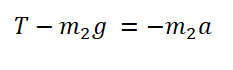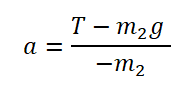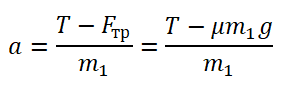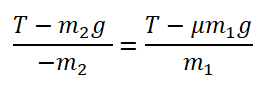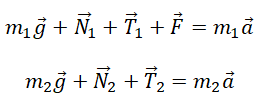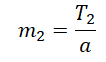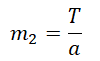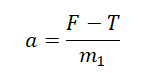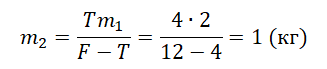Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
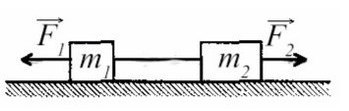
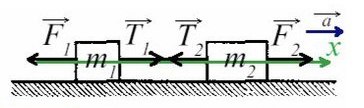
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.
Выразим ускорение:
Ответ: 1 м/с²
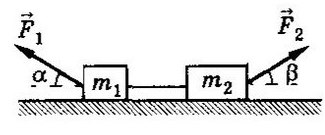
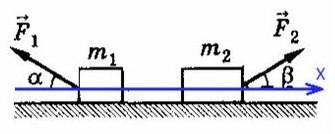
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим уравнения и выразим ускорение:
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
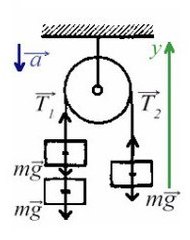
Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
Вычтем из первого уравнения второе:
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
Ответ: 26,64 м
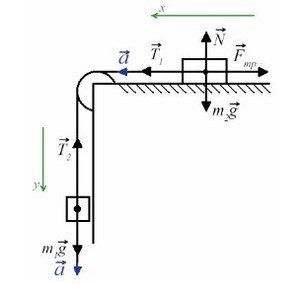
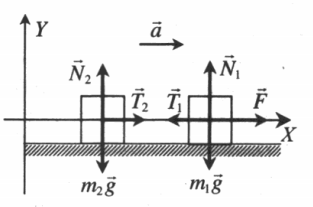
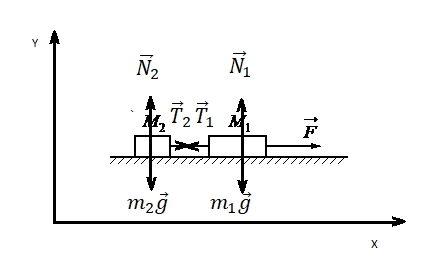
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
Сложим два нижних уравнения для того, чтобы T сократилось:
Выразим ускорение:
Ответ: 2,8 м/с²
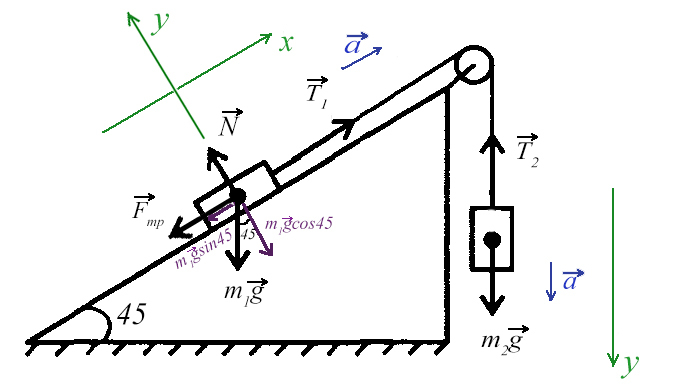
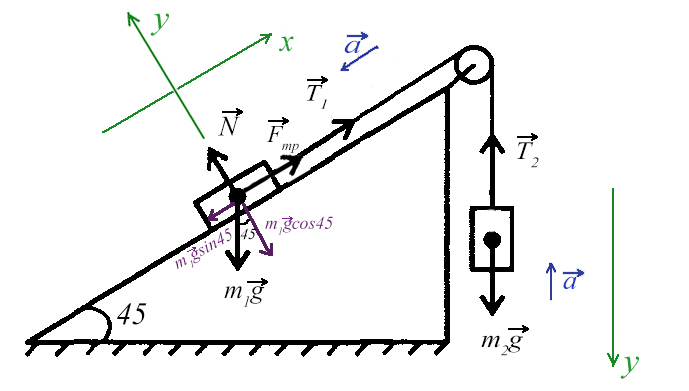
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Ответ: 0,06
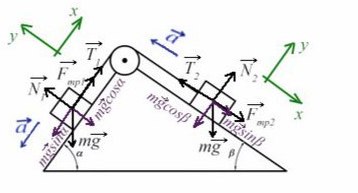
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
Сложим уравнения и сократим на массу:
Выразим ускорение:
Подставив в любое уравнение найденное ускорение, найдем Т:
А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:
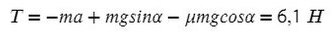
Сложим уравнения
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
Получили, что отношение масс должно быть таким:
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Ответ: от 1,08 до 1,88
Задачи для закрепления.
Система связанных тел.
Будь в курсе новых статеек, видео и легкого технического юмора.
Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
Движение тел по горизонтали без трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
Движение по горизонтали с учетом сил трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
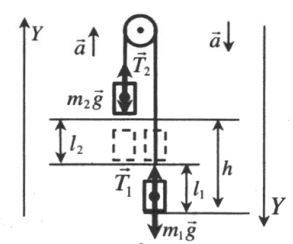
Вертикальное движение тел (m1 > m2)
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
Решение
Расстояние между телами определяется формулой: h = l1 + l2 = 2l.
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОY для 1 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
На один из грузов положили довесок
Решение
II закон Ньютона для 1 тела:
II закон Ньютона для 2 тела:
Проекция на ось ОУ для 1 тела:
Проекция на ось ОУ для 2 тела:
III закон Ньютона:
Вес довеска определяется по формуле:
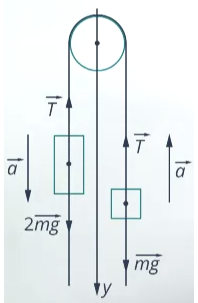
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
Строим чертеж:
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
Сделаем несколько преобразований:
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
Задание EF17717
Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F1 и F2, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, которые действуют на 1 и 2 тело. Выбрать систему координат.
3.Записать для каждого тела второй закон Ньютона в векторной форме.
4.Записать для каждого тела второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Выразить формулу для вычисления силы, действующей на первое тело.
6.Подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные:
• Масса тела 1: m1 = 1 кг.
• Масса тела 2: m2 = 1 кг.
• Сила натяжения нити: Т = 15 Н.
• Сила, действующая на второе тело, равна: F2 = 21 Н.
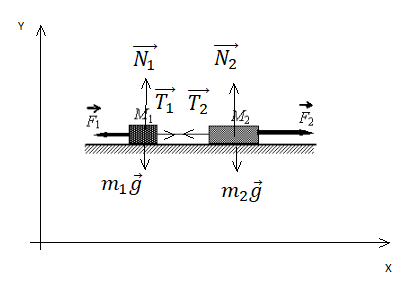
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
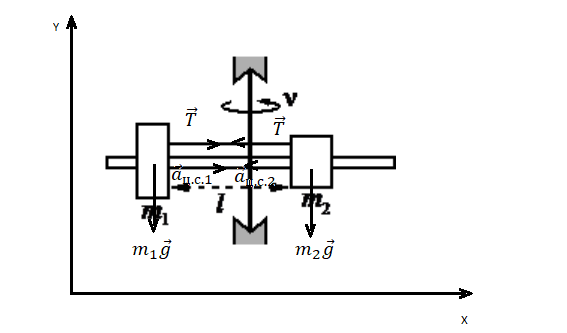
Задание EF18920
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
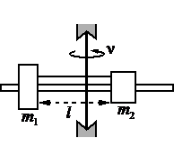
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
Запишем второй закон Ньютона для первого и второго груза соответственно:
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
Подставим радиус второй окружности и выразим радиус первой окружности:
Следовательно, центростремительное ускорение первого груза равно:
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
Подставим известные данные и вычислим силу натяжения нити:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17647
По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
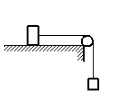
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
• Записать исходные данные.
• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.
• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.
• Записать второй закон Ньютона для обоих тел в виде проекций на оси.
• Вывести формулу для вычисления искомой величины.
• Подставить известные данные и вычислить искомую величину.
Решение
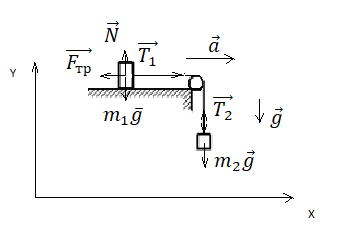
Запишем исходные данные:
• Масса первого тела (движущегося по плоскости) равна: m1 = 0,9 кг.
• Масса второго тела (подвешенного к нити) равна: m2 = 0,3 кг.
• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
Запишем проекцию на ось ОУ для груза на нити:
Выразим из этого выражения ускорение и получим:
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
Приравняем правые части уравнений и получим:
Произведем вычисления:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22698
Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?
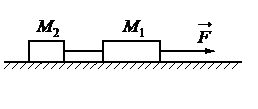
Алгоритм решения
1.Записать исходные данные.
2.Выполнить чертеж, указав все силы, действующие на каждый из грузов.
3.Записать второй закон Ньютона для обоих тел.
4.Записать второй закон Ньютона в проекциях на ось ОХ.
5.Применить третий закон Ньютона.
6.Выразить массу второго груза (найти общее решение).
Решение
Запишем исходные данные:
• Масса первого груза равна: m1 = 2 кг.
• Сила натяжения нити равна: T = 4 Н.
• Модуль силы, которая действует на систему тел: F = 12 Н.
Выполним чертеж:
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
Из первого выражения выразим ускорение и подставим его во второе:
Подставим в формулу и получим:
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5k
Решение задач о движении связанных тел
План урока
- Сила натяжения нити
- Примеры решения задач
Цели урока
- Знать алгоритм решения задач о движении связанных тел
- Уметь применять второй и третий законы Ньютона для решения задач на движение связанных тел
Разминка
- Сформулируйте третий закон Ньютона.
- В каких случаях возникает сила упругости?
- Куда направлена сила упругости?
Сила натяжения нити
Решение задач о движении связанных тел осуществляется по уже изученному нами алгоритму.
В данном блоке задач особое внимание следует уделить силам упругости, возникающим в нити при движении связанных тел. Вспомним, что сила упругости, возникающая в нерастяжимой нити, называется сила натяжения нити и обозначается T→.
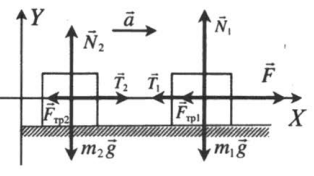
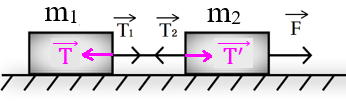
Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рассмотрим, какие силы возникают в системе из двух брусков, связанных невесомой нитью, если на один из них подействовать с некоторой силой F (рис. 1).
В результате действия силы F брусок 2 приходит в движение, нить, связывающая бруски, начинает действовать на брусок 1 с силой T→1. По третьему закону Ньютона брусок действует на нить с силой T→ такой, что T→=-T→1.
Аналогичные рассуждения применимы ко второму бруску: нить действует на него с силой T→2, брусок действует на нить с силой T’→ такой, что T→’=-T→2.
Таким образом, силы T→ и T’→ действуют на нить, а силы T→1 и T→2 – на связанные бруски.
Если натянутая нить невесома, силы упругости, возникающие в различных частях нити, равны по модулю:
T→=T→’.
Так как T→=-T→1 и T→’=-T→2, справедливо будет записать следующее равенство:
T→=T→1=T→’=T→2.
При решении задач может быть нецелесообразно рисовать силы T→ и T’→, возникающие в нити, за исключением случая, когда нить обладает массой и данные силы не равны друг другу (решение подобной задачи рассмотрено в примере 3).
Примеры решения задач
Пример 1
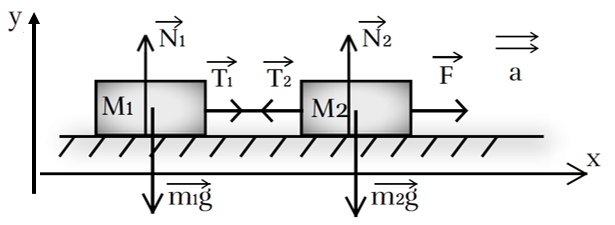
Два бруска массами m1 = 2 кг и m2 = 6 кг связаны легкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 10 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков. Поверхность и бруски считать гладкими.
Решение
1. После того, как на второй брусок начинает действовать сила F, система начинает двигаться поступательно, поэтому оба тела можно принять за материальные точки.
Рис. 2. Иллюстрация к примеру 1
2. В качестве тела отсчета выберем неподвижную плоскость, по которой движутся бруски. Пусть ось ОХ направлена в сторону движения брусков: так как сила F направлена вправо, система будет двигаться в направлении данной силы (рис. 2). Ось OY направлена перпендикулярно оси ОХ.
Изобразим силы, действующие на бруски. Силы упругости, возникающие в нити, изображать не обязательно, так как в данном случае мы не будем применять второй закон Ньютона к нити, связывающей тела.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго бруска:
m1·g→+T→1+N→1=m1·a→;
F→+m2·g→+T→2+N→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси:
OY: N1-m1·g=0;
OX: T1=m1·a;
OY: N2-m2·g=0;
OX: F-T2=m2·a;
5. Как мы уже знаем, при движении связанных невесомой нитью тел силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
T1=T2=T.
6. Обратим внимание, что для решения поставленной задачи достаточно решить систему из уравнений на ось OX.
Решаем полученную систему относительно неизвестного ускорения методом сложения:
T=m1·aF-T=m2·a
Тогда
a=Fm1+m2=102+6=1,25 м/с2.
Ответ: a=1,25 м/с2.
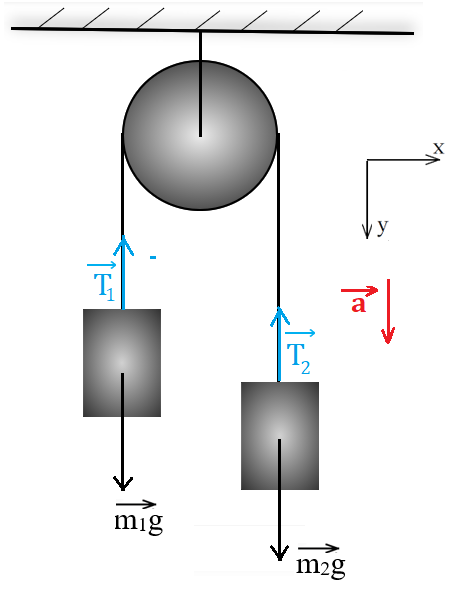
Пример 2
Через неподвижный невесомый блок перекинута легкая нерастяжимая нить. К концам нити прикрепляют грузы массами
m1 = 5 кг и m2 = 10 кг, затем их одновременно отпускают. Найти ускорение системы грузов.
Решение
Рис. 3. Иллюстрация к примеру 2
1. После того, как грузы отпускают, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
2. В качестве тела отсчета выберем неподвижную плоскость, к которой прикреплен блок. Пусть ось ОY направлена в сторону движения брусков: так как брусок массой m2 тяжелее, система будет двигаться в направлении силы m2·g→ (рис. 3).
Ось OХ направлена перпендикулярно оси ОY.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
m1·g→+T→1=m1·a→;
m2·g→+T→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтем, что в выбранной системе отсчета проекции ускорения и сил на ось абсцисс равны нулю, поэтому проекции на данную ось можно не рассматривать.
Так как первое тело движется вверх, проекция ускорения данного тела на ось ординат будет отрицательна.
OY: m1·g-T1=-m1·a;
OY: m2·g-T2=m2·a.
5. Как мы уже знаем, при движении тел, связанных невесомой нитью, силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
T1=T2=T.
6. Решаем полученную систему относительно неизвестного ускорения методом сложения:
m1·g-T=-m1·am2·g-T=m2·a
Тогда
a=m1·g-m2·g-m1-m2=5·10-10·10-5-10≈3,3 м/с2.
Ответ: a=3,3 м/с2.
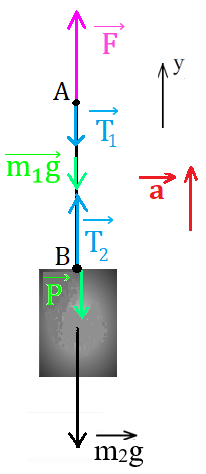
Пример 3
К одному концу нерастяжимой веревки массой 0,5 кг привязывают груз массой 2 кг. Веревку вместе с грузом поднимают вертикально вверх, прикладывая силу, равную 50 Н. Найти ускорение системы, а также модули сил упругости, действующие на противоположные концы веревки.
Решение
1. Веревка по условию задачи нерастяжима, примем, что груз и веревка движутся поступательно, поэтому оба тела можно принять за материальные точки.
Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчета выберем поверхность Земли. Ось ОY направим в сторону движения системы – в направлении действия силы F→ (рис. 4). Обозначим массу груза m2, массу веревки m1.
К верхнему концу веревки, к точке А, по условию приложена сила F→, в этой точке возникает сила упругости T→1, действующая на источник силы F→ (например, на руку человека, который тянет веревку).
В месте крепления груза, в точке В, на веревку действует вес груза P→, в результате в этой точке возникает сила упругости T→2, действующая на груз.
3. Запишем второй закон Ньютона в векторной форме для веревки и для груза:
F→+m1·g→+P→=m1·a→;
m2·g→+T→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на ось ординат:
OY: F-m1·g-P=m1·a;
OY: T2-m2·g=m2·a.
5. По третьему закону Ньютона силы T→2 и P→ равны по модулю и противоположны по направлению:
P=T2.
6. Решаем полученную систему с учетом соотношения:
F-m1·g-T2=m1·aT2-m2·g=m2·a
Тогда
a=F-g·m1+m2m1+m2=50-10·(0,5+2)0,5+2=10 м/с2.
Найдем Т2:
T2=m2·g+m2·a=40 Н.
Наконец, найдем значение силы Т1: согласно третьему закону Ньютона, данная сила будет равна по модулю и противоположна по направлению силе, с которой веревку тянут вверх:
T1=F=50 Н.
Ответ: a=10 м/с2; T1=50 Н; T2=40 Н.
Упражнение 1
1. Два бруска массами m1 = 1 кг и m2 = 3 кг связаны легкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 20 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков, если коэффициент трения между поверхностью и брусками равен 0,4.
2. На нерастяжимой невесомой нити, перекинутой через неподвижный блок, подвешены грузы массами 300 и 500 г. Какова сила натяжения нити во время движения?
3. Тепловоз массой 80 т тянет два вагона массой по 20 т каждый с ускорением 0,2 м/с2. Найти силу тяги тепловоза, если коэффициент трения равен 0,005.
Ответы
Упражнение 1
1. а = 1 м/с2.
2. T = 3.75 Н.
3. F = 30 кН.
Динамика движения системы связанных тел
В механике под связанными телами понимают тела, перемещение которых ограничено другими телами.
При решении задач, в которых рассматривается движение системы связанных между собой тел, необходимо записать уравнения движения (второй закон Ньютона) для каждого тела в отдельности. Также записывают уравнения, выражающие кинематические условия, которые связывают ускорения отдельных тел системы. В результате получают систему уравнений, в которой число уравнений равно числу неизвестных величин.
Если тела связаны нитью, массой которой можно пренебречь, силу натяжения нити считают одинаковой по всей ее длине. Если нить перекинута через блок, то равенство сил натяжения со стороны соседних частей нити выполняется только в том случае, когда можно пренебречь массами нити и блока, а также силами трения, которые возникают при вращении блока.
Рассмотрим подробнее основные модели движения систем связанных тел.
Движение по горизонтальной плоскости
Движение в вертикальной плоскости
Движение по наклонной плоскости
| Понравился сайт? Расскажи друзьям! | |
Динамика прямолинейного движения связанных тел
Динамика прямолинейного движения связанных тел
Основная задача динамики прямолинейного движения связанных тел
Основной задачей динамики при рассмотрении движения связанных тел в разных системах отсчета является объяснение причин, которые определяют характер движения. При этом возникает необходимость понять, при каких условиях системы тел движутся по прямой линии, в каком случае их траекторией является кривая, в результате действия каких причин тела движутся равномерно, ускоренно или замедленно.
При изучении поведения систем связанных тел со скоростями много меньшими скорости света используют классические законы Ньютона:
Если тела не взаимодействуют с другими телами или действие других тел скомпенсировано, то скорость системы не изменяется ни по модулю, ни по направлению. Система перемещается равномерно и прямолинейно.
Сила ($overline{F}$), вызывающая ускорение системы тел ($overline{a}$), в инерциальной системе отсчета пропорциональная массе ($m$) тел, умноженной на его ускорение:
[overline{F}=moverline{a}left(1right).]
Силы взаимодействия тел равны по величине, направлены вдоль одной прямой и имеют противоположные направления.
Если не указано иное, то связи, обычно нити, считают нерастяжимыми и невесомыми. В таком случае при рассмотрении движения связанных тел необходимо помнить, что ускорение движения тел в системе одинаково (результат действия связей). Силу натяжения нитей считают равной по всей длине нити.
В некоторых случаях можно выбирать разные системы координат при рассмотрении движения разных тел системы.
Схема решения типовой задачи при движении связанных тел
- Графически изображаем ситуацию, описанную в задаче. Рисуем чертеж, изображаем силы, скорости движения тел, ускорения. Выбираем и изображаем системы отсчета.
- Записываем основной закон динамики поступательного движения (второй закон Ньютона) в векторной форме, необходимые кинематические уравнения движения, другие необходимые законы и формулы, например, основной закон динамики вращательного движения, формулу силы трения и т.д.
- Проектируем векторные уравнения на оси систем координат.
- Решаем уравнения.
- Проводим необходимые вычисления, предварительно убедившись, что все величины записаны в единой системе единиц.
Примеры задач с решением
Пример 1
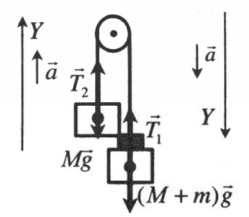
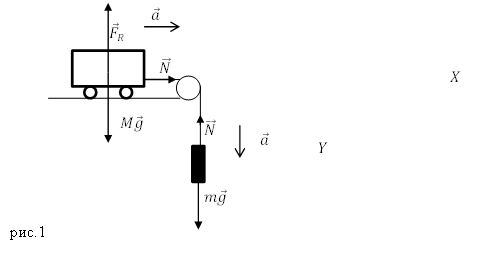
Задание. На горизонтальной поверхности находится тележка, имеющая массу $M$. К ней привязана невесомая, нерастяжимая нить. Нить перекинута через невесомый блок. Ко второму концу нити прикреплен груз массой $m$ (рис.1). С каким ускорением будет двигаться тележка. Силы трения не учитывать.
Решение. Изобразим силы, которые действуют на тележку и груз на рис.1. и ускорения движения тел системы. Помним, что сил трения нет. Отметим, что ускорения связанных тел (тележки и груза) будут одинаковы, кроме этого силы натяжения нити ($overline{N}$), действующие на тележку и на груз равны по величине (блок невесомый), но имеют разные направления (рис.1). Запишем второй закон Ньютона для тележки:
[{overline{F}}_R+Moverline{g}+overline{N}=Moverline{a}left(1.1right).]
Основной закон динамики для груза имеет вид:
[moverline{g}+overline{N}=moverline{a} left(1.2right).]
Систему отсчета свяжем с Землей, запишем проекции уравнения (1.1) на оси координат:
[left{ begin{array}{c}
X:N=Ma \
Y:Mg=F_R end{array}
right.left(1.3right).]
В проекциях на эти же оси координат уравнение (1.2) даст одно скалярное уравнение:
[left{ begin{array}{c}
X:mg-N=ma \
Y:0 end{array}
right.left(1.4right).]
Из первого уравнения системы (1.3) и уравнения (1.4) имеем:
[mg-Ma=ma left(1.5right).]
Выразим из (1.5) искомое ускорение:
[a=frac{m}{M+m}.]
Ответ. $a=frac{m}{M+m}$
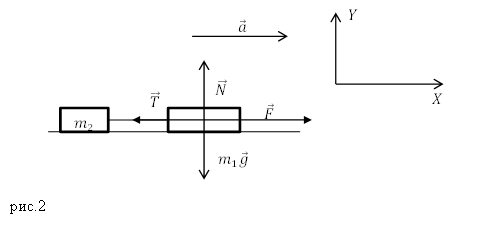
Пример 2
Задание. Два груза массами $m_1 и m_2,$ связанные невесомой нитью, скользят по гладкой поверхности. На груз массы $m_1 $действует с силой F направленной горизонтально (рис.2). Каково ускорение грузов? Какой будет сила натяжения нити, связывающей эти грузы? Силу трения грузов о поверхность не учитывайте. textit{}
Решение. На рис. 2 изобразим силы, действующие на груз массы $m_1$ (рис.2).
В соответствии со вторым законом Ньютона запишем:
[m_1overline{g}+{overline{N}}_1+overline{F}+overline{T}=m_1overline{a}left(2.1right).]
Систему отсчета свяжем с Землей, выберем направления осей координат (рис.2).
Для решения задачи нам потребуется проекция уравнения (2.1) только на ось Y:
[F-T=m_1a left(2.2right).]
В уравнении (2.2) мы имеем две неизвестные величины: сила натяжения нити ($T$) и ускорение тела ($a$). Для нахождения ускорения с которым движется первое тело и вся система из связанных тел, выясним, какие силы действуют на систему, если оба тела считать одним целым. Тогда на систему массой $m_1+m_2$ действует одна сила $overline{F}$. В этом случае второй закон Ньютона принимает вид:
[left(m_1+m_2right)overline{a}=overline{F}+left(m_1+m_2right)overline{g}+overline{N}left(2.3right).]
В проекции на ось Y формулы (2.3) получим:
[left(m_1+m_2right)a=F left(2.4right).]
Из (2.4) ускорение тел равно:
[a=frac{F}{m_1+m_2}left(2.5right).]
Из (2.2) и (2.5) получим силу натяжения нити равной:
[T=Fleft(1-frac{m_1}{m_1+m_2}right). ]
Ответ.$ 1)a=frac{F}{m_1+m_2}.$ 2) $T=Fleft(1-frac{m_1}{m_1+m_2}right)$
Читать дальше: закон всемирного тяготения, сила тяжести.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!