Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.
Что такое P-значение
P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.
Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.
Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.
Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.
Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном
- Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
- Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
- Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.
Статистическая значимость
Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.
Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.
Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.
Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.
Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.
Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.
Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.
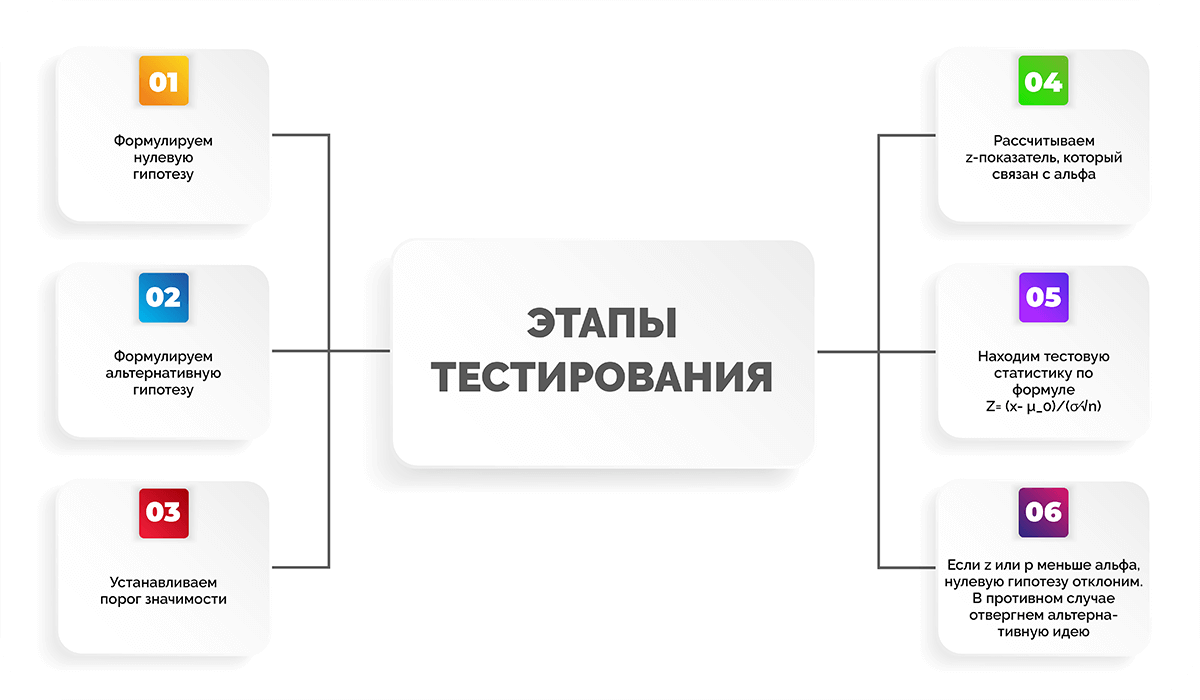
Все тестирование можно разделить на несколько этапов:
- Формулируем нулевую гипотезу.
- Формулируем альтернативную гипотезу.
- Устанавливаем порог значимости.
- Рассчитываем z-показатель, который связан с альфа.
- Находим тестовую статистику по формуле
.
- Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.
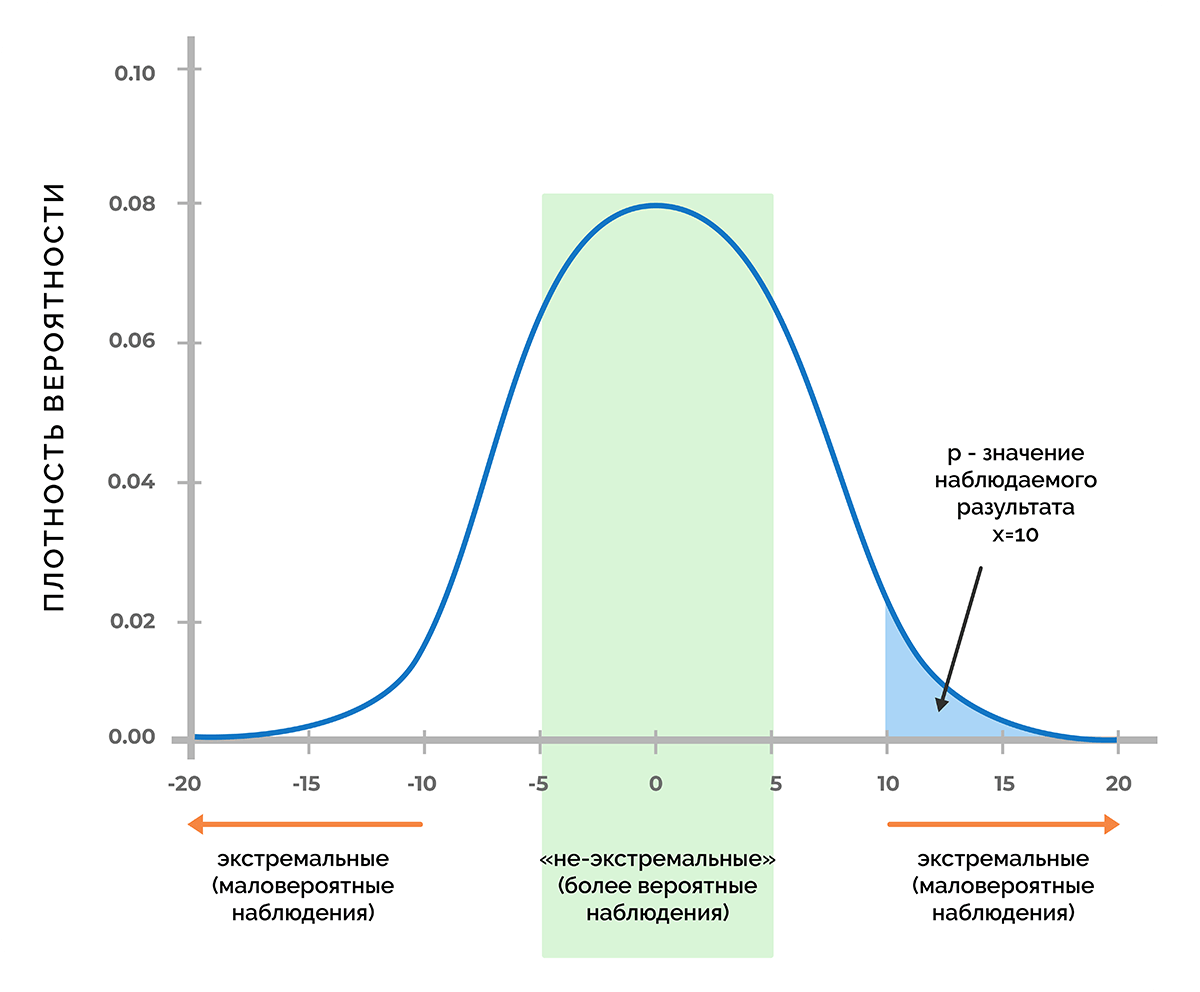
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.
Порог вероятности
В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.
Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.
Доверительные уровни
Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.
Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.
|
Доверительный уровень |
Стандартное отклонение (z-оценка) |
Вероятность (p-уровень) |
|
90% |
< -1,65 или > +1,65 |
< 0,10 |
|
95% |
< -1,96 или > +1,96 |
< 0,05 |
|
99% |
< -2,58 или > +2,58 |
< 0,01 |
Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.
Проверка статистических гипотез
Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).
Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.
Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии
Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.
В статистике применяется рандомизация и нормализация нулевой гипотезы.
Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.
Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.
Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.
Подход p-value к проверке гипотез
Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.
Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.
Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.
Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».
Как рассчитать P-value
Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.
Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.
Как рассчитать p-значение, используя тестовую статистику
Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.
Левосторонний эксперимент:
P-value = cdf (x)
Правосторонний эксперимент:
P-value = 1 – cdf (x)
Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}
Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.
Пошаговый алгоритм расчета p-значения
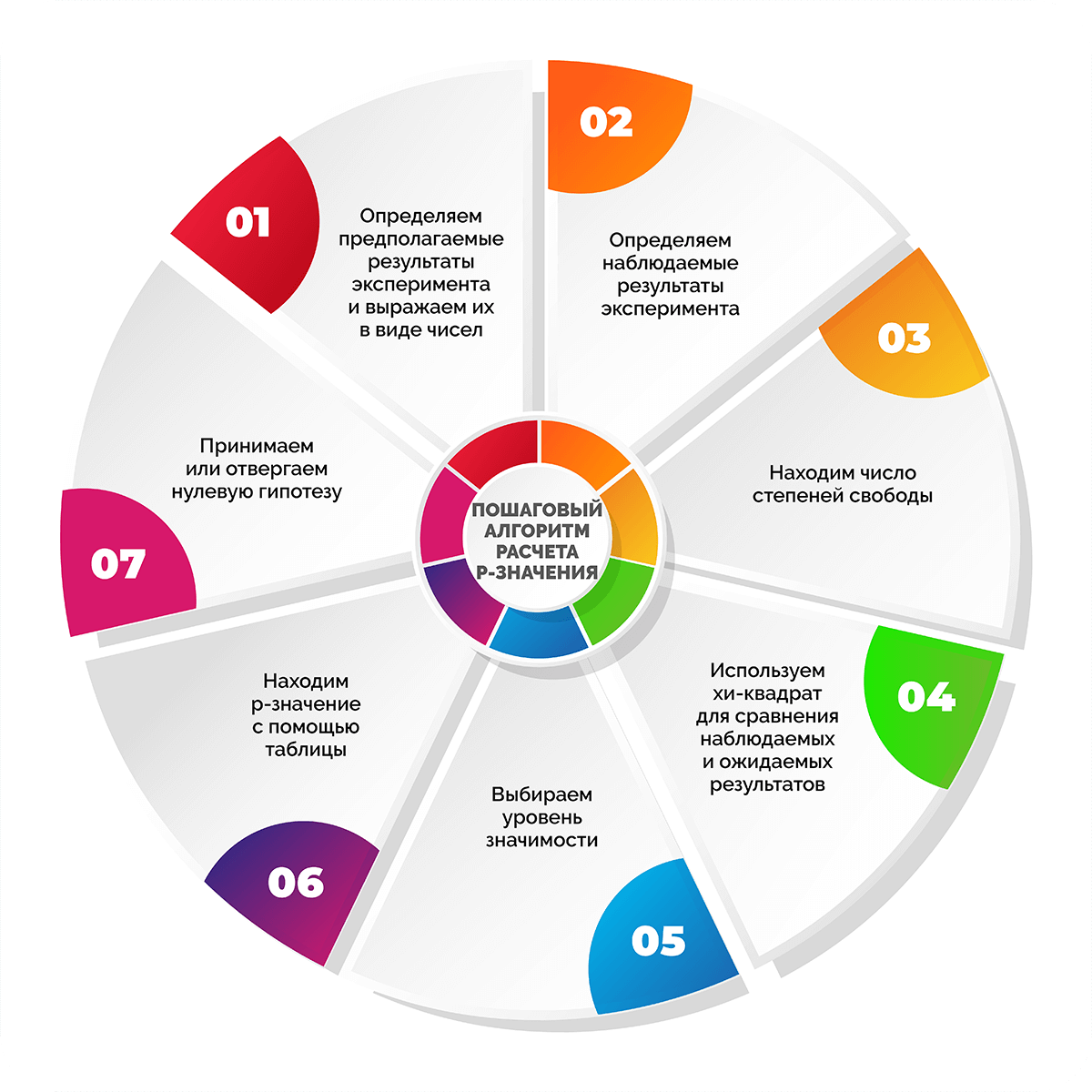
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.
Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.
Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.
Шаг 3. Находим число степеней свободы
Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.
Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.
В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.
Число степеней свободы = 2 – 1 = 1.
Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.
Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов
Хи-квадрат (х2) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.
где:
о – наблюдаемое значение;
е – ожидаемое значение.
Подставляем наши цифры в уравнение и учитываем, что 
х2 = ((220 – 200)2/200) + ((80 – 100)2/100) = ((20)2/200)) + ((-20)2/100) = (400/200) + (400/100) = 2 + 4 = 6.
Шаг 5. Выбираем уровень значимости
Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.
Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.
В нашем случае примем статистическую значимость, равную 0,05.
Шаг 6. Находим p-значение с помощью таблицы
Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.
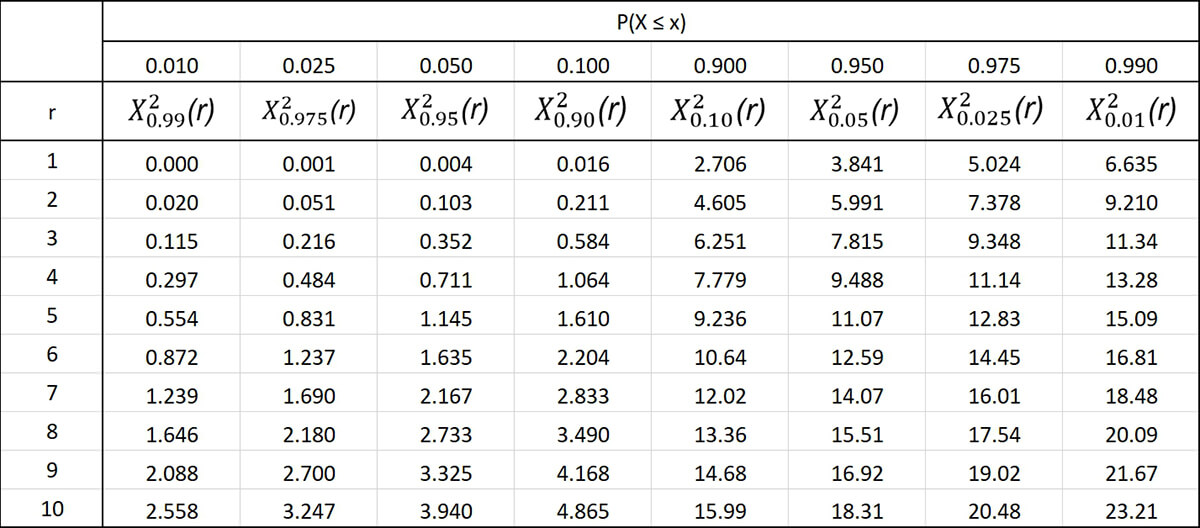
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.
Шаг 7. Принимаем или отвергаем нулевую гипотезу
Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.
В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.
Как интерпретировать P-значение
P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.
P-значение – это…
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
Что нужно помнить о P-значениях
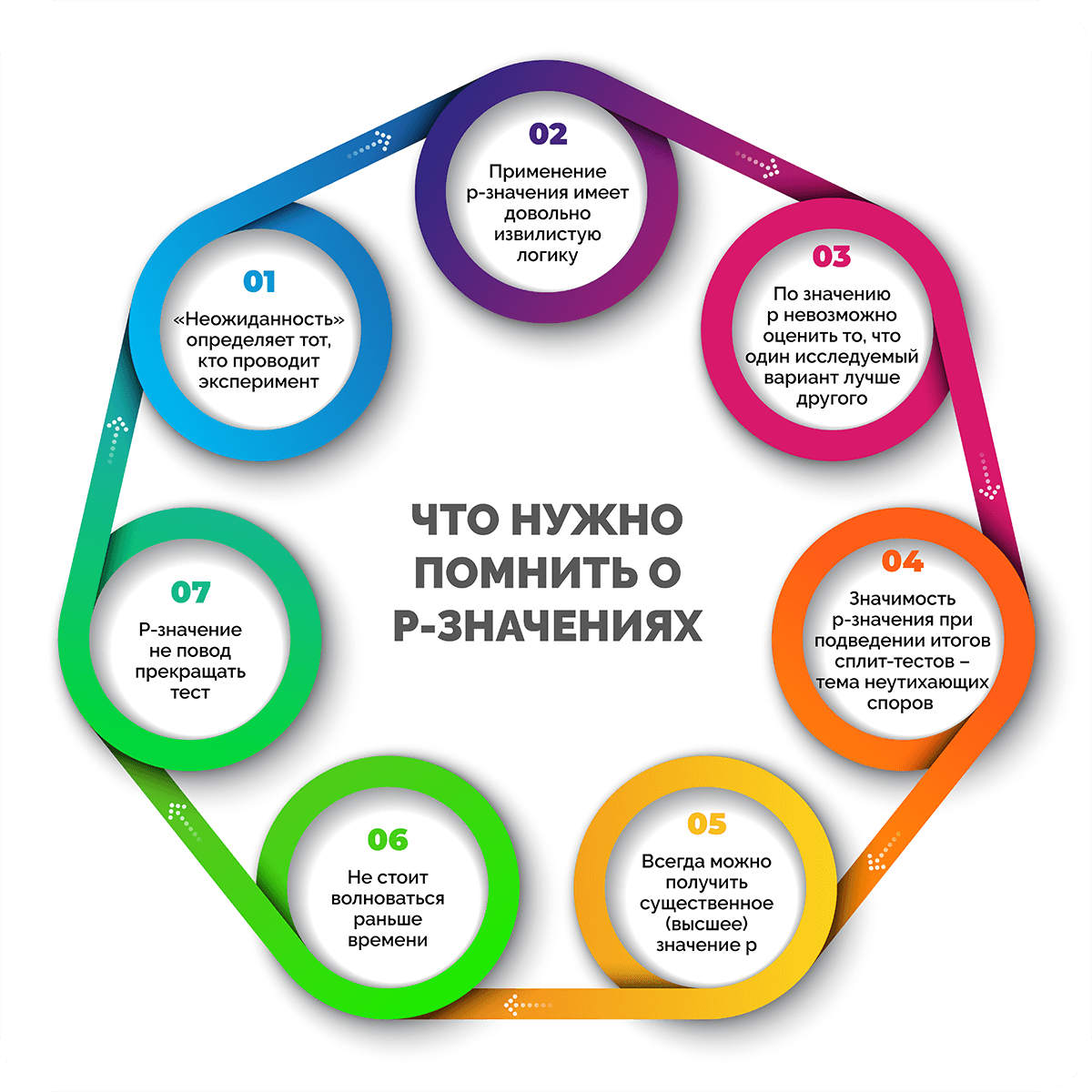
- «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
- Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
- По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
- Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
- Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
- Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
- P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.
Примеры интерпретации P-значений
На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.
По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.
Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.
Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.
Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.
Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.
Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.
Часто задаваемые вопросы
P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.
Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.
Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.
Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:
- При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
- Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.
Заключение
Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид:
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Стандартная методика проверки статистических гипотез
- 2 Вычисление пи-величины
- 3 Вычисление ROC-кривой
- 4 Литература
- 5 См. также
- 6 Ссылки
Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.
Другая интерпретация:
уровень значимости — это такое (достаточно малое) значение вероятности события, при котором событие уже можно считать неслучайным.
Уровень значимости обычно обозначают греческой буквой (альфа).
Стандартная методика проверки статистических гипотез
В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка
.
Чрезмерное уменьшение уровня значимости (вероятности ошибки первого рода) может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна (это называется ложноотрицательным решением, false negative).
Вероятность ошибки второго рода связана с мощностью критерия
простым соотношением
.
Выбор уровня значимости требует компромисса между значимостью и мощностью или
(что то же самое, но другими словами)
между вероятностями ошибок первого и второго рода.
Обычно рекомендуется выбирать уровень значимости из априорных соображений.
Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться,
и выбор часто сводится к назначению одного из популярных вариантов
.
В докомпьютерную эпоху эта стандартизация позволяла сократить объём справочных статистических таблиц.
Теперь нет никаких специальных причин для выбора именно этих значений.
Существует две альтернативные методики, не требующие априорного назначения .
Вычисление пи-величины
Достигаемый уровень значимости или пи-величина (p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия .
где
— критическая область критерия.
Другая интерпретация:
достигаемый уровень значимости или пи-величина — это вероятность, с которой (при условии истинности нулевой гипотезы) могла бы реализоваться наблюдаемая выборка, или любая другая выборка с ещё менее вероятным значением статистики
.
Случайная величина имеет равномерное распределение.
Фактически, функция приводит значение статистики критерия
к шкале вероятности.
Маловероятным значениям (хвостам распределения) статистики соотвествуют значения
, близкие к нулю или к единице.
Вычислив значение на заданной выборке
,
статистик имеет возможность решить,
является ли это значение достаточно малым, чтобы отвергнуть нулевую гипотезу.
Данная методика является более гибкой, чем стандартная.
В частности, она допускает «нестандартное решение» — продолжить наблюдения, увеличивая объём выборки, если оценка вероятности ошибки первого рода попадает в зону неуверенности, скажем, в отрезок .
Вычисление ROC-кривой
ROC-кривая (receiver operating characteristic) — это зависимость мощности от уровня значимости
.
Методика предполагает, что статистик укажет подходящую точку на ROC-кривой, которая соответствует компромиссу между вероятностями ошибок I и II рода.
Литература
- Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006.
- Цейтлин Н. А. Из опыта аналитического статистика. — М.: Солар, 2006. — 905 с.
- Алимов Ю. И. Альтернатива методу математической статистики. — М.: Знание, 1980.
См. также
- Проверка статистических гипотез — о стандартной методике проверки статистических гипотез.
- Достигаемый уровень значимости, синонимы: пи-величина, p-Value.
Ссылки
- P-value — статья в англоязычной Википедии.
- ROC curve — статья в англоязычной Википедии.
Два термина, которые студенты часто путают в статистике, — это p-значение и альфа .
Оба термина используются в тестах гипотез , которые представляют собой формальные статистические тесты, которые мы используем, чтобы отвергнуть или не отвергнуть какую-либо гипотезу.
Например, предположим, что мы выдвигаем гипотезу о том, что новая таблетка снижает кровяное давление у пациентов в большей степени, чем текущая стандартная таблетка.
Чтобы проверить это, мы можем провести проверку гипотезы, в которой мы определяем следующие нулевые и альтернативные гипотезы:
Нулевая гипотеза: нет никакой разницы между новой и стандартной таблетками.
Альтернативная гипотеза: есть разница между новой таблеткой и стандартной таблеткой.
Если мы предполагаем, что нулевая гипотеза верна, p-значение теста говорит нам о вероятности получения эффекта, по крайней мере, такого же большого, как тот, который мы фактически наблюдали в выборочных данных.
Например, предположим, что мы обнаружили, что p-значение проверки гипотезы равно 0,02.
Вот как интерпретировать это p-значение: если бы действительно не было разницы между новой и стандартной таблетками, то в 2% случаев, когда мы проводим эту проверку гипотезы, мы получили бы эффект, наблюдаемый в данных выборки, или больше. просто из-за ошибки случайной выборки.
Это говорит нам о том, что получение фактических данных выборки было бы довольно редким, если бы действительно не было разницы между новой и стандартной таблетками.
Таким образом, мы были бы склонны отвергнуть утверждение нулевой гипотезы и сделать вывод, что между новой и стандартной таблетками есть разница.
Но какой порог мы должны использовать, чтобы определить, достаточно ли низко наше p-значение, чтобы отвергнуть нулевую гипотезу?
Здесь на помощь приходит альфа!
Альфа-уровень
Альфа-уровень проверки гипотезы — это порог, который мы используем, чтобы определить, достаточно ли низко наше p-значение, чтобы отклонить нулевую гипотезу. Он часто устанавливается равным 0,05, но иногда устанавливается на уровне 0,01 или 0,10.
Например, если мы установим альфа-уровень проверки гипотезы на 0,05 и получим p-значение 0,02, то мы отклоним нулевую гипотезу, поскольку p-значение меньше альфа-уровня. Таким образом, мы пришли бы к выводу, что у нас достаточно доказательств, чтобы сказать, что альтернативная гипотеза верна.
Важно отметить, что альфа-уровень также определяет вероятность ошибочного отклонения истинной нулевой гипотезы.
Например, предположим, что мы хотим проверить, есть ли разница в среднем снижении артериального давления между новой и текущей таблетками. И предположим, что на самом деле нет никакой разницы между двумя таблетками.
Если мы установим альфа-уровень проверки гипотезы на 0,05, то это означает, что если мы повторим процесс выполнения проверки гипотезы много раз, мы ожидаем ошибочного отклонения нулевой гипотезы примерно в 5% проверок.
Как выбрать альфа-уровень
Как упоминалось ранее, наиболее распространенным выбором альфа-уровня проверки гипотезы является 0,05. Однако в некоторых ситуациях, когда неправильные выводы влекут за собой серьезные последствия, мы можем установить альфа-уровень еще ниже, например, 0,01.
Например, в области медицины исследователи обычно устанавливают альфа-уровень равным 0,01, потому что они хотят быть полностью уверенными в надежности результатов проверки гипотезы.
И наоборот, в таких областях, как маркетинг, может быть более распространено устанавливать альфа-уровень на более высоком уровне, например 0,10, потому что последствиями ошибки являются не жизнь и не смерть.
Стоит отметить, что увеличение альфа-уровня теста увеличивает шансы найти результат теста значимости, но также увеличивает вероятность того, что мы неправильно отвергнем истинную нулевую гипотезу.
Резюме:
Вот что мы узнали из этой статьи:
1. Значение p говорит нам о вероятности получения эффекта, по крайней мере, столь же сильного, как тот, который мы фактически наблюдали в выборке данных.
2. Альфа-уровень — это вероятность ошибочного отклонения истинной нулевой гипотезы.
3. Если p-значение проверки гипотезы меньше альфа-уровня, то мы можем отклонить нулевую гипотезу.
4. Увеличение альфа-уровня теста увеличивает вероятность того, что мы сможем найти значимый результат теста, но также увеличивает вероятность того, что мы ошибочно отклоним истинную нулевую гипотезу.
Дополнительные ресурсы
Введение в проверку гипотез
Как написать нулевую гипотезу (5 примеров)
Как отличить левосторонний тест от правостороннего теста
Определение статистической значимости
Статистическая значимость – это вероятность того, что наблюдение не вызвано ошибкой выборки. Это подразумевает, что наблюдение имеет определенную причину. Следовательно, чтобы считать наблюдение статистически значимым, оно должно пройти тестирование.
Чтобы доказать статистическую значимость, набор данных должен отклонить нулевую гипотезу. Нулевая гипотеза. абсолютная истина и всегда прав. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Читать далее. Чтобы доказать ошибочность нулевой гипотезы, p-значение наблюдения должно быть меньше уровня значимости. p-valueP-valueP-Value, или значение вероятности, является решающим фактором для нулевой гипотезы для вероятности того, что предполагаемый результат окажется истинным, будет принят или отклонен, и принятия альтернативного результата в случае отклонения предполагаемых результатов. . Читать дальше — это вероятность того, что наблюдение вызвано случайными факторами.
Оглавление
- Определение статистической значимости
- Понимание уровней статистической значимости
- Тест статистической значимости (P-значение)
- #1 – Статистическая проверка гипотез
- # 2 — Статистически значимое значение p
- Расчет статистической значимости
- Статистическая и практическая значимость
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Статистическая значимость показывает, что наблюдение вызвано конкретной причиной, а не случайным фактором.
- Уровень значимости представлен α. Исследователь устанавливает его значения и обычно составляет 0,01, 0,05 или 0,1.
- Нулевая гипотеза предполагает, что исследование ложно. Однако альтернативная гипотеза, являющаяся предположением исследователя, может оказаться верной, отвергнув нулевую гипотезу.
- Условное значение α = 0,05. Следовательно, если значение p для набора данных ≤ 0,05, то результат статистически значим. Если p-значение > 0,05, то исследование может быть статистически незначимым.
Понимание уровней статистической значимости
Статистическая значимость широко применяется исследователями в качестве инструмента количественного исследования для принятия решений. Этот инструмент применяется в различных областях, таких как бизнес, маркетинг, реклама, инвестиции и финансы.
Следующие два фактора определяют значимость.
- Размер образца: Количество наблюдений в огромной степени влияет на уровень значимости. Большой набор данных (обязательно рандомизированная выборка) часто устраняет ошибку выборкиОшибка выборкиФормула ошибки выборки используется для расчета статистической ошибки, которая возникает, когда человек, проводящий тест, не выбирает выборку, которая представляет всю рассматриваемую совокупность. Формула для ошибки выборки = Z x (σ /√n)подробнее.
- Размер эффекта: Корреляция между двумя наборами данных или переменными называется размером эффекта. Больший эффект sizeEffect SizeEffect size измеряет интенсивность взаимосвязи между двумя наборами переменных или групп. Он рассчитывается путем деления разницы между средними значениями, относящимися к двум группам, на стандартное отклонение. Это статистическая концепция. Следовательно, она подразумевает, что два разных исследования показывают очень похожие значения. Больший размер эффекта указывает на то, что данные статистически более значимы.
Значение альфа (α) представляет собой статистическую значимость. Традиционное значение альфы составляет 0,05, что составляет 5%. Он служит 95% порогом значимости. Это означает, что вероятность точности результата составляет 95%.
Для достижения статистической значимости должно выполняться хотя бы одно из заданных условий:
- Значение p должно быть ниже значения альфа.
- Значения нулевой гипотезы не должны иметь места в доверительном интервале.
Доверительный интервал Доверительный интервал Доверительный интервал относится к степени неопределенности, связанной с конкретной статистикой, и часто используется вместе с пределом погрешности. Доверительный интервал = среднее значение выборки ± критический фактор × стандартное отклонение выборки. read more относится к гарантированному диапазону, в который попадают фактические значения. Для p-значения 0,05, то есть 5%, оставшиеся 95% считаются доверительным интервалом.
Например, в июне 2020 г. ОСИНА Испытание не достигло статистической значимости по своей основной конечной точке. Об этом сообщило агентство Рейтер.
Тест статистической значимости (P-значение)
Статистическая значимость включает в себя нахождение результата и его проверку. Набор данных должен успешно отвергнуть нулевую гипотезу.
#1 – Статистическая проверка гипотез
Гипотеза – это предположение исследователя. Исследователи предполагают, что они получат тот или иной результат еще до проведения теста. Это предположение основано на взаимосвязи между различными переменными или наборами данных.
Два типа гипотез, используемых для анализа данных, следующие:
- Нулевая гипотеза: Теперь, если теория, предложенная исследователями, неверна, гипотеза исследователя считается недействительной. Это обозначается H0.
- Альтернативная гипотеза: Однако, если теория исследователя оказывается верной, она называется альтернативной гипотезой. Обозначается H1.
# 2 — Статистически значимое значение p
Значение p обозначает значение вероятности, то есть вероятность результата, являющегося результатом случайности или совпадения, а не фактов. Таким образом, уровень статистической значимости можно анализировать с помощью p-значения, которое находится в диапазоне от 0 до 1. Статистический результат считается точным, когда p-значение равно или меньше 0,05. Другими словами, вероятность того, что данные были получены случайно или случайно, составляет всего 5%.
Таким образом, тестирование приведет к следующим двум возможностям.
- p-значение ≤ 0,05: значение p, равное или меньшее 0,05, указывает на то, что нулевая гипотеза, вероятно, ложна. Таким образом, есть шансы, что результат будет более статистически значимым.
- р-значение > 0,05: Напротив, значение, превышающее 0,05, означает, что нулевая гипотеза кажется вероятной, и результат может быть статистически незначимым.
Расчет статистической значимости
Рассмотрим следующую задачу на основе гипотетического сценария. Самуэль, владелец парка развлечений, хочет, чтобы гости проводили больше времени в парке. Среднее время, проведенное 20 посетителями парка, составляет 199 минут. Сэмюэл решает установить новые аттракционы. Для теста порог значимости принят равным 5%, среднее значение выборки равно 200 минутам, а стандартное отклонение равно 200 минутам. На основе полученных данных проведите тест значимости для Сэмюэля.
Данные:
- µ = 199 минут
- п = 20
- µ остается 199 минут до установки новых аттракционов
- µ > 199 минут после установки новых аттракционов
- α = 5% или 0,05
- х = 200 минут
- σ = 200 минут
Расчет
Мы будем применять z-тест здесь,
Z = (x̄ — μ) / √ (σ2 / n)
Z = (200 – 199) / √(200 / 20)
Z = 1/3,16228
Z = 0,31623 = 0,3
Теперь давайте определим z-оценку или p-значение для данной z-таблицы:
Z0,000,10,20,30,40,00,500000,503990,507980,511970,51595
Таким образом, p-значение равно 0,51197.
Здесь, p-значение > α, т.е.., 0,51197 > 0,05
Следовательно, нулевая гипотеза может быть верной, и результат не является статистически значимым.
В качестве альтернативы пользователи могут выбирать из различных онлайн-калькуляторов для проведения тестов значимости.
Статистическая и практическая значимость
Статистическая значимость исключает случайное совпадение и указывает на то, что данные являются результатом определенной причины. Однако практическая значимость обнаруживает величину этого эффекта и его актуальность в реальном мире.
В то время как исследователи используют размер выборки и p-значение для установления статистической значимости, размер эффекта наборов данных указывает на практическую значимость.
Таким образом, получение статистической значимости без определения практической значимости было бы не очень полезным.
Часто задаваемые вопросы (FAQ)
Что такое статистическая значимость в исследованиях?
Тесты значимости широко используются в научных, экономических и медицинских исследованиях для определения надежности результатов тестов путем анализа шансов на истинность нулевой гипотезы.
Как определить статистическую значимость?
Шаги для расчета значимости следующие.
1. Найдите нулевую и альтернативную гипотезы, т. е. H0 и H1.
2. Предположим порог значимости или уровень значимости (α).
3. Получите образец и данные для проведения теста.
4. Запустите статистические тесты, такие как z-тест, T-тест, ANOVA или Chi-Square.
5. Проверьте, являются ли данные статистически значимыми, определив p-значение.
6. Интерпретируйте результат или завершите исследование.
Почему значимо значение p, равное 0,05?
Значение p, равное 0,05, представляет собой альфа, т.е. порог статистической значимости. Это граница вероятности, поэтому любое значение, выходящее за ее пределы, считается статистически незначимым. Если p-значение превышает 5%, это указывает на то, что более 5% значений вызваны случайностью. В результате набор данных нельзя использовать в качестве существенного доказательства причинно-следственной связи.
Рекомендуемые статьи
Это было Руководство по статистической значимости и ее значению. Здесь мы обсуждаем тесты значимости (значение p) и то, как понять его уровни, а также примеры и расчеты. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:
- Проверка гипотезы
- Степени свободы
- Тест хи-квадрат в Excel


 .
.