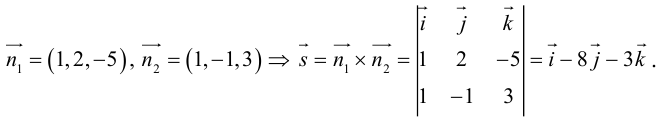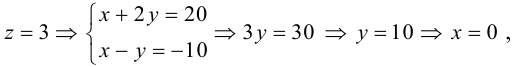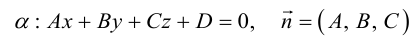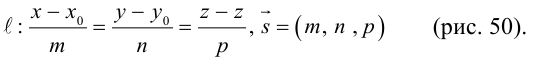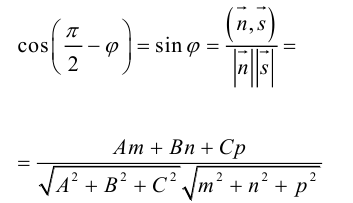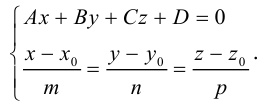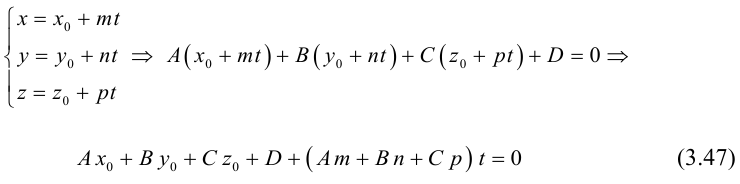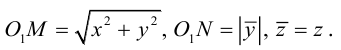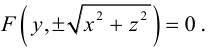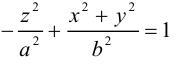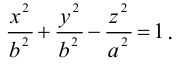Упражнения
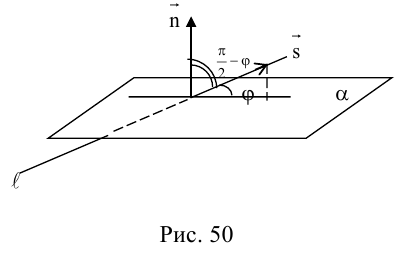
1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .
2. Нарисуйте кривую, задаваемую уравнением r = cos φ .
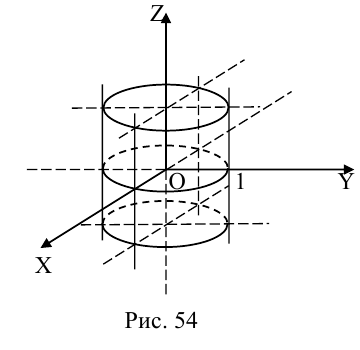
3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением
.
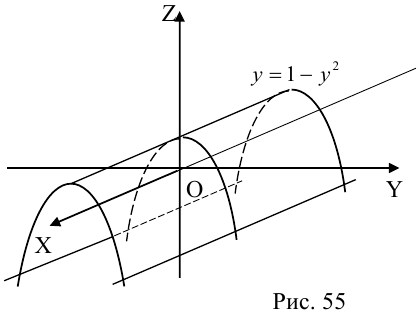
4. Докажите, что уравнение
задает эллипс, если 0 > 1.
5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?
6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?
7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = .
8. Нарисуйте спираль Галилея , которая задается уравнением r = a 2 ( a > 0). Она вошла в историю математики в XVII веке в связи с задачей нахождения формы кривой, по которой двигается свободно падающая в области экватора точка, не обладающая начальной скоростью, сообщаемой ей вращением земного шара.
9. Нарисуйте кривую, задаваемую уравнением r = | |.
10. Нарисуйте кривую, задаваемую уравнением r = .
11. Нарисуйте кривую, задаваемую уравнением r = .
12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.
1. Березин В. Кардиоида //Квант. – 1977. № 12.
2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
3. Берман Г.Н. Циклоида. – М.: Наука, 1975.
4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.
5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.
7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.
8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.
9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.
10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
Декартова система координат: основные понятия и примеры
Понятие декартовой системы координат
Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния нужно пройти строго вперёд, а затем — строго вправо, чтобы оказаться в некоторой другой точке, то вы уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой координат в пространстве.
Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат .
С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.
Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.
Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.
Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.
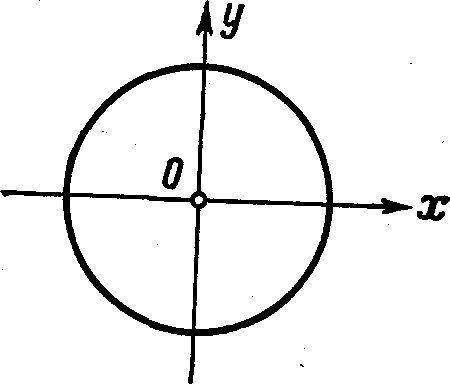
С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x — a)² + (y — b)² = R² .
Сферы применения
Декартова система координат является основой рассмотрения плоских и пространственных объектов во многих разделах математики, и применяется, в частности (все ссылки — работающие):
Прямоугольная декартова система координат на плоскости
Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. Одна из этих осей называется осью Ox , или осью абсцисс, другую — осью Oy , или осью ординат. Эти оси называются также координатными осями. Обозначим через M x и M y соответственно проекции произвольной точки М на оси Ox и Oy . Как получить проекции? Проведём через точку М прямую, перпендикулярную оси Ox . Эта прямая пересекает ось Ox в точке M x . Проведём через точку М прямую, перпендикулярную оси Oy . Эта прямая пересекает ось Oy в точке M y . Это показано на рисунке ниже.
Декартовыми прямоугольными координатами x и y точки М будем называть соответственно величины направленных отрезков OM x и OM y . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 и y = y 0 — 0 . Декартовы координаты x и y точки М называются соответственно её абсциссой и ординатой. Тот факт, что точка М имеет координаты x и y , обозначается так: M(x, y) .
Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.
Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой — в уроке полярная система координат.
Прямоугольная декартова система координат в пространстве
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.
Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Одну из указанных осей называют осью Ox , или осью абсцисс, другую — осью Oy , или осью ординат, третью — осью Oz , или осью аппликат. Пусть M x , M y M z — проекции произвольной точки М пространства на оси Ox , Oy и Oz соответственно.
Проведём через точку М плоскость, перпендикулярную оси Ox . Эта плоскость пересекает ось Ox в точке M x . Проведём через точку М плоскость, перпендикулярную оси Oy . Эта плоскость пересекает ось Oy в точке M y . Проведём через точку М плоскость, перпендикулярную оси Oz . Эта плоскость пересекает ось Oz в точке M z .
Декартовыми прямоугольными координатами x , y и z точки М будем называть соответственно величины направленных отрезков OM x , OM y и OM z . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 , y = y 0 — 0 и z = z 0 — 0 .
Декартовы координаты x , y и z точки М называются соответственно её абсциссой, ординатой и аппликатой.
Попарно взятые координатные оси располагаются в координатных плоскостях xOy , yOz и zOx .
Задачи о точках в декартовой системе координат
Пример 1. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось абсцисс.
Решение. Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, и ординату (координату на оси Oy , которую ось абсцисс пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось абсцисс:
Пример 2. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось ординат.
Решение. Как следует из теоретической части этого урока, проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, и абсциссу (координату на оси Ox , которую ось ординат пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось ординат:
Пример 3. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Ox .
Решение. Поворачиваем на 180 градусов вокруг оси Ox направленный отрезок, идущий от оси Ox до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Ox , будет иметь такую же абсциссу, что и данная точка, и ординату, равную по абсолютной величине ординате данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Ox :
Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
Пример 4. Определить, в каких квадрантах (четвертях, рисунок с квадрантами — в конце параграфа «Прямоугольная декартова система координат на плоскости») может быть расположена точка M(x; y) , если
Пример 5. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Oy .
Продолжаем решать задачи вместе
Пример 6. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Oy .
Решение. Поворачиваем на 180 градусов вокруг оси Oy направленный отрезок, идущий от оси Oy до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Oy , будет иметь такую же ординату, что и данная точка, и абсциссу, равную по абсолютной величине абсциссе данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Oy :
Пример 7. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно начала координат.
Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:
Пример 8. В декартовой системе координат в пространстве даны точки
Найти координаты проекций этих точек:
1) на плоскость Oxy ;
2) на плоскость Oxz ;
3) на плоскость Oyz ;
4) на ось абсцисс;
5) на ось ординат;
6) на ось апликат.
1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :
2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :
3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :
4) Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, а ордината и апликата проекции равны нулю (поскольку оси ординат и апликат пересекают ось абсцисс в точке 0). Получаем следующие координаты проекций данных точек на ось абсцисс:
5) Проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, а абсцисса и апликата проекции равны нулю (поскольку оси абсцисс и апликат пересекают ось ординат в точке 0). Получаем следующие координаты проекций данных точек на ось ординат:
6) Проекция точки на ось апликат расположена на самой оси апликат, то есть оси Oz , а следовательно имеет апликату, равную апликате самой точки, а абсцисса и ордината проекции равны нулю (поскольку оси абсцисс и ординат пересекают ось апликат в точке 0). Получаем следующие координаты проекций данных точек на ось апликат:
Пример 9. В декартовой системе координат в пространстве даны точки
Найти координаты точек, симметричных этим точкам относительно:
7) начала координат.
1) «Продвигаем» точку по другую сторону оси Oxy на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxy , будет иметь абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную по величине апликате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxy :
2) «Продвигаем» точку по другую сторону оси Oxz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxz , будет иметь абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную по величине ординате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxz :
3) «Продвигаем» точку по другую сторону оси Oyz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oyz , будет иметь ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную по величине абсциссе данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oyz :
По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.
4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:
5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:
6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:
7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:
Декартовы координаты точек плоскости. Уравнение окружности
| Числовая ось |
| Прямоугольная декартова система координат на плоскости |
| Формула для расстояния между двумя точками координатной плоскости |
| Уравнение окружности на координатной плоскости |
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
http://function-x.ru/geometry_coordinates_cartesian.html
http://www.resolventa.ru/demo/him/diagege.htm
Линия в полярной системе координат
Краткая теория
В полярной системе координат точка задается полярным углом φ и полярным радиусом r.
φ — угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки)
r — расстояние от заданной точки до полюса
Если совместить начало декартовых координат с полюсом, а ось абсцисс с полярной осью, то между полярной и декартовой системой координат может быть установлена однозначная связь.
Пример решения задачи
Задача
Линия задана
уравнением
в полярной
системе координат. Требуется:
Решение
Построение линии по точкам
Построим линию по
точкам, предварительно заполнив таблицу значений r и j:
|
|
|
|
|
|
| 1 | 0 | 1 | 9 | 0,556 |
| 2 |
|
0,924 | 8,772 | 0,570 |
| 3 |
|
0,707 | 8,121 | 0,616 |
| 4 |
|
0,383 | 7,148 | 0,699 |
| 5 |
|
0,000 | 6,000 | 0,833 |
| 6 |
|
-0,383 | 4,852 | 1,031 |
| 7 |
|
-0,707 | 3,879 | 1,289 |
| 8 |
|
-0,924 | 3,228 | 1,549 |
| 9 |
|
-1 | 3 | 1,667 |
| 10 |
|
-0,924 | 3,228 | 1,549 |
| 11 |
|
-0,707 | 3,879 | 1,289 |
| 12 |
|
-0,383 | 4,852 | 1,031 |
| 13 |
|
0,000 | 6,000 | 0,833 |
| 14 |
|
0,383 | 7,148 | 0,699 |
| 15 |
|
0,707 | 8,121 | 0,616 |
| 16 |
|
0,924 | 8,772 | 0,570 |
| 17 |
|
1 | 9 | 0,556 |
Используя данные
таблицы, строим линию.
- Отмечаем полюс и указываем масштаб.
- С помощью транспортира прочерчиваем
угловые направления - Циркулем и линейкой отмечаем найденные
точки - Отложенные точки соединяем линией
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
График в полярной
системе координат имеет вид:
Уравнение линии в декартовой прямоугольной системе координат
Найдем уравнение
данной линии в декартовой системе координат:
Подставляя в исходное
уравнение в полярных координатах, получаем:
Полученная линия
-эллипс
Уравнения фигур
Уравнение фигуры — это уравнение с двумя переменными x и y, для которого выполняются два условия: 1) координаты любой точки фигуры F удовлетворяют этому уравнению.
Содержание:
Понятие уравнения фигур
Название этого раздела означает: геометрические фигуры можно задавать уравнениями (некоторые фигуры можно задавать неравенствами).
Известно, что точки плоскости и пространства задаются их координатами, геометрические фигуры могут задаваться уравнениями или неравенствами: 


Говорят, что фигура F задается уравнением в прямоугольных координатах, если точка принадлежит фигуре F тогда и только тогда, когда координаты этой точки удовлетворяют данному уравнению. Это означает, что выполняются два условия:
1. Если точка принадлежит фигуре F, то ее координаты удовлетворяют данному уравнению.
2. Если числа х, у, г удовлетворяют данному уравнению, то точка с такими координатами принадлежит фигуре F.
Второе условие можно выразить иначе: координаты любой точки, не принадлежащей фигуре F, не удовлетворяют данному уравнению.
Например, прямая, перпендикулярная оси Ох и проходящая через точку М(2, 0), на оси Ох задается уравнением х = 2 (рис. 2.461). Действительно, каждая точка, лежащая на этой прямой, имеет одну и ту же координату 2. А любая точка, не лежащая на этой прямой, имеет другое значение координаты х, нежели 2. Ось Оу задается уравнением х = 0.
Аналогично прямая, перпендикулярная оси Оу и проходящая через точку Щ0, 3), имеет уравнение у = 3 (рис. 2.462). Ось Ох имеет уравнение у = 0.
Уравнение прямой
Можно доказать такую теорему.
Теорема 3. Любая прямая в декартовой системе координат хОу имеет уравнение вида 

Выясним, как расположена прямая относительно осей координат, если ее уравнение 
1. 
Таким образом, все точки прямой имеют одну и ту же ординату 
2. 
3. с = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 2.465).
Если в общем уравнении прямой 


Коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью Ох. В уравнении прямой, изображенной на рисунке 2.466, k > 0.
Коэффициент k в уравнении прямой называют угловым коэффициентом прямой.
Уравнения окружности и сферы
Составим уравнение окружности с центром в точке 
1. Возьмем произвольную точку А(х, у) на окружности. Расстояние от нее до центра О равно R.
2. Квадрат расстояния от точки А до точки О равен 
3. Координаты х, у каждой точки А окружности удовлетворяют уравнению
(2, определение окружности).
Получили искомое уравнение. Обратно: любая точка А, координаты которой удовлетворяют уравнению окружности, принадлежит окружности, так как расстояние от нее до точки О равно R. Отсюда следует, что данное уравнение действительно является уравнением окружности с центром в точке О и радиусом R.
Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:
Выведем теперь уравнение сферы. Пусть в пространстве введена прямоугольная система координат и задана сфера S с центром 
Пусть х, у, z — координаты точки М. Согласно формуле расстояния между точками в пространстве, предыдущее равенство можно записывать в координатах так:
Это и есть уравнение сферы S с центром 
Если центр А находится в начале координат, т. е. 
Рассмотрим шар с центром 
По определению, это множество точек М, для которых 

Это неравенство задает шар S с центром 

Если центр шара находится в начале координат, то уравнение шара упрощается и имеет вид:
Два предприятия A и В производят продукцию с одной и той же ценой т за одно изделие. Однако автопарк, обслуживающий предприятие А, оснащен более современными и более мощными грузовыми автомобилями. В результате транспортные расходы на перевозку одного изделия составляют для предприятия А 10 руб. на 1 км, а для предприятия В 20 руб. на 1 км. Расстояние между предприятиями 300 км. Как территориально должен быть разделен рынок сбыта между двумя предприятиями для того, чтобы расходы потребителей при покупке изделий были минимальными?
Решение:
1. Выберем систему координат так, чтобы ось Ох проходила через пункты А и В, а ось Оу — через точку А (построение) (рис. 2.470).
2. Пусть N — произвольная точка, 
3. При доставке груза из пункта А расходы равны 
4. При доставке груза из пункта Б расходы равны 
5. Если для пункта N выгоднее доставлять груз с предприятия А, то 


6. Таким образом, границей этих двух областей для каждой точки, до которой расходы на перевозку груза из пунктов А и Б равны, будет множество точек плоскости, удовлетворяющих уравнению 
7. Выразим 

8. Имея в виду равенство из п. 6, получим:

9. Это есть уравнение окружности (рис. 2.472).
Следовательно, для всех пунктов, попадающих во внутреннюю область круга, выгоднее привозить груз из пункта В, а для всех пунктов, попадающих во внешнюю часть круга, — из пункта А.
Пример 2.
Два наблюдаемых пункта находятся в точках 


Решение:
Из условий задачи имеем:
1. Два наблюдаемых пункта находятся в точках
2. Пункт наблюдения О находится на прямой АВ и удален от А на расстоянии 

3. Наблюдатель идет так, чтобы расстояние до пункта А было в два раза больше, чем до В.
4. По какой линии должен идти наблюдатель?
5. Примем за начало координат наблюдательный пункт О и направление оси Ох будет проходить через пункты А и В (по условию задачи эти три точки находятся на одной прямой) (рис. 2.473).
6. Пусть наблюдатель находится в точке М(х, у). Вычислим расстояние от наблюдателя до пунктов А и В (рис. 2.473):
(1, 2, 3, 5, формула расстояния между точками).
7. По условию задачи имеем: МА = 2MB, т. е.

8. Решая это уравнение, получим:
9. Раскроем скобки и перегруппируем:
10. Наблюдатель должен идти по окружности с центром 

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Уравнение фигуры
Уравнение фигуры F в прямоугольной системе координат — это уравнение с двумя переменными x и y, для которого выполняются два условия:
1) координаты любой точки фигуры F удовлетворяют этому уравнению;
2) любая пара чисел (x; y), удовлетворяющая этому уравнению, является координатами некоторой точки фигуры F.
1) Уравнение вида
где a, b и c — числа (причем a и b не равны нулю одновременно) задаёт в прямоугольной системе координат уравнение некоторой прямой.
2) Уравнение вида
задаёт в прямоугольной системе координат окружность с центром в точке (a;b) и радиусом R.
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
источники:
http://www.treugolniki.ru/uravnenie-figury/
http://www.resolventa.ru/demo/him/diagege.htm
ЛИНИИ,
ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ.
ЛЕКЦИЯ
1
I.
ЛИНИЯ И ЕЕ УРАВНЕНИЯ.
§ 21. О понятии
линии и ее уравнениях.
Определение I.
Уравнением
линии в декартовой системе координат
называется уравнение
F(x,y)=0,
(1) (это неявное уравнение линии) которому
удовлетворяют координаты х, у всех точек
этой линии и только координаты таких
точек.
В частности,
уравнение линии может иметь вид y=f(x)
(явное уравнение) (2).
Уравнением
линии в полярной системе координат
называется уравнение
(3), (это
тоже неявное уравнение) которому
удовлетворяют полярные координаты
и
всех точек этой линии и только координаты
таких точек.
В частности,
уравнение линии в полярных ко-ординатах
может иметь вид
(явное) (4).
Определение II.
Параметрическими
уравнениями линии в декартовой
системе координат называются уравнения
вида
,
где функции
x(t)
и у(t)
имеют одну и ту же область определения,
каждому значению t
из этой области соответствует точка
M(x(t),y(t))
рассматриваемой линии и каждая точка
М этой линии соответствует некоторому
значению t из области определения
функций x(t)
и y(t),
т. е. для любой точки М линии найдется
такое значение t, что x(t)
и y(t)
будут координатами точки М. Аналогично
определяются параметрические уравнения
линии в полярных координатах.
§ 22. Примеры составления уравнений линии.
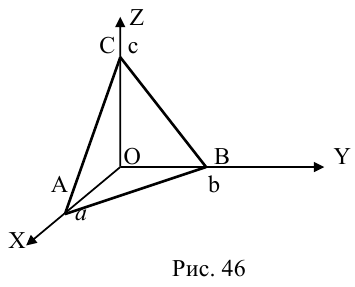
Пример 1.
Рассмотрим окружность S
радиуса r
с центром в точке C(a,b)
заданной
относительно декартовой прямоугольной
системы координат (рис. 46) Пусть М(x,y)
— произвольная точка плоскости. Точка
М
лежит на окружности
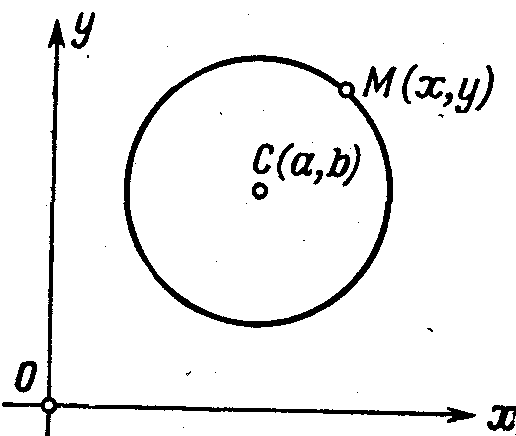
47
S
тогда и только тогда, когда расстояние
между точками М
и С
равно радиусу r
окружности S.
Расстояние между
точками М
и С
равно
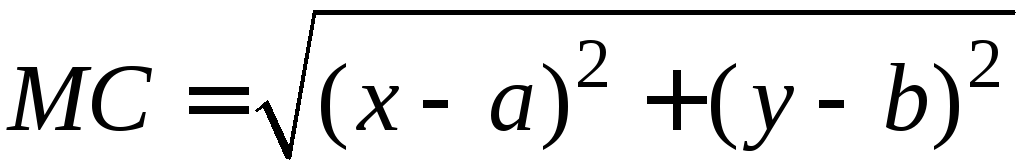
уравнение окружностиS
имеет вид
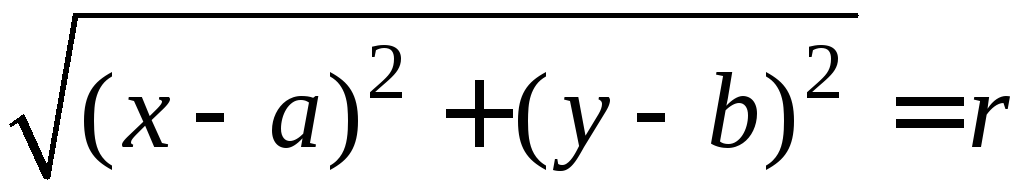
или
(1), или
(1′).
В частности,
уравнение окружности радиуса r
с центром в начале координат имеет
вид (рис.47)
;
(2),(2′).
Уравнения (1′) и
(2′) называются нормальными уравнением
окружности.
Пример 2.
Составить уравнение линии, произведение
расстояний любой точки которой до двух
данных точек F1
и F2
равно данному числу b2.
Решение.
Пусть расстояние между точками F1
и F2
равно 2а.
За начало О
декартовой прямоугольной системы
координат на плоскости примем середину
отрезка F1F2
,
а прямую F1F2
с положительным
направлением от О
к F2
примем за ось Ох.
Точка F1
в выбранной системе координат имеет
координаты: (-а,0),
а точка F2
— (а,0).
Согласно условию задачи
или
.
Применяя формулу расстояния между двумя
точками, находим,
и
соотношение
принимает вид:

Линии, определяемые
этим уравнением, называются овалами
Кассини. Изображения их (для случаев
a>b
, а=b,
а
< b)
даны на рис. 48. Если а=b,
Рис. 48
т. е. если произведение
расстояний от точки М
до точек F1
и F2,
равно квадрату половины расстояния
между точками F1
и F2,
то овал Кассини называется лемнискатой
Бернулли (рис. 49). Уравнение лемнискаты
имеет вид
.
Составим уравнение
лемнискаты еще в полярной системе
координат, принимая точку О за полюс,
а положительную полуось Ох
за полярную ось.
Заменяя в уравнении
лемнискаты х
и у их
выражениями через полярные координаты
получим
или
.
При изменении
от
до 0 функция
возрастает от 0 до
,
а при изменении
от 0 до
— эта функция убывает от
до 0; получается петля, расположенная
в первой и четвертой четвертях; при
изменении
от
до
получается другая петля, расположенная
во второй и третьей четвертях, симметричная
первой относительно полюса.
Рис. 49
Значениям
,
для которыхсоответствуют мнимые значения функции
,
следовательно, этим значениямне соответствуют никакие точки лемнискаты.
Что касается
построения овалов Кассини, то точки
этих линий удобнее всего строить, исходя
из геометрического определения
линии. Уравнения линий иногда
удобно составлять в полярной системе
координат. Рассмотрим следующий пример
линии
.
Подумайте, что это за линия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Аналитическая геометрия
В этой главе все геометрические объекты мы будем определять и изучать с помощью соответствующих уравнений этих объектов и, следовательно, в принципе геометрия может быть изложена без единого чертежа. И, действительно, все чертежи, которые мы будем использовать, будут служить лишь для визуальной иллюстрации наших рассуждений.
Уравнение поверхности в выбранной декартовой системе координат
т. е. в виде связи или зависимости между координатами х, у, z произвольной точки поверхно-аналогично, уравнение
определяет некоторую линию (кривую) в системе координат 
Кривая в пространстве может быть задана как пересечение двух поверхностей и, следовательно, она определяется системой из уравнений этих поверхностей:
Кроме того, кривую на плоскости или в пространстве можно также задать с помощью зависимостей координат произвольной то’жи этой кривой от некоторого параметра, т. е. с помощью параметрических уравнений:
где t — действительный параметр.
Плоскость в пространстве. Различные виды уравнения плоскости
Найдем уравнение плоскости в пространстве с выбранной в нем декартовой системой координат 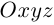
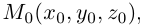
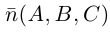
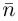
Пусть 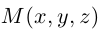
или, учитывая, что 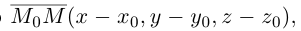
Преобразовав полученное уравнение к виду
мы получим тем самым общее уравнение плоскости.
Рассмотрим теперь некоторые частные случаи общего уравнения плоскости. Если в общем уравнении плоскости отсутствует, одна из координат, то нормальный вектор 
Аналогично, если в общем уравнении плоскости отсутствуют две координаты, то нормальный вектор данной плоскости перпендикулярен соответствующей координатной плоскости и, значит, плоскость расположена параллельно этой координатной плоскости.
Научимся теперь находить уравнение плоскости по трем элементам.
1) Плоскость, проходящая через точку, параллельно двум векторам.
Пусть плоскость 
Обозначим через 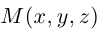
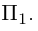
Раскрыв определитель (проще всего, разлагая его по первой строке), получим общее уравнение плоскости
2)Плоскость, проходящая через две точки, параллельно вектору.
Найдем уравнение плоскости 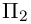
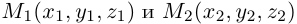
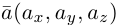
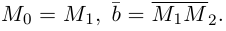
— искомое уравнение плоскости
3)Плоскость, проходящая через три точки.
Если плоскость 
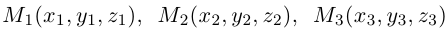
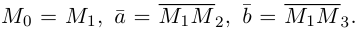
Замечание. Во всех трех случаях уравнение плоскости можно найти, вычислив предварительно ее нормальный вектор. Например, в первом случае в качестве нормального вектора можно взять векторное произведение 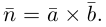
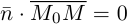
Пример №1
Найти уравнение плоскости 11 ^ — перпендикулярной плоскости
параллельной вектору 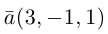
Решение. Из уравнения плоскости 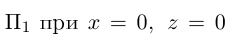
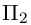
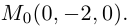
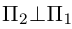
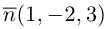
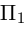
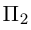
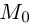
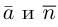
Таким образом, общее уравнение плоскости 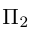
Пусть плоскость 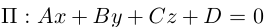
Разделив обе части уравнения плоскости на число D. мы можем записать его в виде:
Числа а, b, с представляют собой величины отрезков, которые плоскость П отсекает на координатных осях. Полученное уравнение называется уравнением плоскости в отрезках.
Найдем теперь формулу для вычисления расстояния от точки 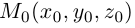
Обозначим искомое расстояние через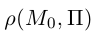
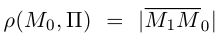
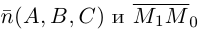
С другой,
так как 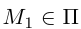
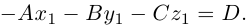
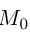
В заключение этого параграфа выясним характер взаимного расположения двух плоскостей. Пусть плоскости заданы своими общими уравнениями:
Очевидно, что угол 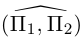
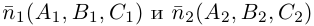
В частности,
Пример №2
Убедиться в том, что плоскость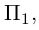
параллельны и найти расстояние между ними.
Решение. Запишем уравнение плоскости II| в отрезках:
Преобразовав его к общему виду, получим:
Так как нормальные векторы 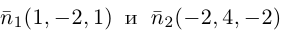
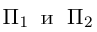
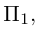
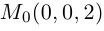
Уравнения прямой в пространстве
Пусть прямая L в пространстве с декартовой системой координат 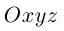
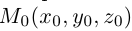
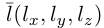
Обозначим через 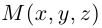
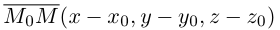
Эта двойная пропорция представляет собой канонические уравнения прямой в пространстве.
Заметим, что в канонических уравнениях прямой формально допускается запись нулей в знаменателях, это означает лишь то, что прямая перпендикулярна соответствующей координатной оси или координатной плоскости.
Если прямая проходит через две точки 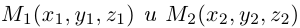
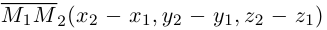
Коллинеарные векторы 
Если точка М перемещается вдоль прямой, параметр t изменяется в пределах от 
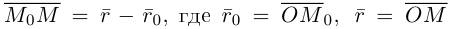
Это уравнение называется векторным уравнением прямой.
Переходя в полученном векторном уравнении к координатам, запишем параметрические уравнения прямой:
Прямую в пространстве можно задать также как пересечение двух плоскостей.
Система
составленная из уравнений этих плоскостей, дает нам общие уравнения прямой в пространстве. Для перехода от общих к каноническим уравнениям прямой, достаточно найти какую-нибудь точку на ней, решив при фиксированном значении одной из координат систему уравнений плоскостей, а также определить направляющий вектор прямой, которым может служить векторное произведение нормальных векторов 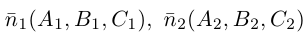
Пример №3
Найти канонические уравнения прямой
Решение. Полагая в данной системе z = 0, получим
Решив эту систему, найдем х = 1, у = —2. Таким образом, мы получили точку 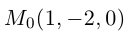
Осталось записать канонические уравнения данной прямой:
Научимся теперь вычислять расстояние от точки до прямой в пространстве. Пусть задана точка 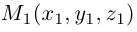
Искомое расстояние 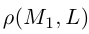
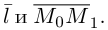
Пусть нам известны канонические уравнения двух прямых в пространстве:
Очевидно,
Один из углов между этими прямыми равен углу между их направляющими векторами 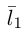
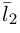
Изучим взаимное расположение прямых 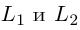
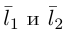
В случае, когда 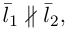
Прямые пересекаются, очевидно, тогда и только тогда, когда векторы 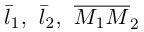
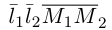
Расстояние 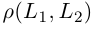
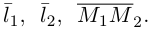
Пример №4
Убедиться в том, что прямые
являются скрещивающимися. Найти расстояние между ними и уравнение общего перпендикуляра к ним.
Решение. Первая прямая проходит через точку 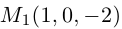
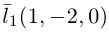
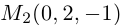
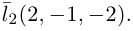
следовательно, прямые 
Осталось найти уравнение общего перпендикуляра к данным прямым. Заметим, прежде всего, что его направляющим вектором является уже вычисленный нами вектор 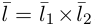
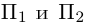
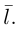
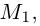
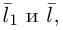
Таким образом, плоскость 
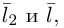
и, стало быть, 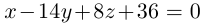
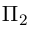
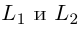
В заключение этого параграфа вычислим угол между прямой L, заданной каноническими уравнениями
и плоскостью П, для которой известно ее общее уравнение
Очевидно, искомый угол 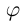
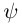
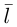
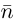
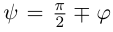
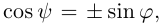
В частности, если
Прямая на плоскости
Для прямой на плоскости наблюдается большее разнообразие ее уравнений, так как на плоскости прямая фиксируется точкой, через которую она проходит и, либо вектором ей перпендикулярным (нормальным вектором), либо вектором ей параллельным (направляющим вектором) и, следовательно, для прямой на плоскости можно записывать как уравнения, характерные для плоскости в пространстве (§1), так и аналоги уравнений прямой в пространстве (§2). Перечислим, не повторяя деталей, изложенных в предыдущих двух параграфах, основные уравнения прямой на плоскости и связанные с ними формулы.
Пусть прямая L на плоскости с выбранной в ней системой координат 
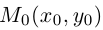
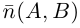
Уравнение такой прямой имеет вид:
откуда после очевидных преобразований получим уравнение
которое представляет собой общее уравнение прямой на плоскости.
Пусть прямая L отсекает на координатных осях 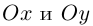
Тогда, как и для плоскости, мы можем записать уравнение прямой в отрезках:
Если прямая L содержит точку 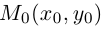
то ее каноническое уравнение имеет вид:
По аналогии с прямой в пространстве, прямая на плоскости может быть задана также векторным уравнением
и параметрическими уравнениями
Расстояние от точки 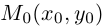
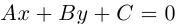
Найдем еще одно уравнение прямой на плоскости, характерное для этого геометрического объекта. Пусть прямая L, заданная своим каноническим уравнением 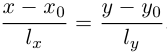
Тогда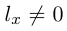
где 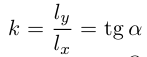
представляет собой уравнение прямой с угловым коэффициентом, которая проходит через точку
Если две прямые на плоскости заданы общими или каноническими уравнениями, то их взаимное расположение исследуется по аналогии с плоскостями или прямыми, заданными такими же уравнениями (§1 или §2). Изучим поэтому взаимное расположение двух прямых, которые заданы уравнениями с угловым коэффициентом. Итак, рассмотрим две прямые
Предположим сначала, что прямые не являются перпендикулярными, обозначим через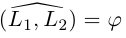
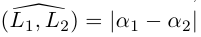
Если же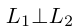
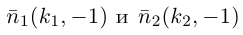
Таким образом, для перпендикулярности прямых 
Очевидно. прямые 
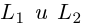
Пример №5
Даны прямая 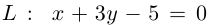
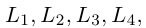
Решение. Прямые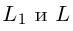
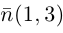
Так как 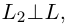
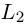
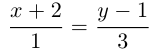
Из уравнения прямой L находим 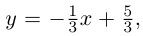
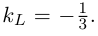
откуда, 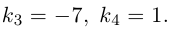
Кривые второго порядка на плоскости
В предыдущих трех параграфах нами были изучены линейные геометрические объекты -плоскость и прямая в пространстве и на плоскости. Мы показали, что в декартовой системе координат они определяются алгебраическими уравнениями первой степени, т. е. линейными уравнениями. Предметом нашего исследования в этом параграфе будут являться кривые второго порядка, т. е. линии на плоскости, уравнения которых в декартовой системе координат Оху имеют вид:
где А, В, С, D, Е, F — действительные числа. Мы убедимся в том, что, за исключением случаев вырождения данное уравнение определяет одну из трех замечательных линий — эллипс, гиперболу или параболу. Приведем сначала геометрическое определение каждой из этих линий и найдем их канонические уравнения.
Эллипс
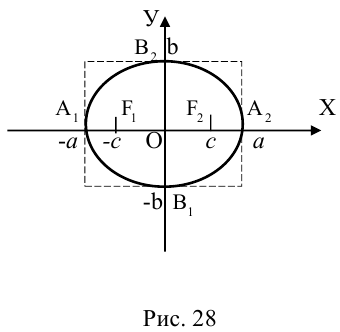
Определение: Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек (фокусов эллипса) есть величина постоянная.
Найдем каноническое уравнение эллипса. Обозначим через 2с фокусное расстояние, т. е. расстояние между фокусами, а через 2а — постоянную сумму расстояний от точек эллипса до фокусов. Из неравенства треугольника следует, что 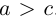
Пусть М(х, у) — произвольная точка эллипса. По определению этой линии,
Упростим последнее уравнение:
откуда, использовав обозначение 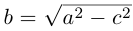
Построим эту линию. Для этого прежде всего заметим, что она симметрична относительно координатных осей и начала координат, так как переменные x и у входят в каноническое уравнение в квадратах. Отсюда следует, что эллипс достаточно построить в первой координатной четверти и затем отразить его относительно координатных осей. Из канонического уравнения эллипса находим:
Очевидно, эта функция определена и убывает при 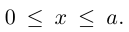
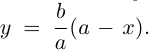
Числа а и b называются соответственно большой и малой полуосями эллипса. Точка O(0,0) -центр эллипса, точки 
Форму эллипса характеризует величина 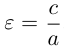
то при 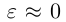
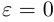
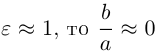
Замечание. В уравнении эллипса может оказаться, что 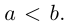
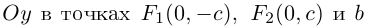
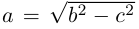
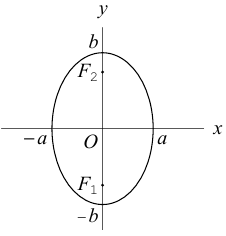
Гипербола
Определение: Гипербола представляет собой линию на плоскости, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек (фокусов гиперболы) есть величина постоянная.
Обозначим и здесь фокусное расстояние через 2с. а через 2а — постоянную абсолютную величину разности расстояний от точек гиперболы до фокусов. Для гиперболы а < с, что следует из неравенства треугольника. Выберем декартову систему координат на плоскости точно также, как и при выводе канонического уравнения эллипса.
По определению гиперболы для произвольной точки М(х, у) этой линии
Избавляясь от корней в этом уравнении, получим:
Обозначая здесь 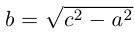
Как видно из ее уравнения, гипербола симметрична относительно координатных осей и начала координат. Из канонического уравнения гиперболы следует, что в первой четверти
Эта функция возрастает, 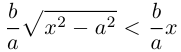
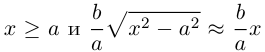
а а а а
Это означает, что в первой четверти гипербола, выходя из точки (а, 0) на оси Ох, приближается
затем при больших значениях х к прямой 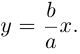
Прямые 
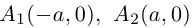
Как и для эллипса, определим эксцентриситет гиперболы как отношение половины фокусного расстояния к действительной полуоси:
Так как
то эксцентриситет гиперболы характеризует величину угла, в котором она располагается. При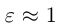
Замечание. В каноническом уравнении гиперболы знаки перед квадратами могут располагаться и в обратном порядке:
В этом случае фокусы и вершины находятся на оси
Парабола
Определение: Параболой называется множество точек плоскости, равноудаленных от. фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы).
Обозначим расстояние от фокуса до директрисы через р. Число р > 0 называется параметром параболы. Выберем удобную систему координат на плоскости: ось Ох направим через фокус F перпендикулярно директрисе D, а начало координат возьмем посередине между директрисой и фокусом.
Если М(х,у) — произвольная точка параболы, то по определению этой кривой
После возведения в квадрат и очевидных преобразований, получим каноническое уравнение параболы:
Очевидно, парабола проходит через начало координат и симметрична относительно оси Ох. Точка O(0,0) называется вершиной параболы, ось Ох — осью параболы.
Замечание. Если бы при выборе системы координат мы направили ее оси в противоположные стороны, то каноническое уравнение параболы приняло бы вид:
Аналогично, уравнения
также определяют параболы, фокусы которых расположены на оси Оу. а директрисы параллельны оси Ох.
Приведение уравнения кривой второго порядка к каноническому виду
Покажем, что общее уравнение кривой второго порядка на плоскости, кроме случаев вырождения, определяет одну из линий — эллипс, гиперболу или параболу.
Выясним сначала, как преобразуются координаты точки на плоскости при параллельном переносе системы координат. Предположим, что осуществлен параллельный перенос системы координат Оху в точку 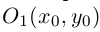
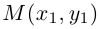
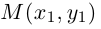
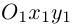
Так как 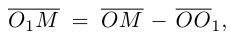
Рассмотрим теперь уравнение второго порядка на плоскости в частном случае, когда оно не содержит произведения координат ху :
причем коэффициенты А и С не равны одновременно нулю. Здесь возможны три случая.
а) АС > 0. Очевидно, всегда можно считать, тгго А > 0, С > 0. Выделяя в уравнении второго порядка полные квадраты по переменным х и у, получим:
где 
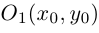
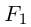
и, следовательно, в смещенной с помощью параллельного переноса в точку 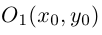
b) АС < 0. Будем считать для определенности, что А > 0. С < 0.
В этом случае исходное уравнение второго порядка также приводится к виду (1). При F = 0 оно определяет пару прямых, проходящих, через точку 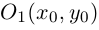
Если же 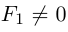
и, стало быть, после параллельного переноса системы координат в точку 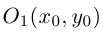
c) АС = 0. Предположим, например, что
Выделяя в данном уравнении второго порядка полный квадрат по переменной у, получим:
С {у ~ Уо)2 + Dx + F1=0.
Если в этом уравнении D = 0, то при 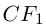
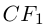
Если же 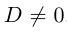
т.е. после параллельного переноса системы координат в точку 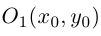
Аналогично. если в исходном уравнении второго порядка 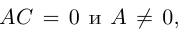
Пример №6
Привести уравнение второго порядка к каноническому виду, назвать и построить кривую:
Решение. Выделяя полные квадраты по обеим переменным, получим:
что представляет собой каноническое уравнение эллипса в смещенной в точку 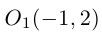
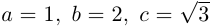
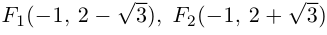
Пример №7
Найти каноническое уравнение параболы с вершиной в точке 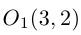
Решение. Фокус параболы находится в точке F(0 , 2), следовательно, уравнение параболы с учетом смещения имеет вид:
Здесь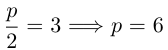
каноническое уравнение параболы.
Замечание. Для приведения к каноническому виду уравнения второго порядка, содержащего произведение координат ху, необходимо кроме параллельного переноса выполнить еще и поворот системы координат на определенный угол. Например, для равносторонней гиперболы ху = 1 следует повернуть систему координат Оху вокруг ее начала на угол 45° против часовой стрелки. Поскольку вершины гиперболы находятся на расстоянии 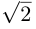
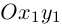
Поверхности второго порядка в пространстве
В заключение этой главы мы изучим поверхности в пространстве, которые в декартовой системе координат задаются алгебраическими уравнениями второй степени. Существуют пять видов таких поверхностей: эллипсоид, гиперболоиды, параболоиды, цилиндры второго порядка и конус второго порядка.
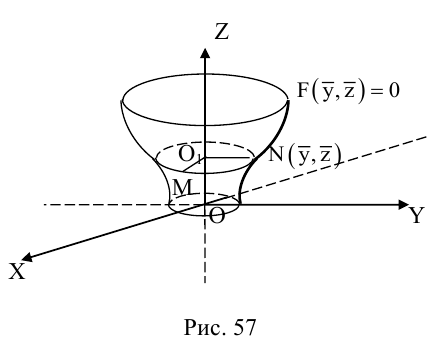
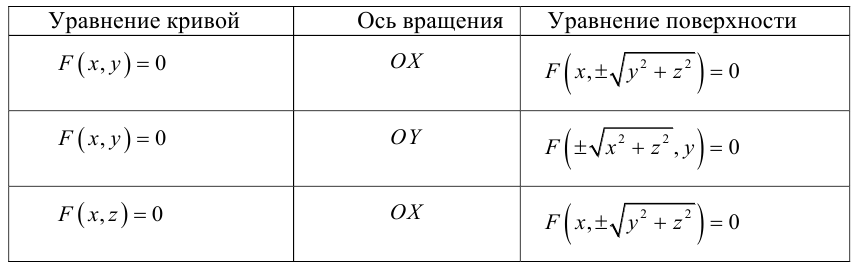
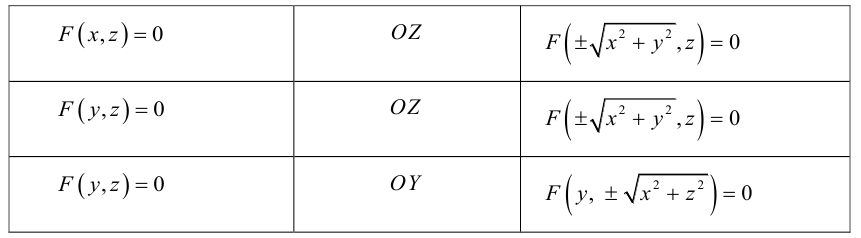
Поверхность вращения
Найдем уравнение поверхности, которая получается вращением некоторой линии вокруг одной из координатных осей. Пусть линия L, которая в координатной плоскости Oyz задается уравнением F(y, z) = 0. вращается вокруг оси Oz.
Пусть M(x,y,z) — произвольная точка на поверхности вращения. Перегоним ее по окружности, расположенной в сечении поверхности плоскостью, проходящей через данную точку перпендикулярно оси Oz, в точку N на линии L. Поскольку расстояние от точки М до оси Oz равно 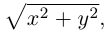
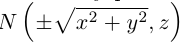
Найдем теперь уравнения поверхностей, которые получаются вращением кривых второго порядка с последующей линейной деформацией этих поверхностей.
Эллипсоид
Возьмем в плоскости Oyz эллипс
и будем вращать его вокруг оси Oz. В результате, как следует из предыдущего пункта, мы получим поверхность с уравнением
которая называется эллипсоидом вращения. Заменив в найденном уравнении координату х на —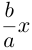
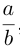
Положительные числа а, b, с называются полуосями эллипсоида.
Очевидно, сечениями эллипсоида плоскостями параллельными координатным, являются эллипсы.
Замечание. В частном случае, когда а = b = с = R эллипсоид превращается в сферу
радиуса R с центром в начале координат.
Гиперболоиды
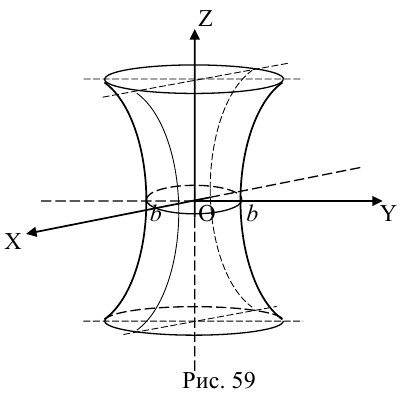
а) Однополостный гиперболоид.
Вращая гиперболу
вокруг оси Oz, получим однополостный гиперболоид вращения с уравнением
После линейной деформации вдоль оси Ох эта поверхность превращается в однополостный гиперболоид общего вида с осью Oz :
Аналогично, уравнения однополостных гиперболоидов с осями Ох и Оу имеют, соответственно, вид:
Сечениями однополостного гиперболоида плоскостями, перпендикулярными его оси, являются эллипсы, а в сечениях плоскостями, перпендикулярными другим координатным осям, располагаются гиперболы.
Двухполостный гиперболоид
Поверхность, полученная вращением вокруг оси Оz гиперболы
вершины которой расположены на оси вращения, называется двухполостным гиперболоидом вращения. Запишем уравнение двухполостного гиперболоида:
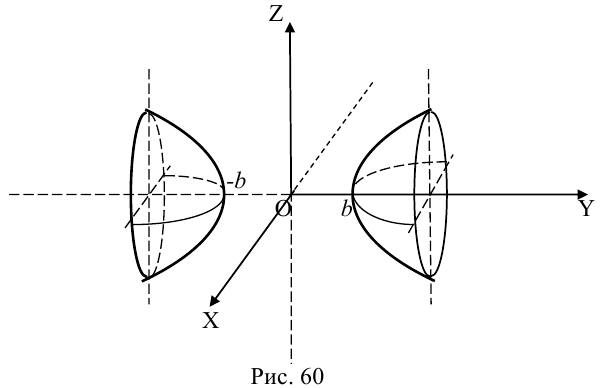
Линейная деформация двухполостного гиперболоида вращения вдоль оси Ох прообразует его в двухполостный гиперболоид общего вида с осью Oz. Уравнение этой поверхности имеет вид:
Двухполостные гиперболоиды с осями Ох и Оу имеют, соответственно, уравнения:
Как и в случае однополостного гиперболоида, сечениями двухполостного гиперболоида плоскостями, параллельными координатным, являются эллипсы и гиперболы.
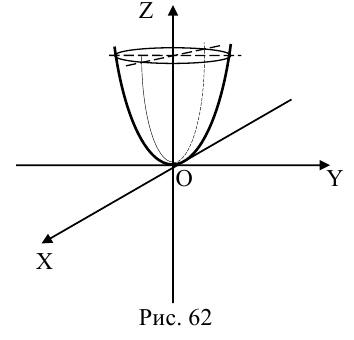
Параболоиды
а) Эллиптический параболоид
Вращение параболы вокруг ее оси приводит к поверхности, которая называется параболоидом вращения. В частности, если параболу с каноническим уравнением 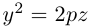
Линейная деформация параболоида вращения вдоль оси Оу превращает его в эллиптический параболоид с уравнением:
Положительные числа p, q называются параметрами параболоида, точка O(0,0) — вершина, ось Oz — ось эллиптического параболоида.
Уравнения эллиптических параболоидов с осями Ох и Оу имеют, соответственно, вид:
Как следует из уравнения эллиптического параболоида, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, а в сечениях плоскостями, параллельными другим координатным, находятся параболы.
Замечание. Изменение знака в правой части уравнения эллиптического параболоида приводит к отражению этой поверхности относительно координатной плоскости, перпендикулярной оси параболоида.
b) Гиперболический параболоид.
Будем поступательно перемещать образующую параболу
расположенную в плоскости Oyz, параллельно самой себе вдоль направляющей параболы
находящейся в плоскости Oxz. Полученная таким образом поверхность называется гиперболическим параболоидом или седловидной поверхностью.
Найдем уравнение этой поверхности. Пусть М(х. у, z) — произвольная точка гиперболического параболоида. По его построению точка М принадлежит параболе с вершиной в точке 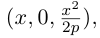
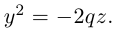
то, подставив в него координаты точки М, мы и получим после несложных преобразований уравнение гиперболического параболоида:
Здесь, как и для эллиптического параболоида, числа р, q — параметры гиперболического параболоида, точка O(0,0) и ось Oz — соответственно вершина и ось гиперболического параболоида.
Замечание 1. Седловидная поверхность может быть также получена перемещением параболы 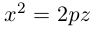
Судя по уравнению гиперболического параболоида, в сечениях этой поверхности плоскостями z = h > 0 находятся гиперболы, действительные оси которых параллельны координатной оси Ох. Аналогично, плоскости z = h < 0 пересекают данную поверхность по гиперболам с действительными осями, параллельными оси Оу. Наконец, плоскость Оху пересекает гиперболический параболоид по двум прямым
Гиперболические параболоиды, осями которых служат координатные оси Ох и Оу, имеют, соответственно, уравнения:
Замечание 2. Отразив седловидную поверхность относительно координатной плоскости, перпендикулярной ее оси, получим гиперболический параболоид, уравнение которого отличается знаком правой части от уравнения исходной поверхности.
Цилиндры второго порядка
Цилиндром второго порядка называется поверхность, полученная перемещением некоторой прямой (образующей) вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей образующую, параллельно фиксированному ненулевому вектору в пространстве.
Ограничимся случаем, когда направляющая расположена в одной из координатных плоскостей, а образующая перпендикулярна этой плоскости. Возьмем для определенности в плоскости Оху кривую второго порядка и будем перемещать прямую, параллельную оси Oz, вдоль этой кривой. Так как проекцией любой точки M(x,y,z) полученного таким образом цилиндра на плоскость Оху является точка N(x,y), принадлежащая кривой второго порядка, то координаты точки М удовлетворяют уравнению этой кривой. Следовательно, уравнением построенного цилиндра является уравнение его направляющей.
Перечислим теперь цилиндры второго порядка.
1) 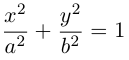
В частности, при а = b мы получим круговой цилиндр.
2 2 X у
2) 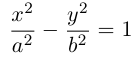
3) 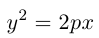
Аналогичные уравнения имеют цилиндры второго порядка, образующие которых параллельны осям Ох и Оу, а направляющие расположены в координатных плоскостях Oyz и Oxz, соответственно.
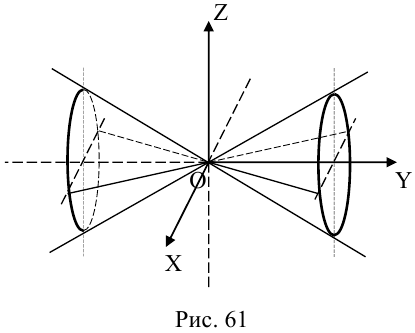
Конус второго порядка
Конус второго порядка представляет собой поверхность, которая может быть получена перемещением прямой (образующей), имеющей неподвижную точку, которая называется вершиной конуса, вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей вершину.
Найдем уравнение конуса, вершина которого совпадает с началом координат, а направляющей служит эллипс с уравнением
расположенный в плоскости z = с, с > 0.
Пусть M(x,y,z) — произвольная точка конуса. Обозначим через 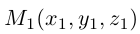
а точки M — уравнениям
Из последних уравнений мы находим:
Подставив найденные выражения для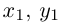
Координатная ось Oz называется осью конуса. Если а = b, то конус является круговым.
Конусы второго порядка с осями Ох и Оу имеют, соответственно, уравнения:
Покажем, что вид конуса второго порядка не зависит от выбора направляющей. Действительно, если в качестве направляющей взять гиперболу
находящегося в плоскости 2 = с, то после рассуждений, аналогичных предыдущим, получим поверхность с уравнением
т. е. конус с осью Ох. Если же за направляющую мы выберем в плоскости z = с параболу с уравнением
то построенный таким образом конус имеет уравнение
Наблюдая со стороны положительной полуоси Оу, повернем систему координат Oxz вокруг оси Оу на угол 45° против часовой стрелки. Тогда произведение xz в системе координат
запишется как 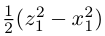
и, стало быть, эта поверхность является конусом с осью
Как следует из уравнения конуса и его построения, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, сечениями конуса плоскостями, параллельными его оси, являются гиперболы, и, наконец, в сечениях конуса плоскостями, параллельными образующей, располагаются параболы.
Приведение уравнения поверхности второго порядка к каноническому виду
По аналогии с уравнением кривой второго порядка (§4, пункт 4), уравнение поверхности второго порядка, не содержащее произведений координат, мы можем за счет выделения полных квадратов привести к уравнению одной из рассмотренных в пунктах 1—5 поверхностей. Следовательно, мы получим одну из поверхностей второго порядка в смещенной с помощью параллельного переноса системе координат. Исключение, правда, составляет случай, когда уравнение поверхности содержит полный квадрат и два линейных слагаемых относительно других координат. Такая поверхность представляет собой параболический цилиндр в смещенной с помощью параллельного переноса и повернутой затем вокруг одной из координатных осей системе координат.
Пример №8
Привести уравнение второго порядка
к каноническому виду, назвать и построить поверхность.
Решение. После выделения полных квадратов по переменным у, z получим:
Переписав это уравнение в виде
мы замечаем, что в смещенной с помощью параллельного переноса в точку 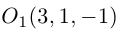
Прямая на плоскости. Общее уравнение прямой на плоскости
Докажем, что всякая прямая на плоскости задается в любой пдск уравнением первой степени относительно двух переменных.
Если A – некоторая точка на прямой 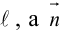
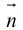
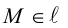
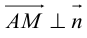
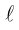
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY .
В этой системе координат
Пусть M (x, y) – произвольная точка
на 
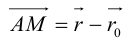
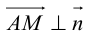
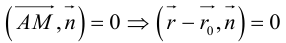

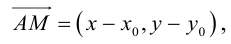
Координаты точек, лежащих на прямой
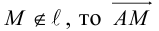
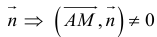
Определение: Любой ненулевой вектор 

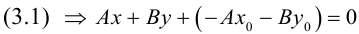
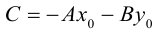
(3.2) – общее уравнение прямой на плоскости,
Уравнение прямой с направляющим вектором
Определение: Любой ненулевой вектор 
Если A – некоторая точка на прямой 
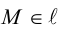
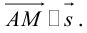

Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY . В этой системе координат
Пусть M (x, y) – произвольная точка на . Тогда 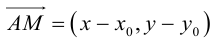
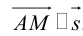
(3.3) – уравнение прямой на плоскости с направляющим вектором.
Если 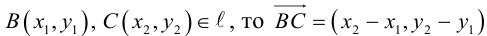
Уравнение прямой с угловым коэффициентом
Пусть 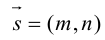
Определение: Угловым коэффициентом прямой 
Очевидно, что если 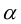
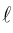
Рассмотрим уравнение (3.3) прямой с направляющим вектором
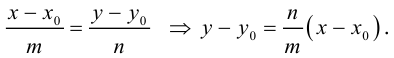
Отсюда следует (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку
Из (3.5) получим 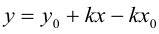
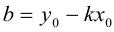
(3.6) – уравнение прямой с угловым коэффициентом.
Угол между прямыми на плоскости
Определение: Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен 0 или
Пусть прямые заданы общими уравнениями.
Условие параллельности прямых:
Условие перпендикулярности прямых:
Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.
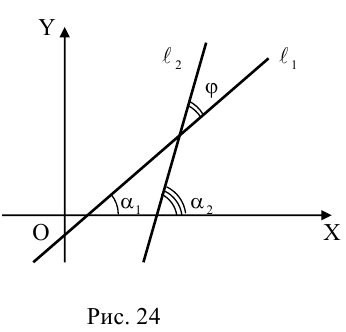
Так как 
Условие параллельности прямых:
Условие перпендикулярности:
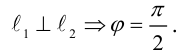
не существует, то
Пример №9
Даны вершины треугольника:
Написать:
а) уравнение медианы AM , б) высоты AH , в) найти угол между AM и AH
(рис. 25).

Перепишем уравнение медианы в общем виде:
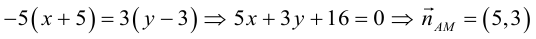
б)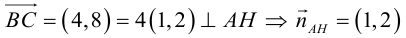
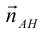
в)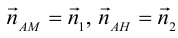
Расстояние от точки до прямой на плоскости
Пусть в некоторой пдск XOY задана прямая 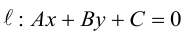
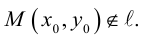
Пусть 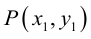
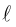
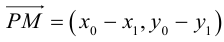
Нормаль
где d – искомое расстояние, 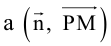
Следовательно,
Так как 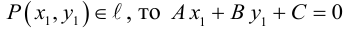
Отсюда
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
Пример №10
Найти длину высоты
Уравнение 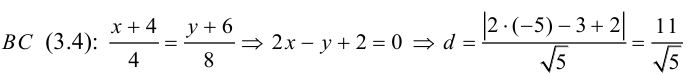
искомая длина высоты АН.
Кривые второго порядка
Окружность
Определение: Кривые второго порядка – плоские линии, которые в пдск XOY задаются уравнениями второй степени относительно двух переменных x,y.
Определение: Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск XOY . Пусть 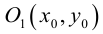
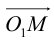
Если точка M (x, y) не лежит на окружности, то 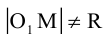
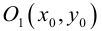
Если 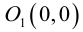
(3.10) – каноническое уравнение окружности.
Пример №11
Показать, что уравнение 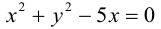
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной x :
Пример №12
Написать уравнение линии центров окружностей
Найдем центр второй окружности:
Уравнение прямой (3.4), проходящей через две точки:
Эллипс
Определение: Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы 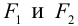
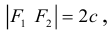
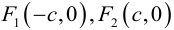
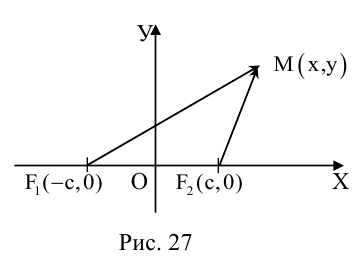
2a>2c определению эллипса.
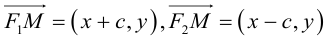
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к
более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
Сложим (3.11) и (3.12) и результат возведем в квадрат:
Так как по определению a>c, то есть 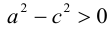
Тогда из (3.13) получим:
(3.14) – каноническое уравнение эллипса.
Исследуем форму эллипса по его каноническому уравнению. Найдем точки пересечения с осями координат:
Из (3.14) следует, что
Значит, эллипс расположен в прямоугольнике со сторонами 
Кроме того, из уравнения следует, что он симметричен относительно OX и OY . O(0,0) – точка пересечения осей симметрии – центр симметрии эллипса.
Ось, на которой лежат фокусы, называется фокальной осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
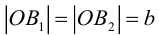
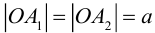
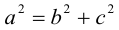
Отношение полуфокусного расстояния к длине большой полуоси 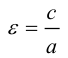
Так как 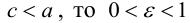
ЗАМЕЧАНИЕ 1. Уравнение эллипса, центр которого 
ЗАМЕЧАНИЕ 2. К кривым второго порядка эллиптического типа относятся также мнимый эллипс
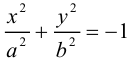
Пример №13
Найти эксцентриситет эллипса 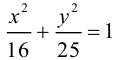
Так как 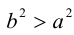
Гипербола
Определение: Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск следующим образом:
ось абсцисс проведем через фокусы 
ка 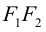
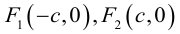
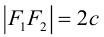
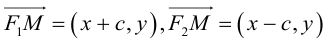
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении:
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:
По определению 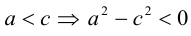
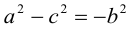
(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична относительно осей координат. Если x=0, 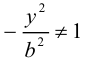
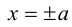
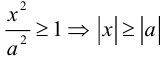
c – полуфокусное расстояние, a – действительная полуось, b – мнимая полуось. Отношение полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом гиперболы: 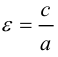
Считая, что 
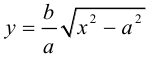
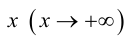
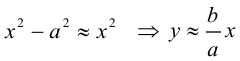
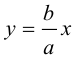
причем ординаты точек на ней меньше соответствующих ординат точек на этой
прямой: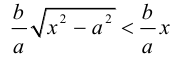
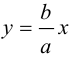
Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой четвертях. Поэтому 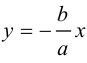
Итак, прямые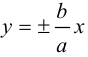
Если фокусы гиперболы лежат на OY , то ее уравнение имеет вид:
Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот (3.19) такие же, как и для (3.18), но действительной является ось OY .
Если a = b, то гипербола называется равносторонней: 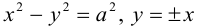
Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на 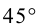
ЗАМЕЧАНИЕ 1. Если центр гиперболы в точке 
ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также пара пересекающихся прямых:
Пример №14
Найти координаты центра и написать уравнения асимптот гиперболы
Приведем данное уравнение к виду (3.20):
Таким образом, 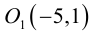
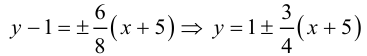
Парабола
Определение: Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).
Пусть расстояние между фокусом F и директрисой DK равно p . Тогда 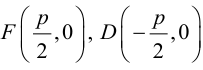
(3.21) – уравнение параболы в выбранной системе координат.
Упростим его:
(3.22) – каноническое уравнение параболы; p называется ее параметром.
Из уравнения следует, что парабола симметрична относительно OX и проходит через начало координат. Кроме того, если 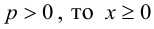
Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид
ЗАМЕЧАНИЕ 1. Если вершина параболы в точке 
ЗАМЕЧАНИЕ 2. К кривым второго порядка параболического типа относятся также 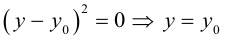
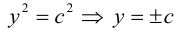
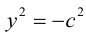
Пример №15
Написать уравнение геометрического места точек, равноудаленных от прямой x + y — 1 = 0 и точки F(-3,2).
По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть M (x, y) – произвольная точка искомой параболы, тогда 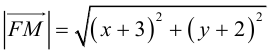
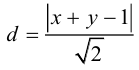
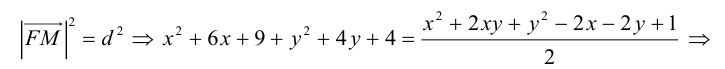
Если оси координат системы XOY повернуть на угол 
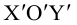
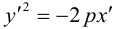
ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.
Преобразования координат на плоскости
Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном n-мерном многообразии.
Параллельный перенос координатных осей
Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат 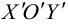
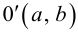
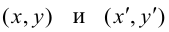
Пусть 
Тогда
так как 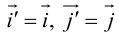
Так как 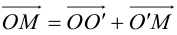
или
(3.23) – формулы параллельного переноса осей пдск.
Поворот координатных осей на угол α
Поворот координатных осей на угол 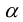
Пусть “новая” пдск 
Из рис. 38 очевидно, что
Так как 
(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.
Если обозначить 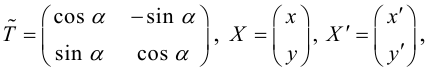
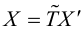
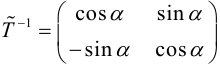
(3.25) – формулы поворота координатных осей на угол 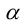
Пример №16
Каким будет уравнение прямой x + y — 1 = 0 после поворота координатных осей на угол
новое уравнение прямой (рис. 39).
Линейные преобразования на плоскости
Рассмотрим систему линейных уравнений:
Каждой точке плоскости M(x, y) по формулам (3.26) можно поставить в соответствие единственную точку 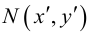
Преобразование (3.26) определяется матрицей 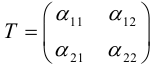
(3.26) можно переписать в виде 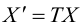
Пример №17
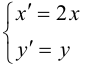
оси OX в 2 раза.
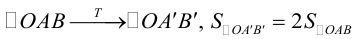
Пример №18
при этом направление обхода 
Определение: Линейное преобразование (3.26) называется невырожденным, если
В этом случае существует обратная матрица 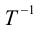
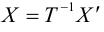
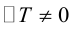
Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.
Пример №19
Пусть 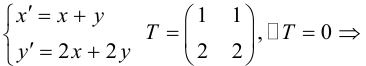
Какими будут образы точек, лежащих, например, на прямой x + y — 1 = 0
(рис. 42)?
Очевидно, что если 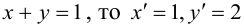
Пример №20
Рассмотрим формулы (3.25):
Очевидно, что поворот осей пдск на угол 
Так как это линейное преобразование невырожденное, то существует
Заметим, что в этом случае
Определение: Матрица A называется ортогональной, если 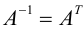
Линейное преобразование, матрица которого ортогональна, называется ортогональным.
Таким образом, поворот координатных осей – ортогональное линейное преобразование.
Можно показать, что если A – ортогональная матрица, то 
Произведение линейных преобразований
Рассмотрим матрицы 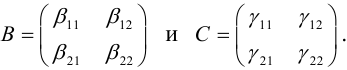
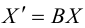
В свою очередь точка N под действием линейного преобразования 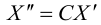
Такое последовательное выполнение линейных преобразований называется их произведением:
Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):
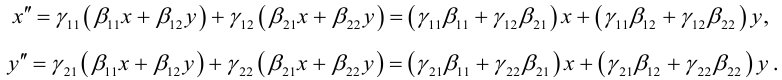
То есть
(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:
Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.
Приведение квадратичной формы к каноническому виду
Определение: Квадратичной формой относительно двух переменных x и y называется однородный многочлен второй степени:
Уравнение 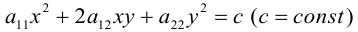
начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).
Предположим, что уравнение 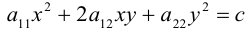
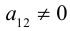
угол 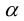
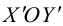
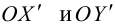
Матрица 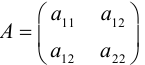
Пусть
Вычислим
Таким образом, квадратичная форма может быть записана в матричном виде:
Пусть x, y – координаты точек плоскости в системе XOY , а 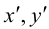
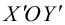
(3.32) – ортогональное линейное преобразование с матрицей
По определению ортогональной матрицы
(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)
Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): 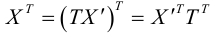
(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.
Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат xy, то 
, где 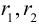
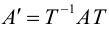
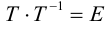
По определению равных матриц имеем:
Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.
Это означает, что 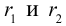
Уравнение (3.36) называется характеристическим уравнением матрицы A (характеристическим уравнением квадратичной формы). Его решения 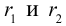
Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.
Вычислим определитель (3.36):
Дискриминант
так как 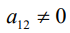
Таким образом, коэффициентами при 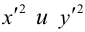
Решим (3.36) и подставим 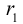
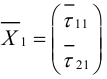
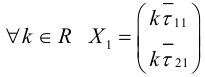
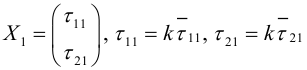
Векторы 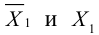
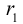
Аналогично подставим 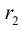
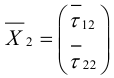
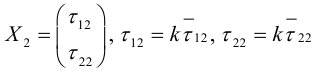
Можно показать, что 
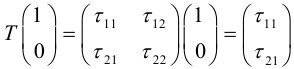
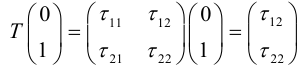
вектор, поэтому ортами “новой” системы координат 
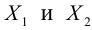
ВЫВОД.
Чтобы привести квадратичную форму к каноническому виду, надо:
- Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при
в каноническом виде квадратичной формы.
- Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат
.При этом если ось
сонаправлена с
– канонический вид, который квадратичная форма имеет в системе
.
Приведение общего уравнения кривой второго порядка к каноническому виду
Общее уравнение кривой второго порядка имеет вид:
В результате невырожденного линейного преобразования с матрицей T квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член 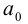
После поворота осей подберем параллельный перенос новой системы 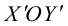
Пример №21
Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:
1) Составим матрицу квадратичной формы:
2) Составим и решим характеристическое уравнение (3.36):
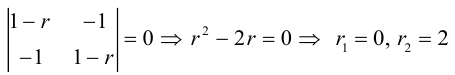
3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):
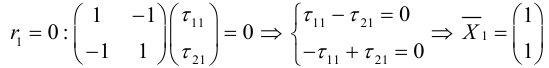
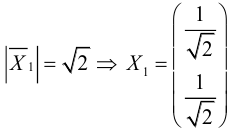
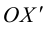
4) Найдем второй единичный собственный вектор, то есть решим (3.35):
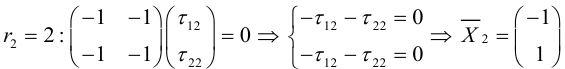
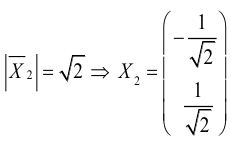
Заметим, что 
В полученной таким образом системе координат 
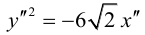
Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.
Плоскость
Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных x, y, z.
Если A – некоторая точка на плоскости 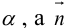
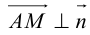
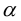
Чтобы вывести уравнение плоскости, зададим в пространстве пдск OXYZ . В этой системе координат
Пусть M(x,y,z) – произвольная точка на плоскости 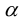
Тогда 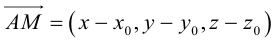
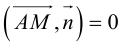
Вычислив скалярное произведение, получим:
Координаты точек, лежащих в плоскости 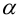
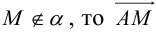
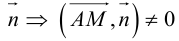
Раскрыв скобки в (3.38), получим 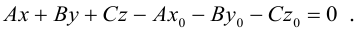
Обозначим 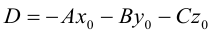
(3.39) – общее уравнение плоскости в пространстве,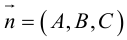
Определение: Любой ненулевой вектор 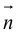
Особые случаи расположения плоскости
Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
, так как
, значит, плоскость
.
, так как
.Значит, плоскость
.
так как
. Значит, плоскость
.
проходит через OX .
проходит через OY .
проходит через OZ .
-
или
.
или
.
-
или
.
– плоскость YOZ .
– плоскость XOZ .
– плоскость XOY .
Уравнение плоскости в отрезках
Пусть плоскость 
Рассмотрим 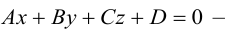
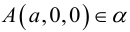
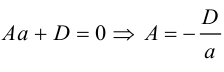
Аналогично 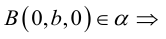
Подставив А, В, С в общее уравнение, получим
(3.40) – уравнение плоскости в отрезках.
Пример №22
Вычислить объем тетраэдра, образованного плоскостями
Перепишем уравнение плоскости в виде (3.40):
уравнение данной плоскости в отрезках. Поэтому (рис. 47)
Уравнение плоскости, проходящей через три точки
Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой:
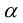
Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости M(x,y,z) . Тогда 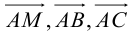
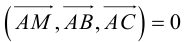
(3.41) – уравнение плоскости, проходящей через три точки.
ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы 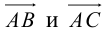
Пример №23
Написать уравнение плоскости, проходящей через точки
Угол между плоскостями
Определение: Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении.
Если плоскости параллельны, то угол между ними равен 0 или 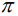
Рассмотрим плоскости 
Очевидно,
или
Если 
Если 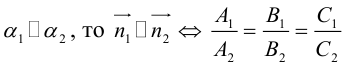
Пример №24
Найти угол между плоскостями
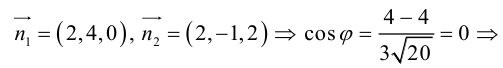
Прямая линия в пространстве
Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей
и
Если 
определяет прямую линию в пространстве.
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами.
Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.
Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.
Канонические уравнения прямой в пространстве
Пусть в некоторой пдск задана прямая 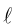
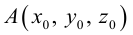
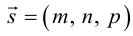
Для произвольной точки 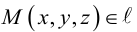
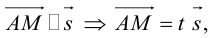
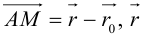
(рис. 49).
Отсюда 
(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:
(3.44) – параметрические уравнения прямой в пространстве, 
Выразим из каждого уравнения (3.44) параметр:
Тогда
(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку 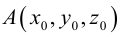
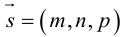
Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей
одна из которых параллельна OZ , а вторая – OY или как
где первая плоскость параллельна OZ , а вторая – OX .
Если прямая 
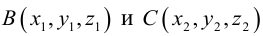
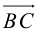
(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.
Угол между прямыми в пространстве
Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:
и
Определение: Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 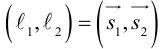
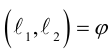
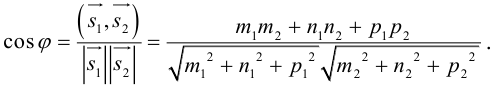
1)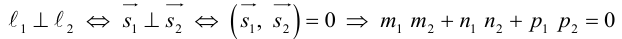
2)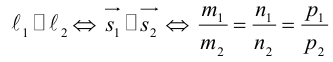
Пример №25
Найти угол между прямой 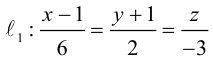
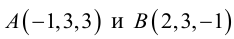
Заметим, что уравнение прямой 
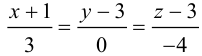
Приведение общих уравнений прямой в пространстве к каноническому виду
Рассмотрим прямую 
Привести эти уравнения к каноническому виду можно двумя способами:
- найти координаты какой-либо точки
, лежащей на
, ее направляющий вектор s и написать уравнения (3.45);
- найти координаты двух точек, лежащих на
, и воспользоваться уравнениями (3.46).
1 способ.
Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц 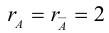
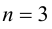
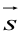
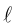
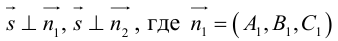
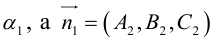
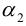
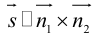
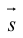
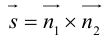
Пример №26
Привести уравнения прямой 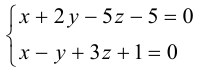
Найдем какое-нибудь частное решение этой системы: пусть, например,
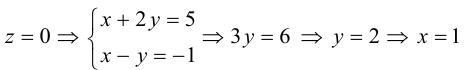
Таким образом, 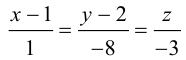
2 способ.
Найдем два произвольных частных решения системы уравнений, задающей прямую.
В рассмотренном примере 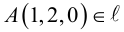
тогда 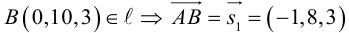
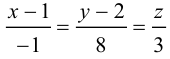
Угол между прямой и плоскостью
Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
и прямая
Определение общих точек прямой и плоскости
Чтобы найти общие точки прямой : 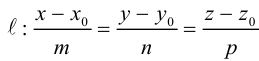
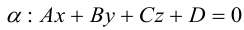
Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):
1) Пусть 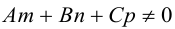
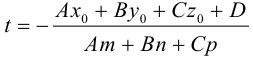
и по формулам (3.44) M(x,y,z) – их точку пересечения.
2) Пусть 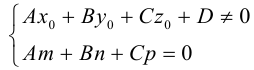
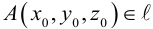
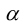
3) Пусть 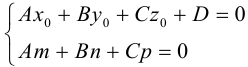
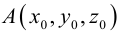
Пример №27
Найти проекцию точки 
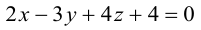
Пусть прямая 
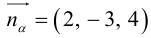
Напишем канонические уравнения прямой (3.45):
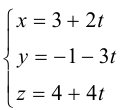
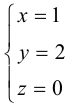
Цилиндрические поверхности
Уравнение F(x, y, z)=0 задает в пространстве некоторую поверхность.
Пусть уравнение содержит только две переменные, например, F(x,y)=0.Рассмотренное в плоскости XOY , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки этой кривой, так как в уравнении отсутствует z , то есть все точки M(x,y,z) у которых х и у связаны соотношением 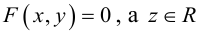
Пример №28
Построить поверхность 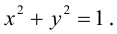
На плоскости это уравнение задает окружность с центром О(0, 0) и R=1.
В пространстве ему удовлетворяют координаты всех точек, проекция которых на плоскость ХОУ лежит на этой окружности. Очевидно, что эта поверхность – круговой цилиндр
(рис. 54).
Цилиндрические поверхности бывают не только круговыми.
Определение: Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.
Для поверхности 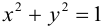
ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность. У поверхности F(y,z) ,образующая параллельна OX , а направляющая лежит в плоскости YOZ . Для поверхности F(x,z) ,образующая параллельна OY , направляющая в плоскости XOZ .
Пример №29
Построить и назвать поверхности 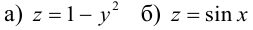
Поверхности вращения
Определение: Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее
плоскости.
Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.
Пусть в плоскости YOZ задана кривая 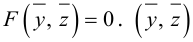
Пусть M(x,y,z) – произвольная точка на поверхности, 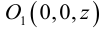
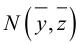
Тогда 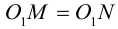
Но
Таким образом, уравнение поверхности вращения получим, если в уравнении кривой 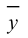
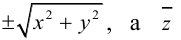
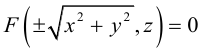
Очевидно, что если кривая F(y,z)=0 вращается вокруг OY , то уравнение
поверхности вращения имеет вид:
Некоторые поверхности второго порядка
1. Пусть эллипс 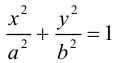
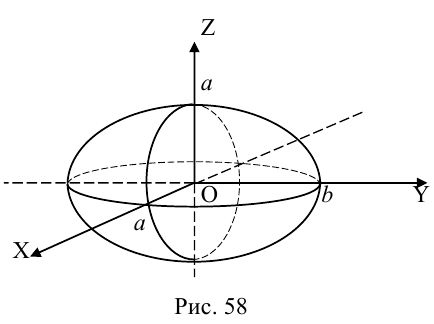
Полученная поверхность является поверхностью второго порядка, так ее уравнение 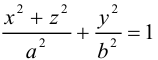
Поверхность, задаваемая уравнением 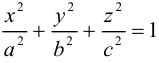
2. Если гипербола 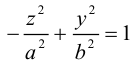
поверхности вращения имеет вид
или
Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).
3. Если гипербола 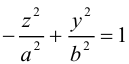
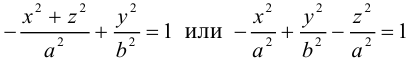
4. Если пара пересекающихся прямых 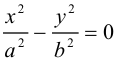
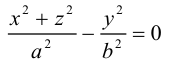
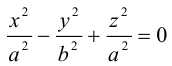
5. При вращении параболы 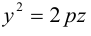
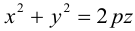
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика























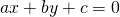
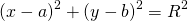

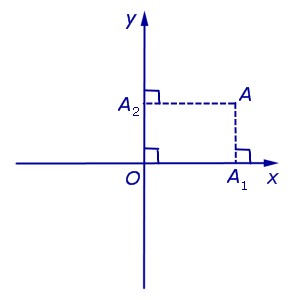
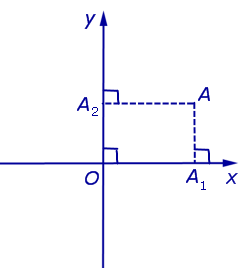
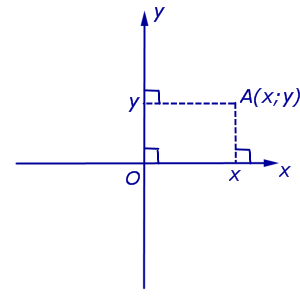
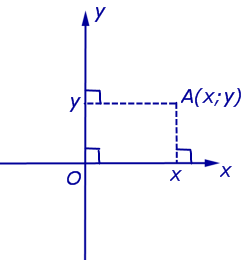
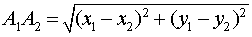
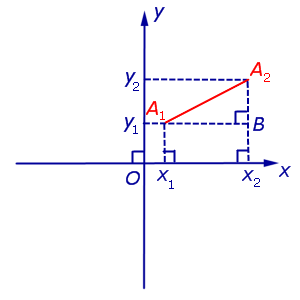
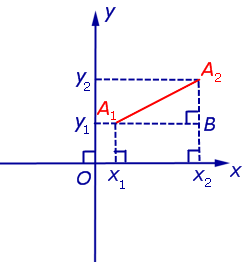
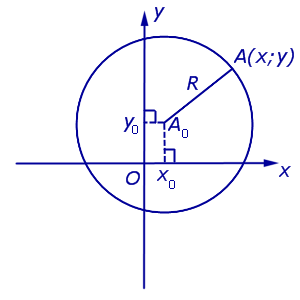
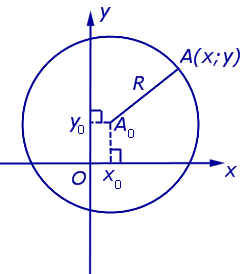
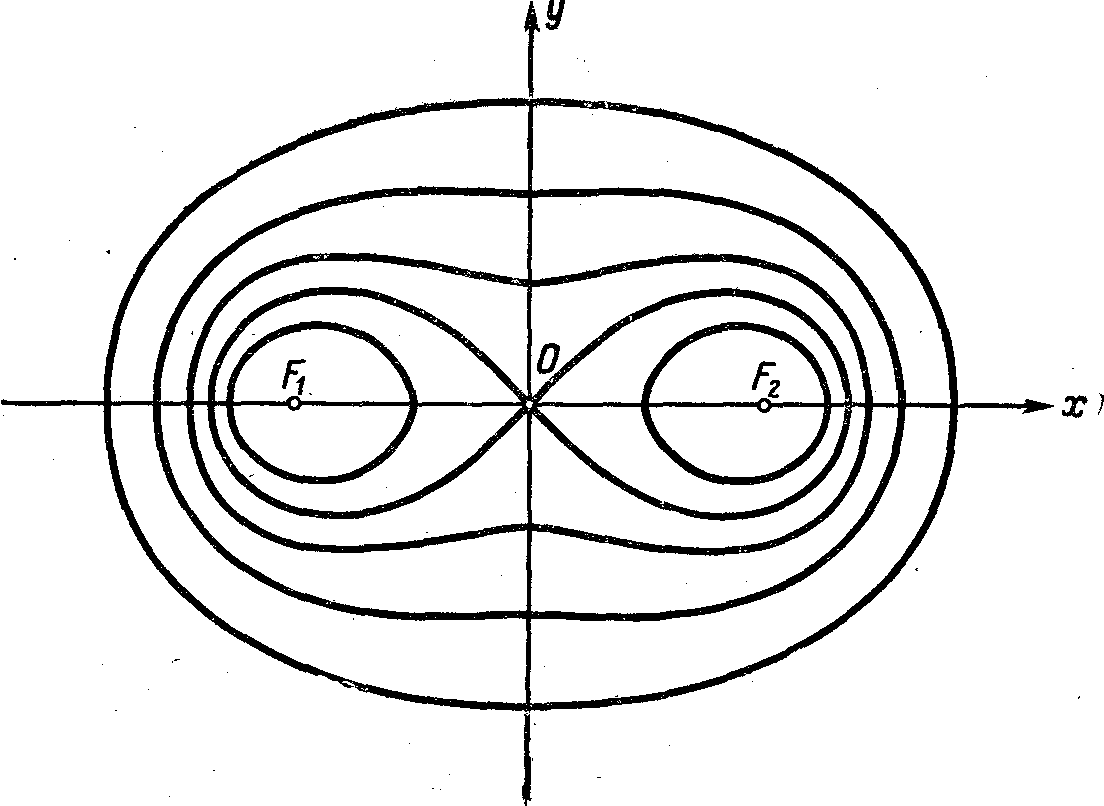
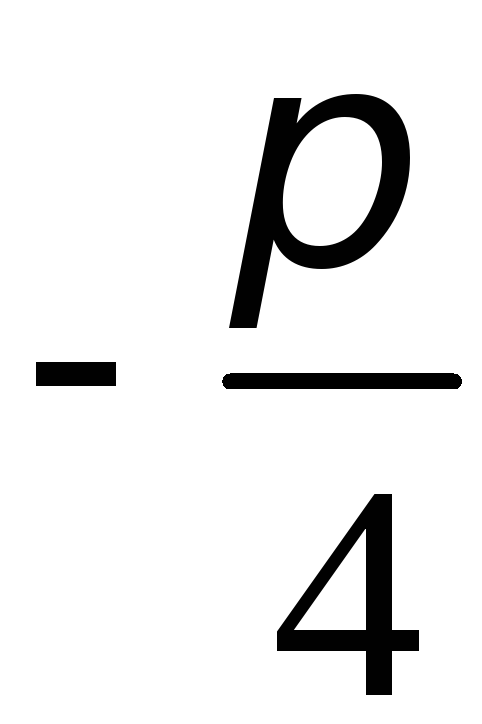
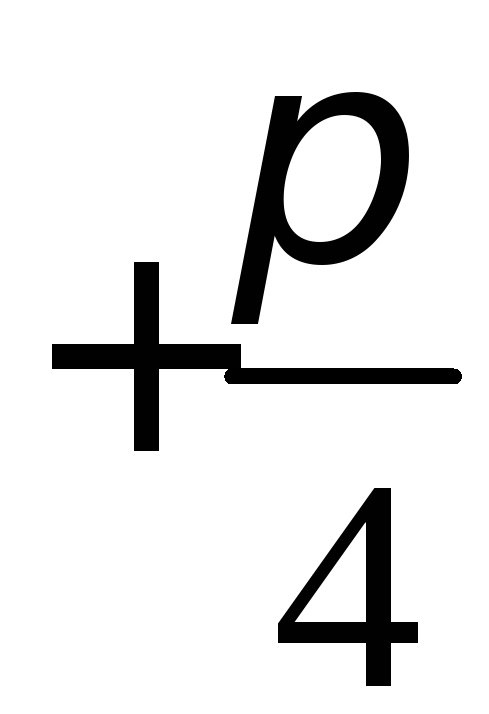

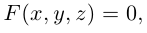
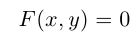
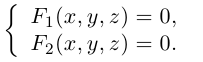

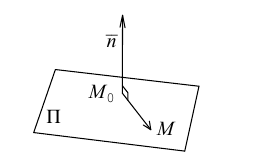
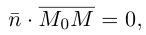
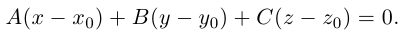
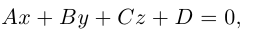
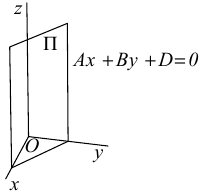
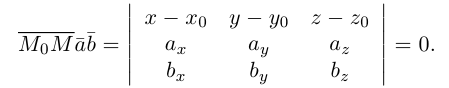
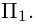
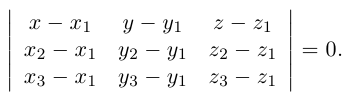
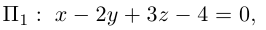
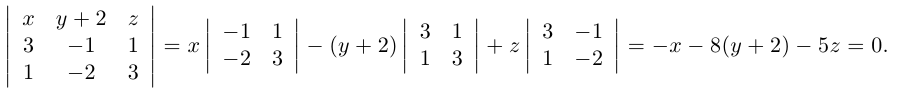
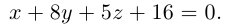
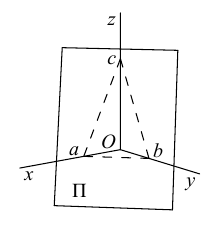
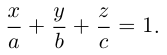
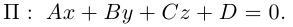
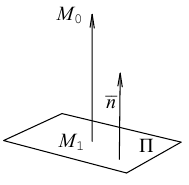
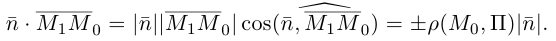
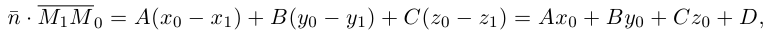
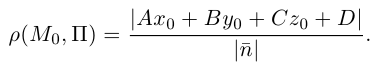
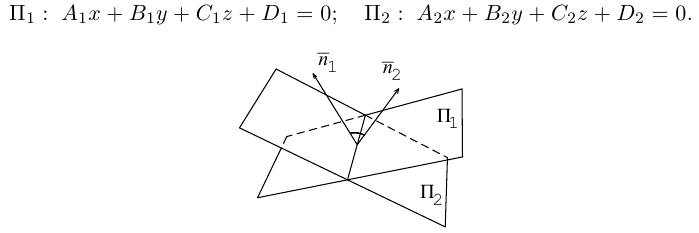
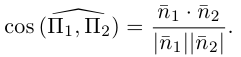
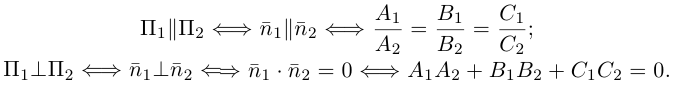
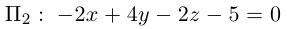
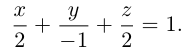
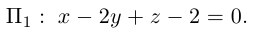
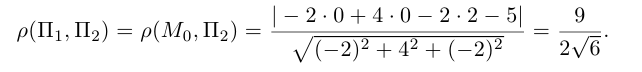
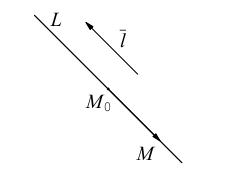
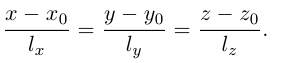
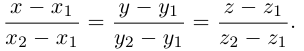
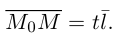
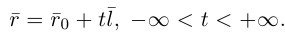
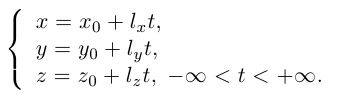
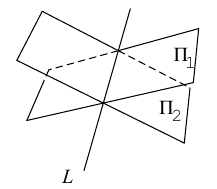
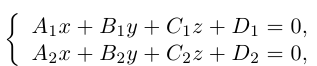
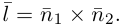
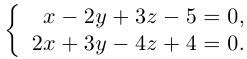
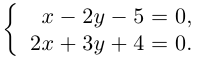
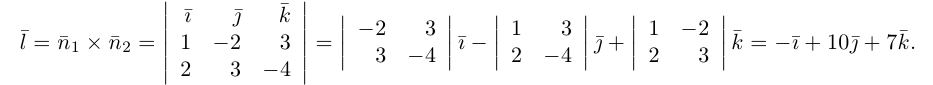
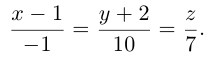
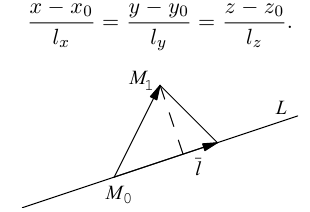
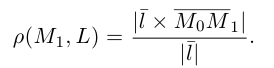
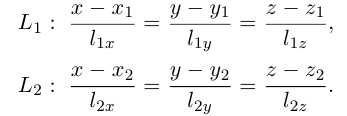
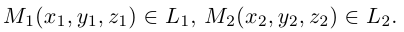
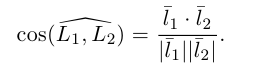
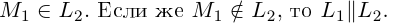
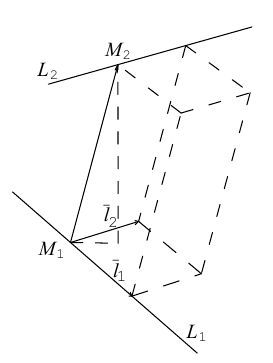
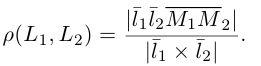
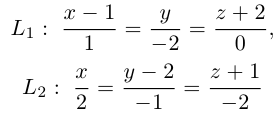
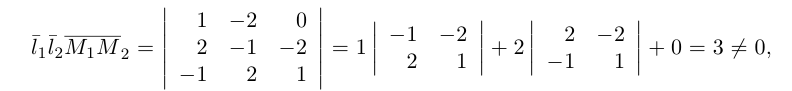
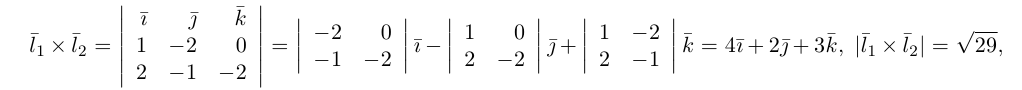
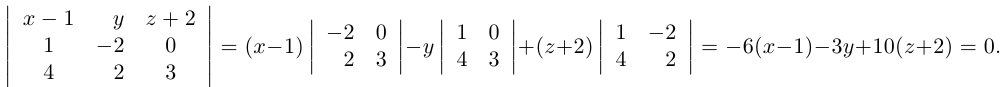
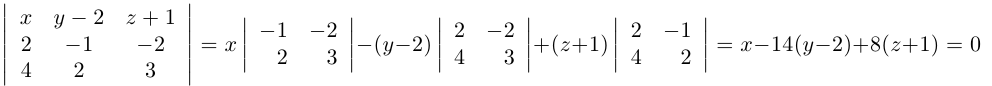
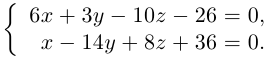
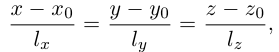
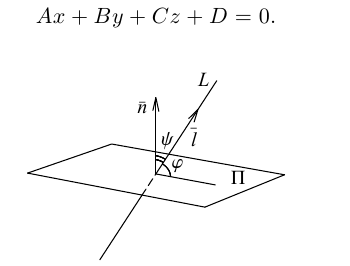
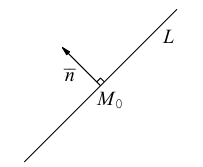
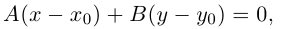
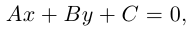
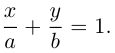
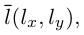
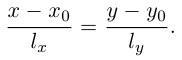
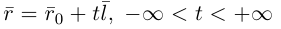
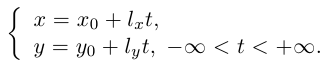
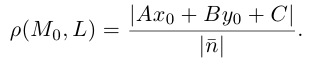
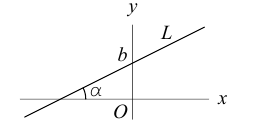
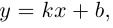
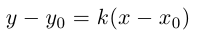
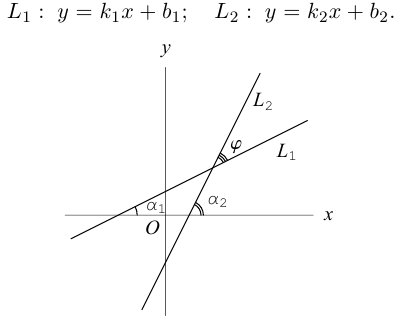
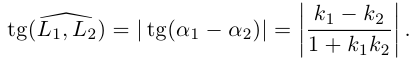
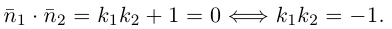
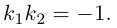
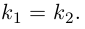
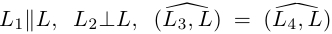
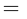
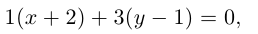
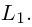
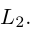
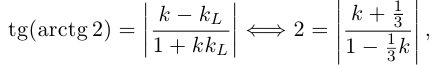
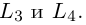
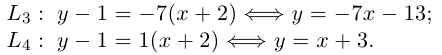
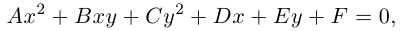
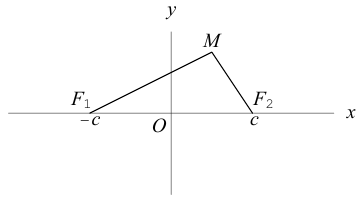
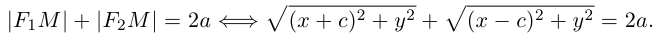
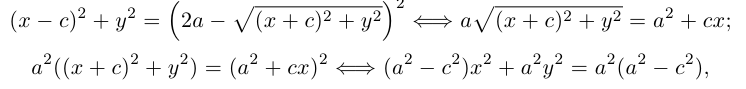
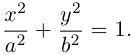
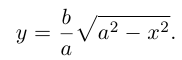
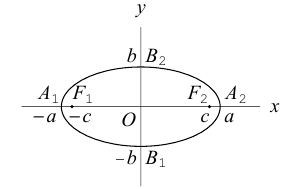
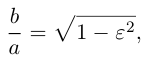
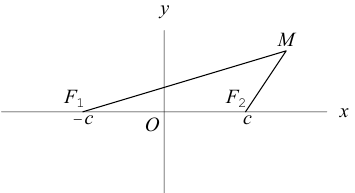
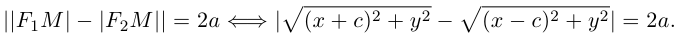
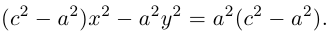
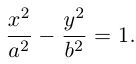
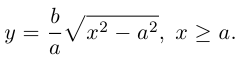
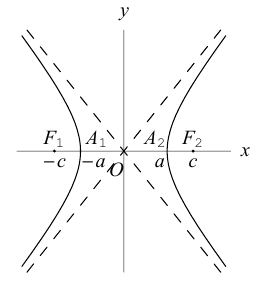
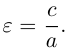
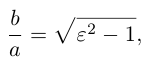
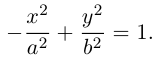
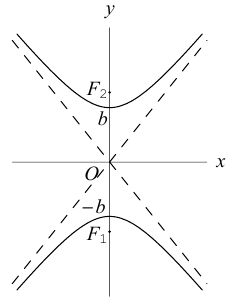
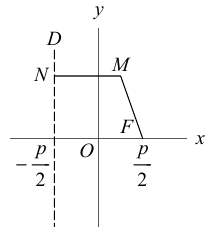
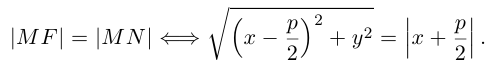
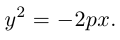
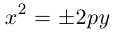
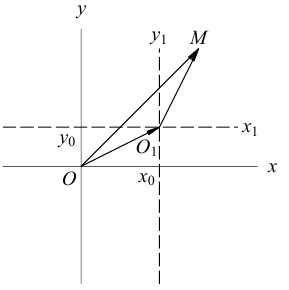
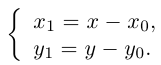
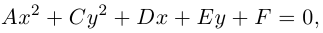
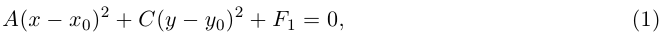
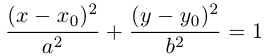
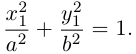
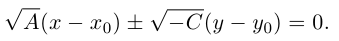
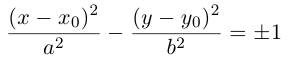
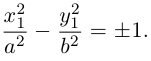
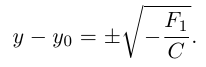
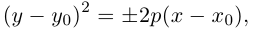
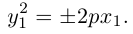
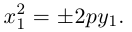
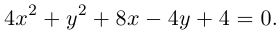
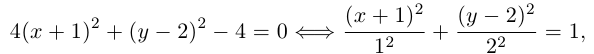
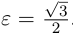
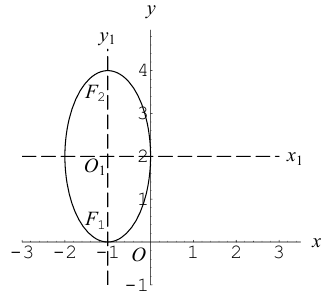
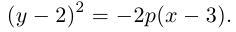
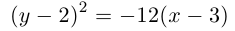
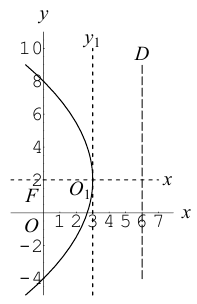
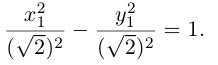
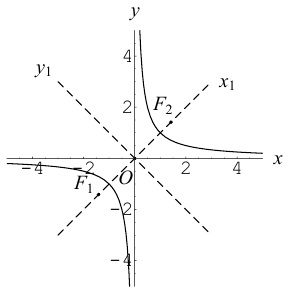
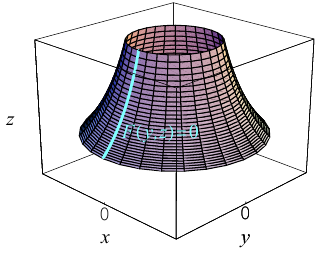
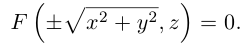
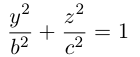
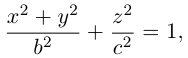
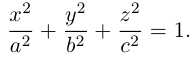
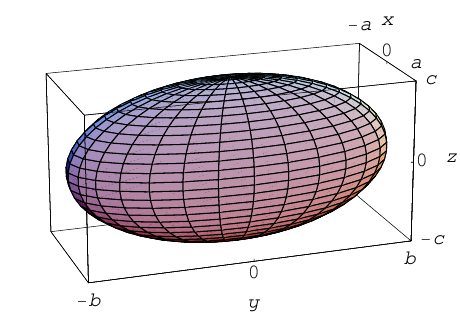
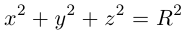
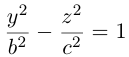
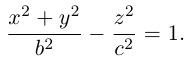
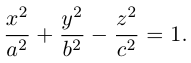
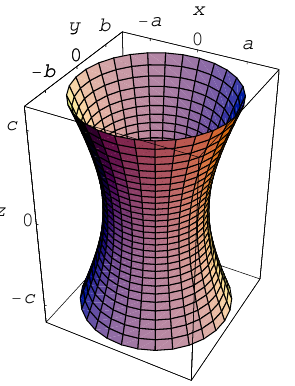
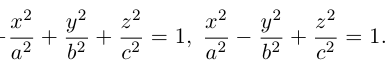
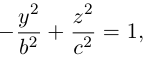
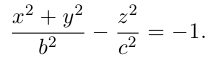
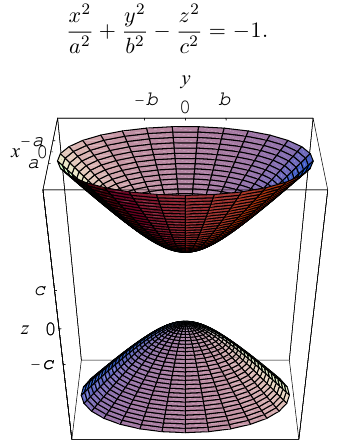
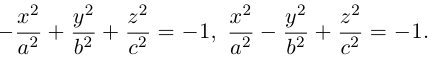
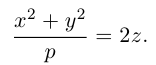
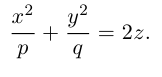
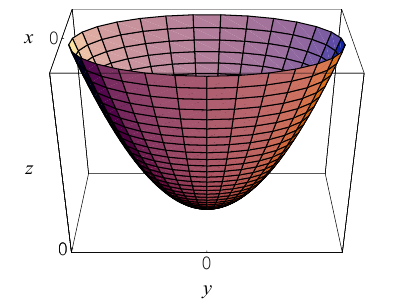
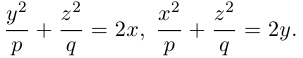
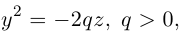
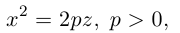
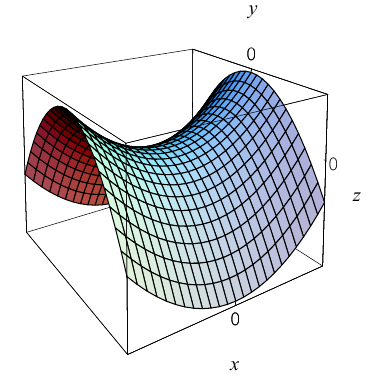
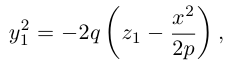
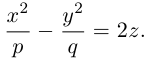
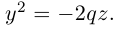
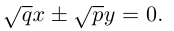
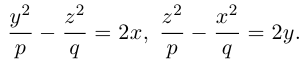
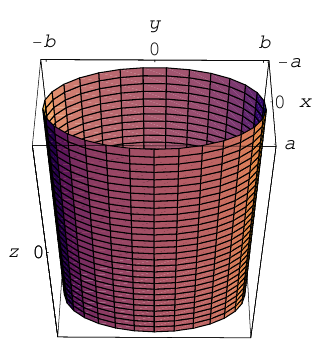
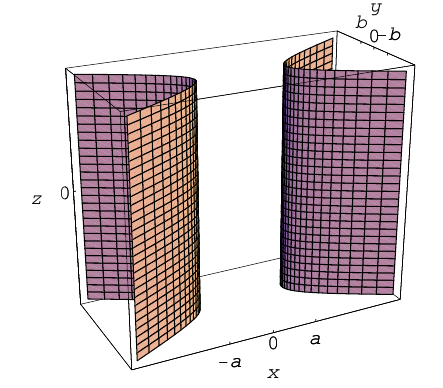
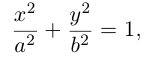
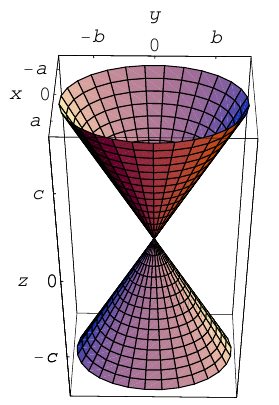
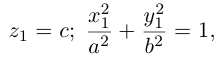
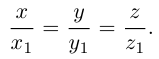
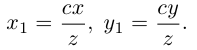
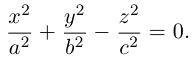
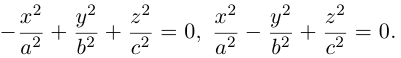
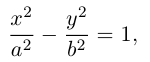
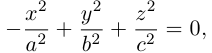
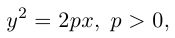
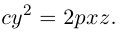
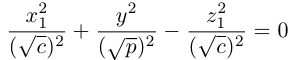
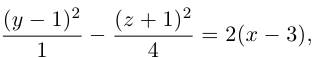
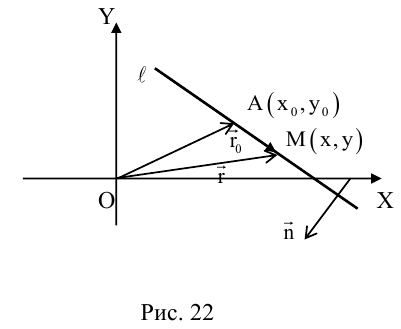
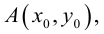
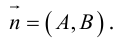


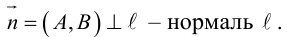
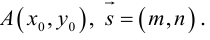


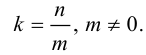
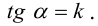
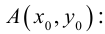


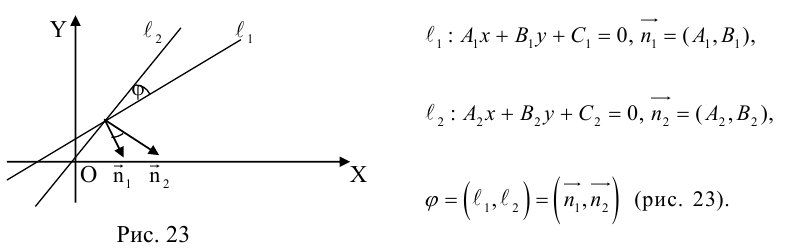
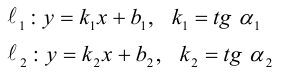
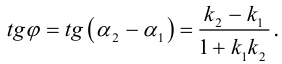
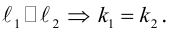
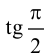
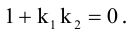
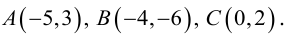
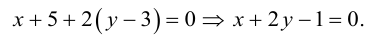
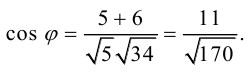
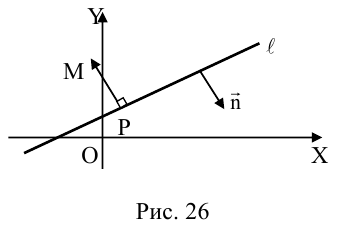

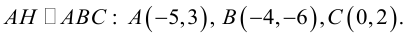
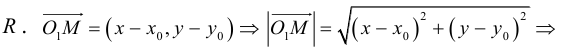


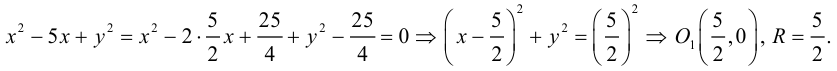
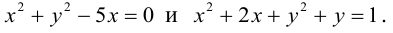
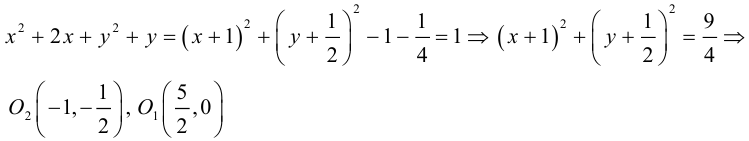
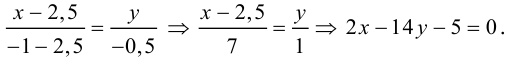
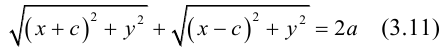
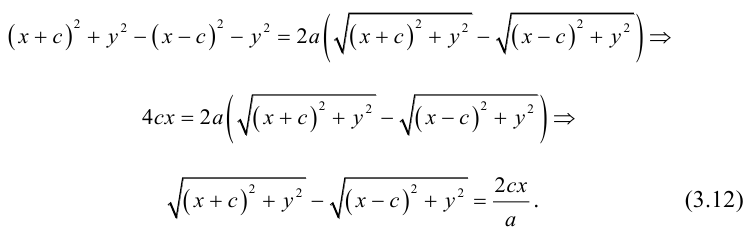
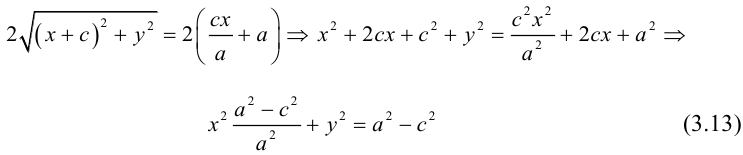

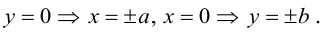
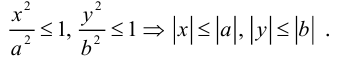

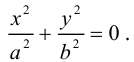
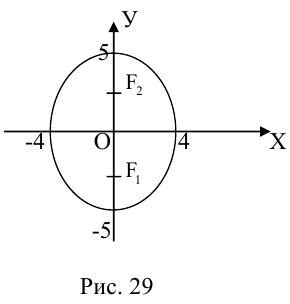
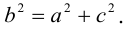
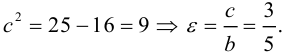
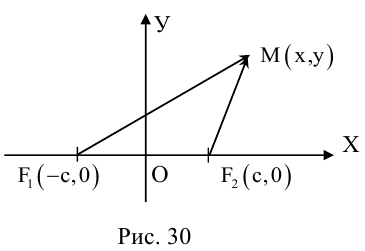
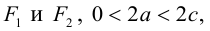
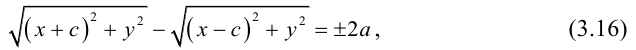


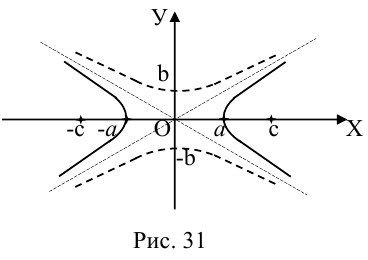

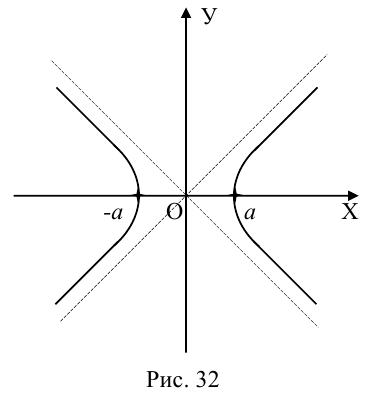
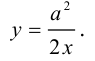
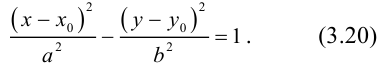
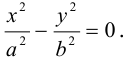
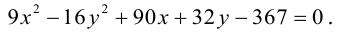
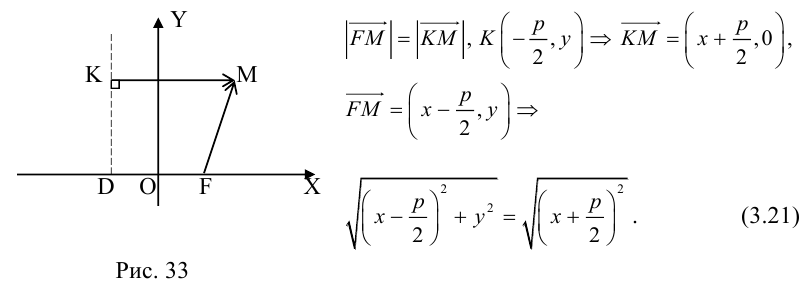
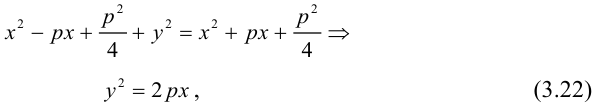
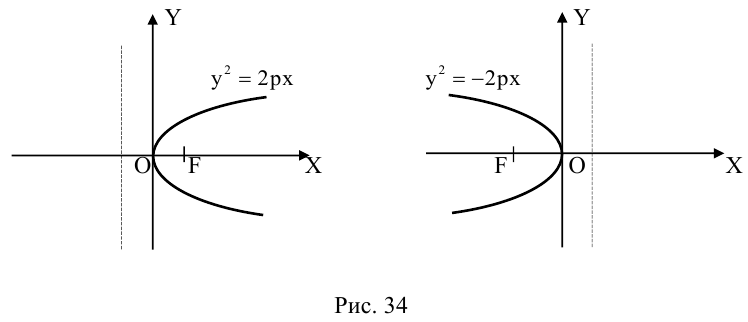
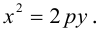
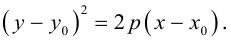
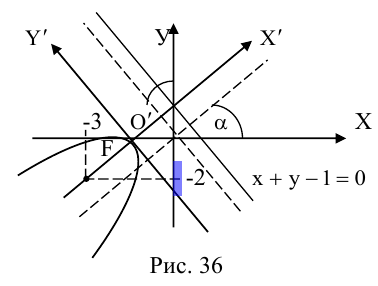
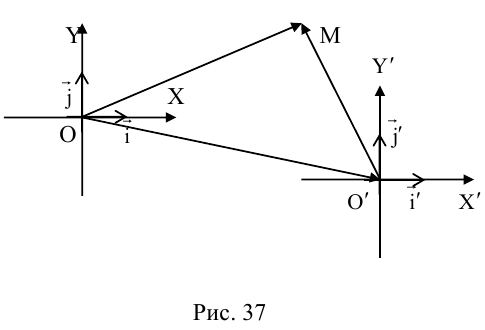
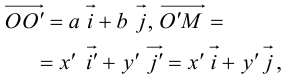
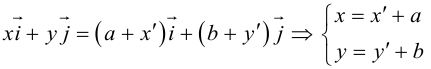

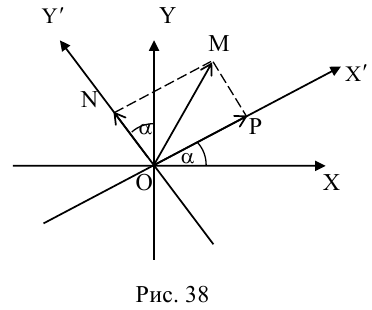

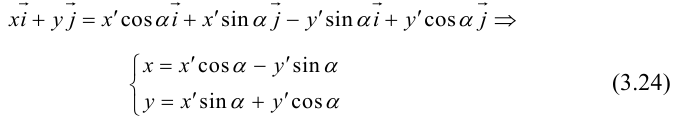
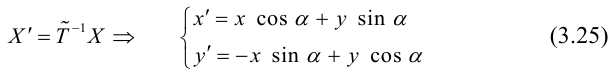
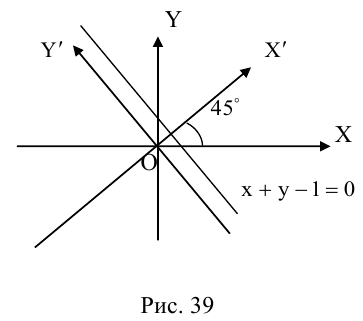
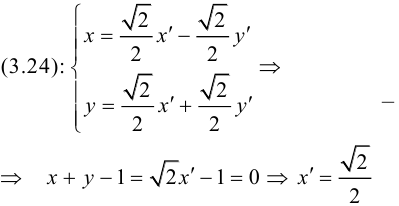

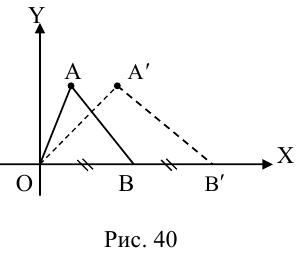
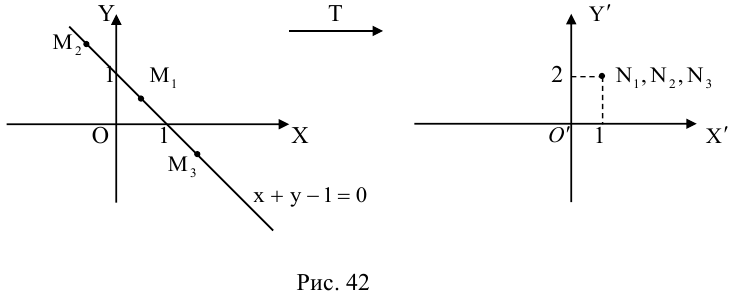
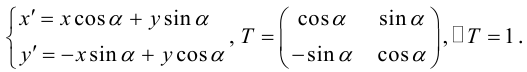
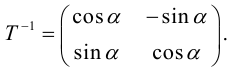
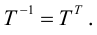

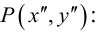

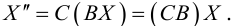
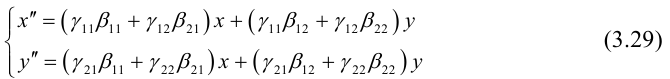
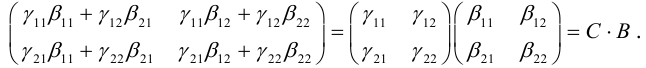
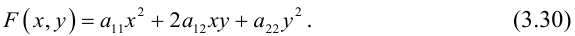
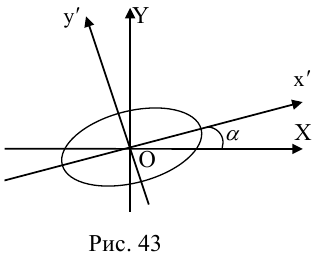
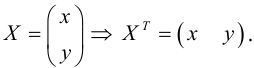
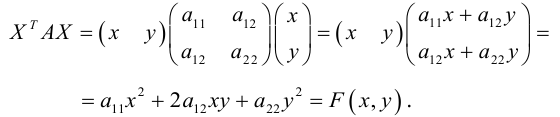

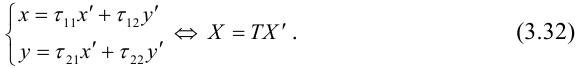
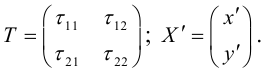

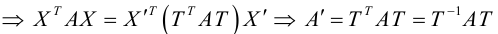
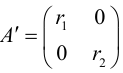
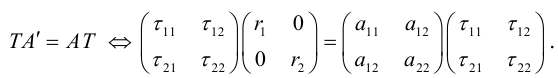
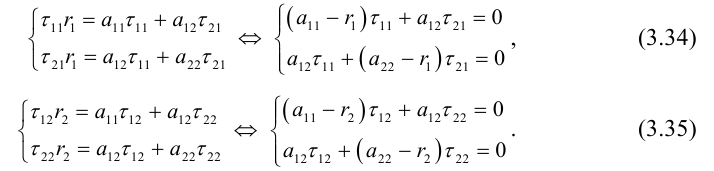
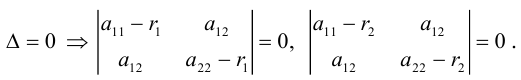
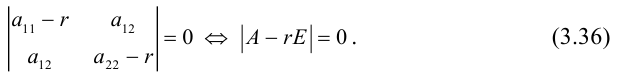
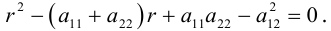
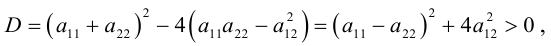
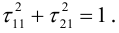
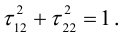
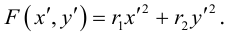
 в каноническом виде квадратичной формы.
в каноническом виде квадратичной формы.  .При этом если ось
.При этом если ось сонаправлена с
сонаправлена с 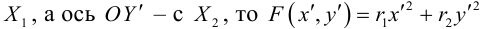 – канонический вид, который квадратичная форма имеет в системе
– канонический вид, который квадратичная форма имеет в системе  .
.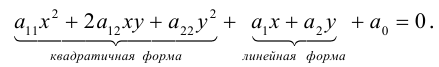
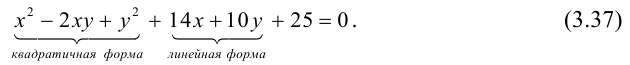
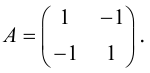
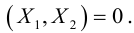
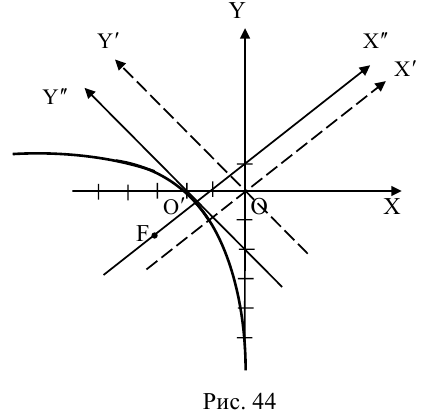
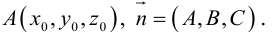
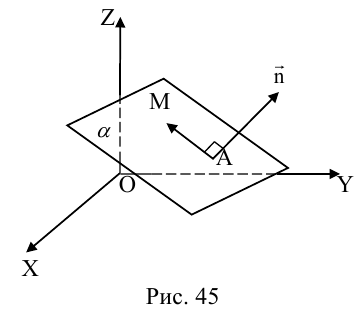
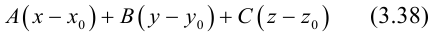

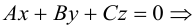 координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат. 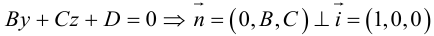 , так как
, так как 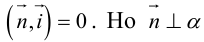 , значит, плоскость
, значит, плоскость  .
. 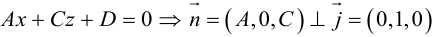 , так как
, так как 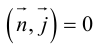 .Значит, плоскость
.Значит, плоскость  .
.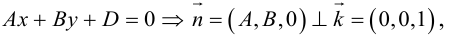 так как
так как 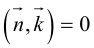 . Значит, плоскость
. Значит, плоскость  .
. 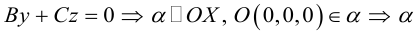 проходит через OX .
проходит через OX . 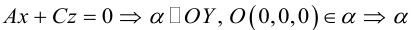 проходит через OY .
проходит через OY . 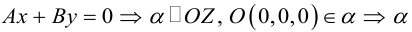 проходит через OZ .
проходит через OZ . 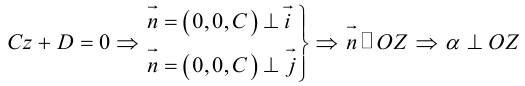 или
или  .
. 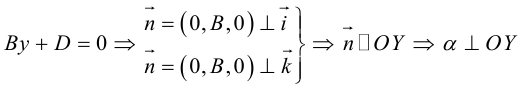 или
или  .
. 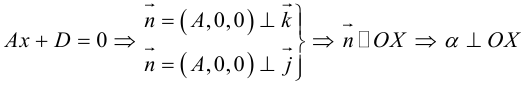 или
или  .
. 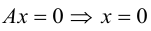 – плоскость YOZ .
– плоскость YOZ . 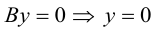 – плоскость XOZ .
– плоскость XOZ . 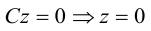 – плоскость XOY .
– плоскость XOY . 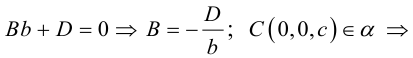
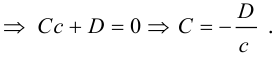
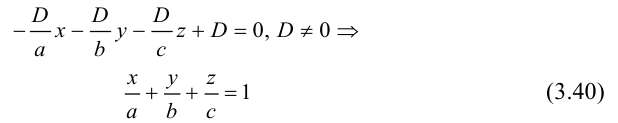
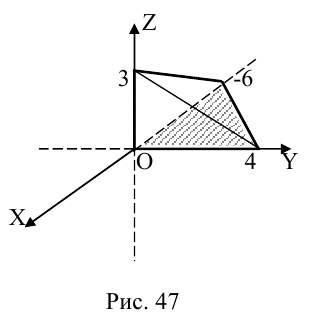
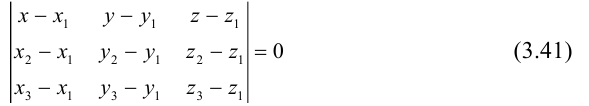
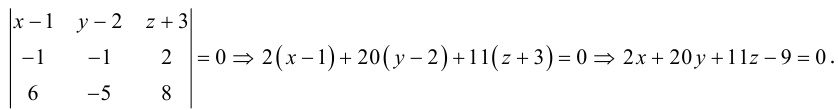
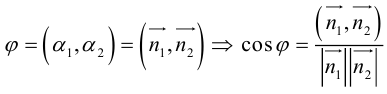
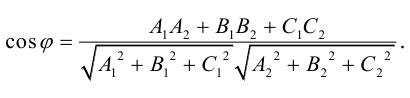
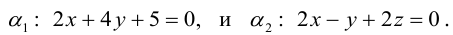
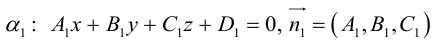
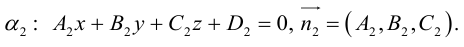
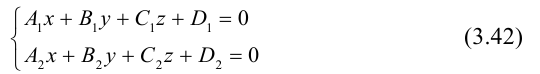

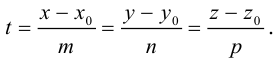

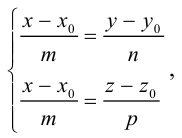
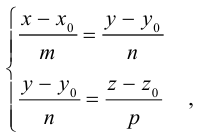

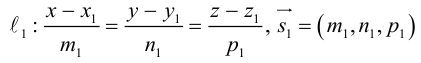
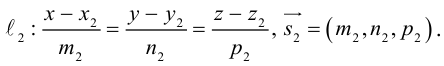
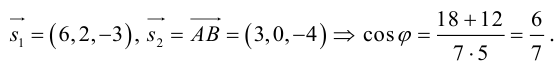
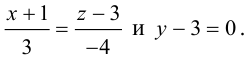
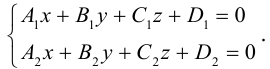
 , лежащей на
, лежащей на