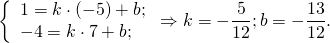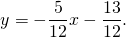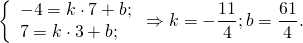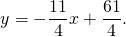Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Пример.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
Решение:
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Уравнение стороны AC —
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Составить уравнение стороны ab треугольника abc
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
УСЛОВИЕ:
Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB
A(-3,8); B(-6;2); C(0,-5)
РЕШЕНИЕ ОТ u821511235 ✪ ЛУЧШЕЕ РЕШЕНИЕ
Добавил vk247797756 , просмотры: ☺ 17346 ⌚ 2018-11-27 17:51:50. математика 1k класс
Решения пользователей
Написать комментарий
Делим обе части равенства на π
и умножаем на 4
+pi k, k in Z
Можно правую часть записать в виде двух ответов:
x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].
x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]
[b]x=-5 – наибольшее отрицательное [/b]
О т в е т. x=1+8n in Z или x=3+ 8n, n in Z
корни чередуются так:
. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .
[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)
a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член
4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0
5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.
∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.
складываем оба равенства:
2* ∠ А=126 градусов.
По формулам приведения:
sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1
sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1
sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z
Найдем корни, принадлежащие указанному отрезку с помощью неравенства:
-286 ° ≤ 90 ° +360 ° *k ≤ 204 °
-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °
-376 ° ≤ 360 ° *k ≤ 114 °
Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]
Значит, указанному отрезку принадлежат два корня:
x=90 ° +360 °* ([green]-1[/green])=-270 °
x=90 ° +360 °*[red]0[/red]=90 °
7. KT- средняя линия трапеции:
Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)
Высоты треугольников АКО и СОК равны половине высоты трапеции
S_( Δ АКО)+S_( Δ COK)=44
S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=
О т в е т. [b]176[/b]
B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды
Что ты хочешь узнать?
Ответ
Проверено экспертом
а) Длина стороны АВ:
б) Уравнение сторон АВ и ВС и их угловые коэффициенты: АВ : Х-Ха = У-Уа
Хв-Ха Ув-Уа
Получаем уравнение в общем виде:
АВ: 4х – 8 = 3у – 6 или
АВ: 4х – 3у – 2 = 0
Это же уравнение в виде у = кх + в:
у = (4/3)х – (2/3).
Угловой коэффициент к = 4/3.
ВС: 2х + у – 16 = 0.
ВС: у = -2х + 16.
Угловой коэффициент к = -2.
в) Внутренний угол В:Можно определить по теореме косинусов.
Находим длину стороны ВС аналогично стороне АВ:
BC = √((Хc-Хв)²+(Ус-Ув)²) = 2.236067977
cos В= ( АВ²+ВС²-АС²) / ( 2*АВ*ВС) = 0.447214
Угол B = 1.107149 радиан = 63.43495 градусов.
Можно определить векторным способом:
Пусть координаты точек
A: (Xa, Ya) = (2; 2) .
B: (Xb, Yb) = (5; 6).
С: (Xc, Yc) = (6; 4).
Находим координаты векторов AB и BС:
AB= (Xb-Xa; Yb-Ya) = ((5 – 2); (6 – 2)) = (3; 4);
BС= (Xc-Xв; Yс-Yв) = ((6 – 5); (4 – 6)) = (1; -2).
Находим длины векторов:
|AB|=√((Xb-Xa)² + (Yb-Ya)^2) = 5 ( по пункту а)
|ВС|=√((Xс-Xв)²+(Yс – Yв) = √(1²+(-2)²) = √5 = 2.236067977 .
b=cos α=(AB*ВС)/(|AB|*|ВС|
AB*ВC = (Xв – Xa)*(Xc – Xв) + (Yв – Ya)*(Yc – Yв) =
= 3*1 + 4*(-2) = 3 – 8 = -5.
b = cosα = |-5| / (5*2.236067977) = 5 / 11.18034 = 0.4472136 20
Угол α=arccos(b) = arc cos 0.4472136 = 1.1071487 радиан = 63.434949°.
г) Уравнение медианы АЕ.
Находим координаты точки Е (это основание медианы АЕ), которые равны полусумме координат точек стороны ВС.
3x – 6 = 3,5y – 7
3x – 3,5y + 1 =0, переведя в целые коэффициенты:
6х – 7у + 2 = 0,
С коэффициентом:
у = (6/7)х + (2/7) или
у = 0.85714 х + 0.28571.
http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik
http://4apple.org/sostavit-uravnenie-storony-ab-treugolnika-abc/
Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:
а) уравнение стороны АС: А(5; 3), С(-4; 15).
Вектор АС = (-4-5; 15-3) = (-9; 12).
уравнение стороны АС: (x – 5)/(-9) = (y – 3)/12 каноническое.
12*(x – 5) — (-9)*(y – 3) = 0,
12х – 60 + 9у – 27 = 0,
12х + 9у – 87 = 0, сократим на 3:
4х + 3у – 29 = 0 общего вида.
Выразим относительно у:
у = (-4/3)х + (29/3) с угловым коэффициентом.
б) длину высоты, проведенной из вершины А.
У прямой, перпендикулярной к прямой общего вида Ах + Ву + С = 0, коэффициенты А и В меняются на В и (-А) или (-В) и А.
Высота, проведенная из вершины А, — это перпендикуляр AD к стороне ВС.
Находим уравнение стороны ВС.
Вектор ВС = (-4-(-11); 15-(-9) = (7; 24).
Уравнение ВС: (x + 11)/7 = (y + 9)/24 каноническое.
24х + 264 – 7у – 63 = 0,
24х – 7у + 201 = 0 общего вида.
Для ВС общего вида 24х — 7у + 201 = 0 уравнение перпендикуляра АD будет таким – АD: 7х + 24у + С = 0.
Подставим координаты точки А(5; 3).
7*5 + 24*3 + С = 0, отсюда С = – 35 – 72 = -107.
Тогда получаем уравнение перпендикуляра AD к стороне BС в общем виде:
AD: 7х + 24у — 107 = 0 общего вида или у = (-7/24)х + (107/24) с угловым коэффициентом.
Находим точку D пересечения перпендикуляра со стороной ВС.
BC: 24х – 7у + 201 = 0 |x24 = 576x — 168y + 4824 = 0
AD: 7х + 24у — 107 = 0 |x7 = 49x + 168y – 749 = 0
625x + 4075 = 0,
x = -4075/625 = -6,52.
y = (24/7)*(-6,52) + (201/7) = -22,3543 +28,7143= 6,36.
D(-6,52; 6,36).
Отрезок AD = √((-6,52-5)² + (6,36-3)²) = √(132,7104 + 11,2896) = √144 = 12.
Можно применить второй вариант определения расстояния от точки А до прямой ВС.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|/√(A² + B²)
Подставим в формулу данные:
d = |24·5 + (-7)·3 + 201|/√(24² + (-7)²) = |120 — 21 + 201|/√(576 + 49) =
= 300/√625 = 12.
в) величину угла В (в радианах).
Находим векторы ВА и ВС.
ВА = (5-(-11); 3-(-9)) = (16; 12),
модуль равен √(16²+ 12²) = √(256 + 144) = √400 = 20.
ВС = (-4-(-11); 15-(-9)) = (7; 24),
модуль равен √(7²+ 24²) = √(49+ 576) = √625 = 25.
Теперь находим косинус угла В:
cos B = (16*7+12*24)/(20*25) = 400/500 = 0,8.
Отсюда угол В = arccos 0,8 = 0,643501 радиан или 57,17432 градуса.
Как составить уравнения сторон треугольника
Есть множество способов определить треугольник. В аналитической геометрии один из этих способов — задать координаты трех его вершин. Эти три точки определяют треугольник однозначно, но для полноты картины нужно еще составить уравнения сторон, соединяющих вершины.
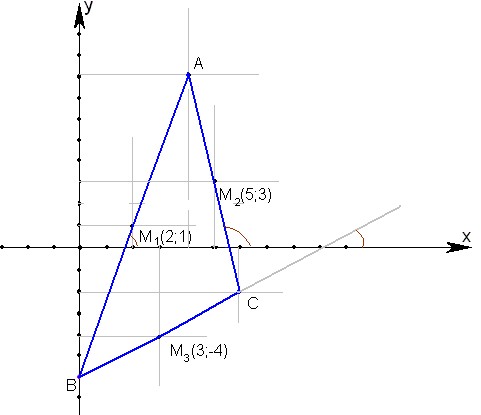
Инструкция
Вам заданы координаты трех точек. Обозначим их как (x1, y1), (x2, y2), (x3, y3). Предполагается, что эти точки являются вершинами некоторого треугольника. Задача состоит в том, чтобы составить уравнения его сторон — точнее уравнения тех прямых, на которых лежат эти стороны. Эти уравнения должны иметь вид:
y = k1*x + b1;
y = k2*x + b2;
y = k3*x + b3.Таким образом, вам предстоит найти угловые коэффициенты k1, k2, k3 и смещения b1, b2, b3.
Убедитесь, что все точки различны между собой. Если какие-то две совпадают, то треугольник вырождается в отрезок.
Найдите уравнение прямой, проходящей через точки (x1, y1), (x2, y2). Если x1 = x2, то искомая прямая вертикальна и ее уравнение x = x1. Если y1 = y2, то прямая горизонтальна и ее уравнение y = y1. В общем случае эти координаты не будут равны друг другу.
Подставляя координаты (x1, y1), (x2, y2) в общее уравнение прямой, вы получите систему из двух линейных уравнений:k1*x1 + b1 = y1;
k1*x2 + b1 = y2.Вычтите одно уравнение из другого и решите полученное уравнение относительно k1:k1*(x2 — x1) = y2 — y1, следовательно, k1 = (y2 — y1)/(x2 — x1).
Подставляя найденное выражение в любое из исходных уравнений, найдите выражение для b1:((y2 — y1)/(x2 — x1))*x1 + b1 = y1;
b1 = y1 — ((y2 — y1)/(x2 — x1))*x1.Поскольку уже известно, что x2 ≠ x1, можно упростить выражение, умножив y1 на (x2 — x1)/(x2 — x1). Тогда для b1 вы получите следующее выражение:b1 = (x1*y2 — x2*y1)/(x2 — x1).
Проверьте, не лежит ли третья из заданных точек на найденной прямой. Для этого подставьте значения (x3, y3) в выведенное уравнение и посмотрите, соблюдается ли равенство. Если оно соблюдается, следовательно, все три точки лежат на одной прямой, и треугольник вырождается в отрезок.
Тем же способом, что описан выше, выведите уравнения для прямых, проходящих через точки (x2, y2), (x3, y3) и (x1, y1), (x3, y3).
Окончательный вид уравнений для сторон треугольника, заданного координатами вершин, выглядит так:(1) y = ((y2 — y1)*x + (x1*y2 — x2*y1))/(x2 — x1);
(2) y = ((y3 — y2)*x + (x2*y3 — x3*y2))/(x3 — x2);
(3) y = ((y3 — y1)*x + (x1*y3 — x3*y1))/(x3 — x1).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.