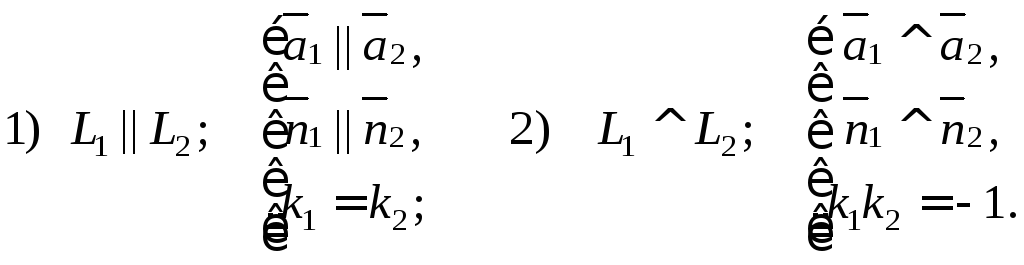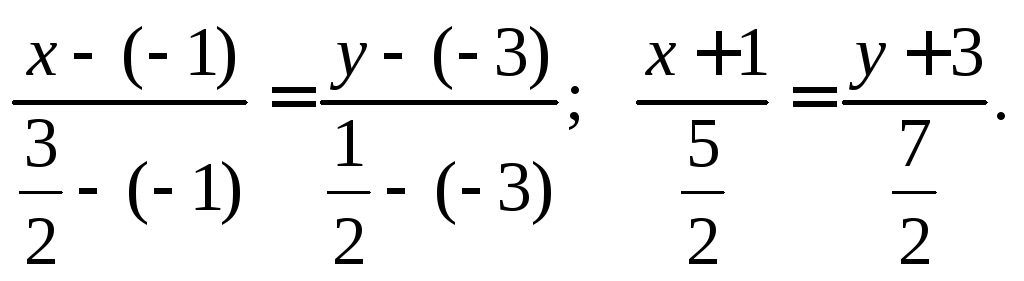Как найти уравнение прямой для медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Пример.

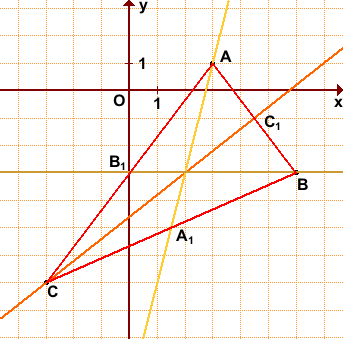
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Решение:

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

1) По формулам координат середины отрезка

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы  BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

C(-3;-7), C(4,5;-1), y=kx+b:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

9.1. Прямая на плоскости

Рассмотрим
различные случаи задания прямой L
на плоскости.

1. Если
задан ненулевой направляющий
вектор

и радиус-вектор
некоторой фиксированной точкито в этом случае радиус-векторпроизвольной точкизадается формулой

(9.1)

где

Уравнение (9.1)
называется
векторно-параметрическим уравнением
прямой L.

2. Если
– координаты точкикоторая лежит на прямойL,
(l, m)
– координаты направляющего вектора
то прямая задаетсяпараметрическими
уравнениями:

3. Если
– направляющий вектор, такой, чтои– точка, через которую проходит прямая,
то имеемканоническое
уравнение:

(9.2)

4. Если прямая L
не параллельна оси Ox,
то для всех направляющих векторов
отношение
По заданному угловому коэффициентуk
прямой L
и точке
уравнение прямойL
может быть задано в следующем виде:

– это уравнение
прямой с угловым коэффициентом
k,
проходящей
через точку
М₀.

В случае, если
– точка пересечения прямойL
с осью Oy,
это уравнение может быть записано в
следующем виде:

5. Координаты
направляющего вектора
прямойL
могут быть найдены, если известны две
точки
иэтой прямой:

Уравнение
прямой, проходящей через две заданные
точки:

(9.3)

6. Если известны
точки пересечения прямой L
с координатными осями, т. е. точки M₀(a,
0) и M₁(0,
b),
то справедливо уравнение
«в отрезках»:

7. Положение прямой
на плоскости однозначно определено и
в случае, когда задан ненулевой нормальный
вектор
этой прямой и точкаУсловие перпендикулярности векторовпозволяет перейти к векторному уравнению

и затем к его
координатной форме:

или

(9.4)

где

Уравнение (9.4)
называется общим
уравнением прямой
L.

8. Если в качестве
нормального вектора берется единичный
вектор
направленный из начала координат в
сторону прямой, т. е.

то справедливо
нормальное
уравнение
прямой L
на плоскости:

где
– расстояние от начала координат до
прямой.

Величина
δ(M₀,
L)
= x₀cos α
+ y₀cos β
– p,
где

называется отклонением точки М₀
от прямой L.
При этом δ
< 0, если точки M₀
и O(0,
0) лежат по одну сторону от прямой L,
δ
> 0 – если по разные. Расстояние d(M₀,
L)
от точки до прямой равно абсолютному
значению отклонения.

От общего уравнения
прямой к нормальному можно перейти с
помощью умножения на нормирующий
множитель:

где

Расстояние от
точки M₀(x₀,
y₀)
до прямой L:
Ax
+ By
+ C
= 0 может быть
найдено по формуле

(9.5)

Угол между прямыми
легко найти с помощью косинуса угла
между их направляющими или нормальными
векторами, а также по формуле

где k₁
и k₂
– угловые коэффициенты прямых.

При этом возможны
частные случаи:

Здесь L₁
и L₂
– прямые на плоскости, для которых
– угловые коэффициенты соответственно
прямыхи

В полярной системе
координат уравнение прямой имеет вид

ρcos(φ
– φ₀)
= p,

где p
– длина перпендикуляра, проведенного
из полюса к прямой, φ₀
– угол между полярной осью и перпендикуляром.

Пример 1.
Даны вершины треугольника ABC:
A(1, 2),
B(–1, –3),
C(2, –1).
Найти:

1) уравнение прямой
BC;

2) уравнение высоты
AH
и ее длину;

3) уравнение медианы
BM;

4) угол между прямыми
BM
и AH;

5) уравнения
биссектрис внутреннего и внешнего углов
при вершине А.

Решение.
1) Для составления уравнения прямой BC
воспользуемся заданными координатами
точек B,
C
и уравнением прямой (9.3), проходящей
через две заданные точки. Так как B(–1,
–3), C(2,
–1), имеем:

Последнее уравнение
приведем к общему уравнению, использовав
основное свойство пропорции:

2(x
+ 1) = 3(y
+ 3) или 2x
– 3y
– 7 = 0.

Таким образом,
окончательно получаем:

ВС:
2x
– 3y
– 7 = 0.

2) Для построения
уравнения высоты АН
воспользуемся условием перпендикулярности
прямых AH
и ВС:
нормальным вектором прямой ВС
является
,
т. е.Этот вектор можно рассматривать как
направляющий вектор прямойАН.
Следовательно, каноническое уравнение
прямой AH
согласно формуле (9.2) имеет вид:

(9.6)

где А(1,
2)АН.

В общем виде получим
АН:
3х
+ 2у
– 7 = 0.

Чтобы найти длину
высотыАВС,
опущенной из вершины А,
воспользуемся формулой расстояния
(9.5):

3) Для составления
уравнения медианы ВМ
найдем координаты точки М,
являющейся серединой отрезка AC:

Получим M(3/2,
1/2). Запишем уравнение прямой BM
по двум известным точкам B(–1,
–3) и
используя формулу (9.3):

Приведя его к
общему уравнению, получим:

ВМ:
7x
– 5y
– 8 = 0.

4) Угол φ
между прямыми BM
и AH
найдем, используя угол между их нормальными
векторами:

Получаем

5) Пусть точка M(x,
y)
лежит на биссектрисе угла BАС.
Тогда по свойству биссектрисы d(M,
AB)
= d(M,
AC).
Запишем уравнения прямых АВ
и
АС. Имеем:

Следовательно,

Аналогично

т. е.

Используем формулу
расстояния (9.5):

Следовательно,

По основному
свойству пропорции и свойству модуля
имеем:

Итак, получили две
биссектрисы (внутреннего и внешнего
углов при вершине А):

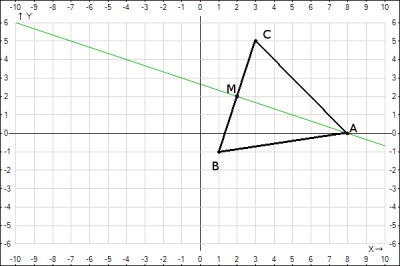
Пример 2.
Даны две точки A(–3,
и B(2,
2). На оси Ox
найти такую точку M,
сумма расстояний от которой до двух
заданных точек была бы наименьшей.

Решение.
Воспользуемся утверждением, смысл
которого состоит в следующем: наименьший
путь между двумя точками достигается
в случае движения по прямой. Тогда задача
будет заключаться в поиске точки
пересечения прямой AB
(рис. 9.1) с осью Ox,
где B
– точка, симметричная точке В
относительно оси Ox
(или в нахождении точки пересечения
прямой AB
с осью Ox,
где A
– точка, симметричная точке А
относительно оси Ox).

Рис. 9.1

Точки B(2,
–2) и A(–3,
определяют прямую AB:

т. е.
или

Значит, для
нахождения координат искомой точки М
осталось решить систему уравнений:

Решаем ее:

Итак, точка М(1,
0) является искомой.

Задания

Соседние файлы в папке Часть 2

• #
• #
• #
• #
• #
• #
• #
• #
• #

1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)

Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть

(х-0) = k•(-1)

(y-4) = k•(-4)

откуда получаем -х=k и -y/4 +1 = k, приравниваем k

-x = -y/4 + 1 или

4x — y = -4

2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М — середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)

Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)

Получаем (x-3)/2 = (y-1)/0,5

0,5х — 1,5 = 2y — 2

x — 4y = -1

3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0

AB (3-0; 1-4) = AB(3; -3)

CH (x-2; y-(-3))

<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0

3x-6 — 3y — 9 = 0

x-y = 5 — получили уравнение прямой высоты CH

Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)

x+y = 4

Точка Н — пересечение этих двух прямых:

Решая систему уравнений подстановкой, находим х=4,5; y=-0,5

CH (4,5-2; -0,5+3) = CH(2,5; 2,5)

|CH| = √(2,5² + 2,5²) = 2,5•√2

Ответ:

1) 4x — y = -4;

2) x — 4y = -1;

3) 2,5•√2

Лучший ответ

0 Голосов

Posted Декабрь 5, 2013 by Вячеслав Моргун 1. Вычислить длину медианы АМ. Для нахождения длины медианы найдем координату точки M, зная координаты точки A найдем расстояние между этими точками, которое рассчитывается по формуле  $$d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2} quad (1)$$Найдем координаты точки M, которая находится по середине между точками B(1;-1) и  C(3;5), координаты рассчитываются по формуле $$M(frac{x_B+x_C}{2};frac{y_B+y_C}{2})$$ подставляем значения координат и получаем $$M(frac{1+3}{2};frac{-1+5}{2}) => M(2;2)$$ Найдем длину медианы, подставим координаты точек в формулу (1) $$d_{AM} = sqrt{(8-2)^2+(0-2)^2} = 2sqrt{10}$$ 2. Уравнение медианы AM. Известны две точки A и M через которые проходит медиана. Для составления уравнения медианы, воспользуемся формула уравнения прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек и получаем уравнение медианы$$frac{x-8}{2-8}=frac{y-0}{2-0} => y = -frac{1}{3}x+frac{8}{3}$$ 3. Наносим полученные точки и уравнение прямой на декартовую систему координат.

Другие ответы