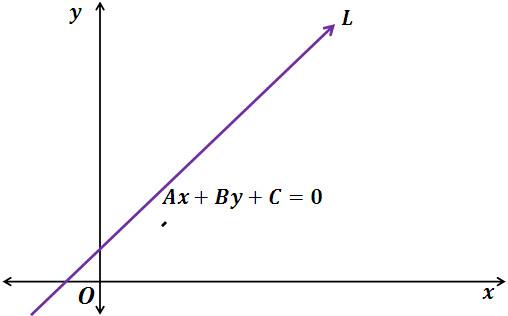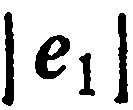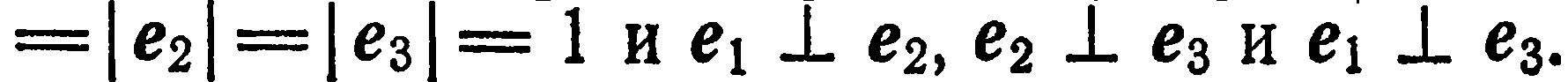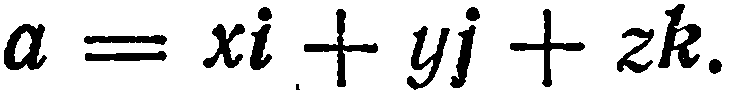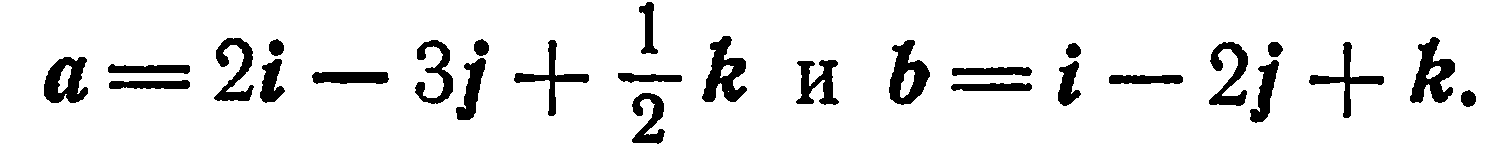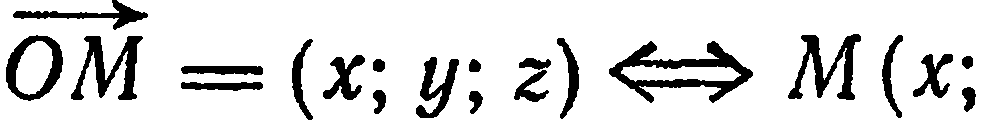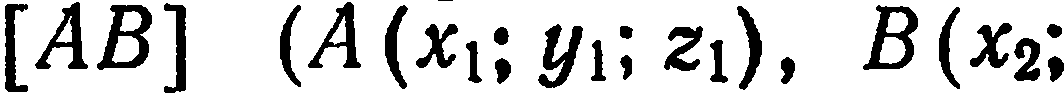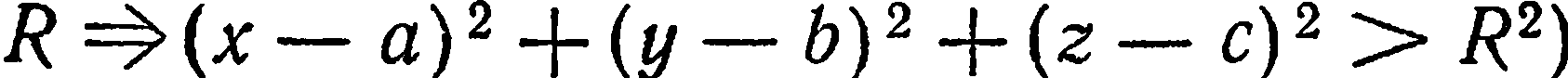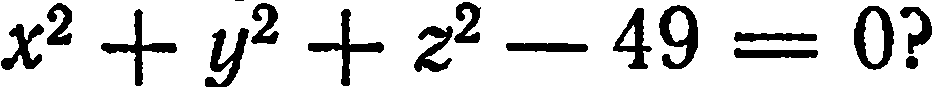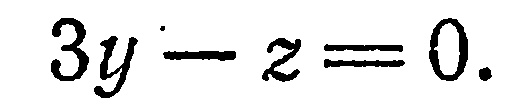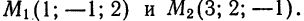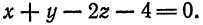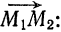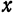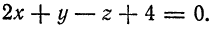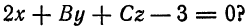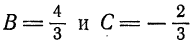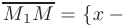Направляющий вектор прямой, координаты направляющего вектора прямой
С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
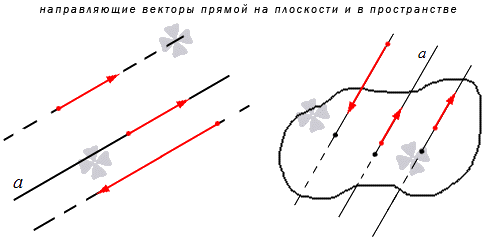
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .
Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
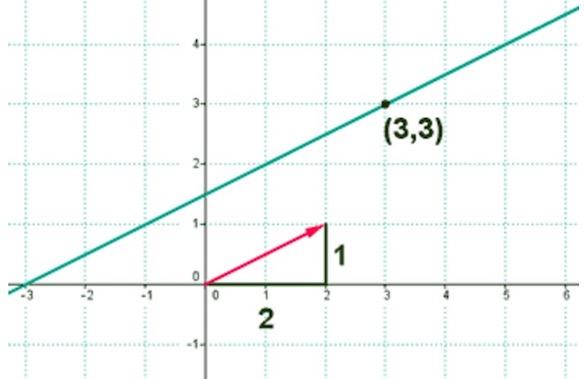
Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.
Ответ: 4 , — 3 .
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .
А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.
У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.
Ответ: ( 0 , 1 )
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10
Получившееся равенство преобразовываем и получаем:
3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.
Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0
Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .
Решение
Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .
Решение
Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .
У нас получится:
n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →
Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: — 20 , 10 , 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Направляющий вектор прямой: определение и примеры
Важным геометрическим объектом, который изучают в плоском пространстве, является прямая. В трехмерном же пространстве, помимо прямой, появляется еще плоскость. Оба объекта удобно задавать с помощью направляющих векторов. Что это такое, как применяют эти вектора для определения уравнений прямой и плоскости? Эти и другие вопросы освещаются в статье.
Прямая и способы ее задавания
Каждый школьник хорошо представляет, о каком геометрическом объекте идет речь. С точки зрения математики, прямая представляет собой набор точек, которые в случае их попарного произвольного соединения между собой приводят к получению совокупности параллельных векторов. Это определение прямой используют для написания уравнения для нее как в двумерном, так и в трехмерном пространстве.

Для описания рассматриваемого одномерного объекта пользуются разными видами уравнений, которые перечислены в списке ниже:
- общего вида;
- параметрическое;
- векторное;
- каноническое или симметричное;
- в отрезках.
Каждый из названных видов имеет некоторые преимущества по отношению к другим. Например, уравнением в отрезках удобно пользоваться при изучении поведения прямой относительно осей координат, уравнение общего вида удобно при нахождении направления, перпендикулярного заданной прямой, а также при вычислении угла ее пересечения с осью x (для плоского случая).

Поскольку тема данной статьи связана с направляющим вектором прямой, то далее будем рассматривать только уравнение, где этот вектор является принципиальным и содержится явно, то есть векторное выражение.
Задание прямой через вектор
Предположим, что у нас имеется некоторый вектор v¯ с известными координатами (a; b; c). Поскольку координат три, то вектор задан в пространстве. Как изобразить его в прямоугольной системе координат? Делается это очень просто: на каждой из трех осей откладывается отрезок, длина которого равна соответствующей координате вектора. Точка пересечения трех перпендикуляров, восстановленных к плоскостям xy, yz и xz, будет концом вектора. Началом же его является точка (0; 0; 0).
Тем не менее приведенное положение вектора не является единственным. Аналогичным образом можно нарисовать v¯, располагая его начало в произвольной точке пространства. Эти рассуждения говорят о том, что задать конкретную прямую с помощью вектора нельзя. Он задает семейство из бесконечного числа параллельных прямых.
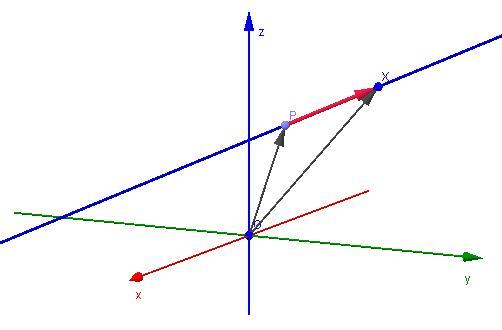
Теперь зафиксируем некоторую точку P(x0; y0; z0) пространства. И зададим условие: через P должна проходить прямая. В этом случае вектор v¯ тоже должен содержать эту точку. Последний факт означает, что можно задать одну единственную прямую, используя P и v¯. Она запишется в виде следующего уравнения:
Здесь Q — любая точка, принадлежащая прямой. Эту точку можно получить, подобрав соответствующий параметр λ. Записанное уравнение называется векторным, а v¯ получил название направляющего вектора прямой. Располагая его так, чтобы он проходил через P, и изменяя его длину с помощью параметра λ, мы получаем каждую точку Q прямой.
В координатной форме уравнение запишется так:
(x; y; z) = (x0; y0; z0) + λ × (a; b; c)
И в явном (параметрическом) виде можно записать:
Если в приведенных выражениях исключить третью координату, то мы получим векторные уравнения прямой на плоскости.
Для каких задач полезно знать направляющий вектор ?
Как правило, это задачи на определение параллельности и перпендикулярности прямых. Также определяющий направление прямой вектор используется при вычислении дистанции между прямыми и точкой и прямой, для описания поведения прямой относительно плоскости.
Две прямые будут параллельными, если таковыми являются их направляющие вектора. Соответственно, перпендикулярность прямых доказывается с помощью перпендикулярности их векторов. В этих типах задач достаточно рассчитать скалярное произведение рассматриваемых векторов, чтобы получить ответ.
В случае задач на вычисление расстояний между прямыми и точками направляющий вектор входит явно в соответствующую формулу. Запишем ее:
Здесь P1P2¯ — построенный на точках P1 и P2 направленный отрезок. Точка P2 является произвольной, лежащей на прямой с вектором v¯, точка же P1 является той, до которой следует определить расстояние. Она может быть как самостоятельной, так и принадлежать другой прямой или плоскости.
Отметим, что рассчитывать расстояние между прямыми имеет смысл только тогда, когда они являются параллельными или скрещивающимися. Если же они пересекаются, то d равно нулю.
Приведенная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой, только в этом случае P1 должна принадлежать плоскости.
Решим несколько задач, чтобы нагляднее показать, как пользоваться рассматриваемым вектором.
Задача на составление векторного уравнения
Известно, что прямая описывается следующим равенством:
Следует написать соответствующее выражение в векторной форме.
Это типичное уравнение прямой, известное каждому школьнику, записано в общем виде. Покажем, как его переписать в векторной форме.
Выражение можно представить в виде:
Видно, что если его раскрыть, то получится исходное равенство. Теперь разделим его правую часть на два вектора так, чтобы только один из них содержал иксы, имеем:
(x; y) = (x; 3 × x) + (0; -4)
Остается вынести x за скобки, обозначить его греческим символом и поменять вектора правой части местами:
(x; y) = (0; -4) + λ × (1; 3)
Мы получили векторную форму записи исходного выражения. Координаты направляющего вектора прямой равны (1; 3).
Задача на определение взаимного расположения прямых
В пространстве заданы две прямые:
(x; y; z) = (1; 0; -2) + λ × (-1; 3; 1);
(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)
Они являются параллельными, скрещивающимися или пересекающимися?
Ненулевые вектора (-1; 3; 1) и (1; 2; 0) будут направляющими для этих прямых. Выразим в параметрической форме эти уравнения и подставим координаты первого во второе. Получаем:
x = 3 + γ = 1 — λ => γ = -2 — λ;
y = 2 + 2 × γ = 3 × λ => γ = 3 / 2 × λ — 1;
z = 2 = -2 + λ => λ = 4
Подставляем найденный параметр λ в два уравнения выше, получаем:
γ = 3 / 2 × λ — 1 = 5
Параметр γ не может одновременно принимать два разных значения. Это означает, что прямые не имеют ни одной общей точки, то есть являются скрещивающимися. Параллельными они не являются, так как ненулевые векторы не параллельны друг другу (для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго).
Математическое описание плоскости
Для задания плоскости в пространстве приведем уравнение общего вида:
A × x + B × y + C × z + D = 0
Здесь латинские большие буквы представляют собой конкретные числа. Первые три из них определяют координаты нормального вектора плоскости. Если его обозначить n¯, тогда:
Этот вектор является перпендикулярным плоскости, поэтому его называют направляющим. Его знание, а также известные координаты какой-либо точки, принадлежащей плоскости, однозначно задают последнюю.
Если точка P(x1; y1; z1) плоскости принадлежит, тогда свободный член D рассчитывается следующим образом:
D = -1 × (A × x1 + B × y1 + C × z1)
Решим пару задач с использованием общего уравнения для плоскости.
Задача на нахождение нормального вектора плоскости
Плоскость задана в следующем виде:
(y — 3) / 2 + (x + 1) / 3 — z / 4 = 1
Как найти направляющий вектор для нее?
Из приведенной выше теории следует, что координаты нормального вектора n¯ являются коэффициентами, стоящими перед переменными. В связи с этим для нахождения n¯ следует записать уравнение в общем виде. Имеем:
1 / 3 × x + 1 / 2 × y — 1 / 4 × z — 13 / 6 = 0
Тогда нормальный вектор плоскости равен:
Задача на составление уравнения плоскости
Даны координаты трех точек:
Как будет выглядеть уравнение плоскости, содержащей все эти точки.
Через три точки, которые одной прямой не принадлежат, можно провести только одну плоскость. Чтобы найти ее уравнение, сначала вычислим направляющий вектор плоскости n¯. Для этого поступим следующим образом: найдем произвольные два вектора, принадлежащие плоскости, и вычислим их векторное произведение. Оно даст вектор, который этой плоскости будет перпендикулярен, то есть n¯. Имеем:
M1M2¯ = (1; -1; 5); M1M3¯ = (-1; -2; -2);
n¯ = [M1M2¯ × M1M3¯] = (12; -3; -3)
Возьмем точку M1 для составления выражения плоскости. Получаем:
D = -1 × (12 × 1 + (-3) × 0 + (-3) × 0) = -12;
12 × x — 3 × y — 3 × z — 12 = 0 =>
4 × x — y — z — 4 = 0
Мы получили выражение общего типа для плоскости в пространстве, определив сначала направляющий вектор для нее.
Свойство векторного произведения следует запомнить при решении задач с плоскостями, поскольку оно позволяет простым способом определять координаты нормального вектора.
Уравнения плоскости, компланарной двум неколлинеарным векторам
Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .
Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.
Пусть в координатном пространстве заданы:
б) два неколлинеарных вектора (рис.4.15).
Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).
Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:
Параметрическое уравнение плоскости
Пусть в координатном пространстве заданы:
б) два неколлинеарных вектора (рис.4.15).
Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).
Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :
где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.
Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:
где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.
1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.
2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:
Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:
3. Направляющие векторы плоскости определяются неоднозначно.
4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:
1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;
2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;
3) записать параметрическое уравнение (4.20).
5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:
и записать общее уравнение плоскости в форме (4.14):
6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.
Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:
а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;
б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и
Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:
1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;
2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;
3) записываем параметрическое уравнение плоскости (4.20):
б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и
Составляем уравнение (4.14):
Тот же результат можно получить, записывая уравнение (4.18):
http://1ku.ru/obrazovanie/41097-napravljajushhij-vektor-prjamoj-opredelenie-i-primery/
http://mathhelpplanet.com/static.php?p=uravneniya-ploskosti-komplanarnoi-dvum-nekollinyearnym-vektoram

1. Общее уравнение плоскости
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0 , где А, В, С – координаты вектора
N = Ai + Bj + Ck -вектор нормали к плоскости. Возможны следующие частные случаи:
A = 0 – плоскость параллельна оси Ох
B = 0 – плоскость параллельна оси Оу C = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
A = B = 0 – плоскость параллельна плоскости хОу A = C = 0 – плоскость параллельна плоскости хОz B = C = 0 – плоскость параллельна плоскости yOz A = D = 0 – плоскость проходит через ось Ох
B = D = 0 – плоскость проходит через ось Оу C = D = 0 – плоскость проходит через ось Oz
A = B = D = 0 – плоскость совпадает с плоскостью хОу A = C = D = 0 – плоскость совпадает с плоскостью xOz B = C = D = 0 – плоскость совпадает с плоскостью yOz
2. Уравнение поверхности в пространстве
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
3. Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какиелибо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе
|
координат. |
||||||
|
Для того, чтобы произвольная точка M (x, y, z) |
лежала в одной плоскости с точками |
|||||
|
M1, M2 , M3 необходимо, чтобы векторы M1M 2 , M1M 3 , M1M были компланарны, т.е |
||||||
|
M1M = {x − x1 ; y − y1 ; z − z1} |
||||||
|
( M1M 2 , M1M 3 , M1M ) = 0. Таким образом, M1M 2 |
= {x2 − x1 ; y2 |
− y1 ; z2 − z1} |
||||
|
M1M 3 |
= {x3 − x1 ; y3 − y1 ; z3 − z1} |
|||||
|
x − x1 |
y − y1 |
z − z1 |
||||
|
Уравнение плоскости, проходящей через три точки: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
35

4. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и векторa = (a1, a2 , a3 ) .
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную
|
точку М(х, у, z) параллельно вектору a . |
||||||||||
|
Векторы M1M = {x − x1 ; y − y1 ; z − z1} |
и вектор a = (a , a |
2 |
, a |
3 |
) |
должны быть |
||||
|
M1M 2 = {x2 − x1 ; y2 − y1 ; z2 − z1} |
1 |
|||||||||
|
x − x1 |
y − y1 |
z − z1 |
||||||||
|
компланарны, т.е. ( M1M , M1M 2 , a ) = 0.Уравнение плоскости: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||||||
|
a1 |
a2 |
a3 |
5. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости
Пусть заданы два вектора a = (a1, a2 , a3 ) и b = (b1,b2 ,b3 ) , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы a,b, MM1 должны быть компланарны.
|
x − x1 |
y − y1 |
z − z1 |
|||
|
Уравнение плоскости: |
a1 |
a2 |
a3 |
= 0 . |
|
|
b1 |
b2 |
b3 |
6. Уравнение плоскости по точке и вектору нормали
Теорема. Если в пространстве задана точка M0 (x0 , y0 , z0 ) , то уравнение плоскости, проходящей через точку M0 перпендикулярно вектору нормали N ( A, B,C) имеет вид: A(x − x0 ) + B ( y − y0 ) + C (z − z0 ) = 0 .
7. Уравнение плоскости в отрезках
Если в общем уравнении Ax + By + Cz + D = 0 поделить обе части на (-D)
|
− |
A |
x − |
B |
y − |
C |
z − 1 = 0 , заменив − |
D |
= a, |
− |
D |
= b, |
− |
D |
= c , получим уравнение плоскости |
||||||||
|
A |
B |
C |
||||||||||||||||||||
|
D |
D |
D |
||||||||||||||||||||
|
в отрезках: |
x |
+ |
y |
+ |
z |
= 1 . Числа a, b, c являются точками пересечения плоскости соответственно |
||||||||||||||||
|
a |
b |
c |
||||||||||||||||||||
с осями х, у, z.
8. Уравнение плоскости в векторной форме
r n = p, где r = xi + yj + zk — радиусвектор текущей точки M (x, y, z) ,
n = i cosα + j cos β + k cosγ — единичный вектор, имеющий направление, перпендикуляра,
опущенного на плоскость из начала координат. α, β и γ — углы, образованные этим вектором с осями х, у, z. p – длина этого перпендикуляра. В координатах это уравнение имеет вид:
x cosα + y cos β + z cosγ − p = 0
36
9. Расстояние от точки до плоскости
Расстояние от произвольной точки M0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 равно:
d = Ax0 + By0 + Cz0 + D

Пример. Найти уравнение плоскости, проходящей через точки А(2,-1,4) и В(3,2,-1) перпендикулярно плоскости x + y + 2z − 3 = 0 .
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0 , вектор нормали к этой плоскости n1 (A,B,C). Вектор AB (1,3,-5) принадлежит плоскости. Заданная нам плоскость,
перпендикулярная искомой имеет вектор нормали n2 (1,1,2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
|
n = AB × n |
i |
j |
k |
= i |
3 |
− 5 |
− j |
1 |
− 5 |
+ k |
1 |
3 |
= 11i − 7 j − 2k. |
||||||||
|
2 |
= |
1 |
3 |
− 5 |
|||||||||||||||||
|
1 |
1 |
2 |
1 |
2 |
1 |
1 |
|||||||||||||||
|
1 |
1 |
2 |
|||||||||||||||||||
Таким образом, вектор нормали n1 (11,-7,-2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11.2+ 7.1− 2.4 + D = 0; D = −21. Итого, получаем уравнение плоскости: 11x − 7 y − 2z − 21 = 0
10.Уравнение линии в пространстве
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0 . Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана какимлибо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
F(x, y, z) = 0
Тогда пару уравнений Ф(x, y, z) = 0 назовем уравнением линии в пространстве.
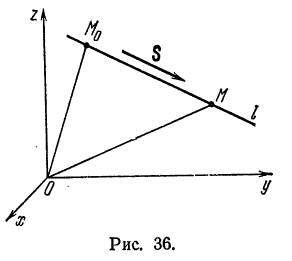
11. Уравнение прямой в пространстве по точке и направляющему вектору
Возьмем произвольную прямую и вектор S (m, n, p), параллельный данной прямой. Вектор S называется направляющим вектором прямой.
На прямой возьмем две произвольные точки M0 (x0 , y0 , z0 ) и M (x, y, z) .
z
37
z
S M1
M0
r0 r
Обозначим радиусвекторы этих точек как r0 и r , очевидно, что r − r0 = M0 M .
Т.к. векторы М0 М и S коллинеарны, то верно соотношение М0 М = St , где t – некоторый параметр. Итого, можно записать: r = r0 + St .
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
x = x0 + mt
Это векторное уравнение может быть представлено в координатной форме: y = y0 + nt
z = z0 + pt
Преобразовав эту систему и приравняв значения параметра t, получаем канонические
|
уравнения прямой в пространстве: |
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
m |
n |
|||||
|
p |
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора S , которые могут быть вычислены по формулам:
|
cosα = |
m |
; cos β = |
n |
; cosγ = |
p |
. |
||
|
+ n2 |
+ p2 |
+ n2 + p2 |
m2 + n2 + p2 |
|||||
|
m2 |
m2 |
Отсюда получим: m : n : p = cosα : cos β : cosγ .
Числа m , n , p называются угловыми коэффициентами прямой. Т.к. S — ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
12. Уравнение прямой в пространстве, проходящей через две точки
Если на прямой в пространстве отметить две произвольные точки M1 (x1, y1, z1 ) и
M2 (x2 , y2 , z2 ), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
|
x2 − x1 |
= |
y2 − y1 |
= |
z2 − z1 |
. |
|
m |
n |
||||
|
p |
38
Содержание
- Уравнения плоскости в координатной форме
- Общее уравнение плоскости
- Уравнение плоскости, проходящей через три точки
- Параметрические уравнения плоскости
- Уравнения плоскости в векторном виде
- Векторное параметрическое уравнение плоскости
- Нормальное векторное уравнение плоскости
- Уравнение плоскости, проходящей через три точки
Определение. Направляющими векторами плоскости называются два неколлинеарных вектора, лежащих в этой плоскости.
Уравнения плоскости в координатной форме
Общее уравнение плоскости в декартовой системе координат:
при этом вектор с координатами является нормальным вектором к плоскости.
Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой, можно получить, если решить систему уравнений
Здесь
и
— координаты трёх точек плоскости. Заметим, что уравнений в системе три, а переменных — четыре. То есть решение этой системы мы получаем с точностью до коэффициента. Этот коэффициент роли не играет — после подстановки решения в уравнение плоскости на него можно сократить. Рассмотрим это на примере.
Пример. Составить уравнение плоскости, проходящей через точки
и
Решение. Составляем систему уравнений
Числа выражаем через
:
Получаем уравнение плоскости
или, после сокращения на ,
Параметрические уравнения плоскости:
Здесь — некоторая точка плоскости,
и
— координаты направляющих веторов плоскости,
— параметры.
Уравнения плоскости в векторном виде
Векторное параметрическое уравнение плоскости:
где — направляющие векторы плоскости,
— радиус-вектор некоторой фиксированной точки плоскости.
Это уравнение также можно записать в виде
То есть для того, чтобы вектор был радиус-вектором некоторой точки плоскости, необходимо, чтобы вектора
и
лежали в одной плоскости, то есть их смешанное произведение было равно нулю.
Нормальное векторное уравнение плоскости:
где — нормальный вектор плоскости.
Это уравнение также можно записать в виде
Если вектор — единичный (его длина равна
), то величина
есть расстояние от точки
до плоскости. Смысл этого уравнения в том, что проекция радиус-вектора любой точки плоскости на нормаль к ней есть постоянная величина, равная расстоянию до этой плоскости.
Уравнения плоскости, компланарной двум неколлинеарным векторам
Напомним, что три или более векторов называются компланарными, если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам.
Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.
Пусть в координатном пространстве заданы:
а) точка ;
б) два неколлинеарных вектора (рис.4.15).
Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.16).
Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения
Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:
(4.18)
Параметрическое уравнение плоскости
Пусть в координатном пространстве заданы:
а) точка ;
б) два неколлинеарных вектора (рис.4.15).
Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку
Выберем на плоскости произвольную точку . Обозначим
-радиус-векторы точек
и
(рис.4.16).
Точка принадлежит заданной плоскости тогда и только тогда, когда векторы
и
компланарны (см. разд. 1.3.2). Запишем условие компланарности:
где
— некоторые действительные числа (параметры). Учитывая, что
получим векторное параметрическое уравнение плоскости:
(4.19)
где — направляющие векторы плоскости, а
— радиус-вектор точки, принадлежащей плоскости.
Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:
(4.20)
где и
— координаты направляющих векторов
и
соответственно. Параметры
в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины
пропорциональны расстоянию от заданной точки
до точки
принадлежащей плоскости. При
точка
совпадает с заданной точкой
. При возрастании
(или
) точка
перемещается в направлении вектора
(или
), а при убывании
(или
) — в противоположном направлении.
Замечания 4.4.
1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.
2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору
для этой плоскости. Поэтому их скалярное произведение равно нулю:
Следовательно, координаты и
направляющих векторов
и
плоскости и ее нормали связаны однородными уравнениями:
3. Направляющие векторы плоскости определяются неоднозначно.
4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:
1) найти любое решение уравнения
определяя тем самым координаты точки
принадлежащей плоскости;
2) найти любые два линейно независимых решения
однородного уравнения
определяя тем самым координаты решения
и
направляющих векторов
и
плоскости;
3) записать параметрическое уравнение (4.20).
5. Чтобы перейти от параметрического уравнения плоскости к общему, достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:
и записать общее уравнение плоскости в форме (4.14):
6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.
Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки
и
(см. рис.4.11). Требуется:
а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;
б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам
и
Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:
1) находим любое решение уравнения , например,
следовательно, точка
принадлежит плоскости;
2) находим два линейно независимых (непропорциональных) решения однородного уравнения например
и
следовательно, векторы
являются направляющими для плоскости;
3) записываем параметрическое уравнение плоскости (4.20):
б) Координаты середины отрезка
были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов
и
Составляем уравнение (4.14):
Тот же результат можно получить, записывая уравнение (4.18):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Векторный базис в пространстве:
Пусть 
Определение:
Векторным базисом пространства называется тройка некомпланарных векторов, взятых в определенном порядке.
Очевидно, что существует бесконечное множество базисов пространства. Пусть 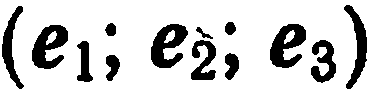

Это означает, что для любого вектора 
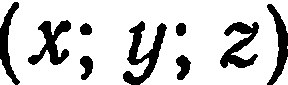
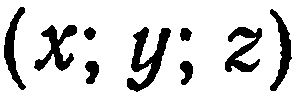
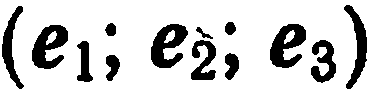

Числа 

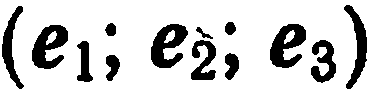


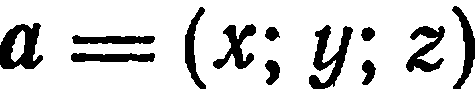
Определение:
Базис 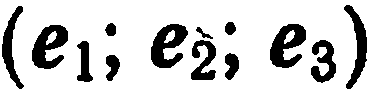
Базисные векторы прямоугольного базиса обозначают через 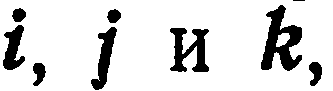
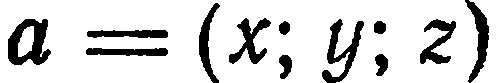
Пример:
Даны векторы:
Найти координаты векторов 
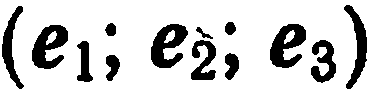
Решение. Имеем:
Применив правила действия над векторами, заданными координатами, находим:
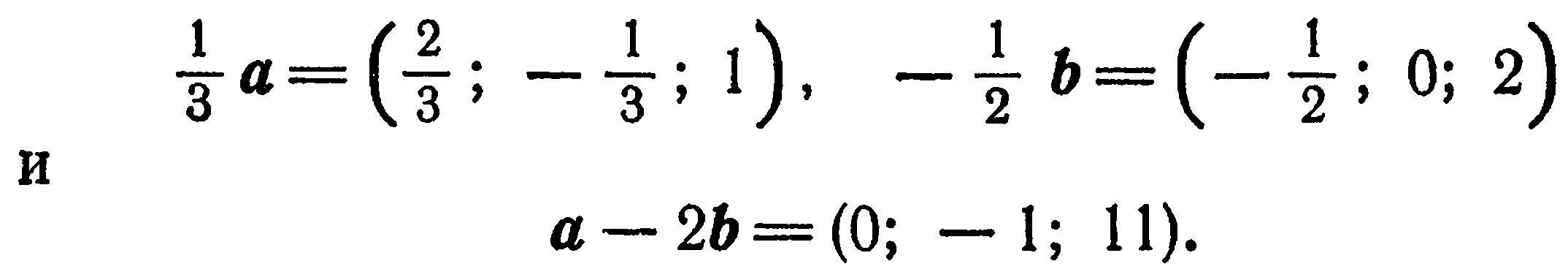
Пример:
Найти длину вектора 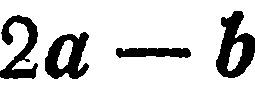
Решение:
Известно, что если 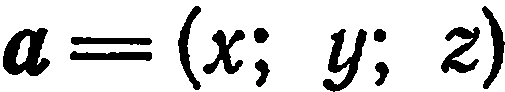
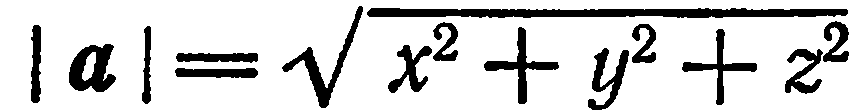
поэтому
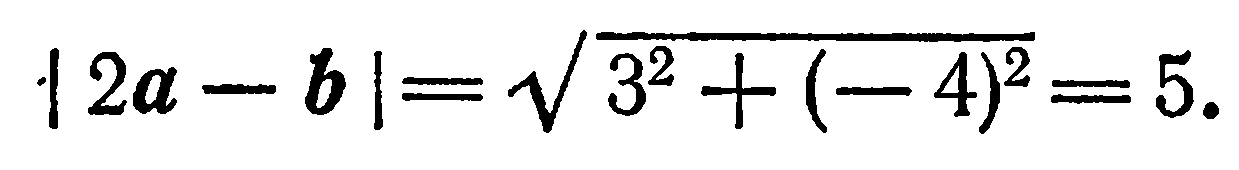
Прямоугольные координаты в пространстве
Определение:
Декартовой системой координат в пространстве называется совокупность фиксированной точки 

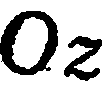

Пусть 



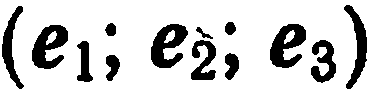
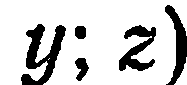

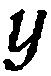
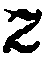
Определение:
Прямоугольной декартовой (или просто прямоугольной) системой координат в пространстве называется совокупность фиксированной точки 
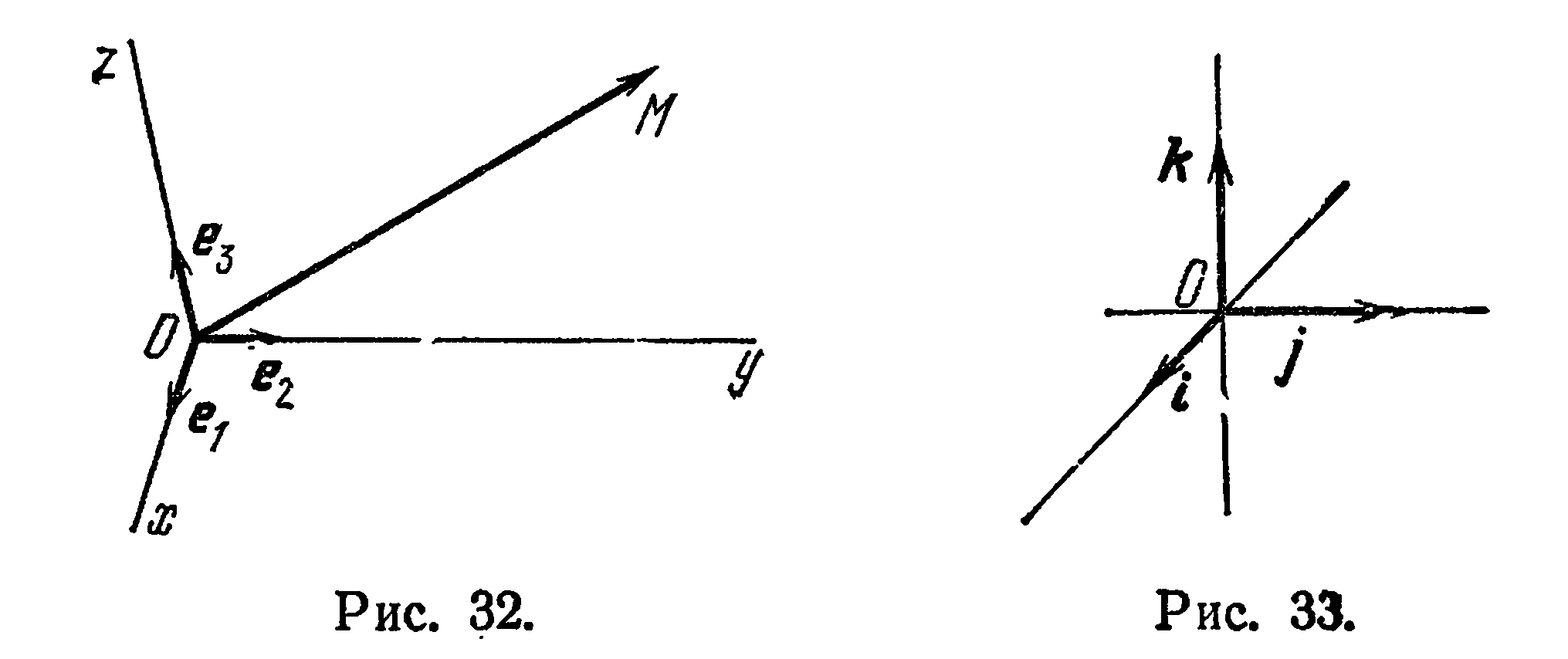
Прямоугольная система координат хорошо известна по школьному курсу, поэтому на ее описании мы здесь останавливаться не будем.
Введение прямоугольной системы координат в пространстве дает возможность решать много геометрических задач так, как это делалось в плоскости.
Например, можно показать, что координаты точки 
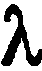
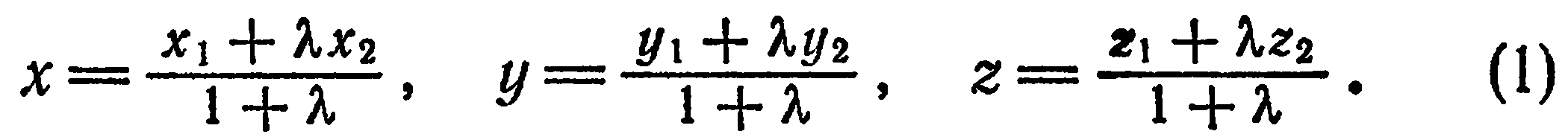
Понятие об уравнении поверхности и линии в пространстве
Пусть множество решений уравнения
не пусто. Тогда каждой тройке чисел 
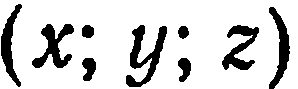
Обратно, пусть в пространстве заданы некоторая поверхность и прямоугольная система координат 
Определение:
Уравнением данной поверхности в системе координат 
Пример:
Найти уравнение сферы радиуса 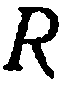
Решение:
Пусть 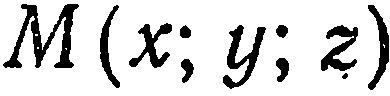
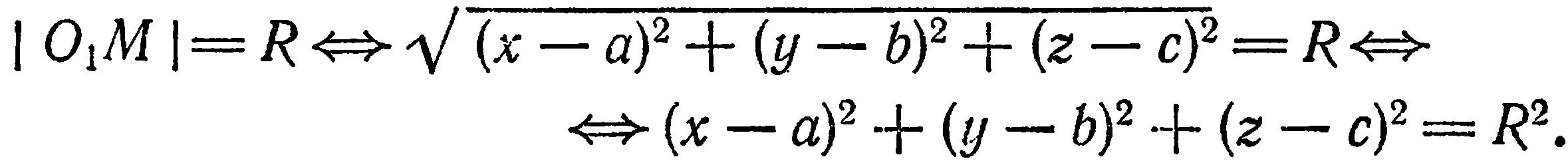
Уравнение 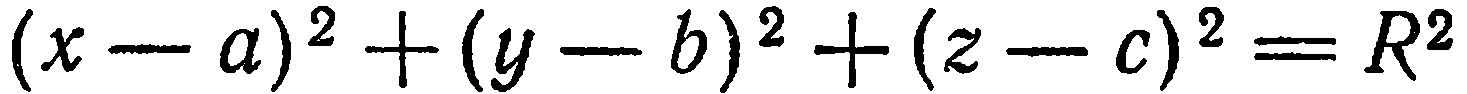
Линия в пространстве рассматривается как линия пересечения двух поверхностей, т. е. как множество точек, общих двум поверхностям. Так, если 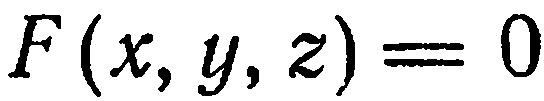
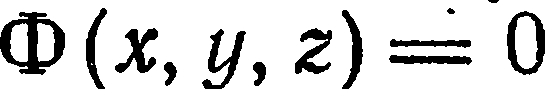
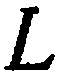
уравнений. Таким образом, система уравнений

определяет рассматриваемую линию 
Например, система
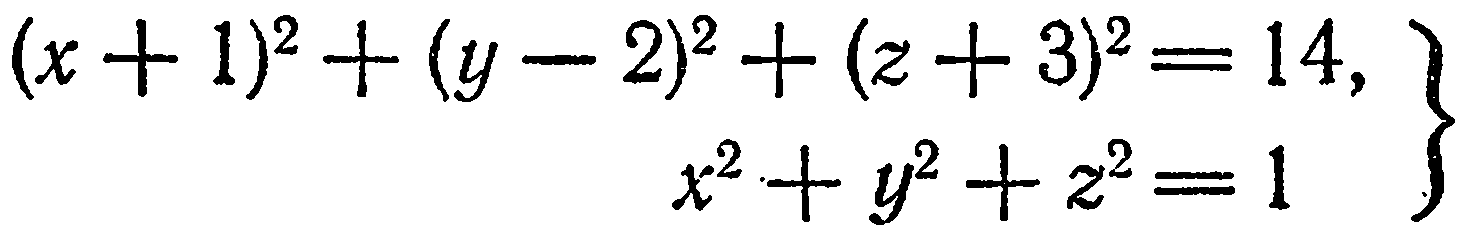
определяет окружность (как линию пересечения двух сфер).
Отметим, что если известно уравнение поверхности (линии), то относительно любой точки пространства можно решить вопрос: лежит эта точка на данной поверхности (линии) или нет?
Пример:
Лежит ли точка 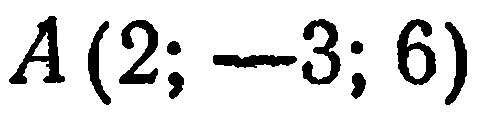
Решение:
Подставив в данное уравнение вместо текущих координат 
Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором
Пусть в прямоугольной системе координат 
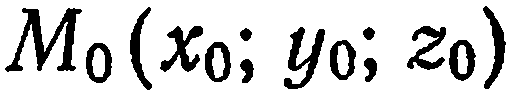
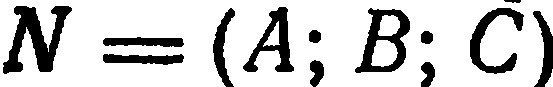

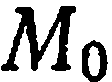
перпендикулярной вектору 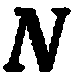
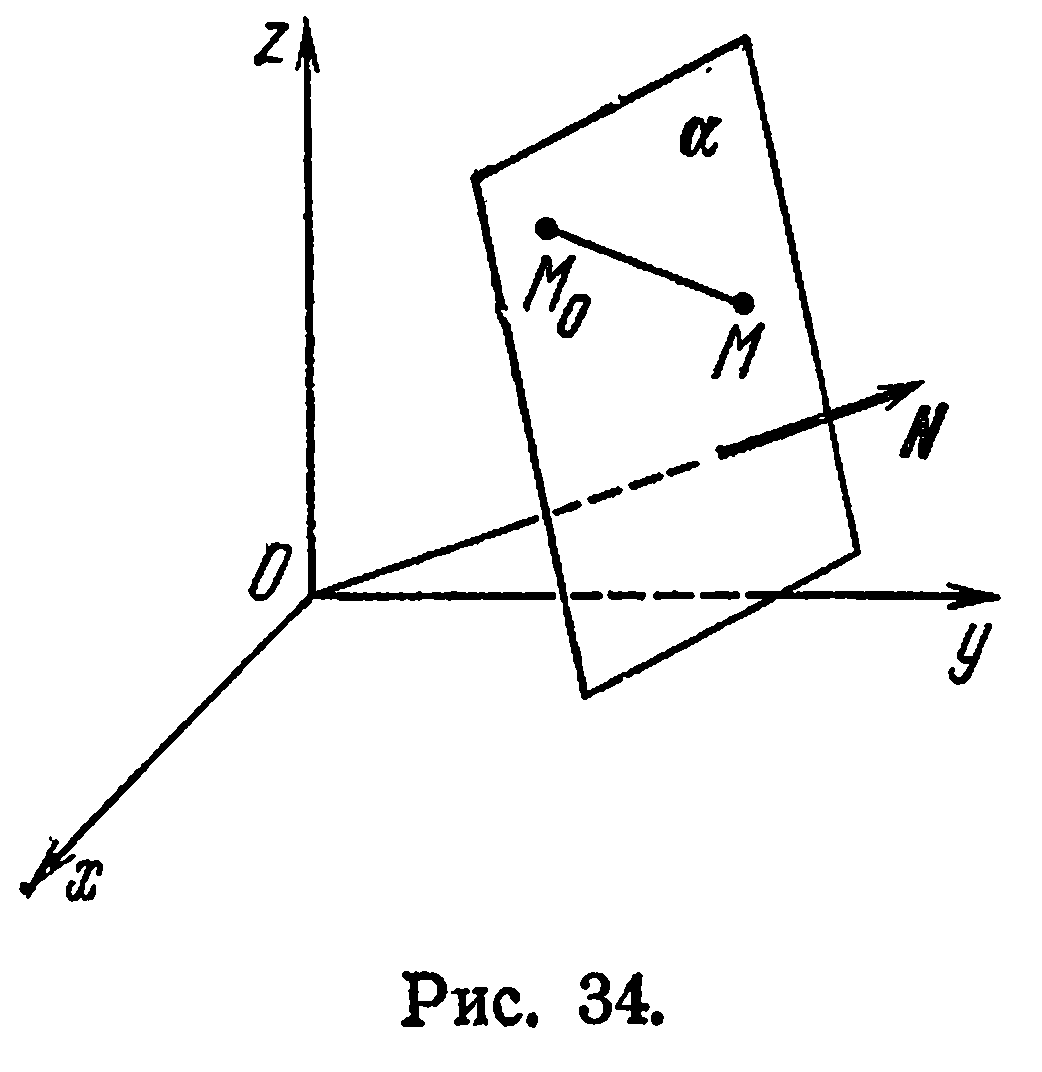
Определение:
Любой ненулевой вектор, перпендикулярный к плоскости 
Очевидно, что положение плоскости 

Возьмем на плоскости 
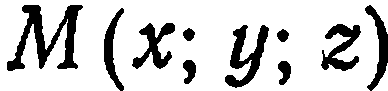

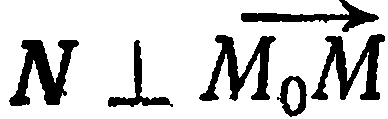
Учитывая, что 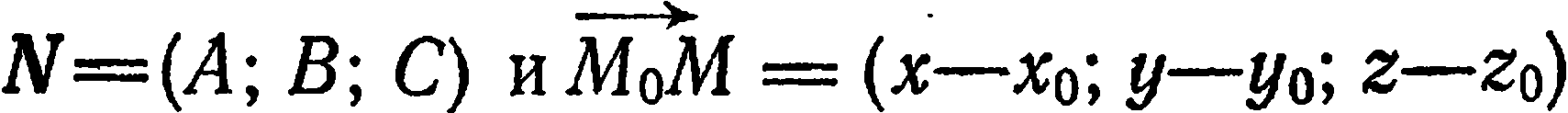
Уравнение (2) называется уравнением плоскости, проходящей через данную точку 
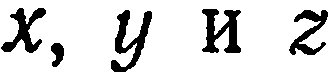
Заметим, что если коэффициентам 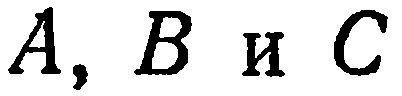
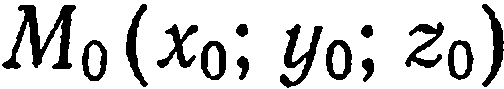
Пример:
Составить уравнение плоскости, проходящей через точку 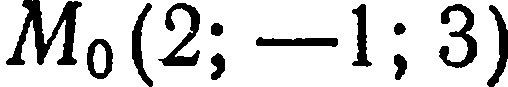

Решение:
Имеем 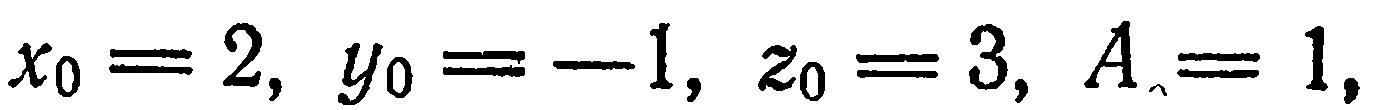
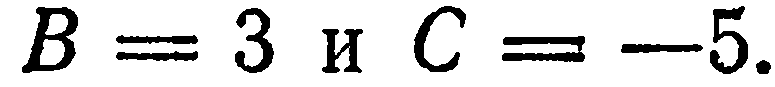
(2), получим
или
Общее уравнение плоскости и его частные случаи
В предыдущем параграфе мы показали, что в прямоугольной системе координат 
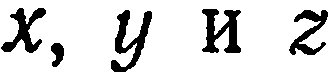
в прямоугольной системе координат 
Так как уравнение (1) является уравнением первой степени, то по крайней мере один из коэффициентов 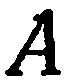
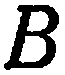

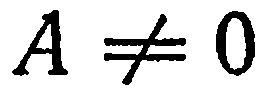
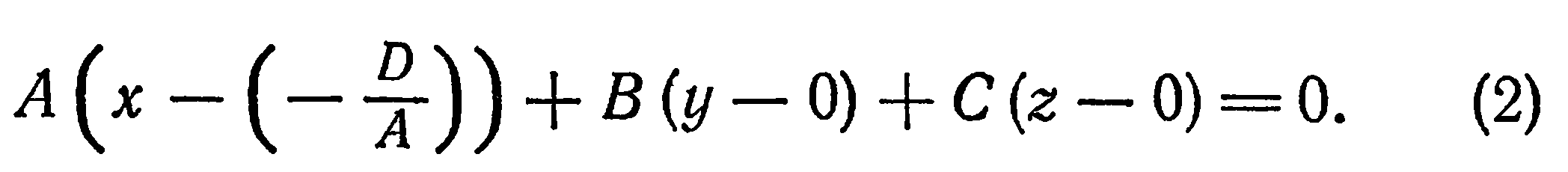
Это уравнение имеет вид уравнения (2) из предыдущего параграфа и, следовательно, оно определяет единственную плоскость, проходящую через точку 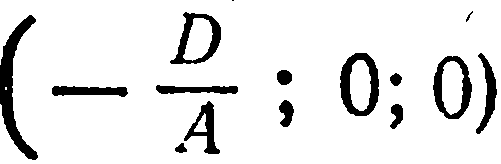
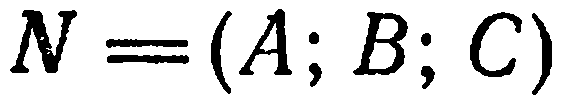
плоскость.
Уравнение (1) называется общим уравнением плоскости.
Рассмотрим некоторые частные случаи уравнения (1) (плоскость, определяемую этим уравнением, обозначим через 
1. Свободный член 
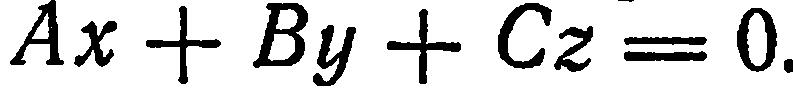
1. Один из коэффициентов при текущих координатах равен нулю. Пусть 
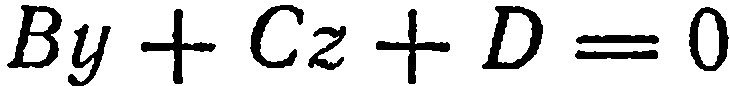
Аналогично, 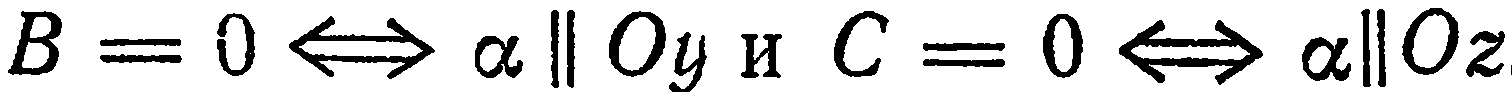

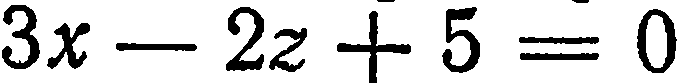


1. Свободный член и один из коэффициентов при текущих координатах равны нулю. Пусть, например, 


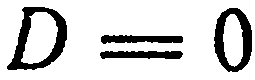

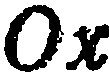
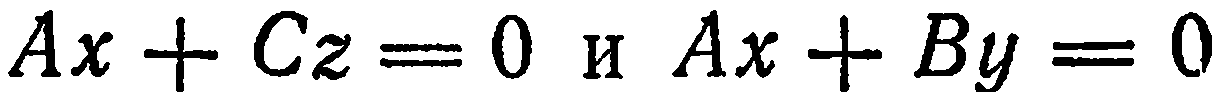


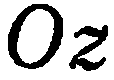
4. Два коэффициента при текущих координатах равны нулю. Пусть, например, 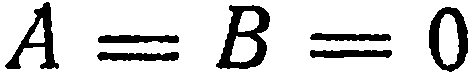
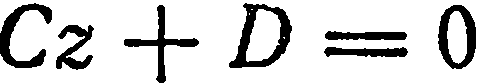
Следовательно, данная плоскость параллельна координатной плоскости 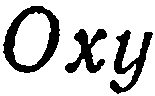
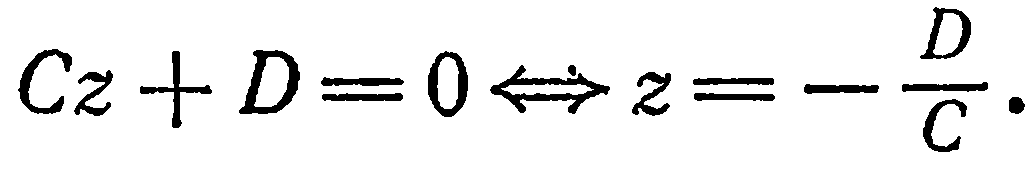
Положив
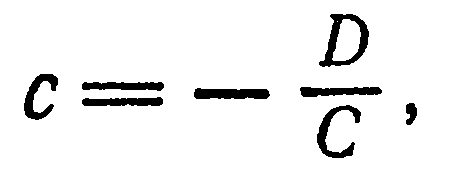
получим
Это уравнение показывает, что все точки данной плоскости имеют одну и ту же апликату, т. е. данная плоскость параллельна плоскости 
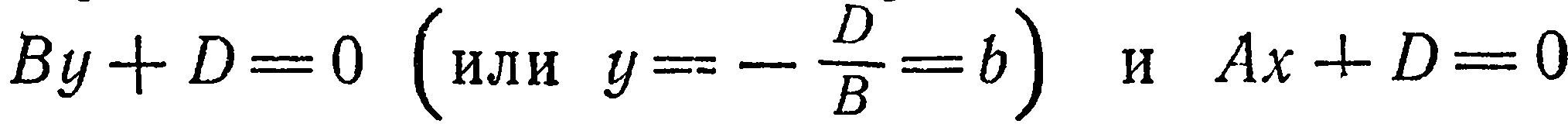
определяют плоскости, соответственно параллельные координатным плоскостям 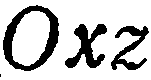

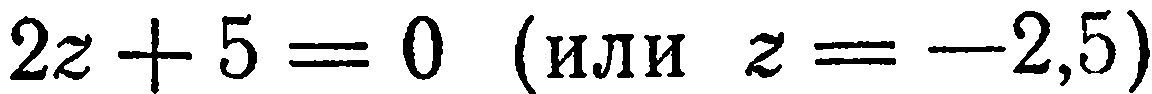
от нее.
5. Свободный член и два коэффициента при текущих координатах равны нулю. Пусть, например, 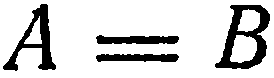
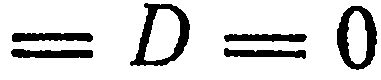
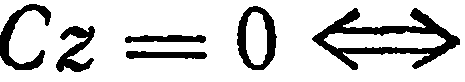

Аналогично, 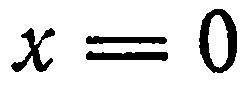

Пример:
Составить уравнение плоскости, проходящей через ось 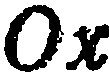
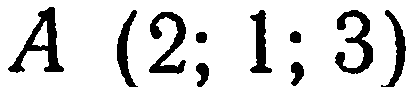
Решение. Так как искомая плоскость проходит через ось 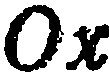

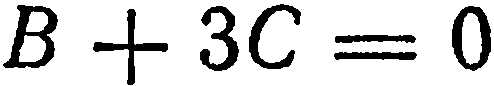
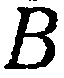

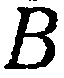
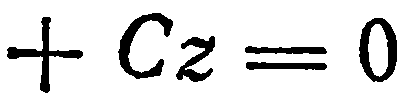

Пример:
Построить плоскость
Решение:
Для построения плоскости достаточно построить три ее точки. Проще всего найти точки пересечения плоскости с осями координат. Положив в данном уравнении 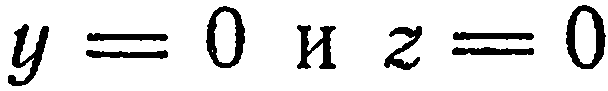

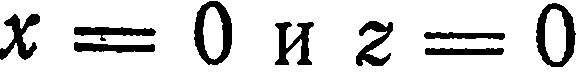

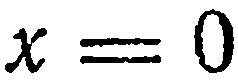

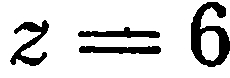
плоскость пересекает оси 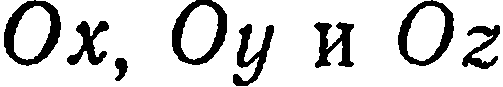
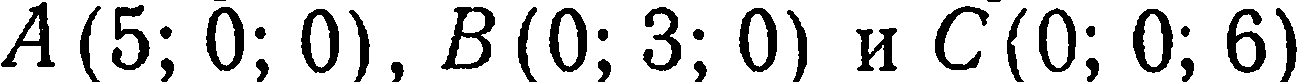
Пример:
Составить уравнение плоскости, проходящей через три точки 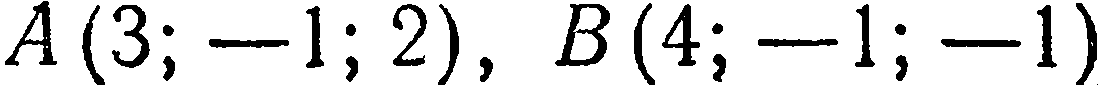
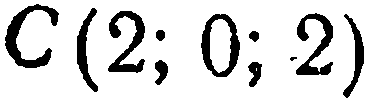
Решение:
Пусть искомое уравнение имеет вид (1). Так как каждая из данных точек принадлежит данной плоскости, то координаты этих точек удовлетворяет уравнению (1), т.-е.
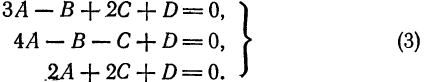
Решим эту систему, приняв за неизвестные коэффициенты 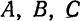
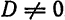
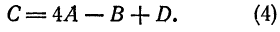
Подставив это значение 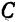
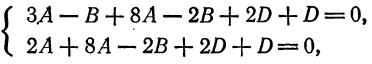
или
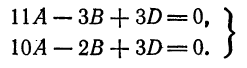
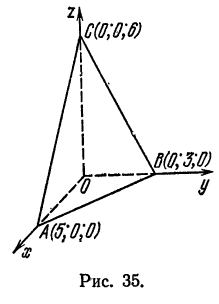
Отсюда 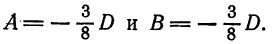
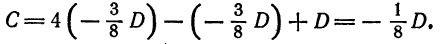
Заменив найденными значениями 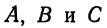
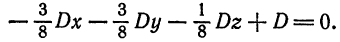
Отсюда
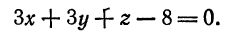
Уравнения прямой, проходящей через данную точку с заданным направляющим вектором
Пусть в прямоугольной системе координат 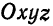
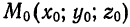
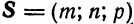
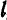
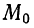
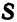
Определение:
Любой ненулевой вектор 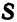
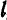
Положение прямой 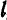
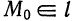
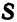
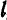
Возьмем на прямой 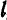
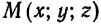
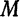
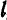
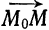
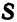
соответствующих координат. Следовательно,
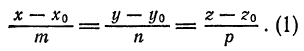
Уравнения (1) называются уравнениями прямой, проходящей через данную точку 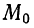
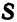
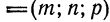
Пример:
Составить уравнения прямой, проходящей через точку 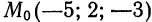
соединяющему точки
Решение:
За направляющий вектор искомой прямой примем вектор 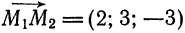
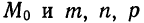
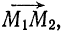
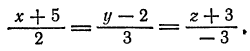
Отметим, что если прямая 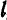
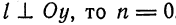
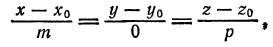
Пример:
Составить уравнения прямой, проходящей через точку 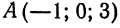
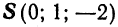
Решение:
Согласно уравнениям (1) имеем
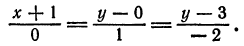
Другие формы уравнений прямой в пространстве
Параметрические уравнения прямой
В предыдущем параграфе мы показали, что точка 
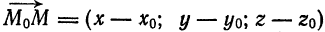
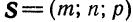
где 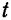
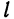
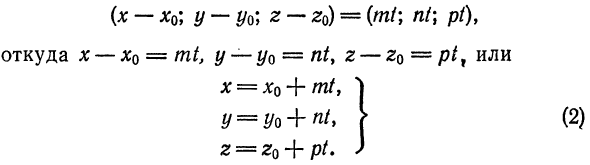
Уравнения (2) называются параметрическими уравнениями прямой.
Пример:
Найти точку пересечения прямой 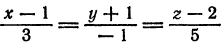
Решение:
Представим данные уравнения прямой в параметрическом виде, для чего перепишем их следующим образом:
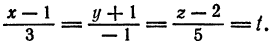
Отсюда
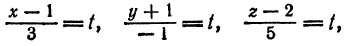
или
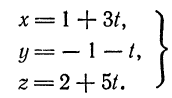
Очевидно, что. для нахождения координат искомой точки нужно решить систему
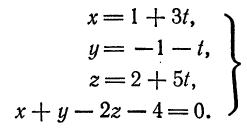
Заменив в последнем уравнении 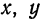
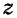
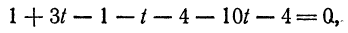
откуда 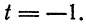
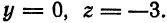
Уравнения прямой, проходящей через две данные точки
Пусть требуется найти уравнения прямой 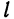
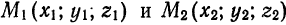
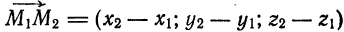
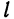
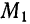
направляющий вектор
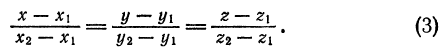
Пример:
Дан треугольник с вершинами 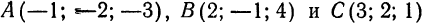
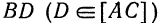
Решение:
Находим координаты точки 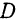
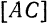
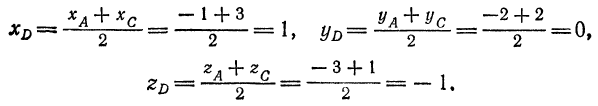
Напишем искомые уравнения как уравнения прямой, проходящей через точки 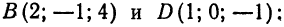
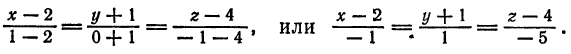
3. Общие уравнения прямой. Рассмотрим систему
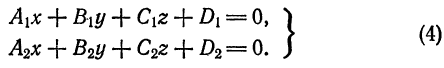
Каждое из уравнений системы (4) в прямоугольной системе координат 
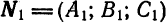
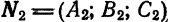
Пример:
Привести к каноническому виду общие уравнения прямой
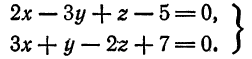
Решение:
Исключив сначала 
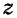
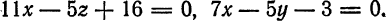
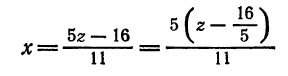
и
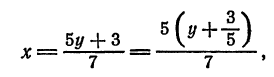
откуда
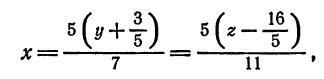
или
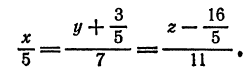
Некоторые задачи на прямую и плоскость в пространстве
Пусть прямая 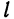
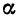
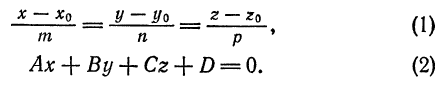
Решая задачи на прямую и плоскость, следует помнить, что для прямой (1) основной характеристикой является направляющий вектор 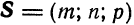
Мы рассмотрим несколько наиболее часто встречающихся задач на прямую и плоскость в пространстве.
Угол между прямой и плоскостью
Предположим сначала, что прямая 
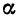
Непосредственно из рис. 37
нетрудно заметить, что синус угла 
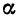
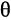
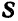
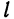
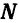
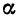
Но
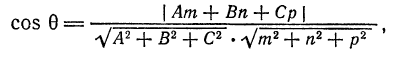
Следовательно
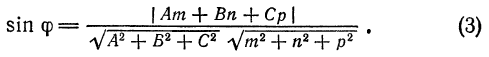
Пример:
Найти угол между прямой
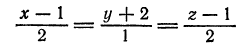
и плоскостью
Решение:
Имеем: 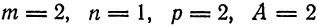
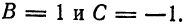
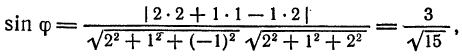
откуда 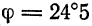
Условия параллельности прямой и плоскости
Прямая 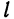
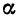
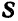
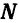
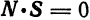
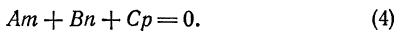
Мы видим, что формула (3) справедлива и в случае 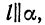
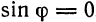
Пример:
При каком значении 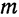
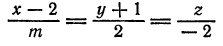
параллельна плоскости
Решение:
По формуле (4) имеем
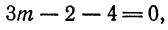
откуда 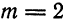
Условие перпендикулярности прямой и плоскости. Прямая 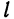
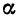
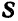
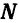

Из этих условий, в частности, следует, что формула (3) сохраняет смысл и при 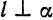
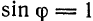
Пример:
При каких значениях 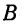
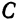
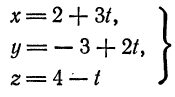
перпендикулярна плоскости
Решение:
Из уравнения прямой имеем 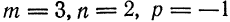
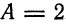
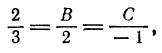
откуда
Уравнения прямой и плоскости в пространстве
Уравнение плоскости, проходящей через точку пространства 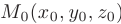
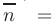
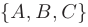
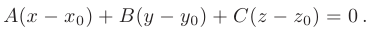
Это уравнение вытекает из условия ортогональности (см. п.2.4.) векторов 
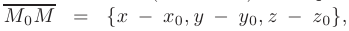
где 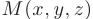
Обозначив

получим общее уравнение плоскости в пространстве:
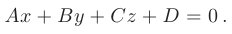
Если прямая параллельна вектору 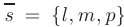
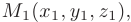
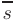
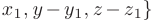
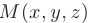
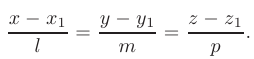
Эти уравнения называются каноническими уравнениями прямой линии в пространстве.
Уравнение прямой, проходящей через две точки пространства
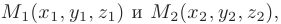
записывается в виде
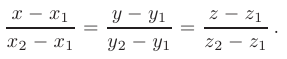
Направляющий вектор этой прямой 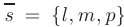
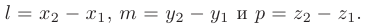
Интерпретируя координаты точек
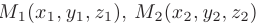
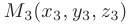
как координаты трех радиус-векторов
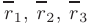
и используя условие компланарности векторов
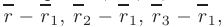
получим запись уравнения плоскости, проходящей через эти точки, в виде определителя третьего порядка
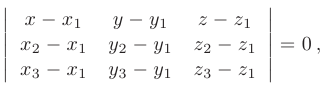
где 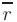
Пример:
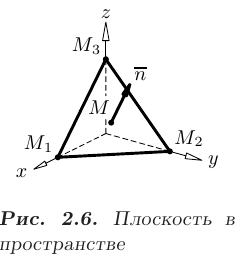
Даны координаты вершин пирамиды 
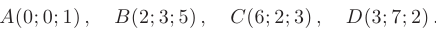
Требуется составить: 1) уравнения прямой 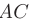
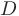
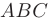
► 1. Составим уравнения прямой 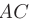
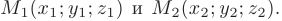
Подставив координаты точек 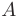
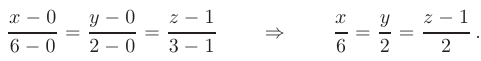
Окончательный вид уравнений прямой 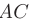
- Составим уравнение грани
, используя формулу уравнения плоскости, проходящей через три заданные точки пространства
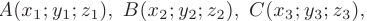
- приведенную в п. 2.6. Подставляя координаты точек
получаем
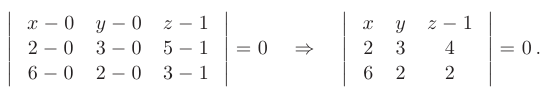
Раскладывая последний определитель по первой строке, выводим искомое уравнение плоскости, проходящей через три заданные точки пространства 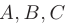
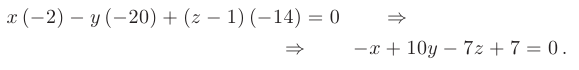
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Помощь по математике
Возможно эти страницы вам будут полезны:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат